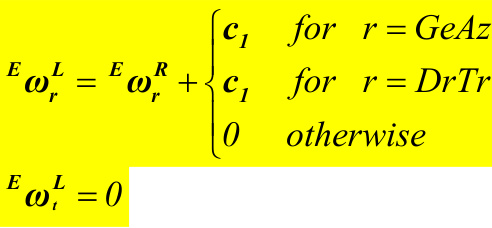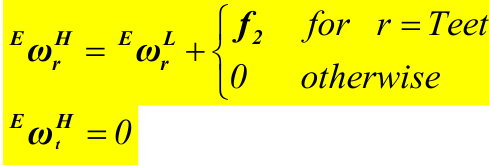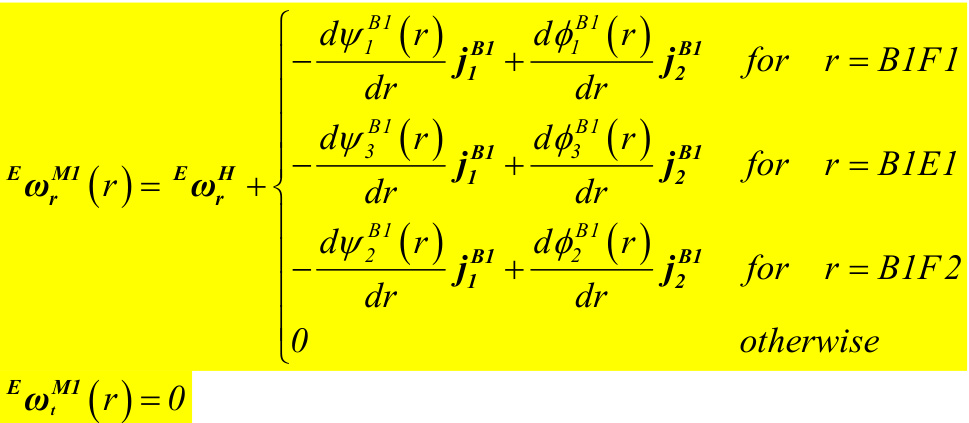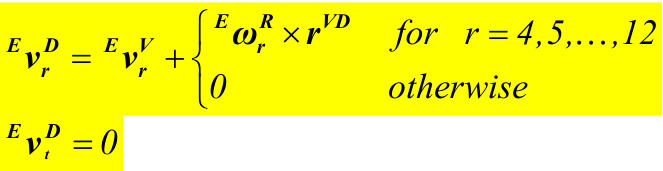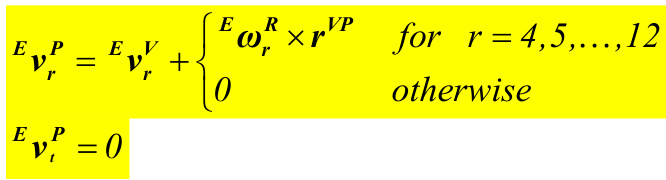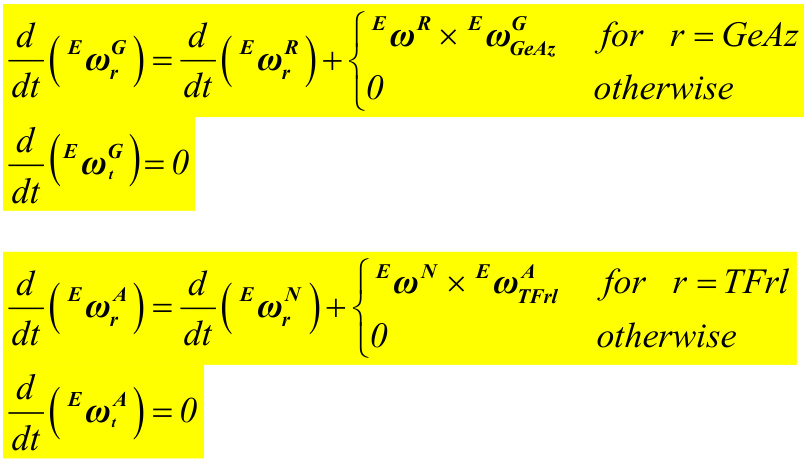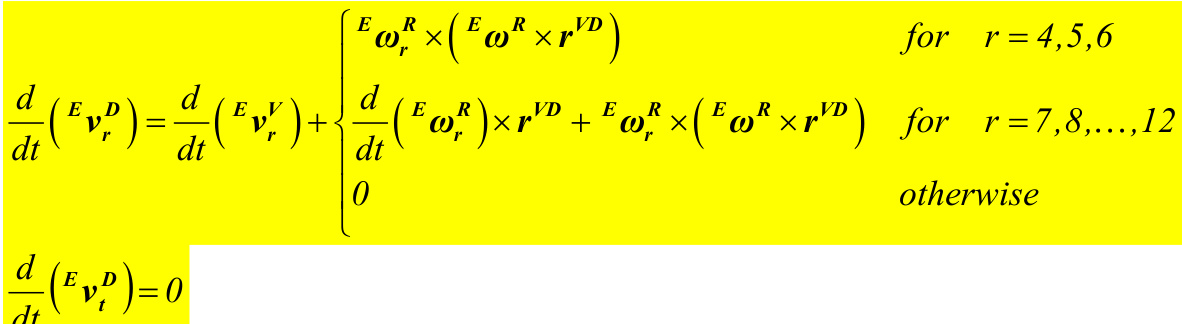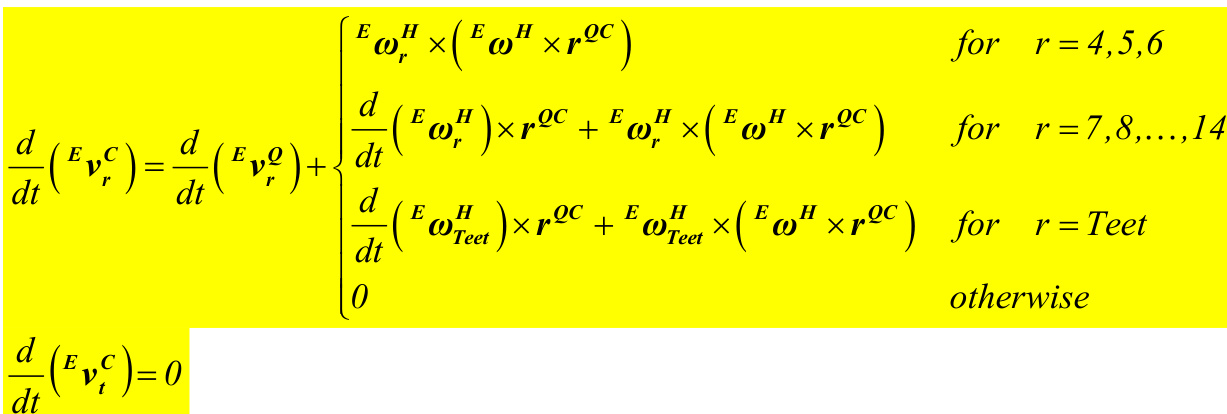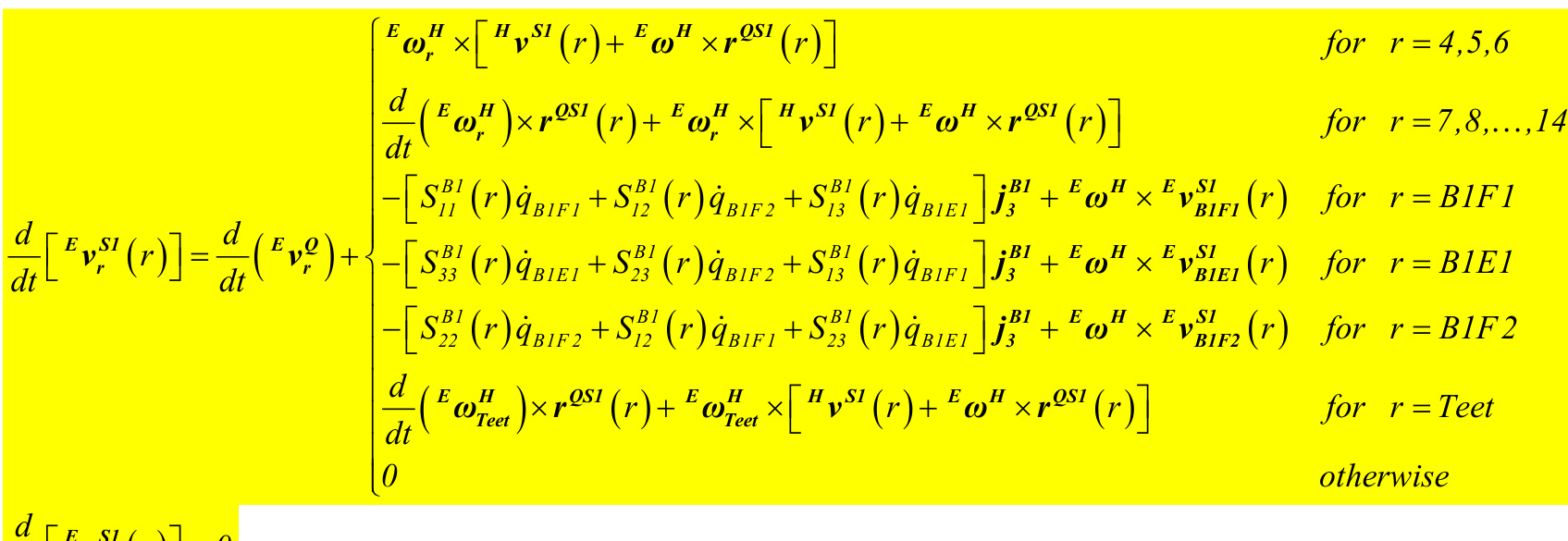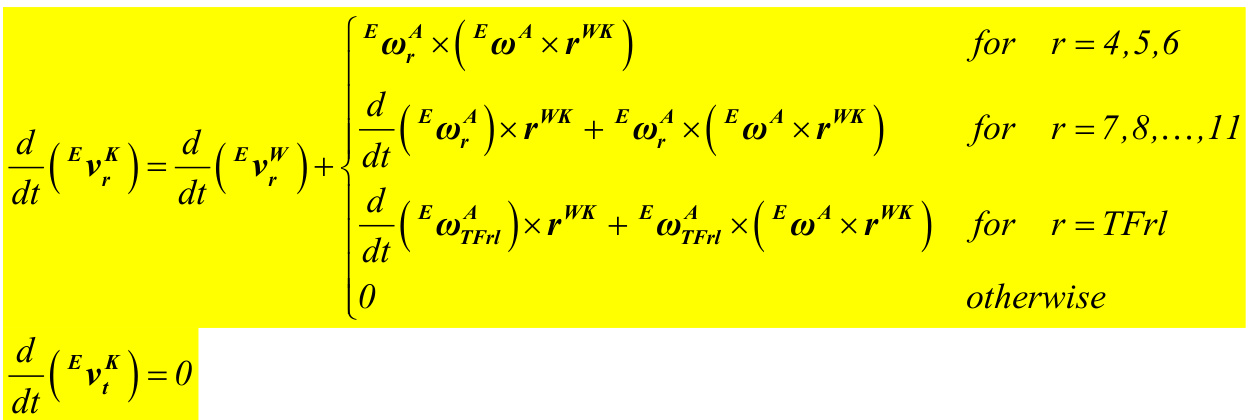obsidian_backup/力学书籍/FASTKinematics/auto/FASTKinematics.md

There are several points on a 2-bladed turbine: Z (platform reference), Y (platform mass center), T (tower node), O (tower-top / base-plate / yaw bearing mass center), U (nacelle mass center), V (arbitrary point on rotor-furl axis), W (arbitrary point on tail-furl axis), D (center of mass of structure that furls with the rotor [not including rotor]), IMU (nacelle inertial measurement unit), P (teeter pin), SG [shaft strain gage location: i.e., a point on the shaft a distance ShftGagL towards the nacelle from point P (or point Q for a 3-blader since point P does not exist)], Q (apex of coning angle), C (hub mass center), S1 (blade node for blade 1), S2 (blade node for blade 2), I (tail boom mass center), J (tail fin mass center), and K (tail fin center-of-pressure). There are also several reference frames: E (earth / inertial), X (platform / tower base), F (tower element body), B (tower-top / base plate), N (nacelle), R (structure that furls with the rotor—generator housing, etc…), L (low speed shaft on rotor end of LSS-compliance), H (hub / rotor), M1 (blade 1 element body), M2 (blade 2 element body), G (fixed in the high speed shaft / generator), and A (tail). The following are derivations of the position vectors, angular velocities, linear velocities, partial angular velocities, partial linear velocities, angular accelerations, and linear accelerations of all these points on the 2-bladed turbine (point SG’s velocities and accelerations are not derived since they wont be used in the ensuing analysis). The velocities and accelerations of points on a 3-bladed turbine are very similar.

ZO =[qTFA1+qTFA2]a1 + Ptfm Re f+TowerHt 21S1T1F+A(S1TT1SwSr(FTlwerxFLl) eqxT2LFA) 1qT+2SSS12T2F+AS(2TT2SSw(rTFlwerxFLl) exqT2LF) A2qT2+SS 22S+1T2F2AS(1T2TSSw(rTFwlerxFLle) xqLTF) A1qTqSTSF1Aq2TSS 2 u +[qTSS1+qTSS 2]a3

OU =NacCMxnd1+NacCMznd2−NacCMynd3 rVD=(RFrlCMxn−RFrlPntxn)rf1+(RFrlCMzn−RFrlPntzn)rf2−(RFrlCMyn−RFrlPntyn)rf3 rVIMU= \big(N c I M U x n-R F r l P n t x n\big)r f_{I}+\big(N c I M U z n-R F r l P n t z n\big)r f_{J}-\big(N c I M U y n-R F r l P n t y n+R F r l P n t z n\big) )rf3 rVP= −RFrlPntxnrf1+(Twr2Shft−RFrlPntzn)rf2−(Yaw2Shft−RFrlPntyn)rf3+OverHangc1

PSG = ShftGagLc

PQ= −UndSlingg rQC=HubCMg

\begin{array}{r l}&{\Bigr|\int_{I}^{B I}+\Bigr[\psi_{I}^{B I}\left(r\right)q_{B I F I}+\psi_{2}^{B I}\left(r\right)q_{B I F2}+\psi_{3}^{B I}\left(r\right)q_{B I E I}\Bigr]\dot{j}_{2}^{B I}}\\ &{\Bigr.}\\ &{\Bigr.\Bigr.\Bigr.\Bigr.\qquad^{2}+S_{33}^{B I}\left(r\right)q_{B I E I}^{2}+2S_{I2}^{B I}\left(r\right)q_{B I F I}q_{B I F2}+2S_{23}^{B I}\left(r\right)q_{B I F2}q_{B I E I}+2S_{I3}^{B I}\left(r\right)q_{B I F I}q_{B I E I}\Bigr]\Biggr\}.}\end{array}
$$$$
\begin{array}{l}{{\displaystyle7.8I F I+\phi_{2}^{B I}\left(r\right)q_{B I F2}+\phi_{3}^{B I}\left(r\right)q_{B I E I}\biggr]\dot{J}_{I}^{B I}+\left[\psi_{I}^{B I}\left(r\right)q_{B I F I}+\psi_{2}^{B I}\left(r\right)q_{B I F I2}+\psi_{3}^{B I}\left(r\right)q_{B I E I}\right]\dot{J}_{I}^{B I}+\cdots}}\\ {{\displaystyle:R a d-\frac{I}{2}\Bigl[S_{I I}^{B I}\left(r\right)q_{B I F I}^{2}+S_{22}^{B I}\left(r\right)q_{B I F2}^{2}+S_{33}^{B I}\left(r\right)q_{B I E I}^{2}+2S_{I2}^{B I}\left(r\right)q_{B I F I}q_{B I F2}+2S_{23}^{B I}\left(r\right)q_{B I F}^{2}\Bigr]\dot{J}_{I}^{B I}\,,}}\end{array}

where,

The equation for r^{\varrho s2}\left(r\right) is similar.

Note limit on r : 0≤r≤TipRad−HubRad=BldFlexL

\pmb{r}^{o w}=T F r l P n t x n\pmb{d}_{\jmath}+T F r l P n t z n\pmb{d}_{\jmath}-T F r l P n t y n\pmb{d}_{\jmath}

r^{\prime\prime}=\left(B o o m C M x n-T F r l P n t x n\right)t f_{I}+\left(B o o m C M z n-T F r l P n t z n\right)t f_{J}-\left(B o o m C M y n-T F r u n t z n\right)t f_{I}=0. TFrlPntyn)tf3

r^{\mu\nu}=\left(T F i n C M x n-T F r l P n t x n\right)t f_{I}+\left(T F i n C M z n-T F r[P n t z n)t f_{J}-\left(T F i n C M y n-T F i n C M z n\right)t f_{I}\right).

r^{W K}=\left(T F i n C P x n-T F r l P n t x n\right)t f_{I}+\left(T F i n C P z n-T F r l P n t z n\right)t f_{2}-\left(T F i n C P y n-T F r u n t z n\right)t f_{I}.

Angular Velocities:

${}\pmb{\omega}^{X}=\dot{q}{R}\pmb{\Sigma}{I}+\dot{q}{Y}\pmb{\Sigma}{2}-\dot{q}{P}\pmb{\Sigma}{3}$

EωF( h)=EωX dφ1TSS ( h) qTSS1 + dφ2TSS ( h) qTSS 2 a dφ1 ( h) qTFA1 + dφ2TFA ( h) qTFA2 dh dh dh dh

dφ1TSS( h) dφ2TSS( h) dφ1TFA( h) dφ2TFA( h) ω ω qTSS1+ qTSS 2 a1 qTFA1+ qTFA2 a3 dh dh dh dh h =TwrFlexL h =TwrFlexL h =TwrFlexL h =TwrFlexL

{}^{E}{\pmb\omega}^{N}={}^{E}{\pmb\omega}^{B}+\dot{q}_{\mathrm{{}}\scriptscriptstyle{Y a w}}{\pmb d}_{z}

{}^{E}{\pmb\omega}^{R}={}^{E}{\pmb\omega}^{N}+\dot{q}_{R F r l}{\pmb r}{\pmb f}{\pmb\dot{a}} where, r f\!\!a=\!c o s\left(R F r l S k e w\right)\!c o s\left(R F r l T i l t\right)\!d_{I}+s i n\left(R F r l T i l t\right)\!d_{J}-s i n\left(R F r l T i l t\right)\!d_{I}-s i n\left(R F r l T i l t\right)\!d_{I}+s i n\left(R F r l T i l t\right)\!d_{I}. lSkew) cos (RFrlTilt)d3

{}^{E}{\pmb\omega}^{L}={}^{E}{\pmb\omega}^{R}+\dot{q}_{D r T r}{\pmb c}_{I}+\dot{q}_{G e A z}{\pmb c}_{I}

EωM1(r )=EωH dψ1B1(r ) dr qB1F1 +dψ2B1(r ) dr qB1F 2 dψ3B1(r ) dr qB1E1 j1B1 dφ1B1(r )qB1F1+dφ2B1(r ) qB1F 2 +dφ3B1(r ) dr qB1E1 2

The equation for ^{E}\pmb{\omega}^{M2}\left(r\right) is similar.

Since the generator is attached to the high speed shaft which may or may not rotate in the opposite direction of the low speed shaft and since q_{G e A z} represents the position of the low speed shaft near the entrance of the gearbox,

{}^{E}{\pmb\omega}^{G}={}^{E}{\pmb\omega}^{R}+G e n D i r\cdot G B R a t i o\cdot{\dot{q}}_{G e d z}{\pmb{c}}_{I}

where, $G e n D i r=\binom{-I}{I}\quad f o r,,,,G B,R e,\nu e r s e=T r u e}\ {,,,,G\d{p},,,,G B,R e,\nu e r s e=F a l s e}$

{}^{E}{\pmb\omega}^{A}={}^{E}{\pmb\omega}^{N}+\dot{q}_{{}_{T F r l}}t{\pmb f}\dot{\pmb u} where, tfa=cos (TFrlSkew) cos (TFrlTilt)d1+sin (TFrlTilt)d2−sin (TFrlSkew) cos (TFrlTilt)d3

Linear Velocities: {}^{E}{\pmb{\nu}}^{Z}=\dot{q}_{S g}\bar{\sf z}_{I}+\dot{q}_{H\nu}\bar{\sf z}_{2}-\dot{q}_{S w}\bar{\sf z}_{3}

{}^{E}{\pmb{\nu}}^{Y}={}^{E}{\pmb{\nu}}^{Z}+{}^{E}{\pmb{\omega}}^{X}\times{\pmb{r}}^{Z Y}

{}^{E}{\nu}^{T}\left(h\right)={}^{E}{\nu}^{Z}+{}^{X}{\nu}^{T}\left(h\right)+{}^{E}{\omega}^{X}\times{r}^{Z T}\left(h\right)

where,

XvT( h)=φ1TFA( h) qTFA1+φ2TFA( h) qTFA2a1 S1T1FA( h) qTFA1qTFA1+S2T2FA( h) qTFA2qTFA2+S1T2FA( h)(qTFA1qTFA2+qTFA1qTFA2) +S1T1SS( h) qTSS1qTSS1+S2T2SS( h) qTSS 2qTSS 2+S1T2SS( h)(qTSS1qTSS 2+qTSS1qTSS 2) +φ1TSS( h) qTSS1+φ2TSS( h) qTSS 2a3

{}^{E}{\nu}^{o}={}^{E}{\nu}^{Z}+{}^{X}{\nu}^{o}+{}^{E}{\omega}^{X}\times{r}^{Z O} where,

XvO=[qTFA1+qTFA2]a1 S1T1FA(TwrFlexL) qTFA1qTFA1+S2T2FA(TwrFlexL) qTFA2qTFA2+S1T2FA(TwrFlexL)(qTFA1qTFA2+qTFA1qTFA2) +S1T1SS(TwrFlexL) qTSS1qTSS1+S2T2SS(TwrFlexL) qTSS 2qTSS 2+S1T2SS(TwrFlexL)(qTSS1qTSS 2+qTSS1qTSS 2) +[qTSS1+qTSS 2]a3

\begin{array}{l}{{{^E}_{\nu}{^U}={^E}_{\nu}{^o}+{^E}_{\omega}{^N}\times r^{o U}}}\\ {{{}}}\\ {{{^E}_{\nu}{^V}={^E}_{\nu}{^o}+{^E}_{\omega}{^N}\times r^{o V}}}\\ {{{}}}\\ {{{^E}_{\nu}{^D}={^E}_{\nu}{^V}+{^E}_{\omega}{^R}\times r^{V D}}}\end{array}

The equation for E_{\nu}^{\phantom{\mu\nu}}{}^{m U} is similar.

{}^{E}{\pmb{\nu}}^{P}={}^{E}{\pmb{\nu}}^{V}+{}^{E}{\pmb{\omega}}^{R}\times{\pmb{r}}^{V P}

EvQ=EvP+EωH×r

×

EvS1(r )=EvQ+HvS1(r )+EωH×rQS1(r )

where,

HvS1(r )=φ1B1(r ) qB1F1+φ2B1(r ) qB1F 2+φ3B1(r ) qB1E1j1B1+ψ1B1(r ) qB1F1+ψ2B1(r ) qB1F 2+ψ3B1(r ) qB1E1j2B1 S1B11(r ) qB1F1qB1F1+S2B21(r ) qB1F 2qB1F 2+S3B31(r ) qB1E1qB1E1 +S1B21(r )(qB1F1qB1F 2+qB1F1qB1F 2)+S2B31(r )(qB1F 2qB1E1+qB1F2qB1E1)+S1B31(r )(qB1F1qB1E1+qB1F1qB1E1)

The equation for \boldsymbol{\varepsilon}_{\boldsymbol{\nu}}^{s_{2}}\left(\boldsymbol{r}\right) is similar.

\begin{array}{r l}&{^{E}_{\nu}\psi^{\nu}=^{E}_{\nu}\!\!\!\phantom{^{(0)}}^{\!\!E}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! 

Partial Angular Velocities:

Recall that: ^{E}\!\omega^{N_{i}}\left(\dot{q},q,t\right)\!=\!\!\left(\sum_{r=l}^{22}\d^{E}\omega_{r}^{N_{i}}\left(q,t\right)\!\dot{q}_{r}\right)\!+\!\;^{E}\!\omega_{t}^{N_{i}}\left(q,t\right) for each rigid body N_{i} in the system. Note that all of the {}^{E}{\pmb{\omega}}_{t}^{N_{i}} terms are zero as will be shown.

z1 for r=R z3 for r=P EωX= 7 for r=Y 0 otherwise EωtX = 0

<html>

E (h) の + E	dpi TFA h a3 for r =TFAl
	dh dpi TSS h a1 for r =TSS1
	dh dΦ2 TFA (h) a3 for r=TFA2
	dh dΦ2 TSS h a for r =TSS2 dh otherwise
0 0F (h) =0

</html> <html>

Q	dpIFA TFA (h) dh	a3 for r =TFAl h=TwrFlexL
	d$iss T'SS (h) dh	for r = TSS1 h=TwrFlexL
	dΦ2 TFA (h dh TSS	a3 for r=TFA2 h=TwrFlexL
	dp? h dh	a for r =TSS2 h=TwrFlexL
E =0	0	otherwise

</html>

d for r=Yaw
E ω ω 0 otherwise
E ω

rfa for r=RFrlω ω0 otherwiseE ω R =0

The equations for ^{E}\pmb{\omega}_{r}^{M2}\left(r\right) and ^{E}\pmb{\omega}_{t}^{M2}\left(r\right) are similar.

Partial Linear Velocities:

Recall that: ^{E}\nu^{X_{i}}\left(\dot{q},q,t\right)=\left(\sum_{r=I}^{22}\varepsilon_{r}^{\phantom{R}}\left(q,t\right)\dot{q}_{r}\right)+^{E}\nu_{t}^{X_{i}}\left(q,t\right) for each point X_{i} in the system. Note that all of the \ensuremath{\boldsymbol{\varepsilon}}_{\ensuremath{\boldsymbol{\nu}}_{t}^{X_{i}}} terms are zero as will be shown.

7 for r=Sg z3 for r=Sw for r=Hv 0 otherwise v = 0

E ωr X ×r ZY for r=4,5,6 0 otherwise = 0

EvrT( h)=EvrZ+ $\begin{array}{r l r}&{\left{\begin{array}{l l}{\varepsilon_{\omega}^{x}\times r^{z T}\left(h\right)}&{f o r}&{r=d,5,6}\ {\phi_{l}^{T R L}\left(h\right)a_{l}-\left[S_{l l}^{T R L}\left(h\right)q_{T E A l}+S_{l2}^{T R L}\left(h\right)q_{T E A l}\right]a_{2}}&{f o r}&{r=T F A l}\end{array}\right.}\ &{\left{\begin{array}{l l}{\phi_{l}^{T S S}\left(h\right)a_{3}-\left[S_{l l}^{T S S}\left(h\right)q_{T S S l}+S_{l2}^{T S S}\left(h\right)q_{T S S2}\right]a_{2}}&{f o r}&{r=T S S I}\ {\phi_{2}^{T R L}\left(h\right)a_{l}-\left[S_{22}^{T R L}\left(h\right)q_{T E A2}+S_{l2}^{T R L}\left(h\right)q_{T E A l}\right]a_{2}}&{f o r}&{r=T F A2}\end{array}\right.}\ &{\left}\phi_{2}^{T R L}\left(h\right)a_{l}-\left[S_{22}^{T R L}\left(h\right)q_{T E A2}+S_{l2}^{T R L}\left(h\right)q_{T E A l}\right]a_{2}}&{f o r}&{r=T F A2}\ &{\phi_{2}^{T S S}\left(h\right)a_{3}-\left[S_{22}^{T S S}\left(h\right)q_{T S S2}+S_{l2}^{T S S}\left(h\right)q_{T S S l}\right]a_{2}}&{f o r}&{r=T S S2}\ {0}&{o t h e r w i s e}\end{array}\right.}\end{array}$ \boldsymbol{\varepsilon}_{\boldsymbol{\nu}_{t}^{T}}(h)\!=\!\boldsymbol{\ O}

\begin{array}{r}{\left[\begin{array}{l l l}{\varepsilon_{\omega}^{\scriptscriptstyle X}\times r^{2\theta}}&{f o r}&{r=\mathscr{I},\mathscr{S},\theta}\\ {a_{I}-\Big[S_{I I}^{\scriptscriptstyle T\scriptscriptstyle F\scriptscriptstyle L}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle A I}+S_{I2}^{\scriptscriptstyle T\scriptscriptstyle L}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle A2}\Big]a_{2}}&{f o r}&{r=T F A I}\\ {a_{3}-\Big[S_{I I}^{\scriptscriptstyle T\scriptscriptstyle S\scriptscriptstyle S}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle S\scriptscriptstyle I}+S_{I2}^{\scriptscriptstyle T\scriptscriptstyle S\scriptscriptstyle S}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle S\scriptscriptstyle S2}\Big]a_{2}}&{f o r}&{r=T S S I}\\ {a_{I}-\Big[S_{22}^{\scriptscriptstyle T\scriptscriptstyle E\scriptscriptstyle A}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle A2}+S_{I2}^{\scriptscriptstyle T\scriptscriptstyle E\scriptscriptstyle A}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle A I}\Big]a_{2}}&{f o r}&{r=T F A2}\\ {a_{3}-\Big[S_{22}^{\scriptscriptstyle T\scriptscriptstyle S\scriptscriptstyle S}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle A2}+S_{I2}^{\scriptscriptstyle T\scriptscriptstyle S\scriptscriptstyle S}\big(T w r F l e x L\big)q_{T r\scriptscriptstyle A2}}&{f o r}&{r=T S S2}\\ {\theta}&{o t h e r w i s e}\end{array}\right]}\end{array}

ω × OU for r=4,5,,11 otherwise

OV for r=4,5,,11 ω × otherwise EvV =0

The equations for E_{\nu_{r}}^{\,,\,\,\,\,\mu\nu} and EvIMU are similar.

\begin{array}{r l r}&{}&{f o r\ \ r}\\ &{}&{\left\{\phi_{l}^{B I}\left(r\right)j_{l}^{B I}+\psi_{l}^{B I}\left(r\right)j_{2}^{B I}-\left[S_{1l}^{B I}\left(r\right)q_{B I F I}+S_{12}^{B I}\left(r\right)q_{B I F I}+S_{13}^{B I}\left(r\right)q_{B I E I}\right]j_{3}^{B I}\ \ \ f o r\ \ r}\\ &{}&{\left\{\phi_{3}^{B I}\left(r\right)j_{l}^{B I}+\psi_{3}^{B I}\left(r\right)j_{2}^{B I}-\left[S_{33}^{B I}\left(r\right)q_{B I E I}+S_{23}^{B I}\left(r\right)q_{B I F I}+S_{13}^{B I}\left(r\right)q_{B I F I}\right]j_{3}^{B I}\ \ \ f o r\ \ r}\\ &{}&{\left\{\phi_{2}^{B I}\left(r\right)j_{l}^{B I}+\psi_{2}^{B I}\left(r\right)j_{2}^{B I}-\left[S_{22}^{B I}\left(r\right)q_{B I F I}+S_{12}^{B I}\left(r\right)q_{B I F I}+S_{23}^{B I}\left(r\right)q_{B I E I}\right]j_{3}^{B I}\ \ \ f o r\ \ r}\\ &{}&{\left\{\varepsilon_{O H}^{B I}\times r^{Q S I}\left(r\right)\right.}\\ &{}&{\left.\rho t\rightarrow r^{r}\left(r\right)}\\ &{}&{\left.\rho t h e r w i\right.}\end{array} =4,5,,14 =B1F1 =B1E1 =B1F2 =Teet ise \boldsymbol{\varepsilon}_{\boldsymbol{\nu}_{t}^{S I}}\left(\boldsymbol{r}\right)=\boldsymbol{\ O}

The equations for ^E_{\nu_{r}^{S2}}\left(r\right) and ^E_{\nu_{t}^{S2}}\left(r\right) are similar.

ω ×r OW for r=4,5,,11 0 otherwise E = 0

Angular Accelerations:

Recall that: ^{E}\pmb{\alpha}^{N_{i}}\left(\ddot{q},\dot{q},q,t\right)\!=\!\left(\sum_{r=l}^{22}^{E}\pmb{\omega}_{r}^{N_{i}}\left(q,t\right)\ddot{q}_{r}\right)\!+\!\left[\sum_{r=l}^{22}\frac{d}{d t}\!\left(^{E}\pmb{\omega}_{r}^{N_{i}}\left(q,t\right)\right)\!\dot{q}_{r}\right]\!+\!\frac{d}{d t}\!\left(^{E}\pmb{\omega}_{t}^{N_{i}}\left(q,t\right)\right)\!\left(^{E}\pmb{\omega}_{p}^{N_{i}}\left(q,t\right)\right), for each rigid body N_{i} in the system. Note that the \frac{d}{d t}\Big(^{E}\omega_{r}^{N_{i}}\Big) terms are all vector functions of \left({\dot{q}},q,t\right) and that all of the \frac{d}{d t}\Big(^{E}\omega_{t}^{N_{i}}\Big) terms are zero as will be shown.

\begin{array}{l}{\displaystyle\frac{d}{d t}\Big(\sp\varepsilon\omega_{r}^{X}\Big)=O}\\ {\displaystyle\frac{d}{d t}\Big(\sp\varepsilon\omega_{{r}}^{X}\Big)=O}\end{array}

\begin{array}{l l}{\displaystyle\frac{d}{d t}\Big[^{\varepsilon}\pmb{\omega}_{r}^{F}\left(h\right)\Big]\!=\!\left\{\!\!\begin{array}{l l}{\displaystyle\varepsilon_{\pmb{\omega}}^{\varepsilon}\!\times^{\varepsilon}\!\omega_{r}^{F}\left(h\right)}&{\displaystyle f o r\;\;r=7,\delta,...,l O}\\ {\displaystyle\theta}&{o t h e r w i s e}\end{array}\!\right.}\\ {\displaystyle\frac{d}{d t}\Big[^{\varepsilon}\pmb{\omega}_{\prime}^{F}\left(h\right)\Big]=O}\end{array}
\begin{array}{l}{\displaystyle\frac{d}{d t}\Big({}^{E}{\omega}_{r}^{B}\Big)=\left\{{\!\!\begin{array}{l l}{\displaystyle E_{{\pm}}{\omega}^{X}\times{}^{E}{\omega}_{r}^{B}}&{\displaystyle f o r\ \ r=7,\mathrm{}\mathrm{\it{\mathscr{S}}},\ldots,{\it{\it{10}}}}\\ {\displaystyle O}&{\ o t h e r w i s e}\end{array}}\right.}\\ {\displaystyle\frac{d}{d t}\Big({}^{E}{\omega}_{{\iota}}^{B}\Big)=\cal{O}}\end{array} E E N for r=Yaw
d E ω Yaw
ω ω
dt d otherwise
d E
ωt =0
dt

The equations for {\frac{d}{d t}}\Big[^{\,E}\pmb{\omega}_{r}^{{\scriptscriptstyle M}2}\,\big(r\big)\Big]  and d Eω \frac{d}{d t}\Big[^{\,E}\pmb{\omega}_{t}^{{M}2}\left(r\right)\Big] are similar.

Linear Accelerations:

Recall that: \varepsilon_{\mathbf{}}\boldsymbol{\alpha}^{X_{i}}\left(\ddot{q},\dot{q},q,t\right)\!=\!\!\left(\sum_{r=l}^{22}\varepsilon_{\nu_{r}^{X_{i}}}\left(q,t\right)\ddot{q}_{r}\right)\!+\!\!\left[\sum_{r=l}^{22}\!\frac{d}{d t}\!\left({^{\varepsilon}\nu_{r}^{X_{i}}}\left(q,t\right)\right)\!\dot{q}_{r}\right]\!+\!\frac{d}{d t}\!\left({^{\varepsilon}\nu_{{^I}}^{X_{i}}}\left(q,t\right)\right)\!\left({^{\varepsilon}\nu_{{^I}}^{X_{i}}}\left(q,t\right)\right)\!+\!\frac{d}{d t}\!\left({^{\varepsilon}\nu_{{^I}}^{X_{i}}}\left(q,t\right)\right)\!+\!{^{\varepsilon}\nu_{{^I}}^{X_{i}}}\left(q,t\right), for each point X_{i} in the system. Note that the {\frac{d}{d t}}{\Big(}^{E}\nu_{r}^{X_{i}}{\Big)} terms are all vector functions of \left({\dot{q}},q,t\right) and that all of the {\frac{d}{d t}}{\Big(}^{E}\nu_{t}^{X_{i}}{\Big)} terms are zero as will be shown.

\begin{array}{l}{\displaystyle\frac{d}{d t}\Big(\sp\varepsilon\pmb{\nu}_{r}^{z}\Big)=O}\\ {\displaystyle\frac{d}{d t}\Big(\sp\varepsilon\pmb{\nu}_{{\pmb\nu}}^{z}\Big)=O}\end{array}

ω ω × for r=4,5,6 v dt otherwise (EvtY) =0 dt ddt $\iota_{\Psi_{r}^{T}}(h)!!!\int_{=!!!!!!\int_{0}^{M}}!\left[!!!\begin{array}{l l l}{\varepsilon_{\omega_{r}^{X}\times\left[!!!\begin{array}{l}{x}{\nu}{\nu^{r}\left(h\right)+}^{\varepsilon}\omega^{X}\times r^{Z r}\left(h\right)!!\right]}}&{f o r}&{r=d,5,6}\ {-\left[!!\begin{array}{l l l}{S_{11}^{T R A}\left(h\right)\dot{q}{T r A l}+S{12}^{T R A}\left(h\right)\dot{q}{T r A l}]!!\right]a{2}+}&{\varepsilon_{\omega}^{X}\times^{E}\nu_{T R A l}^{T}\left(h\right)}&{f o r}&{r=T R A l}\ {-\left[!!\begin{array}{l l l}{S_{11}^{T S B}\left(h\right)\dot{q}{T S S1}+S{12}^{T S B}\left(h\right)\dot{q}{T S S2}}\end{array}\right]a{2}+}&{\varepsilon_{\omega}^{X}\times^{E}\nu_{T S S1}^{T}\left(h\right)}&{f o r}&{r=T S S I}\ {-\left[!!\begin{array}{l l l}{S_{22}^{T R A}\left(h\right)\dot{q}{T R A2}+S{12}^{T R A}\left(h\right)\dot{q}{T R A l}\right]a{2}+}&{\varepsilon_{\omega}^{X}\times^{E}\nu_{T R A2}^{T}\left(h\right)}&{f o r}&{r=T F A2}\ {-\left[!!\begin{array}{l l l}{S_{22}^{T R A}\left(h\right)\dot{q}{T S2}+S{12}^{T R A}\left(h\right)\dot{q}{T R A l}}\end{array}\right]a{2}+}&{\varepsilon_{\omega}^{X}\times^{E}\nu_{T R S2}^{T}\left(h\right)}&{f o r}&{r=T F A2}\ {-\left[!!\left[S_{22}^{T S S}\left(h\right)\dot{q}{T S S2}+S{12}^{T S S}\left(h\right)\dot{q}{T S S1}\right]a{2}+}&{\varepsilon_{\omega}^{X}\times^{E}\nu_{T S S2}^{T}\left(h\right)}&{f o r}&{r=T S S2}\ {0}&{o t h e r w i s e}\end{array}\right]$ d[EvtT(h )]=0

The equations for \frac{d}{d t}\big(\varepsilon_{\nu_{r}^{I M U}}\big) and \frac{d}{d t}\big(\boldsymbol{\varepsilon}_{\boldsymbol{\nu}_{t}^{I M U}}\big) are similar.

dtEvtS1(r )=0

The equations for \frac{d}{d t}\Big[^{\varepsilon}\nu_{r}^{s_{2}}(r)\Big] and \frac{d}{d t}\Big[^{\varepsilon}\nu_{t}^{s2}\left(r\right)\Big] are similar.