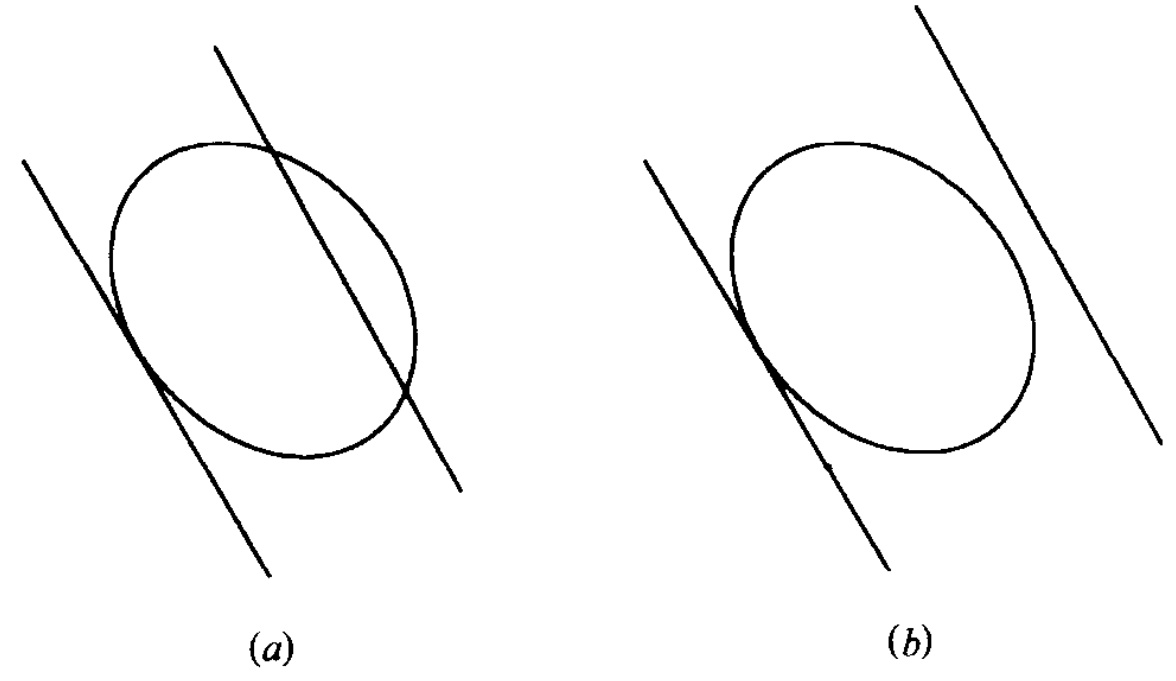obsidian_backup/线性化求解器/参考文献/飞行器系统辨识学/auto/飞行器系统辨识学.md

国防科研试验工程技术系列教材空气动力系统

飞行器系统辨识学

专业装 福村工作委员会

飞行器系统辨识学

中国人民解放军总装备部军事训练教材编辑工作委员会

國防工草岛版社·北京·

图书在版编目 （CIP)数据

飞行器系统辨识学/中国人民解放军总装备部军事训练教材编辑工作委员会编.一北京：国防工业出版社，2003.5

国防科研试验工程技术系列教材·空气动力系统ISBN7-118-02971-8

I.飞.．．Ⅱ.中.．．Ⅲ.系统辨识－应用－飞行器 -空气动力学－教材IⅣ.V417

中国版本图书馆CIP数据核字（2002)第078321号

國防 草 \frac{\phi}{\phi} 版 \dot{\pmb{\mathcal{T}}}^{\pmb{\mathcal{k}}} 出版发行
（北京市海淀区紫竹院南路23号）
（邮政编码100044）
国防工业出版社印刷厂印刷
新华书店经售

开本 850\times1168 1/32印张 18\% 470千字2003年5月第1版 2003年5月北京第1次印刷印数:1一2000册 定价：41.00元

《国防科研试验工程技术系列教材》总编审委员会

名誉主任委员 程开甲 李元正

主 任 委 员胡世祥

副主任委员段双泉尚学琨褚恭信马国惠
委 员 (以下按姓氏笔画排列)王国玉　刘　强　刘晶儒 张忠华李济生　邵发声周铁民　姚炳洪姜世忠 徐克俊 钱卫平常显奇萧泰顺 穆 山

办公室主任 任万德

办公室成员王文宝冯许平　左振平朱承进余德泉 李钢杨德洲 邱学臣郑时运 聂 陶有勤 郭诠水钱玉民

《国防科研试验工程技术系列教材·空气动力系统》编审委员会

主任委员董臻东

副主任委员 陈作斌 乐嘉陵
委 员张涵信 王侃 张志成 萧泰顺刘义信 范召林 郭隆德 杨祖清桂业伟
主 编 张涵信
副主编萧泰顺张志成王侃
秘 书 赵志根 沈秀春

飞行器系统辨识学

主编 蔡金狮副主编 汪清 王文正主审 陈士橹 曾颖超

著作人员

第1章 蔡金狮
第2章 蔡金狮
第3章汪清董能力蔡金狮
第 4 章 蔡金狮 王文正
第5章 王文正蔡金狮
第6章 蔡金狮
第7章 蔡金狮
第8章 蔡金狮 王文正
第9章蔡金狮万宗国
第 10章汪清蔡金狮
第 11章 董能力 蔡金狮
第 12 章 钱炜祺 蔡金狮

总序

当今世界，科学技术突飞猛进，知识经济迅速兴起，国力竞争越来越取决于各类高技术、高层次人才的质量与数量，因此，作为人才培养的基础工作一—教材建设，就显得格外重要和紧迫。为总结、巩固国防科研试验的经验和成果，促进国防科研试验事业的发展，加快人才培养，我们组织了近千名专家、学者编著了这套系列教材。

建国以来，我国国防科研试验战线上的广大科技人员，发扬“自力更生、艰苦奋斗、科学求实、大力协同、无私奉献”的精神，经过几十年的努力，建立起了具有相当规模和水平的科研试验体系，创立了一系列科研试验理论，造就了一支既有较高科学理论知识、又有实践经验，勇于攻关、能打硬仗的优秀科技队伍，取得了举世瞩目的成就。这些成就对增强国防实力，带动国家经济发展，促进科技进步，提高国家和民族威望，都发挥了重要作用。

编著这套系列教材是国防科研试验事业继往开来的大事，它是国防科研试验工程技术建设的一个重要方面，是国防科技成果的一个重要组成部分，也是体现国防科研试验技术水平的一个重要标志。它承担着记载与弘扬科技成就、积累和传播科技知识的使命，是众多科技工作者用心血和汗水凝成的科技成果。编著该套系列教材，旨在从总体的系统性、完整性、实用性角度出发，把丰富的实践经验进一步理论化、科学化，形成具有我国特色的国防科研试验理论与实践相结合的知识体系。一是总结整理国防科研试验事业创业40年来的重要成果及宝贵经验；二是优化专业技术教材体系，为国防科研试验专业技术人员提供一套系统、全面的教科书.满足人才培养对教材的急需；三是为国防科研试验提供有力的技术保障；四是将许多老专家、老教授、老学者广博的学识见解和丰富的实践经验总结继承下来。

这套系列教材按国防科研试验主要工程技术范畴分为：导弹航天测试发射系统、导弹航天测量控制系统、试验通信系统、试验气象系统、常规兵器试验系统、核试验系统、空气动力系统、航天医学工程系统、国防科技情报系统、电子装备试验系统等。各系统分别重点论述各自的系统总体、设备总体知识，各专业及相关学科的基础理论与专业知识，主要设备的基本组成、原理与应用，主要试验方法与工作程序，本学科专业的主要科技成果，国内外的最新研究动态及未来发展方向等。

这套系列教材的使用对象主要是：具有大专以上学历的科技与管理干部，从事试验技术总体、技术管理工作的人员及院校有关专业的师生。

期望这套系列教材能够有益于高技术领域里人才的培养，有益于国防科研试验事业的发展，有益于科学技术的进步。

《国防科研试验工程技术系列教材》总编审委员会1999年10月

序

空气动力试验与研究是国防科研试验的重要组成部分。

新中国成立以来，我国从事航空、航天空气动力研究的科技人员坚持“自力更生、艰苦奋斗、团结协作、科学求实”的精神，建立了尺寸、速度、性能相配套的各类气动试验设备，开展了气动理论、数值计算、气动试验及模型自由飞研究，承担并完成了一系列航空、航天、兵器武器的试验、计算任务，为我国武器装备的发展作出了重要贡献。

中国空气动力研究与发展中心的广大科技人员，在空气动力试验设备的研制、空气动力试验、计算方法研究及完成航空、航天、兵器等各类武器的试验与设计中，积累了丰富的实践经验，取得了丰硕的科研成果。为了更有效地培养和造就新一代空气动力学研究人才，促进我国空气动力事业的不断巩固和发展，在总装备部的领导下，我们组织有关专家和科技人员编写了这套系统、全面总结几十年来理论与实践经验成果的空气动力系列教材。

本套教材是以具有大专以上学历，从事空气动力研究的科技人员为主要适用对象，既可作为空气动力试验研究的中、高级技术人员的学习指导用书，亦可作为院校空气动力学相关专业的帅生参考用书。

本套教材共分13卷。包括：《分离流与旋涡运动的结构分析》《计算流体力学及应用》、《低速风洞试验》、《高速风洞试验》、《高超声速气动力试验》《高超声速气动热和热防护》、《再人物理》《高低速风洞气动与结构设计》、《高低速风洞测量与控制系统设计》《高超声速试验设备设计》、《飞行器系统辩识学》、《模型目由飞试验》和《流动显示技术》。

本套教材在编写过程中，得到了总装备部领导、机关，型号部门和国内空气动力研究单位的大力支持与协作，在此一并表示衷心的感谢。由于本套教材涉及专业面广，包含内容多，编者水平有限，书中难免有错误或疏漏之处，诚请读者予以指正。

《国防科研试验工程技术系列教材·空气动力系统》编审委员会2001年3月

前言

飞行器系统辨识是将系统辨识理论应用于飞行器动力学系统,阐述如何从飞行器飞行试验的遥外测数据、风洞实验模型的动态实验数据和流场参数实测数据、弹道靶自由飞模型的光测、雷测数据以及飞行器模型测热实验的温度数据等诸多类实测数据中辨识出飞行器的气动力参数、气动热参数、工程湍流模型参数和惯性仪表误差系数等，以建立正确的飞行器动力学系统数学模型。它在飞行武器研制的设计、试验、定型鉴定的全过程，特别是在飞行器系统仿真建模与飞行故障分析中，有着广泛的应用前景。同时也是国防科研各试验系统进行飞行试验和风洞实验数据处理的有用工具。

本书是按国防科研试验工程系列教材的要求，在蔡金狮等所著《动力学系统辨识与建模》和《飞行器系统辨识》两本专著的基础上进一步充实、提高而成的。全书分理论与应用两大部分。理论部分在专著的内容上进行了精简，补充了部分新近发展的辨识方法；应用部分增补了大量本系统辨识研究组最近的研究成果。特别是汪清博士的非线性非定常气动力建模和神经网络建模，王文正博士的集员辨识和基于广义频率响应函数系统辨识，钱炜祺博士的分布参数系统辨识及气动热参数辨识和工程湍流模型辨识，董能力博士的正交最小二乘法应用及惯性仪表误差系数辨识等，都有其独到之处。王文正和董能力还介绍了新近发展的 H_{\infty} 郑识和小波分析辨识法。全书由蔡金狮、汪清、王文正负责统稿，并请陈士橹院士、曾颖超教授负责审稿。编著中突出了系统辨识理论的新发展，拓展了系统辨识在航空航天领域的应用范围，使本书既具有较高的理论价值，又具有较高的实用价值。

书中未说明的符号均按中华人民共和国国家标准GB/T14410-93《飞行力学概念、量和符号》定义。

希望本书的出版，对我国特别是对国防科研各试验系统及有关研究院所的飞行器系统辨识研究和实际应用工作有所促进。

著者2002年4月

内容简介

本书将系统辨识理论应用于飞行器动力学系统，阐述如何从飞行试验的遥外测数据、风洞实验模型的动态实验和流场参数实测数据、弹道靶自由飞模型的光测数据以及飞行器模型测热实验的温度数据等各类数据中辨识出飞行器的气动力参数、气动热参数、工程湍流模型参数和惯性仪表误差参数，以建立正确的飞行器动力学系统数学模型。

全书分理论与应用两部分。理论部分简明论述系统辨识基本理论与方法；应用部分密切结合飞行器试验中实际问题，给出实例、具体算法和公式，是一部理论与实践密切结合的系统辨识教材。

本书读者对象是在航空、航天、兵器领域中从事系统辨识、动力学特性研究，特别是从事飞行器飞行试验和风洞实验的数据处理和分析的研究员、工程师、实验师和高校教师、研究生；也可作为系统控制、系统仿真、系统辨识研究专业人员的参考资料。

目录

第1章绪论·…·
1.1 系统辩识与建模 2
1.2 系统辨识基本思想 3
1.3 系统辩识主要内容 5
1.4 系统辨识主要功用 8
1.5 动力学系统辨识· 10
1.5.1 集中参数系统辨识 12
1.5.2 分布参数系统辨识 12
1.6飞行器系统辨识.... 13
1.6.1 气动力参数辨识 14
1.6.2 气动热参数辨识 15
1.6.3 工程湍流模型辩识 16
1.6.4 惯性仪表误差系数辩识 16
第2章 飞行器动力学系统模型 ... 18
2.1飞行器动力学系统数学模型 18
2.1.1 常用坐标系 19
2.1.2 飞行器刚体动力学方程·· 20
2.1.3 热传导方程·…· 23
2.1.4 流体动力学方程 ..·24
2.2空气动力学数学模型 26
2.2.1 代数模型 26
2.2.2 积分方程模型 30
2.2.3微分方程模型 32
2.3推力与环境数学模型 34
2.3.1 推力数学模型 34
2.3.2 重力数学模型 36
2.3.3标准大气密度 37
2.3.4大气湍流模型 38
参考文献….. 40
第3童模型辨识 42
3.1概述 ····· 42
3.2建模准则 42
3.2.1最大信息量准则 43
3.2.2最大可信度准则 44
3.2.3 \pmb{F} 统计检验 45
3.2.4最小预测误差平方和准则 47
3.3优选算法 48
3.3.1逐步回归法 49
3.3.2主成分分析法 52
3.3.3 正交最小二乘法 54
3.3.4数据分割技术 + 60
3.4神经网络建模方法 61
3.4.1神经网络和学习算法 62
3.4.2非线性系统建模 ·· 65
3.5基于小波分析的系统辨识方法 67
3.5.1小波分析方法 68
3.5.2时变系统的辨识 71
3.5.3 分形信号的辨识 73
3.5.4半参数模型的小波辨识 75
参考文献….. 76
4章飞行状态估计 79
4.1 概述 79
4.2卡尔曼滤波算法 80
4.2.1最小方差估计 81
4.2.2 卡尔曼滤波 82
87
4.2.3 广义卡尔曼滤波
4.2.4增广的广义卡尔曼滤波 90
4.2.5修正增益广义卡尔曼滤波 ...91
4.2.6平方根分解滤波··. ... 94
4.3分割算法 103
4.3.1分割定理·... .... 104
4.3.2广义分割算法·…. 108
4.3.3广义多分割算法· 114
4.3.4广义分割辨识算法· 118
参考文献 .... .….123
5章参数估计…. 125
5.1概述……. 125
5.2线性模型参数估计 126
5.2.1最小二乘法···· 127
5.2.2递推最小二乘法·· 128
5.2.3渐消记忆的递推估计法. 129
5.2.4 贝叶斯法··· 130
5.2.5 岭估计法···· 131
5.2.6 超椭球法· 132
5.2.7 主成分法···· 134
5.2.8 特征根法··· 135
5.2.9贝叶斯主成分法(PB回归法) 136
5.3最大似然法 ···· 137
5.3.1最大似然准则· .... 137
5.3.2非线性动力学系统最大似然算法 ..….140
5.3.3线性系统最大似然算法· 145
5.3.4修正最大似然准则· 148
5.3.5输出误差法·. ..·149
5.3.6方程误差法· .…·150
5.3.7最大似然近似算法· 152
5.3.8最大似然递推算法· 155
5.4非统计类参数估计方法--集员辨识 157
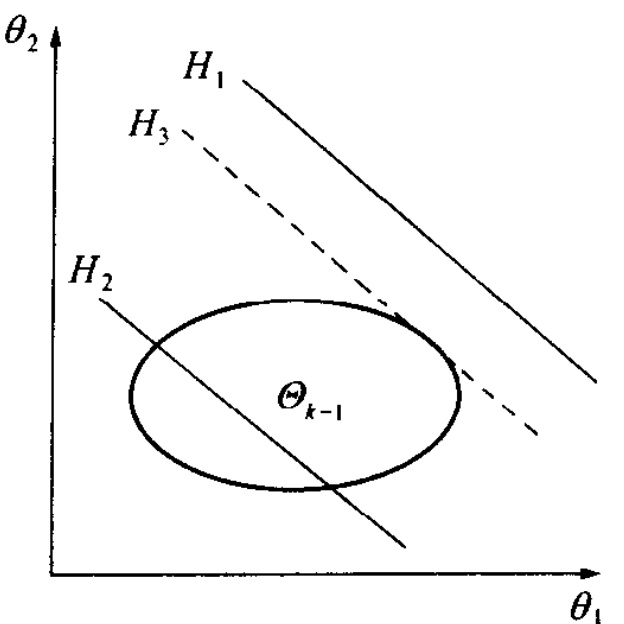
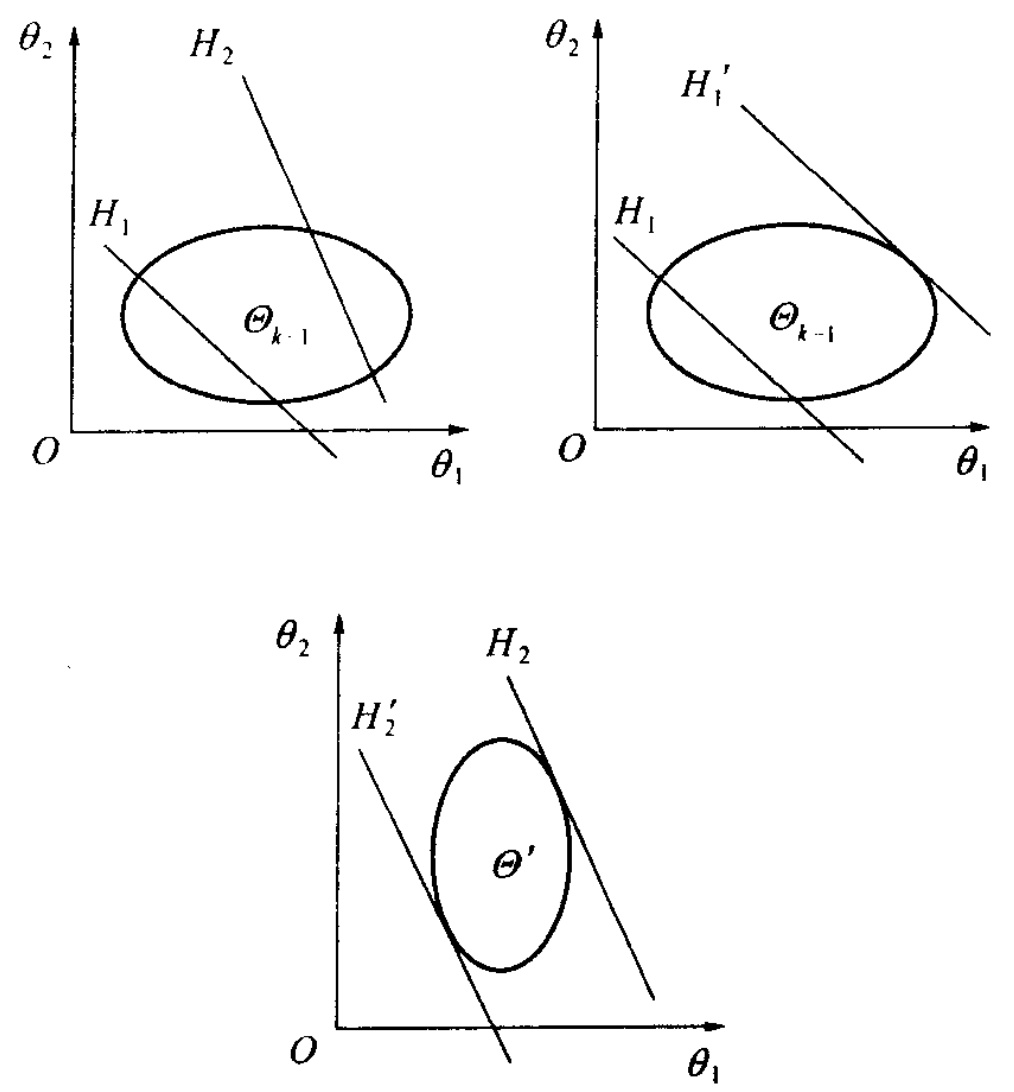
5.4.1线性系统参数估计的边界椭球法·· 157
5.4.2线性系统参数估计的改进凸多面锥法·· 167
5.4.3非线性系统参数的集员辨识·· 175
5.5 基于广义频率响应函数(GFRF)的系统辨识 181
5.5.1 多项式类非线性连续模型的GFRF描述· 181
5.5.2 多项式类非线性离散模型的GFRF描述· 184
5.5.3 GFRF的辨识方法· 186
5.5.4 基于 GFRF 的 H_{2} 辨识··· 193
5.6.1 闭环系统可辨识性的基本概念· 204
5.6.2 闭环系统的辨识方法及可辨识性· 206
5.6.3 最小二乘法在闭环辨识中的应用··· 211
5.6.4 辅助变量法在闭环辨识中的应用···· 216

第6章频域辨识算法 221

6.1 概述 221
6.2 频域分析的基础知识 222
6.2.1 傅里叶变换···· 222
6.2.2 离散傅里叶变换 223
6.2.3 复随机变量·· 225
6.2.4 随机过程…·· 226
6.2.5 平稳随机过程 228
6.2.6 随机过程的傅里叶变换 229
6.2.7 随机过程的谱密度··· 230
6.3 最大似然法 232
6.3.1 似然准则推导 233
6.3.2 最大似然算法··· 235
6.3.3 离散型最大似然算法 240
6.3.4 输出误差法···· 242
6.3.5 方程误差法·· 243
6.3.6 零添补技术 244

参考文献 246

第7章试验设计和最优输入 247

7.1输人设计 247

7.2输出设计 250
7.2.1输出信号测量要求· 250
7.2.2运动轨迹的测量 252.
7.2.3数据采集系统.….. 253
7.3几何、物理和环境参数测量 ·· 254
7.3.1几何、物理参数的测定 254
7.3.2环境参数测量·. 255
7.4最优输人设计 255
7.4.1最优输人设计准则· ..256
7.4.2最优输人算法…… 258
7.4.3应用实例…·.. 265
参考文献 270
育 8章辨识准度与系统验证 271
8.1概述.·. 271
8.2参数估计准度评价准则 271
8.2.1估计偏差... 271
8.2.2估计分散度·…. 272
8.2.3克拉马-罗不等式 272
8.2.4 不确定度椭球 ….·. ··· 274
8.3估计准度评价的简化算法 274
8.3.1灵敏度.. 274
8.3.2相关性· 275
8.3.3克拉马-罗界 276
8.3.4修正的克拉马-罗界 277
8.4参数的置信区间估计· 278
8.4.1线性系统置信区间估计· 279
8.4.2非线性系统置信区间估计 280
8.4.3非线性因子估计算法 281
8.5准度的工程判断 283
8.6系统验证 284
参考文献 ..·285
官 9 童试验数据预处理及相容性检验 .... 286
9.1概述…….….. ... 286
9.2飞行试验数据的预处理.…. ..286
9.2.1测量数据由电码到物理量的转换 .….287
9.2.2零位修正... ..... 288
9.2.3 野值的识别、剔除与补正 ..289
9.2.4 试验数据加密与采样时刻校正…·. .….291
9.2.5 传感器安装位置校正···· .. 292
9.2.6 数据平滑和微分平滑 293
9.2.7 数据的低通数字滤波···· 296
9.2.8数据的时间迟后修正·· 300
9.3数据相容性检验和数据重建 .·303
9.3.1相容性检验基本方程及算法·…· . 304
9.3.2四元素相容性检验模型…··. .... 311
9.3.3飞行数据相容性检验实用算法· ... 313
9.4气动参数可辨识性分析和预估计 ... 317
9.4.1参数可辨识性分析 317
9.4.2参数预估计…..... ..321
参考文献 ..... 323
官10章气动力参数辨识 ….325
10.1概述…·.. ..325
10.2固定翼飞行器气动参数辨识· 326
10.2.16 自由度模型气动参数辨识 ...· 326
10.2.2纵向气动参数辨识··· .... 344
10.2.3横侧向气动参数辨识…·.. 347
10.2.4静不稳定飞行器气动参数辨识 352
10.3旋翼飞行器气动参数辨识 357
10.3.1 6 自由度模型气动参数辨识 .357
10.3.2含旋翼自由度模型气动参数辨识…· 361
10.4自旋飞行器气动参数辨识…···…· ….365
10.4.1 等效舵偏角和气动力数学模型 366
10.4.2气动参数辨识数学模型 .367
10.5再人体气动参数辨识 ... 374
10.5.1 再人体气动力矩导数辨识 374
10.5.2 小不对称气动参数辨识 378
10.5.3 再人攻角和气动力导数估计 383
10.6 弹丸气动参数辨识 386
10.6.1 太阳方位计的姿态测定 387
10.6.2 弹丸气动参数辨识数学模型 388
10.6.3 气动参数辨识对测试准度的要求 392
10.7 鱼雷水动力参数辨识 394
10.7.1 鱼雷动力学系统基本方程 394
10.7.2 水动力参数辨识基本方程 401
10.7.3 辨识仿真算例 406
10.8 地面试验气动参数辨识 407
10.8.1 弹道靶自由飞试验气动参数辨识 408
10.8.2 风洞自由振荡试验气动参数辨识 414
10.8.3 大攻角非定常气动力参数辨识 418
423

参考文献

第 11章惯性仪表误差系数辨识 425

11.1 概述 425
11.2 制导工具误差-般模型 427
11.2.1 加速度表误差 428
11.2.2 陀螺漂移误差 431
11.2.3 平台角偏差 433
11.2.4 误差模型 436
11.3 误差系数估计 437
11.3.1 工具误差的试验 438
11.3.2 工具误差的观测方程 439
11.3.3 工具误差辨识难题 440
11.3.4 仿真应用算例 442
11.4 天地关系检验与地面数据纠错 447
11.4.1 组合不变量 448
11.4.2 天地关系是否一致的检验 451
11.4.3 变量重组与地面数据纠错 455
11.4.4仿真算例 457
11.5实测数据处理· 459
11.5.1 实测数据 459
11.5.2 误差模型的初选 462
11.5.3 工具误差系数估计 466
附录A 静态误差模型中的环境函数··· 472
参考文献 478
育 12 章分布参数系统辨识 480
12.1 概述 480
12.2 基本辨识算法· 481
12.2.1 基函数方法 482
12.2.2 伴随方程法 488
12.2.3 灵敏度法 493
12.3再人飞行器气动热参数辨识· 495
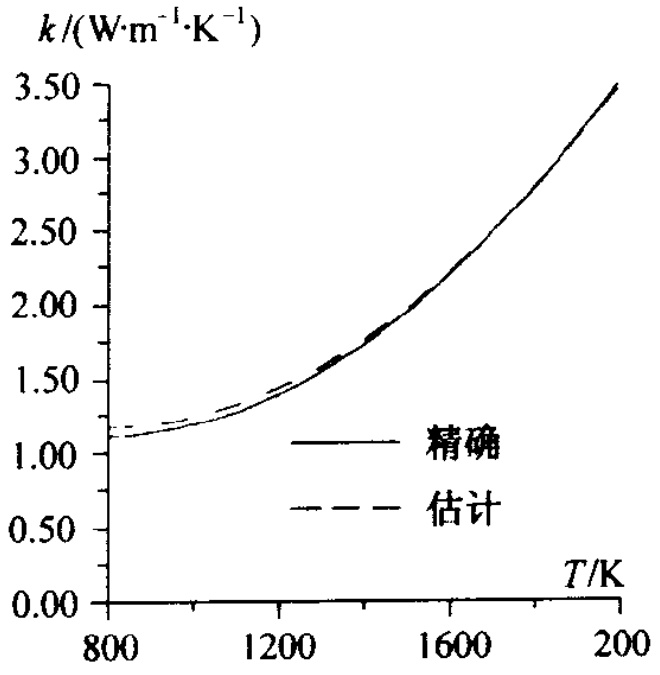
12.3.1 非线性热传导系数的辨识算法 497
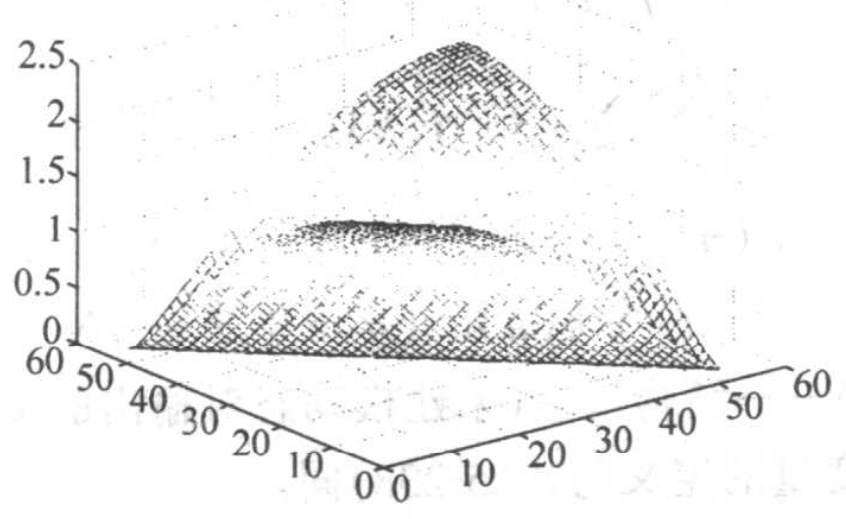
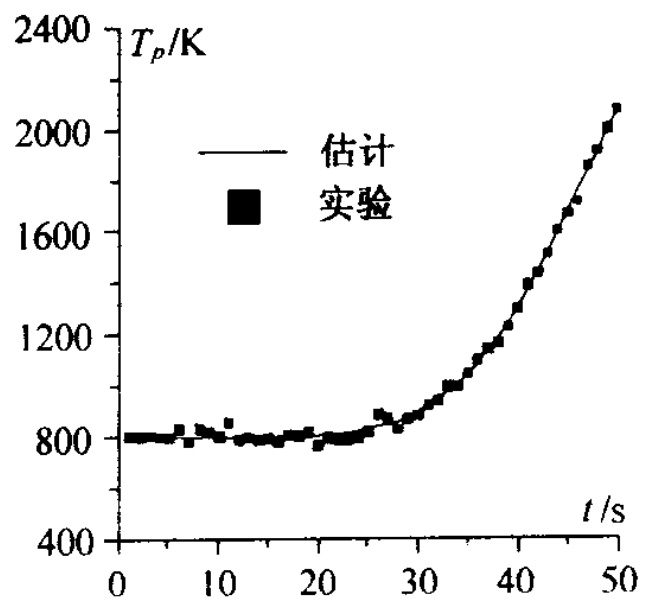
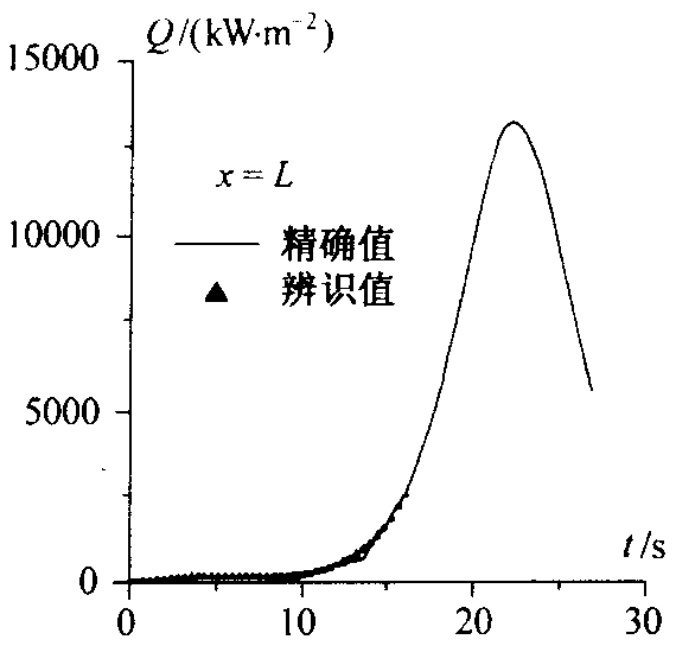
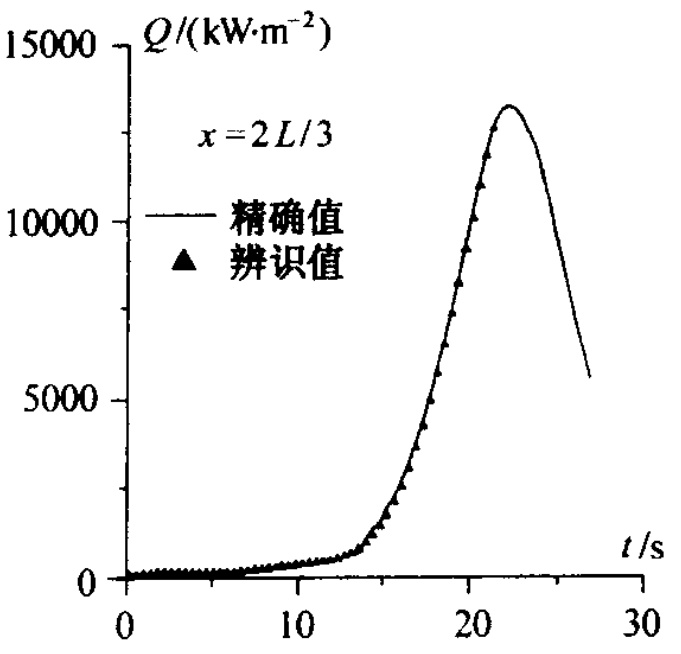
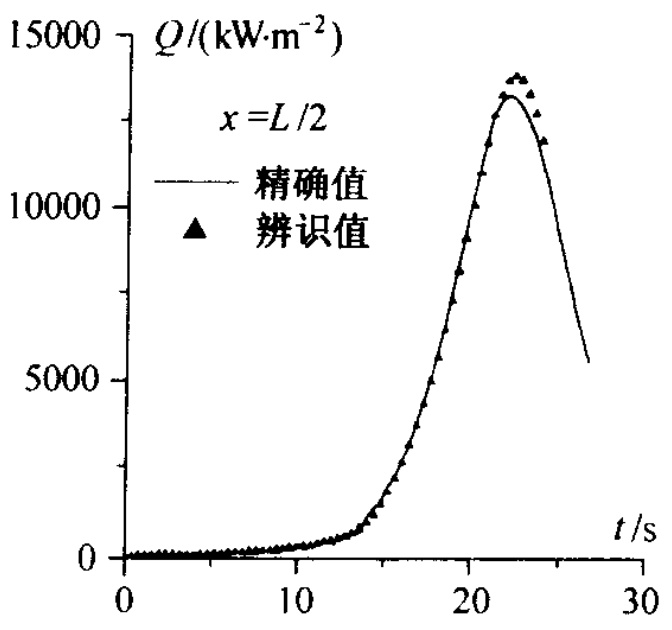
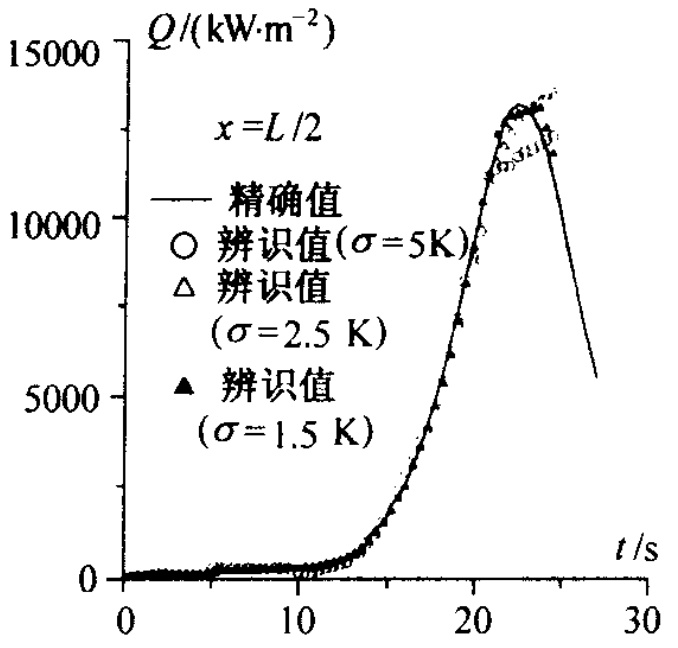
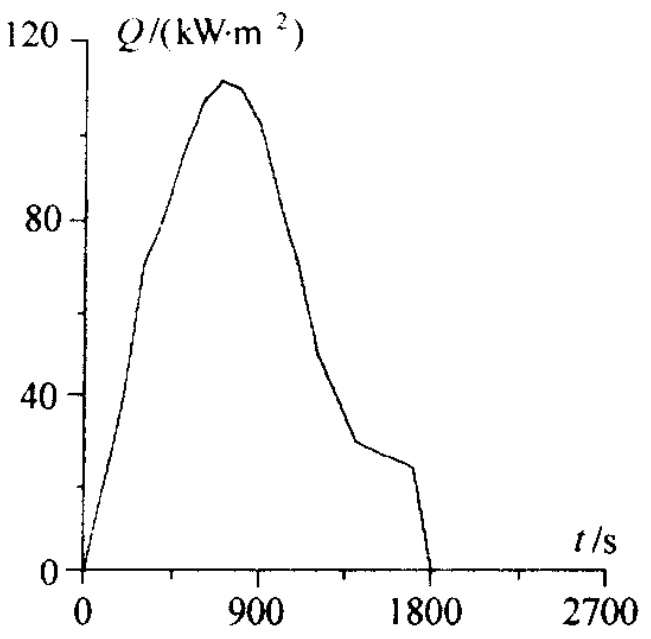
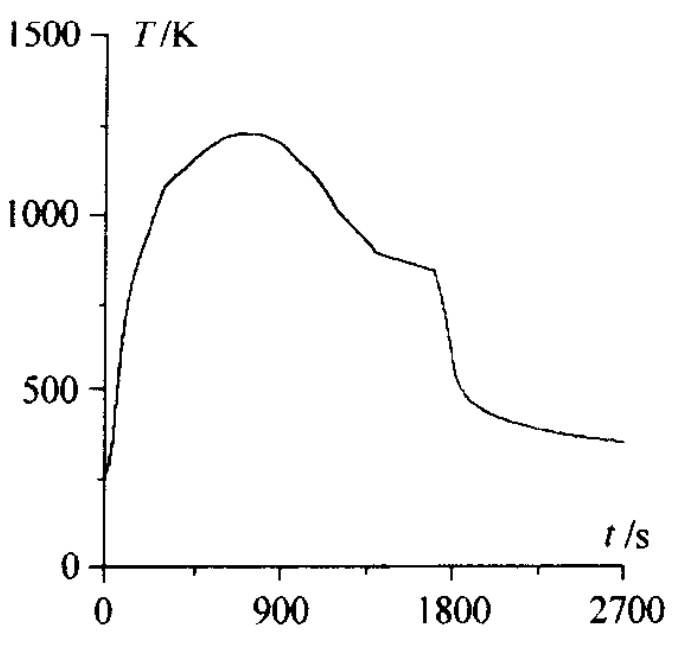
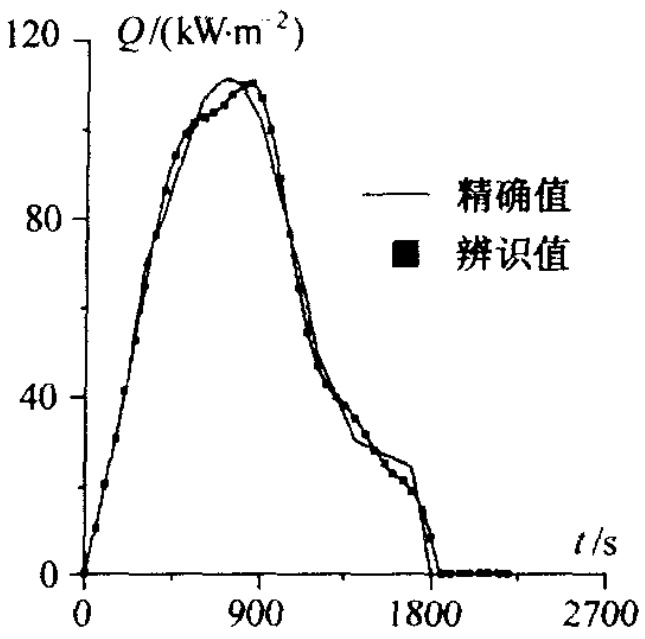
12.3.2 再人飞行器表面热流辨识· 505
12.4 工程湍流模型辨识 522
12.4.1 不可压湍流流动数值模拟方法 526
12.4.2 k^{-}\varepsilon 两方程模型参数辨识研究 535
12.4.3 对标准 k\!-\!\varepsilon 两方程模型结构改进的探讨 545
参考文献 556

第1章 绪 论

系统辨识是利用系统运行或试验过程中测得的系统输人-输出数据建立系统数学模型的技术科学。所谓系统数学模型是系统本质特征的数学抽象。人们对客观事物的认识都是由表及里、去粗取精、从定性到定量，最终希望能确定出反映所研究系统各内部因素(系统状态参数)之间以及内部因素与外部因素(外作用)之间本质特征的定量关系，以便更深刻地了解系统内在规律和特性,这些定量关系就是系统的数学模型。建立了系统的正确数学模型，可认识系统的现在，并预测系统的未来。

系统辨识的先导性工作可追溯到16世纪德国天文学家开普勒的工作，他根据布拉赫的火星观测记录数据，采用观测比较法，发现了行星运动三大定律，建立了行星运动的一种数学模型，为牛顿理论奠定了基础。18世纪德国数学家高斯在行星运动轨道的预报研究中开创性地提出最小二乘法，奠定了系统辨识中参数估计方法的基石，它作为新近发展的各类参数估计方法在特定条件下的特定形式，至今仍得到广泛应用。现代控制理论和电子数字计算技术的蓬勃发展，提供了通过试验数据建立数学模型的系统辨识学的理论和技术基础。近三十年来，现代控制理论的平滑、滤波、预测和参数估计，系统论的系统分析方法和建模思想以及数值计算方法和优化算法广泛应用于自然科学、社会科学和工程设计实践中的各个领域，与各领域的专业知识相结合，使系统辨识理论和技术得以蓬勃发展为一门技术科学。

飞行器动力学系统辨识是将飞行器作为一个动力学系统，采用系统辨识理论与技术，利用飞行器在飞行试验或地面试验中测量所得数据，建立飞行器系统的数学模型。系统的数学模型是系统定量研究的手段，它在所研究的主题范围内描述系统的主要特征，当研究的主题不同，所建立的数学模型也不同。飞行器按所研究的问题的性质可以作为刚体动力学系统、弹性体动力学系统、弹性体与液体耦合动力学系统等，当研究飞行器的防热问题时，还可作为热力学系统来建立数学模型。本书系统论述飞行器系统辨识的理论基础，并着重阐述系统辨识理论在飞行器研制和飞行试验过程中所遇到的空气动力学、飞行动力学问题中的具体应用，既有系统的理论，又有工程实践的经验总结。

1.1 系统辨识与建模

系统是由内部相互联系、相互制约、相互作用的各组元构成，是具有整体功能和综合行为的统一体。系统接受外部因素的制约和作用。系统是一个高度概括、高度抽象的概念，已广泛应用于科学研究、工程技术、经济研究、社会管理各个领域。在数学上，系统的基本特性可以用状态参数加以描述，状态参数一经确定，系统也就确定。系统数学模型是系统本质特征的数学抽象，是建立系统状态参数之间以及与外作用之间最主要的相互作用、相互制约的数学表达式。研究系统不同侧面的特性，则反映系统基本特性的状态参数也不同。例如，研究飞行器的轨道特性，其状态参数是速度、位置等：研究飞行器的弹性特性，其状态参数则是广义坐标、振型等。因此，描述系统不同基本特性的数学模型也不同。企图建立一一个描述系统全面特性的统一的数学模型是不科学的，即使可能也是不经济的。

系统数学模型有两类建模方法：理论建模和实验建模。理论建模是从已知的原理、定律和定理出发，通过机理分析研究，找出系统内在的运动规律，推导出系统中各状态参数与外作用之间的解析关系式一一数学模型。这类问题的基本规律已知，在控制论中称之为“白箱”问题。实验建模是直接从系统运动或试验中测量系统的外作用和系统的响应数据，应用辨识方法，建立系统的数学模型。这类方法适用于系统的客观规律不清楚的情况，称之为“黑箱”问题。在科学实践中经常遇到的问题是已知系统满足的某些基本定律，但又有些机理还不清楚，有待研究，这就要求理论建模与实验建模结合起来，对机理已知的部分采用理论建模、给出解析表达式，对机理不清楚的部分采用实验建模，确定其数学模型。这类问题称为“灰箱”问题。飞行器动力学系统满足牛顿第二定律，故飞行器动力学系统辨识是典型的“灰箱”问题，需要辨识的对象是动力学系统的简化数学模型和外作用力的数学模型。

1.2 系统辨识基本思想

系统辨识的基本思想是根据系统运行或试验测得的数据，按照给定的“系统等价准则”从一群候选数学模型集合中，确定出一个与系统特性等价的数学模型。这里有三个问题：如何确定候选数学模型集；如何确定辨识准则，即以什么准则判定系统的数学模型与真实系统是等价的；依据给定的辨识准则，从候选模型集合中选出正确数学模型的数学工具和算法。

1）候选数学模型集

对于“黑箱”问题，在早期，候选模型集通常取为最简单的线性代数模型集，之后推广为多项式模型集。随着电子数值计算技术的快速发展，较为复杂的样条函数模型集、指数函数模型集、超越函数模型集，甚至有限元、有限体积元、神经网络元构成的模型集都可被作为候选数学模型集。对于“灰箱”问题，由于系统应满足的某些定律已知，可以根据这些定律建立系统必须满足的状态方程组。对于不同类型的系统,状态方程组可以是代数方程组、常微分方程组、偏微分方程组、积分方程组及其组合形式。状态方程组就是候选数学模型集应满足的约束条件。

2）辨识准则

最早的辨识准则是高斯提出的、已得到广泛应用的最小二乘准则。随着现代控制理论和统计理论的发展，又提出了最小方差准则、最大似然准则、贝叶斯准则、 H_{\infty} 准则等辩识准则。辨识理论还证明了各种辨识准则能使辨识所得数学模型渐近趋于真实系统的条件。

3）辨识算法

对于给定的候选数学模型集，根据辨识准则建立辨识方程组之后，系统辨识问题就化成了一个极值优化计算问题。对于线性系统，应用最小二乘准则，常可得到解析解；对于非线性系统，采用较为复杂的辨识准则，则辨识方程组成为非线性方程组，问题成了含有微分、积分方程的泛函极值问题，无解析解。通常采用迭代算法求解，也可采用逐点递推逼近算法求解。

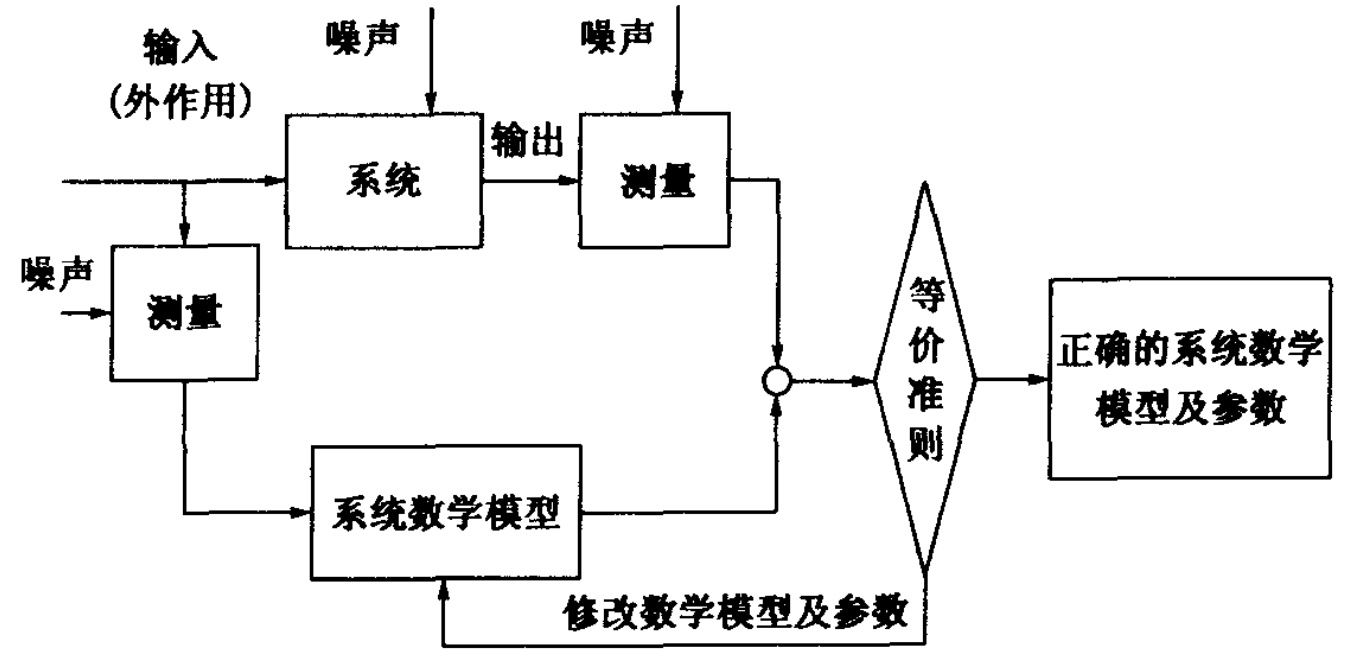
总之，系统辨识就是通过测量系统在外作用（输人）下的系统动态响应（输出）数据，按照确定的辨识准则，从这些试验数据建立反映系统本质属性的数学模型，并确定出模型中的未知参数，系统辨识的示意框图见图 1-1。

图 1-1 系统辨识示意框图

系统辨识和系统分析是互逆的两种手段。系统分析是已知系统所服从的基本定律，建立了系统的数学模型，研究系统对各种外作用的响应历程。系统辨识则相反，给定了系统的外作用和响应历程，要求确定系统的数学模型，通常称系统分析为正问题，系统辨识为反问题。系统辨识、系统分析和系统控制的研究对象和问题有密切的关系：给定系统的外作用和系统数学模型，求解系统的响应是系统分析问题；给定系统数学模型和系统响应，求解系统外作用规律是系统控制设计问题；给定系统的外作用及系统的响应，求解系统的数学模型是系统辨识问题。

1.3 系统辨识主要内容

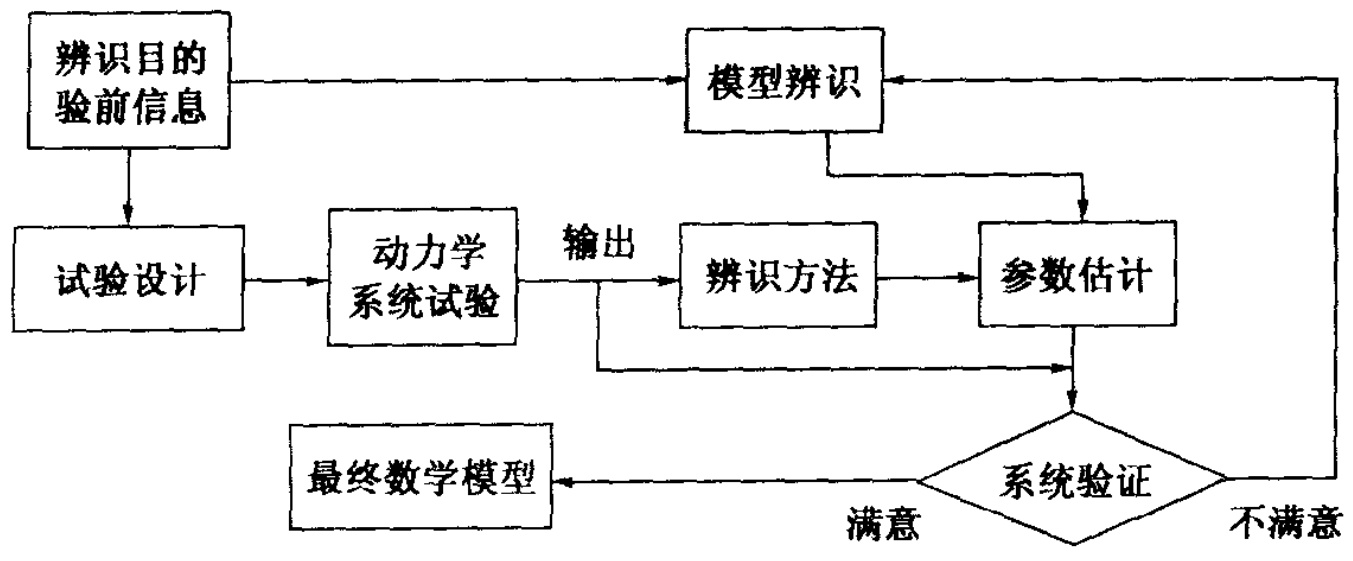
系统辨识的主要任务是建立系统的数学模型。建立数学模型过程可分为四步，也是系统辨识四个主要研究内容一一试验设计、模型辨识、参数估计和系统验证，参见图1-2。

图 1-2系统辨识基本过程

1）试验设计

试验设计是系统辨识的重要环节，是系统辨识能否成功的基础。试验设计的主要目的是确保试验能为系统辨识提供含有尽可能多信息的试验数据，使之足以辨识出正确的系统数学模型。试验设计主要包含：输人、输出参数的选择，输人信号优化设计，数据采样速率和采样长度的确定等。

试验设计的第一步是系统输人的选择，使系统输人能激发系统的主要动态特性。输人优化设计是使系统输出的有用信息量达到极大。对于不可加外作用的系统，应给系统加上一定的初始扰动，以激发待辨识系统的动态特性。其次是输出传感器的选择，传感器量程、测量精准度和安装位置的设计。之后是数据采样系统设计，数据采集速率和采集长度的确定。

飞行试验前，数据遥测系统（包括传感器选择）和数据采集系统的设计必须考虑系统辨识的需求。必须事先作系统辨识仿真计算，才能确保飞行试验能获得真正有用的信息。

2）模型辩识

模型辩识是建模过程的关键。模型辨识的主要任务是确定系统数学模型的结构形式，数学模型结构形式的选择很大程度取决于对系统本质属性的了解。实践证明，如果模型结构形式选得不合适，那么不论采用什么辨识准则和参数估计方法都无法提高辨识结果的准确度。对于飞行器系统辨识，系统应满足的基本定律（牛顿力学定律、胡克定律、傅氏定律、质量守恒定律、能量守恒定律等）是已知的，待辨识的数学模型常常是系统的外作用力数学模型或某子系统的数学模型。

模型辨识是根据系统的输人-输出试验数据，利用建模准则，在满足系统的约束条件下，从候选的模型集合选择出与系统的输人-输出特性最等价的数学结构形式。对于单输人-单输出系统，状态参数和控制参数都只有一个，通常采用多项式模型，模型辨识就是模型阶次的确定。

3）参数估计

数学模型结构形式确定后，问题就成了根据辨识准则和试验数据求取模型中的待定参数，即参数估计问题，这是系统辨识定量研究的核心。参数估计包括辨识准则的确定和优化算法两部分，辨识准则将参数估计问题转化为泛函极值问题。目前常用的辨识准则有最大似然准则、贝叶斯准则、最小方差准则等。经验证明，最大似然准则和牛顿-拉夫逊优化算法在动力学系统辨识中最实用、最有效，并得到广泛的应用。

输人-输出数据中含有常值偏差成分，在参数估计中无法消除其影响。数据中还有高频噪声、时间延迟等误差，为消除这些误差会使参数估计增加很大的计算量。通常在参数估计之前先进行数据预处理和相容性检验，消除常值偏差、高频噪声、时间延迟等，以减少参数估计的工作量并提高辨识准度。

4）系统验证

系统辨识的目的是建立反映系统本质属性的数学模型，由于辨识过程中含有不少人为的主观因素，特别是候选数学模型集的选定很大程度上取决于人的主观意识，因此在模型辨识和参数估计之后，应对辨识所得数学模型和相应参数的正确性进行验证，以确认所得模型是否确实反映了系统的本质属性。

实践是检验真理的惟一标准。正确的数学模型要在设计实践中不断应用,长期考验,才能确定其正确应用范围。例如，气动力线性模型于1911年提出，经九十多年应用，其适用范围已较清楚。飞行器研制周期短，试验次数少，经过系统辨识所得数学模型的正确性，通常采用以下几种工程办法进行验证：

（1）利用数学模型的预测功能进行验证。基于系统的本质属性不应随不同试验数据而改变的想法可推知：利用相同条件下的一部分试验数据辨识出的正确数学模型应能预测另一部分试验数据的特性；若采用辨识出的数学模型对另一部分数据进行预测的结果与试验数据相差很大，则该模型不是正确数学模型。

（2）利用不同试验方法所得结果相互比较进行验证。例如，气动力参数可以从飞行试验数据辨识出，也可以用理论计算和风洞实验获得，若几种研究手段所得结果较为一致，也就验证了模型正确性：若不同研究手段所得结果不一致，则必须深人分析，找出令人信服的原因，否则结果不可信。

（3）利用不同途径获得的结果互相验证。例如，由惯性仪表误差系数辨识结果可以预测落点精度，而实际飞行时也可测得落点偏差，两者的一致性也是误差系数数学模型正确性的验证。

（4）利用数学模型和实测数据的残差进行验证。正确数学模型与实测数据的残差应该是零均值噪声，否则说明模型与实测数据间仍有系统偏差。

1.4 系统辨识主要功用

系统辨识已在自然科学、技术科学、社会科学、经济活动和工程实践中的各个领域得到广泛的应用，概括起来，其主要功用有下述5个方面。

1）建模与仿真

系统仿真是系统研究的重要手段。在工程实践中，一个大工程系统的研制过程，从设计、试制、试验到定型的全过程中，系统仿真是贯彻始终的重要研究手段。系统仿真可用于优选设计参数、预测系统性能、复现系统事故、节省实物试验次数，从而大大节省系统研制经费，缩短研制周期，提高产品质量。在系统仿真中，有些部件采用实物，而有些组元无法用实物，需代之以数学模型，因此经过系统辨识建立正确数学模型就成了系统仿真的关键环节。例如，在战术导弹打靶仿真中，控制系统的执行元件、旋转台、目标源等都可以采用实物，但导弹所受外作用力，特别是空气动力是飞行状态参数的函数，无法用实物实现，应代之以数学模型。该数学模型是否正确就决定了系统仿真的置信度。因此，采用系统辨识方法辨识出导弹的外作用力的数学模型，特别是气动力数学模型，是飞行器系统仿真技术的关键环节之一。

2）性能预测

根据系统过去运行中的实测数据建立反映系统本质属性的数学模型，可以用来预测系统的未来行为。例如，利用民航旅客数年分月的统计数据建立的数学模型，已成功地用于预测旅客的淡旺季节。类似的方法，也已用于股市行情预测、飞行轨道预测、卫星寿命预测等。

3）故障诊断

系统在正常运行中的试验数据所辨识出的正确数学模型，可以不断预测系统状态参数或某重要观测量的变化，当系统运行中测得的系统某观测量与数学模型预测的观测值相差很大时，说明系统的本质属性发生了变化，系统已出现故障，故系统辨识可用于系统故障诊断。例如,大型吊桥的弹性结构系统的频率、结构物理参数和模态参数是确定的，通过随时测量结构系统特定点的位移、应变或过载，可实时辨识其结构物理参数和模态参数，当某个参数发生较大变化时，就说明吊桥结构系统出现故障，可用于预测结构某部位可能已破损或将出现断裂。为了能够预测系统较细微的变化，以确保安全，故障诊断的系统辨识准度要求较高。

4）自适应控制

自适应控制系统能根据系统的状态和环境参数变化，自动调节控制系统的相应系数，以达到最佳控制状态。系统实时辨识是自适应控制系统的重要组成部分，自适应控制在工业生产过程控制中已得到广泛应用，在飞行器研制中也有广泛应用前景。例如，战术导弹的机动性与导弹的静稳定裕度和动压关系很大，实时辨识导弹动力学系统与静稳定裕度和动压密切相关的参数，并据之实时改变控制系统的增益系数，可提高导弹的可控性和机动性。战略导弹主动段的控制精度取决于系统的制导工具误差，若能实时辩识导弹惯性仪表误差系数，并对导弹主动段关机参数进行自适应调节，可提高导弹的命中精度。

5）质量监控

大型工业生产过程由多个生产环节构成，若通过系统辨识建立产品质量指标与生产过程中各状态参数和外加元素输人量之间的数学模型，在生产过程实时监测系统的状态参数和外加元素的输人量，可以实时预测产品质量指标，并通过外加元素来实时控制，以确保产品优质。例如，金属冶炼过程，通过系统辨识建立金属质量指标与主要冶炼过程中熔液的温度、成分、外加元素输人量之间的数学模型，就可以进行质量监控，并通过温控、外加元素输人量来保证产品优质。

1.5 动力学系统辨识

动力学是研究物体在外力作用下运动规律的学科；动力学系统是研究物体在外力作用下的运动规律和力学特性的力学系统。刚体动力学、结构动力学和飞行动力学是比较成熟的动力学学科。动力学理论应用于各技术领域就形成各类动力学分支，如燃气轮机动力学、热流体动力学、液压管路动力学等，以分别研究各类动力学系统的动态特性。飞机、导弹、汽车、轮船和鱼雷在操纵力和外力作用下的航行品质和操纵性、稳定性研究；液体在管路中的流动、振动和在贮箱中的晃动研究；桥梁、建筑物等弹性体在外载荷下的振动研究；机械系统，如激振器、振动台的动态特性研究；人机系统中，人的振动特性和跟随特性研究；热交换器的传热过程以及燃气轮机、喷气发动机的动态研究等，都可当成动力学系统，研究其动态特性。

动力学系统辨识是动力学研究的逆问题，它利用系统在试验和运行中测得的输人-输出数据，采用系统辨识技术，建立反映系统的本质动态特性的数学模型，并辨识出数学模型中的待定系数。动力学系统遵循牛顿力学定律、质量守恒定律、能量守但定律等基本物理定律，所以系统的基本数学模型（动力学系统的状态方程组）是已知的，需要辨识的只是动力学方程组中的某些待定因素，诸如外作用、系统固有特性（固有频率、固有阻尼比、模态参数、结构参数）等，是典型的“灰箱”问题。动力学系统辨识通常分两步进行：首先根据系统特性和力学基本定律，采用推理方法，建立系统动力学方程组一一状态方程组，这是理论建模阶段；然后利用系统试验或系统运行中测得的输人-输出数据，辨识出动力学方程组中的待定因素，包括建立外作用的数学模型（外作用与系统状态参数的定量关系式），辨识出系统的模态参数和结构参数等，这是实验建模阶段。对大多数动力学系统，理论建模工作比较成熟，有现成完整的动力学方程组，系统辨识只是建立系统中外作用的数学模型和辨识系统中的待定参数。由于动力学系统的状态方程组多数是偏微分方程组、微分-积分方程组、非线性常微分方程组和超越代数方程组，在这么复杂的约束条件下进行系统辨识是极为困难的。

一个动力学系统在不同的研究领域有不同的含义和不同的数学模型。例如，飞行器作为一个动力学系统，当研究其飞行轨迹时，可将其作为质点处理，建立质点动力学方程组；当研究其操纵性、稳定性等飞行品质以及姿态对轨迹的影响时，需将飞行器作为一个刚体处理,建立刚体动力学模型,辨识飞行器的运动周期、阻尼和气动力数学模型；当研究飞行器结构振动、颤振、抖振、气动弹性耦合特性时，应将飞行器作为一个弹性体处理，建立弹性体动力学模型，辨识系统振动模态参数、结构参数、非定常气动力模型。

动力学系统按其不同的数学描述方法而划分为集中参数系统和分布参数系统两大类。两类系统因数学描述方法不同，其数学处理方法和所用数学工具也不同。当系统的状态参数仅是时间的函数时，描述系统特性的状态方程组为常微分方程组，系统称为集中参数系统；当系统的状态参数是时间和空间的函数时，描述系统特性的状态方程为偏微分方程组，系统称为分布参数系统。飞行器刚体运动的状态参数（飞行速度和飞行姿态等）都是时间的函数，状态方程组通常取为6自由度动力学方程组，是常微分方程组，属集中参数系统，故飞行器刚体运动的气动力参数辨识属集中参数系统辨识。描述飞行器热传导过程的状态参数（温度等）是时间和空间的函数,其状态方程——热传导方程是偏微分方程组，故飞行器气动热参数辨识属分布参数系统辩识。工程湍流模型的建模研究有着广阔的工程应用前景，流场状态参数满足的纳维-斯托克斯方程（NS方程）是偏微分方程组，故工程湍流模型辨识也是分布参数系统辨识。

动力学系统辨识是辨识理论在动力学系统中的应用，它建立数学模型的基础和出发点是力学定律。建模的基本方法是现代控制论中的滤波、预测和估计理论，而系统辨识是系统论的组成部分，所以动力学系统辨识是介于应用力学（如飞行动力学、流体力学、结构动力学等）现代控制论、系统论之间的交叉学科。

1.5.1 集中参数系统辨识

集中参数系统的数学模型是常微分方程组，设系统的状态参数矢量为 \pmb{x} ，观测矢量为 \pmb{y} ，则集中参数系统的状态方程组可写成下列通用形式

\left\{{\pmb x}\;=\;{\pmb f}(\,{\pmb x}\,,{\pmb u}\,,{\pmb\theta}\,;{\pmb t}\,)\right.

式中 $\pmb{x}(,t,)-$ 维状态矢量;

\pmb{u}\left(\pmb{t}\right)-\quad 维控制矢量；$\theta\mathrm{-}\mathrm{-},!!!!!!!!!!!!!!!!!!!!!!!!!!!!\theta}\longrightarrow!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!$ 维待估计参数矢量；f -—一非线性函数。

描述观测矢量 \pmb{y} 与状态矢量 \pmb{x} 关系式的观测方程组通常取为离散形式

{\bf y}\left(\,t_{i}\,\right)\;=\;{\pmb h}\left(\,{\pmb x}\left(\,t_{i}\,\right),{\pmb u}\left(\,t_{i}\,\right),{\pmb\theta}\,;\,t\,\right)\;+\;{\pmb\varepsilon}\left(\,t_{i}\,\right)

式中 \pmb{\varepsilon}(t_{i}) ———观测噪声；

h一一代数表达式。

集中参数系统辨识问题就是在状态方程组（1-1）和观测方程组（1-2)约束下,对于给定的控制矢量 \pmb{u}\left(\begin{array}{r}{t_{i}}\end{array}\right) 和观测矢量 {\pmb y}\left({\pmb t}_{i}\right) 的实测数据，寻求最优满足辨识准则的参数 \pmb{\theta}

1.5.2分布参数系统辨识

分布参数系统的数学模型是偏微分方程组，设系统的状态参数矢量是u，时间参数是t，位置矢量为x，待估计参数矢量为0，则分布参数系统的状态方程组可写成卜列通用形式

\left\{\begin{array}{l l l}{\displaystyle E\big(\,u\,,x\,,\pmb{\theta}\,;t\,\big)\,=\,0}&{x\in\,\Omega}&{t\in[0,T]}\\ {\displaystyle B\big(\,u\,,x\,,\pmb{\theta}\,;t\,\big)\,=\,0}&{x\in\,\partial\Omega}&{t\in[0,T]}\\ {\displaystyle I\big(\,u\,,x\,,\pmb{\theta}\,;0\big)\,=\,0}&{x\in\,\Omega}\end{array}\right.

式中 \pmb{E} —基本方程；

\pmb{B} 一一边界条件；I—初始条件；\Omega ——状态矢量的定义域；\partial\Omega -边界。

通常描述观测矢量 \pmb{y} 与状态矢量 \pmb{u} 关系式的观测方程组取为离散形式的代数方程式

\begin{array}{r}{\pmb{y}(\pmb{x}_{i j}\,,t_{i})\;=\;\pmb{h}\left(\pmb{u}\left(\pmb{x}_{i j}\,,\pmb{\theta}\,,t_{i}\right);t\right)\,+\,\pmb{\varepsilon}\left(t_{i}\right)}\end{array}

分布参数系统辨识问题就是在状态方程组（1-3）和观测方程组（1-4)约束下，对于给定的观测矢量 {\bf y}\left({x}_{i j},{t}_{i}\right) 的实测数据，应用系统辨识算法，求出最优满足辨识准则的待估计参数 \pmb\theta_{\circ}

1.6飞行器系统辩识

飞行器是个极其复杂的系统，飞行器研制是包括设计、试制、试验、定型、生产的庞大系统，飞行器设计包括外形设计、结构设计、控制系统设计、制导系统设计、动力系统设计、供电系统设计等。设计应确定飞行器有足够的刚度、强度、热防护性能、飞行稳定性、飞行品质和作战性能，并应考虑经济性和可维护性。在飞行器的方案设计阶段、初步设计阶段和型号设计阶段，都必须建立各分系统具有不同近似程度、反应系统不同侧面的数学模型,进行系统分析和系统仿真，以确保各系统的性能达到战术技术指标，满足设计技术要求。为确保建立正确的系统数学模型，在不同设计、试制、试验阶段，要进行多次分系统和全系统的试验，包括在地面缩比尺度的模型试验，地面全尺寸的模拟试验、空中缩比模型试验和全尺寸飞行器的飞行试验。利用这些试验的实测数据,通过系统辩识建立飞行器各分系统的数学模型，是飞行器研制过程中的有力工具。

系统辨识在飞行器设计中的应用始于气动力参数辨识，至今已有八十多年的历史，应用广泛，也最为成功。目前，世界各强国的各大飞机和导弹研制部门都有自己的气动参数辨识软件包。气动热参数辨识研究也有三十多年了，美国、俄罗斯已在高超声速冉人体飞行试验中应用。本书在阐述系统辨识基本理论与方法之后，将着重论述辨识理论在气动力参数、气动热参数和工程瑞流模型辨识中的应用。对于武器试验基地关心的惯性仪表误差系数辨识也专辟一章论述。

1.6.1 气动力参数辨识

在飞行器系统仿真中，气动力数学模型是仿真软件的关键，模型正确与否决定着仿真系统的置信度。大气层内飞行器的飞行轨迹、飞行稳定性、机动性和可控性都取决于飞行器所承受的气动力。

气动力数学模型是建立作用于飞行器的空气动力(升力、阻力、侧向力；俯仰、偏航、滚转气动力矩)与飞行器运动状态参数(速度、角速率、攻角、侧滑角、飞行高度等)和控制输人(升降舵、副翼、方向舵;各控制舵面的偏转角等)之间的解析关系式。数学模型的参变量采用满足相似律的无量纲参数表示。

气动力参数辨识通常假定飞行器是刚体动力学系统，其状态方程组满足牛顿第二定律，因此试验时观测量是反映质心运动和绕质心转动的物理量。对于风洞或弹道靶中的缩比模型自由飞试验，观测量是模型质心的位置和模型相对于地球坐标系的姿态角；对于飞行试验,观测量则常常是过载和角速率,也可测量质心位置和姿态角，有时还测量攻角、侧滑角等。

气动力参数辨识是飞行器系统辨识中发展最为成熟的一个领域，已成功地应用于飞机、战术导弹、战略导弹,并拓展应用到其他运动体,例如鱼雷的水动力参数辨识。目前,国内外各主要飞行器设计部都开发有自己的气动参数辨识软件包，其中应用最广泛的有最大似然法、增广的广义卡尔曼滤波法、分割辨识算法和建模前估计法等。已发展了适用于不同的观测噪声和过程噪声特性的辨识算法，正在发展非线性系统、带有滞迟效应的非定常气动力数学模型。

1.6.2 气动热参数辨识

超高声速飞行器再人大气层时，表面形成高达几千摄氏度的等离子气体层，热防护设计成了再人体设计中的关键课题。特别是再人飞船的最大热流量发生在非平衡气流区域，非平衡热流的计算和直接测量在理论上和地面模拟都很不成熟。因此,从飞行试验数据辨识气动热参数更显出其重要性。

气动热辨识是在已知导热系数的条件下通过测量飞行器内部温度的时间历程数据，辨识飞行器表面气动加热的热流参数或热流历程；也可以通过测量表面热流和内部温度历程，辨识飞行器材料的导热系数。在某些条件下，也可以通过测量温度分布和温度历程，辨识热流和导热系数，它可以是参数估计，也可以是函数估计问题。热传导问题是个分布参数系统问题，热传导方程是含有时间和空间自变量的偏微分方程组；气动热流辨识是个在偏微分方程组约束下的泛函极值问题，而且是数学病态问题。除了极简单的一元线性热传导问题的特定情况有解析解外，通常要求采用有限差分法、有限元法或有限体积法求解偏微分方程并进行选代求解极值，其计算比气动力参数辨识繁杂得多。

飞行器气动热辨识的试验主要在地面上的电弧加热器上进行缩比模型试验，通常测量热流或温度。飞行试验时，由于飞行器外壁处于高温状态无法测量热流，仅测量飞行器内各层的温度历程。再人体防热材料的导热系数很小，内壁温升很小，为获得较多热信息，需要在飞行器壁上嵌装特殊设计的温度传感器。飞船返回舱或航天飞机,再人的飞行时间较长，只需在舱外壁的隔热层之外安装温度传感器就可获取足以辨识气动热参数的信息。

当系统的物性参数与温度无关时，系统是线性系统，已发展较为成熟的热流辨识算法，不仅可作参数估计，而且可进行函数估计，特定条件下还有解析解。当系统物性参数与温度有关时，热流辨识成了非线性系统辨识问题，虽已发展了特定函数法和正则化法等算法，但还有待改进。

1.6.3 工程瑞流模型辨识

飞行器在稠密大气中的空气绕流多是处于湍流流态。湍流不仅是流体力学界关注的百年理论难题，也是飞行器设计过程中必须解决的空气动力学中的工程实践问题。目前湍流数值模拟有直接模拟、大涡模拟和雷诺平均方程法三类方法。由于目前计算机内存和运算速度所限，前两类方法至今仍处于理论研究阶段,工程上解决湍流流动的常用方法仍是雷诺平均方程法。

雷诺平均方程法假定流动速度由时均速度和脉动速度合成，对流动速度应满足的NS方程作时间平均，得到时均速度应满足的NS方程，并引进了一个新未知量一雷诺应力。建立雷诺应力与时均速度的数学关系式就是工程湍流模型。随着人们对湍流认识的不断深人，工程湍流模型也不断得到改进和完善，已解决了不少工程实践中提出的实际课题。

工程湍流模型辨识是将某一湍流流场作为一系统，以含有工程湍流模型的NS方程作为系统的状态方程,以流场的速度场测量值、湍动能、压力场的测量值作为观测量，建立观测方程。通过湍流机理研究分析，建立工程湍流模型结构形式，形成模型候选集，最后采用分布参数系统辨识的方法来确定湍流模型结构中的未知部分，以达到改进工程湍流模型的目的。

1.6.4 惯性仪表误差系数辨识

洲际导弹的落点精度主要取决于导弹主动段火箭停火点状态参数的误差。引起导弹停火点参数误差的主要因素是惯性制导系统惯性仪表的测量误差。建立惯性仪表误差系数的正确数学模型，可以实时校正关机点参数，提高导弹命中精度，故惯性仪表误差系数辨识是系统辨识在飞行器研制中的一个重要应用。

惯性仪表误差系数数学模型是建立误差系数和飞行状态参数及其导数的关系式。其辨识建模的基本思想是利用弹上遥测系统和外测（雷测、光测)系统两种测量手段同时测量的飞行状态参数之差进行误差系数辨识。遥测系统采用惯性仪表进行测量，其测量值含有惯性仪表与飞行状态参数有关的系统误差和测量随机误差，故遥测值与外测值之差可作为辨识惯性仪表误差系数的信息源，目前还没找到误差系数与状态参数之间的物理定律，无法建立状态方程，误差系数辨识是作为“黑箱”问题处理，其候选数学模型取为多项式模型集，通过 F 检验、正交最小二乘法或主成分分析法等方法确定数学模型结构形式，再进行参数估计。由于各误差系数之间的相关性较强，为提高辨识准度可采用特别设计的飞行弹道。此问题并没有很好解决，可望通过建立惯性仪表的数学模型而开发出更有效的方法。

第2章 飞行器动力学系统模型

飞行器系统辨识是利用飞行试验或风洞实验实测的飞行器的过载、角速率、姿态、速度、位置等数据，采用辨识方法，建立描述飞行器基本特性的数学模型的应用性学科。飞行器动力学系统辨识是将飞行器作为动力学系统，着力于建立描述系统动态特性的数学模型。飞行器动力学系统遵循牛顿第二定律、质量守恒和能量守恒定律等，根据这些定律，可以建立动力学系统基本方程，作为系统辨识的状态方程组。对于气动力参数辨识，取飞行器刚体6自由度动力学方程组作为系统状态方程；对于气动热参数辨识，取热传导方程作为系统状态方程；对于工程湍流模型辨识，取NS方程作为系统状态方程。

在本书系统论述辨识理论之前，本章简要介绍飞行器动力学系统的基本方程和外作用力的数学模型，给出用于系统辨识的状态方程的具体表达式。

2.1 飞行器动力学系统数学模型

飞行器动力学系统遵循牛顿第二定律，该系统由质点系（有限质点系或无限质点系）组成，质点系满足牛顿第二定律

\sum_{i}.m_{i}\;\frac{\mathrm{d}\,{\cal V}_{i}}{\mathrm{d}t}\;=\;\sum_{i}{\cal F}_{i}

式中 m;——质点i的质量;

\pmb{V}_{i} ——质点 \lat_{i} 的飞行速度矢量；
\pmb{F}_{i} —质点 _i 所受的外力。

式(2-1)是飞行器动力学系统建模的基本出发点。

研究飞行器的飞行品质、飞行性能和运动稳定性时，通常将飞行器当作刚体处理。经典力学已证明，任何刚体运动皆可分解为刚体质心的位移运动和绕质心的旋转运动，用下列6自由度动力学方程描述

\frac{\mathrm{d}m V}{\mathrm{d}t}\,=\,F

\frac{\mathrm{d}I\pmb{\omega}}{\mathrm{d}t}\,=\,\pmb{M}

式中 m—-飞行器总质量；

V—飞行器质心运动速度；—飞行器惯量矩阵；
\pmb{\omega} -飞行器绕质心的角速度；
\pmb{F} —一作用于飞行器的总外力；
\pmb{M} 一作用于飞行器质心的总外力矩。

对不同工程问题，将式（2-2)和式(2-3)投影到不同的坐标系，导出具体表达式。对于飞行试验，由于遥测传感器固连于飞行体框架上，坐标系采用体轴系较为方便；对于风洞和弹道靶的自由飞或单自由度振荡实验，实测数据是模型的姿态角和位置，则坐标系采用地面固连坐标系较为方便。

2.1.1 常用坐标系

飞行力学常用坐标系在航空界有8种，在航天界有几十种，多数是右手定则笛卡儿坐标系；在国标GB/T14410.1一93和航大部标Q11028-86有严格定义。这里仅介绍飞行器系统辨识中最常用的两种坐标系。

1）地面固连坐标轴系

地面固连坐标轴系（符号 O x_{0}y_{0}z_{0} ，简称 S_{0} ),其原点皆与地面固连。当坐标原点为取飞行器质心，而 \pmb{z} 轴铅垂向卜， _x 轴指向固定的参考飞行方向或特定方向的坐标系,称为飞行器牵连铅垂地面坐标轴系（符号 O x_{g}y_{g}z_{g} 简称 S_{g} )。

2）弹(机)体坐标系

弹体坐标系(符号 {\cal O}x y z ,简称 S_{b} )的原点位于飞行器的质心。对于轴对称体, _{x} 轴(纵轴)取为对称轴,对于面对称体, \pmb{x} 轴处于对称面(飞机参考面)并平行于飞行器机身轴线； _x 轴指向飞行器头部。 _y 轴(横轴)垂直于飞行器参考面,并指向飞行器右方。 \boldsymbol{z} 轴(竖轴)指向下方，与 x\setminus y 轴构成右手坐标系。

弹体坐标系与铅垂地面坐标系的相对方位见图 2-1。其相对关联角度由偏航角 (\,\phi\,) 和俯仰角 (\,\theta\,) 表示。滚转角 \left(\,\phi\,\right) 定义为竖轴与过纵轴的铅垂平面的夹角。

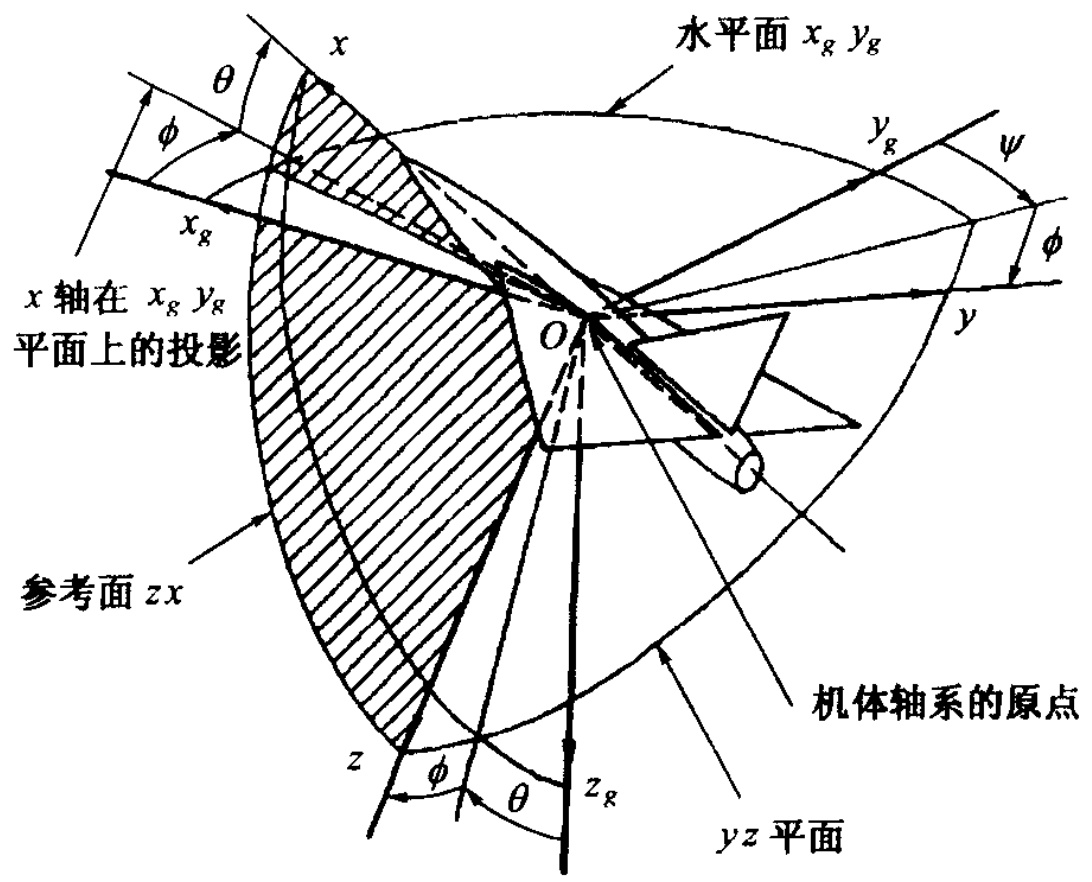
图 2-1弹体坐标系与铅垂地面坐标系的相对方位\mathbf{\xi}O x y z 为机体轴系； O x_{\infty}y_{\pmb{\mathscr{s}}}z_{\pmb{\mathscr{s}}} 为飞机牵连铅垂地面轴系。

飞行器速度 \mathbf{v} 在 O x_{g}y_{g}z_{g} 中的投影为 u_{g}\setminus v_{g}\setminus w_{g} ;在 {\cal O}x y z 中的投影为 {\pmb u}_{\mathrm{~\tiny~`~}}{\pmb v}_{\mathrm{~\tiny~`~}}{\pmb w}_{\mathrm{~\tiny~`~}} 。飞行器角速度 \pmb{\omega} 在 O x_{g}y_{g}z_{g} 中的投影为 \pmb{\mathscr{P}}_{\pmb{\mathscr{g}}} 、q_{g}\setminus r_{g} ,在 O x y z 中的投影为 \phi\,.\,q\,.\,r\,_{\circ}

2.1.2 飞行器刚体动力学方程

飞行器系统辩识常采用弹体坐标系，通常飞行器有一个对称

面,称为面对称飞行器。下面给出面对称飞行器的完整6自由度动力学方程组，也适用于轴对称飞行器。

质心动力学方程组

\begin{array}{r}{\left\{\dot{u}\;=-\;q w\,+\,r v\,+\,g\big(\,n_{x}\,-\,\mathrm{sin}\theta\big)\right.}\\ {\dot{v}\;=-\;r u\;+\;\rho w\,+\,g\big(\,n_{y}\,+\,\mathrm{cos}\theta\mathrm{sin}\phi\big)}\\ {\dot{w}\;=-\;\rho v\;+\;q u\;+\;g\big(\,n_{z}\,+\,\mathrm{cos}\theta\mathrm{cos}\phi\big)}\end{array}

绕质心转动的动力学方程组

\begin{array}{r}{\left\{\begin{array}{l l}{\nu\beta\alpha\nu\alpha\mathrm{e}^{-\mathrm{i}\phi}\mathrm{s}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! 

式中 n_{x}\setminus n_{y}\setminus n_{z} —过载分量，由气动力和推力构成；

C_{l},C_{m},C_{n} 气动力矩分量；动压 \frac{1}{2}\rho V^{2} s ——参考面积；l 参考长度；\rho ——大气密度；I_{x}\,,\,I_{y}\,,\,I_{z} 惯量矩；I_{x z} -惯量积。

姿态角方程组

\left\{\begin{array}{l}{\displaystyle\frac{\mathrm{d}\theta}{\mathrm{d}t}\,=\,q\cos\phi\,-\,r\sin\phi}\\ {\displaystyle}\\ {\displaystyle\frac{\mathrm{d}\phi}{\mathrm{d}t}\,=\,\,\phi\,+\,\tan\theta\,(\,q\sin\phi\,+\,r\cos\phi\,)}\\ {\displaystyle\frac{\mathrm{d}\phi}{\mathrm{d}t}\,=\,\,(q\sin\phi\,+\,r\cos\phi\,)/\cos\theta}\end{array}\right.

位移运动方程组

\left\{\begin{array}{l}{\displaystyle\frac{\mathrm{d}x_{s}^{\prime}}{\mathrm{d}t}=u\cos\theta\cos\phi+\upsilon\left(\sin\theta\cos\phi\sin\phi-\sin\phi\cos\phi\right)+\mathrm{\Lambda}}\\ {\displaystyle\qquad\qquad w\left(\sin\theta\cos\phi\cos\phi+\sin\phi\sin\phi\right)}\\ {\displaystyle\frac{\mathrm{d}y_{s}^{\prime}}{\mathrm{d}t}=u\cos\theta\sin\phi+\upsilon\left(\sin\theta\sin\phi\sin\phi+\cos\phi\cos\phi\right)+\mathrm{\Lambda}}\\ {\displaystyle\qquad w\left(\sin\theta\sin\phi\cos\phi-\cos\phi\sin\phi\right)}\\ {\displaystyle\frac{\mathrm{d}z_{s}^{\prime}}{\mathrm{d}t}=-\ u\sin\theta+\upsilon\cos\theta\sin\phi+\{\upsilon\cos\theta\cos\phi\}}\end{array}\right.,

式中 x_{g}^{\prime}\,\sqrt{y_{g}^{\prime}}\,\sqrt{z_{g}^{\prime}} —飞行器质心位置在铅垂地面坐标轴系的坐

以上列出了飞行器系统辨识中常用的动力学方程组。在状态方程中，重力是高度和经纬度的函数,推力是高度与大气环境的函数,气动力是多个飞行状态参数的非线性函数。飞行器动力学系统辨识就是要通过飞行试验和地面实验的实测数据，采用系统辨识的方法来建立重力、推力和气动力的数学模型。对于飞行武器，假定重力是高度和经纬度的已知函数就已有足够精准度了，在多数情况下，假定重力是常数对于确定飞行位置和姿态所带来的误差小于千分之一，故在飞行力学研究中，常取之为已知函数。重力模型的研究由地球物理学家进行。火箭发动机的推力主要取决于燃料、温度及燃烧压力，与飞行状态参数关系很小，飞行中的推力可取为地面实验测得的推力加上高空修正，也可通过实测燃烧室压力加以校正。航空发动机构造比较复杂,通过系统辨识建立数学模型，至今在国际上仍处于探索阶段，推力性能主要仍依赖于地面实验。因此,空气动力建模是飞行器系统辨识的主要研究对象。

2.1.3 热传导方程

飞行器气动热参数辨识是根据飞行试验中测得的飞行器上特定点的温度时间历程数据，估计飞行器的热传导系数和外气流对它的热流率，而不是测量气体绕流流场中的温度时间历程数据来辨识气体的热传导系数和热流率。因此，飞行器气动热参数辨识的状态方程不是描述气体流场热传导特性的能量守恒方程，而是取飞行器固壁的热传导方程作为辨识的状态方程，其通式、边界条件和初始条件为

\left\{\begin{array}{l l}{\rho\,c_{p}\left(\displaystyle\frac{\partial T}{\partial t}\right)=\mathrm{div}(\boldsymbol{k}\,\,\nabla\,\,T)}&{(\boldsymbol{x}\,,\boldsymbol{y}\,,z)\in\Omega\,,t\in[\,t_{0}\,,t_{f}]}\\ {-\,\boldsymbol{k}\,\,\nabla\,\,\,T(\boldsymbol{x}\,,\boldsymbol{y}\,,z\,;t)=q(\boldsymbol{x}\,,\boldsymbol{y}\,,z\,;t)}&{(\boldsymbol{x}\,,\boldsymbol{y}\,,z)\in\partial\Omega,t\in[\,t_{0}\,,t_{f}]}\\ {T(\boldsymbol{x}\,,\boldsymbol{y}\,,z\,;t_{0})=t(\boldsymbol{x}\,,\boldsymbol{y}\,,z)}&{(\boldsymbol{x}\,,\boldsymbol{y}\,,z)\in\Omega}\end{array}\right.

式中 q ——热流密度；

p一一固壁材料密度；cp—比定压热容;$k$ -导热系数；T 温度；div——散度；\mathbf{v} —梯度；\Omega 一一一流场区域；\partial\Omega ——区域边界。

飞行器多为薄壳结构，许多问题可简化为一维问题，其状态方

程组简化为

\left\{\begin{array}{l l}{\displaystyle\rho c_{p}(\boldsymbol{x})\frac{\partial T}{\partial t}\!=\!\frac{\partial}{\partial\boldsymbol{x}}\!\left(k(\,T)\frac{\partial T}{\partial\boldsymbol{x}}\right)}&{(0\!\!\le\!x\!\le\!L\,,t_{0}\!\!\leqslant\!t\!\leqslant\!t_{f})}\\ {\displaystyle-\,k(\,T)\frac{\partial T}{\partial\boldsymbol{x}}\!=\!q(\,t\,)}&{(\boldsymbol{x}=\boldsymbol{0},t_{0}\!\leqslant\!t\!\leqslant t_{f})}\\ {\displaystyle-\,k(\,T)\frac{\partial T}{\partial\boldsymbol{x}}\!=\!q_{\mathrm{Loss}}(\,t\,)}&{(\boldsymbol{x}=L\,,t_{0}\!\leqslant\!t\!\leqslant t_{f})}\\ {\displaystyle T(\,x\,,t_{0})=T(\,t_{0})}&{(0\!\leqslant x\!\leqslant L)}\end{array}\right.

2.1.4 流体动力学方程

工程湍流模型辨识是利用湍流流动中测得的速度场、湍动能场、压力场、摩擦力系数等实验数据，采用辨识方法来建立工程湍流模型的结构形式并估算出其中的未知待定系数。湍流流动满足由质量守恒定律、动量守恒定律、能量守恒定律导出的粘性流体动力学方程。故工程湍流模型辨识的状态方程取为NS方程,其笛卡儿坐标系的表达式通常写为

\frac{\partial\,\mathbf{V}}{\partial t}\,+\,\frac{\partial\mathbf{E}_{i}}{\partial x}\,+\,\frac{\partial\mathbf{F}_{i}}{\partial y}\,+\,\frac{\partial\mathbf{G}_{i}}{\partial z}\,=\,\frac{\partial\mathbf{E}_{v}}{\partial x}\,+\,\frac{\partial\mathbf{F}_{v}}{\partial y}\,+\,\frac{\partial\mathbf{G}_{v}}{\partial z}

<html>

	pu 20 E,	E, =	pu 2 ou 力 and mnd (E, + p)u [0		F;	2d ano 2. 20 + mad (E, + p)v
	m0 imnd mao + D L(E, + p)u.	E心	TII xy	F	0 xy y	0 xz G Tyz 二 Tzz

</html>

{\begin{array}{r l}{\tau_{x x}\,=\,{\frac{\mu}{3}}\left[4\,{\frac{\partial u}{\partial x}}\,-2\left({\frac{\partial v}{\partial y}}+{\frac{\partial w}{\partial z}}\right)\right]}&{\tau_{y y}\,=\,{\frac{\mu}{3}}\left[4\,{\frac{\partial v}{\partial y}}\,-2\left({\frac{\partial w}{\partial z}}\,+{\frac{\partial u}{\partial x}}\right)\right]}\\ &{\tau_{x y}\,=\,\mu\left[{\frac{\partial u}{\partial y}}\,+{\frac{\partial v}{\partial x}}\right]}&{\tau_{y z}\,=\,\mu\left[{\frac{\partial v}{\partial z}}\,+{\frac{\partial w}{\partial y}}\right]}\\ {\tau_{x z}\,=\,\mu\left[{\frac{\partial u}{\partial z}}\,+{\frac{\partial w}{\partial x}}\right]}&{\tau_{z z}\,=\,{\frac{\mu}{3}}\left[4\,{\frac{\partial w}{\partial z}}\,-2\left({\frac{\partial u}{\partial x}}\,+{\frac{\partial v}{\partial y}}\right)\right]}\end{array}}

{\begin{array}{r l}&{\sigma_{x}\,=\,u\tau_{x x}\,+\,v\tau_{x y}\,+\,w\tau_{x z}\,+\,k\,{\frac{\partial\,T}{\partial\,x}}}\\ &{}\\ &{\sigma_{y}\,=\,u\tau_{x y}\,+\,v\tau_{y y}\,+\,w\tau_{y z}\,+\,k\,{\frac{\partial\,T}{\partial\,y}}}\\ &{}\\ &{\sigma_{z}\,=\,u\tau_{x z}\,+\,v\tau_{y z}\,+\,w\tau_{z z}\,+\,k\,{\frac{\partial\,T}{\partial\,z}}}\end{array}}

E_{t}\,=\,\rho\left(\,e\,+\,\frac{u^{2}\,+\,v^{2}\,+\,w^{2}}{2}\right)

式中 下标“”——无粘流参数；

下标“ \pmb{\tau} ”—粘性流参数；

\pmb{\hat{p}} -一压力；
\rho —一密度；
T —温度；
e 一一内能；
\tau_{i j} 一粘性应力张量；
k 一一热传导系数；
\pmb{\mu} 一一粘性系数。

对于湍流流动,式(2-10)中的状态参数均含有随机脉动量,难于直接求解。工程应用上都对它进行雷诺平均，导出带有雷诺应力的均值方程组。不同雷诺应力表达方式就形成不同的工程湍流模型。目前工程上应用最为广泛的是 k^{-}\varepsilon 两方程涡粘性模型，对不少工程问题给出较为满意的结果；但对于大分离流区、激波边界层干扰区以及方截面管流中的二次流等各向异性较强的区域的模拟比较差。本书在讨论了工程湍流辨识的一般算法之后，将着重对 k\!-\!\varepsilon 两方程湍流模型进行辨识研究，并讨论各种因素对辨识结

果的影响。

2.2 空气动力学数学模型

飞行器动力学系统的外作用力辨识中，最重要的是空气动力数学模型的辨识。空气动力是飞行器外形和飞行状态参数的函数。严格地说，空气动力与状态参数和飞行器外形的关系服从偏微分方程组、偏微分-积分方程组。对某些情况，例如湍流情况、分离流状态，甚至迄今还没有建立完备的方程组。建立空气动力与状态参数的简化数学模型是飞行器设计计算、仿真系统研制和飞行特性分析所必不可少的。常用的气动力数学模型有代数模型、积分模型和微分方程模型三类。近来，又发展了利用神经网络和小波理论的建模方法。

2.2.1 代数模型

早期，简化的气动力数学模型是代数模型，早在1911年布莱恩(G.H.Bryan)就给出了飞机的气动力线性数学模型(3。近来为适应飞机失速/过失速/尾旋特性的研究，克莱恩（V.Klein）采用多项式模型和样条函数模型开展大攻角气动力数学模型研究，给出了非线性代数模型的实用算法[4]

1）线性气动力模型

飞行器气动力线性数学模型假定气动力参数是飞行状态参数和控制输人的线性函数。设气动力参数 \pmb{\theta}=(\,C_{A}\,,\,C_{Y}\,,\,C_{N}\,,\,C_{l} ?Cm,C,)T,C; 为气动力和力矩在体轴系的投影。飞行状态参数x=（1,x2,,x,）T,飞行控制输人u=（a，，0,）T,则气动力数学模型的一般形式为

C_{i}\ =\ \sum_{j\ =1}^{n}C_{i x_{j}}x_{j}\ +\ \sum_{k}C_{i\delta_{k}}\delta_{k}

式中 c_{i x_{j}}- 气动力系数 C_{i} 对状态参数 x_{j} 的气动导数；

Ci, 气动力系数 C_{i} 对 \delta_{k} 的舵面效率。

在建模过程中，应根据各气动力系数的物理意义加以简化。例如，俯仰力矩系数通常与偏航角速度、方向舵等参数无关，只需表示为

C_{m}\;=C_{m0}(\,\alpha_{0}\,,\,\delta_{e0}\,)\;+\;C_{m a}(\,\alpha\;-\;\alpha_{0}\,)\;+

C_{m\hat{\delta}_{\epsilon}}(\,\delta_{e}\,-\,\delta_{e0}\,)\,+\,C_{m q}\,\frac{q l}{2\,V}

而 C_{m\delta_{r}}.C_{m r} 等皆恒为零。式(2-12)是早期常用的气动力数学模型。之后经多年飞行试验和风洞实验结果表明，飞机尾翼产生的气动力和气动力矩不仅依赖于瞬时攻角，而且与攻角变化率有关，气动力数学模型应计人攻角迟滞效应才能更好描述气动特性。小攻角时的迟滞效应可近似为与 \dot{\pmb{\alpha}} 成正比，故俯仰力矩系数的线性气动模型为

C_{m}\;=C_{m0}(\,\alpha_{0}\,,\delta_{e0}\,)\;+\;C_{m a}(\,\alpha\;-\;\alpha_{0}\,)\;+

C_{m\delta_{e}}\,(\,\delta_{e}\,-\,\delta_{e0}\,)\,+\,C_{m q}\,\frac{q l}{2\,V}\,+\,\dot{C}_{m\dot{a}}\,\frac{\dot{\alpha}l}{2\,V}

其他气动力和气动力矩系数有类似表达式。

2）多项式模型

大攻角飞行状态下的气动力已不是攻角等状态参数的线性模型，必须计及非线性效应。多项式模型是线性模型的直接推广。设飞行器的状态参数和控制输人参数都以 {\pmb x}=(\,x_{1}\,,x_{2}\,,\cdots,x_{n}\,)^{\textup T} 表示，则多项式模型的一般表达式为

C_{m}\left(\,t\,\right)\;=\;\sum_{i_{1}=0}^{N_{1}}\cdots\sum_{i_{p}=0}^{N_{p}}C_{m\,\Pi x_{k}^{i_{k}}}\prod_{k\,=\,1}^{p}\,x_{k}^{i_{k}}(\,t\,)

式中 x_{k}^{i_{k}}- 飞行状态参数和控制输人参数 x_{k} 的 i_{k} 次幂；

通常式(2-14)中的每一项由 1\!\sim\!3 个状态参数或控制输人参数乘积组成,而幂次方通常取 0\!\sim\!3 ，个别项的幂次可根据验前信息（理论计算或地面试验信息）进行选取，取比较高的幂次。

美国研究后掠翼战斗机F-4E在失速/尾旋飞行区域的气动力数学模型时，采用多项式模型获取大攻角的稳定和控制导数。

F-4E战斗机飞行在 12\mathbf{km} ,采用升降舵使攻角从 15^{\circ} 升到 40^{\circ} 在 25^{\circ} 时出现失速，不稳定的侧向运动产生滚转偏离。假定飞行中推力是常数，试验中测量了线加速度、角度和角速率数据，采用回归法求出的气动力系数模型为[5]

\begin{array}{r l}&{\left\{C_{A}=C_{A0}+C_{A^{\prime}}a^{2}+C_{A^{\prime}}a^{4}+C_{A\mu}\beta+C_{A\,a}\frac{q I}{2V}\right.}\\ &{\left.\left|C_{Y}=C_{Y0}+C_{Y\mu}\beta+C_{Y\mu^{3}}\beta^{3}+C_{Y\mu\mu}\beta+C_{Y\lambda}\frac{\beta-I}{\beta^{\prime}}+C_{Y\mu}\frac{r I}{2V}\right.}\\ &{\left.\left\{C_{N}=C_{N0}+C_{N a}a+C_{N a}a^{2}+C_{N\beta^{2}}\beta^{2}+C_{N\mu}\frac{q I}{2V}+C_{N\beta_{a}^{2}}\beta+C_{N\mu_{a}^{2}}\alpha\hat{S}_{a}\right.\right.}\\ &{\left.\left.C_{i}=C_{i0}+C_{i\mu}\beta+C_{i\mu^{2}}a^{2}\beta+C_{i\nu}\frac{r I}{2V}\right.\right.}\\ &{\left.\left.C_{m}=C_{m0}+C_{m0}a+C_{m0}a^{2}+C_{m^{3}}a^{3}+C_{m\mu}\beta+C_{m\mu}\frac{q I}{2V}+C_{m\lambda}\hat{\sigma}_{e}\right.\right.}\\ &{\left.\left.C_{n}=C_{n0}+C_{n0}a+C_{m\mu}\beta\right.\right.}\\ &{\left.\left.C_{n}=C_{n0}+C_{n0}a+C_{m\mu}a\beta\right.\right.}\\ &{\left.\left.C_{n}=C_{n0}+C_{n0}a+C_{m\mu}\beta\right.\right.}\end{array}

3）样条函数模型

样条函数也是简单、方便的代数型非线性模型构式，其优点是可以用低阶项很好地逼近各种非线性,而且在给定区域不出现零点。样条函数有单变量和双变量之分,其一般表达式为：

单变量 _{m} 阶样条函数

S_{m}\left(\alpha\right)\;=\;\sum_{\stackrel{i\,=\,0}{i\,=\,0}}^{m}C_{i}a^{i}\;+\;\sum_{\stackrel{i\,=\,1}{i\,=\,1}}^{k}D_{i}\left(\,\alpha\;-\;\alpha_{i}\,\right)_{+}^{m}

双变量 m+n 阶样条函数

\begin{array}{l}{{\displaystyle S_{m n}\big(\,\alpha\,,\beta\big)\,=\,\sum_{i\,=\,0}^{m}\,\sum_{j\,=\,0}^{n}C_{i j}\alpha^{i}\beta^{j}\,+\,\sum_{i\,=\,1}^{k}P_{i}\big(\,\beta\big)\big(\,\alpha\,-\,\alpha_{i}\,\big)_{+}^{m}\,+}}\\ {{\displaystyle\sum_{j\,=\,1}^{l}Q_{j}\big(\,\alpha\,\big)\big(\,\beta\,-\,\beta_{j}\,\big)_{+}^{n}+\,\sum_{i\,=\,1}^{k}\,\sum_{j\,=\,1}^{l}D_{i j}\big(\,\alpha\,-\,\alpha_{i}\,\big)_{+}^{m}\,\,(\,\beta\,-\,\beta_{j}\,)_{+}^{n}}}\end{array}

式中

\bigl(\,\alpha\,-\,\alpha_{i}\,\bigr)_{\,+}^{\,m}\,=\,\left\{\begin{array}{l l}{{\bigl(\,\alpha\,-\,\alpha_{i}\,\bigr)^{\,m}}}&{{\alpha\,\geqslant\,\alpha_{i}}}\\ {{{\,0}}}&{{\,\alpha\,<\,\alpha_{i}}}\end{array}\right.

(\,\beta\,-\,\beta_{j}\,)_{\,+}^{\,n}=\,\left\{\!\!\begin{array}{l l}{{(\,\beta\,-\,\beta_{j}\,)^{\,n}}}&{{\beta\geqslant\beta_{j}}}\\ {{0}}&{{\beta<\,\beta_{j}}}\end{array}\right.

\alpha_{i}\ldots\beta_{j} 是已知节点： ;P_{i}(\beta),Q_{j}(\alpha) 分别为 \pmb{n} 阶和 _{m} 阶多项式； C_{i} 、D_{i}\,.C_{i j} 和 D_{i j} 是常数。通常 ^{m} 和 \pmb{n} 取为 0\!\sim\!2 ,否则可能因待辨识参数过多而无法进行参数估计。

根据建模的“最节省原则”，阶数要尽量取小。通常 _{m} 取为0、1 或 2。0阶样条相当于用阶梯函数逼近非线性函数；1阶样条相当于逐段用折线逼近非线性函数。双变量样条函数的 ^{m} 和 \pmb{n} 通常只取0或1。否则辨识方程将很复杂。阶次 \mathbf{\nabla}m 和 \pmb{n} 也可以通过拟合气动力理论计算和风洞实验结果来确定。

样条函数模型与多项式模型一样，模型阶次的选取是人为的，选择不合适会导致较大误差，而且模型中各项的物理意义不是那么明确。

美国采用多项式样条函数研究轻型飞机在失速/过失速区的气动力数学模型[6]

轻型飞机在 2\mathtt{k m} 作低空飞行，关掉发动机使飞机处于配平状 态。给一扰动后任其阻尼掉，当回到配平状态后再给一扰动，每次 试验约 3\mathbf{min} 可作7次扰动，飞机落到 1\mathtt{k m} 后再爬升到 2\mathtt{k m} ，继续 做试验。

样条函数节点取为 \alpha=10^{\circ}\!\sim18^{\circ} ,每隔 0.5^{\circ} 放一个节点，样条函数模型取为

C_{A}\,=C_{A0}\,+\,C_{A a}a\,+\,\sum_{i=1}^{k}C_{A a i}\bigl(\,\alpha\,-\,\alpha_{i}\,\bigr)_{+}+\,\sum_{i\,=1}^{k}C_{A q i}\bigl(\,\alpha\,-\,\alpha_{i}\,\bigr)_{+}^{0}\,\,\frac{q l}{2V}\,+

C_{A q}\,\frac{q l}{2\,V}\,+\,C_{A\delta_{\epsilon}}\delta_{e}\,+\,C_{A\delta_{\epsilon}7}\delta_{e}\,(\,\alpha\,-\,\alpha_{7})_{\,+}^{0}\,+\,C_{A\delta_{\epsilon}13}\delta_{e}\,(\,\alpha\,-\,\alpha_{13})_{\,+}^{0}

C_{N}\,=C_{N0}\,+\,C_{N\alpha}\alpha\,+\,\sum_{i\,=\,1}^{k}C_{N\alpha i}\,(\,\alpha\,-\,\alpha_{i}\,)_{+}+\,\sum_{i\,=\,1}^{k}C_{N\beta i}\,(\,\alpha\,-\,\alpha_{i})_{+}^{0}\,\frac{q l}{2\,V}\,+

30

C_{N q}\,\frac{q l}{2V}\,+\,C_{N\delta}\delta_{e}\,+\,C_{N\delta_{\epsilon}7}\delta_{e}(\,\alpha\,-\,\alpha_{7})_{+}^{0}+\,C_{N_{\epsilon}13}\delta_{e}(\,\alpha\,-\,\alpha_{13})_{+}^{0}

C_{m}\;=C_{m0}\,+\,C_{m a}\alpha\,+\,\sum_{i\,=\,1}^{k}C_{m a i}\bigl(\,\alpha\,-\,\alpha_{i}\,\bigr)_{+}+\,\sum_{i\,=\,1}^{k}C_{m q}\bigl(\,\alpha\,-\,\alpha_{i}\,\bigr)_{+}^{0}\,\,\frac{q l}{2V}\,+

C_{m q}\,\frac{q l}{2\,V}\,+\,C_{m\hat{\phi}}\hat{o}_{e}\,+\,C_{m\hat{\phi}_{e}\,}7\hat{\partial}_{e}\,(\alpha\,-\,\alpha_{7})_{+}^{0}+\,C_{m\hat{\phi}_{e}13}\hat{\partial}_{e}\,(\alpha\,-\,\alpha_{13})_{+}^{0}

2.2.2 积分方程模型

20 世纪70年代以来托巴克(M.Tobak)[7采用阶跃响应的方法建立了气动力系数与飞行状态参数变化历程的积分关系式，给出了气动力系数非线性、非定常数学模型的一般表达式，包括有分叉点和有迟滞现象的非单值非线性气动系数的一般表达式。其基本思想是将飞行状态参数的时间历程分成无数个阶跃函数之和，并将气动力系数作为气动力对这些阶跃函数的响应的总和，得到积分方程形式的气动力数学模型。其一般表达式为

C_{m}(\mathbf{\Psi}_{t})\,=C_{m}(\mathbf{\Psi}-\infty)+\int_{-\infty}^{t}C_{m a}\big[\alpha\big(\hat{\mathbf{\xi}}\big),\hat{\partial}_{e}\big(\hat{\mathbf{\xi}}\big),q(\hat{\mathbf{\xi}});t,\tau\big]\,\frac{\mathrm{d}\alpha(\tau)}{\mathrm{d}\tau}\mathrm{d}\tau\,+\,\frac{\mathrm{d}\alpha(\tau)}{\mathrm{d}\tau}\int_{-\infty}^{t}C_{m a}(\mathbf{\Psi}_{t})\,\frac{\mathrm{d}\alpha(\tau)}{\mathrm{d}\tau}\mathrm{d}\tau.

\begin{array}{l}{{\displaystyle\int_{-\infty}^{t}C_{m\delta_{\epsilon}}\left[\left.\alpha\left(\xi\right),\delta_{e}\left(\xi\right),q\left(\xi\right);t\,,\tau\right]\,\frac{\mathrm{d}\delta_{e}\left(\tau\right)}{\mathrm{d}\tau}\mathrm{d}\tau\,+}}\\ {{\displaystyle\frac{1}{2\,V}\!\!\int_{-\infty}^{t}C_{m q}\left[\left.\alpha\left(\xi\right),\delta_{e}\left(\xi\right),q\left(\xi\right);t\,,\tau\right]\frac{\mathrm{d}q\left(\tau\right)}{\mathrm{d}\tau}\mathrm{d}\tau}}\end{array}

式中 方括号——表示泛函关系式；

\xi\mathrm{-}\,\overline{{\tau}}\,\mathrm{,}\,t 之间的变量；

α、、q——均为的任意函数。

可见，此数学模型极为复杂，无法直接用于参数辨识，必须加以简化。有三种简化方法：

(1）对 \boldsymbol{\xi} 的函数作线性逼近,取 \alpha\left(\,\pmb{\xi}\,\right)=\alpha\left(\,\tau\,\right)-\dot{\alpha}\left(\,\tau\,\right)\left(\,\tau-\,\pmb{\xi}\,\right), 通常用于快速机动的飞行器。

\begin{array}{l}{{\sum_{m}\left(t\right)=C_{m}\left(\mathrm{\boldmath~-~}\infty\right)+}}\\ {{\displaystyle\int_{-\infty}^{t}\,C_{m\alpha}\big[\alpha\big(\tau\big),\dot{\alpha}\big(\tau\big),\dot{\delta}_{e}\big(\tau\big),\dot{\delta}_{e}\big(\tau\big),q\big(\tau\big),\dot{q}\big(\tau);t,\tau\big]\frac{\mathrm{d}\alpha\big(\tau\big)}{\mathrm{d}\tau}\mathrm{d}\tau+}}\\ {{\displaystyle\int_{-\infty}^{t}\,C_{m\dot{\delta}_{e}}\big[\alpha\big(\tau\big),\dot{\alpha}\big(\tau\big),\dot{\delta}_{e}\big(\tau\big),\dot{\delta}_{e}\big(\tau\big),q\big(\tau\big),\dot{q}\big(\tau);t,\tau\big]\frac{\mathrm{d}\dot{\delta}_{e}\big(\tau\big)}{\mathrm{d}\tau}\mathrm{d}\tau+}}\\ {{\displaystyle\frac{l}{2V}\displaystyle\int_{-\infty}^{t}\,C_{m\dot{\delta}}\big[\alpha\big(\tau\big),\dot{\alpha}\big(\tau\big),\dot{\delta}_{e}\big(\tau\big),\dot{q}\big(\tau\big),\dot{q}\big(\tau);t\,\tau\big]\frac{\mathrm{d}q\big(\tau\big)}{\mathrm{d}\tau}\mathrm{d}\tau}}\end{array}

(2）忽略状态参数变化率对气动导数的影响，取 \alpha\left(\,\xi\,\right)=\,\alpha (\tau) 。通常用于飞行器缓变运动。

\begin{array}{l}{{\displaystyle}}\\ {{\displaystyle}=C_{m}\big(-\infty)+\int_{-\infty}^{t}C_{m a}\big[\alpha(\tau),\delta_{e}(\tau),q(\tau);t\,-\,\tau\big]\,\frac{\mathrm{d}\alpha(\tau)}{\mathrm{d}\tau}\mathrm{d}\tau\,+}}\\ {{\displaystyle}}\\ {{\displaystyle\int_{-\infty}^{t}C_{m\delta_{e}}\big[\alpha\big(\tau)\,,\delta_{e}(\tau)\,,q\big(\tau)\,;t\,-\,\tau\big]\,\frac{\mathrm{d}\delta_{e}(\tau)}{\mathrm{d}\tau}\mathrm{d}\tau\,+}}\\ {{\displaystyle}}\\ {{\displaystyle\frac{l}{2{\cal V}}\!\!\int_{-\infty}^{t}C_{m q}\big[\alpha\big(\tau)\,,\delta_{e}(\tau)\,,q\big(\tau)\,;t\,-\,\tau\big]\,\frac{\mathrm{d}q\,(\tau)}{\mathrm{d}\tau}\mathrm{d}\tau}}\end{array}

(2 -21)

（3）忽略飞行状态参数对气动导数的影响，认为气动导数与瞬时变量 \alpha(\,\tau){\,,\delta_{e}(\,\tau)\,,\boldsymbol{q}\,}(\,\tau) 无关，俯仰力矩系数可近似表示为

\begin{array}{l}{{\displaystyle C_{m}\left({\bf\Pi}_{t}\right)\,=\,C_{m}\left({\bf\Pi}-{\bf\Pi}\infty\right)\,+\,\int_{-\infty}^{t}C_{m a}\left({\bf\Pi}_{t}\,-{\bf\Pi}_{\tau}\right)\,\frac{\mathrm{d}\alpha}{\mathrm{d}\tau}\mathrm{d}\tau}\ +}\\ {{\displaystyle\int_{-\infty}^{t}C_{m\delta_{\epsilon}}\left({\bf\Pi}_{t}\,-{\bf\Pi}_{\tau}\right)\,\frac{\mathrm{d}\hat{\delta}_{e}}{\mathrm{d}\tau}\mathrm{d}\tau}\,+\,\frac{l}{2\,V}{\displaystyle\int_{-\infty}^{t}C_{m q}\left({\bf\Pi}_{t}\,-{\bf\Pi}_{\tau}\right)\,\frac{\mathrm{d}q}{\mathrm{d}\tau}\mathrm{d}\tau}\,}}\end{array}

上式改写成平衡值 C_{m}(\infty) 和剩余值 C_{m F} 之和,则成了

\begin{array}{l}{{\displaystyle\left({\bf\Pi}_{t}\right)\,=\,C_{m0}\,+\,C_{m a}\left(\infty\right)\alpha\left({\bf\Pi}_{t}\right)\,+\,C_{m\hat{\delta}_{\epsilon}}\left(\infty\right)\hat{\partial}_{\epsilon}({\bf\Pi}_{t})\,+\,\frac{l}{2\,V}C_{m q}q\,-}}\\ {{\displaystyle\int_{-\infty}^{t}C_{m a F}\bigl(t\,-\,\tau\bigr)\dot{\alpha}\bigl({\bf\Pi}_{\tau}\bigr){\bf d}\tau\,-\,{\bf\prod}_{-\infty}^{t}C_{m\hat{\delta}_{\epsilon}}\bigl(t\,-\,\tau\bigr)\dot{\delta}_{\epsilon}\bigl({\bf\Pi}_{\tau}\bigr){\bf d}\tau\,-}}\\ {{\displaystyle\frac{l}{2\,V}\!\!\int_{-\infty}^{t}\!C_{m q F}\bigl(t\,-\,\tau\bigr)\dot{q}\,\bigl({\bf\Pi}_{\tau}\bigr){\bf d}\tau\,}}\end{array}

式中，前四项为定常项，后三项为非定常项。

以上只给出平面俯仰运动下的俯仰力矩系数的数学模型。当飞行器作空间运动时， C_{m}\left(\r_{t}\right) 不仅是 \alpha\setminus q\setminus\delta_{e} 等的函数，还是 \beta,r\,, \delta_{r} 、"等的函数，其具体表达式比上面所给公式还复杂些，但类似上面推导方法，很容易写出其具体表达式。当气动力参数不是状态参数的单值函数时，例如出现迟滞效应，气动力参数出现分叉和多值现象，这时应在分叉点采用差分公式，而其余区域仍用上述公式。

美国采用阶跃过渡函数模型研究高性能战斗机F-15的 3/8缩比遥控模型飞机在过失速/尾旋区域的气动力模型[8]

遥控数据包括三个角速率、三个姿态角、三个加速度、动压、静压、攻角和侧滑角等。以法向力为例，其阶跃过渡函数为

C_{N}(\,t\,)\;=\;C_{N}(\,\alpha\,,\delta_{e}\,,q\,)\,+\,\int_{0}^{t}C_{N\alpha F}(\,\alpha\,,t\,-\,\tau\,)\,\dot{\alpha}\,(\,\tau\,)\,\mathrm{d}\tau

C_{N} 对 \delta_{e} 和 q 是线性关系，上式可简化为

\begin{array}{l}{{\displaystyle C_{N}(\,{\alpha}\,)\,+\,\,C_{N\hat{\alpha}_{e}^{\hat{\alpha}}}\hat{\sigma}_{e}\,+\,C_{N q}\,\frac{q l}{2\,V}\,+\,\int_{0}^{t}C_{N a F}(\,t\,-\,\tau\,)\,\dot{\alpha}\,(\,\tau\,)\,\mathrm{d}\tau\,=\,}}\\ {{\displaystyle C_{N0}\,+\,C_{N a}\alpha\,(\,t\,)\,+\,\,C_{N_{a}^{\;\;2}}\alpha^{2}\bigl(\,t\,)\,+\,\,C_{N a}{}^{\;3}\alpha^{3}\bigl(\,t\,\bigr)\,+\,\,C_{N\hat{\theta}_{e}^{\hat{\theta}}}\hat{\sigma}_{e}\,+\,}}\\ {{\displaystyle C_{N q}\,\frac{q l}{2\,V}\,+\,\sum_{i=1}^{10}C_{N a F}(0.1\,i\,)\,\dot{\alpha}\,(\,t\,-\,0.1\,i\,)}}\end{array}

上述数学模型的过渡函数只有一秒种的记忆时间，也即气动力的非定常效应是受一秒种以内的扰动的影响。此记忆时间的长度取决于攻角振荡的频率和飞机特征长度与飞行速度之比值，也是为了使模型简化而选取的。式中α是采用改进的时间历程的导数计算法求得的，整个模型结构是采用系统辨识、数据分析、控制设计和系统估算的软件包“MATRIXx"求出的。

2.2.3 微分方程模型

20世纪80年代初柯曼（M.T.TomaH）首先提出用微分方程模型描述大攻角非定常气动系数，着重研究大攻角分离流引起的气动力迟滞效应。其基本思想是，飞行器大攻角气动力的迟滞效应主要是气动分离引起的，可以用一个与气流分离有关的变量 \xi （称之为内在变量)来描述。目前这理论还不完备，但已有了成功的应用实例[9]。

设飞行状态变量为 \pmb{x} ,控制输人为 \pmb{u} ，气动力和力矩系数构成矢量 \pmb{\theta}=(\,C_{x}\,,C_{y}\,,C_{z}\,,C_{l}\,,C_{m}\,,C_{n}\,)^{\textup T} ,则气动力非线性微分方程模型的通式可写成

\begin{array}{l}{\displaystyle{D_{i}\left[\,\pmb{\theta}\,,\frac{\mathrm{d}\pmb{\theta}}{\mathrm{d}t},\cdots,\frac{\mathrm{d}^{n}\pmb{\theta}}{\mathrm{d}t^{n}}\,\right]=}}\\ {\displaystyle{N_{i}\left[\,\pmb{x}\,,\frac{\mathrm{d}\pmb{x}}{\mathrm{d}t}\,,\cdots,\frac{\mathrm{d}^{p}\pmb{x}}{\mathrm{d}t^{p}}\,;\pmb{u}\,,\frac{\mathrm{d}\pmb{u}}{\mathrm{d}t}\,,\cdots,\frac{\mathrm{d}^{r}\pmb{u}}{\mathrm{d}t^{r}}\,;\pmb{\xi}\,,\frac{\mathrm{d}\pmb{\xi}}{\mathrm{d}t}\,,\cdots,\frac{\mathrm{d}^{q}\pmb{\xi}}{\mathrm{d}t^{q}}\,\right]}}\end{array}

式中 D_{i}[\cdots]_{\star}N_{i}[\cdots]. 光滑函数关系。

对于二元翼型的不可压缩粘性分离流、细长三角翼大攻角俯仰振荡运动、飞机大攻角俯仰振荡运动等状态，柯曼给出了式（2-24）的简化数学表达式。对于二元翼和三角翼运动的气动力数学模型中的各参数有明确物理意义，但推广到全机运动时，数学模型中的气动参数缺乏明确的物理意义。文献[10提出了直接建立气动力系数的微分方程数学模型的想法。模型中的各参数有比较明确的物理意义。以法向力系数 C_{N} 为例，数学模型为

C_{N}\;=\;\sum_{\substack{\prime\,=\,0}}^{\hat{P}}C_{N\alpha}^{\;\;}\alpha^{j}\;+\;C_{N\dot{\alpha}}\;\frac{\dot{\alpha}l}{2\,V}\,+\,C_{N q}\;\frac{q l}{2\,V}\,+\,^{\cdot}\,C_{N n u}\;\Biggr\lfloor

\tau_{1}~\frac{\mathrm{d}C_{N n u}}{\mathrm{d}t}~+~C_{N n u}~=~\sum_{j\,=\,1}^{n}\,\sum_{i\,=\,0}^{n\,-\,j}A_{i j}\alpha^{i}\left(\frac{\dot{\alpha}l}{2\,V}\right)^{j}

Cv表达式的第1项为大攻角静态气动力系数,第2、3项为线性非定常气动力系数,CNnu为非线性非定常气动力系数,满足一阶常微分方程。式(2-25)中， C_{N a^{\prime}}\ldots C_{N\dot{a}}\ldots C_{N q}\ldots\tau_{1}\ldots A_{i j} 等为待辨识的气动系数。图 2-2 给出 Cv(α)辨识结果与风洞实验结果的比较,两者吻合得很好。式(2-25)不仅各项有明确的物理意义，而且 C_{N n u} 满足一阶微分方程，因此系统辨识的状态方程组与定常气动参数辨识时的形式类同，仅仅多加一个常微分方程，辨识软件无须做较大的更改。可以证明，式(2-25)相当于气动力系数对阶跃输人的响应历程呈指数衰减律时的式(2-23)[11},这说明积分方程和微分方程型数学模型是一致的。

上述三种数学模型中的各个参数都清楚地显示出它们与各状态参数的关系，相比较而言，有物理意义。而近来发展的神经网络法，因神经元和权因子较多，比较难于说明所建模型中各个参数的物理意义，但因其应用广泛，本书在第3章将作专门介绍。

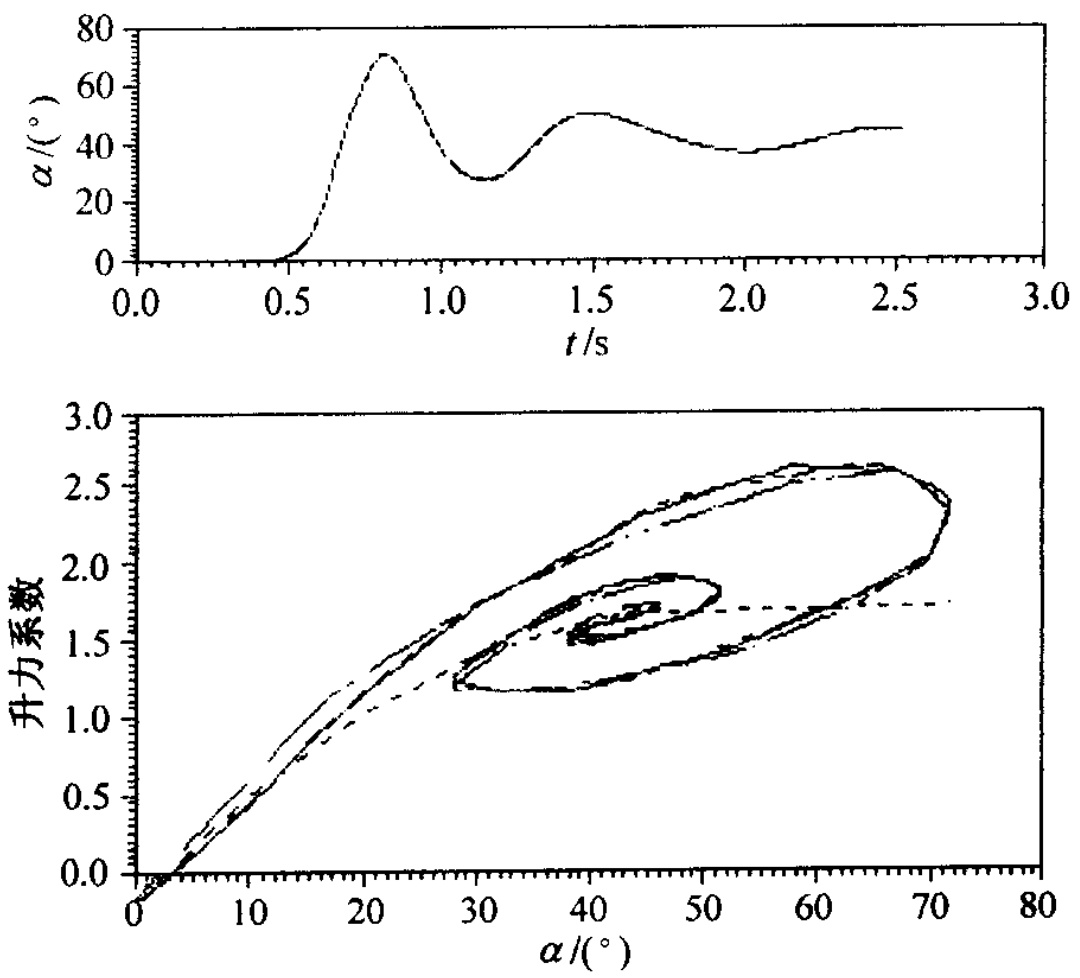
图 2-2自由振荡风洞实验结果与数学模型计算结果比较-—动态试验数据：----柯曼模型辨识结果；-·-·-文献[11]辨识结果。

2.3 推力与环境数学模型

飞行器动力学系统辨识中，推力、重力和地球大气通常是作为已知测量参数，本节给出辨识中常采用的推力、重力和大气数学模型。

2.3.1 推力数学模型

推力是飞行器动力学系统的动力，是飞行的基础，飞行器的推力由发动机提供，常用发动机有活塞式发动机、火箭发动机、燃气涡轮发动机和冲压发动机等。发动机装人飞行器之前，在地面进行了充分的全尺寸试验，发动机推力数据基本上依赖于地面试验结果。20多年来，发动机数字仿真和专家系统研究得到较快进展，已建立了各类发动机的数学模型，给出发动机推力与发动机内部状态参数的泛函关系。发动机数学模型必须经过飞行试验验证，故发动机系统参数辨识是一个正在蓬勃发展的热门课题，但还不很成熟。本节只是给出推力的表达式和近似公式，以便利用地面推力试验结果建立飞行器动力学系统的状态方程组。

1）活塞式发动机

活塞式发动机是用活塞发动机带动螺旋桨产生推力，推力公式为

R\,=\,\frac{750\,N_{A}\eta_{A}}{V}

式中 N_{A} —发动机功率，以马力计；

7A——螺旋桨效率;
V-—飞行速度。

推力 R 随高度变化有下列经验公式[12]

R(H)\,=\,\left\{1.11{\left[{\frac{\rho(H)}{\rho_{0}}}\right]}\sqrt{\frac{T_{0}}{T(H)}}\,-\,0.11\right\}\!R_{0}

式中 下标 \mathbf{\omega}^{\ast}\mathbf{0}^{\ast\ast} ——海平面参数；

H 海拔高度；
T —热力学温度。

2）火箭发动机

火箭发动机，不论液体火箭或固体火箭都是高压燃气由喷管向后排出而产生推力。根据动量守恒定理，得推力公式为

R\;=\;\dot{m}\,V_{e x}\,+\,\left(\,\dot{\,}p_{e x}\,-\,\rlap/p\,\right)S_{e x}

式中下标“ex” 一—喷管出口处参数；

m——从喷管喷出的秒质量流量。

若 R\left(0\right) 是海平面条件下地面试验时测得的推力，则由式(2-28)得

R(H)\;=\;R({\bf0})\;+\;[\;\rho({\bf0})\;-\;\rho(H)\;]S_{e x}

3）燃气涡轮发动机

燃气涡轮发动机是目前航空界最常用发动机，已发展了涡轮喷气、涡轮螺桨、涡轮风扇、涡轮轴和螺桨风扇等多种类型。这类发动机由进气道、压气机、燃烧室和涡轮组成。发动机的推力等于发动机进口与发动机喷管出口气流的秒动量之差。对涡轮喷气发动机有[13]

{\cal R}\;=\;\dot{m}_{A}\left(\frac{\dot{m}_{A}\;+\;\dot{m}_{L}}{\dot{m}_{A}}V_{e x}\;-\;V\right)+\;S_{e x}\left(\frac{}{}\hat{p}_{e x}\;-\;{\rlap/p}\right)\approx

\dot{m}_{A}\left(\,V_{e x}\,-\,V\,\right)\,+\,\left(\,\phi_{e x}\,-\,\rlap/p\,\right)S_{e x}

式中 $\dot{m}_{A}-\mathrm{~\}$ 单位时间进人发动机的空气质量；

m,——单位时间消耗的燃料质量。

对涡轮螺桨发动机，大部分能量用于驱动螺桨，用于喷流推进的 V_{e x} 较小，推力公式为[14]

R\;=\;\frac{750N_{A}\eta_{A}}{V}\;+\;\dot{m}_{A}\big(\,V_{e x}\,-\,V\,\big)\;+\;\big(\,\dot{p}_{e x}\,-\,\dot{p}\,\big)\,S_{e x}

燃气涡轮发动机中的 V_{e x} 和 \dot{m}_{A} 是外界大气温度、飞行速度、燃烧室压力、涡轮燃烧室温度以及膨胀效率、压缩效率的函数，自前还没有将地面试验结果推广到飞行器的简单近似公式。

4）冲压发动机

冲压发动机由扩压器、燃烧室和尾喷管组成。若在扩压器和燃烧之间装火箭发动机就构成火箭-冲压发动机。其推力表达式也由式（2-30)表示[15]

2.3.2 重力数学模型

飞行器在空中飞行时，除承受气动力和推力外,还受地球引力

的作用。地球引力是保守力场,计人地球的椭球度影响的引力正常位势 \boldsymbol{U} 可近似表示为[16]

U\,=\,\frac{G M}{r}\biggl[1\,-\,\frac{J_{2}}{2}\biggl(\frac{a_{e}}{r}\biggr)^{2}\bigl(3\sin^{2}{\phi}\:-\:1\bigr)\,\biggr]

式中 GM—地球引力常数；

\alpha_{e} ——正常地球赤道半径；一计算点至地心的距离；
\phi —一计算点地心纬度。

对飞行轨道而言， \alpha_{e}/r{\ll}1\,,J_{2}{\approx}10\,^{-\,3} ，可见式（2-33）的第二项小于千分之一。故飞行器动力学系统辨识中可以忽略地球扁度对引力的影响。地球引力可近似表示为

g^{\mathrm{~*~}}=\frac{G M}{r^{2}}\approx\frac{G M}{a_{\it e}^{2}}\biggl(1-\frac{2H}{a_{e}}\biggr)=

9.80\mathrm{~-~}3.073H\times10^{-5}

地面静止物体同时承受地球引力和地球自旋引起的离心力，通常将引力和离心力组合起来定义为重力。重力可以用下列经验公式计算[17]

g\ =9.80612\,+\,(\,-\,258.\,65\mathrm{cos}2\,\phi\ +

0.58\mathrm{cos}^{2}2\oint\mathrm{~-~}0.38H)\times10^{-4}

式中 \phi 和 H ～——分别为飞行器的当地纬度和海拔高度。

2.3.3 标准大气密度

标准大气是国际上公认的，反映中纬度全年大气特征的一种假想的气温、气压和空气密度的垂直分布。各国还通过大量实验分析，给出各特定地区和季节（月份）的理想化的平均大气模式，称为参考大气。这些数据表是飞行器动力学系统数字仿真和辨识仿真中的重要工具，当缺乏大气的实测数据时，可用于提供系统辨识所必需的气象数据。

国际标准化组织已将美国1976年的 50\mathbf{k}m 以下标准大气作为国际标准大气（1SO 2533，1973），将 50\mathrm{km}\!\sim\!80\mathrm{km} 的美国标准大气作为“暂用国际标准大气”。我国也将美国 30\mathrm{km} 以下标准大气作为国家标准（GB1920一80）。美国1976年标准大气共有八个基本表[18]。标准大气可以用解析函数逼近以便于使用

\rho\,=\,1.225(1.0\,-\,2.2556\times10^{-5}H)^{4.2561}\quad(\,H\,=\,0\,\sim\,11000\mathrm{m})

\rho\,=\,0.364\mathrm{exp}\{\frac{11000\,-\,H}{6341.64}\}\quad(\,H\,=\,11000\mathrm{m}\sim25000\mathrm{m})

2.3.4 大气湍流模型

大气湍流是由不同尺度（或不同频率）的湍涡相互叠加而成的随机场，可以近似将大气湍流速度作为一平稳、各态历经、各向同性的随机量，用能量谱密度加以描述。在飞行力学中，常假定飞行器作直线常速运动，且大气湍流“冻结”于初始时刻，根据实测数据确定湍流脉动的相关函数的经验表达式，从而导出其一维谱函数。

1）普雷斯（Press）模型和德莱顿（Dryden）模型

普雷斯最早给出瑞流风纵向（平均风速方向）脉动的相关函数,导出普雷斯模型[20],此模型也称德莱顿模型。

\tilde{r}_{u u}\left(\,\omega\,\right)\,=\,\frac{2\sigma_{u}^{2}L_{u}}{\pi V}\,\frac{1}{1\,+\,\left(\,L_{u}\omega/V\,\right)^{2}}

\tilde{r}_{_{\alpha_{\texttt{g}}^{\alpha}}}(\,\omega\,)\,=\,\frac{2\,\sigma_{_{w}}^{2}L_{w}}{\pi\,V^{3}}\,\frac{1\,+\,12(\,L_{w}\omega/\,V\,)^{2}}{[\,1\,+\,4(\,L_{w}\omega/\,V\,)^{2}\,]^{2}}

\tilde{r}_{\beta_{g}\beta_{g}}(\,\omega\,)\,=\,\frac{2\sigma_{v}^{2}L_{v}}{\pi V^{3}}\,=\,\frac{1+12(\,L_{v}\omega/V)^{2}}{[\,1+\,4(\,L_{v}\omega/V)^{2}\,]^{2}}

式中,湍流尺度L;和湍流强度o;(i=u,,w)按下式确定：

晴空湍流

L_{u}\,=\,2L_{v}\,=\,2L_{w}\,=\,530\mathrm{m}\qquad(\,H\geqslant530\mathrm{m})

L_{u}\,=\,2L_{v}\,=\,65\,.7\,H^{1/2}\qquad L_{w}\,=\,0\,.5\,H\qquad(\,H\,<\,530\mathrm{m})

有许多实测结果图表[19],数值仿真计算时,可偏保守地取为

<html>

H/m	0	100	1000	10000	20000	26000
O,o/(m/s)	2.1	2.05	1.80	1.40	1.0	0

</html>

\mathcal{O}_{\tau\varepsilon}. 由下式求得

\sigma_{\it z}^{2}\,=\,\frac{L_{w}}{L_{v}}\sigma_{\it v}^{2}

风暴湍流

\begin{array}{l}{{L_{u}\,\,=\,2\,L_{v}\,=\,2\,L_{w}\,=\,530\mathrm{m}}}\\ {{\sigma_{u}\,=\,\,\sigma_{v}\,=\,\sigma_{w}\,=\,6\,.4\mathrm{m}/\mathrm{s}}}\end{array}

2）布蕾恩(Bullen)模型

布蕾恩提出较广泛的一类风纵向脉动的相关函数，导出一类纵向脉动和横向脉动的谱密度表达式，称为布蕾恩模型。

\tilde{r}_{u u}(\,\omega\,)\,=\,\frac{2\sigma_{u}^{2}L_{u}}{\pi V}\,\frac{1}{\left[\,1\,+\,(\,a\omega/V\,)^{2}\,\right]^{\,N+1/2}}

\tilde{r}_{w w^{\prime}}(\,\omega\,)\,=\,\frac{2\sigma_{w}^{2}L_{w}}{\pi V}\,\frac{1\,+\,2({\cal N}+1)(\,\alpha\omega/V)^{2}}{\left[\,1\,+\,(a\omega/V)^{2}\,\right]^{\,N+3/2}}

式中

a\;=\;\frac{L_{u}\left(N\,-\,1\right)!}{\sqrt{\pi}\left(N\,-\,\frac{1}{2}\right)!}\;=\;\frac{\displaystyle{\cal T}(N)\,L_{u}}{\displaystyle{\sqrt{\pi}\,{\cal I}\left(N\,+\,\frac{1}{2}\right)}}\;

当 \ N=1/2 时，布蕾恩模型化为德莱顿模型。

3）冯·卡曼（VonT．Karman)模型

布蕾恩模型的 N 取为 1/3 时，即化为冯·卡曼模型，其频谱为

\hat{r}_{u u}(\omega)\;=\;\frac{2\sigma_{u}^{2}L_{u}}{\pi V}\;\frac{1}{[\,1\,+\,(\left.a L_{u}\omega/V)^{2}\right]^{5/6}}

\tilde{r}_{_{\alpha_{\kappa}^{\alpha}}}(\,\omega\,)\;=\;\frac{1}{V^{2}}\tilde{r}_{w w}(\,\omega\,)\;=\;\frac{2\sigma_{w}^{2}L_{w}}{\pi\,V^{3}}\,\frac{1\,+\,8(2a L_{w}\omega/V)^{2/3}}{\,[\,1\,+\,(2a L_{w}\omega/V)^{2}\,]^{11/6}}

\tilde{r}_{\beta_{\kappa}^{\beta_{\kappa}}}(\,\omega\,)\,=\,\frac{2\sigma_{v}^{2}L_{v}}{\pi\,V^{3}}\,\frac{1\,+\,8(2\,\alpha L_{v}\omega/\,V\,)^{2/3}}{[\,1\,+\,(2\,a L_{v}\omega/\,V\,)^{2}\,]^{11/6}}

式中： a=1.339 。湍流尺度和湍流强度满足下式：

晴空湍流

\begin{array}{c c}{{L_{u}\,=\,2L_{v}\,=\,2L_{w}\,=\,762\mathrm{m}}}&{{(\,H\gg762\mathrm{m}\,)}}\\ {{{}}}&{{{}}}\\ {{L_{u}\,=\,2\,L_{v}\,=\,83\,.4\,H^{1/3}}}&{{L_{w}\,=\,0\,.\,5H}}&{{(\,H<762\mathrm{m})}}\end{array}

\bar{\sigma}_{u}\,\setminus\bar{\sigma}_{v} 同德莱顿模型， {\sigma}_{w} 由下式计算

\sigma_{\,w}^{2}\;=\;\left(\frac{L_{w}}{L_{v}}\right)^{2/3}\sigma_{\,z}^{2}

风暴湍流

L_{u}\,=\,2L_{v}\,=\,2L_{w}\,=\,762\mathrm{m}

\sigma_{u}\ =\ \sigma_{v}\ =\ \sigma_{w}\ =\ 6.4\mathrm{m/s}

4）角速率湍流脉动模型

大气湍流引起飞行器的附加角速度可以由湍流速度对 x\setminus y\setminus \mathfrak{z} 求导而取得，但目前采用的是从试验数据拟合所得的谱密度，具体表达式为

\tilde{r}_{p p}(\,\omega\,)\,=\,\frac{0.2\sigma_{w}^{2}}{L_{w}V}\;\frac{\left[\pi L_{w}/(2\,l\,)\,\right]^{1/3}}{1+\left[4\,l\omega/(\,\pi V\,)\,\right]^{2}}

\tilde{r}_{q q}(\mathbf{\Sigma}\omega)\;=\;\frac{\omega^{2}}{1\,+\,[\,4l\omega/(\pi V)\,]^{2}}\,\tilde{r}_{\mathbf{\Sigma}_{\alpha_{\kappa}^{\beta}}}(\mathbf{\Sigma}\omega)\;

对于大型运输机，翼展与湍流的横向尺度相比已不可忽略，上述频谱公式需引进修正因子[21]。

参考文献

1蔡金狮.动力学系统辨识与建模.北京：国防工业出版社，1991

2 Meirovitch L, Norris M A.Parameter Identification in Distributed Spacecraft Structurc.AAS 85-670,1985
3 Bryan G H.Stability in Aviation, 1911
4 Klein V,etc.Determination of Airplane Model Structure from Flight Data Using Splines and Stepwise Regression. NASA TP-2126,1983
5 Klein V,Batterson J G.Determination of Airplane Model Structure from Flight Data by Using Modified Stepwise Regression. NASA TP-1916, 1981
6 Batterson J G. Analysis of Oscillatory Motion of a Light Airplane at High Value of Lift Coefficient. NASA TM-84563, 1983
7 Tobak M, Schiff L B. Aerodynamic Mathematical Modelling--Basic Concepts.AGARD LS-114,paper 1,1981
8 Gupta N K, lliff K W . Identification of Aerodynamic Indicial Functions Using Flight Data. AIAA 82-1375 ,1982
9 Goman M G,eic . Mathematical Description of Longitudinal Aerodynamic Characteristics of an Aircraft at High Angles of Attack with Accounting for Dynamic Effects of Separated Flow . Preprint of TsAGI, Moscow, N.9, 1990,56pp
10汪清,蔡金狮．飞机大攻角非定常气动力建模与辨识．航空学报,1996,17(4)： 391 ~ 398
11 Cai Jinshi, Wang Qing. Nonlinear Unsteady Aerodynamic Mathematical Models for Aircraft . First Asian CFD Conference ,January 16-19,Paper IB3,1995
12A.A.巴佳金，Φ.A.穆哈麦多夫．轻型飞机设计．航空工业部601所译.1985
13张逸民．航空涡轮风扇发动机．北京：国防工业出版社，1985
14A.J.克莱什金．喷气发动机原理．秦鹏译．北京：国防工业出版社，1977
15B.C.朱也夫,B.C.马卡伦．冲压和火箭-冲压发动机原理．刘兴洲等译．北京： 国防工业出版社,1975
16李瑞浩．重力学引论．北京：地震出版社，1988
17叶笃正等．动力气象学．北京：科学出版社,1988
18 U.S.A.Standard Atmosphere.NOAA, NASA, U.S.A.Air Force, Washington D.C. , 1976
19曲延禄．外弹道气象学概论．北京：气象出版社,1987
20J．泰勒．飞机载荷手册．黄舜琪等译．北京：国防工业出版社，1974
21 Military Specification Flying Qualities of Piloted Airplanes. MIL-F-8785C, 1980
22 Akaike H.A New Look at the Statistical Model Identification. IEEE Trans. 1974,AC19(6) :716 ~ 722
23 Fiske P H, Price C F.A New Approach to Model Structure Identification.AIAA 77- 1171,1977
24 Klein V,Batterson J G, Murphy P C. Determination of Model Structure and Parameters of an Airplane from Pre- and Post-Stall Flight Data.AIAA 81-1866,1981

第3章模型辨识

3.1概述

在大多数系统辨识问题中，人们事先并不确知待辨识系统的模型结构，而只能根据对待辨识系统的认识和建模目的，确定待辨识系统数学模型的结构形式（候选模型集）。这就需要通过模型辨识确定系统的最优模型结构，然后才能进行系统的状态估计和参数估计。

模型辨识是系统辨识的重要步骤之一。它是根据试验或运行过程中测量的输人输出数据，从给定的候选模型集中确定最优数学模型的过程。

模型辨识的关键是建模准则和优选算法。因此，本章着重阐述飞行器系统辨识中常用的儿种建模准则和优选算法，并在最后介绍新近发展的非线性系统神经网络建模方法。

3.2建模准则

由于实测数据含有各种测量噪声和过程噪声，不能仅以对实测数据拟合误差最小作为建模准则，否则建立的模型将含有噪声特性。建模准则应能使优选出的模型具有以下性质[1,2] :

（1）模型能很好地拟合现有的飞行试验数据；
（2）模型能预测类似条件下的实测数据；
（3）模型各项具有明确的物理意义；
（4）在性能相当的条件下是阶次最低的模型。
迄今，已发展了多种建模准则。下面介绍几种飞行器系统辨

识中常用的建模准则，各种准则各有特点，各有其适用范围。这些准则，是在处理实际统计数据中产生的经验方法。

3.2.1 最大信息量准则

最大信息量准则是由日本赤池（H.Akaike)教授提出的l²,称为赤池信息准则（AIC),是统计模型优选中应用很广泛的信息准则。其形式为

\mathrm{AIC}\,=\,-\,2\mathrm{ln}\cdot （模型的最大似然准则） ^+ 2(模型的独立参数个数）

该式中，第一项是最大似然函数，它衡量模型的拟合程度，表示在模型的独立参数相同的情况下，似然函数最大的模型是最优模型；第二项可以解释为对增加参数个数的一种惩罚，当第一项差别不大时，第二项起作用，从而参数个数少的模型是较优的模型。AIC准则第二项的系数有各种不同取法，有人取为3、4、5，使模型独立参数个数的多少在模型优选中占的地位不同。

似然函数定义为在给定模型 M_{i} 下观测数据 Y_{N} 的条件概率。因此，对于给定的任意两个候选模型 M_{1}(\,m_{1},\,\hat{\theta}_{1}) 和 M_{2}(\,m_{2}\,,\hat{\theta}_{2}) ，最大信息量准则为

\ln\frac{P(~Y_{N}~!~M_{1}\,,\hat{\theta}_{1})}{P(~Y_{N}~!~M_{2}\,,\hat{\theta}_{2})}\,-\,k\,(\,m_{1}\,-\,m_{2}){\binom{<~0~}{>~0~}} 时取 M_{\mathrm{i}} 模型时取 M_{2} 模型式中 Y_{N} ——观测矢量数据集合；

\hat{\theta}_{1}\,,\hat{\theta}_{2}\,,m_{\,1}\,,m\,^{-} —分别为模型参数的最大似然估计和待估计参数的个数。

1{\leqslant}k{\leqslant}3 ，当 k=1 时就是赤池信息准则。

具体算法：提出候选的数学模型集，对每个模型用最大似然法进行参数估计（参见5.3节），由式（3-2）选择最优模型。

从近代统计理论的观点看，此准则比较严格，但计算量太大，对每个候选模型都要进行参数的最大似然估计，计算其似然函数。

当候选模型较多时，所费机时是惊人的。这种方法适用于任意概率密度函数的观测矢量数据 Y_{N} ，但要求知道观测矢量的概率密度函数。

3.2.2 最大可信度准则

模型的最大可信度准则是选取可信度最大的模型为最优模型。首先需要定义模型的可信度，然后采用广义卡尔曼滤波算法逐点计算模型的可信度，可信度最大者为最优模型。可以取在给定观测量下,模型为最优模型的概率 P_{M_{i}}(\,Y_{k}\,) 为可信度3]；也可以新息 \left[\:Y(\,k\,)\:-\:\hat{Y}(\,k\,\mid\,k\:-\:1\,,M_{i}\,)\:\right] 平方和之逆为可信度；或者以残差 [\:Y(\,k\,)\:-\:\hat{Y}(\,k\:\mid\:k\,,M_{i}\,)\,] 平方和之逆为可信度，等等。

设一组候选模型 M_{i}\;(\;i\;=\;1\,,\,2\,,\,\cdots\,,\,q\;) 是相互独立的，即M_{i}\bigcap M_{j}=\Phi\left(\;i\neq j\;\right), \pmb{\varPhi} 为空集，并且其中有一个最优模型，即P(\bigcup_{i=1}^{q}M_{i})=1\,,P\left(\,M_{i}\,\right)>0 。对于给定的观测数据 Y_{N}=\left(\,\mathbf{y}\,,\,\mathbf{y}_{2}\,,\, \cdots,{\mathfrak{y}}_{N})^{\mathrm{T}} ,利用贝叶斯公式,可得 M_{i} 为最优模型的概率为

P_{M_{i}}(\,Y_{k}\,)\equiv\!P(\,M_{i}\,|\,Y_{k}\,)\,=\,P(\,M_{i}\,|\,y_{k}\,,\,Y_{k-1}\,)\,=

\frac{P(\,\mathbf{y}_{k}\,|\,M_{i}\,,\,Y_{k-1})\,P(\,M_{i}\,|\,Y_{k-1})}{\sum_{j\,=\,1}^{q}P(\,\mathbf{y}_{k}\,|\,M_{j}\,,\,Y_{k-1})\,P(\,M_{j}\,|\,Y_{k-1})}\,=

\frac{P(\boldsymbol{y}_{k}\,|\,M_{i}\,,\,\boldsymbol{Y}_{k-1})P_{M_{i}}(\boldsymbol{Y}_{k-1})}{\displaystyle\sum_{j=1}^{q}P(\boldsymbol{y}_{k}\,|\,M_{j}\,,\,\boldsymbol{Y}_{k-1})P_{M_{j}}(\boldsymbol{Y}_{k-1})}

假设系统的状态参数和观测量是高斯分布，则有

P(\,y_{k}\,|M_{i}\,,Y_{k-1})\approx\frac{\exp\Bigl[-\,\frac{1}{2}{\pmb v}_{i}^{T}(\,k\,)\,{\pmb B}_{i}^{\,-1}(\,k\,)\,v_{i}(\,k\,)\,\Bigr]}{\left(2\pi\right)^{m/2}\,\vert\,{\pmb B}_{i}(\,k\,)\,\vert^{\,1/2}}

式中 {\pmb v}_{i}\setminus{\pmb B}_{i} 一一分别为广义卡尔曼滤波的新息和新息协方差矩 阵（参见4.2节）;

_{m} —观测矢量的维数。

具体算法：给出一组候选模型 M_{i}(\,i=1\,,2\,,\cdots,q\,) 和相应的待估计参数 \theta_{i j}({\bf\chi}_{i}=1,2,\cdots,q\,;j=1,2,\cdots,p\,) 。采用增广的广义卡尔曼滤波（参见4.2.4节)进行状态 \pmb{x} 和参数 \theta_{i j} 的递推估计，并用式(3-3)和式(3-4)计算各个 M_{i} 对应的可信度 P_{M_{i}}(\,Y_{k}\,) ,比较各个模型的可信度。在计算过程中，对可信度明显低的模型可以及时淘汰，以节省时间；对可信度明显优于其他模型者，可及时确定为最优模型。

这种方法需要预知系统的过程噪声和观测噪声协方差矩阵。它不必像最大似然准则那样反复迭代求解，花费大量机时，但仍需对每个模型逐点计算，也颇费机时。

3.2.3 {\pmb F} 统计检验

在飞行器系统辨识问题中，有相当一部分属于线性模型的辨识问题。例如，采用多项式和样条函数构成的气动力非线性模型，关于飞行状态变量是非线性的，但关于待估计参数却是线性的。再如，惯性仪表误差系数辨识问题中，误差模型通常都是线性的。

对于线性模型， F 统计检验{4]是最广泛使用的模型假设检验，其优点是有现成的优化标准程序，计算工作量远小于前两种准则。 F 统计检验与 AIC准则是渐近等价的[6]。经验表明,多数情况下用此准则和用其他准则所得结果相差不多[7]

线性模型的一般形式为

y\;=\;\theta_{0}\:+\:\theta_{1}x_{1}\:+\:\theta_{2}x_{2}\:+\:\cdots\:+\:\theta_{m}x_{m}\:+\:\varepsilon

式中 y——因变量(预报量);

x_{i} —一自变量(预报因子);

\theta_{i} ——待定参数；
\pmb{\varepsilon} 一——随机误差，服从 N(\mathbb{0},\sigma^{2}) 分布。

先讨论对参数的 F 检验。由统计理论知

\hat{\theta}_{i}\simeq{\cal N}(\theta_{i}\,,S_{i i}\sigma^{2})

Q/\sigma^{2}\sim\,\chi^{\,2}(N\,-\,m\,-\,1)

式中 \hat{\theta}_{i}\longrightarrow\theta_{i} 的最小二乘估计;

S_{i i} 一—回归分析的法方程系数矩阵之逆的主对角线元素；\boldsymbol{Q} 回归方程（3-5）采用 _{m} 个参数拟合后的残差平方和；

N —数据总点数。

从而

\begin{array}{l}{{F_{\boldsymbol{\rho}}\equiv\!\frac{\displaystyle(\hat{\theta}_{i}\,-\,\theta_{i})^{2}/(\,S_{i\boldsymbol{\sigma}}\sigma^{2})}{\displaystyle{Q/[\,(N\,-\,m\,-\,1)\,\sigma^{2}]}}\,=\,}}\\ {{\qquad\frac{\displaystyle(N\,-\,m\,-\,1)(\,\hat{\theta}_{i}\,-\,\theta_{i})^{2}}{S_{i i}Q}\sim F(1,N\,-\,m\,\,-\,1)}}\end{array}

给定一个显著性水平 \pmb{\alpha} ,可以根据上式对参数 \theta_{i} 做 F 检验。检验假设为

\begin{array}{r}{H_{0}:\,\theta_{i}\,=\,0}\\ {H_{1}:\,\theta_{i}\neq\mathbf{0}}\end{array}

检验的统计量为

F_{\it\hat{p}}\ =\ \frac{\left(\,N\,-\,m\,-\,1\,\right)\hat{\theta}_{i}^{2}}{S_{i i}Q}

当 F,<F。(1,N- m一1)时,回归系数 0;接近零,可以将x;从回归方程（3-5）中剔除。 F_{\alpha}(1,N-m-1) 是给定显著性水平后，由F 分布表查得的常数。

对整个回归方程也需要检验，判断其优劣。通常采用下列三个标准。

第一个标准是表征预报因子与预报量之间相关性的复相关系数：

R^{2}\,=\,\frac{\displaystyle\sum_{i=1}^{N}\,(\hat{y}_{i}\,-\,\bar{y}\,)^{2}}{\displaystyle\sum_{i\,=\,1}^{N}\,(\,y_{i}\,-\,\bar{y}\,)^{2}}

式中

\begin{array}{c}{{\hat{y}_{i}\;=\;\hat{\theta}_{0}\,+\,\displaystyle\sum_{j\,=\,1}^{m}\hat{\theta}_{j}x_{j}({\bf\theta}_{i}\,)}}\\ {{\overline{{{y}}}\;=\;\displaystyle\frac{1}{N}\sum_{i\,=\,1}^{N}y_{i}}}\end{array}

由于残差平方和

Q\ =\ \sum_{i\,=\,1}^{N}\,(\,y_{i}\,-\,\hat{y}_{i}\,)^{2}\,=\,\sum_{i\,=\,1}^{N}\,(\,y_{i}\,-\,\bar{y}\,)^{2}\,-\,\sum_{i\,=\,1}^{N}\,(\,\hat{y}_{i}\,-\,\bar{y}\,)^{2}

当 R 趋于1时， \boldsymbol{Q} 趋于0。所以， R 趋于1的程度表征着数据的拟合程度。

第二个标准是整个模型的 F 检验值：

F_{\dot{r}}\equiv\frac{\displaystyle{\sum_{i=1}^{N}\,(\hat{y}_{i}\,-\,\bar{y}\,)^{2}}\Big/(\,m\sigma^{2})}{\displaystyle{Q/[\,(N\,-\,m\,-\,1)\,\sigma^{2}\,]}}\,=\,\frac{\displaystyle{(\,N\,-\,m\,-\,1\,)\,R^{2}}}{m\,(1\,-\,R^{2})}

R 越趋向 1,F 值就越大，反映拟合越好；回归方程独立参数的个数 m 越多， F 值就越小，这是对增加参数个数惩罚，反映出要求模型的独立参数少。因此， F 取最大值为最佳模型。

第三个标准是残差序列应相当于白噪声，否则，说明还有重要因素未列人模型。

逐步回归法（参见3.3.1节)是应用 F 统计检验建模的有效算法。

3.2.4 最小预测误差平方和准则

一个好的模型不仅应能拟合好现有的试验数据，而且应该能够预测类似条件下的试验数据。根据这一原则，产生了最小预测误差平方和准则8

对于线性回归模型（3-5），定义平均平方预测误差

\mathrm{MSPE}\,=\,E\,[\,(\,y\,-\,\hat{y}\,)^{2}\,]

\hat{y} 是 y 的预估值。由上述定义可推得\mathrm{MSPE}\,=\,E\,\{\,[\,y\,-\,E(\,y\,)\,]^{2}\,\}\,+\,E\,\{\,[\,\hat{\,y}\,-\,E(\,y\,)\,]^{2}\,\}\,= E\,\{[\,y\,-\,E(y)\,]^{2}\,\}\,+\,E\,\{\,[\,{\hat{y}}\,-\,E({\hat{y}}\,)\,]^{2}\,\}\,+\,[\,E(y)\,-\,E({\hat{y}}\,)\,]^{2}\,= \sigma^{2}\,+\,\mathrm{Var}(\,\hat{y}\,)\,+\,[\,E(\,y\,)\,-\,E(\,\hat{y}\,)\,]^{2}

式中：第一项为响应方差，与回归方程所选项数无关，仅是测量误差 \varepsilon 的方差；第二项为预测方差，通常是回归方程的项数越多，\operatorname{Var}(\,{\hat{y}}\,) 也越大，故项数过多的模型，由于 \operatorname{var}(\hat{y}) 加大，其平均平方预测误差MSPE必然比最小值大；第三项为预测偏差的平方，当回归方程的项数太少，模型不完备时，必将导致较大的预测偏差，从而使MSPE加大。因此,MSPE最小的模型为最优模型。

具体算法：将实测数据分成两部分，一部分用于估计候选模型集中各模型的待定系数 \pmb{\theta} ；求得 \hat{\pmb{\theta}} 之后，再用第二部分数据计算各模型的平均平方预测误差，MSPE最小者为最优模型。

在上述算法中，可以用 (N-1) 个点进行估计，而只用一个点进行预测,称之为 PRESS 准则[9]

\mathrm{PRESS}=\sum_{i=1}^{N}\left\{y(i)-\hat{y}[i\left|x(1),\cdots,x(i\,-1),x(i+1),\cdots,x(N)\right.]\right\}^{2}

通常采用下式计算

\mathrm{PRESS}=\sum_{\mathrm{~}i=1}^{N}\,\frac{\left[\,\boldsymbol{y}(\,i\,)\,-\,\boldsymbol{\hat{y}}(\,i\,)\,\right]^{2}}{1\,-\,\pmb{x}(\,i\,)(\,\mathbf{X}^{\mathrm{T}}\pmb{X})^{-1}\pmb{x}^{\mathrm{T}}(\,i\,)}

式中 {\mathfrak{y}}({\mathfrak{i}}) 第 _i 个点的观测值;

\hat{y}\left(\,i\,\right) ——第 _i 个点的预测值；\pmb{X} —一回归方程的系数矩阵；
x(i) ——系数矩阵 \pmb{X} 的第 _i 行构成的行矢量。

3.3优选算法

对于每种建模准则,均需采用相应的算法来实现对模型的优选。由于与最大信息量准则和最大可信度准则相应的最大似然辨

识算法和增广的广义卡尔曼滤波算法有另章讨论,这里仅给出模型优选中常用的逐步回归法、主成分分析法、正交最小二乘法。数据分割是系统建模中的一项重要技术，本节一并给出。

3.3.1 逐步回归法

逐步回归法是采用 F 检验来考察预报因子与预报量相关性的显著性水平，逐项将影响显著的预报因子选人，并将相应的影响小的因子剔除，以建立最优数学模型的方法。

对于系统试验获取的 N 组测量数据 x_{k}\,,\,x_{1k}\,,\,x_{2k}\,,\,\cdots,\,x_{m k}\,(\,k =1,2,\cdots,N) ,要求建立 y 与 x_{i} 之间的最佳回归方程

y\;=\;\theta_{0}\:+\:\theta_{1}x_{1}\:+\:\theta_{2}x_{2}\:+\:\cdots\:+\:\theta_{m}x_{m}

上述方程中的有些 x_{i} 与 y 无关，其对应的 \theta_{i} 应等于零。我们的目的是从 x_{1},x_{2},\cdots,x_{m} 中选出对 y 影响最大的因子，以构成最优数学模型。具体做法是，在整个候选模型集的各个元素 x_{i} 中,按其对预报量 y 作用的显著性水平挑选出一个最重要的元素，先建立只包含这个元素的回归方程；接着对剩下的其他元素计算偏回归平方和，再引人一个最显著元素，建立具有两个元素的回归方程；之后，每引人一个元素或从回归方程中剔除一个元素，都要对回归方程中的每个元素作显著性检验，把最不显著的元素从方程中剔除，并从不属于回归方程的元素中挑选最显著的元素进人方程。反复选人和剔除，直到回归方程既不需要再引入新元素，也不能剔除任-元素为止。这时，回归方程中的所有元素都是显著性元素，此方程即为 F 检验法所确定的最优数学模型。

逐步回归法可分以下4 步进行[10]

（1）确定模型候选元素。根据系统的物理意义选定候选的模型元素，形成候选模型集。

（2）计算相关矩阵。对所有的候选项，计算相关矩阵，正则化为主对角线元素为1的矩阵

50

\left(\begin{array}{l l l l l}{r_{11}}&{r_{12}}&{\cdots}&{r_{1m}}&{r_{1y}}\\ {r_{21}}&{r_{22}}&{\cdots}&{r_{2m}}&{r_{2y}}\\ {\cdots}&{\cdots}&{\cdots}&{\cdots}&{\cdots}\\ {r_{m1}}&{r_{m2}}&{\cdots}&{r_{m m}}&{r_{m y}}\\ {r_{y1}}&{r_{y2}}&{\cdots}&{r_{y m}}&{r_{y y}}\end{array}\right)

式中

r_{i j}\,=\,l_{i j}/\,\sqrt{l_{i i}l_{j j}}

l_{i j}\;=\;\sum_{k\,=\,1}^{N}\,(\,x_{i k}\,-\,\bar{x}_{i}\,)\,(\,x_{j k}\,-\,\bar{x}_{j}\,)

\bar{x}_{i}\;=\;\frac{1}{N}\sum_{k\,=\,1}^{N}x_{i k}\;\qquad(\,i\,,j\;=\;1\,,2\,,\cdots,m\,,y\,)

由此构成线性回归的法方程

\begin{array}{r l r}{\lefteqn{r_{11}\hat{\theta}_{1}^{\prime}\,+\,r_{12}\hat{\theta}_{2}^{\prime}\,+\,\cdots\,+\,r_{1m}\hat{\theta}_{m}^{\prime}\,=\,r_{1y}}}\\ &{}&\\ {r_{21}\hat{\theta}_{1}^{\prime}\,+\,r_{22}\hat{\theta}_{2}^{\prime}\,+\,\cdots\,+\,r_{2m}\hat{\theta}_{m}^{\prime}\,=\,r_{2y}}\end{array}

r_{m1}\hat{\theta}_{1}^{'}\,+\,r_{m2}\hat{\theta}_{2}^{'}\,+\,\cdots\,+\,r_{m m}\hat{\theta}_{m}^{'}\,=\,\,r_{m y}

式中： \hat{\theta}_{i}^{'}\ =\ \hat{\theta}_{i}\ \sqrt{l_{i i}/l_{y y}}\,,\hat{\theta}_{i} 为 \theta_{i} 的估计值。

（3）筛选模型候选元素。

\textcircled{1} 判断已选元素和待选元素。令 f_{i}=\left.r_{i y}r_{y i}/\,r_{i i}\right. ,可以根据 f_{i} 的符号判定 x_{i} 是否已选人模型。 f_{i}\!<\!0 的元素为已选人模型的元素(已选元素),而 f_{i}\!>\!0 的元素为未选人模型的元素（待选元素）。

\textcircled{2} 剔除已选元素和变换。对已选元素计算其对回归方程的贡献 v_{i}^{2}=\mid f_{i}\mid ,找出其中最小者 v_{\mathrm{min}} ,判断下式是否成立

v_{\mathrm{min}}^{2}(\,N\mathrm{~-~}m\,\mathrm{~-~}1)/r_{s y}<\,F_{a}(\,1\,,N\mathrm{~-~}m\,\mathrm{~-~}1)

若式(3-12)成立,说明它所对应的 x_{\mathsf{m i n}} 贡献很小,应从模型中剔除，并作下列矩阵变换

r_{i j}\,=\,\left\{\!\!\begin{array}{l l}{{r_{i j}\,-\,r_{i k}r_{k j}/\,r_{k k}\quad}}&{{(i\not=k\,,j\not=k\,)}}\\ {{r_{k j}/\,r_{k k}\quad}}&{{(i\,=\,k\,,j\not=k\,)}}\\ {{-\,\,r_{i k}/\,r_{k k}\quad}}&{{(i\not=k\,,j\,=\,k\,)}}\\ {{1/\,r_{k k}}}&{{(i\,=\,k\,,j\,=\,k\,)}}\end{array}\!\!\right.

式中： \pmb{k} 为对应于 x_{\operatorname*{min}} 的下标。上述变换的计算结果， r_{i y} 给出 \hat{\theta_{i}^{'}} r_{y y} 给出标准残差平方和， r_{i j} 给出 \left(\mathbf{\nabla}r_{i j}\right)^{\mathrm{~-~}1} 矩阵的相应元素。

若式（3-12）不成立，表示无任何元素需要剔除。

\textcircled{3} 选人待选元素和变换。对待选元素计算其对回归方程的贡献 v_{i}^{2}=\mid f_{i}\mid ,找出其中最大者 \pmb{v}_{\mathrm{max}} ,判断下式是否成立

v_{\mathrm{max}}^{2}(N\mathrm{~-~}m\mathrm{~-~}2)/(r_{y y}\mathrm{~-~}v_{\mathrm{max}}^{2})\geqslant F_{\alpha}(1,N\mathrm{~-~}m\mathrm{~-~}2)

若式(3-14)成立,说明它所对应的 x_{\mathrm{{max}}} 贡献较大，应选人模型,并作式(3-13)的矩阵变换,其中 \pmb{k} 为对应于 x_{\tt m a x} 的下标。

若式（3-14）不成立，说明无任何元素需要选人回归方程。

若既无已选元素需要剔除，也无待选元素需要选人，所得方程即为最优回归方程。

\circledast 计算回归结果。

残差平方和 \begin{array}{r l}&{Q=l_{s p}r_{s p}}\\ &{\sigma=\sqrt{{l_{y}}{r_{g}}/{\left({N-m}\right)}}}\\ &{R=\sqrt{1-r_{s p}}}\\ &{F=(N-m-1)R^{2}/[\left({m\left(1-R^{2}\right)}\right]}\\ &{\hat{\theta}_{i}=\ r_{i y}\sqrt{{l_{y}}/{l_{i a}}}}\\ &{\sigma_{i}=\sigma\sqrt{{r_{i a}}/{l_{i a}}}}\\ &{\hat{\theta}_{0}=\bar{y}-\frac{\sqrt{1}}{\sqrt{1-\hat{\theta}}}\hat{\theta}_{i}\bar{x}_{i}}\end{array}
回归方程的标准差
复相关系数
F 检验值
回归系数
回归系数的标准差
常数项

在处理实际问题时，往往明确要求某些模型项进人回归方程。例如，多项式形式的飞行器气动力数学模型必须包含重要的线性项。为此,在采用逐步回归法进行模型辨识时，可以先将线性项直接选人回归方程，然后再对非线性项进行筛选，称之为修正的逐步回归法[111。

3.3.2 主成分分析法

主成分估计是克服回归方程系数矩阵复共线性所带来的困难，改进线性模型参数估计的一种常用方法。这里，采用主成分分析的基本思想和方法对线性回归方程中的预报因子进行筛选，以确定最优的数学模型结构。

对于线性模型(3-5)和系统试验获取的 N 组测量数据 y_{k} 1k，2k，"，mk（k=1,2，,N）,构成线性回归方程

\mathbf{y}\:=\:\theta_{0}\mathbf{1}\:+\:\mathbf{X}\pmb{\theta}\:+\:\pmb{\varepsilon}

式中 \mathbf{y}\!\!\longrightarrow\!\!N 维矢量,预报量测量数据；

_{1\longrightarrow N} 维矢量，其元素均为1；
\pmb{X}\mathrm{-}\!\!\longrightarrow\!\!\!N\times\pmb{m} 维矩阵，预报因子测量数据；
\theta_{0} -一常数项，待估计参数；
\theta\!\cdots m 维矢量，待估计参数；
\varepsilon\!-\!N 维矢量，测量噪声序列。

对其正则化，即令

\begin{array}{c}{{y_{k}^{'}\,=\,(\,y_{k}\,-\,\bar{y}\,)/\,S_{y}}}\\ {{{}}}\\ {{x_{i k}^{'}\,=\,(\,x_{i k}\,-\,\bar{x}_{i}\,)/\,S_{i}}}\end{array}

S_{\,y}^{2}\;=\;\sum_{k\,=\,1}^{N}\,(\,y_{k}\:-\:\overbar{y}\,)\,(\,y_{k}\:-\:\bar{y}\,)

\overline{{y}}\;=\;\frac{1}{N}\sum_{k\,=\,1}^{N}y_{k}

\ddot{x}_{i}\,=\,\frac{1}{N}\sum_{k\,=\,1}^{N}x_{i k}\qquad(\,i\,=\,1\,,2\,,\cdots,m\,)

得

\mathbf{y}^{\prime}\;=\;\pmb{X}^{\prime}\pmb{\theta}^{\prime}\;+\;\pmb{\varepsilon}^{\prime}

\pmb{\theta} 的估计值 \pmb{\hat{\theta}} 与 \pmb{\theta}^{\prime} 的估计值 \hat{\pmb{\theta}}^{\prime} 之间具有下列关系

\hat{\theta}_{i}\,=\,(\,S_{y}/S_{i}\,)\,\hat{\theta}_{i}^{\prime}

常数项 \theta_{0} 的估计值 \boldsymbol{\hat{\theta}}_{0} 为

\hat{\theta}_{0}\;=\;\bar{y}\;-\;\sum_{i\;=\;1}^{m}\hat{\theta}_{i}\bar{x}_{i}

考虑正则化的线性回归方程（3-16），为方便起见，略去矢量和矩阵的上标，即

\pmb{y}\;=\;\pmb{X}\pmb{\theta}\;+\;\pmb{\varepsilon}

假设矩阵 (\pmb{X}^{\mathrm{T}}\pmb{X}) 的 _m 个特征值为 \lambda_{1}\!\geqslant\!\lambda_{2}\!\geqslant\!\cdots\!\geqslant\!\lambda_{m} ，其对应的标准正交特征矢量为 P_{1},P_{2},\cdots,P_{m} ，则有

X^{\mathrm{{T}}}X\,=\,P A P^{\mathrm{{T}}}

式中

\begin{array}{c}{{{\bf A}\,=\,\mathrm{diag}(\,\lambda_{1},\lambda_{2},\cdots,\lambda_{m}\,)}}\\ {{{\bf P}\,=\,\left(\,P_{1},P_{2}\,,\cdots,P_{m}\,\right)}}\end{array}

令 \pmb{Z}=\pmb{\Sigma}\pmb{P} ,矩阵 \mathbf{Z} 的列矢量 \mathbf{Z}_{1},\mathbf{Z}_{2},\cdots,\mathbf{Z}_{m} 构成了 \pmb{m} 个主成分。这 _{m} 个主成分具有如下性质：

\overline{{{z}}}_{i}\;=\;\frac{1}{N}\sum_{k\,=\,1}^{N}z_{i k}\;=\;0\qquad(\,i\;=\;1\,,2\,,\cdots,m\,)

S_{i j}^{\,^{\ast\,2}}\,=\,\,\sum_{k=1}^{N}\,(\,z_{i k}\,-\,\overline{{z}}_{i}\,)\,(\,z_{j k}\,-\,\overline{{z}}_{j}\,)\,=\,\left\{\begin{array}{l l}{{\lambda_{i}\,}}&{{\,\imath\,=\,\jmath}}\\ {{0}}&{{\,i\,\neq\,j}}\\ {{(\,i\,,j\,=\,1,2,\cdots,m\,)}}\end{array}\right.

\boldsymbol{r}_{i j}^{\star}=\frac{\boldsymbol{S}_{i j}^{\star\,2}}{\boldsymbol{S}_{i i}^{\star}\boldsymbol{S}_{j j}^{\star}}=\left\{\begin{array}{l l}{1}&{i=j}\\ {0}&{i\neq j}\end{array}\right.\qquad(\,i\,,j=1\,,2\,,\cdots,m\,)

表明 m个主成分之间相互独立、正交,其偏差平方和逐渐递减,即\lambda_{1}\geq\lambda_{2}\geq\cdots\geq\lambda_{m}0

引人新参数 β= PTθ,代人式(3-17)得

\pmb{y}\pmb{\textrm{=}}\pmb{Z}\pmb{\beta}+\pmb{\varepsilon}

式中 Z^{\mathrm{T}}Z=A 。

特征值 \lambda_{i} 度量了第 _i 个主成分 \mathbf{Z}_{i} 在 N 次试验中取值变化的大小。如果 \lambda_{i}{\approx}0 ,则该主成分在 N 次试验中取值的变化很小，对回归方程的贡献也就很小，可以从回归方程中剔除。

假设 \lambda_{r+1}\,,\lambda_{r+2}\,,\cdots,\lambda_{m} 接近于零,则剔除主成分 {\bf Z}_{r+1}\,,{\bf Z}_{r+2}\,, ： \cdot,\mathbf{Z}_{m\circ}\ \beta 的前 ^r 个分量 \pmb{\beta}_{\textup{I}}=(\,\beta_{1}\,,\,\beta_{2}\,,\cdots,\,\beta_{r}\,)^{\textup{T}} 采用最小二乘估计,后 \left(\textit{\textbf{m}}-\textit{\textbf{r}}\right) 个分量 \beta_{n}=(\beta_{r+1},\beta_{r+2},\cdots,\beta_{m})^{\scriptscriptstyle\mathrm{T}} 以0作为估计值。为此,将矩阵 \pmb{\Lambda} 和 \pmb{P} 分块为

\begin{array}{r}{\textbf{A}=\left.\left(\begin{array}{c c}{\textbf{A}_{\mathrm{I}}}&{\ \ 0}\\ {\mathbf{0}}&{\ \textbf{A}_{\mathrm{I}}}\end{array}\right)\quad\quad\textbf{\textit{P}}=\left.\left[\begin{array}{c c}{\textbf{p}_{\mathrm{I}}}&{\ \textbf{p}_{\mathrm{I}}}\end{array}\right]\right.}\end{array}

于是

\hat{\pmb{\beta}}_{1}\,=\,\left[\pmb{\Lambda}_{1}^{\,\,\,-1}\quad0\right]\pmb{Z}^{\mathrm{T}}\pmb{y}

从而

\hat{\pmb\theta}\ =\ \pmb P_{1}[\pmb A_{1}^{-1}\quad0]\pmb Z^{\mathrm{T}}\pmb y

\pmb{\hat{\theta}} 称为 \pmb{\theta} 的主成分估计。

主成分估计的一个关键问题是如何确定 \pmb{\tau} 。关于 \pmb{r} 的确定问题可参考有关文献 [12\!\sim\!15]

基于主成分分析筛选变量的具体算法[16]:对于特征值 \lambda_{1}\geqslant \lambda_{2}\!\ge\!\cdots\!\geqslant\lambda_{m} ，若 \lambda_{m}\!\approx\!0 ，表示相应的主成分 \mathbf{Z}_{m} 对模型的贡献最小，找出此特征值对应的特征矢量 \pmb{P_{m}} 中所占权数最大的分量，设为 \pmb{\hat{p}_{i m}} ，即是说在贡献最小的主成分中起主要作用的是第 _i 个变量，因此决定剔除第 _i 个变量。之后再作主成分分析，进行变量的剔除，直至最小的特征值不是很小为止。

3.3.3 正交最小二乘法

在非线性系统辨识中，最经常考虑的用于非线性近似的表达式有沃特拉（Volterra）级数或其他相关的函数表达式。这样做的一个主要的困难是往往对非常简单的非线性系统进行辨识时，需要非常繁多的参数。多项式模型是动力学系统中最为普遍的近似表达式之一，它具有很多优点，其参数是线性的，但有时即使是中等程度的阶数,其模型项也是相当的多。

20世纪80年代后期，为有效地解决在非线性模型辨识中的两大主要困难，即数值病态和结构选择问题，英国系统辨识专家比林斯(Billings)等人发展了正交最小二乘技术。该项技术被广泛应用于包括非线性气动力在内的非线性系统的建模中[17,18]

1）正交最小二乘参数估计考虑参数线性的多项式模型

y(k)\,=\,\sum_{i\,=\,1}^{p}\theta_{i}x_{i}(\,k\,)\,+\,\varepsilon(\,k\,)\qquad(\,k\,=\,1,2,\cdots,N)

式中 \mid x_{i}(\,k\,)\,\mid_{i\,=\,1}^{\!\,\,\rlap/p} 多项式模型中的不同项；

\pmb{\dot{p}} —系数的个数；

\epsilon\left(k\right) 一一均值为零的白噪声序列。

式(3-19)可以认为是在由矢量组 \{\,\pmb{x}_{i}\}_{i}^{\,\pmb{p}}=\mathbf{1} 张成的 \pmb{\hat{p}} 维欧氏空间中的估计问题，由欧氏空间理论知，对于 \pmb{\dot{p}} 维欧氏空间中的任一基,均可找到一组正交基 w_{1},\cdots,w_{p}, ，于是,式(3-19)可通过正交变换化成 \pmb{\dot{p}} 维欧氏空间中正交基的线性组合形式

y(k)=\sum\limits_{i=1}^{p}g_{i}w_{i}(k)+\varepsilon(k)

其中 \{g_{i}\}_{i=1}^{\,p} 是常系数， \{\ w_{i}\}_{i=1}^{\pmb{\phi}} 是由 \{\,\pmb{x}_{i}\}_{i=1}^{\,\pmb{p}} 生成的构成 \pmb{\hat{p}} 维欧氏空间的正交基。由 w_{i} 之正交性，可求得观测量 \b{y} 在正交基 w_{1} \cdots,\pmb{w}_{p} 上的投影 g_{1},\cdots,g_{p}\circ 田 {\pmb{\ g}}_{i}{\pmb{\psi}}_{i} 之大小,即可方便地判断出模型中该项贡献的大小，从而对模型实施筛选，进行模型辨识，同时进行参数的估计。

\{w_{i}\}_{i=1}^{p} 是在采样的数据段正交化后的序列，满足

\overline{{w_{i}(\,k\,)w_{j+1}(\,k\,)}}\;=\;{\bf0}\;\;\;\;\;\;\;\;\;(\,i\;=\;1\,,2\,,\cdots,j\,)

式中，上横线表示对时间取平均。

根据式(3-20)和式(3-21）,可以得到系数 \{\,g_{i}\,\}_{i=1}^{\ p} 的估计值

56

\hat{g_{i}}\;=\;\frac{\widehat{y(\,k\,)\,w_{i}(\,k\,)}}{\overline{{{w_{i}^{2}(\,k\,)}}}}\qquad(\,i\;=\;1,2,\cdots,\rho\,)

然后可得到式（3-19)中未知系数的估计值

\hat{\theta}_{m}\;=\;\sum_{i\,=\,m}^{\hbar}\hat{g_{i}}v_{i}\;\;\;\;\;\;\;\;\;(\;m\;=\;1\,,2\,,\cdots,\rlap/p)

其中

\begin{array}{r}{\eta_{i j}=~1}\\ {\eta_{i}=-~\displaystyle\sum_{r_{i}=\ m}^{i-1}\eta_{r i}v_{r}}&{(i~=~m~+1,m~+2,\cdots,p)}\\ {\eta_{i j}~=~\displaystyle\frac{\overline{{w_{j}(k)\,x_{j}(k~)}}}{\overline{{w_{i}^{2}(k)}}}~~~~~}&{(i~=~1,2,\cdots,j~-1;j~=~2,3,\cdots,p)}\end{array}

上面的正交化过程采用格拉姆-施密特（Gram-Schmidt)正交化方法。其基本步骤是：首先取 x_{1},x_{2},\cdots,x_{p} 中任一项作为正交基中的第一个矢量，可令

{\pmb w}_{1}\,=\,{\pmb x}_{1}

选定一个正交基之后，根据 x_{2} 与 x_{1} 之间的关系，可确定第二个正交基。

再令第二个正交基为

\pmb{\{\psi_{2}}\;=\;\pmb{x_{2}}\,-\;\eta_{12}\,\pmb{w_{1}}}

由正交特性,根据正交矢量之内积为0,可确定系数 \pmb{\eta}_{12} ，记二矢量间的内积为 (\,{\pmb x}_{1},{\pmb x}_{2}) ,有

\begin{array}{r l r}{\left(\,\pmb{\psi}_{1},\pmb{w}_{2}\,\right)\!\!\!}&{=}&{\!\!\!\!\!\left(\pmb{x}_{2}\,-\,\eta_{12}\,\pmb{x}_{1},\pmb{x}_{1}\,\right)\,=}\\ &{}&{\!\!\!\!\!\left(\pmb{x}_{2}\,,\pmb{x}_{1}\right)\,-\,\eta_{12}(\,\pmb{x}_{1}\,,\pmb{x}_{1}\,)\,=\,0}\end{array}

于是有

\eta_{12}\;=\;\frac{\displaystyle\sum_{k\,=\,1}^{N}w_{1}(\,k\,)\,x_{2}(\,k\,)}{\displaystyle\sum_{k\,=\,1}^{N}w_{1}(\,k\,)\,w_{1}(\,k\,)}

同理可构造

\begin{array}{c}{{\displaystyle w_{i}(\,k\,)\,=\,x_{i}(\,k\,)\,-\,\sum_{j=1}^{i-1}\eta_{j i}w_{j}(\,k\,)}}\\ {{\displaystyle\sum_{\eta_{j i}}^{N}w_{j}(\,k\,)\,x_{i}(\,k\,)}}\\ {{\displaystyle\sum_{k\,=\,1}^{N}w_{j}(\,k\,)\,w_{j}(\,k\,)}}\end{array}\quad\begin{array}{c}{{\displaystyle(\,i\,=\,2,3,\cdots,p\,)}}\\ {{\displaystyle(\,i\,=\,2,3,\cdots,p\,)}}\end{array}

于是，利用格拉姆-施密特正交方法可将式（3-19)转化为

y(k)=\sum\limits_{i=1}^{p}g_{i}w_{i}(k)+\varepsilon(k)

式中， g_{i} 满足

g_{\pmb{\mathscr{s}}\!}\,=\,\theta_{\pmb{\mathscr{p}}}

g_{j}~=~\theta_{j}~+~\sum_{i\,\,i\,j\,i}^{\,\,\,\,\,\,\,\beta}\eta_{j i}\theta_{i}~~~~~~~~(j~=~\!\!\!\!\slash~-~1~,~\!\!\!\!\slash~-~2,\cdots,1)

由式(3-23)及式(3-27）,可得 \pmb{\hat{g}}_{L S} （最小二乘估计）

\hat{g}_{i L S}\,=\,\frac{\displaystyle\sum_{k\,=\,1}^{N}y(k)\,w_{i}(k)}{\displaystyle\sum_{k\,=\,1}^{N}w_{i}(k)\,w_{i}(k)}

由此可得关于 \pmb{\theta} 的估计 \hat{\pmb{\theta}}

\hat{\theta}_{p}\;=\;\hat{g}_{p}

\hat{\theta}_{j}\ =\ \hat{g}_{j}\,-\,\sum_{i\,\,j+\,{\bf1}}^{\bar{p}}\eta_{j i}\hat{\theta}_{i}\qquad(j\ =\ \bar{p}\,-\,1\,,\,\beta\,-\,2\,,\cdots\,,1)

上述的正交化过程实际上是把矩阵 \pmb{X} 进行 {\pmb Q}{\pmb R} 分解，即化为一正交阵与一上三角阵之积。

引理：设 \pmb{A}\in\pmb{R}^{m}^{\times\ n} \operatorname{rand}(\,\mathbf{A}\,)=n\;,m\!\geqslant\!n ,则 \pmb{A} 有分解式

\mathbf{A}\ =\ Q\mathbf{R}

其中 \boldsymbol{Q}\in\mathbb{R}^{m\times n} ， \pmb{R}\in\mathbb{R}^{n\times n} ,且满足 \pmb{Q}^{\mathrm{T}}\pmb{Q}=\pmb{I},\pmb{R} 为非奇异三角阵。

设 F\in\mathbb{R}^{n\times\star} ,且 \boldsymbol{F}=\mathtt{d i a g}(\,r_{11}\,,r_{22}\,,\cdots,r_{n n}\,)\,, r_{i i} 为 \pmb{R} 矩阵的对 角元素，则有

{\bf A}\ =\ Q F F^{-1}R\ =\ Q_{1}R_{1}

Q_{1}^{\mathsf{T}}Q_{1}\;=\;\pmb{F}^{\mathsf{T}}Q^{\mathsf{T}}Q\pmb{F}\,=\,\pmb{F}^{\mathsf{T}}\pmb{F}\,=\,\mathrm{diag}(\,r_{11}^{2},r_{22}^{2},\cdots,r_{n n}^{2}\,)

式中： \pmb{R}_{1}=\pmb{F}^{-1}\pmb{R} ,仍为上三角阵，但其对角元素全为1。这就是上述正交化过程的矩阵表述。其中

\pmb{{\cal W}}_{1}\,=\,\pmb{{\cal Q}}_{1}

\pmb{\eta}\,=\,\pmb{R}_{1}

\pmb{g}\ =\ \pmb{R}_{1}\pmb{\theta}

2）结构确定

在多项式模型中，模型项数随着阶数的增加会迅速增加，在这方面有许多有效的方法，其中之一就是比林斯于1989年提出的误差缩减率试验法[19]。考虑等效模型(3-20),设模型中有 \scriptstyle n_{\theta} 项,对其取积并求时间平均，有

\overline{{{y^{2}(\,k\,)}}}\;=\;\sum_{i\,=\,1}^{\mathfrak{n}_{\theta}}g_{\,i}^{2}\:\overline{{{w_{\,i}^{2}(\,k\,)}}}\;+\;\overline{{{\xi}^{2}(\,k\,)}}

如果模型中没有任何项，即 {\pmb n}_{\pmb\theta}={\bf0} ，此时的平均二乘预测误差最大，并等于 \sqrt{y^{2}(k)} 。从式(3-37)可知，每当模型中引人一项，比如第 _i 项 g_{i}w_{i}(k) ,则预测误差将减少 g_{\,i}^{2}w_{\,i}^{\,2}(\,k\,) 。设该项减少与总误差的比为

[\,E R R\,]_{_{i}}\approx\frac{\hat{g}_{_{i}}^{2}\,\overline{{{w_{i}^{2}(k\,)}}}}{\overline{{{y^{2}(k\,)}}}}\qquad(\,i\,=\,1,2,\cdots,n_{\theta})

这样的处理使我们不必对候选模型中的每一项进行估计，计算其显著性和对观测数据的贡献，而且ERR检验是正交估计算法的一附带结果。

\left[\boldsymbol{E}\boldsymbol{R}\boldsymbol{R}\right]_{i} 的数量值提供了一个是否包含该项进人模型的标志，根据各个候选项的误差缩减率的大小可以方便地确定各项的相对重要程度，误差缩减率越大，则相对而言此项越重要，在模型选择时具有优先地位。模型项数的确定，可以参考最终预测误差准则、赤池信息准则、贝叶斯信息判据、模型或施瓦茨（Schwarz）

信息判据等。另一种办法是观察相应各项的ERR 值,若出现ERR值的突然大幅度降低，则预示着截断点的到来。

例：考虑如下非线性映射模型

\begin{array}{l}{\left\{x(k)\,=\,1.0\,-\,1.4x^{2}(k\,-\,1)\,+\,y(k\,-\,1)\right.}\\ {\left.y(k)\,=\,0.3x(k\,-\,1)\,+\,\varepsilon(k\,)\right.}\end{array}

其中， \varepsilon\left(\boldsymbol{k}\right)\sim N(0,9.2\times10^{-4}) ，估计结果的前6项如表3-1所列。

表 3-1 基于 ERR 值的模型选择示例

<html>

模型项	参数估计值	ERR 值
x²(k -1)	-1.3993	0.0849
Constant	1.0004	0.83815
r²(k-1)x(k-3)	- 0.0004	0.425× 10~
x(k-2)	0.2993	0.0769
r(k-1)x(k-2)x(k-3)	- 0.0015	0.185 × 10 ~ 7
x(k - 1)x²(k-3)	-0.0005	0.431 x 10 ~ 7

</html>

从表 3-1 中第 3 列的 ERR 值数据可以看出,第 5 行以下的ERR值很小，模型可以在此处截断，使模型仅包含前4项，再用4项模型重新进行参数估计和判断，得到估计的最终结果为

x\left(k\right)\,=\,0.99\,-\,1.39x^{2}(\,k\,-\,1)\,+\,0.30x\left(\,k\,-\,2\right)

考察模型选项是否满足要求，设模型中已包含了 \pmb{n}_{\pmb{\theta}} 项,当

\sum_{i\,=\,1}^{n_{\theta}}\,[\,E R R\,]_{i}\times100\geqslant C_{s}\qquad(1\leqslant n_{\theta}\leqslant p\,)

说明所选模型项已足够了。 C_{s} 为模型完备水平，根据实际情况给定。如果考虑现有的所有模型项，式（3-39）仍不满足，则说明候选模型不完备，需要重新建模，或对模型进行改进，考虑其他模型。这是正交最小二乘估计方法在模型辨识上的一项重要功能。

对于具有多输人-多输出的多变量模型，可以用类似的方法进行估计和结构确定[18]。

正交最小二乘估计和传统的主成分估计虽然都是确定模型中的主项，但前者不仅考虑了回归函数矩阵，同时考虑了待估参数，即用二者之积在观测量中所占的比重作为选项的标准，而主成分估计仅是考虑函数矩阵的特征值大小，因而它是不完备的，依赖于刻度因子的选取。正交最小二乘估计采用格拉姆-施密特正交化方法进行模型变换，避免了矩阵求逆和求特征值的运算。而且当矩阵条件数很大时，矩阵求逆和求特征值会导致较大的误差，而矩阵求逆或求特征值正是主成分估计方法所不可避免的。

3.3.4 数据分割技术

数据分割是系统建模中经常使用的一种实用技术，它能够在-定程度上克服非线性给系统建模所带来的困难。当然，数据分割技术并不是一种独立的建模方法，它需与前述优选算法结合使用，以提高所建模型的准度。

设有系统

y(\mathbf{\boldsymbol{\mathit{t}}}\,)\,=\,f{\bigl[}\,x_{1}(\,\iota\,)\,,x_{2}(\,\iota\,)\,,\cdots,x_{m}(\,\iota\,)\,{\bigr]}

期望通过数据分割消除 _y(t) 对某个变量 x_{i}\left(t\right) 的非线性依赖性。为此,对 x_{i}(t) 的取值区间进行分割

x_{i0}<x_{i1}<x_{i2}<\cdots<x_{i p}

并在子集 \{\,x_{1}\,,\cdots,x_{i\,-\,1}\,,x_{i\,+\,1}\cdots,x_{m}\,\} 上重新定义 y(t)

{\bf y}\left(\,\overline{{x}}_{i}\,,t\,\right)=

\begin{array}{r}{\left\{f_{1}\big[x_{1}(t),\cdots,x_{i-1}(t),x_{i+1}(t),\cdots,x_{m}(t)\big]\right.x_{i}\in[x_{i0},x_{i1})}\\ {\left.f_{2}\big[x_{1}(t),\cdots,x_{i-1}(t),x_{i+1}(t),\cdots,x_{m}(t)\big]\right.x_{i}\in[x_{i1},x_{i2})}\\ {\qquad\qquad\qquad\qquad\left.\cdots\cdots\cdots\cdots}\\ {\left.f_{p}\big[x_{1}(t),\cdots,x_{i-1}(t),x_{i+1}(t),\cdots,x_{m}(t)\big]\right.x_{i}\in[x_{i\beta-1},x_{i\beta}]}\end{array}

式中

\bar{x}_{i}\,=\,\frac{x_{i j-1}\,+\,x_{i j}}{2}\qquad(j\,=\,1,2,\cdots,p\,)

随着分割的细化,x;的子区间变小,在各子区间内,y随x;的变化可以忽略。

现以偏航力矩系数Cn为例，阐述数据分割技术在飞行器气

动力模型辨识中的应用[20]

假设飞机作横侧机动,但攻角有一变化范围，为 20^{\circ}\!\sim\!30^{\circ} 。在此攻角范围内，由于分离对升力面的影响，横侧气动力和力矩系数通常非线性地依赖于攻角 \pmb{\alpha} ,即有

C_{n}\;=\;C_{n}\left(\,\alpha\,,\beta\,,\phi\,,r\,,\delta_{a}\,,\delta_{r}\,\right)

采用数据分割技术，在如下的几个分离的子区间内对飞行数据进行分析

\left\{\begin{array}{l l}{{C_{n}\,(\,\overline{{{\alpha}}}\,=\,21^{\circ}\,)\,=\,C_{n}\,(\,{\beta},{\phi}\,,r\,{,}\delta_{a}\,,\delta_{r}\,)_{\alpha\,\in\,[\,20^{\bullet}\,,22^{\bullet}\,)}}}\\ {{\null}}\\ {{C_{n}\,(\,\overline{{{\alpha}}}\,=\,23^{\circ}\,)\,=\,C_{n}\,(\,{\beta},{\phi}\,,r\,,\delta_{a}\,,\delta_{r}\,)_{\alpha\,\in\,[\,22^{\bullet}\,,24^{\bullet}\,)}}}\\ {{\null}}\\ {{\qquad\qquad\qquad\qquad\cdots\cdots\cdots\cdots}}\\ {{C_{n}\,(\,\overline{{{\alpha}}}\,=\,29^{\circ}\,)\,=\,C_{n}\,(\,{\beta},{\phi}\,,r\,,\delta_{a}\,,\delta_{r}\,)_{\alpha\,\in\,[\,28^{\bullet}\,,30^{\bullet}\,]}}}\end{array}\right.

也就是说，将所有 \alpha\in[20^{\circ},22^{\circ}) 的数据放在一组进行分析；将所有\alpha\in\{22^{\circ},24^{\circ}\} 的数据作为第二组进行分析；依次类推。

如果在某个子区间内出现 C_{n} 对 \pmb{\alpha} 的依赖性，则对该子区间再作分割。当然，必须保证分割后的每个子区间内包含足够的数据点。

这样，就可以采用前述的建模准则和优选算法，在 \pmb{\alpha} 的各个子区间进行模型辨识和参数估计，以建立 C_{n} 的模型，模型参数为该子区间中点 \breve{\pmb{\alpha}} 处的气动导数值。

利用数据分割技术，可以将多次机动数据放在一起进行分析处理。

3.4 神经网络建模方法

传统的系统建模方法，首先需要根据物理机理、试验观测、建模经验等确定系统输出与输人之间的关系式，给出候选模型集。然后，再应用模型辨识和参数估计方法确定最优的数学模型。这对于线性系统来说是容易实现的，但对于非线性系统，往往难以给出适当的数学模型结构，或者由于模型中的未知参数过多而无法辨识,或者由于非线性的影响模型辨识和参数估计十分困难。特别是对“黑箱”系统，无法给出候选模型集。神经网络系统理论的诞生和发展，为非线性系统建模开辟了一条新的途径。

由于神经网络能够逼近任意非线性映射，因而在非线性系统建模领域具有巨大的潜力。与传统的建模方法相比,基于神经网络的系统建模具有如下特点L21]：

（1）不要求建立实际系统的数学模型，因为神经网络已作为系统的一种模型,其可调参数反应在网络内部的连接权值和阀值上，通过调整这些权值和阀值，使网络输出逼近实际系统的输出。

（2）神经网络学习算法的收敛速度不依赖于系统的维数，只与网络及算法本身有关，而传统的建模方法中，辨识算法随模型待估计参数的增加而变得很复杂。

（3）神经网络作为实际系统的模型，实际上也是系统的一个物理实现，可以用于在线控制。

3.4.1 神经网络和学习算法

神经网络是模拟人脑神经思维机理和神经元细胞间结构的一种方法。它具有快速并行处理、高度容错、联想记忆和自组织学习能力等优点，并且可以逼近任意非线性函数，因而得到广泛应用。

神经网络的种类很多,在系统建模与控制中常用的有[22~24] :多层前馈网络、径向基函数网络、函数变换网络、霍普菲尔德网络、博尔茨曼机等。这里，仅介绍最常用的多层前馈网络及其学习算法。

1）多层前馈神经网络

多层前馈神经网络由一个输人层、一个或多个隐层和一个输出层构成，每层均含有若干个神经元。输人和输出层中神经元的个数是由问题本身决定的，隐层中神经元个数的选取目前还没有严格的理论指导。图3-1示出了三层前馈神经网络的结构。

网络中各神经元的输人-输出关系为

n e t_{i,k}\;=\;\sum_{j}\,(\,w_{i,j,k}O_{j,k-1}\,)\,+\,b_{i,k}

O_{i,k}\,=\,f(\,n e t_{i,k}\,)

式中 $n e t_{i,,,k}-$ 第 k 层第 _i 个神经元的输人；

O_{i,k} -该神经元的输出；bi,k—阀值；
\boldsymbol{w}_{i,j,k} 第 \pmb{k} 层第 _i 个神经元与第（k－1)层第 j 个神经元之间的连接权值；
f(\,\cdot\,) ——神经元的激励函数。

图 3-1 三层前馈神经网络

神经网络的学习算法要求激励函数至少是一次可微的。对于隐层神经元，激励函数一般取为 s 型函数，输人和输出神经元取为线性函数。例如

隐层神经元 f(\mathbf{\Delta}x)=\frac{1-\mathrm{e}^{\mathbf{\Gamma}^{a x}}}{1+\mathrm{e}^{-\mathbf{\Gamma}_{a x}}} 输人和输出神经元 f(\v{x}\,)=\v{x}

2）BP学习算法

神经网络通过对输人和输出样本的学习，调整神经元的连接权值和阀值，使网络输出拟合实际系统的输出。学习过程由正向传播和反向传播组成。在正向传播过程中，输人信号从输人层经隐层逐层处理，传向输出层。如果在输出层不能得到期望的输出，则转人反向传播，将误差信号沿原来的通路返回，通过修正各层神经元的权值和阀值，使误差信号最小。

对给定的输人和输出对，误差定义为

E\,=\,\frac{1}{2}\sum_{j\,=\,1}^{q}\,(\,d_{j}\,-\,O_{j\,,\,n}\,)^{2}

式中 \pmb{\pi} 神经网络总层数；

q 输出神经元的个数；
d_{j} --给定的输出。

误差利用当前的学习参数值在前向通道中计算。

学习参数 w_{i,j,k} 和 b_{i,k} 的修正公式为

\begin{array}{r}{w_{i,j,k}^{(r)}\;=\;w_{i,j,k}^{(r-1)}\;-\;\eta\Bigg(\frac{\partial E}{\partial w_{i,j,k}}\Bigg)^{(r)}\;}\\ {b_{i,k}^{(r)}\;=\;b_{i,k}^{(r-1)}\;-\;\xi\Bigg(\frac{\partial E}{\partial b_{i,k}}\Bigg)^{(r)}\;\;\;\;}\end{array}

式中 \boldsymbol{r} —迭代步数；

\pmb{\eta} 和 \xi 学习步长。

由式（3-44）和式（3-45)可得如下偏导数计算公式

\frac{\partial n e t_{i,k}}{\partial w_{i,j,k}}\:=\:O_{j,k-1}\quad\quad\frac{\partial n e t_{i,k}}{\partial b_{i,k}}\:=\:1\quad\quad\frac{\partial O_{i,k}}{\partial n e t_{i,k}}\:=\:f^{\prime}(\,n e t_{i,k})

记 {\partial E}/{\partial n e t_{i,k}}=\delta_{i,k} ，于是 \pmb{{\cal E}} 关于学习参数的偏导数可以表示为

\frac{\partial E}{\partial w_{i,j,k}}\,=\,\left(\frac{\partial E}{\partial n e t_{i,k}}\right)\left(\frac{\partial\,n e t_{i,k}}{\partial\,w_{i,j,k}}\right)=\,\delta_{i,k}O_{j,k-1}

\frac{\partial E}{\partial b_{i,k}}\:=\:\:\left(\frac{\partial E}{\partial n e t_{i,k}}\right)\left(\frac{\partial n e t_{i,k}}{\partial b_{i,k}}\right)=\:\delta_{i,k}

式(3-46)和式(3-47)中，神经元的输出 O_{j,k\,-\,1} 在前向通道中计算，即利用式（3-44）和式（3-45），由输人层通过各隐层到输出层，逐层递推计算。而 \delta_{i,k} 是输出误差对神经元输人的偏导数，需通过误差在神经网络上反向传播得到，即利用下式，由输出层经隐层向输出层，逐层反向递推计算。

\delta_{i\,,\,k}\,=\,\left\{\!\!\!\begin{array}{l}{{d_{i}\,-\,\,O_{i\,,\,n}}}\\ {{f^{\prime}(\,n e t_{i\,,\,k}\,)\sum_{j}\big(\,\delta_{j\,,\,k+1}\,w_{j\,,\,i\,,\,k+1}\,\big)}}\end{array}\!\!\right. \pmb{k} 为输出层其他

以上给出了神经网络学习算法的全部计算公式，这种学习算法称为误差反向传播算法，简称BP算法。

标准BP算法是一种简单的最速下降寻优算法，因而不可避免地存在一些明显的缺点：

（1）局部极小值问题。这是非线性最优化算法普遍存在的问题。

（2）学习步长的选择。如果 \pmb{\eta} 和 \xi 选择得太小，收敛速度减慢，相反， \pmb{\eta} 和 \xi 选择得太大,可能导致发散。

（3）收敛速度。在极小点附近，收敛速度缓慢。

迄今已提出了许多方法来克服标准BP算法的上述局限性，如各种自适应变步长 BP 算法[25,26] 、共轭梯度法[27] 、麦夸特-莱温伯格算法[28]、拟牛顿法[29] 、牛顿法[30]、卡尔曼滤波法[31]等。

3.4.2 非线性系统建模

对于一般的多输人-多输出非线性动态系统，可将输出看作是输人的非线性泛函，即

\begin{array}{r}{\left\{y_{1}(t)\,=\,f_{1}\big[\,x_{1}(\,\hat{\xi}\,)\,,x_{2}(\,\hat{\xi}\,)\,,\cdots\,,x_{m}\,(\,\hat{\xi}\,)\,\big]\right.}\\ {\,}\\ {\left.y_{2}(t)\,=\,f_{2}\big[\,x_{1}(\,\hat{\xi}\,)\,,x_{2}(\,\hat{\xi}\,)\,,\cdots\,,x_{m}\,(\,\hat{\xi}\,)\,\big]\right.}\\ {\,}\\ {\left.\qquad\qquad\cdots\cdots\cdots\cdots\cdots\right.}\\ {\,}\\ {y_{n}(t)\,=\,f_{n}\big[\,x_{1}(\,\hat{\xi}\,)\,,x_{2}(\,\hat{\xi}\,)\,,\cdots\,,x_{m}(\,\hat{\xi}\,)\,\big]}\end{array}

式中 \xi\!\in\!\left(\,-\,\infty\,,t\,\right]

f_{i} ——输人时间历程的非线性泛函。

假设系统无分叉现象，输出对输人的记忆时间是有限的，则可以用有限个采样值代替式（3-48）中的时间历程 x_{i}(\xi) ，从而将式（3-48）写成差分形式

\left\{y_{1}(k)\,=\,f_{1}[\,x_{1}(k),\cdots,x_{1}(k\,-\,p_{1});\cdots;x_{m}(k),\cdots,x_{m}(k\,-\,p_{m})\,]}\\ {y_{2}(k)\,=\,f_{2}[\,x_{1}(k),\cdots,x_{1}(k\,-\,p_{1});\cdots;x_{m}(k),\cdots,x_{m}(k\,-\,p_{m})\,]}\\ {\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\cdots.........}\\ {y_{n}(k)\,=\,f_{n}[\,x_{1}(k),\cdots,x_{1}(k\,-\,p_{1});\cdots;x_{m}(k),\cdots,x_{m}(k\,-\,p_{m})\,]}\end{array}\right.

这里的 f_{i} 为非线性函数。

根据式(3-49)即可建立该系统的神经网络模型。该系统可有两种或两种以上的神经网络模型结构,图3-2给出了两种最基本的模型结构。图中， \begin{array}{r}{\pmb{x}=\left[\,x_{1}\left(\,k\,\right),\cdots,x_{1}\left(\,k\,-\,p_{1}\,\right),\cdots,\,x_{m}\left(\,k\,\right),\cdots,\,\right.}\end{array} x_{m}\left(\boldsymbol{k}-\boldsymbol{\phi}_{m}\right)\left]^{\mathrm{T}},\boldsymbol{y}=\left[\,\boldsymbol{y}_{1}(\boldsymbol{k})\,,\boldsymbol{y}_{2}(\boldsymbol{k})\,,\cdots,\boldsymbol{y}_{n}(\boldsymbol{k})\,\right]^{\mathrm{T}}\circ

图3-2 非线性动态系统的神经网络模型

\left(\footnote{C o t h i s i s t h i s t h i s w i l l a d d r e v a t u r e.T e l}\right) 单个神经网络的模型结构； (\,b\,)\;\,n 个神经网络组成的模型结构。

图 3^{-2}(\,a\,) 为单个多层前馈神经网络的模型结构，输人和输出神经元分别为

_{x_{1}}(k),\cdots,_{x_{1}}(k-\rho_{1}),\cdots,_{x_{m}}(k),\cdots,_{x_{m}}(k-\rho_{m})

输出： y_{1}(\,k\,)\,,y_{2}(\,k\,)\,,\cdots,y_{n}(\,k\,)

学习准则为

J(\,\pmb\theta)\;=\;\sum_{\stackrel{i\,=\,1}{i\,=\,1}}^{n}\,(\,y_{i}\;-\;y_{i m}\,)^{2}

图 3{-}2(\,b\,) 为由 \pmb{n} 个多层前馈神经网络组成的模型结构，第 i 个神经网络的输人和输出神经元为

_{x_{1}}(k),\cdots,_{x_{1}}(k-p_{1});\cdots;x_{m}(k),\cdots,x_{m}(k-p_{m})

学习准则为

J(\,\pmb\theta_{i}\,)\;=\;(\,y_{i}\,-\,y_{i m}\,)^{2}

神经网络的隐层数通常取为1或2，隐层神经元的个数可根据具体问题选定，也可以应用有关神经网络结构的自学习方法来确定。

上述神经网络建模方法，实际上是将非线性动态系统看作“黑箱”问题，用神经网络来模拟系统的外部特性，从而使网络的输人输出与系统的输人输出相拟合。若系统是“灰箱”问题，即对系统有一定的先验知识，则建模时应充分利用这些先验知识，而仅对未知部分用神经网络模拟[32]

3.5基于小波分析的系统辨识方法

小波分析是20世纪80年代以来出现的新数学方法[33,34]由于小波分析在时域和频域都具有良好的局部化特性，在分析中具有变焦功能，其理论研究不断深化，应用范围迅速扩大,在函数论、算子论、偏微分方程、非线性分析、数值分析、信号处理与传输、图像分析和处理、天体物理以及分形理论等方面，都获得了重要的应用。

小波分析在信号去噪、频率辨识等方面都有了一般应用，在著名的应用软件MATLAB里就有这方面的例子和工具。小波在概率统计和系统辨识方面真正的应用研究还是近十年来的事，1993年米切尔(Michail)等将小波用于时变系统的辨识[35]，1992 年格列高里(Gregory)等将小波用于分形信号的辨识和估计[36],1994年安东尼亚茨（Antoniads）等将小波分析成功地应用在非参数密度估计和回归估计方面[37.38],发展了一套令人关注的新的非参数估计方法。小波估计相对于其他正交级数估计来说，具有较为理想的大样本性质，因此，在最近几年，基于小波分析的系统辨识方

法得到了广泛的研究[39.40]

3.5.1 小波分析方法

小波分析是为克服傅里叶分析在非线性分析和时频局部化等方面的缺陷而发展起来的，是对傅里叶分析的重大突破。傅里叶分析将信号分解成若干不同频率的正弦曲线的组合，小波分析则是将信号分解成由母小波的伸缩和平移构成的小波的组合。傅里叶变换中不包含信号在时间上的特征，从而丢失了信号的时间信息。它对于平稳信号或随时间变化不大的信号分析是十分合适的，给出近乎完美的结果。当信号中包含非平稳或暂态特性（如突变、漂移、事件起始和结束）时，傅里叶分析不适用。为解决傅里叶分析中无时间信息这一问题，盖柏提出了加窗傅里叶分析的概念，但由于其时频窗大小是固定的，而实际上我们希望对于高频的信息，时间间隔要相对的小，以得到较好的精度；对于低频信息，要求相对较大的时间间隔以给出完全的信息，即要求时频窗的大小随频率变化。因此盖柏变换仍然未能很好地解决时频局部化问题。小波变换则很好地解决了这一问题，满足了人们对信号分析的需要。自其思想形成以来，经过迈耶、迈拉特和道比切丝等人的研究[41,42],小波分析变成了系统的科学分析方法,其后更是得到了迅猛的发展,关于其理论研究和应用研究的文献浩如烟海。在国际互联网上也有大量的关于小波分析和应用的网站。感兴趣的读者可以参考有关小波方面的著作和文献，也可在相应的网站上寻找有关的资源[40]

迈耶对小波函数的定义为：函数 \phi(t) 是小波函数,如果满足

C_{\psi}\,=\,\int_{0}^{+\infty}\,\frac{|\,\hat{\psi}(\,\omega)\,|^{\,2}}{\omega}\mathrm{d}\omega<+\,\infty

或

\int_{-\infty}^{+\infty}\psi(\mathbf{\Psi})\,\mathrm{d}t\;=\;0

式中 上标“。”—函数的傅里叶变换。

一般地，人们将 \psi(\,t\,) 称为母小波,而将其伸缩和平移

\psi_{a\,,\,b}(\,t\,)\;=\;\mid a\mid^{-1/2}\psi\left({\frac{t\,-\,b}{a}}\right)

称为真正的小波函数，简称小波。其中 \alpha\,,\,b\in R a\neq0 从式(3-50)和式(3-51)知小波函数具有如下性质：

（1）母小波函数无零频分量；
（2）小波函数为带通的；
（3）小波函数是振荡的且随时间的延伸快速衰减。函数 f(t) 的小波变换定义为

\begin{array}{l}{\displaystyle F(\,a\,,b\,)\,=\langle\,f(\,t\,)\,,\psi_{a\,,b}(\,t\,)\,\rangle\,=\,}\\ {\displaystyle\mid a\mid^{-1/2}\!\!\int_{\,-\,\infty}^{+\,\infty}\!\!f(\,t\,)\,\psi^{\star}\left(\frac{t\,-\,b}{a}\right)\!\mathrm{d}t}\end{array}

式中 上标“ \clubsuit ”—函数的共轭。

函数 f(\iota) 的小波逆变换或重建定义为

f(\,t\,)\,=\,\frac{1}{C_{\phi}}\!\int_{0}^{+\infty}\,\mid\,\alpha\mid\,^{-1/2}\!\!\int_{-\infty}^{+\infty}\!F(\,\alpha\,,b\,)\,\phi\!\left(\frac{\,t\,-\,b\,}{a}\right)\!d b\,\,\frac{\mathrm{d}a}{a^{2}}

式（3-50）是小波逆变换存在的条件。令式（3-53）中的参数α=ao",b= nboαg",其中 m 和n 为整数,ag和 bo 为常数且\boldsymbol{a}_{0}\not=0 ，特别地令 a_{0}=2\,,b_{0}=1 ，可得到离散信号 f(k) 的离散小波变换

F(\,m\,,n\,)\,=\,2^{m/2}\sum_{k}f(\,k\,)\,\psi^{\ast}\,(\,2^{m}k\,-\,n\,)

相应地有 f(k) 的重构公式

f(\,k\,)\;=\;\sum_{m}\,\sum_{n}F\,(\,m\,,n\,)\,\psi(\,2^{m}k\,-\,n\,)

目前，人们已构造了很多的小波函数，其中较为著名的有莫勒特（Morlet）小波、墨西哥帽小波、哈（Haar）小波及道比切丝（Daubechies）小波等，其定义和形式可参见相关的著作。

多分辨分析是小波分析的核心内容，它将小波的构造纳人了一个统一的框架之中。其中一维多分辨分析的定义如卜：

L^{2}(R) 的一个多分辨分析是 L^{2}(R) 的一列单调上升的子空间 V_{j}(j\in Z) ,它们满足

(1) \bigcap_{\infty}^{+\infty}{\cal V}_{j}=\{0\}\,,\bigcup_{-\infty}^{+\infty}\,{\cal V}_{j} 在 L^{2}(R\,) 中稠密； (2) \forall\;f\!\in\!L^{2}(\,R\,)\,,\,\forall\;j\!\in\!Z\,,\,f(\;t\,)\!\in\!V_{j}{\leftrightarrow}f(2\,t\,)\!\in\!V_{j+1}\,; (3) \forall\;f\!\in\!L^{2}(\;R\;)\,,\;\forall\;k\!\in\!Z,f\!(\;t\,)\!\in\!V_{0}\!\!\leftrightarrow\!f\!(\;t-k\;)\!\in\!V_{0}\,;

（4）存在-个函数 g\left(\mathit{t}\right)\in V_{0} ,使 g\left(\,t\,-\,\pmb{k}\,\right)\left(\,k\in Z\,\right) 构成空间\ensuremath{\boldsymbol{V}}_{0} 的利兹(Riesz)基。

研究表明，如果 V_{j}\left(\,j\in Z\right) 是一个多分辨分析，则存在惟一的函数 \varphi(\mathbf\xi_{t}\,)\in L^{2}\left(\,R\,\right),\,\varphi_{j,\,k}\left(\,t\,\right)=2^{j/2}\,\varphi\left(2^{j}t\,-\,k\,\right)\left(\,j\,,k\in Z\,\right) ，使\{\;\varphi_{j\,,\,k}\,(\,t\,)\,,k\in Z\} 是空间 V_{j}(j\in Z) 的一个规范正交基。 \varphi(t) 称为尺度函数，又称为父小波函数。人们发现，母小波函数 \psi^{(\,t\,)} 将由父小波函数 \varphi(t) 生成，即有尺度方程

\begin{array}{r}{\left\{\varphi(\mathbf{\alpha})\;=\;\displaystyle\sum_{n}\!\!\!h\left(\mathbf{\alpha},\right)\varphi(2t\mathbf{\alpha}-\mathbf{\alpha}n\left)\right.}\\ {\left.\varphi(\mathbf{\alpha})\;=\;\displaystyle\sum_{n}\!\!\!g(\mathbf{\alpha},\right)\varphi(2t\mathbf{\alpha}-\mathbf{\alpha}n\left)\right.}\end{array}

式中 g(\,n\,)=(\,-\,1\,)^{\,-\,n}h\,(\,1-\,n\,)

h\left(\,n\,\right) ———滤波器系数。

而 \psi_{j^{\,},\,k}^{\,}(\,t\,)=2^{j^{\,}/2}\,\psi_{}^{\,}(\,2^{j}t\,-\,k\,)\,(\,j\,,k\in Z\,) ,构成 L^{2}(R) 的规范正交基[50]。

信号 f(\,t\,) 在 j 尺度上的平滑表示为

P f_{\ A}^{j}\;=\;\left\langle\,f(\,t\,)\,,\varphi_{j\,,\,k}(\,t\,)\,\right\rangle

在 j 尺度上的细节表示为

P f_{\cal D}^{j}\;=\;\left\langle f(\,t\,)\,,\psi_{j\,,\,k}(\,t\,)\right\rangle

f(t)在j－1尺度上的平滑和细节可由j尺度上的平滑分解得到

\left\{{\cal P}f_{\mathrm{\scriptsize~A}}^{j\mathrm{\scriptsize~1}}\,=\,\sum_{l}\!h\,(\,l\,-\,2\,n\,)\,{\cal P}f_{\mathrm{\scriptsize~A}}^{j}}\\ {\ensuremath{\ P}f_{\mathrm{\scriptsize~D}}^{j\mathrm{\scriptsize~-1}}\,=\,\sum_{l}\!g(\,l\,-\,2\,n\,)\,{\cal P}f_{\mathrm{\scriptsize~A}}^{j}}\end{array}\right.

同时，又有重构式

P f_{A}^{j}\ =\ \sum_{\iota}\,\bigl[\,h\,\big(\,n\,-\,2\,\iota\,\big)P f_{A}^{\,j-1}\,+\,g\,\big(\,n\,-\,2\,\iota\,\big)P f_{\phantom{A}D}^{\,j-1}\,\bigr]

式(3-60)和式(3-61)就是著名的迈拉特小波快速算法。给定多分辨深度为 J ,则有

f(\,t\,)\;=\;P f_{\,A}^{\;-\,J}\,+\,\sum_{j\,=\,-1}^{-J}P f_{\,D}^{\,j}

二维以上的小波分析可参考有关的著作和文献。小波分析应用的关键在于，对面向某一具体问题时，如何合理地选择小波，这仍然是一个开发性的课题，至今还没有统一的方法。在系统辨识方面，首先是将系统进行小波级数展开，然后对小波系数和系统特性参数进行辨识，最后重构系统。

3.5.2 时变系统的辨识

实际应用中多数信号并不满足平稳假设，这就使包括时变谱分析在内的非平稳信号处理得到越来越广泛的研究。如果能用时变参数模型来描述这类系统，则对系统的描述要简略得多。时变模型源于语音分析，现在，它大量地出现在如回音对消、时滞估计和阵列处理等系统辨识问题中。

时变系统辨识最普遍的方法是采用自适应方法，该方法假定系统的时变较为缓慢，它不能处理变化迅速的系统，无法跟随系统的时间演化。另-一种方法是对时变系数进行建模，假定这些系数轨道具有一定的概率结构并认为它们是随机过程，然后用卡尔曼滤波估计这些系数。这类方法面临着系数轨道模型确定和如何估计的问题。由于小波能很好地模拟系统轨道的局部和全局特征，若系统中的时变系数能在一系列小波正交基上展开，即时变系数的演化可由少量小波基的组合构成,则时变系统辨识问题等效于估计展开式上的时不变系数。这种方法称为时变系统的多分辨小波建模法。

考察离散的 \pmb{\dot{p}} 阶时变自回归（TV-AR）过程模型

y(\,n\,)\;=\;\sum_{k\,=\,1}^{p}a\left(\,n\,;k\,\right)y(\,n\,-\,k\,)\,+\,\epsilon\left(\,n\,\right)

式中 y(\,n\,) -—系统的观测数据；

\alpha\left(\,n\,;k\,\right) —随时间演化的系数；\pmb{\epsilon}\left(\,n\,\right)\!\sim\!N(\mathbf{0}\,,\sigma^{2})\,_{\circ}

若系统的阶数与 _n 有关,可取 \pmb{\phi}=\operatorname*{max}\pmb{\phi}_{n}\circ

根据离散小波变换和重构的迈拉特算法，对给定 k\;,a\left(\;n\;;k\;\right) 的平滑和细节分别为

\begin{array}{r c l}{{\xi_{\mathrm{\tiny~-1},\mathrm{\tiny~m}}^{k}}}&{{=}}&{{\displaystyle\sum_{l}\!h\left(\mathit{l}\right)a\left(2\,m\,-\,{l}\,;k\,\right)}}\\ {{\xi_{\mathrm{\tiny~-1},m}^{k}}}&{{=}}&{{\displaystyle\sum_{l}\!g\left(\mathit{l}\right)a\left(2\,m\,-\,{l}\,;k\,\right)}}\end{array}

式中 h\left(\,n\,\right),g(\,n\,)- 完全重构滤波器对。

a\left(\,n\,;k\,\right) 的重构为

a\left(\!\!\begin{array}{c}{{\!\displaystyle{n}\,{;}\,k}}\end{array}\!\!\right)\ =\ \sum_{m}\zeta_{\ \ \ 1,\,m}^{\,\,k}h\left(\,n\ -\,2\,m\,\right)\ +\ \sum_{m}\hat{\xi}_{\ \ \ 1,\ m}^{\,\,k}g\left(\,n\ -\,2\,m\,\right)

类似式(3-61)和式(3-66)有

\zeta_{\,j\,,n}^{\,k}\;=\;\sum_{m}\zeta_{\,j\,-1\,,\,m}^{\,k}h\left(\,n\;-\,2\,m\,\right)\;+\;\sum_{m}\hat{\xi}_{\,j\,-1\,,\,m}^{\,k}g\left(\,n\;-\,2\,m\,\right)

设 a\left(\,n\,;k\,\right) 的最后分解尺度为 J ,根据文献[35],尺度为 j 时的传递函数为

\begin{array}{c}{{H^{J}(\,z\,)\,=\,H(\,z\,)H(\,z^{2})\cdots H(\,z^{2^{-J-1}})}}\\ {{\,}}\\ {{\,)\,=\,H(\,z\,)H(\,z^{2})\cdots H(\,z^{2^{-j-2}})\,G(\,z^{2^{-j-1}})(\,j\,=-\,1,\cdots,\,-\,J)}}\end{array}

令 h^{J}(\,n\,)\,,g^{j}(\,n\,) 分别是上两式的逆 \pmb{z} 变换,于是有[35]

a\left(\;n\;,k\;\right)\;=\;\sum_{n}\zeta_{\;J\;,m}^{\;k}h^{J}\bigl(\;n\;-\;2^{-J}m\;\bigr)\;+\;\sum_{j\,=\,1}^{J}\sum_{m}\hat{\xi}_{\;j\,,m}^{\;k}g^{j}\bigl(\;n\;-\;2^{-j}m\;\bigr)

式中 m\in[0\,,2^{j}N-1\,]\,;

N —观测数据的长度。

将式(3-70)代人式(3-63)有

y^{\l}(\ n\r)\r=\sum_{k=1}^{\beta}\sum_{m}\zeta_{\textsc{j},m}^{k}\bigl[\,h^{J}(\n u\r-\l2^{-J}m\ n)_{\l}y(\ n\mathrm{~-~}k\r)\,\bigr]\,+\,}\\ {\sum_{k=1}^{\beta}\sum_{j=-1}^{-J}\sum_{m}\hat{\xi}_{\,j,m}^{\,k}[\,g^{j}(\ n\r-\l2^{-j}m\ n)_{\l}y(\ n\mathrm{~-~}k\r)\,]\,+\,\varepsilon(\ n\r)}\end{array}

于是,问题变为对 \zeta_{j,m}^{k},\xi_{j,n}^{k} 的估计。

如果小波正交基是紧致的,则 \sum\limits_{j=m}^{k}\sum\limits_{m}^{k}f_{j}^{k} m中不为零的分量较少，可使估计的精度提高并降低计算量。在时变系统的辨识中，关键的问题是完全重构滤波器对 \boldsymbol{h}\left(\boldsymbol{n}\right),\boldsymbol{g}\left(\boldsymbol{n}\right) 的选择以及多分辨长度的确定。后者可根据 F 统计检验或赤池信息准则进行确定，前者根据小波正交基构造中的方法进行构造。

文献[35]给出了应用的例子，该方法比卡尔曼滤波结果要好得多。该方法可以推广到时变ARMAX过程。

3.5.3分形信号的辨识

小波分析与分形几何具有深刻的内在联系，它们在尺度变换上具有一致性，从本质上讲，分形分析和小波分析都是尺度变换。

自然界中有很多信号具有分形结构[43,分形信号的频谱呈负幂次律，可用 1/f^{\gamma} 来表示，其中 f 是频率， 0{\leqslant}\gamma{\leqslant}2 ，即具有分形标度不变性，这类信号或现象称为 1/f 信号或现象43]，自然界中典型的 1/f 信号是音乐，分形之父曼德勃罗对许多音乐进行了分析和比较，其著作中对此有精辟的论述。这类信号或过程在数学上难于处理，使许多涉及这类信号的经典信号处理问题十分困难。当这类信号被白噪声污染后，如何从观测数据中分析系统的分形特征以及系统信号的重构是一个重要课题。由于小波分析与分形的本质相似性，用小波来处理其辨识问题是一个自然而又具有创新的选择。

假使我们得到了一个均值为零的高斯 1/f 过程 x\left(\t\right) 的观测数据 r(\,t\,)

r\left(\,t\,\right)\;=\;x\left(\,t\,\right)\;+\;w\left(\,t\,\right)\quad\left(\,-\,\infty\,<\,t\,<+\,\infty\,\right)

式中 w(t)- 均值为零的加性白色高斯噪声。

将观测数据向小波基函数上投影得到小波系数 r_{n}^{m}

r_{n}^{m}\,=\,\int_{\,-\infty}^{+\,\infty}\psi_{m\,,\,n}\bigl(\,t\,\bigr)\,r\bigl(\,t\,\bigr)\,\mathrm{d}t

考虑离散情形，采样数据长度为 N=2^{M}{\cal N}_{0}\,,N_{0} 是依赖与滤波器h\left(\,n\,\right) 长度的常数， M 是最大可能的尺度，其中有

\begin{array}{c}{{m\ =\ \{1\,,2\,,\cdots,M\,\}}}\\ {{n\,(\,m\,)\,=\,\,\{1\,,2\,,\cdots,N_{0}2^{\,m\,-\,1}\,\}}}\end{array}

由式(3-72)和式(3-73)有

r_{_n}^{m}\ =\ x_{_n}^{_m}\ +\ w_{_n}^{_m}

显然 {\boldsymbol{\varpi}}_{n}^{m} 独立于 x_{n}^{m} 且对任意小波基它是不相关的，因此可认为r_{n}^{m} 是互相独立、均值为零的高斯随机变量，其方差为

\mathrm{var}r_{_{n}}^{{m}}\;=\;\sigma_{{m}}^{^{2}}\;=\;\sigma^{2}\beta^{^{-\,m}}\;+\;\sigma_{{w}}^{^{2}}

式中 \beta\!=\!2^{\gamma} 。

令

\theta\:=\:(\,\beta\,,\sigma^{2}\,,\sigma_{\mathrm{\scriptsize~w}}^{2}\,)

上式就是待估计的参数。可用最大似然法估计，估计出 \hat{\beta}_{M L} 后即可得到分形信号的特征参数的估计

谱指数

相似参数

\begin{array}{r l}&{\hat{\gamma}_{{\scriptscriptstyle M L}}\,=\,\log_{2}\hat{\beta}_{{\scriptscriptstyle M L}}}\\ &{\hat{D}_{{\scriptscriptstyle M L}}\,=\,(\,5\,-\,\hat{\gamma}_{{\scriptscriptstyle M L}}\,)/2}\\ &{\hat{H}_{{\scriptscriptstyle M L}}\,=\,(\,\hat{\gamma}_{{\scriptscriptstyle M L}}\,-\,1\,)/2}\end{array}

估计的似然函数为

L\left(\boldsymbol{\Theta}\right)\,=-\,\frac{1}{2}\sum_{m\,=\,1}^{M}\sum_{n\,\in\,n\left(m\right)}\left\{\frac{1}{\sigma_{m}^{2}}\!\left(\,r_{n}^{m}\,\right)^{2}\,+\,\ln(2\pi\sigma_{_m}^{2}\,)\,\right\}

实际上有

L\left(\Theta\right)\;=-\;\frac{1}{2}\sum_{m\,=\,1}^{M}n\left(\,m\,\right)\Biggl\{\frac{\hat{\sigma}_{\,m}^{2}}{\sigma_{\,m}^{2}}\,+\,\ln(2\pi\sigma_{\,m}^{2}\,)\Biggl\}

式中

\hat{\sigma}_{\,m}^{2}\;=\;\frac{1}{n\left(\,m\,\right)}\sum_{n\,\in\;n\left(\,m\,\right)}\left(\,r_{n}^{m}\,\right)^{2}

有了 \boldsymbol{\Theta} 的估计，可以对信号 x(t) 进行估计，有

\hat{x}_{n}^{m}\;=\;\bigg[\frac{\hat{\sigma}^{2}\hat{\beta}^{-m}}{\hat{\sigma}^{2}\beta^{-m}\,+\,\hat{\sigma}_{\,w}^{2}}\bigg]r_{n}^{m}

最后得到 1/f 信号的最优估计为

\hat{x}\left(\,t\,\right)\;=\;\sum_{m\,=\,1}^{M}\sum_{n\,\in\;n\left(\ m\right)}\left[\frac{\hat{\sigma}^{2}\hat{\beta}^{-m}}{\hat{\sigma}^{2}\beta^{m}\,+\,\hat{\sigma}_{w}^{2}}\right]r_{n}^{m}\phi_{m\,,\,n}\left(\,t\,\right)

3.5.4 半参数模型的小波辨识

设有半参数回归模型

式中

\begin{array}{r l r}&{}&{\mathbf{y}\,=\,\mathbf{X}\pmb{\theta}\,+\,\pmb{g}\,+\,\pmb{\varepsilon}}\\ &{}&{\mathbf{y}\simeq(\,y_{1}\,,y_{2}\,,\cdots,y_{n}\,)^{\mathrm{T}}\,;}\\ &{}&{\pmb{g}=(\,g(\,t_{1})\,,g(\,t_{2})\,,\cdots,g(\,t_{n}\,)\,)^{\mathrm{T}}\,;}\end{array}

g\left(t\right) 一定义在[0,1]上的未知布雷尔(Borel)函数,是非参数分量；

X{\longrightarrow}\,n\times\,\phi 矩阵；

\pmb{\theta}=(\,\theta_{1}\,,\theta_{2}\,,\cdots,\theta_{p}\,)^{\mathrm{T}}. —未知参数分量；
\pmb{\varepsilon}=(\,\pmb{\varepsilon}_{1}\,,\pmb{\varepsilon}_{2}\,,\cdots\,,\pmb{\varepsilon}_{n}\,)^{\mathrm{T}}. 一—零均值的随机误差。

辨识的基本问题是根据 {\mathbf y}\,,{\pmb X}\,,{\pmb t} 来估计 \pmb\theta 及 g(t)

假定找到了属于苏伯勒夫(Sobolev)空间的尺度函数 \varphi ,其伴随的多分辨分析为 \{\,V_{m}\,\{\mathrm{~,~}V_{m} 的再生核为

E_{m}\left(\,t\,,s\,\right)\,=\,2^{m}E_{0}(2^{m}t\,,2^{m}s\,)\,=\,2^{m}\sum_{k\,\epsilon\,z}\varphi(2^{m}t\,-\,k\,)\,\varphi(2^{m}s\,-\,k\,)

当 t_{i}({\it i}=1,2,\Lambda,n\,) 为常量时,定义 g(t) 的估计为

\hat{g}_{0}(\,t_{i}\,,\,\pmb\theta\,)\;=\;\sum_{i\,=\,1}^{n}\big(\,y_{i}\,-\,\pmb x_{i}^{\mathrm{T}}\pmb\theta\,\big)\!\!\int_{\,s_{i-1}}^{s_{i}}\!\!\!E_{m}(\,t\,,s\,)\,\mathrm{d}s

式中 t_{i}\in[\;s_{i\,-\,1}\,,s_{i}\,)\,,[\;s_{i\,-\,1}\,,s_{i}\,) 为[0,1]上的分割。

求极小值问题

\operatorname*{min}\sum_{i\,=\,1}^{n}\big(\,y_{i}\,-\,\pmb{x}_{i}^{\mathrm{T}}\pmb{\theta}\,-\,\hat{g}_{0}\big(\,t_{i}\,,\pmb{\theta}\,\big)\,\big)^{2}

则有

\hat{\pmb{\theta}}\;=\;(\,\widetilde{\pmb{X}}^{\scriptscriptstyle\mathrm{T}}\widetilde{\pmb{X}}\,)^{-1}\,\widetilde{\pmb{X}}^{\scriptscriptstyle\mathrm{T}}\,\widetilde{\pmb{y}}

式中 \widetilde{\pmb X}=(\,\pmb I-\pmb S)\pmb X\,.

\mathbf{\calS}=\left(\mathbf{\Sigma}_{s_{i j}}\right)_{n\,\times\,n}\,,s_{i j}=\,\int_{s_{{j}-1}}^{s_{{j}}}\!\!\!\!\cal E_{m}\left(\mathbf{\Sigma}_{t_{i}}\,,s\right)\!\mathrm{d}s\,;

\tilde{\bf y}=(\,{\bf I}-{\bf S}\,)\,{\bf y}\,_{\circ}

将式（3-89）代人式（3-88）得到非参数分量 g\!\left(\,t\,\right) 的估计。上述估计是偏回归估计。

参考文献

1蔡金狮．动力学系统辨识与建模．北京：国防工业出版社，1991

2蔡金狮等．飞行器系统辨识.北京：宇航出版社，1995

3 Akaike H.A New Look at the Statistical Model Identification.IEEE Transactions, 1974,AC-19(6) :716 ~722
4 Fisk P H, Price C F.A New Approach to Model Structure Identification.AIAA 77- 1171,1997
5 Astrom K J, Eykhoff P.System Identification-—- A Survey. Automatica, 1971, 7(2) : 123~162
6 Soderstrom T.On Model Structure Testing in System Identification. International Journal of Control, 1977,26(1) : 1 ~ 18
7 Gupta N K, Hall W E Jr, Trankle T L.Advanced Methods of Model Structure Determination from Test Data.AIAA 77-1170,1977
8 Taylor L W Jr.Application of a New Criterion for Modeling Systems.AGARD CP-172, Paper 4,1974
9 Klein V,Batterson J G, Murphy P C.Determination of Model Structure and Parameters of an Airplane from Pre and Post-Stail Flight Data.A1AA 81-1866,1981
10冯康．数值计算方法．北京：国防工业出版社，1978
11 Klein V,Batterson J G, Murphy P C.Determination of Airplane Model Structure from

Flight Data by Using Modified Stepwise Regression. NASA TP-1916, 1981

12张金槐．线性模型参数估计及其改进．长沙：国防科技大学出版社,1991
13刘伯生，白堤．测量系统的系统误差主成分估计方法．宇航学报,1986,(2)
14李本津．主成分估计特征根筛选与残差平方和．飞行器测控技术,1989，（4)
15安鸿光等．时间序列的分析与应用．北京：科学出版社,1986
16李乃宏，现场条件下有控飞行器气动参数辨识的理论及应用研究[博士学位论 文］.哈尔滨工业大学，1992
17 Aguirre L A.Retrieving Dynamical Invariants from Chaotic Data Using NARMAX Models. International Journal of Bifurcation & Chaos,1995,5:449 ~ 474
18 Morelli , E A.Global Nonlinear Aerodynamic Modeling Using Multivariate Orthogonal Functions. Journal of Aircraft, 1995,32 :270 ~ 278
19 Billings,S.A. Identification of MIMO Nonlinear Systems Using a Forward- Regression Orthogonai Estimator. Intermational Journal of Control, 1989 ,49 :2157-2189
20 Batterson J G, Klein V.Partitioning of Flight Data for Aerodynamic Modeling of Aircraft at High Angles of Attack. Journal of Aircraft,1989,26(4) :334 ~- 339
21焦李成．神经网络系统理论．西安:西安电子科技大学出版社,1990
22 Narendra K S,etc. Identification and Control of Dynamical System Using Neural Networks. IEEE Transactions on Neural Networks, 1990,1(1)
23 Chen S, Billings S A. Neural Networks for Nonlinear Dynarmic Systerm Modeling and Identification. International Journal of Control, 1992 ,56(2)
24 Hunt K J,etc.Neural Networks for Control Systems—A Survey. Automatica,1992,29 (6)
25邓志东,孙增圻．利用线性再励的自适应变步长快速 BP算法．模式识别与人工 智能,1993,6(4)
26雷鸣，关雅,杨叔子．非线性时序建模与预测的神经网络法．华中理工大学学报， 1993,21(1)
27 Battiti R. Accelerated Backpropagation Learning : Two Optimization Methods. Complex Systems, 1989,3(4)
28 Kollias S, Anastassion D.Adaptive Training of Multilayer Neural Networks Using a Least Squares Estimation Technique.IEEE Transactions on Circuits and Systems, 1989,36(8)
29 Watrous R L . Learning Algorithms for Connectionist Network. IEEE First International Conference on Neural Networks, San Diego,1987
30 Rarker D B. Optimal Algorithms for Adaptive Networks: Second Order Back Propagation, Second Order Direct Propagation, and Second Order Hebbian Learning. Proceedings of the 1987 International Joint Conference on Neural Networks, San Diego,1987
31 Singhal S, Wu L. Training Feed-forward Networks with the Extended Kalman Algorithm. Proceedings of the 1989 International Conference on ASSP,Glasgow, Scotland, 1989
32汪清．飞机大攻角非定常气动力建模及其应用研究［博士学位论文］。西安：西北 工业大学，1994
33Y.迈耶．小波与算子，尤众译，北京：世界图书出版公司，1992
34徐佩霞，孙功宪，小波分析与应用实例，合肥：中国科技大学出版社，1996
35 Tsatsanis M K, Giannakis G B. Time- Varying System Identification and Model Valida. tion Using Wavelets. IEEE Trans.Signal Processing,1993 ,41(12) :3512 ~ 3523
36 Wornell G W ,Oppenheim A V. Estimation of Fractal Signals from Noisy Measurements Using Wavelets. IEEE Trans.Signal Processing,1992,40(3) :611 ~ 623
37 Antoniads. Wavelet Methods of Curve Estimation. JASA,1994,89 :1340-- 1353
38 Kerkyacyarian.Density Estimation in Besov Spaces.Statist.Probab. Lett. , 1992, 13: 15~24
39 Donoho.Adapting to Unknown Smoothness via Wavelet Shrinkage. JASA, 1995, 90: 1200 ~1224
40李建平,唐远炎．小波分析方法的应用，重庆：重庆大学出版社,1999
41Mallat S. A Theory for Multi-resolution Signal Decomposition : the Wavelet Representation. IEEE Trans. Patt.Anal. Machine. Intell. ,1989,11(7) :674 ~ 693
42 Daubechies I.Orthonormal Bases of Compactly Supported Wavelets.Commun.Pure Appl. Math. ,1988,XLI:909 ~ 996
43敖力布,林鸿溢．分形学导论．包头:内蒙古人民出版社,1996
44 Barnsley M F, Devaney R L, Mandelbrot B, etc.The Science of Fractal Images.Springer-Verlag Worid Publishing Corp,1990

第4章 飞行状态估计

4.1概述

飞行器状态估计是飞行器系统辨识的组成部分，是气动参数估计的前提。在飞行状态估计问题中，状态变量 \pmb{x} 既是随机矢量，又是时变过程，即飞行器的状态（位置、速度等)是一个随机矢量过程。如果我们把状态和观测量在某些离散时刻 \pmb{t}_{k} 进行采样，则构成两个随机矢量序列 {\pmb x}(t_{k}) 和 {\mathfrak{y}}({t_{k}}) ，简记为 x(k) 和 {\mathfrak{y}}({\pmb k})_{\mathfrak{c}} 本章的目的是研究如何用观测量序列 {\mathfrak{y}}(k) 对状态序列 x(k) 做出尽可能精确的估计。

将使用直至第 k 时刻的观测量 {\mathfrak{y}}({\mathfrak{k}}) 对第 j 时刻的状态 \pmb{x}(j) 进行的估计记作 \hat{\pmb{x}}\left(\,j\,\vert\,k\,\right) ，则上述估计问题依据 j 与 k 的不同关系分别称为预报 (j>k) 、滤波 (\,j=k\,) 和平滑 (j<k) 。对实时辨识和自适应控制而言，比较感兴趣的估计问题是滤波和预报，对数据的事后处理和离线辨识则侧重于滤波和平滑。无论哪一种估计问题，它们的实用算法都是卡尔曼滤波及其相应的改进、推广与发展，而其数学基础是最小方差估计和线性最小方差估计。因此，本章首先介绍估计问题的数学基础一-一-最小方差估计，然后给出卡尔曼滤波的基本公式-—线性递推估计及其推广-—广义卡尔曼滤波和增广的厂义卡尔曼滤波，进而介绍用于改进滤波算法的两种方法-一一修正增益广义卡尔曼滤波和平方根滤波，最后介绍20世纪70年代发展起来的分割算法。本章介绍的状态估计方法已被推广应用于进行参数估计。

4.2 卡尔曼滤波算法

卡尔曼滤波是20世纪60年代初由卡尔曼（R.E.Kalman)i1)和布西(R.Buey)[2]首先提出的。他们为了解决线性最小方差估计公式难以实际计算的困难，提出了一套状态估计的递推计算公式,获得了现代控制理论中的一个突破性结果,并首先将其应用于线性离散系统和线性连续系统。其后，这种状态的递推估计算法又被推广到非线性系统[3]。由于卡尔曼滤波算法适用于计算机递推计算，在工程中得到非常广泛的应用。

20 世纪 70 年代初,贾温斯基(A. H. Jazwinski)[4]和盖尔布(A.Gelb)[5]采用增广未知参数为状态的办法将卡尔曼滤波用于参数估计。由于算法简单，且可能发展成实时估计而得到了广泛应用。但在应用过程中,常出现有偏估计和发散现象。1979 年荣(L.Ljung)[6}研究了广义卡尔曼滤波用于线性系统参数估计时的渐近特性，指出由于广义卡尔曼滤波计算过程中没有计人参数·的变化对增益的影响，因此用它进行参数估计常常导致有偏估计或发散，特别是对过程噪声和观测噪声的特性不甚了解的情况尤为严重。故近来人们建议广义卡尔曼滤波只用于状态估计，而不用于参数估计。但有时由于实时估计的需要，仍有不少人还在研究广义卡尔曼滤波用于参数估计的问题。

20 世纪80 年代,斯皮尔(J.L.Speyer)[7]等针对动力学系统辨识中存在的一类所谓“可修正非线性系统”，提出了修正增益广义卡尔曼滤波算法，实现了对状态方程的精确线性化，从而解决了广义卡尔曼滤波算法的近似线性化问题。然而，这种算法只适用于一类特殊的非线性函数一—可修正非线性函数，并且在精确线性化过程中， \pmb{D} 函数的选取与计算也需要一定的技巧。

平方根滤波是为了改善卡尔曼滤波的收敛性和提高算法的数值稳定性提出的{8,实现的途径是对滤波的协方差阵进行均方根分解，以保证滤波过程中 \pmb{P} 阵的正定性。

4.2.1 最小方差估计

1）最优估计准则

最小方差估计的最优估计准则是要求估计量 \hat{\pmb{x}} 与被估计量 \pmb{x} 的误差 \tilde{\pmb{x}}=\pmb{x}-\hat{\pmb{x}} 的均方误差阵最小，即

J\;=\;E\,\{\left[\frac{}{}\pmb{x}\left(\pmb{k}\;\right)\;-\;\pmb{\hat{x}}\left(\pmb{k}\;\middle|\;k\;\right)\right]\left[\pmb{x}\left(\pmb{k}\;\right)\;-\;\pmb{\hat{x}}\left(\pmb{k}\;\middle|\;k\;\right)\right]^{\mathrm{T}}\}\;=\;E\left[\frac{}{}\pmb{\tilde{x}}\pmb{\tilde{x}}^{\mathrm{T}}\right]

为最小。式中： \hat{\pmb{x}}(\pmb{k}\mid\pmb{k}) 表示 x(k) 的最小方差估计。

2）最小方差估计的计算与统计特性

设 \pmb{x} 和 \pmb{y} 是两个联合高斯分布的随机矢量，的最方差估计 \hat{\pmb{x}} 就是 \pmb{x} 的条件均值

\hat{\pmb{x}}\;=\;E\left[\,{\pmb{x}}\;|\,{\pmb{y}}\,\right]\;=\;\int_{-\infty}^{\infty}{\pmb{x}}\beta\,(\,\dot{\pmb{x}}\,|\,y\partial\rangle\partial\!\!\!\!\slash\;\;\;

最小方差阵为

E\,\big[\,\widetilde{\textbf{\em x}}\,\widetilde{\textbf{\em x}}^{\intercal}\,\big]\,=\,E\,\big\{\,\big[\,{\pmb{\mathscr{x}}}\,-\,E(\,{\pmb{\mathscr{x}}}\,|\,{\pmb{\mathscr{y}}}\,)\,\big]\,[\,{\pmb{x}}\,-\,E\,\langle\,{\pmb{\mathscr{x}}}_{\leqslant}|\,{\pmb{\mathscr{y}}}\,)\,]^{\mathrm{T}}\big\}^{\mathrm{KJ}}\,\mathcal{\,(}\,\pmb{\mathscr{y}}\,\mathcal{A}_{3}^{\intercal}\,)

最小方差估计的统计特性是无偏的，并且其均方误差阵等于其估计误差的方差阵[9]。即

E(\,{\hat{\pmb x}}\,)\,=E{\left[\,E(\,{\pmb x}\,|\,{\pmb y}\,)\,\right]}\,=\,\int_{\,-\infty}^{\infty}E(\,{\pmb x}\,|\,{\pmb y}\,)\,\phi(\,{\pmb y}\,)\mathrm{d}{\pmb y}\,=

\int_{-\infty}^{\infty}\Big[\int_{-\infty}^{\infty}\pmb{x}\phi\big(\pmb{x}\,\vert\,\pmb{y}\,\big)\mathrm{d}\pmb{x}\,\big]\,\phi(\pmb{y})\mathrm{d}\pmb{y}\,=

\int_{-\infty}^{\infty}\Big[\int_{-\infty}^{\infty}\pmb{x}\phi\big(\pmb{x}\,,\pmb{y}\big)\mathrm{d}\pmb{x}\mathrm{d}\pmb{y}\;=\;E\big(\pmb{x}\,\big)

E(\stackrel{\sim}{\bf x})\,=\,E(\,{\pmb x}\,-\,\hat{\pmb x}\,)\,=\,E(\,{\pmb x}\,)\,-\,E(\,\hat{\pmb x}\,)\,=\,0

E(\widetilde{\textbf{\em x}}\widetilde{\textbf{\em x}}^{\intercal})\;=\;E\big[\,\big(\,{\pmb x}\:-\:\hat{\pmb x}\,\big)\big(\,{\pmb x}\:-\:\hat{\pmb x}\,\big)^{\intercal}\,\big]\;=

E\left\{\left[\,{\pmb x}\,-\,\hat{\pmb x}\,-\,E({\pmb x}\,-\,\hat{\pmb x}\,)\,\right]\left[\,{\pmb x}\,-\,\hat{\pmb x}\,-\,E({\pmb x}\,-\,\hat{\pmb x}\,)\,\right]^{\mathrm{T}}\right\}

3）线性最小方差估计的计算与统计特性

令 \pmb{x} 和 \pmb{y} 分别表示 \pmb{n} 维和 ^{m} 维高斯随机矢量。假使 \pmb{x} 和 \pmb{y} 是联合高斯随机矢量,其均值为 m_{x}\setminus m_{y} ,协方差阵为

82

P~=~\left[\!\!{\begin{array}{l l}{P_{x x}}&{P_{x y}}\\ {P_{y x}}&{P_{y y}}\end{array}}\!\!\right]

则最小方差估计和估计误差方差阵分别为[9]

\hat{\pmb{x}}\;=\;E\left[\,{\pmb{x}}\;|\,{\pmb y}\,\right]\;=\;{\pmb m}_{x}\,+\,P_{x y}\,P_{y y}^{\,-\,1}(\,{\pmb y}\,-\,{\pmb m}_{y})

E\big(\stackrel{\sim}{{\pmb x}}\tilde{{\pmb x}}^{\intercal}\big)\;=\;E\,\big\{\,[\,{\pmb x}\;-\;\hat{\pmb x}\,]\,[\,{\pmb x}\;-\;\hat{\pmb x}\,]^{\intercal}\,\big\}\;=\;\;\;\;\,

P_{x x}\:-\:P_{x y}P_{y y}^{-1}P_{y x}

式(4-6)和式(4-7)是推导卡尔曼滤波的基本公式。在高斯分布的假设条件下，最小方差估计是观测矢量 \pmb{y} 的线性函数，并且具有以下性质：

(1) \widetilde{\pmb{x}} 具有零均值；
(2) \widetilde{\pmb{x}} 和 \pmb{y} 独立;
(3) \widetilde{\pmb{x}} 的协方差阵为 \pmb{P}_{x x}-\pmb{P}_{x y}\pmb{P}_{y y}^{-1}\pmb{\mathscr{P}}_{y x}\circ

4.2.2 卡尔曼滤波

上节给出了最小方差估计和估计误差方差阵的计算公式(4-6)和式（4-7），但直接应用这两个公式进行计算是相当困难的。首先,矩阵Py的求逆计算量很大,有时难以实现;其次,在获得k次测量后求 \hat{\pmb{x}}\left(\,j\,\left|\,k\,\right) 时,要用到 k 次全部测量值 \mathbf{y}\left(\,1\,\right),\,\mathbf{y}\left(\,2\,\right),\cdots, y(k）,随着k的增加,数据存储量越来越大,也达不到实时估计的要求。为此，卡尔曼一布西等找到了一套状态估计的递推计算公式,解决了上述两个困难。本书给出线性离散系统和线性连续系统的卡尔曼滤波基本公式。

1）线性离散系统

线性离散系统的状态方程和观测方程可由下式表示

\pmb{x}\left(\,k\,\right)\,=\,\pmb{\phi}(\,k\,,k\,-\,1)\,\pmb{x}\left(\,k\,-\,1\,\right)\,+\,\pmb{T}(\,k\,,k\,-\,1)\,\pmb{\eta}(\,k\,-\,1)

E\left[\,{\pmb x}\left(0\right)\,\right]\;=\;\bar{\pmb x}\left(0\,\right)

\mathbf{y}(k)\;=\;{\pmb H}({\pmb k}\,)\,{\pmb x}({\pmb k}\,)\,+\,{\pmb\varepsilon}({\pmb k}\,)

式中 \scriptstyle{\pmb x}\longrightarrow{\pmb n} 维状态矢量；

{\underline{{\pmb{\phi}}}}{\underline{{\longrightarrow}}}{\underline{{n}}}\times{\underline{{n}}} 维转移矩阵；
\Gamma\!\longrightarrow\!n\times q 维过程噪声分布矩阵；
\eta\!-\!-\!q 维过程噪声矢量；
\scriptstyle{\mathbf{y}}\longrightarrow m 维观测矢量；
H{\longrightarrow}\,m\times n 维观测矩阵；
\varepsilon\!\longrightarrow\!m 维观测噪声矢量。

假设 \pmb{\eta}(k) 和 \varepsilon(k) 是互不相关的零均值高斯白噪声。即 \left\{\begin{array}{l}{{E[\,\pmb{\eta}(\,k\,)\,]\,=\,0\,,E[\,\pmb{\varepsilon}(\,k\,)\,]\,=\,0\,,E[\,\pmb{\eta}(\,k\,)\,\pmb{\varepsilon}^{\mathrm{T}}(\,k\,)\,]\,=\,0}}\\ {{E[\,\pmb{\eta}(\,k\,)\,\pmb{\eta}^{\mathrm{T}}(\,l\,)\,]\,=\,Q\left(\,k\,\right)\hat{\partial}_{k l}\,,E[\,\pmb{\varepsilon}(\,k\,)\,\pmb{\varepsilon}^{\mathrm{T}}(\,l\,)\,]\,=\,\pmb{R}\left(\,k\,\right)\hat{\partial}_{k l}}}\end{array}\right.

(4 - 10)

式中 Q\left(k\right) -—-过程噪声协方差矩阵；

\pmb R\left(k\right) —一观测噪声协方差矩阵。

转移矩阵 \pmb{\phi}(k\,,k-1) 满足

\left\{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\pmb{\phi}(t\,,t_{k-1})\,=\,{\cal F}(\,t\,)\,\pmb{\phi}(t\,,t_{k-1})\,}&{(t_{k-1}<\,t\,<\,t_{k})}\\ {\pmb{\phi}(t_{k-1},t_{k-1})\,=\,{\cal I}}\end{array}\right.

式中 \pmb{F} --线性系统状态方程中的系数矩阵；

I—单位阵。

现假设已知 k-1 步的状态估计 \hat{\pmb{x}}\left(\,\pmb{k}\mathrm{~-~}\!\,1\,\left|\,\pmb{k}\mathrm{~-~}\!\,1\,\right\rangle 和误差协方差阵 P(\,k\,-1\mid k\,-1\,) ,推导第 k 步的 \hat{\pmb{x}}\left(\hat{\pmb{k}}\left|\hat{\pmb{k}}\right.\right) 和 \textstyle P(k\mid k) 。

已知 \hat{\pmb{x}}(\,\pmb{k}\,-1\,\}\,\pmb{k}\,-1\,) ，可利用式(4-8)对 \pmb{x}(\pmb{k}) 做一步估计：

x\left(\,k\,\right)\,=\,\pmb{\Phi}\!\left(\,k\,,k\,-\,1\,\right)\pmb{x}\left(\,k\,-\,1\,|\,k\,-\,1\,\right)\,+

\pmb{T}(\,k\,,\pmb{k}\,-\,1\,)\,\pmb{\eta}(\,k\,-\,1\,)

只利用状态方程得到 \textbf{\em x}(\textbf{\em k}) 的一步预报估计，记为\hat{\mathbf{x}}(\,\pmb{k}\,\!\mid\!\pmb{k}\,-1) ：而同时利用观测信息得到 x(k) 的最小方差估计，记

为 \hat{\pmb{x}}(\pmb{k}\mid\pmb{k}) 。对式(4-12)两端取均值,并考虑到过程噪声 \pmb{\eta} 的均 值为零，得

\hat{\pmb{x}}\big(\,k\mid k\,-\,1\,\big)\;=\;\pmb{\Phi}\big(\,k\,,k\,-\,1\,\big)\,\hat{\pmb{x}}\big(\,k\,-\,1\mid k\,-\,1\,\big)

式(4-13)为状态预测方程。

设 \hat{\pmb{x}}(\pmb{k}\mid\pmb{k}) 是 \hat{\pmb{x}}(\pmb{k}\mid\pmb{k}-\mathbf{1}) 和 {\mathfrak{y}}(k) 的线性组合，有

\hat{\pmb{x}}\left(\,k\,\vert\,k\,\right)\:=\:{\pmb{K}}_{1}(\,k\,)\,\hat{\pmb{x}}\left(\,k\,\vert\,k\,-\,1\right)\,+\,{\pmb{K}}(\,k\,)\,{\pmb{y}}(\,y\,)

将式（4-9）代人式（4-14），并记估计误差 \widetilde{\textbf{\em x}}(\textbf{\em k}\,|\,\pmb{k}\,)\,=\,\pmb{x}\,(\textbf{\em k})\,- \hat{\pmb{x}}\left(\,k\mid k\,\right),\widetilde{\pmb{x}}\left(\,k\mid k-1\,\right)=\pmb{x}\left(\,k\,\right)-\hat{\pmb{x}}\left(\,k\mid k-1\,\right) ，可得

\widetilde{\pmb{x}}(\,k\,|\,k\,)\,=-\,\left[\,K_{1}(\,k\,)\,+\,K(\,k\,)H(\,k\,)\,-\,I\,\right]\pmb{x}(\,k\,)\,+

\pmb{K}_{1}(\,k\,)\widetilde{\pmb{x}}(\,k\,|\,k\,-\,1)\,-\,\pmb{K}(\,k\,)\,\pmb{\varepsilon}(\,k\,)

对式（4-15)两端取均值,考虑到 E\left[\,{\pmb v}\left(\,k\,\right)\,\right]={\bf0} ，而且无偏估计要求误差 \widetilde{\pmb{x}} 的均值为零，推得

K_{1}(\,k\,)\,+\,K(\,k\,)\,H(\,k\,)\,-\,I\,=\,{\bf0}

将式（4-16）代人式（4-14），推得状态估计校正方程为

\begin{array}{l}{\hat{\pmb{x}}(\,k\,|\,k\,)\,=\hat{\pmb{x}}(\,k\,|\,k\,-\,1)\,+}\\ {\pmb{K}(\,k\,)[\,{\pmb{y}}(\,k\,)\,-\,H(\,k\,)\,\hat{\pmb{x}}(\,k\,|\,k\,-\,1)\,]}\end{array}

下面推导误差协方差阵预测方程和校正方程。将式（4-8）减去式（4-13）得

\begin{array}{c}{{\widetilde{\pmb{x}}\left(\,k\:\middle\vert\,k\:-1\right)\:=\pmb{\Phi}(\,k\:,k\:-1)\,\widetilde{\pmb{x}}\left(\,k\:-1\,\middle\vert\,k\:-1\right)\,+}}\\ {{\pmb{T}(\,k\:,k\:-1)\,\pmb{\eta}(\,k\:-1)}}\end{array}

记

\begin{array}{l}{{\pmb{P}(\,k\,|k\,-1)\,=\,E\bigl[\,\widetilde{\pmb{x}}(\,k\,|k\,-1)\widetilde{\pmb{x}}^{\intercal}(\,k\,|k\,-1)\,\bigr]}}\\ {{\pmb{P}(\,k\,|k\,)\,=\,E\bigl[\,\widetilde{\pmb{x}}(\,k\,|k\,)\,\widetilde{\pmb{x}}^{\intercal}(\,k\,|k\,)\,\bigr]}}\end{array}

将式(4-18)两端都右乘以自身的转置,并取均值,状态x与过程噪声独立无关,可得到下列协方差阵预测方程

\pmb{P}(\pmb{k}\,,\pmb{k}\,-\,1)\,=\pmb{\Phi}(\pmb{k}\,,\pmb{k}\,-\,1)\,\pmb{P}(\pmb{k}\,-\,1\,|\,\pmb{k}\,-\,1)\,\pmb{\Phi}^{\mathrm{T}}(\pmb{k}\,,\pmb{k}\,-\,1)\,+

\pmb{{\cal T}}(\,k\,,k\,-\,1)\,\pmb{{\cal Q}}\left(\,k\,-\,1\,\right)\pmb{{\cal T}}^{\mathrm{T}}(\,k\,,k\,-\,1)

利用式（4-15)和式（4-16)可得

\widetilde{\pmb{x}}(\,\pmb{k}\,|\,\pmb{k}\,)\,=\,\left[\,\pmb{I}\,-\,\pmb{K}(\,\pmb{k}\,)\,\pmb{H}(\,\pmb{k}\,)\,\right]\widetilde{\pmb{x}}\left(\,\pmb{k}\,|\,\pmb{k}\,-\,1\right)\,-\,\pmb{K}(\,\pmb{k}\,)\,\pmb{\nu}(\,\pmb{k}\,)

根据 \textstyle P(k\mid k) 的定义,利用式(4-20),考虑到 \tilde{\textbf{\textit{x}}}(\textbf{\em k}|\textbf{\em k}-1) 与{\pmb v}\left(\,{\pmb k}\,\right) 独立无关，可得下列协方差阵校正方程

\begin{array}{l}{{\pmb{P}}(\pmb{k}\mid\pmb{k})\,=\big[\,{\pmb{I}}\,-\,{\pmb{K}}(\,\pmb{k}\,){\pmb{H}}(\,\pmb{k}\,)\,\big]{\pmb{P}}(\,\pmb{k}\,|\,\pmb{k}\,-\,1)}\\ {\big[\,{\pmb{I}}\,-\,{\pmb{K}}(\,\pmb{k}\,){\pmb{H}}(\,\pmb{k}\,)\,\big]^{\mathrm{T}}\,+\,{\pmb{K}}(\,\pmb{k}\,){\pmb{R}}(\,\pmb{k}\,){\pmb{K}}^{\mathrm{T}}(\,\pmb{k}\,)}\end{array}

现在用最小方差判据 J\left(k\right) 取极小值来确定卡尔曼增益矩阵\kappa(\,k\,)\,_{\circ}

\begin{array}{l}{\pmb{K}(\pmb{k}\,)=\mathrm{ARGmin}J(\pmb{k}\,)\,=}\\ {\mathrm{ARGmin}E[\,\widetilde{\pmb{x}}^{\mathrm{T}}(\,\pmb{k}\,|\,\pmb{k}\,)\,\widetilde{\pmb{x}}(\,\pmb{k}\,|\,\pmb{k}\,)\,]\,=}\\ {\mathrm{ARGtr}[\,\pmb{P}(\,\pmb{k}\,|\,\pmb{k}\,)\,]}\end{array}

将式(4-21)代人式(4-22),令 \j(k) 对 \pmb{K}(\pmb{k}) 的偏导数等于零，可以推出

\begin{array}{l}{{\pmb{K}}({\pmb{k}})\,={\pmb{P}}({\pmb{k}}\,|{\pmb{k}}\,-1){\pmb{H}}^{\mathrm{T}}({\pmb{k}})\,\cdot}\\ {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\ {{\pmb{\lfloor}{}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}}\end{array}

将式（4-23）代人式（4-21），经过整理可得下列协方差阵的校正方程

P(k\,|k)\,=\,\left[\,I\,-\,K(k)\,H(k)\,\right]P(k\,|k\,-\,1)

至此，我们已得到以下线性离散系统的卡尔曼滤波算式

状态预测方程

\begin{array}{c}{{{\widetilde{\bf x}}(\,k\mid k\,-\,1)\,=\,{\pmb\Phi}(\,k\,,k\,-\,1){\star}(\,k\,-\,1\,|\,k\,-\,1)\,{;}}}\\ {{{\bf\widehat{x}}(\,0\,|\,0\,)\,=\,{\bar{\bf x}}(\,0)}}\end{array}

状态校正方程

\hat{\pmb{x}}(\,k\,|\,k\,)\,=\,\hat{\pmb{x}}(\,k\,|\,k\,-\,1)\,+\,{\pmb{K}}(\,k\,)[\,{\pmb{y}}(\,k\,)\,-\,{\pmb{H}}(\,k\,)\hat{\pmb{x}}(\,k\,|\,k\,-\,1)\,]

误差协方差阵预测方程

\begin{array}{c}{{P(\,k\,|\,k\,-1)\,=\pmb{\Phi}(\,k\,,k\,-1)\,P(\,k\,-1\,|\,k\,-1)\,\pmb{\Phi}^{\mathrm{T}}(\,k\,,k\,-1)\,+}}\\ {{\pmb{\qquad\qquad\qquad\qquad\quad}\,\pmb{\Gamma}(\,k\,,k\,-1)\,\pmb{Q}(\,k\,-1)\,\pmb{\Gamma}^{\mathrm{T}}(\,k\,,k\,-1)}}\\ {{\pmb{P}(\,0\,|\,0\,)\,=\pmb{P}(0)}}&{{(4\,-2)}}\end{array}

误差协方差阵校正方程

\begin{array}{r}{\begin{array}{c}{P\big(\,k\,|\,k\,\big)\,=\big[\,I\,-\,K(k\,)H(k\,)\big]P(k\,|\,k\,-\,1)\,=\,}\\ {\big[\,I\,-\,K(k\,)H(k\,)\big]P(k\,|\,k\,-\,1)\big[\,I\,-\,K(k\,)H(k\,)\,\big]^{\mathrm{T}}\,+\,}\\ {K(k\,)R(k\,)K^{\mathrm{T}}(k\,)\qquad\qquad\qquad\qquad\quad(4\,-\,28\,)}\end{array}}\end{array}

增益矩阵

\begin{array}{l}{{\pmb{K}}({\pmb{k}})\,={\pmb{P}}({\pmb{k}}\,|{\pmb{k}}\,-1)\,{\pmb{H}}^{\mathrm{T}}({\pmb{k}}\,)\,\cdot}\\ {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[\,H({\pmb{k}}\,)\,{\pmb{P}}({\pmb{k}}\,|{\pmb{k}}\,-1)\,{\pmb{H}}^{\mathrm{T}}({\pmb{k}}\,)\,+\,{\pmb{R}}({\pmb{k}}\,)\,\right]^{-1}}}\end{array}

在状态估计误差协方差阵校正方程（4-28）中，给出了两种等价的表达式。尽管后者会增加一定的计算量，但因其在数值计算中能够始终保持 P 为正定，因而在实际计算中经常使用后者。

2）线性连续系统

线性连续系统的状态方程和观测方程可由下式表示

\pmb{\dot{x}}\left(\,t\,\right)\;=\;\pmb{F}(\,t\,)\,\pmb{x}\left(\,t\,\right)\,+\,\pmb{T}(\,t\,)\,\pmb{\eta}(\,t\,)\,;

E\left[\,{\pmb x}\,(\,t_{0}\,)\,\right]\;=\;\mp\,(\,t_{0}\,)

\mathbf{y}(t)\,=\,{\pmb H}(\,t\,)\,{\pmb x}\left(\,t\,\right)\,+\,{\pmb\varepsilon}(\,t\,)

式中 {\pmb x}\!-\!\!\longrightarrow{\pmb n} 维状态矢量；

n—q维过程噪声矢量；

\pmb{y} 和 \pmb{\varepsilon} 一分别为 ^{m} 维观测矢量知 \pmb{m} 维观测噪声矢量；

\mathbf{\cal{F}}(\mathbf{\lambda}_{t})\,,\mathbf{\cal{T}}(\mathbf{\lambda}_{t})\,,\mathbf{\cal{H}}\left(\mathbf{\lambda}_{t}\right). 分别为连续的 \,n\times n\,,\,n\times q\,,m\times n 维矩

阵。

假设随机过程 \left\{\,\pmb{\eta}\left(\,t\,\right)\right\} 和 \pmb{\varepsilon}(\pmb{\,t})\} 是互不相关的零均值高斯白噪声，其协方差阵分别为

\begin{array}{r}{E\big[\,{\pmb\eta}(\,t)\,{\pmb\eta}^{\mathrm{T}}(\,\tau)\,\big]\,=\,{\pmb Q}(\,t)\delta(\,t\,-\,\tau)}\\ {E\big[\,{\pmb\varepsilon}(\,t)\,{\pmb\varepsilon}^{\mathrm{T}}(\,\tau)\,\big]\,=\,{\pmb R}(\,t\,)\delta(\,t\,-\,\tau)}\end{array}

则卡尔曼滤波算式如下：

状态最优滤波方程

\frac{\mathrm{d}\hat{\pmb{x}}(\,t\,\vert\,t\,)}{\mathrm{d}t}\,=\,\pmb{F}(\,t\,)\hat{\pmb{x}}(\,t\,\vert\,t\,)\,+\,\pmb{K}(\,t\,)\big[\,\pmb{y}(\,t\,)\,-\,\pmb{H}(\,t\,)\hat{\pmb{x}}(\,t\,\vert\,t\,)\,\big]

\hat{\mathbf{x}}(\,t_{0}\,|\,t_{0})\,=\,\bar{\mathbf{x}}\,(\,t_{0})

误差协方差矩阵方程

\begin{array}{l}{\displaystyle\frac{\mathrm{d}P(t\,|\,t)}{\mathrm{d}t}=F(t)P(t\,|\,t)+P(t\,|\,t)F^{\mathrm{T}}(t)}\\ {\displaystyle\qquad\qquad+\,\pmb{\Gamma}(t)\underline{{Q(t)}}\underline{{\Gamma}}^{\mathrm{T}}(t)-P(t\,|\,t)\underline{{H}}^{\mathrm{T}}(t)\pmb{R}^{-1}(t)\underline{{H}}(t)P(t\,|\,t)}\end{array}

P(\,t_{0}\,|\,t_{0})\;=\;P(\,t_{0})

滤波增益矩阵

\pmb{K}(\pmb{t})\:=\:\pmb{P}(\pmb{t}\mid\pmb{t})\pmb{H}^{\operatorname{T}}(\pmb{t})\pmb{R}^{-1}(\pmb{t})

卡尔曼滤波算式适用于满足下述条件的系统：

(1）初始状态 x(0)是高斯随机矢量,其均值为x(0l0),它独立于 n(k)和 ε(k),且具有非负定的 n × n 维协方差阵E[x(0)·\mathbf{x}^{\mathrm{T}}(0)\,]=P(0\,|\,\mathbf{0})\,_{\circ}

(2）过程噪声和观测噪声都是互不相关的零均值高斯白噪声，并且其协方差矩阵 \pmb{Q} 非负定、 \pmb{R} 正定。

4.2.3 广义卡尔要滤波

在飞行器系统辨识中，经常遇到的是非线性连续－离散系统，即状态方程是非线性连续方程，观测方程是离散型的。将卡尔曼滤波推广用于非线性系统称之为广义卡尔曼滤波。非线性连续～离散系统的状态方程和观测方程为：

状态方程

\begin{array}{c}{{\pmb{\dot{\pmb{x}}}\left(\,t\,\right)\,=\,\pmb{\mathcal{f}}[\,{\pmb{x}}\left(\,t\,\right),{\pmb{\mathfrak{u}}}\left(\,t\,\right),\pmb{\theta}\,;t\,]\,+\,\pmb{\Gamma}(\,t\,)\,\pmb{\eta}(\,t\,)\,;}}\\ {{\pmb{E}}\left[\,{\pmb{x}}\left(\,t_{0}\,\right)\,\right]\,=\,\pmb{\bar{x}}\left(\,t_{0}\,\right)\,}}\end{array}

观测方程

\begin{array}{r}{\textbf{y}\!\left(\,k\,\right)\,=\,h\left[\,\pmb{x}\left(\,k\,\right),\pmb{u}\left(\,k\,\right),\pmb{\theta}\,;k\,\right]\,+\,\pmb{\varepsilon}\left(\,k\,\right)}\end{array}

式中 x\!\in\!R^{n}\,,\pmb{u}\!\in\!R^{r}\,,\mathbf{y}\!\in\!R^{m} 一状态矢量、控制矢量和观测矢量；\theta\in R^{p} 一参数矢量；

f、h——相应维的非线性实值函数；\pmb{T} —过程噪声分布矩阵；

\pmb{\eta}(t) 和 \pmb{\varepsilon}(\pmb{k}) 一分别为过程噪声和观测噪声。假定为互不相关的零均值高斯白噪声，即

\left\{\begin{array}{l}{{E[\,\pmb{\eta}(t)\,=\,0,\quad E[\,\pmb{\varepsilon}(k)\,]\,=\,0,\quad E[\,\pmb{\eta}(t)\pmb{\varepsilon}^{\mathrm{T}}(k)\,]\,=\,0}}\\ {{E[\,\pmb{\eta}(t)\,\pmb{\eta}^{\mathrm{T}}(\tau)\,]\,=\,Q(t)\delta(t\,-\,\tau),\quad E[\,\pmb{\varepsilon}(k)\pmb{\varepsilon}^{\mathrm{T}}(j)\,]\,=\,\pmb{R}(k)\,\hat{\delta}_{k j}}}\end{array}\right.

其广义卡尔曼滤波算式为：

状态预测方程

\left\{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}}\hat{\pmb{x}}\big(\,t\,\big|\,t_{k-1}\big)\,=\,\pmb{f}\big[\,\hat{\pmb{x}}\big(\,t\,\big|\,t_{k-1}\big)\,,\pmb{u}\big(\,t\,\big)\,,\pmb{\theta}\,;t\,\big]}\\ {\hat{\pmb{x}}\big(\,t_{0}\,\big|\,t_{0}\big)\,=\,\bar{\pmb{x}}\big(\,t_{0}\big)\quad\big(\,t\,\in\,\big[\,t_{0}\,,t_{k}\,\big]\,\big)}\end{array}\right.

状态校正方程

\begin{array}{l}{\hat{\pmb{x}}\left(\,k\,|\,k\,\right)\,=\hat{\pmb{x}}\left(\,k\,|\,k\,-1\right)\,+\,{\pmb{K}}\left(\,k\,\right)}\\ {\left[\,{\pmb{y}}\left(\,k\,\right)\,-\,{\pmb{h}}\left(\,\hat{\pmb{x}}\left(\,k\,|\,k\,-1\right),\pmb{u}\left(\,k\,\right),\pmb{\theta}\,;k\,\right)\,\right]}\end{array}

误差协方差阵预测方程

\begin{array}{l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}{P}(\,t\\mid t_{k-1})\,=\,F(\,t\,){P}(\,t\mid t_{k-1})\,+\,}\\ {\displaystyle\qquad\qquad\qquad\quad{P}\big(\,t\mid t_{k-1}\big){F}^{\mathrm{T}}\big(\,t\,\big)\,+\,{F}(\,t\,){Q}(\,t\,){\cal T}^{\mathrm{T}}(\,t\,)}\end{array}

P(\,t_{0}\,|\,\,t_{0})\;=\;P(\,t_{0})

式中 \pmb{F}(\pmb{\mathrm{\Delta}}t)=\frac{\partial\pmb{f}}{\partial\pmb{x}}\bigg|_{\pmb{x}=\pmb{\hat{x}}(\pmb{\mathrm{\Delta}}t)}|_{\pmb{t}_{k-1}})

误差协方差阵校正方程

P\!\left(\,k\;|\,k\,\right)\;=\;\left[\,I\,-\,K\!\left(\,k\,\right)H\!\left(\,k\,\right)\right]P\!\left(\,k\;|\,k\;-\,1\right)

滤波增益矩阵

\begin{array}{l}{{\displaystyle{\cal K}(k)\,={\cal P}(k\,|k\,-1)H^{\mathrm{T}}(k)\;\cdot}}\\ {{\displaystyle\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}}\\ {{\displaystyle\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}}\end{array}

式中 H(k)=\frac{\partial\,\pmb{h}}{\partial\pmb{x}}\,\Bigg|_{\pmb{x}=\pmb{\hat{x}}(\pmb{k}\mid\pmb{k}-\pmb{1})}

对于连续-离散系统的另一解法，是将连续状态模型离散化，对状态方程积分，求得转移矩阵 \Phi(k,k-1) ，然后再用离散系统的算式进行计算。其算式为：

预测方程

\hat{\pmb{x}}(\,k\,\left|\,k\,-1\right.)\,=\,\hat{\pmb{x}}(\,k\,-1\,\left|\,k\,-1)\,+\int_{t_{k-1}}^{t_{k}}\pmb{f}[\,x\,(\,t\,)\,,\bar{u}\,(\,k\,)\,,\theta\,;t\,]\mathrm{d}t

\hat{\bf{\sigma}}(0\,|\,0)\;=\;{\bf{\sigma}}_{x}(0)

P\left(\,k\;|\,k\,-\,1\,\right)\,=\,\pmb{\phi}\left(\,k\;,k\,-\,1\,\right)P\left(\,k\,-\,1\,|\,k\,-\,1\,\right)\,\cdot

\pmb{\mathcal{P}}^{\mathrm{T}}(k\,,k\,-\,1)\,+\,\Delta t\pmb{T}(k\,-\,1)\pmb{Q}(k\,-\,1)\pmb{T}^{\mathrm{T}}(k\,-\,1)

P(0\,|\,0)\:=\:P(0)

式中

\begin{array}{l}{{\displaystyle\overline{{{u}}}\left(k\right)~=~\left[~{u}\left(k~-1\right)~+~{u}\left(k\right)\right]/2}}\\ {{\displaystyle\Phi(k,k~-1)~=~\mathrm{e}^{F(k)\Delta t}}}\\ {{\displaystyle\Delta t~=~t_{k}~-~t_{k-1}}}\\ {{\displaystyle F(k)~=~\frac{\partial{f}}{\partial{x}}\Bigg|_{s=\hat{x}(k)\Delta t-1}}}\end{array}

\begin{array}{c}{{\pmb{K}(\pmb{k})=\pmb{P}(\pmb{k}\mid\pmb{k}-1)\pmb{H}^{\mathrm{T}}(\pmb{k})\cdot}}\\ {{\left[\pmb{H}(\pmb{k})\pmb{P}(\pmb{k}\mid\pmb{k}-1)\pmb{H}^{\mathrm{T}}(\pmb{k})+\pmb{R}(\pmb{k})\right]^{-1}}}\\ {{\hat{\pmb{x}}(\pmb{k}\mid\pmb{k})\!=\pmb{\hat{x}}(\pmb{k}\mid\pmb{k}-1)+\pmb{K}(\pmb{k})\cdot}}\\ {{\pmb{x}\in\{\pmb{k}\}}}\end{array}

\left[{\pmb y}({\pmb k})-{\pmb h}(\hat{\pmb x}({\pmb k}\left|{\pmb k}-1),{\pmb u}({\pmb k}),{\pmb\theta},{\pmb k})\right.\right]

\pmb{P}(\pmb{k}\mid\pmb{k})\,=\pmb{[I\,-\,\pmb{K}(k\,)\,H(k\,)\,]\,\pmb{P}(k\,|\,\pmb{k}\,-\,1)}\,=

\left[\,I\,-\,K(\,k\,)H(\,k\,)\,\right]P(\,k\,|\,k\,-\,1)

[\,I\,-\,K(\,k\,)H(\,k\,)\,]^{\mathrm{T}}\,+\,K(\,k\,)R(\,k\,)K^{\mathrm{T}}(\,k\,)

由式（4-44）给出的状态估计误差协方差阵传播公式是在假定 \Delta t 足够小的条件下而近似获得的[10]

在飞行器系统辨识中，当系统可近似看成时不变系统，且过程噪声和观测噪声的统计特性变化不大时，在其运动偏离标准轨线较小的情况下，对状态估计可近似使用稳态滤波，而式（4-43）一式(4-47）称为时变滤波。在稳态滤波情况下，滤波增益矩阵 \pmb{K} 和状态估计误差协方差矩阵 \pmb{P} 均是常数。即

\pmb{K}\:=\:P H^{\operatorname{T}}[\,H P H^{\operatorname{T}}\,+\,\pmb{R}\,]^{-1}

式中 \pmb{H}=\frac{\partial\pmb{h}}{\partial\pmb{x}}\bigg|_{\pmb{x}=\pmb{x}(\mathbf{\mu_{0}})}\circ\pmb{P} 通过稳态黎卡提方程的一阶近似获得

{\pmb F}{\pmb P}\,+\,{\pmb P}{\pmb F}^{\mathrm{T}}\,-\,\frac{1}{\Delta t}{\pmb P}{\pmb H}^{\mathrm{T}}\,[\,{\pmb H}{\pmb P}{\pmb H}^{\mathrm{T}}\,+\,{\pmb R}\,]^{-1}{\pmb H}{\pmb P}\,+\,{\pmb I}{\pmb Q}{\pmb I}^{\mathrm{T}}\,=\,0

式中 \pmb{F}=\frac{\partial\pmb{f}}{\partial\pmb{x}}\Bigg|_{\pmb{x}=\pmb{\xi}(\pmb{\xi}_{0})},

4.2.4 增广的广义卡尔曼滤波

广义卡尔曼滤波算法还可推广用于参数估计。设 \pmb{\theta} 是待估参数矢量，因常值参数 \pmb{\theta} 满足

故将方程（4-50)增补到状态方程中，从而导出增广非线性系统。对增广的非线性系统进行广义卡尔曼滤波，便可获得增广状态的准最小方差估计，也就是对未知参数矢量0做近似最小方差估计。这种将广义卡尔曼滤波用于系统参数估计的方法称为增厂的广义卡尔曼滤波。特别需要强调的是，增广后的系统一定是非线性的，即使对状态 \pmb{x} 而言是线性系统，由于参数0增厂为状态，{\pmb\theta}^{\mathrm{T}}{\pmb x} 项就成了非线性项，故对增广后的状态矢量而言必定是非线性系统。

以式（4-35)和式（4-36）描述的非线性连续一离散系统为例，其增广后的非线性系统为

\begin{array}{r}{\left[\dot{\pmb{x}}\right]=\;\left[\!\!\begin{array}{c}{\pmb{f}\!\left[\,\pmb{x}\left(t\,\right),\pmb{u}\left(t\,\right),\pmb{\theta}\,;t\,\right]}\\ {\pmb{\theta}}\end{array}\!\!\right]+\;\pmb{\Gamma}(t\,)\!\left[\!\!\begin{array}{c}{\pmb{\eta}\!\left(t\,\right)}\\ {\pmb{\eta}}\end{array}\!\!\right]}\end{array}

\mathbf{y}\left(\,k\,\right)\;=\;h\left[\,\pmb{x}\left(\,k\,\right),\pmb{u}\left(\,k\,\right),\pmb{\theta}\left(\,k\,\right)\,+\,\pmb{\varepsilon}\left(\,k\,\right)

记

\begin{array}{r l r}{\pmb{x}_{a}\;=\;\left(\begin{array}{c}{\pmb{x}}\\ {\pmb{\theta}}\end{array}\right),}&{{}\pmb{f}_{a}\;=\;\left(\begin{array}{c}{\pmb{f}}\\ {\pmb{0}}\end{array}\right),}&{\pmb{\eta}_{a}\;=\;\left(\begin{array}{c}{\pmb{\eta}}\\ {\pmb{0}}\end{array}\right),}\end{array}

\pmb{h}_{a}\left[\,\pmb{x}_{a}\,,\pmb{u}\,;\pmb{k}\,\right]\:=\:\pmb{h}\left[\,\pmb{x}\,,\pmb{u}\,,\pmb{\theta}\,;\pmb{k}\,\right]

则有

{\pmb x}_{a}\;=\;f_{a}\!\left[\,{\pmb x}_{a}\!\left(\,t\,\right),{\pmb u}\!\left(\,t\,\right);t\,\right]\,+\,{\pmb T}\!\left(\,t\,\right){\pmb\eta}_{a}\!\left(\,t\,\right)

\begin{array}{r}{\mathbf{y}(\,k\,)\;=\;h_{a}\big[\,\pmb{x}_{a}(\,k\,)\,,\pmb{u}\left(\,k\,\right)\,;k\,\big]\,+\,\pmb{\varepsilon}\big(k\,\big)\;}\end{array}

式（4-53）、式（4-54)与方程（4-35)、式（4-36)具有同样的描述形式，只是把参数矢量θ隐含于增广状态x。中。因此，由式（4-53）式（4-54)推得的广义卡尔曼滤波算式与基于式（4-35）、式(4-36）推出的广义卡尔曼滤波算式结构完全相同，只需将其中的x换成xa、f换成fa、h换成h。即可[11]

4.2.5 修正增益广义卡尔曼滤波

修正增益广义卡尔曼滤波是针对一类所谓“可修正非线性”的非线性系统导出的广义卡尔曼滤波算法。它与一般非线性系统广义卡尔曼滤波算法的区别在于，在状态方程的线性化处理过程中没做任何近似。在飞行器系统辨识中，有些非线性系统满足“可修正非线性”的要求，故这个算法在飞行器系统辨识中得到了应用。

定义：函数 f(\,x\,):I R^{n}{\rightarrow}I R^{n} 称为可修正非线性函数，如果对于任意状态 \pmb{x} 和已知状态 \hat{\pmb{x}} ,都有一个 n\times n 维矩阵 D:I R^{n}\times I R^{n} \to I R^{n\times n} 存在,使得

{\pmb f}(\,{\pmb x}\,)\,-\,{\pmb f}(\,{\pmb\hat{\pmb x}}\,)\,=\,{\pmb D}(\,{\pmb y}\,^{\star}\,,{\pmb\hat{\pmb x}}\,)(\,{\pmb x}\,-\,{\pmb\hat{\pmb x}}\,)

式中 {\bf y}^{\star} 一—已知函数或数值。

如果非线性系统式（4-35)和式(4-36)中的非线性函数 \pmb{f} 满足可修正非线性要求，即

\begin{array}{r l}&{\left[\,\mathbf{x}\left(\,t\,\right),\pmb{u}\left(\,t\,\right),\pmb{\theta}\,;t\,\right]\;=}\\ &{\pmb{f}\big[\,\hat{\mathbf{x}}\left(\,t\,\big\vert\,t_{k-1}\right),\pmb{u}\left(\,t\,\right),\pmb{\vartheta}\,;t\,\right]\,+\,\pmb{D}\big[\,\mathbf{y}^{\,\ast}\left(\,t\,\right),\hat{\mathbf{x}}\left(\,t\,\big\vert t_{k-1}\right),}\\ &{\pmb{u}\left(\,t\,\right),\pmb{\theta}\,;t\,\right]\big[\,\mathbf{x}\left(\,t\,\right)\,-\,\hat{\mathbf{x}}\left(\,t\,\big\vert t_{k-1}\right)\big]\big(\,t\,\in\,\left[\,t_{k-1},t_{k}\,\right]\big)}\end{array}

则以矩阵 \pmb{D} 代替式 (4-38)\sim 式（4-42）中的矩阵 \pmb{F}(t) ，便构成如下修正增益广义卡尔曼滤波算法：

状态预测方程

\begin{array}{l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\pmb{\hat{x}}\left(\,t\,\left|t_{k-1}\right\rangle\,=\,\pmb{f}\big[\,\pmb{\hat{x}}\left(\,t\,\left|t_{k-1}\right\rangle,\pmb{u}\left(\,t\,\right),\pmb{\theta}\,;t\,\right]\right.}\\ {\displaystyle\left.\pmb{\hat{x}}\left(\,t_{0}\,\left|\,t_{0}\right\rangle\,=\,\pmb{\bar{x}}\left(\,t_{0}\right)\left(\,t\,\in\,\left[\,t_{k-1},t_{k}\,\right]\,\right)\,\right.}\end{array}

状态校正方程

\begin{array}{r}{\hat{\pmb{x}}(\pmb{k}\,|\pmb{k})=\hat{\pmb{x}}(\pmb{k}\,|\pmb{k}-1)+\pmb{K}(\pmb{k})\,|\,\pmb{y}(\pmb{k})-}\\ {\pmb{h}[\hat{\pmb{x}}(\pmb{k}\,|\,\pmb{k}-1),\pmb{u}(\pmb{k}),\pmb{\theta};\pmb{k}\,]\}}\end{array}

误差协方差阵预测方程

\frac{\mathrm{d}}{\mathrm{d}t}\pmb{P}\big(\ t\,\lvert t_{k-1}\big)\,=\pmb{D}\big[\,\pmb{y}^{\mathrm{~*~}}(\ t\,)\,,\hat{\pmb{x}}\big(\ t\,\lvert t_{k-1}\big)\,,\pmb{u}\,(\ t\,)\,,\pmb{\theta}\,;t\,\big]

\begin{array}{r l}&{\pmb{P}(\,t\,|\,t_{k-1})\,+\,\pmb{P}(\,t\,|\,t_{k-1})\pmb{D}^{\mathrm{T}}[\,\pmb{y}^{\ast}\,(\,t\,)\,,\hat{\pmb{x}}(\,t\,|\,t_{k-1})\,,}\\ &{\pmb{u}(\,t\,)\,,\pmb{\theta}\,;t\,]\,+\,\pmb{T}(\,t\,)\,\pmb{Q}(\,t\,)\pmb{T}(\,t\,)}\\ &{\pmb{P}(\,t_{0}\,|\,t_{0})\,=\,\pmb{P}(\,t_{0})}\end{array}

误差协方差阵校正方程

P(k\,|k)\,=\,\left[\,I\,-\,K(\,k\,)H(\,k\,)\,\right]P(\,k\,|\,k\,-\,1)

滤波增益矩阵

\begin{array}{c}{{\displaystyle{\pmb K}\left({\pmb k}\mid{\pmb k}\right)\,={\pmb P}\left({\pmb k}\mid{\pmb k}\,-1\right){\pmb H}^{\mathrm{T}}\left({\pmb k}\,\right)\left[{\pmb H}\left({\pmb k}\,\right)\,\right.\,}}\\ {{\displaystyle{\pmb P}\left({\pmb k}\mid{\pmb k}\,-1\right){\pmb H}^{\mathrm{T}}\!\left({\pmb k}\,\right)\,+\,{\pmb R}\left({\pmb k}\,\right)\right]^{-1}}}\\ {{\displaystyle{\pmb H}\left({\pmb k}\,\right)=\frac{{\partial\pmb h}}{{\partial\pmb x}}\,\Bigg\vert_{{\pmb x}\,=\,{\pmb\hat{\kappa}}\,\left({\pmb k}\,\right\vert\,{\pmb k}\,-1\right)}}}\end{array}

式中

同理，对于增广后的非线性系统式（4-51）～式（4-54），如果非线性函数 f_{a} 满足可修正非线性要求，即

f_{a}[\,{\pmb x}_{a}(t),{\pmb u}(t),t\,]\,={\pmb f}_{a}[\,\hat{\pmb x}_{a}(t\,|\,t_{b-1}),{\pmb u}(t);t\,]\,+

\begin{array}{r l r}{\lefteqn{{D_{a}[y_{a}^{*}\left(t\right),\hat{x}_{a}(t\,|\,t_{k-1}),\pmb{u}(t);t\,][x_{a}(t)-\hat{x}_{a}(t\,|\,t_{k-1})]}}}\\ &{}&{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\\ &{}&{\quad\quad\quad\quad\quad\quad\quad\quad\quad\big({t\in[t_{k-1},t_{k}\,]}\big)}\end{array}

则将式(4-56)～式(4-61)中的 \pmb{x} 换成 \pmb{x}_{a}\,,\pmb{f} 换成 f_{a},h 换成 \pmb{h}_{a}\,,\pmb{D} 换成 \pmb{D}_{a} ,便可对增广非线性系统式（4-51）～式（4-54)构成修正增益广义卡尔曼滤波算法[11]

修正增益广义卡尔曼滤波与前述广义卡尔曼滤波的不同之处是，其状态方程的线性化是精确的，而前述广义卡尔曼滤波算法是对状态方程非线性函数采用台劳级数展开，仅保留一阶项，忽略所有二阶以上高次项得到的。

应用修正增益广义卡尔曼滤波算法的关键是，能够找到函数矩阵 \pmb{D} （或 \pmb{D}_{a} ）,使得非线性函数 \pmb{f} （或 f_{a} )是可修正的。通常，一个简单处理办法是把方程（4-55）中的 \pmb{y}^{\star} 直接取为

\textbf{y}^{\star}\left(\,t\,\right)\;=\;\pmb{H}\left(\,t\,\right)\pmb{x}\left(\,t\,\right)

在实际应用中，如果系统中的待估计参数与状态参数、控制参数以乘积型出现，则对用于参数估计的增广非线性系统而言，一般可以找到相应的 {\pmb D}_{a} 矩阵。在飞行器气动参数辨识中，由于气动参数通常是与状态参数、控制参数同时以乘积型出现，故修正增益广义卡尔曼滤波算法已在飞行器气动参数辨识中得到应用。然而，对于具体问题，如何选取待估计参数和 \pmb{D} (或 \pmb{{D}}_{a} ）矩阵是件颇费脑筋的事。

4.2.6 平方根分解滤波

由于计算机有限字长等因素的影响，常会使广义卡尔曼滤波中的滤波误差协方差阵 \textstyle P(k\mid k) 失去半正定性，从而导致滤波过程发散。尽管可采用所谓稳定形式的广义卡尔曼滤波以保证\textstyle P(k\mid k) 的正定性,但正如安德森（B.D.O.Anderson)所指出，其非负定性不会自动得到保证[12]。平方根滤波是保证滤波稳定性的有效方法。所谓平方根滤波，就是令 \pmb{P}=\pmb{S}\pmb{S}^{\mathrm{T}} 导出的算法。由矩阵条件数

\operatorname{Cond}(P)\,=\,\operatorname{Cond}(\,S\mathbf{S}^{\mathrm{T}})\,=\,[\operatorname{Cond}(\,S)\,]^{2}

可见，平方根滤波两倍有效于普通卡尔曼滤波。

目前平方根滤波可分为两类，即协方差平方根滤波和信息平方根滤波。限于篇幅，这里只讨论前者，信息平方根滤波请参见参考文献[8,13] 。

1）协方差平方根分解滤波算法

对于由式（4-35）所描述的非线性系统，对普通广义卡尔曼滤波，令

\begin{array}{r l}&{\left\{P\big(k\,|k\big)\,=\,\pmb{S}\big(k\,|k\big)\pmb{S}^{\mathrm{T}}\big(k\,|k\big)\right.}\\ &{\left.\left\{P\big(k\,|k\,-\,1\big)\,=\,\pmb{S}\big(k\,|k\,-\,1\big)\,\pmb{S}^{\mathrm{T}}\big(k\,|k\,-\,1\big)\right.}\\ &{\left.\left(\pmb{Q}\big(k\,-\,1\big)\,=\,\pmb{W}_{d}\big(k\,-\,1\big)\,\pmb{W}_{d}^{\mathrm{T}}\big(k\,-\,1\big)\right.\right.}\end{array}

式中 \mathbf{S}\in\mathbb{R}^{n\times\,n}- 一上或下三角阵。

可由乔莱斯基(Cholesky)分解产生。假定 \boldsymbol{F}\,,H\,,\boldsymbol{\Phi} 已求得。首先考虑时间更新，由

\begin{array}{c}{{|\emph{k}-1\rangle\,=\,\pmb{\Phi}(k\,,k\,-\,1)P(k\,-\,1\,|\,k\,-\,1)\,\pmb{\Phi}^{\mathrm{T}}(k\,,k\,-\,1)\,+}}\\ {{}}\\ {{\pmb{T}(k\,-\,1)\,\pmb{Q}(k\,-\,1)\,\pmb{T}^{\mathrm{T}}(k\,-\,1)}}\end{array}

有

\begin{array}{r c l}{{}}&{{\tilde{S}(k\,|\,k\,-1)\,=}}\\ {{}}&{{}}&{{}}\\ {{}}&{{\left[\,\pmb{\Phi}(k\,,\rlap/,k\,-1)S(k\,-1\,|\,k\,-1)\,\stackrel{!}{,}\,\pmb{\Gamma}(k\,-1)\,W_{d}(k\,-1)\right](4\,-65)}}\end{array}

式中 s(k|k-1)∈Rn×(n+q)

由于以上直接的时间更新将使协方差平方根阵 \tilde{\pmb{S}}\left(\,\pmb{k}\ \middle|\,\pmb{k}\ -1\,\right) 增维，计算上这是不希望的。为此，可通过格拉姆-施密特正交化过程或计算上更有效地修正格拉姆-施密特正交化过程或豪西候德尔(Househoulder)变换构造正交变换 Tl8],TE R(n+q)×(n+q),且 \pmb{T}\pmb{T}^{\mathrm{T}}=\pmb{I} ，使

\tilde{\textbf{\textit{S}}}(\,k\mid k\,-\,1\,)\,T\,=\,[\,{\textbf{\textit{S}}}(\,k\mid k\,-\,1\,)\,\mid\,{\cal O}\,]

注意，此处有

\begin{array}{c}{{\tilde{\bf{S}}(k\,|k\,-\,1)\,{\bf{T}}{\bf{T}}^{\mathrm{T}}\tilde{\bf{S}}^{\mathrm{T}}(k\,|k\,-\,1)\,=\,}}\\ {{{\bf{S}}(k\,|k\,-\,1)\,{\bf{S}}^{\mathrm{T}}(k\,|k\,-\,1)}}\end{array}

通过修正格拉姆-施密特正交化方法，可导出如下的平方根滤波的时间更新算式：

令

\begin{array}{r}{\begin{array}{r l r}{\lefteqn{\textbf{A}^{1}=\tilde{S}(\,k\,|\,k\,-1)\,=}}\\ &{}&{\left[\,\tilde{\pmb{\phi}}(\,k\,,k\,-1)\,S(\,k\,-1\,|\,k\,-1)\,\left\,\right\,|\,{\pmb{\Gamma}}(\,k\,-1)\,W_{d}(\,k\,-1)\,\right]^{\mathrm{T}}}\end{array}}\end{array}

96

\left\{{C_{k_{i}}}\atop=\sqrt{\left({\frac{{A_{k}^{k}}^{\top}A_{k}^{k}}{A_{k}^{k}}}\right)}}&{\quad\displaystyle({A_{k}^{k}}^{\top}=({A_{k}^{k}})^{\top}}\\ {\atop\displaystyle A_{k_{i}}^{k}={\left\{\!\!\begin{array}{l l}{0}&{\!\!\begin{array}{l}{(j=1,2,\cdots,k-1)}\\ {a^{k}}\end{array}\right.}}\\ {\left\{{\left({\frac{1}{\alpha^{k}}}\right)}A_{k}^{k\top}\right\}}&{\quad(j=k+1,\cdots,n)}\end{array}}}\\ {A_{j}^{k+1}={A_{j}^{k}}-{C_{k}}[(1/\alpha^{k})A_{k}^{k}]}&{\quad(j=k+1,\cdots,n)}\end{array}}\right.

则

\pmb{S}(\pmb{k}\mid\pmb{k}\,-\,1\,)\,=\,\pmb{C}^{\mathrm{T}}

式中 \mathbf{A}_{j}^{k} 代表 A^{k} 的第 j 列。

可见,时间更新并没有显式地计算正交阵 \pmb{T}

对于平方根滤波的测量更新，可通过标量量测迭代 m 次实现。令观测阵H=（HT，H，·,HH）T,由广义卡尔曼滤波,对标量量测 \pmb{z}_{j} 有

\begin{array}{c}{{S(k\mid k)S^{\mathrm{T}}(k\mid k)\;=\;}}\\ {{{}}}\\ {{S(k\mid k-1)[\,I\,-\,f\pmb{f}^{\mathrm{T}}/\alpha\,]S^{\mathrm{T}}(k\mid\!k-1)}}\end{array}

即

\pmb{S}(\,k\,|\,k\,)\,=\,\pmb{S}(\,k\,|\,k\,-\,1)(\,I\,-\,f\pmb{f}^{\mathrm{T}}/\alpha\,)^{1/2}

式中 \pmb{f}=\pmb{S}^{\mathrm{T}}(\,\pmb{k}\,\,|\,\pmb{k}\,-1\,)\,\pmb{H}_{j}^{\mathrm{T}},

\alpha=(f^{\mathrm{T}}f+R_{j j})\sp{\textnormal{-}1}. —标量；

进一步，对 j=1,2,\cdots,m ,可获得测量更新方程如下：

\begin{array}{r l}&{\pmb{f}=\pmb{S}^{\mathrm{T}}(\pmb{k}\mid\pmb{k}\,-\,1)\,\pmb{H}_{j}^{\mathrm{T}}}\\ &{\pmb{b}\,=1/(\pmb{f}^{\mathrm{T}}\pmb{f}\,+\,\pmb{R}_{j j}\,)}\\ &{\pmb{r}\,=1/[1+\,(\,b R_{j j}\,)^{1/2}\,]}\end{array}

\begin{array}{r l r}&{\hat{\pmb{x}}(\,k\,|\,k\,)\!\!\!}&{=\!\hat{\pmb{x}}(\,k\,|\,k\,-1)\!\!\!}&{{}+}\\ &{\quad}&{\pmb{K}(\,k\,|\,k\,)\!\!\}\,\vert\,z_{j}\,-\,h_{j}[\,\hat{\pmb{x}}(\,k\,|\,k\,-1)\,,\pmb{u}(\,k\,)\,,\pmb{\theta}\,]\,\vert\,}\\ &{\quad}&{\pmb{S}(\,k\,|\,k\,)\!\!\}\,=\!\pmb{S}(\,k\,|\,k\,-1)\,-\,r{\pmb{K}(\,k\,|\,k\,)\!\!}\,\pmb{f}^{\mathrm{T}}\,}\end{array}

因此,由式(4-64)式 (4-68)\sim 式(4-70)及式(4-73）即构成了平方根滤波算法。

2）快速三角化协方差平方根滤波算法

对于以上的平方根滤波算法，在测量校正时常会使S失去上或下三角性，从而导致计算量及存储量成倍增加。下面基于卡尔森(N.A.Carlson)的工作[14],采用乔莱斯基分解给出非线性连续-离散系统的快速三角化协方差平方根滤波算法，可有效地保证\mathbf{S}(\,k\,\left|\,k\,\right) 始终是上三角的。为了说明的方便，仍以标量量测推导，可自然地推广到矢量量测情形。

快速三角化平方根滤波的时间校正方程仍同上节，对于测量校正，由上节的推导有

S(\,k\,|\,k\,)\,=\,S(\,k\,|\,k\,-\,1)[\,I\,-\,f f^{\mathrm{T}}/\alpha\,]^{1/2}

令 A=\left[\,I-f\pmb{f}^{\mathrm{T}}/\alpha\,\right]^{1/2} 为上三角阵，则 \pmb{S}\left(\pmb{k}\mid\pmb{k}\right)=\pmb{S}\left(\pmb{k}\mid\pmb{k}-1\right)\pmb{A} 亦为上三角阵。采用乔莱斯基分解有

A\ =\ a^{D}\ –\ f\ ^{*}\ c^{D}

这里， {\pmb a}^{D}\,,{\pmb C}^{D} 为对角阵，其元素 a_{i},C_{i} 可由下式获得

\left\{\begin{array}{l l}{\alpha_{0}\,=\,r}\\ {\quad}\\ {\alpha_{i}\,=\,\,\alpha_{i-1}\,+\,f_{\,i}^{\,2}}&{(\,i\,=\,1,2,\cdots,n\,)}\\ {\quad}\\ {\alpha_{i}\,=\,\,(\,\alpha_{i-1}/\alpha_{i}\,)^{1/2}}&{(\,i\,=\,1,2,\cdots,n\,)}\\ {\quad}\\ {C_{i}\,=\,f_{\!i}\,(\,\alpha_{i-1}\alpha_{i}\,)^{1/2}}&{(\,i\,=\,1,2,\cdots,n\,)}\end{array}\right.

此处 \alpha_{n}{\overset{=}{\overline{{\cdots}}}}\alpha\,,f_{i} 为 \pmb{f} 的第 _i 元素， r 为相应于 \pmb{h} 的观浏噪声方差。

\begin{array}{l}{\left\{{\pmb f}^{*}\;=\;\left[{\pmb0},{\pmb f}^{(1)},\cdots,{\pmb f}^{(n-1}\right]\right.}\\ {\left.\right\}{\pmb f}^{(i)}=\;\left(f_{1},f_{2},\cdots,f_{i},0,\cdots,0\right)^{\intercal}}\end{array}

因此， \pmb{S}(\pmb{k}\mid\pmb{k})=\pmb{S}(\pmb{k}\mid\pmb{k}-1)\,\pmb{A} ,可由递推计算 s f^{\star} 的 \pmb{S f}^{(i)} 列(以\pmb{b}_{i} 表示)

\left\{b_{0}\;=\;0\right.\qquad}\\ {\left.b_{i}\;=\;b_{i-1}\,+\,S_{i}\bigl(\,k\,\bigl|\,k\,-\,1\bigr)\,f_{i}\right.\qquad\qquad}&{{}\left(\,i\;=\;1,2,\cdots,n\,\right)}\\ {\left.S_{i}\bigl(\,k\,\bigl|\,k\,\bigr)\;=\;S_{i}\bigl(\,k\,\bigl|\,k\,-\,1\bigr)\,a_{i}\,-\,b_{i-1}C_{i}\quad(\,i\;=\;1,2,\cdots,n\,)\,\right.}

这里， \pmb{S}_{i} 表示 \pmb{S}(\pmb{k}\mid\pmb{k}-1) 的第 _i 列,且 \pmb{S}_{i} 和 \pmb{b}_{i} 在第 i 个元以下的元素为零。因此,有

\left\{\begin{array}{l}{{b_{n}\,=\,\displaystyle\sum_{i=1}^{n}S_{i}f_{i}\,=\,S f\equiv K a}}\\ {{\displaystyle\hat{\mathbf{x}}\,(\,k\,|\,k\,)\,=\,\hat{\mathbf{x}}\,(\,k\,|\,k\,-\,1)\,+\,(\,b_{n}/\alpha_{n}\,)\,[\,z_{j}\,-\,\hat{y}_{j}\,(\,k\,|\,k\,-\,1)\,]}}\end{array}\right.

令

\pmb{H}\;=\;(\pmb{H}_{1}^{\mathrm{T}},\pmb{H}_{2}^{\mathrm{T}},\cdots,\pmb{H}_{m}^{\mathrm{T}})^{\mathrm{T}}

快速三角化平方根滤波算法的观测校正可归纳如下

\left\{\begin{array}{l l}{f(k)=s^{\top}(k\mid k-1)H_{j}^{\top}(k)}\\ {\alpha_{0}=R_{i j}}\\ {b_{0}(k)=0}\\ {a_{i}=\alpha_{i-1}+f_{i}^{2}(k)}\\ {a_{i}=(\alpha_{i-1}/\alpha_{i})^{1/2}}\\ {C_{i}=f_{i}(k)/(\alpha_{{\alpha_{i-1}}})^{1/2}}\\ {b_{i}(k)=b_{i-1}(k)+S_{i}(k\mid k-1)f_{i}(k)}\\ {S_{i}(k\mid k)=S_{i}(k\mid k-1)\alpha_{i}-b_{i-1}(k)C}\end{array}\right.

\hat{\pmb{x}}(\,k\mid k\,)\;=\;\hat{\pmb{x}}\left(\,k\:\middle|\,k\;-\;1\,\right)\;+

\pmb{b}_{n}\left(\,k\,\right)\mid z_{j}\,-\,h_{j}\left[\,\pmb{\hat{x}}\left(\,k\,\left|\,k\,-\,1\,\right),\pmb{u}\left(\,k\,\right),\pmb{\theta}\,\right]\,\right\}

\left(\,i\;=\;1\,,2\,,\cdots,n\,;\;j\;=\;1\,,2\,,\cdots,m\,\right)

\pmb{S}(\,k\,|\,k\,)\,=\,[\,\pmb{S}_{1}(\,k\,|\,k\,)\,,\pmb{S}_{2}(\,k\,|\,k\,)\,,\cdots,\pmb{S}_{n}(\,k\,|\,k\,)\,]

新息方差阵 \pmb{{\cal B}}=\pmb{{\cal H}}\pmb{{\cal P}}\pmb{{\cal H}}^{\mathrm{T}}+\pmb{{\cal R}} ，可由下式计算

\begin{array}{r}{\left\{B_{i i}\;=\;a_{n}^{(i)}\right.\quad\quad\quad\quad\quad\quad\left.(i\;=1,2,\cdots,m)\quad}\\ {\quad\quad\quad\quad\quad\left.\quad B_{i j}\;=\;[f^{(i)}(k)]^{\mathrm{T}}f^{(j)}(k)\quad(i\,,j\,=\,1,2,\cdots,m\,{.})\right.}\end{array}

式中 \alpha_{\;\prime a}^{\;(\;i\;)} -相应于 \pmb{H}_{i} 分量求得的量。

3. {\bf{\nabla}}U{\bf{\cal D}}U^{\mathrm{~T~}} 协方差分解滤波算法

改善广义卡尔曼滤波算法数值特性的另一途径是对协方差阵\pmb{P} 进行 U D U^{\mathcal{T}} 分解,即

\pmb{P}(\pmb{k}\mid\pmb{k})\,=\,\pmb{U}(\,\pmb{k}\mid\pmb{k}\,)\,\pmb{D}(\,\pmb{k}\,\mid\pmb{k}\,)\,\pmb{U}^{\mathrm{T}}(\,\pmb{k}\,\mid\pmb{k}\,)

P\big(\,k\,\big|\,k\,-\,1\big)\:=\:\pmb{U}\big(\,k\,\big|\,k\,-\,1\big)\pmb{D}\big(\,k\,\big|\,k\,-\,1\big)\,\pmb{U}^{\mathrm{T}}\big(\,k\,\big|\,k\,-\,1\big)

式中 \pmb{U} 单位上三角阵；

D-———对角阵。

使用与后向乔莱斯基分解密切相关的算法可唯一确定 \pmb{D} 及U ，仍以标量量测推导该算法。由广义卡尔曼滤波算法，有

\begin{array}{r}{P(\boldsymbol{k}\mid\boldsymbol{k})\,=P(\boldsymbol{k}\mid\boldsymbol{k}\,-\,1)\,-\,}\end{array}
$$$$
\begin{array}{c}{{{\pmb{F}}\lbrace\,{\pmb{\mathscr{R}}}\,|{\pmb{\mathscr{R}}}\,-\,{\pmb{\mathscr{1}}}\,{\pmb{\mathscr{\kappa}}}^{\intercal}\,-}}\\ {{\pmb{\mathscr{P}}\left(\,{\pmb{\mathscr{k}}}\,|{\pmb{\mathscr{k}}}\,-\,1\right){\pmb{\mathscr{h}}}\left(\,1/\alpha\,\right){\pmb{\mathscr{h}}}^{\intercal}{\pmb{\mathscr{P}}}\left(\,{\pmb{\mathscr{k}}}\,|{\pmb{\mathscr{k}}}\,-\,1\right)}}\\ {{\pmb{\mathscr{x}}}={\pmb{\mathscr{h}}}^{\mathrm{T}}{\pmb{\mathscr{P}}}\left(\,{\pmb{\mathscr{k}}}\,\big|{\pmb{\mathscr{k}}}\,-\,1\right){\pmb{\mathscr{h}}}+{\pmb{\mathscr{r}}}\,;}\end{array}

式中

——相应于 \pmb{h} 的观测噪声方差。

由式（4-83）和式（4-84），有

\pmb{U}(\pmb{k}\mid\pmb{k})\pmb{D}(\pmb{k}\mid\pmb{k})\,\pmb{U}^{\mathrm{T}}(\pmb{k}\mid\pmb{k})\,=

\begin{array}{l}{{\pmb U(k\,|k\,-1)\pmb D(k\,|k\,-1)\,\pmb U^{\operatorname{T}}(k\,|k\,-1)\,-}}\\ {{(1/\alpha)\big[\pmb U(k\,|k\,-1)\pmb D(k\,|k\,-1)\pmb U^{\operatorname{T}}(k\,|k\,-1)\pmb h\big]\,-}}\\ {{\pmb h^{\operatorname{T}}\pmb U(k\,|k\,-1)\pmb D(k\,|k\,-1)\pmb U^{\operatorname{T}}(k\,|k\,-1)\,=}}\\ {{\pmb U(k\,|k\,-1)\,\pmb D(k\,|k\,-1)\,-}}\\ {{(1/\alpha)\big[\pmb D(k\,|k\,-1)\pmb U^{\operatorname{T}}(k\,|k\,-1)\pmb h\big]\,\cdot}}\\ {{[\pmb D^{\operatorname{T}}(k\,|k\,-1)\pmb U^{\operatorname{T}}(k\,|k\,-1)\pmb h\big]^{\operatorname{T}}\big[\pmb U^{\operatorname{T}}(k\,|k\,-1)\pmb\)}}\end{array}

定义

\left\{\begin{array}{l l}{\pmb{f}=\pmb{U}^{\operatorname{T}}(\pmb{k}\mid\pmb{k}-1)\,\pmb{h}}\\ {\pmb{V}=\pmb{D}(\pmb{k}\mid\pmb{k}-1)\,\pmb{f}}\end{array}\right.

将其代人式（4-85），得

\begin{array}{r l}{\pmb{U}(k\left|k\right.)\pmb{D}(k\left|k\right.)\pmb{U}^{\mathrm{T}}(k\left|k\right.)\:=}&{{}}\\ {\pmb{U}(k\left|k\right.-1)[\pmb{D}(k\left|k\right.-1)\:-}&{{}}\\ {\left.\left(1/\alpha\right)\pmb{V}\pmb{V}^{\mathrm{T}}\right]\pmb{U}^{\mathrm{T}}(k\left|k\right.-1)}&{{}}\end{array}

令

\begin{array}{c}{{\overline{{{U}}}\left(\,k\;|k\,-\,1\right)\overline{{{D}}}\left(\,k\;|k\,-\,1\right)\overline{{{U}}}^{\mathrm{T}}(\,k\;|k\,-\,1)\,=}}\\ {{{}}}\\ {{{}}}\\ {{{\pmb{D}}\left(\,k\;|k\,-\,1\right)\,-\,\left(1/\alpha\right){\bf{V}}{\bf{V}}^{\mathrm{T}}}}\end{array}

式中 \bar{\pmb{U}} —单位上三角阵；

\bar{\pmb{D}} —对角阵。

则由式(4-87)～式(4-88),有

\begin{array}{l}{{\pmb{U}(k\mid k)\,{\pmb{D}}(k\mid k)\,{\pmb{U}}^{\mathrm{T}}(k\mid k)\,=\,}}\\ {{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 

由于 \pmb{U}(\pmb{k}\mid\pmb{k}-1) 和 \overbar{U}(k\mid k-1) 均为上三角阵,从而

\left\{\begin{array}{l}{{\pmb U(k\,|k)\,=\,\pmb U(k\,|k\,-\,1)\,\vec{\pmb U}(k\,|k\,-\,1)}}\\ {{\pmb D(k\,|k)\,=\,\vec{\pmb D}(k\,|k\,-\,1)}}\end{array}\right.

因此,广义卡尔曼滤波的 {\pmb U}{\pmb D}{\pmb U}^{\mathrm{T}} 分解滤波的测量修正就成了分解对称阵 \left\{\pmb{D}-\left(1/\alpha\right)\pmb{V}\pmb{V}^{\intercal}\right\} 为 \overline{{{\cal U}{\cal D}}}\,\,\overleftarrow{{\cal U}}^{T} 形式的问题。 \bar{\pmb{U}}\setminus\bar{\pmb{D}} 可由下式递推一列一列地产生。

\left\{\begin{array}{l l}{\alpha_{0}\,=\,r}\\ {\alpha_{j}\,=\,\displaystyle\sum_{k=1}^{j}D_{k k}\cdot f_{k}^{\,2}\,+\,r}\\ {\overline{{D_{j j}}}\,=\,D_{j i}\alpha_{j-1}\slash\alpha_{j}}\\ {\overline{{U}}_{i j}\,=\,\displaystyle\left\{\begin{array}{l l}{\displaystyle-\,D_{i}f f_{j}/\alpha_{j-1}}&{(i\,=\,1,2,\cdots,j\,-\,1)}\\ {\displaystyle1}&{(i\,=\,j)}\\ {\displaystyle0}&{(i\,=\,j+1,j+2,\cdots,n)}\end{array}\right.}\end{array}\right.

式中 r-—相应于 \pmb{h} 的观测噪声方差。

因此,由式(4-90)和式(4-91)即可计算 \pmb{U}(\pmb{k}\mid\pmb{k}) 和 \pmb{{\cal D}}(k\mid k) 但为了计算的有效性，常采用下式递推计算。

\left\{\begin{array}{l l}{\alpha_{i}\,=\,\alpha_{i-1}+f_{i}v_{i}}\\ {\ }\\ {D_{i i}(k\,|\,k)\,=\,D_{i i}(k\,|\,k\,-\,1)\,\cdot\,\alpha_{i-1}/\alpha_{i}}\\ {\ }\\ {b_{i}\,\gets\,v_{i}}\\ {\dot{p}_{i}\,=\,-\,f_{i}/\alpha_{i-1}}\\ {\bigcup_{j i}(k\,|\,k\,)\,=\,\,U_{j i}(k\,|\,k\,-\,1)\,+\,b_{j}P_{i}\Bigg\}(j\,=\,1,2,\cdots,i\,-\,1)}\\ {b_{j}\gets b_{i}\,+\,U_{j i}(k\,|\,k\,-\,1)\,v_{i}}\end{array}\right.

符号 ^{6}\cdots 表示替换。从而

\left\{\begin{array}{l l}{b\,\,=\,\left[\,b_{1}\,,b_{2}\,,\cdots,b_{n}\,\right]^{\mathrm{T}}}\\ {\,}\\ {K(\,k\,|\,k\,)\,=\,\,b/\alpha_{n}}\\ {\,}\\ {\hat{\mathbf{x}}\left(\,k\,\middle\vert\,k\,\right)\,=\,\,\hat{\mathbf{x}}\left(\,k\,\middle\vert\,k\,-\,1\right)\,+\,K(\,k\,\middle\vert\,k\,)\left[\,z_{i}\,-\,y_{i}\,\right]}\end{array}\right.

式(4-83)、式(4-86)式(4-92)式(4-93)即构成了 {\bf{\nabla}}U{\bf{\cal D}}U^{\mathrm{T}} 分解滤波的测量校正。

观测阵 H=(\,H_{1}^{\mathrm{T}},H_{2}^{\mathrm{T}},\cdots,H_{m}^{\mathrm{T}}\,)^{\mathrm{T}} ，可逐个分量进行以上过程，完成 {\bf{\nabla}}U{\bf{\cal D}}U^{\mathrm{T}} 分解滤波的量测校正。对于 ^{m} 个分量，可计算得到f^{\,1}\,,f^{\,2}\,,\cdots,f^{\,m} 及 \alpha_{\,n}^{\,1}\,,\alpha_{\,n}^{\,2}\,,\cdots,\alpha_{\,n}^{\,m}\,\circ

新息阵 \pmb{B}=\pmb{H}\pmb{P}\pmb{H}^{\mathrm{T}}+\pmb{R} ，可由下式计算

B_{i j}\,=\,\binom{\alpha_{n}^{i}}{f^{\,i}V^{j}}\quad(\,i\,=\,j\,=\,1\,,2\,,\cdots,m\,)

对于 {\pmb U}{\pmb D}{\pmb U}^{\dagger} 分解滤波的时间校正，令

\left\{\begin{array}{l l}{\textbf{\em Y}=\left[\,\Phi(k\,|\,k\,-\,1)\,U(k\,|\,k\,-\,1)\,\right\,\colon\,\Gamma(\,k\,-\,1)\,\right],}\\ {\textbf{\em Y}\in\,\mathbb{R}^{n\times(n+q)}}\\ {\tilde{\textbf{\em D}}=\,\left[\,\mathbf{\overset{|}{\mathfrak{D}}}\,\right.\,\left.0\,\right],\tilde{\textbf{\em D}}\in\,R^{(\,n+q)\times(\,n+q\,)}}\\ {\textbf{\em0}\textbf{\em g}}\end{array}\right.

则

\begin{array}{l}{\displaystyle P\big(k\;|k-1\big)\,=\,}\\ {\displaystyle\pmb\Phi\big(k\,,k\,-1\big)\,\pmb P\big(k\,-1\,|\,k\,-1\big)\,\cdot}\\ {\displaystyle\pmb\Phi^{\mathrm{T}}\big(k\,,k\,-1\big)\,+\,\pmb{T}\big(k\,-1\big)\,\pmb Q\big(k\,-1\big)\,\pmb{T}^{\mathrm{T}}\big(k\,-1\big)\,=\,}\\ {\displaystyle\pmb U\big(k\,|k-1\big)\,\pmb{D}\big(k\,|k-1\big)\,\pmb U^{\mathrm{T}}\big(k\,|k-1\big)\,\qquad\qquad(4\,-9)\,=\,1}\end{array}

同样，为了不使计算过程增维，使用类似于4.2.6.1节中的过程，但此处采用修正加权的格拉姆一施密特正交化过程计算18），从而产生下列时间校正方程。

令 \pmb{Y}^{\mathrm{T}}\mp\left(\,\pmb{a}_{1}\,,\pmb{a}_{2}\,,\cdots,\pmb{a}_{n}\,\right),\pmb{a}_{i}\in\mathbb{R}^{(\,n\,+\,q\,)\,\times\,1} 。对 \,k=n\;,n-1\,,\cdots, 1,计算

\left\{\begin{array}{l l}{C_{k}\ =\ \tilde{D}\left(k\ |k\ -1\right)a_{k}\,,}\\ {C_{k j}\ =\ \tilde{D}_{j j}\left(k\ |k\ -1\right)a_{k j}\quad(j\ =\ 1,2,\cdots,n\ +\ q)}\\ {D_{k k}\left(k\ |k\ -1\right)\ =\ a_{k}^{\top}C_{k}}\\ {d_{k}\ =\ C_{k}/D_{k k}(\,k\ |k\ -1)}\\ {U_{j k}(\,k\ |k\ -1)\ =\ a_{j}^{\top}d_{k}}\\ {a_{j}\ =\ a_{j}\ -\ U_{j k}(\,k\ |k\ -1)a_{k}\displaystyle\right\}(j\ =\ 1,2,\cdots,k\ -1)}\end{array}\right.

这里， U_{j k} 表示 \pmb{U} 的第 (\,j\,,k\,) 个元素。由此即产生了 \pmb{U}(\pmb{k}\mid\pmb{k}-1) 和 \pmb{{\cal D}}(\pmb{\mathscr{k}}\mid\pmb{\mathscr{k}}-1)

由以上的测量和校正方程即构成了完整的 \pmb{U}\pmb{D}\pmb{U}^{\textnormal{T}} 分解滤波算法，它可以保证 \pmb{P} 的正定性及 \pmb{U} 的三角性。由于 {\displaystyle{\cal U}{\bf D}{\bf U}^{{\mathbb T}}=} (\mathbf{\nabla}U\mathbf{D}^{1/2})(\mathbf{\nabla}U\mathbf{D}^{1/2})^{\mathrm{T}} ,因此， {\pmb U}{\pmb D}{\pmb U}^{\mathrm{T}} 滤波仍属平方根滤波。

4.3分割算法

继20世纪60年代卡尔曼-布西滤波算法之后，70年代以来，莱尼奥梯斯(D.G.Lainiotis)用他所证明的分割定理[15],得到了新的滤波和平滑算法——-分割算法[16,17]。它是以卡尔曼-布西滤波算法为基础，根据贝叶斯后验估计原理，给出的一种解耦求解系统状态与参数均未知的非线性估计问题的方法。从本质上讲，“分割”表示的意义在于，把原问题分割成了两个互相分离的比较简单的相似子问题，从而导致问题的简化。广义分割算法!8推广了原来的分割算法，这种推广表现在对算法初始条件的要求上，即放弃了对状态滤波估计初值必为零的限制，代之以任意标称状态初值即可。广义分割算法虽可将状态估计与参数估计分割开来，但在进行参数估计时，每步都要求解信息矩阵之逆，当参数较多时，计算工作量较大，因而又提出了将估计问题的初始条件分割成任意数目的联合高斯随机矢量之和的广义多分割算法[19],从而简化矩阵求逆运算。

当分割算法用于估计系统未知参数时，既可类似于广义卡尔曼滤波将参数增广为状态来实现，又可优于广义卡尔曼滤波，将状态和参数分离进行估计。同时，基于分割算法导出的广义分割辨识算法[20]还有助于提高辨识准度。然而,分割算法计算量较大，约束条件苛刻，影响了它的具体应用。

4.3.1 分割定理

1）连续非线性系统

对于连续非线性动力学系统，其状态方程和观测方程可以表示为

\left\{\begin{array}{l}{\dot{\pmb{x}}(t)\,=\,f[\pmb{x}(t),\pmb{u}(t),\pmb{\theta};t]\,+\,\pmb{F}(\pmb{\theta},t)\pmb{\eta}(t)\,\,\,\,(t\in[t_{0},t_{f}])}\\ {\pmb{E}\{\pmb{x}(t_{0})\}\,=\,\pmb{x}(t_{0}\,|\,t_{0};\pmb{\theta})}\\ {\pmb{E}\{\lceil\pmb{x}(t_{0})\,-\,\pmb{x}(t_{0}\,|\,t_{0};\pmb{\theta})\rceil[\pmb{x}(t_{0})\,-}\\ {\pmb{x}(t_{0}\,|\,t_{0};\pmb{\theta})]^{\top}\}\,=\,\pmb{P}(t_{0}\,|\,t_{0};\pmb{\theta})}\end{array}\right.

{\bf y}(t)\,=\,{\pmb h}\big[{\pmb x}(t),{\pmb u}(t),{\pmb\theta};t\,\big]\,+\,{\pmb\varepsilon}(t)\,\quad(t\,\in\,[\,t_{0},t_{f}])

初始状态 {\pmb x}\left(\,t_{0}\,\right) 与过程噪声 \pmb{\eta}\left(\pmb{\,t}\right) 和观測噪声 \pmb{\varepsilon}\left(\begin{array}{r l}\end{array}\right) 无关；\pmb{\eta}(t) 和 \pmb{\varepsilon}(t) 是互不相关的零均值白色高斯噪声，相应的协方差阵分别为 Q\left(\t\right) 和 \pmb{R}\left(\begin{array}{r l}\end{array}\right) ；未知参数 \pmb{\theta} 是概率密度函数为 p\left(\,\pmb\theta\,\right) 的随机变量。则在给定了观测记录 \pmb{Y}\left(\,t\,,t_{0}\right)=\lbrace\textbf{y}(\,t\,)\,;\,t\in\left(\,t_{0}\,,t_{f}\,\right)\rbrace 之后， \pmb{x}(t) 的最小方差滤波估计 \hat{\pmb{x}}(\pmb{t}\mid\pmb{t}) 及其相应的误差协方差矩阵 \pmb{P}(\pmb{t}\mid\pmb{t}) 由下式给出（分割定理）

\hat{\pmb{x}}(\,t\,|\,t\,)\,=\,\int_{\hat{\pmb{x}}}(\,t\,\left|\,t\,;\pmb{\theta}\,\right)\phi(\,\pmb{\theta}\,\mid\,t\,)\mathrm{d}\pmb{\theta}

\pmb{P}(\pmb{t}\mid t\,)\,=\,\int\{\pmb{P}(\,t\,\vert\,t\,;\pmb{\theta}\,)\,+\,\big[\,\hat{\pmb{x}}(\,t\,\vert\,t\,)\,-\,\hat{\pmb{x}}(\,t\,\vert\,t\,;\pmb{\theta}\,)\,\big]\,\

[\,\hat{\pmb{x}}\,(\,t\,|\,t\,)\,-\,\hat{\pmb{x}}\,(\,t\,|\,t\,;\pmb{\theta}\,)\,]^{\mathrm{T}}\,\}\,\rho\,(\,\pmb{\theta}\,|\,t\,)\,\mathrm{d}\,\pmb{\theta}

式中 \hat{\pmb{x}}\left(\,t\,\left|\,t\,;\pmb{\theta}\,\right),\pmb{\mathscr{P}}\left(\,t\,\left|\,t\,;\pmb{\theta}\,\right) 分别是状态矢量的 \pmb{\theta} 条件最小

方差滤波估计和相应的 \pmb{\theta} 条件误差协方差矩阵。

分别定义为

\begin{array}{c}{{\hat{\pmb{x}}(\,t\,|\,t\,;\pmb{\theta})\,=\,E\,\mathrm{i}\,\pmb{x}(\,t\,)\mid\,\pmb{Y}(\,t\,,t_{0}\,)\,;\pmb{\theta}\mid}}\\ {{}}\\ {{\pmb{P}(\,t\,|\,t\,;\pmb{\theta})\,=\,E\,\mathrm{i}\,\!\left[\,\pmb{x}(\,t\,)\,-\,\hat{\pmb{x}}(\,t\,|\,t\,;\pmb{\theta})\,\right]\!\left[\,\pmb{x}(\,t\,)\,-\,\right]\,}}\\ {{}}\\ {{\hat{\pmb{x}}(\,t\,|\,t\,;\pmb{\theta})\,\right]^{\mathrm{T}}\mid\,\pmb{Y}(\,t\,,t_{0}\,)\,;\pmb{\theta}\,\mathrm{j}}}\end{array}

它们是相应的 \pmb\theta 条件下广义卡尔曼滤波器的输出。

\frac{\mathrm{d}}{\mathrm{d}t}\hat{\pmb{x}}\left(\,t\mid t\,;\pmb{\theta}\,\right)\;=\;\pmb{f}[\,\hat{\pmb{x}}\left(\,t\mid t\,;\pmb{\theta}\,\right),\pmb{u}\left(\,t\,\right),\pmb{\theta}\,;t\,]\;+

\pmb{K}(\mathbf{\nabla}t\mathbf{\Omega},\pmb{\theta})\,\pmb{v}\left(\mathbf{\Omega}_{t}\mid t\mathbf{\Omega};\pmb{\theta}\right)

\frac{\mathrm{d}}{\mathrm{d}t}\pmb{P}(\,t\,|\,t\,;\pmb{\theta}\,)\,=\,\pmb{F}(\,t\,,\pmb{\theta}\,)\,\pmb{P}(\,t\,|\,t\,;\pmb{\theta}\,)\,+\,\pmb{P}(\,t\,|\,t\,;\pmb{\theta}\,)\,\pmb{F}^{\mathrm{T}}(\,t\,,\pmb{\theta}\,)\,+

\begin{array}{c}{{\pmb{T}(\,t\,,\pmb{\theta})\,\pmb{Q}\left(\,t\,\right)\pmb{T}^{\mathrm{T}}(\,t\,,\pmb{\theta})\,-\,\pmb{P}(\,t\,|\,t\,;\pmb{\theta})\,\pmb{H}^{\mathrm{T}}(\,t\,,\pmb{\theta})\,\cdot}}\\ {{\pmb{R}^{-1}(\,t\,)\,\pmb{H}(\,t\,,\pmb{\theta})\,\pmb{P}(\,t\,|\,t\,;\pmb{\theta})}}\end{array}

式中

\begin{array}{r l r}&{}&{{\pmb v}(\,t\,|\,t\,;\pmb\theta)\,=\,{\pmb y}(\,t\,)\,-\,{\pmb h}\big[\,{\pmb x}(\,t\,)\,,{\pmb u}(\,t\,)\,,\pmb\theta\,;t\,\big]}\\ &{}&{{\pmb K}(\,t\,,\pmb\theta)\,=\,{\pmb P}(\,t\,|\,t\,;\pmb\theta){\pmb H}^{\mathrm{T}}(\,t\,,\pmb\theta){\pmb R}^{-1}(\,t\,)}\end{array}

{\cal F}\,=\,\frac{\partial{\pmb f}}{\partial{\pmb x}}\qquad{\quad\pmb H}\,=\,\frac{\partial{\pmb h}}{\partial{\pmb x}}

{\pmb\theta} 的后验概率密度函数 {\pmb\mathscr{p}}(\,\pmb\theta\,|\,t\,) 为

\phi(\pmb\theta\mid t)\,=\,\frac{A(\,t\,\left|\pmb\theta\right.\right)\phi(\pmb\theta)}{\displaystyle\int_{\pmb\Lambda(\,t\,\left|\pmb\theta\right.)\phi(\pmb\theta)\mathrm{d}\pmb\theta}}

式中 \Lambda(t\,|\,\pmb\theta) ———似然比。

\Lambda\left(\,t\,\left|\,\pmb\theta\,\right\rangle\,=\exp\left\{\int_{0}^{t}\hat{h}^{\mathrm{T}}(\,\pmb x\,,u\,,\pmb\theta\,;\sigma\,)\,{\pmb R}^{-1}(\,\sigma\,)\,{\pmb y}(\,\sigma\,)\mathrm{d}\sigma\,-\right.

\frac{1}{2}\!\!\int_{0}^{\iota}\parallel\hat{\pmb{n}}\left(\pmb{x}\,,\pmb{u}\,,\pmb{\theta}\,;\sigma\right)\parallel_{\pmb{R}^{-1}\left(\sigma\right)}^{2}\!\!\mathrm{d}\sigma\,\bigr\}

其等价形式为

\begin{array}{r}{\phi(\pmb{\theta}\mid t)\,=\,\frac{L\left(\,t\,\left|\pmb{\theta}\right.\right)\,\phi\left(\pmb{\theta}\right)}{\displaystyle\int\!L(\,t\,\left|\pmb{\theta}\right.)\,\phi(\pmb{\theta})\mathrm{d}\pmb{\theta}}}\end{array}

式中

L\left(\,t\,\left|\,\pmb\theta\,\right\rangle\,=\,\exp\bigg\{-\,\frac{1}{2}{\int_{0}^{t}\,\left\|\right.\,\pmb v\left(\,\sigma\,\middle|\,\sigma\,;\pmb\theta\,\right)\,\right\|\,\stackrel{2}{\scriptstyle\_{R}-1}\!_{(\sigma)}}\mathrm{d}\sigma\,\bigg\}

2）离散系统

离散系统的分割定理与连续系统类似。设其状态方程和观测方程分别为

\pmb{x}\left(\,k\,+\,1\,\right)\;=\;\pmb{\Phi}\!\left(\,k\,+\,1\,,k\,;\pmb{\theta}\,\right)\pmb{x}\left(\,k\,\right)\,+\,\pmb{T}\!\left(\,k\,\right)\pmb{\eta}\!\left(\,k\,\right)

(\,k\,=\,0\,,1\,,2\,,\cdots,N\,)

\begin{array}{r}{\textbf{y}\!\left(\,k\,\right)\,=\,h\left(\,\pmb{x}\left(\,k\,\right),\pmb{u}\left(\,k\,\right),\pmb{\theta}\,;t_{k}\,\right)\,+\,\pmb{\varepsilon}\left(\,k\,\right)}\end{array}

(\,t_{k}\,=\,t_{0}\,,t_{1}\,,t_{2}\,,\cdots,t_{N}\,)

相应的假设条件与连续系统类似。则在给定观测记录 YN={y1，y_{2},\cdots,y_{N}\} 之后，其最小方差滤波估计 \hat{\pmb{x}}(\pmb{k}\mid\pmb{k}) 和相应的误差协方差矩阵 \textstyle P(k\!\mid\!k) 为（分割定理）

\hat{\pmb{x}}(\,\pmb{k}\mid\pmb{k}\,)\,=\,\int_{\pmb{x}}\pmb{\hat{x}}\left(\,\pmb{k}\mid\pmb{k}\,;\pmb{\theta}\,\right)\phi(\,\pmb{\theta}\mid\pmb{k}\,)\mathrm{d}\pmb{\theta}

P\!\left(\,k\left|\,k\,\right)\,=\!\int\!\{\,P\!\left(\,k\left|\,k\,;\theta\right)\,+\,\left[\,x\left(\,k\left|\,k\,\right)\,-\,\hat{x}\left(\,k\left|\,k\,;\theta\right)\right.\right]\,\;

[\,\hat{\pmb{x}}(\,\pmb{k}\,|\,\pmb{k}\,)\,-\,\hat{\pmb{x}}\,(\,\pmb{k}\,|\,\pmb{k}\,;\pmb{\theta}\,)\,]^{\mathrm{T}}\,\}\,\rho\,(\,\pmb{\theta}\,|\,\pmb{k}\,)\,\mathrm{d}\theta

(4 - 115)

式中 \hat{\pmb{x}}(\,\pmb{k}\,|\,\pmb{k}\,;\pmb{\theta}\,)\,,\pmb{P}(\,\pmb{k}\,|\,\pmb{k}\,;\pmb{\theta}\,) —分别是状态矢量的 \pmb{\theta} 条件最小

方差估计和相应的 {\pmb\theta} 条件误差协方差矩阵。

分别定义为

\hat{\pmb{x}}\left(\,k\:\middle\vert\,k\,;\pmb{\theta}\,\right)\;=\;E\left\{\,{\pmb{x}}\left(\,k\,\right)\,\vert\,\left.\right.\,Y_{k}\,;\pmb{\theta}\,\right\}

P(\,k\,|\,k\,;\pmb\theta\,)\;=\;E\,\{\,[\,{\pmb\ x}\,(\,k\,)\,-\,\hat{\pmb x}\,(\,k\,|\,k\,;\pmb\theta\,)\,]\,\}

[\,{\pmb x}\,(\,{\pmb k}\,)\,-\,\hat{\pmb x}\,(\,{\pmb k}\,\vert\,{\pmb k}\,;{\pmb\theta}\,)\,]^{\mathrm{T}}\,\vert\,\,{\pmb Y}_{\pmb k}\,;{\pmb\theta}\,\vert

它们是相应的 \pmb{\theta} 条件广义卡尔曼滤波器的输出

\begin{array}{c}{{\pmb{\hat{x}}\left(\,k\:\middle\vert\,k\,;\pmb{\theta}\right)\,=\pmb{\Phi}\left(\,k\:,k\:-\:1\,;\pmb{\theta}\right)\pmb{\hat{x}}\left(\,k\:-\:1\:\middle\vert\:k\:-\:1\,;\pmb{\theta}\right)\,+}}\\ {{\pmb{K}\left(\,k\:,\pmb{\theta}\right)\pmb{\nu}\left(\,k\:\middle\vert\,k\:-\:1\,;\pmb{\theta}\right)}}\end{array}

\pmb{\nu}(\pmb{k}\mid\pmb{k}-1;\pmb{\theta})\,=

\mathbf{y}(k)\,-\,h[\,\hat{\pmb{x}}(\,k\,\vert\,k\,-\,1,\pmb{\theta})\,,\pmb{u}(k\,)\,,\pmb{\theta}\,;t_{k}\,]

{\pmb K}({\pmb k}\,,{\pmb\theta})\,=\,{\pmb P}({\pmb k}\,|{\pmb k}\,-\,1\,;{\pmb\theta}){\pmb H}^{\mathrm{T}}({\pmb k}\,,{\pmb\theta}){\pmb B}^{-1}({\pmb k}\,) (4 -120) \pmb{B}\left(\pmb{k}\right)\,=\,\pmb{H}\left(\pmb{k}\,,\pmb{\theta}\right)\pmb{P}\left(\pmb{k}\,\middle|\,\pmb{k}\,-\,1\,;\pmb{\theta}\right)\pmb{H}^{\mathrm{T}}\left(\pmb{k}\,,\pmb{\theta}\right)\,+\,\pmb{R}\left(\pmb{k}\,\right) (4 -121)

P(\,k\,\left|\,k\,-\,1\,;\,\pmb\theta\,)\,=\,\pmb{\Phi}(\,k\,,k\,-\,1\,;\,\pmb\theta\,)

\pmb{P}(\pmb{k}\,-\,1\,|\,\pmb{k}\,-\,1\,;\pmb{\theta})\pmb{\Phi}^{\mathrm{T}}(\,\pmb{k}\,,\pmb{k}\,-\,1\,;\pmb{\theta}\,)\,+

\pmb{{\cal T}}(\,k\,)\,\pmb{{\cal Q}}(\,k\,-\,1\,;\pmb{\theta}\,)\,\pmb{{\cal T}}^{\mathrm{T}}(\,k\,)

P\!\left(\,k\left|k\,;\theta\right.\right)\,=\left[\,I\,-\,K\!\left(\,k\,,\theta\right)\,-\,H\!\left(\,k\,,\theta\right)\right]P\!\left(\,k\left|k\,-\,1\,;\theta\right.\right)

\left[\,I\,-\,K\!\left(\,k\,,\pmb\theta\right)\,-\,H\!\left(\,k\,,\pmb\theta\right)\,\right]^{\mathrm{T}}\,+

\pmb{K}(\,\pmb{k}\,,\pmb{\theta}\,)\,\pmb{R}\left(\,\pmb{k}\,\right)\pmb{K}^{\mathrm{T}}(\,\pmb{k}\,,\pmb{\theta}\,)

\pmb{H}\left(\pmb{k}\,,\pmb{\theta}\right)=\frac{\partial\pmb{h}\left[\pmb{x}\left(\pmb{k}\,\right),\pmb{u}\left(\,\pmb{k}\,\right),\pmb{\theta}\,;t_{k}\,\right]}{\partial\pmb{x}}\,\Bigg|_{\pmb{x}=\pmb{\hat{x}}\left(\,\pmb{k}\,\right|\,\pmb{k}\,-\,1;\,\pmb{\theta}\right)}

\pmb\theta 的后验概率密度函数 p(\pmb\theta\mid k) 由下述贝叶斯公式给出

p(\,\pmb\theta\mid\pmb k\,)\,=\,\frac{L(\,\pmb k\,\mid\pmb k\,;\pmb\theta\,)_{\mathscr P}(\,\pmb\theta\,\mid\pmb k\,-\,1)}{\displaystyle\int\!L(\,\pmb k\,\mid\pmb k\,;\pmb\theta\,)_{\mathscr P}(\,\pmb\theta\,\mid\pmb k\,-\,1\,)\,\mathrm d\pmb\theta}

式中

\begin{array}{c}{{\displaystyle{L\left(\,k\:\middle\vert\,k\,;\theta\right)\:=\:}}}\\ {{\displaystyle{\mid B\left(\,k\,\right)^{-1/2}\mathrm{exp}\left\{\,-\,\frac{1}{2}\,\left\Vert\begin{array}{l}{{\!v\left(\,k\:\middle\vert\,k\,-\,1\,;\theta\right)\,\left\Vert\begin{array}{l}{{\!B^{-1}}\!}\\ {{\!B^{-1}}\!}\!\end{array}\right\}}}}\end{array}

上述分割定理把求解 x(t) 的非线性滤波估计问题分割为两部分：一是对系统状态的条件最优估计；二是基于参数的后验概率密度对状态的校正。即它是在卡尔曼一布西滤波的基础上，利用贝叶斯后验估计原理形成的。从式(4-100)和式(4-114)可以看出: \pmb{x}(t) （或 \pmb{x}(\pmb{k})) 的最小方差估计 \pmb{\hat{x}}(\pmb{\ell}\mid t) （或 \hat{\pmb{x}}(\pmb{k}\mid\pmb{k})) 是条件估计 \hat{{\pmb x}}(\,t\,|\,t\,;{\pmb\theta}\,) （或 \hat{\mathbf{x}}\left(\,k\mid k\,;\theta\,\right)) 的加权积分。正如非线性系统的贝叶斯滤波估计一样，若不对分布函数施加特殊的假设条件，这种估计方法也只有理论意义。在服从高斯分布的假设条件下，虽然计算仍较复杂，但仍可以实现。

4.3.2 广义分割算法

莱尼奥梯斯应用分割定理导出了分割滤波算式和平滑算式，将状态参数 x(t) 的滤波估计 \hat{x}_{0}(t\mid t) 分解为求初始状态为零的状态滤波估计 \pmb{\dot{x}}(\pmb{\tau}\mid t) 和对状态初值的平滑估计 \pmb{\dot{x}}(\mathbf{\nabla}t_{0}\mid t\mathbf{\Omega}) ，称为分割算法。后来，他又解除了对状态初值必为零的限制，推导出适合于任意标称初始状态的分割滤波和平滑算法，称之为广义分割算法。

1）连续非线性系统

系统模型仍如式（4-98）和式（4-99）所列。

设初始状态 {\boldsymbol x}(\,t_{0}\,) 可以表示为两个相关随机矢量之和，即

x\left(\,t_{0}\,\right)\;=\;\,{\pmb x}_{n}\,+\,{\pmb x}_{r}

式中 x_{n} 一正则初始条件；

x,—— 剩余初始条件，是未知随机参数。两者的联合高斯概率密度函数是

\phi\left(\,\mathbf{x}_{n}\,,\,\mathbf{x}_{r}\,\right)\;=\;N\left\{{\binom{{\hat{\mathbf{x}}}_{n}}{\hat{\mathbf{x}}_{r}}}\,,\,{\binom{P_{n}}{P_{n r}^{\mathrm{T}}}}\quad\quad P_{n r}\right\}\quad

则 {\pmb x}\left({t_{0}}\right) 的均值和方差分别为

\hat{\pmb{x}}\left(\,t_{0}\,\right)\;=\;\hat{\pmb{x}}_{n}\,+\,\hat{\pmb{x}}_{r}

\mathbf{\cal{P}}\left(\mathbf{\Lambda}_{t_{0}}\right)\;=\;\mathbf{\cal{P}}_{n}\;+\;\mathbf{\cal{P}}_{r}\;+\;\mathbf{\cal{P}}_{n r}\;+\;\mathbf{\cal{P}}_{n r}^{\mathrm{T}}

将 x_{r} 作为分割定理中的未知参数矢量 \pmb{\theta} ，则在给定 \pmb{x}_{r} 条件下， \pmb{x}(t) 及其协方差矩阵的卡尔曼-布西滤波方程为

\frac{\mathrm{d}}{\mathrm{d}t}\hat{\pmb{x}}\left(\,t\mid t\,;\pmb{x}_{r}\,\right)\,=\,\pmb{f}\big[\,\hat{\pmb{x}}\left(\,t\,\left|\,t\,;\pmb{x}_{r}\,\right),\pmb{u}\left(\,t\,\right),\pmb{x}_{r}\,;t\,\right]\,+\,\pmb{K}\left(\,t\,,\pmb{x}_{r}\,\right)\,\times

\left[\,{\pmb{y}}(\,t\,)\,-\,{\pmb{h}}\left(\,{\pmb{\hat{x}}}\left(\,t\,\left|\,t\,;{\pmb{x}}_{r}\right),{\pmb{u}}\left(\,t\,\right),{\pmb{x}}_{r}\,;t\,\right)\,\right]

\begin{array}{l}{{\displaystyle t\,;{\pmb x}_{r}\,)\,=\,{\pmb F}(t){\pmb P}(t\,|\,t\,;{\pmb x}_{r})\,+\,{\pmb P}(t\,|\,t\,;{\pmb x}_{r}){\pmb F}^{\mathrm{T}}(t)\,+}}\\ {{\displaystyle\,{\pmb T}(t\,){\pmb Q}\,(t){\pmb T}^{\mathrm{T}}(t\,)\,-\,{\pmb P}(t\,|\,t\,;{\pmb x}_{r}){\pmb H}^{\mathrm{T}}(t\,)}}\\ {{\displaystyle\,{\pmb R}^{-1}(t\,){\pmb H}(t\,){\pmb P}(t\,|\,t\,;{\pmb x}_{r})\,\qquad\qquad(4\,\cdot{\pmb\ x}_{r})}}\\ {{\displaystyle\,{\pmb K}(t\,,{\pmb x}_{r})\,=\,{\pmb P}(t\,|\,t\,;{\pmb x}_{r}){\pmb H}^{\mathrm{T}}(t\,){\pmb R}^{-1}(t\,)\,\qquad(4\,\cdot{\pmb\xi})}}\end{array}

初始条件为

\begin{array}{r l}{\hat{\pmb{x}}\left(\,t_{0}\,\middle\vert\,t_{0};\,\pmb{x}_{r}\,\right)\,=\,E\left[\,\pmb{x}\left(\,t_{0}\,\right)\,\middle\vert\,\pmb{x}_{r}\,\right]\,=\,E\left[\,\left(\,\pmb{x}_{n}\,+\,\pmb{x}_{r}\,\right)\,\middle\vert\,\pmb{x}_{r}\,\right]\,=\,}&{{}}\\ {E\left[\,\pmb{x}_{n}\,\middle\vert\,\pmb{x}_{r}\,\right]\,+\,\pmb{x}_{r}\,=\,}&{{}}\\ {\hat{\pmb{x}}_{n}\,+\,\pmb{p}_{n},\pmb{p}_{r}^{-1}\!\left[\,\pmb{x}_{r}\,-\,\hat{\pmb{x}}_{r}\,\right]\,+\,\pmb{x}_{r}\,=}&{{}}\\ {\left[\,\hat{\pmb{x}}_{n}\,-\,\pmb{p}_{n}\pmb{p}_{r}^{-1}\hat{\pmb{x}}_{r}\,\right]\,+\,\left[\,I\,+\,\pmb{p}_{n}\pmb{p}_{r}^{-1}\right]\,\pmb{x}_{r}\,\,\,\,(\,\mpb{x}_{r}\,+\,\neq\,\pmb{x}_{r}\,)}\\ {\pmb{p}\left(\,t_{0}\,\middle\vert\,t_{0}\,;\,\pmb{x}_{r}\,\right)\,=\,\pmb{P}\left[\,\left(\,\pmb{x}_{n}\,+\,\pmb{x}_{r}\,\right)\,\middle\vert\,\pmb{x}_{r}\,\right]\,=\,\,\pmb{P}\left(\,\pmb{x}_{n}\,\middle\vert\,\pmb{x}_{r}\,\right)\,=\,}&{{}}\end{array}

考虑到 \pmb{P}(\,t\,|\,t\,;\pmb{x}_{r}\,) 和 \textstyle\kappa(\,t\,,\pmb{x}_{r}\,) 不是 \pmb{x_{r}} 的显函数，简记为 \pmb{P_{n}} (\,t\,\,|\,t\,) 和 \pmb{K}_{n}(\,t\,);\hat{\pmb{x}}(\,t\,|\,t\,;\pmb{x}_{r}) 的初值是 \pmb{x}_{r} 的显函数，可以将 x_{r} 从 \hat{\pmb{x}^{}} \left(\,t\,\,|\,t\,;x_{r}\,\right) 中分离出来。在滤波值附近,式(4-130)的近似线性化微分方程可以写成

\begin{array}{r l r}{\lefteqn{\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{\boldsymbol{x}}}\left(\,t\,|\,t\,;\pmb{x}_{r}\right)\,=}}\\ &{}&{\left[\,\pmb{F}(\,t\,)\,-\,\pmb{K}_{n}(\,t\,)\,\pmb{H}(\,t\,)\,\right]\hat{\mathbf{\boldsymbol{x}}}\left(\,t\,|\,t\,;\pmb{x}_{r}\right)\,+\,\pmb{K}_{n}(\,t\,)\,\mathbf{\boldsymbol{y}}(\,t\,)}\end{array}

对式(4-135)积分，可以将 \hat{\pmb{x}}(\,t\,|\,t\,;\pmb{x}_{r}\,) 写成下列形式

\hat{\pmb{x}}(\,t\mid t\,;\,{\pmb x}_{r}\,)\,=\,\pmb{\Phi}_{n}\,(\,t\,,t_{0}\,)\,\hat{\pmb{x}}_{n}\,(\,t_{n}\mid t_{0}\,)\,+

\int_{t_{0}}^{t}\pmb{\Phi}_{n}\left(\,\sigma\,,t_{0}\right)\pmb{K}_{n}\left(\,\sigma\,\right)\pmb{y}\left(\,\sigma\,\right)\mathrm{d}\sigma\,+\,\pmb{\Phi}_{n}\left(\,t\,,t_{0}\right)\left[\,\pmb{I}\,+\,\pmb{P}_{n r}\pmb{P}_{r}^{\,-1}\,\right]\pmb{x}_{r}

\Phi_{n} 满足下列方程

\frac{\mathrm{d}}{\mathrm{d}t}\pmb{\phi}_{n}(\,t\,,\pmb{x}_{0}\,)\,=\,\left[\,\pmb{F}(\,t\,)\,-\,\pmb{K}_{n}(\,t\,)\,\pmb{H}(\,t\,)\,\right]\pmb{\phi}_{n}(\,t\,,\pmb{x}_{0})

\pmb{\cal P}_{n}(\,t_{0}\,,t_{0})\,=\,I

令

\begin{array}{r}{\hat{\pmb{x}}_{n}\left(\,t\,\middle\vert\,t\,\right)\ =\pmb{\Phi}_{n}\left(\,t\,,t_{0}\,\right)\hat{\pmb{x}}_{n}\left(\,t_{0}\,\middle\vert\,t_{0}\right)\ +\ \ }\\ {\displaystyle\int_{t_{0}}^{t}\pmb{\Phi}_{n}\left(\,\sigma\,,t_{0}\,\right)\pmb{K}_{n}\left(\,\sigma\,\right)\mathbf{y}\left(\,\sigma\,\right)\mathrm{d}\sigma}\end{array}

则式（4-136)可记为

\begin{array}{c}{\hat{\pmb{x}}\left(\,t\left|t\,;\pmb{x}_{r}\right.\right)\,=}\\ {\pmb{\dot{x}}_{n}(\,t\left|t\,\right)\,+\,\pmb{\Phi}_{n}(\,t\left|t\,,t_{0}\right)\left[\,\pmb{I}\,+\,\pmb{P}_{n r}\pmb{P}_{r}^{-1}\,\right]\pmb{x}_{r}}\end{array}

即

\hat{\pmb{x}}(\,t\,|\,t\,)\;=\;\hat{\pmb{x}}_{n}(\,t\,|\,t\,;\pmb{x}_{r}\,=\,0)

将式(4-139)代人式(4-135),与式(4-131)、式(4-132)一起构成标

称状态变量 \pmb{\dot{x}}_{n}(t\,|\,t) 的内嵌卡尔曼-布西滤波：

\frac{\mathrm{d}}{\mathrm{d}t}\hat{\pmb{x}}_{n}\left(\,t\,\middle\vert\,t\,\right)\,=\,\left[\,{\pmb{F}}(\,t\,)\,-\,{\pmb{K}}_{n}(\,t\,)\,{\pmb{H}}(\,t\,)\,\right]\hat{\pmb{x}}_{n}\left(\,t\,\middle\vert\,t\,\right)\,+\,{\pmb{K}}_{n}(\,t\,)\,{\pmb{y}}(\,t\,)

\begin{array}{l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}P_{n}(\,t\,|\,t)\,={\cal F}(\,t\,)P_{n}(\,t\,|\,t\,)\,+}\\ {\displaystyle P_{n}(\,t\,|\,t){\cal F}^{\mathrm{T}}(\,t\,)+\,{\cal F}(\,t\,){\cal Q}(\,t){\cal F}^{\mathrm{T}}(\,t\,)\,-}\\ {\displaystyle P_{n}(\,t\,|\,t\,){\cal H}^{\mathrm{T}}(\,t\,){\cal R}^{-1}(\,t\,){\cal H}(\,t\,)P_{n}(\,t\,|\,t\,)\,\,}\\ {\displaystyle K_{n}(\,t\,)\,=\,P_{n}(\,t\,|\,t\,){\cal H}^{\mathrm{T}}(\,t\,){\cal R}^{-1}(\,t\,)}\end{array}

初始条件为

\begin{array}{r l}&{\hat{x}_{n}(\,t_{0}\,|\,t_{0})\,=\,\hat{x}_{n}\,-\,P_{n r}P_{r}^{-1}\hat{x}_{r}}\\ &{\,}\\ &{P_{n}(\,t_{0}\,|\,t_{0})\,=\,P_{n}\,-\,P_{n r}P_{r}^{-1}P_{n r}^{\,\mathrm{T}}}\end{array}

应用分割定理,将式（4-138)代人式(4-100）,并注意到 \pmb\theta= \pmb{x}_{r} ，得

\begin{array}{r}{\hat{\pmb{x}}(\mathrm{\boldmath~\ensuremath{\it~t}~}|\mathrm{\boldmath~\tau~})\,=\hat{\pmb{x}}_{n}(\mathrm{\boldmath~\ensuremath{\tau}~}|\mathrm{\boldmath~\tau~})\,+\,\pmb{\Phi}_{n}(\mathrm{\boldmath~\ensuremath{\tau}~},t_{0})[\mathrm{\boldmath~\ensuremath{\cal~I}~}+\,P_{n r}P_{r}^{-1}]\bigg[\pmb{x}_{r}\beta(\mathrm{\boldmath~\ensuremath{\tau}~}\!_{r}|\mathrm{\boldmath~\tau~})\mathrm{d}x\,=\pmb{\mathrm{\boldmath~\delta~}}}\\ {\hat{\pmb{x}}_{n}(\mathrm{\boldmath~\ensuremath{\tau}~}|\mathrm{\boldmath~\tau~})\,+\,\pmb{\Phi}_{n}(\mathrm{\boldmath~\ensuremath{\tau}~},t_{0})\big[\mathrm{\boldmath~\cal~I~}+\,P_{n r}P_{r}^{-1}\big]\hat{\pmb{x}}_{n}(\mathrm{\boldmath~\ensuremath{\tau}~}_{0}|\mathrm{\boldmath~\tau~})}\end{array}

式中

\hat{\b{x}}_{r}(\,t_{0}\,|\,t\,)\,=\,\int_{\mathbf{\}}\pmb{x}_{r}\beta(\,\pmb{x}_{r}\,|\,t\,)\mathrm{d}\pmb{x}_{r}

将式(4-145)、式(4-138)和 P\left(\,t\,\left|\,t\,;\pmb{x}_{r}\,\right)=P_{n}\left(\,t\,\left|\,t\,\right) 代人分割定 理式(4-101),得

\begin{array}{r l r}&{}&{P\big(\,t\,\big|\,t\,\big)\,=P_{n}(\,t\,\big|\,t\,)\,+\,\pmb{\Phi}_{n}(\,t\,,t_{0})\big[\,I\,+\,P_{n r}P_{r}^{-1}\,\big]\,P_{r}(\,t_{0}\,\big|\,t\,)}\\ &{}&{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(4\,-4\,)}\\ &{}&{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad(4\,-1)^{2}}\end{array}

{\cal P}_{r}(\,t_{0}\,|\,\,t\,)\,=

\int[\hat{\textbf{\em x}}_{r}(\,t_{0}\mid t\,)\,-\,{\pmb x}_{r}\,][\,\hat{\textbf{\em x}}_{r}(\,t_{0}\mid t\,)\,-\,{\pmb x}_{r}\,]^{\mathrm{T}}\hat{p}(\,{\pmb x}_{r}\mid t\,)\mathrm{d}x_{r}

下面推导 \hat{\pmb{x}}_{r}(t_{0}\mid t) 和 P_{n}\left(\,t_{0}\,\right|\,t\,\right) 的表达式。由分割定理的公式(4-108),得

\phi(\,\pmb{x}_{r}\,|\,t\,)\,=\,\frac{\Lambda\left(\,t\,|\pmb{x}_{r}\right)\phi\left(\pmb{x}_{r}\right)}{\displaystyle\int_{}^{}\!\!\Lambda\left(\,t\,|\pmb{x}_{r}\right)\phi\left(\pmb{x}_{r}\right)\mathrm{d}\pmb{x}_{r}}

式中

\Lambda\left(\,t\,|\,x_{r}\,\right)\,=\exp\{\int_{t_{0}}^{t}\hat{h}^{\mathrm{T}}(\,x\,,u\,,x_{r}\,;\sigma\,)\,R^{\,-1}(\,\sigma\,)\,y(\,\sigma\,)\mathrm{d}\sigma\,-

\frac{1}{2}\!\int_{t_{0}}^{t}\parallel\hat{\pmb{h}}\left(\pmb{x}\,,\pmb{u}\,,\pmb{x}_{r}\,;\sigma\right)\parallel_{\pmb{R}^{-1}\left(\sigma\right)}^{2}\!\mathrm{d}\sigma\,\right\}

因为先验密度是 \boldsymbol{p}(\boldsymbol{x}_{r}) 高斯的,即

\phi(\,\pmb{x}_{r}\,)\,=\,K\exp\Big\{-\,\frac{1}{2}\,\left\|\textbf{\em x}_{r}\,-\,\bar{\mathfrak{x}}_{r}\,\right\|\,_{P_{r}^{-1}}^{2}\Big\}

所以后验密度 \phi^{(\xi_{r}^{*},\,\{t\})} 也是高斯的。将式(4-150)和式(4-151)代人式（4-149),将 \pmb{\hat{h}} 对 \pmb{x} 做泰勤展开，保留一阶项，并利用式(4-146)和式(4-148）,整理可得 \hat{\pmb{x}}_{r}(\hat{\tau}_{0}\}\ t) 和 \mathbf{\mathcal{P}}_{r}(\mathbf{\mathcal{x}}_{0}\mid t) 的表达式

\hat{\pmb{x}}_{r}(\,t_{0}\,|\,\,t\,)\,=

\begin{array}{c}{{\star_{r}\star\star_{0}|\,\iota\,,\,\prime\,\,}}\\ {{\hphantom{(}}}\\ {{\mathnormalfont\begin{array}{r l}{{P_{r}(\,t_{0}\,|\,t)\,\mathrm{\boldmath~\xi~}[\,{\bar{\imath}}\,+\,{P_{n r}}{P_{r}^{-1}}]^{\mathrm{T}}M_{n}(\,t\,,t_{0}\,)\,+\,{P_{r}^{-1}}\hat{{\pmb x}_{r}}\,\bigr\}\,\left(4\cdot152\right)}}\\ {{\hphantom{(}}}\\ {{\mathnormalfont\qquad\qquad\qquad\qquad\quad}{\mathnormalfont\,{P_{r}}(\,t_{0}\,|\,t\,)\,=}}\\ {{\{\,[\,I+\,{P_{n r}}{P_{r}^{-1}}]^{\mathrm{T}}{\bf{O}}_{n}(\,t\,,t_{0}\,)\,[\,I+\,{P_{n r}}{P_{r}^{-1}}\,]\,+\,{P_{r}^{-1}}\,\}\,-1}}\end{array}}}\end{array}

式中

\begin{array}{c}{{\pmb{M}_{n}(t,t_{0})\,=}}\\ {{\displaystyle{\int}_{t_{0}}^{t}\pmb{\Phi}_{n}^{\mathrm{T}}(\sigma,t_{0})\pmb{H}^{\mathrm{T}}(\sigma)\pmb{R}^{-1}(\sigma)[\,{\pmb{y}}(\sigma)\,-\,\pmb{H}(\sigma)\hat{\pmb{x}}_{n}(\sigma\,|\,\sigma)\,]\mathrm{d}\sigma}}\end{array}

\begin{array}{r l}{~~}&{{}\pmb{\cal O}_{n}\left(\,t\,,t_{0}\,\right)\,=}\end{array}

\int_{t_{0}}^{t}\pmb{\Phi}_{n}^{\top}(\,\sigma\,,t_{0}\,)\,\pmb{H}^{\mathrm{T}}(\,\sigma\,)\,\pmb{R}^{-1}(\,\sigma\,)\,\pmb{H}(\,\sigma\,)\,\pmb{\Phi}_{n}(\,\sigma\,,t_{0}\,)\,\pmb{\mathrm{d}}\sigma

2）离散系统

设离散系统状态方程和观测方程如下

\pmb{x}\left(\,k\,+\,1\,\right)\;=\;\pmb{\Phi}\!\left(\,k\,+\,1\,,k\,;\pmb{x}_{r}\,\right)\pmb{x}\left(\,k\,\right)\,+\,\pmb{T}\!\left(\,k\,\right)\pmb{\eta}\!\left(\,k\,\right)

(k\,=\,0\,,1\,,2\,,\cdots,N)

\begin{array}{r}{\textbf{y}(k)\;=\;h\left[\,\pmb{x}\left(\,k\,\right),\pmb{u}\left(\,k\,\right),\pmb{x}_{r}\,;t_{k}\,\right]\;+\;\pmb{\varepsilon}\left(\,k\,\right)}\end{array}

(\,t_{k}\,=\,t_{0}\,,t_{1}\,,t_{2}\,,\cdots,t_{N}\,)

初始条件

\pmb{x}(0)\;=\;\pmb{x}_{n}\;+\;\pmb{x}_{r}

P\!\left(0\right)\;=\;P_{n}\:+\:P_{r}\:+\:P_{n r}\:+\:P_{n r}^{\mathrm{\,T}}

类似于连续系统的推导过程，可得如下滤波算法

\hat{\pmb{x}}(\,k\,\vert\,k\,)\,=\,\hat{\pmb{x}}_{n}(\,k\,\vert\,k\,)\,+\,\pmb{\Phi}_{n}(\,k\,,0)[\,I\,+\,{\pmb P}_{n r}{\pmb P}_{r}^{\,-1}]\,\hat{\pmb{x}}_{r}(0\,\vert\,k\,)

\begin{array}{l}{{\displaystyle{\cal P}\big(\,k\,|\,k\big)\,=\,{\cal P}_{n}(\,k\,|\,k\,)\,+\,\Phi_{n}(\,k\,,0)\big[\,I\,+\,{\cal P}_{n}{\cal P}_{r}^{-1}\big]\,{\cal P}_{r}(0\,|\,k\,)\,}}\\ {{\displaystyle\qquad\qquad\qquad\big[\,I\,+\,{\cal P}_{n r}{\cal P}_{r}^{-1}\big]^{\mathrm{T}}\Phi_{n}(\,k\,,0)}}\\ {{\hat{\kappa}_{n}(k\,|\,k)\,=\,\Phi_{n}(\,k\,,0)\big[\hat{\kappa}_{n}\,-\,{\cal P}_{n r}{\cal P}_{r}^{-1}\hat{\kappa}_{r}\big]\,+\,}}\\ {{\displaystyle\qquad\qquad\qquad\sum_{i=1}^{k}\,\Phi_{n}(\,k\,,i\,)\,{\cal K}_{n}(\,i\,)\,{\bf y}(\,i\,)\,=\,}}\end{array}

\pmb{\Phi}(k\,,k\,-1)\hat{\pmb{x}}_{n}(k\,-1\,|\,k\,-1)\,+\,K_{n}(k)

[\,y(k)\,-\,H(k)\Phi(k\,,k\,-\,1)\hat{x}_{n}(k\,-\,1\,|\\,k\,-\,1)\,](

\pmb{\phi}_{n}(k\,|k\,-1)\,=\,[\pmb{I}\,-\,\pmb{K}_{n}(k)\pmb{H}(k)]\pmb{\phi}_{n}(k\,|k\,-1)

K_{n}(k)\,=\,P_{n}(k\,|\,k\,-\,1)H^{\mathrm{T}}(k)B_{n}^{-1}(k)

\begin{array}{r}{P_{n}(k\,|\,k\,-1)\,=\pmb{\Phi}(k\,,k\,-1)P_{n}(k\,-1\,|\,k\,-1)\pmb{\Phi}^{\mathrm{T}}(k\,,k\,-1)\,+}\end{array}

\pmb{T}(\pmb{k}\mathrm{~-~}1)\pmb{Q}(\pmb{k}\mathrm{~-~}1)\pmb{T}^{\mathrm{T}}(\pmb{k}\mathrm{~-~}1)

B_{n}(k)\,=\,H(k)P_{n}(k\,|\,k\,-1)H^{\mathrm{T}}(k)\,+\,R(k)

P_{n}\big(k\,|k\big)\,=\,\big[\,I\,-\,K_{n}(k)H(k)\,\big]P_{n}\big(k\,|k\,-1\big)

\hat{x}_{r}(0\,|\,k)\,=\,P_{r}(0\,|\,k)\,\{\,[\,I\,+\,P_{n r}P_{r}^{-1}]^{\mathrm{T}}M_{n}(k\,,0)\,+\,P_{r}^{-1}\hat{x_{r}}\}

{\cal P}_{r}(0\,|\,k)\,=\,\{\,[\,I+{\cal P}_{w}{\cal P}_{r}^{-1}]^{\mathrm{T}}{\cal O}_{n}(k\,,0)[\,I+{\cal P}_{n}{\cal P}_{r}^{-1}]+{\cal P}_{r}^{-1}\}^{-1}

式中

H(k)\,=\,{\frac{\partial h}{\partial x}}\,\bigg|_{t\,=\,t_{k}}

{\pmb M}_{n}({\pmb k}\,,0)\,=\,\sum_{i=1}^{k}{\pmb\Phi}_{n}^{\mathrm{T}}({\pmb i}\,-\,1,0){\pmb\Phi}^{\mathrm{T}}({\pmb i}\,,i\,-\,1){\pmb H}^{\mathrm{T}}({\pmb i}\,){\pmb B}_{n}^{-1}({\pmb i})\,\,.

[\,y(i)\textrm{--}H(i)\Phi(i\,,i\,-\,1)\hat{x}_{n}(i\,-\,1\,|\,i\,-\,1)\,]

(4 - 171)

\begin{array}{l}{{\displaystyle{\bf O}_{n}(k,0)=\sum_{i=1}^{k}\pmb{\Phi}_{n}^{\mathrm{T}}(i-1,0)\pmb{\Phi}^{\mathrm{T}}(i,i-1)\pmb{H}^{\mathrm{T}}(i)\pmb{B}_{n}^{-1}(i)}}\\ {{\displaystyle\pmb{H}(i)\pmb{\Phi}(i,i-1)\pmb{\Phi}_{n}(i-1,0)\qquad\qquad\quad(4.}}\end{array}

4.3.3 广义多分割算法

广义分割算法将状态估计和参数估计分割开来，在进行参数估计时，每步都要求解信息矩阵之逆，当参数较多时，计算工作量较大。广义多分割算法将估计问题的初始条件分割成任意数目的联合高斯随机矢量之和,这些联合高斯随机矢量可以是统计相关的，采用广义多分割算法，可以将矩阵求逆降维运算，甚至简化成简单的标量除法，从而节省计算机时。

广义多分割算法是将初始状态分解为多个高斯统计矢量，并逐个将分割开的状态和参数矢量作为剩下的状态和参数矢量的条件估计，逐个应用分割定理推导出来。也即，先将 \pmb{x}_{1} 作为 {\pmb x}_{2},{\pmb x}_{3},\cdots,{\pmb x}_{L} 的条件估计，应用分割定理估计 \hat{{\pmb x}}_{1}(t\,|\,t) ;再将 \pmb{x}_{2} 作为 x_{3},x_{4},\cdots,x_{L} 的条件估计，应用分割定理估计 \pmb{\dot{x}}_{2}(\pmb{\tau}\mid\pmb{\ell}) ,直至 \hat{\pmb{x}}_{L}(t\,|\,t)

下面给出初始状态分割为多个相关的高斯统计矢量的广义多

分割算法。

状态方程

\pmb{\dot{x}}(\pmb{\mathit{t}})\;=\;\pmb{F}(\pmb{\mathit{t}})\,\pmb{x}\left(\pmb{\mathit{t}}\,\right)\,+\,\pmb{\Gamma}\pmb{\eta}(\pmb{\mathit{t}}\,)

观测方程

\mathbf{y}(\mathbf{\theta}_{t})\;=\;\pmb{H}(\mathbf{\theta}_{t})\,\pmb{x}(\mathbf{\theta}_{t})\,+\,\pmb{\varepsilon}(\mathbf{\theta}_{t})

噪声 \pmb{\eta}(t) 和 \pmb{\varepsilon}(t) 仍假定为分别具有方差矩阵 Q\left(\,t\,\right) 和 \pmb{R}\left(\pmb{\,t}\right) 的互不相关的零均值高斯白噪声。初始条件为

\pmb{x}\left(t_{0}\right)\;=\;\sum_{k\,=\,1}^{L}\pmb{x}_{k}

相应的联合概率密度函数是正态分布随机矢量， \pmb{x}_{k}\left(\pmb{k}=1,2\right ?$\cdots,L)$ 是相关的，即有

\begin{array}{r}{\phi\left(\mathbf{\Omega}_{x_{1}},\mathbf{\Omega}_{x_{2}},\cdots,\mathbf{\Omega}_{x_{L}}\right)\;=\;N\left[\begin{array}{c}{\left[\hat{\mathbf{r}}_{1}\right]}\\ {\hat{\mathbf{x}}_{2}}\\ {\vdots}\\ {\vdots}\\ {\left[\mathbf{\Omega}_{P_{L}}^{\mathrm{T}}\right]}\end{array},\;\left[\begin{array}{c c c c}{P_{11}}&{P_{12}}&{\cdots}&{P_{1L}}\\ {P_{12}^{\mathrm{T}}}&{P_{22}}&{\cdots}&{P_{2L}}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ {P_{1L}^{\mathrm{T}}}&{P_{2L}^{\mathrm{T}}}&{\cdots}&{P_{L L}}\end{array}\right]\right]}\end{array}

式中 \hat{x}_{k}\longrightarrow n 维矢量；

\boldsymbol{P}_{k j}\longrightarrow\boldsymbol{n}\times\boldsymbol{n} 维矩阵。

\boldsymbol{x}\left(t_{0}\right) 的均值和方差可写成

\pmb{x}\left(\mathbf{\eta}_{t_{0}}\right)\;=\;\sum_{k\,=\,1}^{L}\hat{x}_{k\,}

\mathbf{\mathit{P}}(\mathbf{\mathit{\tau}}_{t_{0}})\;=\;\sum_{k\;=\;1}^{L}P_{k k}\;+\;\sum_{k\;=\;1}^{L\;-1}\sum_{j\;=\;k\;+\;1}^{L}{\left[\mathbf{\mathit{\tau}}P_{k j}\;+\;P_{k j}^{\mathrm{\scriptscriptstyle{T}}}\right]}

观测数据

Y(\mathbf{\boldsymbol{\mathit{t}}}\,,t_{0})\;=\;\{\,\mathbf{\boldsymbol{y}}(\mathbf{\boldsymbol{\sigma}})\,;t_{0}\leqslant\sigma\leqslant t\,\}

或

\mathbf{\calY}(N)\;=\;\{\:\mathbf{\caly}(k)\!\;;k\;=\;1,2,\cdots,N\}

应用分割定理于式(4-175）,类似于式(4-145)和式(4-147)的推导过程，可得 \pmb{x}(t) 最小方差滤波估计的多分割算法如下

\hat{\pmb{x}}(\ t\mid t\,)\;=\;\hat{\pmb{x}}_{1}(\ t\mid t\,)\;+\;\sum_{k\,=\,2}^{L}\pmb{\Phi}_{k k}(\ t\,,t_{0}\,)\,\hat{\pmb{x}}_{k}(\ t_{0}\mid t\,)\;\ (4\,-1

P\left(\,t\,|\,t\,\right)\,=\,P_{1}(\,t\,|\,t\,)\,+\,\sum_{k\,=\,2}^{L}\,\bar{\Phi}_{k k}\left(\,t\,,\,t_{0}\,\right)P_{k}\left(\,t_{0}\,|\,\,t\,\right)\,\bar{\Phi}_{k k}^{\,\mathrm{T}}\left(\,t\,,\,t_{0}\,\right)

式中 \hat{\pmb{x}}_{1}(t\mid t) —给定观测量 \pmb{Y}_{N} 和 \pmb{x}_{k}=\mathbf{0}(k=2,3,\cdots,L) 条件下 {\pmb x}(t) 的数学期望;

\hat{\pmb{x}}_{k}(t_{0}\mid t) 一—给定观测量 \pmb{Y}_{N} 和 \pmb{x}_{i}=\pmb{0}\,(\,i=k+1\,,k\,+2\,,\cdots, L ）条件下 \pmb{x}_{k} 的数学期望；

\pmb{P}_{1}(t\mid t) —给定观测量 \pmb{Y}_{N} 和 \pmb{x}_{k}=\mathbf{0}(\,k=2\,,3\,,\cdots,L\,) 条件下 \pmb{x}(t) 的协方差矩阵；

\boldsymbol{P}_{k}(t_{0}\mid t) 一—一一给定观测量 \pmb{Y}_{N} 和 {\pmb x}_{i}={\bf0}\,(\,i=k+1\,,k+2\,,\cdots, L )条件下 \pmb{x}_{k} 的协方差矩阵。即

\begin{array}{l}{{\hat{\mathbf{x}}_{k}(t\,|\,t)\,=\,E\left\{\,\mathbf{x}(\,t\,)\,|\,\mathbf{\deltaY}_{N}\,\right\}\,}}\\ {{\hat{\mathbf{x}}_{1}(t\,|\,t)\,=\,E\left\{\,\mathbf{x}(\,t\,)\,|\,\mathbf{\deltaY}_{N}\,;\mathbf{x}_{2}\,=\,0,\mathbf{x}_{3}\,=\,0,\cdots,\mathbf{x}_{L}\,=\,0\,\right\}}}\\ {{\hat{\mathbf{x}}_{k}(\,t_{0}\,|\,t)\,=\,E\left\{\,\mathbf{x}_{k}\,|\,\mathbf{Y}_{N}\,;\mathbf{x}_{k+1}\,=\,0,\mathbf{x}_{k+2}\,=\,0,\cdots,\mathbf{x}_{L}\,=\,0\,\right\}}}\\ {{\,\,\,P(\,t\,|\,t)\,=\,E\left\{\,\mathbf{x}(\,t\,)\,-\,\hat{\mathbf{x}}(\,t\,|\,t)\,\right\}[\,\mathbf{x}(\,t)\,-\,\hat{\mathbf{x}}(\,t\,|\,t)\,]^{\mathrm{T}}\,\big|\,\mathbf{\deltaY}_{N}\,\right\}}}\\ {{\,\,\,P_{1}(t\,|\,t)\,=\,E\left\{\,\big[\,\mathbf{x}(\,t\,)\,-\,\hat{\mathbf{x}}_{1}(\,t\,|\,t)\,\big][\,\mathbf{x}(\,t)\,-\,\hat{\mathbf{x}}_{1}(\,t\,|\,t)\,\big]^{\mathrm{T}}\,\big|\,\mathbf{\deltaY}_{N}\,\right\}}}\end{array}

{\pmb x}_{2}\,=\,{\bf0}\,,\,\,{\pmb x}_{3}\,=\,{\bf0}\,,\cdots,\,\,{\pmb x}_{L}\,=\,{\bf0}\,\}

\pmb{P}_{k}(\,t_{0}\,|\,t\,)\;=\;E\,\{\,[\,\pmb{x}_{k}\,-\,\hat{x}_{k}(\,t_{0}\,|\,t\,)\,]\,[\,\pmb{x}_{k}\,-\,\hat{x}_{k}(\,t_{0}\,|\,t\,)\,]^{\mathrm{T}}\,|\,\pmb{Y}_{N}\,; {\pmb x}_{k\,+\,1}\,=\,0\,,\,\,{\pmb x}_{k\,+\,2}\,=\,0\,,\cdots,{\pmb x}_{L}\,=\,0\,\}

式(4-181)和式(4-182)中的 \hat{\pmb{x}}_{1}(\pmb{\tau}\mid t) 和 \boldsymbol{P}_{1}(\ t\mid t) 满足卡尔曼-布西滤波方程

\frac{\mathrm{d}}{\mathrm{d}t}\hat{\pmb{x}}_{1}(\,t\,|\,t\,)=\left[\pmb{F}(\,t\,)-\pmb{K}_{1}(\,t\,)\pmb{H}(\,t\,)\right]\hat{\pmb{x}}_{1}(\,t\,|\,t\,)+\pmb{K}_{1}(\,t\,)\,\pmb{y}(\,t\,)

(4 -183)

\frac{\mathrm{d}}{\mathrm{d}t}\pmb{P}_{1}(\,t\,|\,t\,)=\pmb{F}(\,t\,)\pmb{P}_{1}(\,t\,|\,t\,)+\pmb{P}_{1}(\,t\,|\,t\,)\pmb{F}^{\mathrm{T}}(\,t\,)+\pmb{I}\pmb{Q}(\,t\,)\pmb{I}^{\mathrm{T}}-\pmb{F}(\,t\,)\pmb{I}^{\mathrm{T}}(\,t\,)

\pmb{P}_{1}(\,t\,|\,t\,)\,\pmb{H}^{\mathrm{T}}(\,t\,)\,\pmb{R}^{\mathrm{-1}}(\,t\,)\,\pmb{H}(\,t\,)\,\pmb{P}_{1}(\,t\,|\,t\,)

\pmb{K}_{1}(\pmb{\mathit{t}})=\pmb{P}_{1}(\pmb{\mathit{t}}\mid\pmb{\mathit{t}})\,\pmb{H}(\pmb{\mathit{t}})\,\pmb{\mathbf{R}}^{\mathrm{~-~}1}(\pmb{\mathit{t}}\mid\pmb{\mathit{\Psi}})

初始条件为

\begin{array}{c}{{\hat{\mathbf{x}}_{1}(\,t_{0}\,|\,\,t_{0})\;=\;{\pmb{{\cal E}}}\left\{\,{\pmb{x}}_{1}\,|\,{\pmb{x}}_{2}\,=\,0\,,{\pmb{x}}_{3}\,=\,0\,,\cdots,{\pmb{x}}_{L}\;=\,{\bf0}\,\right\}}}\\ {{{}}}\\ {{{\pmb{P}}_{1}(\,t_{0}\,|\,\,t_{0})\,=\,{\pmb{P}}_{1}\,|\,_{\,{\pmb{\lambda}}_{1}{\bf1}}}}\end{array}

式(4-181)和式(4-182)中的 \hat{\pmb{x}}_{k}(\,t_{0}\,|\,\,t\,)\,,\pmb{P}(\,t_{0}\,|\,\,t\,) 和 \Phi_{k k}\left(\textbf{\em t},t_{0}\right) 满足下列方程式

\hat{\pmb{x}}_{k}\left(\,t_{0}\,\vert\,\,t\,\right)\;=\;{\pmb{P}}_{k}\left(\,t_{0}\,\vert\,\,t\,\right)\left[\,M_{k}(\,t\,,t_{0}\,)\,+\,{\pmb{P}}_{k\,\vert\,\,k\,\vert\,}^{\,-1}\,\hat{\pmb{x}}_{k\,\vert\,\,k\,\vert}\,\right]

\pmb{P}_{k}(\,t_{0}\,|\,t\,)\,=\,[\,\pmb{I}\,+\,\pmb{P}_{k\,|\,|\,k\,|}\,\pmb{O}_{k k}(\,t\,,t_{0}\,)\,]^{-1}\pmb{P}_{k\,|\,|\,k\,|}

{\pmb{M}}_{k}\left({\bf\Delta}_{t}\,,t_{0}\right)\;=\int_{t_{0}}^{t}\pmb{\Phi}_{k k}^{\mathrm{T}}\left({\bf\Delta}_{\sigma}\,,t_{0}\right){\pmb{H}}^{\mathrm{T}}\left({\bf\Delta}_{\sigma}\right){\pmb{R}}^{\;-1}({\bf\Delta}_{\sigma})\left\{{\pmb{\mathrm{\Delta}}}_{{\bf{y}}}({\bf\Delta}_{\sigma})\,-\,{\pmb{\cal{H}}}({\bf\Delta}_{\sigma})\,\times\right.

\{\,\hat{\pmb{x}}_{1}(\,\sigma\,|\,\sigma\,)\,+\,\sum_{i\,=\,2}^{k-1}\pmb{\Phi}_{i i}\(\,\sigma\,,t_{0}\,)\,\hat{\pmb{x}}_{1}(\,t_{0}\,|\,\sigma\,)\,\bigr]\,\}\,\mathrm{d}\sigma

{\pmb{\cal O}}_{k j}({\bf\beta},t_{0})\,=\,\int_{t_{0}}^{t}{\pmb{\Phi}}_{k j}^{\mathrm{T}}\,\!\left({\pmb{\sigma}}\,,t_{0}\right){\pmb{\cal H}}^{\mathrm{T}}({\pmb{\sigma}})\,{\pmb{\cal R}}^{-1}({\pmb{\sigma}})\,{\pmb{\cal H}}({\pmb{\sigma}})\,{\pmb{\Phi}}_{k j}({\pmb{\sigma}}\,,t_{0})\mathrm{d}{\pmb{\sigma}}

(4 - 189)

\begin{array}{c}{\pmb{\Phi}_{i j}(\,t\,,t_{0})\,=\,\pmb{\Phi}_{i-1,j}(\,t\,,t_{0})\,+}\\ {\pmb{\Phi}_{i-1,j\,-1}(\,t\,,t_{0})\,\pmb{P}_{i-1}(\,t_{0}\,|\,t\,)[\pmb{P}_{i-1}^{\,-1}\mid_{\{1\}}\pmb{P}_{i-1,j\,1\,\mid\,j-1\}\,-}\\ {\pmb{O}_{i-1,j}(\,t\,,t_{0})\,]\qquad(\,i\,\in\,[3,L\,]\,;\,j\,\in\,[1,L\,]\,)}\end{array}

\pmb{\phi}_{2,j}(\pmb{t}\,,t_{0})\,=\,\pmb{\Phi}_{2}(\pmb{t}\,,t_{0})[\pmb{I}\,+\,\pmb{P}_{1,j\,|\,1|}\,]\qquad(\substack{j\in\,[2,L\,]})

\Phi_{2}(\,t\,,t_{0}\,) 为转移矩阵，满足下列方程

\begin{array}{r l}&{\left\{\frac{\mathrm{d}}{\mathrm{d}t}\pmb{\Phi}_{2}(\,t\,,t_{0})\,=\,\left[\pmb{F}(\,t\,)\,-\,\pmb{K}_{1}(\,t\,)\,\pmb{H}(\,t\,)\right]\pmb{\Phi}_{2}(\,t\,,t_{0})\right.}\\ &{\left.\right.}\\ &{\left.\left.\pmb{\Phi}_{2}(\,t_{0}\,,t_{0})\,=\,\pmb{I}\right.}\end{array}

式中 \hat{\mathbf{x}}_{k}\mid\{k\} 和 P_{k}\{\}_{k}\} 是 \mathbf{\Deltax}_{k}(2{\leqslant}k{\leqslant}L) 的高斯条件概率密度的数 学期望和协方差矩阵。即

\begin{array}{r}{\mathop{\cal p}\left(\,\pmb{x}_{k}\,|\,\pmb{x}_{k+1}\,,\pmb{x}_{k+2}\,,\cdots\,,\pmb{x}_{L}\,\right)\;=\;{\cal N}(\,\pmb{\hat{x}}_{k}\,|\,\mathbf{\,}_{{k}}\,|\,,\pmb{{r}}_{k}\,|\,_{\mid k\downarrow}\,)}\end{array}

\hat{\pmb{x}}_{k}\mid_{\{k\}}=\hat{\pmb{x}}_{k}+\sum_{j\mathop{=}k+1}^{L}{\pmb{P}}_{k j}\mid_{\{k\}}(\pmb{x}_{j}-\,\hat{\pmb{x}}_{j})

P_{k}\mid_{\{k\}}\;=\;P_{k k}\;-\;\sum_{\substack{j\,=\,k\,+\,1}}^{L}P_{k j}\mid_{\{k\}}P_{k j}^{\mathrm{T}}\mid_{\{k\}}

以上给出了初始条件分解为 L 个统计相关矢量的广义多分割算法。当分解的初始条件矢量统计无关时，则 P_{k j}\!\equiv\!\!\:=\!\!\:0(k\!\neq\!j) 算式将大大简化。

将广义多分割算法用于参数估计时，通常取状态矢量 \pmb{x}(t) 作为 \pmb{x}_{1} ，而将待辨识的参数 \theta_{1},\theta_{2},\cdots,\theta_{p} 等作为 \pmb{x}_{2},\pmb{x}_{3},\cdots,\pmb{x}_{L}\circ\pmb{x}_{k} (k\geqslant2) 可以是矢量，也可以是标量，视具体物理问题而定。

4.3.4 广义分割辨识算法

前面讨论的广义分割算法是全量的递推估计算法。如果将分割算法应用于线性化的偏量方程，通过估计参数的偏差 \delta\pmb{\theta} 逐次修正待估计参数 \pmb{\theta} ，从而逼近参数真值，就可以推导出选代型的厂义分割辨识算法（或分割辨识算法）。

将待估参数 \pmb{\theta} 增广为状态矢量，构成增广矢量 x_{a} ，则描述非线性连续动力学系统的状态方程和观测方程为

x_{_a}\;=\;f_{a}\left(\,x_{a}\,,\,u\,;\,t\,\right)\,+\,T\eta_{a}

\mathbf{y}\big(k\big)\,=\,h\big[\,{\pmb{x}}_{a}\left(~k~\right),\pmb{u}\left(~k~\right);t_{k}\,\big]\,+\,\pmb{\varepsilon}\big(k~\big)

式中

\begin{array}{l l}{{{\pmb x}_{a}\;=\;{\left[\!\!\begin{array}{l}{{\pmb x}}\\ {{\pmb\theta}}\end{array}\!\!\right]}}}&{{{\pmb f}_{a}\;=\;{\left[\!\!\begin{array}{c}{{\pmb f}\!\left({\pmb x}\,,{\pmb u}\,,{\pmb\theta}\,;t\right)}\\ {{\pmb\theta}}\end{array}\!\!\right]}}}\\ {{{\pmb\eta}_{a}\;=\;{\left[\!\!\begin{array}{c}{{\pmb\eta}\!\left(t\,\,t\right)}\\ {{\pmb\eta}\!\left({\pmb\eta}\right)}\end{array}\!\!\right]}}}&{{{\pmb x}_{a}\!\left({\pmb0}\right)\;=\;{\left[\!\!\begin{array}{l}{{\pmb x}\!\left({\pmb0}\right)}\\ {{\pmb\theta}\!\left({\pmb0}\right)}\end{array}\!\!\right]}}}\end{array}

选择一条参考轨道 \pmb{x}_{a}^{\star} ,将式(4-196)和式(4-197)在参考轨道 上作台劳展开,取一阶线性近似，得

\begin{array}{r l}{\delta\mathbf{\dot{x}}_{a}(\mathbf{\Delta}t)\;=\;\mathbf{F}_{a}(\mathbf{\Delta}t)\,\delta\mathbf{\dot{x}}_{a}(\mathbf{\Delta}t)\,+\,\mathbf{\Delta}\mathbf{\Gamma}\pmb{\eta}_{a}(\mathbf{\Delta}t)}&{}\\ {\delta\mathbf{y}(\mathbf{\Delta}k)\;=\;H_{a}(\mathbf{\Delta}k)\,\delta\mathbf{\dot{x}}_{a}(\mathbf{\Delta}k)\,+\,\pmb{\varepsilon}(\mathbf{\Delta}k)}&{}\end{array}

式中

{\begin{array}{r l}{F_{a}\,=\,{\cfrac{\partial f_{a}}{\partial x_{a}}}~{\Bigg|}_{\star}\,=\,{\left[\cfrac{\partial f}{\partial x}~{\cfrac{\partial f}{\partial\theta}}\right]}}&{}\\ {\,}&{\,}\\ {H_{a}\,=\,{\cfrac{\partial h}{\partial x_{a}}}~{\Bigg|}_{\star}\,=\,{\left[\cfrac{\partial h}{\partial x}~{\bigg|}~{\cfrac{\partial h}{\partial\theta}}\right]}_{\star}\,=\,{\left[\,H_{x}H_{\theta}\,\right]}}\\ {\,}&{\,}\\ {{\delta x}_{a}\,=\,x_{a}\,-\,x_{a}^{\star}}\end{array}}

\delta\mathbf{x}_{a}(0)\;=\;{\binom{\times(0)\;-\;x^{\star}(0)}{\theta(0)\;-\;\theta^{\star}\;}}

式中角标 *** 表示 x_{a} 和 \pmb{u} 都在参考轨道上取值。对式(4-198)积分，得离散形式的状态方程

\delta\pmb{x}_{a}\left(\,k\,+\,1\,\right)\;=\;\pmb{\Phi}_{a}\left(\,k\,+\,1\,,k\,\right)\delta\pmb{x}_{a}\left(\,k\,\right)\,+\,\pmb{\Gamma}\pmb{\eta}_{a}

式中状态转移矩阵 \pmb{\phi}_{a}(k+1,k) 在参考轨道上取值。且满足

\begin{array}{r}{\left\{\frac{\mathrm{d}}{\mathrm{d}t}\pmb{\Phi}_{a}(\,t\,,t_{k}\,)\,=\,F_{a}\left(\,t\,\right)\pmb{\Phi}_{a}(\,t\,,t_{k}\,)\right.}\\ {\Bigg.}\\ {\pmb{\Phi}_{a}\left(\,t_{k}\,,t_{k}\,\right)\,=\,\pmb{I}\quad\left(\,t\,\in\,\left[\,t_{k}\,,t_{k+1}\,\right]\,\right)}\end{array}

\Phi_{a}(k\,+\,1\,,k\,)\,=\,\left[\begin{array}{c c}{{\Phi_{x}(\,k\,+\,1\,,k\,)}}&{{\Phi_{\theta}(\,k\,+\,1\,,k\,)}}\\ {{}}&{{}}\\ {{0}}&{{I}}\end{array}\right]

要应用前述离散型广义分割算法式 (4\mathrm{-}160)\mathrm{\sim} 式(4-169)于式（4-199）和式（4-200），首先需将初始状态 \delta\pmb{x}_{a} 进行分解。在初始状态 {\pmb x}({\pmb0}) 和 \pmb{\theta} 是两个独立无关的高斯随机矢量的假设条件下，可表示为

\begin{array}{c}{{\delta\hat{\mathbf{x}_{a}}(0)\,=\,\delta\hat{\mathbf{x}_{n}}(0)\,+\,\delta\hat{\mathbf{x}_{r}}(0)}}\\ {{\,}}\\ {{P_{a}(0)\,=\,P_{n}(0)\,+\,P_{r}(0)}}\end{array}

式中

\begin{array}{r l}{\delta\hat{{\mathbf x}}_{a}(0)\;=\;\left[\begin{array}{c c}{\hat{{\mathbf x}}\left(0\right)\,-\,{\mathbf x}^{\star}\left(0\right)}\\ {\hat{{\mathbf e}}\left(0\right)\,-\,{\mathbf6}^{\star}}\end{array}\right]}&{P_{a}\left(0\right)\;=\;\left[\begin{array}{c c}{P_{a}\left(0\right)}&{0}\\ {0}&{P_{\theta}\left(0\right)}\end{array}\right]}\\ {\delta\hat{{\mathbf x}}_{n}\left(0\right)\;=\;\left[\begin{array}{c c}{\hat{{\mathbf x}}\left(0\right)\,-\,{\mathbf\Lambda}_{x}^{\star}\left(0\right)}\\ {0}&{\delta\hat{{\mathbf x}}_{r}\left(0\right)\,=\;\left[\begin{array}{c c}{0}&{0}\\ {\hat{{\mathbf e}}(0)\,-\,{\mathbf6}^{\star}}\end{array}\right]}\end{array}

\begin{array}{r}{P_{n}(0)\;=\;\left[\begin{array}{c c}{P_{x}(0)}&{0}\\ {0}&{0}\end{array}\right]\;\;\;\;\;\;\;\;\;\;\;\;P_{r}(0)\;=\;\left[\begin{array}{c c}{0}&{0}\\ {0}&{P_{\theta}(0)\right]}\end{array}

\delta\hat{\pmb{x}_{n}}(\,\pmb{k}\,\backslash\,\pmb{k}\,) 满足下列卡尔曼滤波公式

\hat{\partial}\hat{\pmb{x}}_{n}\,(\,k\,|\,k\,)\;=\;\hat{\partial}\hat{\pmb{x}}_{n}\,(\,k\,|\,k\,-\,1\,)\,+\,{\pmb{K}}_{n}\,(\,k\,)\,{\pmb{\nu}}\,(\,k\,)

\partial\hat{{x}}_{n}(\,k\,|\,k\,-1)\,=\,\Phi_{x}(\,k\,,k\,-1)\,\partial\hat{{x}}_{n}(\,k\,-1\,|\,k\,-1)

\pmb{\nu}(\,k\,)\;=\;\delta\pmb{y}(\,k\,)\,-\,\pmb{H}_{x}(\,k\,)\,\delta\hat{\pmb{x}}_{n}(\,k\,|\,k\,-\,1)

\pmb{K}_{n}(\pmb{k})\:=\:\pmb{P}_{n}(\pmb{k}\mid\pmb{k}\:-\:1)\,\pmb{H}_{x}^{\mathrm{T}}(\pmb{k})\,\pmb{B}_{x}^{-1}(\pmb{k})

B_{x}(\,k\,)\,=\,H_{x}(\,k\,)\,P_{n}(\,k\,|\,k\,-\,1)\,H_{x}^{\mathrm{T}}(\,k\,)\,+\,R(\,k\,)\,\left(4\right. - 208) P_{n}\left(\,k\mid k\,-\,1\,\right)\,=\,\pmb{\Phi}_{x}\left(\,k\,,k\,-\,1\,\right)P_{n}\left(\,k\,-\,1\,\right)\,.

\pmb{\Phi}_{x}^{\mathrm{T}}(\,k\,,k\,-\,1)\,+\,\overline{{\pmb{\Gamma}}}\pmb{Q}\,(\,k\,-\,1)\,\overline{{\pmb{\Gamma}}}^{\mathrm{T}}

P_{n}(\,k\,)\,=\,\left[\,I\,-\,K_{n}(\,k\,)\,H_{x}(\,k\,)\,\right]P_{n}(\,k\,-\,1)

式中 g\,.\,R\!-\!- 分别是过程噪声 \boldsymbol{w}\left(\right.t\right) 和观测噪声 \pmb{v}(\pmb{k}) 的协方差矩阵。

应用式(4-168)和式(4-169),考虑到 {\pmb x}\left({\pmb0}\right) 与 \pmb{\theta} 独立无关，可得参数的平滑估计算式如下

\delta\hat{x}_{r}(0\,|\,k\,)\;=\;P_{r}(0\,|\,k\,)\,[\,M_{n}(\,k\,,0)\,+\,P_{r}^{\,-1}(0)\,\delta\hat{x}_{r}(0)\,]

P_{r}(0\,|\,k\,)\,=\,[\,\mathbf{\delta}\mathbf{O}_{n}(\,k\,,0)\,+\,P_{r}^{\,-1}(0)\,]^{\,-1}

式中

\pmb{M}_{n}(\emph{k},0)\ =\ \sum_{i\,=\,1}^{\pmb{k}}\pmb{\Phi}_{n}^{\mathrm{T}}(\emph{i}-1,0)\,\pmb{\Phi}_{a}^{\mathrm{T}}(\emph{i},i\,-\,1)\ .

\pmb{H}_{a}^{\mathrm{T}}(\,i\,)\,\pmb{B}_{x}^{-1}(\,i\,)\,\pmb{v}(\,i\,)

{\pmb{\cal O}}_{n}(\,k\,,0\,)\,=\,\sum_{i\,=\,1}^{k}{\pmb{\Phi}}_{a}^{\intercal}(\,i\,-\,1\,,0){\pmb{\Phi}}_{a}^{\intercal}(\,i\,,i\,-\,1){\pmb{\cal H}}_{n}^{\intercal}(\,i\,){\pmb{\cal B}}_{x}^{-1}(\,i\,)

\pmb{H}_{a}\left(\,i\,\right)\pmb{\Phi}_{a}\left(\,i\,,i\,-\,1\,\right)\pmb{\Phi}_{n}\left(\,i\,-\,1\,,0\,\right)

\pmb{\phi}_{n}\left(\,k\,,k\,-\,1\,\right)\;=\;\left[\,I\,-\,K_{n}\left(\,k\,\right)H_{a}\left(\,k\,\right)\,\right]\pmb{\Phi}_{a}\left(\,k\,,k\,-\,1\,\right)

\pmb{\phi}_{n}\left(\,k\,,0\right)\;=\;\prod_{i=1}^{k}\left[\,I\,-\,K_{n}\left(\,i\,\right)H_{a}\left(\,i\,\right)\,\right]\pmb{\Phi}_{a}\left(\,i\,,i\,-\,1\,\right)

对于给定的实测数据组 \pmb{Y}_{N} ，每应用一次式 (4-204)\sim 式(4-216)就可得到状态和参数的一次新的估计值

\hat{\pmb{x}}_{a}\ \mid_{\pmb{\mathscr{s}}+1}\ =\ \hat{\pmb{x}}_{a}\ \mid_{\pmb{\mathscr{s}}}+\ \delta\hat{\pmb{x}}_{a}\ \mid_{\pmb{\mathscr{s}}+1}

以最新得到的状态和参数值作为参考轨道再进行估计，从而提高估计准度。对于第 \pmb{k} 次迭代得到的 \delta\hat{\mathbf{x}}_{a}(\mathbf{0}\mid N) 可写成

\begin{array}{r}{\hat{\delta}\hat{\pmb x}_{a}\left(\mathbf{0}\mid N\right)_{b+1}=\left[\hat{\pmb x}^{\dagger}\left(\mathbf{0}\mid N\right)_{b+1}-\pmb x^{\star}\left(\mathbf{0}\right)\right]=}\\ {\hat{\pmb\theta}(\mathbf{0}\mid N)_{b+1}-\pmb\theta^{\star}\,\Bigg]=}\\ {\left[\hat{\pmb x}(\mathbf{0}\mid N)_{b+1}-\hat{\pmb x}(\mathbf{0}\mid N)_{b}\right]}\\ {\hat{\pmb\theta}_{b+1}-\hat{\pmb\theta}_{b}\,\Bigg]}\end{array}

将式(4-218)代人式(4-211)可得第 \pmb{k} 次迭代所得状态初值和 参数估计值

\begin{array}{c}{{\hat{\pmb{x}}_{a}(0\mid N)_{_{k+1}}=\hat{\pmb{x}}_{a}(0\mid N)_{_{k}}\,+\,\left[\,{\pmb{\cal O}}_{a}(N,0)_{_{k}}\,+\,\right.}}\\ {{\left.\,\right.}}\\ {{\left.\left.\,\right.p_{_{a}}^{-1}(0)\,\right]^{-1}\left[\,M_{a}(N,0)_{_{k}}\,+\,\right.}}\\ {{\left.\left.\,\right.p_{_{a}}^{-1}(0)\,\hat{\pmb{x}}_{a}(0\mid N)_{_{k}}\,-\,\hat{\pmb{x}}_{a}(0\mid N)_{_{k-1}}\,\right]}}\end{array}

\begin{array}{c}{{\hat{\pmb\theta}_{k+1}\,=\,\hat{\pmb\theta}_{k}\,+\,[\,{\pmb\cal O}_{\theta\theta}(N,0)_{k}\,+\,{\pmb P}_{\theta}^{-1}(0)\,]^{-1}\bigl[\,M_{\theta}(N,0)_{\hat{k}}\,+\,}}\\ {{}}\\ {{{\cal P}_{\theta}^{-1}(0)(\,\hat{\pmb\theta}_{\hat{\epsilon}}\,-\,\hat{\pmb\theta}_{k-1}\,)\,\bigr]\qquad\qquad\qquad(4\,\cdot\,\pmb\theta)}}\end{array}

式中

\begin{array}{r l}&{M_{n}(N,0)\ =\ \left[\overset{{N H}_{x}(N,0)}{M_{\theta}}\right]}\\ &{{\bf O}_{n}(N,0)\ =\ \left[\overset{{D}_{x x}(N,0)}{\sum_{x\theta}(N,0)}\quad\overset{{D}_{x\theta}(N,0)}{\sum_{\theta\theta}(N,0)}\right]}\end{array}

\hat{\pmb{x}}(0\,|\,N)_{0}\;=\;\hat{\pmb{x}}(0)\;\;\;\;\;\;\;\;\hat{\pmb{\theta}}_{0}\;=\;\hat{\pmb{\theta}}(0)

M_{n} 和 \pmb{\theta}_{n} 的公式见式(4-213)和式（4-214）， M_{a}\setminus\pmb{\mathscr{O}}_{a} 与 M_{n}\setminus O_{n} 的关系式为

\begin{array}{l}{{{\cal M}_{a}({\cal N},0)\,=\,\left[\,{\cal I}\,-\,{\cal O}_{n}({\cal N},0)\,{\cal P}_{n}(0)\,\right]^{-1}}}\\ {{{}}}\\ {{\quad\left[\,M_{n}({\cal N},0)\,+\,{\cal O}_{n}({\cal N},0)\,\hat{x}_{n}(0)\,\right]}}\\ {{{}.}}\end{array}

\pmb{0}_{a}(N,0)\,=\,\left[\,I\,-\,\pmb{0}_{n}(N,0)\,\pmb{P}_{n}(0)\,\right]^{-1}\pmb{0}_{n}(N,0)

(4 - 222)

对于给定的一组状态初值和参数预估值，由式(4-196)和式（4-197)计算参考轨道 \pmb{x}_{a}^{\star}\left(t\right) 和观测值 {\mathfrak{y}}({\mathfrak{k}}) 。由式(4-198)和式（4-199）构成相应的矩阵 \pmb{F}_{a}\left(\textit{t}\right),\pmb{H}_{a}\left(\textit{k}\right) ，并借助观测数据构成\delta{\pmb v}({\pmb k}) ,继而由式（4-201）求转移矩阵 \Phi_{a} ，再通过式 (4{-}204)\sim 式(4-210)和式（4-211）～式（4-216)分别估计正则状态参数 \delta\hat{\mathbf{x}}_{n} (k\vert k) 、协方差矩阵 \mathop{P_{n}}(k) 、参数偏量 \Delta\theta_{k} 和 P_{\theta}(\mathbf{0}\mid N) 。接着再以新的初始状态和参数更新参考轨道，重复上述过程，直到满足收敛指标 \left|\ \mathbf{\widehat{\theta}}_{k+1}\ -\ \mathbf{\widehat{\theta}}_{k}\ \right|/\left|\ \mathbf{\widehat{\theta}}_{k}\ \right|<\ \varepsilon\ (\ \varepsilon 为给定的收敛指数)为止,则 \hat{\boldsymbol{\theta}}_{k+1} 即为对应于观测量 \pmb{Y_{N}} 的准最小方差估计。

参考文献

1Kalman R E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME, J. Basic Eng. , Ser.D, 1960, 28: 34~45
2 Kalman R E, Bucy R. New Results in Linear Filtering and Prediction Theory. Trans. ASME, J. Basic Eng. , Ser.D, 1961, 83: 95~ 108
3 Bryson A E Jr, Ho Y C. Applied Optimal Control. Waltham, Mass: Blaisdell, 1969
4 Jazwinski A H. Stochastic Processes and Filtering Theory. New York: Academic, 1970
5 Gelb A, et al. Applied Optimal Control. Boston: M.1. T. Press, Cambridge, 1974
6 Ljung L. Asymptotic Behavior of the Extended Kalman Filter as a Parameter Estimator for Linear System. IEEE Trans. , 1979, AC-24(1) : 36~ 50
7 Speyer J L, Crues E Z. On -- line Estimation of Aircraft Stability Derivatives Using the Modified Gain Extended Kaiman Filter. AIAA 85-1762, 1985
8 Maybeck P S. Stochastic Models Estimation And Control, Academic Press, New York,1979
9吴广玉等．系统辨识与自适应控制．哈尔滨：哈尔滨工业大学出版社，1987

10 Maine R E, Iliff K W. Identification of Dynamic Systems. AGARD AG - 300, Vol. 2，1985

11蔡金狮．飞行器系统辨识．北京：宇航出版社，1994

12B.D.O.安德森，J.B.摩尔．最佳滤波．卢伯英译．北京：国防工业出版社，1983

13 Bierman G J. Factorization Methods for Discrete Sequential Estimation. Academic Press, New York, 1977
14 Carlson N A. Fast Triangular Formulation of the Square-Root Filter. AIAA J. , 1973, 11(9): 1259 ~1265
15 Lainiotis D G. Optimal Adaptive Estimation: Structure and Parameter Adaptation. IEEE Trans., 1971,AC-16(2) : 160~ 170
16 Lainiotis D G. Partitioned Estimation Algorithm. Il: Linear Estimation. J. Inform. Sci. , 1974, 7:317-340
17 Eulrich B J. et al. New Identification Algorithm and Their Relationships to Maximum Likelihood Method: the Partitioned Approach. 1978 Joint Auto. Contr. Conf. , Philadelphia, PA, 1978, 2: 231~246
18 Lainiotis D G. A Unifying Framework for Linear Estimation: Generalized Partitioned Algorithm. J. Inform. Sci., 1976, 10(3) : 243~278
19 Lainiotis D G, Andrisani D. Multi-Partitioned Solution for State and Parameter Estimation: Continuous System. Proc. 1978 Joint Auto. Contr. Conf. , Philadelphia, PA, 1978, Vol. 2: 215~229
20 Eulrich B J, Andrisani D, Laniniotis D G. Partitioning Identification Algorithms. IEEE Trans. , 1980, AC - 25(3) : 521~528

第5章参数估计

5.1概述

飞行器动力学系统及其外作用力的数学模型构式确定之后，动力学系统辨识变成了利用飞行或地面试验的实测数据，估计系统数学模型中的未知参数。本章将论述以动力学方程组作为状态方程组，建立试验测得的样本所必须满足的观测方程组，给出未知参数估计的几种常用参数估计方法。参数估计的任务是根据试验测得的样本推断未知参数的数值，为此必须解决参数估计准则和估计算法两个问题。

参数估计准则用以判断参数估计所得的参数值是否是待定参数的真值，最能满足准则要求的参数就作为待估计参数真值的最佳估计。常用准则有最小二乘、最小方差、最小风险、最小预报均方误差等。有了准则，参数估计问题就化为求某准则函数（目标函数）达到极值的优化计算问题。参数估计算法可分为两类：一类是选代算法，这是一种事后处理方法，将整个数据分成几组，一组一组数据进行处理。通常，准则导出的准则函数是待定参数的非线性泛函，无法解析求解，可采用各种迭代算法求解之，例如，牛顿法、梯度法、高斯法等。另一类是递推算法，这是一种实时在线估计算法（当然也可用于事后处理），将数据逐点进行处理，在状态方程组和准则函数的约束下，逐点用新的数据对待估计参数进行更新和修正，直至收敛为止。目前，在系统辨识的众多准则和算法中,最广泛应用的准则是最大似然准则，最常用的算法是修正牛顿-拉夫逊法。

5.2 线性模型参数估计

线性模型的参数估计在飞行器系统辨识中有着广泛的应用，如惯性仪表误差系数的辨识、线性时变离散系统初始状态的辨识及多项式曲线拟合等，都属于线性模型的参数估计问题。解决线性模型参数估计的最小二乘法已广泛应用于工程实践中。线性模型为

\pmb{y}\;=\;\pmb{X}\pmb{\theta}\;+\;\pmb{\varepsilon}

式中y——观测矢量；

\pmb{X} —参数灵敏度系数矩阵；
\pmb\theta 待估参数；
&—测量噪声。

测量噪声满足

（1）零均值： E(\pmb{\varepsilon})=0

（2）测量噪声时序不相关（即白噪声情况）：

\mathrm{cov}(\,\varepsilon\,)\;=\;E(\,\varepsilon_{i}\varepsilon_{j}^{\mathrm{T}})\;=\;B\delta_{i j}

\delta_{i j}\,=\,{\binom{0}{1}}\quad(\,i\neq j\,)

若时序相关（即有色噪声情况）：

\mathbf{cov}(\,\pmb{\varepsilon}\,)\;=\;\pmb{B}

(\pmb{X}^{\top}\pmb{X}) 为线性模型的信息矩阵，信息矩阵的病态是线性模型参数估计的要害。最小二乘法的估计值是无偏估计。但无偏性仅指期望值而言，对小子样试验并不成立。为改善小子样试验估计和信息矩阵病态问题，出现以各种损失函数作为度量估计值优良性的准则，从而引出了不同的参数估计方法。本节针对解决信息矩阵病态的问题，提出各种实用的线性估计方法。

5.2.1 最小二乘法

系统输出的观测值与模型输出之差称为残差 \pmb{v} 。使残差平方和最小的方法即为最小二乘法。

残差平方和为

{\cal J}\;=\;\pmb{\nu}^{\mathrm{T}}\pmb{\nu}\;=\;(\,\pmb{y}\,-\,\pmb{X}\pmb{\hat{\theta}}\,)^{\mathrm{T}}\pmb{B}\,^{-1}(\,\pmb{y}\,-\,\pmb{X}\pmb{\hat{\theta}}\,)

令 \partial J/\partial\hat{\pmb{\theta}}=0 ，求出 \pmb{\hat{\theta}}=\pmb{\hat{\theta}}_{L} ，即为最小二乘估计值。

\hat{\pmb{\theta}}_{L}\:=\:(\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{X})^{-1}\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{y}

当噪声为白噪声且等方差时， {\pmb{{\cal B}}}={\pmb{\sigma}}^{2}{\pmb{\cal I}} , 则

\hat{\pmb{\theta}}_{L}\;=\;(\pmb{X}^{\mathrm{T}}\pmb{X})^{-1}\pmb{X}^{\mathrm{T}}\pmb{y}

最小二乘估计的两个基本特性：

（1）估计值是无偏的，即

E(\hat{\pmb{\theta}}_{L})\,=(\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{X})^{-1}\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{E}(\pmb{y})\,=

(\,{\pmb X}^{\mathrm{T}}{\pmb B}^{-1}{\pmb X})^{-1}{\pmb X}^{\mathrm{T}}{\pmb B}^{-1}[\,{\pmb X}{\pmb\theta}\,+\,E(\,{\pmb\nu})\,]\,=\,{\pmb\theta}

（2）估计值的协方差为

\operatorname{cov}(\hat{\pmb{\theta}}_{L})\;=\;\pmb{{\cal E}}\big[\,\pmb{\theta}\:-\:\hat{\pmb{\theta}}_{L}\,\big)(\,\pmb{\theta}\:-\:\hat{\pmb{\theta}}_{L}\,)^{\mathrm{T}}\,\big]\;=\;(\,\pmb{{\cal X}}^{\mathrm{T}}\pmb{{\cal B}}^{-1}\pmb{{\cal X}}\,)^{-1} (5 - 6)在测量噪声为等方差、白噪声情况下，有

\mathrm{cov}(\,\hat{\pmb{\theta}}_{L}\,)\,=\,\sigma^{2}(\,\pmb{X}^{\mathrm{T}}\pmb{X})^{-1}

最小二乘法估计值的另外两种表示方法：

(1） 在式(5-1)下记

\mathbf G\;=\;{\left[\begin{array}{l l}{\mathbf{y}^{\mathsf{T}}}\\ {\mathbf{X}^{\mathsf{T}}}\end{array}\right]}\left[\,\mathbf{y}\quad\mathbf{X}\,\right]\;=\;{\left[\begin{array}{l l}{\mathbf{y}^{\mathsf{T}}\mathbf{y}}&{\mathbf{y}^{\mathsf{T}}\mathbf{X}}\\ {\mathbf{X}^{\mathsf{T}}\mathbf{y}}&{\mathbf{X}^{\mathsf{T}}\mathbf{X}}\end{array}\right]}

令 \pmb{A} 为正交方阵，使

{\bf A}^{\mathrm{T}}{\bf G}{\cal A}\;=\;{\bf A}\;=\;\mathrm{diag}(\,\lambda_{0}\,,\lambda_{1}\,,\lambda_{2}\,,\cdots,\lambda_{p}\,)

\hat{\theta}_{L\,,\,i}\;=\;\Big(\sum_{j\,=\,0}^{\phi}\alpha_{0j}\alpha_{i j}\big/\lambda_{j}\Big)\,\Big(\sum_{j\,=\,0}^{\phi}\alpha_{0}^{2}\big/\lambda_{j}\Big)

式中 α-——正交方阵 A 的元素；

\pmb{\dot{p}} 一一待估参数的个数。

(2）在式(5-1)下记

\pmb{{\cal D}}\;=\;\pmb{{\cal X}}^{\mathrm{T}}\pmb{{\cal B}}^{-1}\pmb{{\cal X}}

令 \pmb{P} 为 \pmb{D} 的正交方阵，使

P^{\mathrm{T}}D P\;=\;{\cal A}\;=\;\mathrm{diag}(\,\lambda_{1}\,,\lambda_{2}\,,\cdots,\lambda_{\rho}\,)

由式(5-3)得

\begin{array}{r l}{\hat{\theta}_{L}\;=\;{\cal D}^{-1}X^{\top}{\cal B}^{\top\,-1}y}&{}\\ {{\cal P}^{T}\hat{\theta}_{L}\;=\;{\cal P}^{\top}{\cal D}^{-1}X^{\top}{\cal B}^{\,-1}y\;=}\\ {{\cal P}^{\top}{\cal D}^{-1}X^{\top}{\cal B}^{\top\,-1}(X\theta\;+\;\nu\;)\;=}&{}\\ {{\cal P}^{\top}\theta\;+\;{\cal P}^{\top}{\cal D}^{-1}X^{T}{\cal B}^{\top\,-1}\nu\;=}&{}\\ {t\;+\;\mu}\end{array}

式中 {\pmb{t}}={\pmb{P}}^{\mathrm{T}}{\pmb{\theta}} ：\pmb{\mu}\;=\;\pmb{P}^{T}\pmb{D}^{-1}\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{\nu}_{\circ}

因此， \pmb{\hat{\theta}}_{L}=\pmb{P}(\pmb{t}+\pmb{\mu}) ，或

\theta_{L\,,\,i}\,=\,\,\sum_{j\,=\,1}^{\cal P}\,[\,(\,t_{j}\,+\,\mu_{j}\,)\,\rho_{i j}\,]

5.2.2 递推最小二乘法

用上述方法可以给出参数的最小二乘估计，但是观测信息的增加对估计值会有影响。一般地讲，随着信息的不断增加，估计值的精度会越来越高，并趋于稳定，这也是检验估计值是否准确的手段之一。为此产生了计算增加信息后的新的估计值的问题。如何采用简单的算法来求取，就引出了递推最小二乘法。

假设到某时刻 \pmb{\t_{k}} 已经得到最小二乘估计值 \hat{\pmb{\theta}}_{L,k}

\hat{\pmb{\theta}}_{L,\,k}\:=\:\big(\:\pmb{X}_{k}^{\mathrm{T}}\pmb{X}_{k}\:\big)^{-1}\:\pmb{X}_{k}^{\mathrm{T}}\pmb{y}_{k}

当进行第 (k+1) 次观测后,估计值为 \hat{\pmb{\theta}}_{L,k+1\,0}

\hat{\pmb{\theta}}_{L\,,\,k+1}\,=\,\left(\,{\pmb{X}}_{k\,+\,1}^{\mathrm{T}}\pmb{X}_{k\,+\,1}\,\right)^{-1}\pmb{X}_{k\,+\,1}^{\mathrm{T}}\,{\pmb{y}}_{k\,+\,1}

\pmb{X}_{k+1}\;=\;\binom{\pmb{X}_{k}}{\pmb{q}_{k+1}}\,\

\mathbf{y}_{k+1}=\left[\begin{array}{c}{\mathbf{y}_{k}}\\ {\;}\\ {y_{k+1}}\end{array}\right]

式中 {\pmb q}_{k}+{\bf1} 一每递增一步的新息，为行矢量。

由式(5-15)知

X_{k+1}^{\mathrm{T}}X_{k+1}\;=\;X_{k}^{\mathrm{T}}X_{k}\;+\;q_{\;k+1}^{\mathrm{T}}q_{k+1}

再引人矩阵求逆引理

(\pmb{A}\ +\ \pmb{h}^{\mathrm{T}}\pmb{h})^{-1}\ =\ \pmb{A}^{-1}\ -\ \pmb{A}^{-1}\pmb{h}^{\mathrm{T}}(1\ +\ \pmb{h}\pmb{A}^{-1}\pmb{h}^{\mathrm{T}})^{-1}\pmb{h}\pmb{A}^{-1}

式中 \pmb{h} 为行矢量。

于是

\hat{\pmb{\theta}}_{L\,,\,k+1}\;=\;\hat{\pmb{\theta}}_{L\,,\,k}\;+\;{\cal K}_{k}\pmb{v}_{k}

式中

\begin{array}{r l}&{\pmb{K}_{k}\,=\,\pmb{P}_{k}\pmb{q}_{k+1}^{\textsc{T}}(1\,+\,\pmb{q}_{k+1}\,\pmb{P}_{k}\pmb{q}_{k+1}^{\textsc{T}})^{-1}}\\ &{\pmb{v}_{k}\,=\,\pmb{y}_{k+1}\,-\,\pmb{q}_{k+1}\,\hat{\pmb{\theta}}_{L,k}}\\ &{\pmb{P}_{k}\,=\,\left(\pmb{X}_{k}^{\operatorname{T}}\pmb{X}_{k}\right)^{-1}}\end{array}

P_{k+1}\,=\,(\,{\pmb X}_{k+1}^{\mathrm{T}}\,{\pmb X}_{k+1}\,)^{-1}\,=\,P_{k}\,-\,K_{k}q_{k+1}\,P_{k}\,=

(I\,-\,K_{k}q_{k+1})\,P_{k}

递推计算过程为:对某时刻 t_{k} 已估计得到 \hat{\pmb{\theta}}_{L,k}\,,\pmb{P}_{k} ,并有 t_{k+1} 时刻的观测量 y_{k}+10 先构造 {\pmb q}_{k+1} ,然后由式(5-20)计算 \pmb{v}_{\pmb{k}} ，由式 (5-19)计算 \pmb{K}_{k} ,由式(5-18)计算 \hat{\pmb{\theta}}_{L,k+10} 若 {\pmb{\nu}}_{k}\!\rightarrow\!{\bf0} 或 \hat{\theta}_{L,k+1}\rightarrow \hat{\pmb\theta}_{L,k} ,满足给定的收敛条件,则 \hat{\pmb{\theta}}_{L,k+1} 就是估计值。否则由式 (5-21)计算 P_{k+1} ,再重复上述运算过程，向 t_{k+2} 递推,直至收敛为 止。

5.2.3 渐消记忆的递推估计法

随着信息的不断增加，一般地讲，估计精度会越来越高，但在实际使用中，有时会出现估计值精度下降。

由式(5-21)可得

\begin{array}{r l}{\mathbf{\nabla}\cdot\mathbf{P}_{k+1}\:=\:K_{k}\mathbf{q}_{k+1}P_{k}\:=\:}&{}\\ {\mathbf{P}_{k}\mathbf{q}_{\:k+1}^{\mathrm{~T~}}(\:I\:+\:q_{k+1}P_{k}\mathbf{q}_{\:k+1}^{\mathrm{~T~}})^{-1}\mathbf{q}_{k+1}P_{k}\:}&{}\end{array}

由于 \pmb{P_{k}} 为正定,因此 P_{\pmb{k}}q_{\pmb{k}+1}^{\mathrm{~T~}}(1+q_{\pmb{k}+1}P_{\pmb{k}}q_{\pmb{k}+1}^{\mathrm{~T~}})\,^{-1}\,\pmb{q}_{\pmb{k}+1}\,P_{\pmb{k}} 是非负定的,即 \mathbf{\nabla}P_{k}\textrm{--}\mathbf{\nabla}P_{k+1}\!\geqslant\!\mathbf{0} ,从而 \mathbf{\nabla}P_{k}\mathcal{\geq}\mathbf{P}_{k+1} 。

\pmb{P}_{k} 随着增加新的信息有可能最后趋于零，即再增加信息对估计值的改进不再起作用了，这种现象称为数据饱和。为克服这一现象，可以用降低旧数据影响的办法来修改算法，由此出现了渐消记忆的递推估计法。

所谓渐消记忆，就是对每个数据按指数加权，老的数据所加的权按指数衰减。将旧数据乘以一个因子 \rho\,(0\!<\!\rho\!\leqslant\!1) ，即将式(5-15)与式(5-16)改为

\mathbf{{X}}_{k+1}\,=\,{\left[\begin{array}{l}{\rho\mathbf{{X}}_{k}}\\ {\mathbf{{q}}_{k+1}}\end{array}\right]}\qquad\mathbf{{y}}_{k+1}\,=\,{\left[\begin{array}{l}{\rho\mathbf{{y}}_{k}}\\ {\mathbf{{y}}_{k+1}}\end{array}\right]}

相应于式(5-18)、式(5-19)和式(5-21),有

\begin{array}{r}{\hat{\pmb{\theta}}_{L,k+1}\,=\,\hat{\pmb{\theta}}_{L,k}\,+\,{\pmb{K}}_{k}\,(\,y_{k+1}\,-\,q_{k+1}\pmb{\theta}_{L,k}\,)}\end{array}

\pmb{K}_{k}\;=\;P_{k}\pmb{q}_{k+1}^{\mathrm{~T~}}(\,\rho^{2}\:+\:\pmb{q}_{k+1}P_{k}\pmb{q}_{k+1}^{\mathrm{~T~}})^{\;-1}

\mathbf{\calP}_{k+1}\,=\,\frac{1}{\rho^{2}}\big(\,I\,-\,K_{k}q_{k\,+\,1}\big)\,P_{k}

若限定采样点数，当进人一个新数据时，去掉一个旧数据，这种估计称为限定记忆的递推估计[22]

5.2.4 贝叶斯法

最小二乘估计是无偏估计，当信息矩阵不是病态或病态不严重时，最小二乘法可以得到良好的估计值。但是信息矩阵 (\pmb{X}^{\intercal}\pmb{X}) 往往严重病态，导致求逆困难，使估计值精度很差。要解决这个问题，有必要引人各种有偏估计方法，其中利用验前信息来改善信息矩阵病态及提高估计值精度是很有效的方法。贝叶斯法是改善信息矩阵病态的方法之一一，还有龄估计、超椭球约束等均属于这类估计，只是其验前信息的表示方式不一样或选定的损失函数不一样。

贝叶斯法利用基于正态分布的验前信息，其验前期望值 \pmb{\theta}_{0} 与验前协方差阵 {\pmb{{\cal B}}}_{0} 是已知的，因此，除式（5-1)外还增加了验前方程

\pmb{\theta}_{0}\;=\;\pmb{I}\pmb{\theta}\;+\;\pmb{\varepsilon}_{0}

\mathrm{cov}(\,\pmb{\varepsilon}_{0}\,)\;=\;\pmb{B}_{0\,0}

将式(5-1)与式(5-25)综合得

\left[\begin{array}{c}{{\bf y}}\\ {\pmb{\theta}_{0}}\end{array}\right]=\begin{array}{c}{{\left[\begin{array}{c}{{\pmb X}}\\ {{\pmb I}}\end{array}\right]\pmb\theta+\left[\begin{array}{c}{{\pmb\varepsilon}}\\ {{\pmb\varepsilon}_{0}}\end{array}\right]}}\end{array}

贝叶斯法估计值为

\pmb{\dot{\theta}}_{B}\;=\;(\,\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{X}\,+\,\pmb{B}_{0}^{-1}\,)^{-1}(\,\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{y}\,+\,\pmb{B}_{0}^{-1}\,\pmb{\theta}_{0}\,)

贝叶斯法的性质：

(1)估计值是有偏的,即

E(\,\hat{\pmb{\theta}}_{B}\,)\:=\:\pmb{\theta}\:-\:\pmb{D}_{B}^{\,-1}\pmb{B}_{0}^{\,-1}\big(\,\pmb{\theta}\:-\:\pmb{\theta}_{0}\,\big)

其偏度为 \pmb{{\cal D}}_{B}^{\texttt{-}1}\pmb{{\cal B}}_{0}^{\texttt{-}1}(\pmb{\theta}-\pmb{\theta}_{0}) 。

（2）估计值的协方差为

\begin{array}{r l}&{\quad\mathrm{cov}(\,\hat{\pmb{\theta}}_{B}\,)\,\simeq\,{\pmb{{\cal D}}}_{B}^{\,-1}(\,{\pmb X}^{\mathrm{T}}{\pmb B}^{\,-1}{\pmb X}\,)\,{\pmb D}_{B}^{\,-1}}\\ &{^{\mathrm{T}}{\pmb B}^{\,-1}{\pmb X}+{\pmb B}_{0}^{\,-1}\,)}\end{array}

式中 {\pmb{D}}_{B}=\left(\,{\pmb{X}}^{\mathrm{T}}{\pmb{B}}^{\,-\,1}{\pmb{X}}+{\pmb{B}}_{0}^{\,-\,1}\,\right)

根据式（5-12），贝叶斯法估计值的另一种表示式为

\hat{\theta}_{B,\,i}\;=\;\sum_{j\,=\,1}^{\hat{p}}\,[\,(\,t_{j}\,+\,\mu_{j}\,)\,\rho_{i j}\,]

式中 \ensuremath{\boldsymbol{P}}{\longrightarrow}\ensuremath{\boldsymbol{D}}_{B} 的正交矩阵。

5.2.5 岭估计法

岭估计法也是为了解决信息矩阵 (\,X^{\mathrm{T}}X\,) 的病态性质而产生的，它的出发点是要找到一个比最小二乘估计更接近于待估参数真值的估计方法，这就有必要适当增大估计值与真值之间的残差平方和,而适当增大的量是事先给定的，例如给定 \Phi_{0}\left(\,\Phi_{0}>0\,\right) 在增大残差的量 \Phi_{0} 给定后，找出一个新的估计值，使其与待估参数的验前期望值 {\pmb\theta}_{0} 的距离为最短。

对于待估参数 \pmb\theta 的估计值 \pmb{\hat{\theta}} ，由式（5-2)知，它的残差平方和为

\begin{array}{r}{J\;=\;\pmb{\nu}^{\mathrm{T}}\pmb{\nu}\;=\langle\,\pmb{y}\,-\,\pmb{X}\hat{\pmb{\theta}}\,\rangle^{\mathrm{T}}\pmb{B}^{-1}(\,\pmb{y}\,-\,\pmb{X}\hat{\pmb{\theta}}\,)\;=\;}\\ {(\,\pmb{y}\,-\,\pmb{X}\hat{\pmb{\theta}}_{L}\,)^{\mathrm{T}}\pmb{B}^{-1}(\,\pmb{y}\,-\,\pmb{X}\hat{\pmb{\theta}}_{L}\,)\;+}\end{array}

\begin{array}{r l}&{(\hat{\pmb{\theta}}_{L}\,-\,\hat{\pmb{\theta}})^{\mathrm{T}}\pmb{X}(\hat{\pmb{\theta}}_{L}\,-\,\hat{\pmb{\theta}}\,)\,=}\\ &{\pmb{Q}_{L}\,+\,\Delta\pmb{Q}}\end{array}

岭估计就是满足条件

\pmb{\Delta}\pmb{Q}\;=\;(\,\hat{\pmb{\theta}}_{L}\:-\:\hat{\pmb{\theta}}\,)^{\mathrm{T}}\pmb{X}^{\mathrm{T}}\pmb{B}\,^{-1}\pmb{X}(\,\hat{\pmb{\theta}}_{L}\:-\:\hat{\pmb{\theta}}\,)\;=\;\pmb{\Phi}_{0}

且使

(\hat{\pmb{\theta}}\,-\,\pmb{\theta}_{0})^{\mathrm{T}}\pmb{B}_{0}^{-1}(\hat{\pmb{\theta}}\,-\,\hat{\pmb{\theta}}_{0})\,=\,\operatorname*{min}

的一种估计。

岭估计的物理意义是,在超椭球式(5-32)上找出一点 \hat{\pmb{\theta}}_{R} ，使之与 {\pmb\theta}_{0} 的距离最短。运用拉格朗日乘子法，可以推导出岭估计值。令

\begin{array}{l}{{J(\hat{\pmb\theta})\,=\,(\hat{\pmb\theta}\,-\,\pmb\theta_{0})^{\mathrm{T}}{\pmb B}_{0}^{-1}(\hat{\pmb\theta}\,-\,\pmb\theta_{0})\,+}}\\ {{\frac{1}{\lambda^{\ast}}[(\hat{\pmb\theta}_{L}\,-\,\pmb\hat{\pmb\theta})^{\mathrm{T}}{\pmb X}^{\mathrm{T}}{\pmb B}^{-1}{\pmb X}(\hat{\pmb\theta}_{L}\,-\,\pmb\hat{\pmb\theta})\,-\,\pmb\phi_{0}]}}\end{array}

式中 \lambda^{\star} ——拉格朗日乘子。

对函数 \boldsymbol{J}(\hat{\pmb{\theta}}) 求极值，得龄估计值 \hat{\pmb{\theta}}_{R} 为

\pmb{\hat{\theta}}_{R}\ =(\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{X}\ +\ \lambda^{\ \star}\ \pmb{B}_{0}^{\ -1})^{-1}

(\,\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\,\pmb{y}\,+\,\lambda^{\star}\,\pmb{B}_{0}^{-1}\,\pmb{y}\,+\,\lambda^{\star}\,\pmb{B}_{0}^{-1}\,\pmb{\theta}_{0}\,)

显然，当 \lambda^{\star}=0 时，为最小二乘法；当 \lambda^{\star}=1 进，为贝叶斯法。

龄估计的性质：

（1）估计值是有偏的，即

E(\hat{\pmb{\theta}}_{R})\:=\:\pmb{\theta}\:-\:\pmb{D}_{R}^{-1}\pmb{\lambda}\,^{\star}\:\pmb{\cal E}_{0}^{-1}(\vartheta\:-\:\pmb{\theta}_{0})

其偏度为 D_{R}^{\mathrm{~-~}1}\lambda^{\mathrm{~*~}}B_{0}^{\mathrm{~-~}1}(\pmb{\theta}^{\mathrm{~-~}}\ell_{0}^{\mathrm{~*~}})

(2）估计值的协方差为

式中

\begin{array}{c}{{\mathrm{cov}(\hat{\pmb\theta}_{R})\;=\;{\pmb D}_{R}^{-1}(\,{\pmb X}^{\uparrow}{\pmb B}^{-1}{\pmb X}){\pmb D}_{R}^{-1}}}\\ {{({\pmb X}^{\mathrm{T}}{\pmb B}^{-1}{\pmb X}+\lambda^{\star}\,{\pmb B}_{0}^{\sim1})}}\end{array}

5.2.6 超椭球法

如果验前信息不能给出分布，只能给出一个范围，并且要求残差平方和为最小。即在满足给定的约束条件

\mid\theta_{i}\,-\,\theta_{0\,i}\,\mid\,\leqslant d_{i}\;\;\;\;\;\;\;\;(\,i\,=\,1,2,\cdots,p\,)

的前提下，要求

(\,{\bf\vec{y}}\,-\,{\bf X}{\hat{\pmb{\theta}}}\,)^{\mathrm{T}}{\pmb{\cal B}}^{-1}(\,{\bf y}\,-\,{\bf X}{\hat{\pmb{\theta}}}\,)\;=\;\mathrm{min}

将约束条件式（5-38）改写为

\sum_{i\mathop{=}1}^{p}\left(\frac{\theta_{i}\,-\,\theta_{0\,i}}{\sqrt{m_{0}}\,d_{i}}\right)=1\qquad(\,m_{0}\leqslant p\,)

令

G\;=\;\left[\begin{array}{c c c c}{{1}}&{{}}&{{}}&{{0}}\\ {{\sqrt{m_{0}}\,d_{1}}}&{{}}&{{}}&{{}}\\ {{}}&{{\frac{1}{\sqrt{\,m_{0}}\,d_{2}}}}&{{}}&{{}}\\ {{}}&{{}}&{{\cdots}}&{{}}\\ {{}}&{{}}&{{}}&{{\frac{1}{\sqrt{\,m_{0}}\,d_{p}}}}\end{array}\right]

应用拉格朗日乘子法，作函数

\begin{array}{r l}&{J(\hat{\pmb{\theta}})=(\,\pmb{y}\,-\,\pmb{X}\hat{\pmb{\theta}}\,)^{\mathrm{T}}\pmb{B}^{-1}(\,\pmb{y}\,-\,\pmb{X}\hat{\pmb{\theta}}\,)\ +}\\ &{\quad\quad\quad\quad\lambda\,[\,(\,\hat{\pmb{\theta}}\,-\,\pmb{\theta}_{0}\,)^{\mathrm{T}}\pmb{G}^{\mathrm{T}}\pmb{G}\,(\,\hat{\pmb{\theta}}\,-\,\pmb{\theta}_{0}\,)\,-\,1\,]}\end{array}

\frac{\partial J(\pmb{\theta})}{\partial\pmb{\dot{\theta}}}=\mathbf{0} ,求出超椭球法的估计值 \hat{\pmb{\theta}}_{T} 为

\pmb\partial_{T}\,=\,(\,\pmb X^{\operatorname{T}}\pmb B^{-1}\pmb X\,+\,\lambda\pmb G^{\operatorname{T}}\pmb G\,)^{-1}(\,\pmb X^{\operatorname{T}}\pmb B^{-1}\pmb y\,+\,\lambda\pmb G^{\operatorname{T}}\pmb G\pmb\theta_{0})

超椭球法的性质：

（1）估计值是有偏的，即

E(\pmb{\dot{\theta}}_{T})\,=\,\pmb{\theta}\,-\,\pmb{D}_{T}^{\mathrm{T}}\pmb{\lambda}\pmb{G}^{\mathrm{T}}\pmb{G}\,(\pmb{\theta}\,-\,\pmb{\theta}_{0})

其偏度为 D_{T}^{\mathrm{T}}\lambda G^{\mathrm{T}}G(\,\pmb\theta-\pmb\theta_{0}) 。

（2）估计值的协方差为

\begin{array}{c}{{\mathrm{cov}(\hat{\pmb\theta}_{T})\;=\;\pmb{{\cal D}}_{T}^{-1}\big(\,{\pmb X}^{\mathrm{T}}{\pmb B}^{-1}{\pmb X}\big){\pmb D}_{T}^{-1}}}\\ {{\mathrm{}}}\\ {{\pmb D}_{T}=\big(\,{\pmb X}^{\mathrm{T}}{\pmb B}^{\mathrm{-1}}{\pmb X}+{\lambda}{\pmb G}^{\mathrm{T}}{\pmb G}\,\big)_{\circ}}\end{array}

式中

5.2.7 主成分法

贝叶斯法、岭估计法及超椭球法都是利用验前信息来改善设计矩阵的病态,这是显而易见的。但是如果验前信息不可信,反而会导致估计值不正确。为此根据信息矩阵的特征根分析，发现特征根大的成分对测量噪声的反应并不敏感，而特征根小的成分对测量噪声特别敏感。特征根大的成分对线性估计是主要成分，相反特征根小的则可以忽略。由此产生了主成分法。

主成分法是基于信息矩阵 (\pmb{X}^{\mathrm{T}}\pmb{X}) 的特征根的选择，当特征根太小的时候，相应的待估参数不可能估计准确，同时这些参数对线性估计的贡献也不大，若不去掉反而会影响到别的待估参数的估计准度。因此不如不去估计它。而去掉小的特征根后，即使估计值有一定的偏度，但估计值精度大大提高。这就是主成分法的思路。

在信息矩阵中的各分量，由于工程上采用“米·秒·弧度”制作为标准量单位，各分量之间数量相差悬殊，特征根大小与待估参数对线性估计的重要性不一致，为此应该对矩阵 \pmb{X} 进行加权，也就是给一个“刻度”，工程上称为“比例因子”。经比例因子化后，式(5-1)改成

\begin{array}{r}{\textbf{\emph{y}}=\mathbf{\emph{(XF)}}(\mathbf{\emph{F}}^{-1}\,\pmb{\theta})\,+\,\pmb{\varepsilon}\,=\,\widetilde{\mathbf{\emph{X}}}\widetilde{\pmb{\theta}}\,+\,\pmb{\varepsilon}}\end{array}

式中 \scriptstyle F\longrightarrow 比例因子矩阵， \pmb{F}=\mathrm{diag}(~f_{1},f_{2},\cdots,f_{p})_{\circ}

(\widetilde{\pmb{X}}^{\top}\pmb{B}^{\ –1}\widetilde{\pmb{X}}) 是非负定对称矩阵,所以存在正交变换矩阵 \pmb{P} 使得

P^{\mathrm{T}}(\,X^{\mathrm{T}}B^{\mathrm{-}1}X)\,P\;=\;{\bf A}\;=\;\mathrm{diag}(\,\lambda_{1},\lambda_{2},\cdots,\lambda_{\hat{p}}\,)

式中略去了上标号 ^{\bullet}\sim^{\bullet\bullet} ,且 \lambda_{1}{\leqslant}\lambda_{2}{\leqslant}\cdots{\leqslant}\lambda_{p} 。故有

\begin{array}{r l}&{\(X^{\mathrm{T}}B^{-1}X)\;=\;P\Lambda P^{\mathrm{T}}}\\ &{\quad\quad(X^{\mathrm{T}}B^{-1}X)^{-1}\;=\;P A^{\,-1}P^{\mathrm{T}}}\end{array}

\hat{\pmb{\theta}}_{L}\;=\;P\pmb{A}^{\,-1}P^{\mathrm{T}}\pmb{X}^{\mathrm{T}}\pmb{B}^{\,-1}\,\mathbf{y}

\begin{array}{r}{P^{-1}\hat{\pmb{\theta}}_{L}\;=\;{\pmb{A}}^{-1}{\pmb{P}}^{\top}{\pmb{X}}^{\top}{\pmb{B}}^{-1}{\pmb{y}}\equiv{\pmb{d}}\;=\;(\,d_{1},d_{2},\cdots,d_{\cal P}\,)^{\top}}\end{array}

记 \pmb{z}=\pmb{P}^{\mathrm{T}}\pmb{X}^{\mathrm{T}}\pmb{B}^{\mathrm{-1}}\pmb{y} ，则有 \pmb{z}=\pmb{\Delta}d ,即 z_{i}=\lambda_{i}d_{i} 。当信息矩阵严重病

态时，条件数 \lambda_{p}/\lambda_{1}\!\gg\!1 ,故令小的特征根为零，即 \lambda_{1}=\lambda_{2}=\cdots= \lambda_{r}=0 ,则 \hat{\pmb{d}}=(\mathbf{0},\cdots,\mathbf{0},d_{r+1},d_{p})^{\mathrm{T}}. 。主成份估计值 \hat{\pmb\theta}_{P} 为

\hat{\pmb\theta}_{P}\;=\;\pmb{P}\hat{\pmb d}\;=\;{\pmb P}_{2}{\pmb A}_{2}^{-1}{\pmb P}_{2}^{\mathrm{T}}{\pmb X}^{\mathrm{T}}{\pmb B}^{-1}{\bf y}

式中

{\pmb A}\;=\;\binom{{\pmb A}_{1}}{{\bf0}}\;\quad{\bf0}\;\;\}

\pmb{A}_{1}\,=\,\mathrm{diag}(0,0,\cdots,0)

\mathbfcal{A}_{2}\,=\,\mathrm{diag}(\,\lambda_{r+1},\cdots,\lambda_{p})

\pmb{P}\,=\,(\,\pmb{P}_{1}\,\dot{\mathrm{~i~}}\,\pmb{P}_{2})

式中 \scriptstyle P_{1}\longrightarrow\phi\,\times\,r 阶矩阵；

\boldsymbol{P}_{2}{\longrightarrow}\boldsymbol{\phi}\times\left(\boldsymbol{\phi}\boldsymbol{-}\boldsymbol{r}\right) 阶矩阵。

主成分法估计的性质：

（1）估计值是有偏的,即

E(\hat{\pmb{\theta}}_{p})\:=\:\pmb{P}_{1}\pmb{P}_{1}^{\mathrm{T}}\pmb{\theta}

其偏度为 \big(\pmb{I}-\pmb{P}_{1}\pmb{P}_{1}^{\mathrm{T}}\big)\pmb{\theta}_{\epsilon}

（2）估计值的协方差为

\mathrm{cov}(\,\hat{\pmb{\theta}}_{P})\;=\;{\pmb{P}}_{2}{\pmb{A}}_{2}^{\,-\,1}{\pmb{P}}_{2}^{\mathrm{T}}

根据式（5-12），主成分法有另一种表示方法

\hat{\theta}_{P,i}\;=\;\sum_{j\,=\,1}^{\beta}k_{j}\,[\,(\,t_{j}\,+\,\lambda_{j}\,)\,\rho_{i j}\,]

式中

5.2.8 特征根法

从主成分法知，选择主要成分只依赖于信息矩阵，而与观测值无关。特征根法却不同，它既考虑了自变量（灵敏度系数）又考虑了因变量（观测值)的关系。因此，从原理上讲，它比主成分法考虑得更全面。

根据式(5-10),对最小二乘法的估计值

\hat{\theta}_{L\,,\,i}\,=-\,\left(\,\sum_{j\,=\,0}^{\dot{p}}a_{0\,j}a_{i j}/\lambda_{j}\,\right)\Big/\Big(\sum_{j\,=\,0}^{\dot{p}}a_{0\,j}^{2}/\lambda_{j}\,\Big)

式中 \lambda_{j}\big(j=0,1\,,\cdots,p\big)- 矩阵 \pmb{G} (式(5-8))的 (\,\mathfrak{p}+1) 个特征

a_{i j}\big(\,i\,,j=0\,,1\,,\cdots,p\,\big) ——对应的特征矩阵的元素。

对给定的小量 \varepsilon_{\lambda} 和 \varepsilon_{a} ,当

\lambda_{r}\,<\,\pmb{\epsilon}_{\lambda}\qquad\quad\mid\,\alpha_{0r}\,\mid\,<\,\pmb{\epsilon}_{a}

同时满足时,则去掉该项,得到特征根估计 \hat{\theta}_{r\,,\,i}

\hat{\theta}_{r\,,\,i}\;=\;-\;\Bigl.\big(\sum_{j\,=\,r+1}^{\hat{p}}a_{0j}a_{i j}/\lambda_{j}\,\bigr)\Big/\Bigl(\sum_{j\,=\,r+1}^{\hat{p}}a_{0j}^{2}/\lambda_{j}\,\Bigr)

特征根法估计值的性质与主成分法相同，只是 \r^{r} 的含义不同。

5.2.9 贝叶斯主成分法(PB 回归法)

对于上述两类估计，利用验前信息为约束条件的估计和不利用验前信息而依赖于特征根大小的估计,各有其优缺点。为了充分利用验前信息，又采用主成分估计的思路，或者说在主成分法的基础上，附加上验前信息，得到了PB回归方法。

贝叶斯法估计值的公式(5-30)为

\hat{\theta}_{B,\,i}\;=\;\sum_{j\,=\,1}^{p}\,[\,(\,t_{j}\,+\,\mu_{j}\,)\,\rho_{i j}\,]

式中 \pmb{\mathscr{p}}_{i j}\setminus\pmb{\mathscr{\mu}}_{j} 与 B_{0}^{\mathrm{~-~}1} 及 \theta_{0} 有关。

当 \mathbf{\dot{}}B_{\mathbf{0}}^{\mathbf{\mu}-1}\mathbf{=0} 时,式(5-30)与最小二乘法估计值式(5-12)完全一致。

主成分法估计值的公式(5-51)为

\hat{\theta}_{P,\,i}\;=\;\sum_{j\,=\,1}^{\phi}k_{j}\,[\,(\,t_{j}\,+\,\mu_{j}\,)\,\rho_{i j}\,]

式中 k_{j} 取0还是取1,完全取决于舍去的项数 ^r 是多少。而其中 \hat{p}_{i j}\setminus\pmb{\mu}_{j} 与 B_{0}^{\mathrm{~-~}1} 及 \theta_{0} 无关。

因而两类估计法的综合，可归纳为

\hat{\theta}_{P B,\,i}\;=\;\sum_{j\,=\,1}^{\rlap/5}k_{j}\,[\,(\,t_{j}\,+\,\mu_{j}\,)\,\rho_{i j}\,)\,]

式中 {\pmb\mathscr{p}}_{i j}\setminus{\pmb\mathscr{L}}_{j} 与 B_{0}^{\mathrm{~-~}1} 及 {\pmb\theta}_{0} 有关，而 k_{j} 的取值完全决定于 ^r 的大小。

这样，就有

当 \pmb{k}_{j}=1\,,\pmb{B}_{0}^{\,\,\,-\,1}=\mathbf{0} 时，就是最小二乘法；
当 \pmb{k}_{j}\neq1\,,\pmb{B}_{0}^{-\,1}=\mathbf{0} 时，就是主成分法；
当 \mathbf{\dot{}}_{k_{j}}=1\,,\mathbf{{B}}_{0}^{\scriptscriptstyle-1}\neq\mathbf{0} 时，就是贝叶斯法；
当 \pmb{k}_{j}\neq1\,,\pmb{B}_{0}^{-1}\neq0 时，就是PB 回归法。

PB回归法估计值与主成分法从形式上看是相同的，所不同的是,这里矩阵 \pmb{P}=(\pmb{P}_{1}\vdots\pmb{P}_{2}) 是 (\pmb{X}^{\mathrm{T}}\pmb{B}^{\mathrm{-1}}\pmb{X}+\pmb{B}_{0}^{\mathrm{-1}}) ）的正交变换矩阵。

5.3 最大似然法

5.3.1 最大似然准则

最大似然概念是费希尔（R.A.Fisher)引入的，他认为若系统模型是正确的，则有关系统中未知参数的信息全部包含于似然函数之中。对于给定观测量 L ，参数估计的最大似然法就是选取参数 \pmb{\hat{\theta}} 使似然函数 \pmb{L} 达到最大值

\hat{\pmb{\theta}}\,=\,\mathrm{ARG}\,\operatorname*{max}_{\theta\in\theta}L\left(\pmb{\theta}\,\mid\,\pmb{Y}\right)

对给定的-组与参数 \pmb{\theta} 有关的观测矢量组 \mathbf{Y} ,可以取给定 \pmb{\theta} 下 \pmb{Y} 的条件概率 p(\,\pmb{Y}\,|\,\pmb{\theta}\,) 为似然函数。因此,最大似然估计也就是选取参数 \pmb{\hat{\theta}} 使 \mathbf{Y} 出现的条件概率达到最大值

\pmb{\hat{\theta}}\,=\,\mathrm{ARG}\,\underset{\theta\in\Theta}{\operatorname*{max}}(\,\pmb{Y}\,\mid\,\pmb{\theta}\,)

也可以取似然函数为 \ln{\phi}\big(\,\mathbf{Y}\,|\,\pmb{\theta}\,\big) 。这一基本概念适用于线性和非线性系统，有过程噪声和观测噪声的情况。对给定的观测数组 {\bf Y}_{N}=\left({\bf\Phi}_{{\cal{Y}}_{1}}\,,{\bf\Phi}_{{\cal{Y}}_{2}}\,,\,\cdots,{\bf\Phi}_{{\cal{Y}}_{N}}\right),\,{\bf y}_{i} 是 ^{m} 维观测矢量，其条件概率为\phi(\,\mathbf{Y}_{\mathbf{N}}\,|\,\pmb\theta\,) 。连续应用贝叶斯公式，可推得 \phi(\,\mathbf{Y}_{N}\,\backslash\,\theta\,) 的表达式

\begin{array}{l}{{\displaystyle=\,\hat{p}\!\left(\left.\begin{array}{l}{{\bf y}_{N}\,,\,{\cal Y}_{N-1}\,\,\mid\,\,\theta\right)\,=\,}}\\ {{\displaystyle\hat{p}\!\left(\left.\begin{array}{l l}{{\bf y}_{N}\,\mid\,{\bf Y}_{N-1}\,,\,\theta\right)\hat{p}\!\left(\left.y_{N-1}\right.\mid\,\,\theta\right)\,=\,}}\\ {{\displaystyle\hat{p}\!\left(\left.y_{N}\mid\,{\bf Y}_{N-1}\,,\,\theta\right)\hat{p}\!\left(\left.y_{N-1}\right.\mid\,\,{\cal Y}_{N-2}\,,\theta\right)\hat{p}\!\left(\left.Y_{N-2}\right.\mid\,\theta\right)\,=\,}}\\ {{\displaystyle\cdots\,=\,\prod_{i=1}^{N}\,\hat{p}\!\left(\left.y_{i}\mid\,{\bf Y}_{i-1}\,,\theta\right)\quad~~~~~~~~~~~~~~~~~~~~~(5-5)}}\end{array}

由于对数是单调函数，最大似然估计可写成

\hat{\pmb{\theta}}\ =\mathbf{A}\mathbf{R}\mathbf{G}\ \underset{\theta\in\theta}{\operatorname*{max}}\big[\ln{\pmb{\hat{p}}}\big(\ \pmb{Y}_{N}\mid\pmb{\theta}\big)\big]\ =

\mathrm{ARG~}\underset{\boldsymbol{\theta}\in\boldsymbol{H}}{\operatorname*{max}}\Big[\sum_{i\,=\,1}^{N}\ln p\big(\,\boldsymbol{y}_{i}\mid\,\boldsymbol{Y}_{i-1}\,,\boldsymbol{\theta}\,\big)\,\Big]

式中 \ln{\mathop{\:\/D}}\big(\,\pmb{Y}_{N}\,|\,\pmb{\theta}\,\big) 是似然函数。

当观测数据足够多,根据概率论中心极限定理，可以合理地假定 P(\,y_{i}\,|\,\,\mathbf{Y}_{i-1},\pmb{\theta}\,) 是正态分布，由其均值和方差所惟一确定。记其均值（数学期望）为

E\left\{\,\pmb{y}_{i}\mid\;\pmb{Y}_{i-1}\,,\pmb{\theta}\,\right\}\equiv\hat{\pmb{y}}\left(\,i\;\mid\;i\;-1\,\right)

此均值是在给定前（i－1)个观测量的条件下,第 \pmb{i} 个观测量的最优估计。记其协方差为

\begin{array}{r l}&{\mathrm{Cov}\{\,\mathbf{y}_{i}\;\mid\;\mathbf{Y}_{i-1},\pmb{\theta}\,\}\;=}\\ &{E\,\{\,[\,\mathbf{y}_{i}\,-\,\hat{\mathbf{y}}(\,i\,\mid\,i\,-1)\,]\,[\,(\,\mathbf{y}_{i}\,-\,\hat{\mathbf{y}}(\,i\,\mid\,i\,-1)\,]^{\mathrm{T}}\}\equiv}\\ &{E\,\{\,\pmb{\nu}(\,i\,)\,\pmb{\nu}^{\mathrm{T}}(\,i\,)\,\}\equiv\pmb{B}(\,i\,)}\end{array}

式中 \pmb{\nu}(i) ———第 _i 点的新息;

\pmb{{\cal B}}(\pmb{i}) —一趋向于正态分布。

故 {\pmb{y}}_{i}\,,\,{\pmb{Y}}_{i\mathrm{~-~}1} 也趋向正态分布，前面假定概率密度为正态分布是合理的，故有

\begin{array}{r l}&{\displaystyle\ p\big(\,{\mathfrak{y}}_{i}\mid\,{\mathtt{Y}}_{i-1},\theta\big)\approx\frac{\exp\bigg\{-\displaystyle\frac{1}{2}{\mathfrak{v}}^{\mathtt{T}}(i)B^{-1}(\,i)\,{\mathfrak{v}}(\,i\,)\bigg\}}{(2\uppi)^{m/2}\mid\,B(\,i)\mid^{1/2}}}\\ &{\displaystyle\ \ln\big\{\,{\mathfrak{p}}(\,{\mathfrak{y}}_{i}\mid\,{\mathtt{Y}}_{i-1},\theta\,)\,\big\}\ =}\\ &{\displaystyle-\,\frac{1}{2}{\mathfrak{v}}^{\mathtt{T}}(\,i\,)B^{-1}(\,i\,)\,{\mathfrak{v}}(\,i\,)-\displaystyle\frac{1}{2}\ln\mid B(\,i)\mid+\mathrm{const}.}\end{array}

参数 \pmb\theta 的最大似然估计成了\hat{\pmb{\theta}}\ =\mathrm{ARG}\ \underset{\pmb{\theta}\in\pmb{\theta}}{\operatorname*{max}}\big[\ln L\left(\pmb{\theta}\ |\ \pmb{Y}\right)\big]\cdot=

\mathrm{ARG}\operatorname*{max}_{\theta\in\theta}\bigg\{-\frac{1}{2}\sum_{i=1}^{N}\big[\,\pmb{v}^{\mathrm{T}}(i\,)\pmb{B}^{-1}(i\,)\,\pmb{v}(i\,)\,+\,\ln\mid\,\pmb{B}(i\,)\,\mid\,\big]\,\bigg\}

故参数的最大似然估计就是寻求参数 \pmb{\hat{\theta}} ,使下列似然准则函数 J 达到极小值。

J\;=\;\sum_{\scriptscriptstyle{i\,=\,1}}^{\cal N}\;\vert\;\pmb{\nu}^{\mathrm{T}}(\,i\,)\,\pmb{B}^{\,-1}(\,i\,)\,\pmb{\nu}(\,i\,)\,+\,\ln\;\vert\;\pmb{B}(\,i\,)\,\mid\,\mid

可见似然准则函数 J 依赖于新息 \pmb{\nu}(i) 和新息协方矩阵 \pmb{{\cal B}}(\mathfrak{i}) 而两者都是广义卡尔曼滤波的输出。

参数辨识理论证明了最大似然估计的一些重要性质：

(1)若0 是参数9 的最大似然估计,且函数 h(0)满足%0,则 \pmb{\hat{h}}=\pmb{h}\left(\pmb{\hat{\theta}}\right) 是参数 h 的最大似然估计。

(2）若观测量 \pmb{Y}_{N} 是分布函数 p(\,\mathbf{V}_{N}\,;\theta\,) 的随机样本， \pmb{\hat{\theta}} 是参数的最大似然估计,则当样本容量 N{\rightarrow}\infty 时， \pmb{\hat{\theta}} 趋向正态分布

p(\,\hat{\pmb{\theta}}\,;\pmb{\theta})\rightarrow N(\,\pmb{\theta}_{t r}\,;\pmb{P}_{\theta})

式中,协方差矩阵 \scriptstyle{P_{\theta}}

P_{\theta}\,=\,(\,P_{i j}^{\phantom{\,}})\equiv(\,W_{i j}^{\phantom{\,}})^{\,-1}

W_{i j}\;=\;N\Bigg[-\frac{\partial^{2}\:\boldsymbol{\phi}(\:\mathbf{Y}_{N}\!\:;\!\:\pmb{\theta})}{\partial\,\theta_{i}\partial\,\theta_{j}}\Bigg]

（3）当样本容量 N{\rightarrow}\infty 时， \pmb{\hat{\theta}} 的数学期望是 \pmb{\theta}_{t r} ，故最大似然估计是渐近无偏估计。

（4）最大似然估计 \pmb{\hat{\theta}} 是渐近一致的。即当 N{\rightarrow}\infty 时，估计值\pmb{\hat{\theta}} 无限地靠近真值 \pmb{\theta}_{\iota r} 。

（5）最大似然估计 \pmb{\hat{\theta}} 是渐近最有效的。即对于任何一致估计量 \theta^{\prime} ,都有

\operatorname*{lim}_{N\rightarrow\infty}\,\frac{(\,\hat{\pmb{\theta}}_{N}\,-\,\pmb{\theta}_{\iota r}\,)^{2}}{(\,\pmb{\theta}_{N}^{\prime}\,-\,\pmb{\theta}_{\iota r}\,)^{2}}\leq1

可以证明,若存在方差最小的无偏估计(即最有效估计),则它必然是最大似然估计。

以上理论已为实践所证实，最大似然法是飞行器动力学系统辨识最有效、最实用的参数估计方法。

5.3.2 非线性动力学系统最大似然算法

动力学系统的非线运动方程组可写成下列通用形式

\left\{\begin{array}{l l}{\pmb{\mathfrak{x}}\,=\,f(\pmb{x}\,,\pmb{u}\,,\pmb{\theta}\,;\,t)\,+\,{\cal P}(\pmb{\theta}\,,t)\,\pmb{\eta}(\,t\,)}&{(\,t\,\in\,[0,T])}\\ {{\cal E}(\pmb{x}_{0})\,=\,\pmb{x}_{0}(\,\pmb{\theta}\,)}\\ {{\cal E}\,\{\,\vert\,\pmb{x}_{0}\,-\,\pmb{x}_{0}(\,\pmb{\theta}\,)\,\rbrack\,[\,(\pmb{x}_{0}\,-\,\pmb{x}_{0}(\,\pmb{\theta}\,)\,]^{\,T}\,\vert\,=\,\pmb{{\cal P}}_{0}(\,\pmb{\theta}\,)}\end{array}\right.

式中 \pmb{x}(\pmb{t})\longrightarrow\pmb{n} 维状态矢量;

{\pmb u}\left({\bf\Lambda}_{t}\right)\!-\!{\bf\Xi}-\!{\bf\Lambda}_{l} 维控制矢量；{\wp}{\mathrm{-}}\,\ldots 维待估计参数矢量；\scriptstyle{T\longrightarrow n\;\times\;q} 维过程噪声分布矩阵；
{\pmb{\eta}}(\,t\,)\!-\!\,\!\,-q 维随机过程噪声矢量。

描述观测矢量与状态矢量关系式的观测方程组取为离散形式{\bf y}(\,t_{i})\equiv{\bf y}_{i}\;=\;h\left[\,{\pmb{x}}(\,t_{i})\,,\pmb{u}(\,t_{i})\,,\pmb{\theta}\,;t_{i}\,\right]\,+\,{\pmb{\varepsilon}}(\,t_{i})\quad(\,i\;=\,1,2,\cdots,N)

式中 \pmb{\varepsilon}(t_{i}) 观测噪声；

\pmb{\eta}(t) 和 \pmb{\varepsilon}(t_{i}) -一-独立无关的高斯随机白色噪声且均值为零。

\left\{\begin{array}{l}{{E\big[\,\pmb{\eta}(\,t)\,\big]\,=\,0\,,E\big[\,\pmb{v}(\,t_{i}\,)\,\big]\,=\,0\,,E\big[\,\pmb{\eta}(\,t)\,\pmb{\varepsilon}^{\mathrm{T}}\big(\,t_{i}\,\big)\,\big]\,=\,0}}\\ {{E\big[\,\pmb{\eta}(\,t)\,\pmb{\eta}^{\mathrm{T}}(\,\tau\,)\,\big]\,=\,Q\partial\big(\,t\,-\,\tau\,\big)\,,E\big[\,\pmb{\varepsilon}\,\big(\,t_{j}\,\big)\,\pmb{\varepsilon}^{\mathrm{T}}\big(\,t_{k}\,\big)\,\big]\,=\,R\delta_{j k}}}\end{array}\right.

式中 \delta 和 \delta_{j k}\!-\!-\!\delta 函数。在参数估计中， \pmb{f} 和 \pmb{h} 的函数形式是已知的。

问题是在状态方程组（5-69)和观测方程组（5-70)的约束条件下求 \pmb{\hat{\theta}} ,使式(5-64)的 J 取极小值。为此,必须给出 \pmb{\nu}(\,i\,)\,,\pmb{B}(\,i\,) 的表达式，而 \pmb{\nu}(i) 和 \pmb{{\cal B}}(\pmb{i}) 是卡尔曼滤波的输出。应用广义卡尔曼

滤波于式(5-69)和式(5-70)得：

状态预测方程组：

\left\{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}\hat{\pmb{x}}\left(\textit{t}\mid\textit{t}_{i-1}\right)}{\mathrm{d}t}\,=\,\pmb{f}[\hat{\pmb{x}}\left(\textit{t}\mid\textit{t}_{i-1}\right),\pmb{u}\left(\textit{t}\right),\pmb{\theta}\};t\right]}&{\left(\textit{t}\in\left[\textit{t}_{i-1},\textit{t}_{i}\right]\right)}\\ {\displaystyle\pmb{x}(\textbf{0}\mid0)\,=\,\pmb{x}_{0}(\pmb{\theta})}&\end{array}\right.

状态校正方程组：

\hat{\pmb{x}}\left(\,i\,\mid\,i\,\right)\;=\;\hat{\pmb{x}}\left(\,i\,\mid\,i\,-1\,\right)\,+\,{\pmb{K}}\left(\,i\,\right)\pmb{\nu}\left(\,i\,\right)

式中

\pmb{\nu}(\,i\,)\,=\,\pmb{y}(\,i\,)\,-\,\pmb{h}\big[\,\hat{\pmb{x}}\,(\,i\,\mid\,i\,-\,1\,)\,,\pmb{u}\,(\,i\,)\,,\pmb{\theta}\,;t_{i}\,\big]

\pmb{K}(\mathbf{\chi}_{i})\;=\;\pmb{P}(\mathbf{\chi}_{i}\mid\mathbf{\chi}_{i}\;-\;1)\,\pmb{H}^{\mathrm{T}}\pmb{B}(\mathbf{\chi}_{i})^{-1}

H\,=\,{\frac{\partial h}{\partial x}}\,\bigg|_{\,x=\,\dot{x}\,(\,i\,|\,i-1)}

\pmb{B}\left(\mathbf{\Lambda}_{i}\right)\ =\ \pmb{H}\pmb{P}\left(\mathbf{\Lambda}_{i}\ \mid\mathbf{\Lambda}_{i}\ -\ 1\right)\pmb{H}^{\mathrm{T}}\ +\ \pmb{R}

协方差预测方程组：

\left\{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\pmb{P}(t\mid t_{i-1})\,=\,\pmb{F}(t)\pmb{P}(t\mid t_{i-1})+\,\pmb{P}(t\mid t_{i-1})\pmb{F}^{\operatorname{T}}(t)+\,\pmb{T}\pmb{Q}\pmb{F}^{\operatorname{T}}}\\ {\pmb{P}(0\mid0)\,=\,\pmb{P}_{0}(\pmb{\theta})\quad(t\in[t_{i-1},t_{i}])}\end{array}\right.

协方差校正方程组：

\pmb{P}(\mathfrak{i}\ \mid\ i\ )\:=\:\left(\pmb{I}\,-\,\pmb{K}(\,\mathfrak{i}\,)\,\pmb{H}\right)\pmb{P}(\,\mathfrak{i}\ \mid\,\mathfrak{i}\ -\ 1)

式中

{\pmb F}\,=\,\frac{\partial{\pmb f}}{\partial{\pmb x}}\,\bigg|_{{\pmb x}\,=\,\dot{\pmb x}\,(\,t\,|\,t_{i-1})}

式（5-64）、式(5-69）～式(5-80)给出了非线性动力学系统最大似然法的完备方程组。这是在非线性微分方程组 (\,5\,-\,72\,)\sim 式(5-80)的约束条件下求 \pmb{\hat{\theta}} ,使式(5-64)的准则函数 J 达到最小值的泛函极值问题。此方程组复杂，通常无法求得解析解，也无法直接数值积分，只能采用迭代求解算法。泛函极值的迭代求解法已有多种，如梯度法、共轭梯度法、最速下降法、麦夸特法、高斯法等等，实践证明牛顿-拉夫逊法对于动力学系统辨识是最有效的。

采用牛顿-拉夫逊迭代算法求 \hat{\pmb{\theta}} ,先给预估值 \pmb{\theta}_{k} 和状态初值，由式(5-72)、式(5-78)计算 \hat{\pmb{x}}\left(\,i\mid i\mathrm{~-~}1\,\right) 和 \boldsymbol{P}\left(\textit{i}|\textit{i}-1\right) ，由式(5-74)一式(5-77)计算 \pmb{v}\left(\textit{i}\right),\pmb{H}\left(\textit{i}\right),\pmb{B}\left(\textit{i}\right),\pmb{K}\left(\textit{i}\right) ,再由式（5-73）－式(5-79)计算 \hat{\pmb{x}}\left(\it\Delta i\mid\it\Delta i\right) 和 \pmb{P}(\textit{i}|\textit{i}) 。从 i=0 计算到 i=N ,将计算结果代人式(5-64),就可算出相应于 \pmb\theta_{k} 的似然准函数值 J_{k} 。当 J_{k} 不是极小值时，必须调整 \pmb\theta_{k} 使 J_{k+1} 达到极小值,其必要条件为

\frac{\partial J_{k+1}}{\partial\pmb\theta}\,=\,\frac{\partial J\left(\pmb\theta_{k}\,+\,\Delta\pmb\theta_{k}\right)}{\partial\pmb\theta}\,=

\frac{\partial J(\,\pmb{\theta}_{k}\,)}{\partial\pmb{\theta}}\,+\,\frac{\partial^{2}J(\,\pmb{\theta}_{k}\,)}{\partial\pmb{\theta}^{2}}\Delta\pmb{\theta}_{k}\,+\,\hat{\mathrm{0}}(\Delta\pmb{\theta}_{k}^{2}\,)\,=\,0

略去二阶小量， J_{k+1} 达到极值的必要条件成了选取 \Delta\pmb{\theta}_{k} 满足下式

\Delta\pmb{\theta}_{k}\,=-\,M^{-1}\,\frac{\partial J}{\partial\pmb{\theta}}

式中M=300，=1.2.. 称为信息矩阵。式（5-82）是个线性代数方程组，系数矩阵是 {\pmb\mathscr{p}}\times{\pmb\mathscr{p}} 阶。解出 \Delta\pmb{\theta}_{k} 后，再以 \theta_{k+1}= \pmb{\theta}_{k}+\Delta\pmb{\theta}_{k} 重复上述步骤,算出 J_{k+1} ，反复选代直到 J 收敛为止。最后 \pmb{\theta} 的收敛值即为所求 \hat{\pmb\theta}_{\ddot{\diamond}}

现在剩下的问题只是给出 \frac{\partial J}{\partial\theta_{k}} 和 \frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}} 的表达式。对式(5-64)、式(5-74)和式(5-77)求 \pmb{\theta} 偏导数，可得

\begin{array}{l}{\displaystyle\frac{\partial{\cal J}}{\partial\theta_{k}}=\,\sum_{i=1}^{N}\,\left\{2\nu^{\mathrm{T}}(i){\cal B}^{-1}(i)\,\frac{\partial\nu(i)}{\partial\theta_{k}}+\nu^{\mathrm{T}}(i)\,\frac{\partial{\cal B}^{-1}(i)}{\partial\theta_{k}}\pmb{\nu}(i)+\frac{1}{\mid{\cal B}(i)\mid}\frac{\partial\mid{\cal B}(i)\mid}{\partial\theta_{k}}\right\}=}\\ {\displaystyle\sum_{i=1}^{N}\,\left\{2\,\pmb{\nu}^{\mathrm{T}}(i\,){\cal B}^{-1}(i)\,\frac{\partial\,{\pmb{\nu}}(\,i\,)}{\partial\theta_{k}}-\,\pmb{\nu}^{\mathrm{T}}(\,i\,){\cal B}^{-1}(\,i\,)\,\frac{\partial{\cal B}(\,i\,)}{\partial\theta_{k}}{\cal B}^{-1}(\,i\,)\,\pmb{\nu}(\,i\,)\right.+}\\ {\displaystyle\left.\mathrm{tr}\!\left[{\cal B}^{-1}(i\,)\,\frac{\partial{\cal B}(\,i\,)}{\partial\theta_{k}}\right]\right\}\qquad(k\,=\,1,2,\cdots,p)\qquad(5\cdot83)\,,}\end{array}

式中

\frac{\partial\pmb{\nu}(\mathbf{\nabla}i\mathbf{\Gamma})}{\partial\theta_{k}}\,=-\,\pmb{H}\,\frac{\partial\hat{\pmb{x}}(\mathbf{\nabla}i\mathbf{\Gamma}\mid i\mathbf{\Gamma}-\mathbf{1})}{\partial\theta_{k}}\,-\,\frac{\partial\pmb{h}[\hat{\pmb{x}}(\mathbf{\nabla}i\mathbf{\Gamma}\mid i\mathbf{\Gamma}-\mathbf{1})\,,\pmb{u}(i\mathbf{\Gamma})\,,\pmb{\theta}\,;t_{i}]}{\partial\theta_{k}}

\frac{\partial\pmb{B}\left(\mathbf{\chi}_{i}\mathbf{\Lambda}_{i}\right)}{\partial\theta_{k}}\,=\,\frac{\partial\pmb{H}}{\partial\theta_{k}}\pmb{P}(\mathbf{\chi}_{i}\mid\mathbf{\chi}_{i}\mathbf{\Lambda}_{i}-1)\,\pmb{H}^{\mathrm{T}}+\,\pmb{H}\,\frac{\partial\pmb{P}\left(\mathbf{\chi}_{i}\mid\mathbf{\Lambda}_{i}-1\right)}{\partial\theta_{k}}\pmb{H}^{\mathrm{T}}\mathbf{\Lambda}+\pmb{\Lambda}_{i}^{\mathrm{T}}

H P(\textit{i}\mid\textit{i}-1)\:\frac{\partial H^{\mathrm{T}}}{\partial\theta_{k}}+\frac{\partial R}{\partial\theta_{k}}

协方差阵的偏导数由式(5-78)、式(5-79)对 \theta_{k} 求导而得，其预测与校正方程分别为：

预测方程组

\left\{\begin{array}{l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial P(t\mid t_{i-1})}{\partial\theta_{k}}\right)=\frac{\partial\overline{{F}}}{\partial\theta_{k}}P(t\mid t_{i-1})+\boldsymbol{F}\frac{\partial P(t\mid t_{i-1})}{\partial\theta_{k}}+\frac{\partial P(t\mid t_{i-1})}{\partial\theta_{k}}\boldsymbol{F}^{\mathrm{T}}+}\\ {\displaystyle\qquad\qquad\qquad\qquad\quad\;\boldsymbol{P}\big(\mid t_{i-1}\big)\,\frac{\partial\boldsymbol{F}^{\mathrm{T}}}{\partial\theta_{k}}+\frac{\partial\boldsymbol{T}}{\partial\theta_{k}}\boldsymbol{Q}\boldsymbol{F}^{\mathrm{T}}+\boldsymbol{T}\boldsymbol{Q}\,\frac{\partial\boldsymbol{T}^{\mathrm{T}}}{\partial\theta_{k}}}\\ {\displaystyle\frac{\partial P(0\mid0)}{\partial\theta_{k}}=\frac{\partial P_{0}(\theta)}{\partial\theta_{k}}}\end{array}\right.

校正方程组

\frac{\partial P(i\mid i)}{\partial\theta_{k}}=\left[I-K(i)H\right]\frac{\partial P(i\mid i-1)}{\partial\theta_{k}}-\frac{\partial K(i)}{\partial\theta_{k}}\pmb{H}\pmb{P}(i\mid i-1)-\frac{\partial P(i)}{\partial\theta_{k}}\pmb{H}\pmb{P}(i\mid i-1),

\pmb{K}(\textnormal{\em i})~\frac{\partial\pmb{H}}{\partial\theta_{k}}\pmb{P}(\textnormal{\em i}\mid\textnormal{\em i}-1)\quad(\textnormal{\em k}=1,2,\cdots,\textnormal{\em p})

式中

\frac{\partial\pmb{K}(\mathbf{\Sigma}i\mathbf{\Sigma})}{\partial\theta_{k}}\mathbf{\Sigma}=\frac{\partial\pmb{P}(\mathbf{\Sigma}i\mid\mathbf{\Sigma}i\mathbf{\Sigma}-1)}{\partial\theta_{k}}\pmb{H}^{\top}\pmb{B}^{-1}(\mathbf{\Sigma}i\mathbf{\Sigma})\,+\,\pmb{P}(\mathbf{\Sigma}i\mid\mathbf{\Sigma}i\mathbf{\Sigma}-1)\mathrm{~.~}

\frac{\partial\pmb{H}^{\mathrm{T}}}{\partial\theta_{k}}\pmb{B}^{-1}(\,i\,)\,-\,\pmb{K}(\,i\,)\,\frac{\partial\pmb{B}(\,i\,)}{\partial\theta_{k}}\pmb{B}^{-1}(\,i\,)

式(5-84)中的 \partial\hat{\pmb{x}}/\partial\theta_{k} 由状态参数灵敏度方程组积分，将式(5-72)、式(5-73)对 \theta_{k} 求导，求得状态参数灵敏度的预测与校正方程分别为：

状态参数灵敏度预测方程组

\left(\begin{array}{c}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial\hat{\pmb{x}}\left(\ t\mid t_{i-1}\right)}{\partial\theta_{k}}\right)=\,\frac{\partial\pmb{f}\big[\hat{\pmb{x}}\left(\ t\mid t_{i-1}\right),\pmb{u}\left(t\right),\pmb{\theta}\colon t\ \big]}{\partial\theta_{k}}\,+\,\right.

144

\left\{\begin{array}{l l}{\displaystyle\frac{\partial f[\,\hat{\pmb{x}}\,(\ t\ |\ \ t_{i-1})\,\pmb{u}\,(\ t)\,,\pmb{\theta}\,;t\,]}{\partial\pmb{x}}\,\frac{\partial\hat{\pmb{x}}\,(\ t\ |\ \ t_{i-1})}{\partial\theta_{k}}}\\ {\displaystyle\frac{\partial\hat{\pmb{x}}\,(\ 0\ |\ 0)}{\partial\theta_{k}}\,=\,\frac{\partial x_{0}(\,\pmb{\theta}\,)}{\partial\theta_{k}}}\end{array}\right.

状态参数灵敏度校正方程组

\frac{\partial\hat{\pmb{x}}(\textit{i}|\textit{i})}{\partial\theta_{k}}\,=\,\frac{\partial\hat{\pmb{x}}(\textit{i}|\textit{i}-1)}{\partial\theta_{k}}\,+\,\frac{\partial\pmb{K}(\textit{i})}{\partial\theta_{k}}\pmb{\nu}(\textit{i})\,+\,{\pmb{K}}(\textit{i})\,\frac{\partial\pmb{\nu}(\textit{i})}{\partial\theta_{k}}

(\,k\,=\,1\,,2\,,\cdots,p\,)

似然准则函数 {\pmb J} 的二阶导数由式(5-83)对 {\pmb\theta}_{l} 求导而得

\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}}=\sum_{i=1}^{N}\left\{2\,\frac{\partial\,\pmb{\nu}^{\mathrm{T}}(i)}{\partial\theta_{l}}B^{-1}\bigl(i\,\bigr)\,\frac{\partial\,\pmb{\nu}(i)}{\partial\theta_{k}}-2\,\pmb{\nu}^{\mathrm{T}}\bigl(i\,\bigr)\,B^{-1}\bigl(i\,\bigr)\,\frac{\partial\,\pmb{B}(i)}{\partial\theta_{l}}B^{-1}\bigl(i\,\bigr)\,\frac{\partial\,\pmb{\nu}(i)}{\partial\theta_{k}}-\frac{\partial\,\pmb{\nu}^{\mathrm{T}}(i)}{\partial\theta_{l}}B^{-1}\right\}\,.

\begin{array}{r l}&{\frac{1}{n(n-1)}\left[\begin{array}{l}{-\beta_{i j}\tilde{n}^{-1}}&{\beta_{i j}^{-1}(i)\widehat{\beta}_{i k}^{-1}-2\tilde{n}^{\top}(i)B^{\top}(i)\widehat{\beta}_{i j}^{-1}\widehat{\beta}_{i}^{-1}(i)\widehat{\beta}_{i k}^{-1}}\\ {2\nu^{1}(i)B^{-1}(i)\displaystyle\frac{\partial B(i)}{\partial\beta_{i k}}B^{-1}(i)\displaystyle\frac{\partial\tilde{n}^{\top}(i)}{\partial\beta_{i j}}-}\end{array}\right]}\\ &{\mathrm{re}\Big[B^{-1}(i)\displaystyle\frac{\partial B(i)}{\partial\beta_{i j}}B^{-1}(i)\displaystyle\frac{\partial B^{\top}(i)}{\partial\beta_{i k}}\Big]+2\widehat{\beta}_{i j}^{\top}\nabla(i)B^{-1}(i)\nu(i)-}\\ &{\mathrm{re}^{\top}(i)B^{-1}\frac{\partial^{2}B(i)}{\partial\beta_{i j}\partial\beta_{i j}}B^{-1}(i)\nu(i)+\mathrm{re}(B^{-1}(i)\displaystyle\frac{\partial^{2}B^{\top}(i)}{\partial\beta_{i j}\partial\beta_{i j}})\Big]\approx}\\ &{\displaystyle\sum_{i=1}^{n}\Big[\frac{\partial^{2}\Gamma(i)}{\partial\tilde{\beta}_{i j}}B^{-1}(i)\displaystyle\frac{\partial^{2}\Gamma(i)}{\partial\tilde{\beta}_{i j}}-2\nu^{\top}(i)B^{-1}(i)\displaystyle\frac{\partial\tilde{B}(i)}{\partial\tilde{\beta}_{i j}}B^{-1}(i)\displaystyle\frac{\partial^{2}\Gamma(i)}{\partial\tilde{\beta}_{i k}}-}\\ &{2\nu^{\top}(i)B^{-1}(i)\displaystyle\frac{\partial B(i)}{\partial\beta_{i k}}B^{-1}(i)\displaystyle\frac{\partial\nu(i)}{\partial\tilde{\beta}_{i j}}-}\\ &{\mathrm{re}\Big[B^{-1}(i)\displaystyle\frac{\partial B(i)}{\partial\tilde{\beta}_{i j}\partial\beta_{i k}}B^{-1}(i)\displaystyle\frac{\partial\tilde{B}(i)}{\partial\beta_{i j}}\Big]~(l,k=1,2,\cdots,p)}\end{array}

式(5-91)略去了新息及其方差的二阶导数。对于收敛解，二阶导数很快趋于零，可忽略之。整个迭代运算过程只用新息和方差的一阶导数，大大简化了计算工作量，称之为牛顿-拉夫逊算法。通常只需 3\!\sim\!5 次选代就收敛了。上面给出了非线性动力学系统参数估计的最大似然法全部计算公式和计算过程。

5.3.3 线性系统最大似然算法

当动力学系统作小扰动运动时，可以绕平衡状态展开，以扰动量为状态变量，求得描述动力学系统扰动运动的线性动力学方程组，其通式可写成

{\star\!\!\!\!\!\!\!\!\!\!}\;=\;{\cal F}(\,\theta\,,t\,)\,x\,+\,G\,(\,\theta\,,t\,)\,u\,+\,{\cal T}(\,\theta\,,t\,)\,\eta\;\;\;\;(\,t\,\in\,[0\,,T\,]\,)

\,\,y\,(\,t_{k}\,)\,=\,\,H\,(\,\pmb\theta\,,t_{k}\,)\,\pmb x\,(\,t_{k}\,)\,+\,\pmb D\,(\,\pmb\theta\,,t_{k}\,)\,\pmb u\,(\,t_{k}\,)\,+\,\pmb\nu\,(\,t_{k}\,)

(\,k\,=\,1\,,2\,,\cdots,N\,)

它是非线性系统的特殊情况,计算公式与上节完全相同，只是有些公式可以简化，现整理如下

状态预测方程组

\left\{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}\hat{\mathbf{x}}(t\mid t_{i-1})}{\mathrm{d}t}\,=\,\pmb{F}(\theta,t)\pmb{x}(t\mid t_{i-1})\,+\,\pmb{G}(\theta,t)\pmb{u}(t)(t\in[t_{i-1},t_{i}])}\\ {\hat{\mathbf{x}}(0\mid0)\,=\,\pmb{x}_{0}(\theta)}\end{array}\right.

状态校正方程组

{\hat{\pmb{x}}}\left({\begin{array}{c c}{i}\end{array}}{\mid}{\begin{array}{c c}{i}\end{array}}\right)\,=\,{\hat{\pmb{x}}}\left({\begin{array}{c c}{i}\end{array}}{\mid}{\begin{array}{c c}{i}\end{array}}-1\right)\,+\,{\pmb{K}}\left({\begin{array}{c c}{i}\end{array}}\right){\pmb{\nu}}\left({\begin{array}{c c}{i}\end{array}}\right)

协方差预测方程组

\left\{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}P(t\mid t_{i-1})\,=\,F(\pmb\theta,t)P(t\mid t_{i-1})+P(t\mid t_{i-1})F^{\mathrm{T}}(\pmb\theta,t)+I Q T^{\mathrm{T}}}\\ {\displaystyle P(\boldsymbol0\mid\boldsymbol0)\,=\,P_{0}(\pmb\theta)\quad(t\,\in\,[\,t_{i-1},t_{i}]\,)}\end{array}\right.

协方差校正方程

\pmb{P}(\mathfrak{i}\mid\mathfrak{i})\,=\,\left[\,\pmb{I}\,-\,\pmb{K}(\,\mathfrak{i}\,)\,\pmb{H}\,\right]\pmb{P}(\,\mathfrak{i}\,\mid\,\mathfrak{i}\,-\,1)

卡尔曼增益阵

\pmb{K}(\mathbf{\chi}_{i})\;=\;\pmb{P}(\mathbf{\chi}_{i}\mid\mathbf{\chi}_{i}\;-\;1)\,\pmb{H}^{\mathrm{T}}\pmb{B}^{-1}(\mathbf{\chi}_{i})

新息协方差阵

\pmb{B}\left(\mathbf{\chi}_{i}\right)\ =\ \pmb{H}\pmb{P}\left(\mathbf{\chi}_{i}\mid\mathbf{\chi}_{i}\ -1\right)\pmb{H}^{\mathrm{T}}\ +\ \pmb{R}

灵敏度预测方程组

\{\begin{array}{r l}{\displaystyle}&{{}\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial\mathbf{x}\left(t\mid t_{i-1}\right)}{\partial\theta_{k}}\right)=\frac{\partial F}{\partial\theta_{k}}\mathbf{x}\left(i\mid i-1\right)+F\,\frac{\partial\mathbf{x}\left(i\mid i-1\right)}{\partial\theta_{k}}+\frac{\partial G}{\partial\theta_{k}}\mathbf{u}}\end{array}}

\bigl\{\begin{array}{l l}{\,\frac{\partial\hat{\pmb x}\left(0\mid0\right)}{\partial\theta_{k}}\,=\,\frac{\partial\pmb x_{0}(\pmb\theta)}{\partial\theta_{k}}}&{\quad(\,t\,\in\,[\,t_{i-1}\,,t_{i}\,]\,)}\end{array}\bigr.

灵敏度校正方程组

\frac{\partial\hat{\pmb{x}}(\textit{i}\textit{i})}{\partial\theta_{k}}=\frac{\partial\hat{\pmb{x}}(\textit{i}\textit{i}-\mathbf{1})}{\partial\theta_{k}}+\frac{\partial\,{\pmb{K}}(\textit{i})}{\partial\theta_{k}}{\pmb{\nu}}(\textit{i})+\,{\pmb{K}}(\textit{i})\,\frac{\partial\,{\pmb{\nu}}(\textit{i})}{\partial\theta_{k}}

协方差灵敏度预测方程组

\left\{\begin{array}{l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial P\left(\textit{t}|\textit{t}_{i-1}\right)}{\partial\beta_{k}}\right)=\frac{\partial F}{\partial\theta_{k}}P(\textit{t}|\textit{t}_{i-1})+F\,\frac{\partial P\left(\textit{t}|\textit{t}_{i-1}\right)}{\partial\theta_{k}}+\frac{\partial P\left(\textit{t}|\textit{t}_{i-1}\right)}{\partial\theta_{k}}F^{\mathrm{T}}+}\\ {\quad\quad\quad\quad\quad\quad\quad\quad\quad P\left(\textit{t}|\textit{t}_{i-1}\right)\frac{\partial F^{\mathrm{T}}}{\partial\theta_{k}}+\frac{\partial T}{\partial\theta_{k}}Q F^{\mathrm{T}}+\,T Q\,\frac{\partial T^{\mathrm{T}}}{\partial\theta_{k}}}\\ {\displaystyle\frac{\partial P\left(\textit{0}|\textit{0}\right)}{\partial\theta_{k}}\,=\,\frac{\partial P_{0}\left(\theta\right)}{\partial\theta_{k}}\quad\quad\mathrm{(}\textit{t}\in\left[\ t_{i-1},t_{i}\right]\mathrm{)}}\end{array}\right.

协方差灵敏度校正方程组

\frac{\partial P(\textit{i}|\textit{i})}{\partial\theta_{k}}\,=\,\big(\,I\,-\,K(\mathit{i}\,)\,H\big)\,\frac{\partial P(\textit{i}|\textit{i}-1)}{\partial\theta_{k}}\,-\,\frac{\partial K(\mathit{i}\,)}{\partial\theta_{k}}\ .

H P(\textit{i}\mid\textit{i}-1)-K(\textit{i})\,\frac{\partial H}{\partial\theta_{k}}P(\textit{i}\mid\textit{i}-1)

卡尔曼增益灵敏度

\frac{\partial\pmb{K}(\mathbf{\eta}_{i})}{\partial\theta_{k}}\,=\frac{\partial\pmb{P}(\mathbf{\eta}_{i}\mid\mathbf{\eta}_{i}-1)}{\partial\theta_{k}}\pmb{H}^{\operatorname{T}}\pmb{B}^{-1}(\mathbf{\eta}_{i})\,+\,\pmb{P}(\mathbf{\eta}_{i}\mid\mathbf{\eta}_{i}-1)\mathrm{~.~}

\frac{\partial\pmb{H}^{\mathrm{T}}}{\partial\theta_{k}}\pmb{B}^{-1}(\,i\,)\,-\,\pmb{K}(\,i\,)\,\frac{\partial\pmb{B}(\,i\,)}{\partial\theta_{k}}\pmb{B}^{-1}(\,i\,)

新息灵敏度

\frac{\partial\pmb{\nu}(\,i\,)}{\partial\theta_{k}}\,=-\,\pmb{H}(\,\theta\,,t_{i}\,)\;\frac{\partial\hat{\pmb{x}}(\,i\,\mid\,i\,-1\,)}{\partial\theta_{k}}\,-\,\frac{\partial\pmb{H}(\,\theta\,,t_{i}\,)}{\partial\theta_{k}}\;.

\hat{\pmb{x}}(\,i\,\mid\,i\,-\,1\,)\,-\,\frac{\partial{\pmb{D}}(\,\pmb{\theta}\,,t_{i}\,)}{\partial{\pmb{\theta}}_{k}}\pmb{u}\,(\,t_{i}\,)

新息协方差阵灵敏度

\frac{\partial\pmb{B}\left(i\mathbf{\Lambda}\right)}{\partial\theta_{k}}\mathbf{\Lambda}=\frac{\partial\pmb{H}}{\partial\theta_{k}}\pmb{P}\left(i\mathbf{\Lambda}\mid i\mathbf{\Lambda}+1\right)\pmb{H}^{\mathrm{T}}+\pmb{H}\,\frac{\partial\pmb{P}\left(i\mathbf{\Lambda}\mid i\mathbf{\Lambda}-1\right)}{\partial\theta_{k}}\pmb{H}^{\mathrm{T}}\,+

H P(\textit{i}\mid\textit{i}-1)\:\frac{\partial H^{\mathrm{T}}}{\partial\theta_{k}}+\frac{\partial R}{\partial\theta_{k}}

准则函数一阶导数

\frac{\partial J}{\partial\theta_{k}}\;=\;\sum_{i\;=\;1}^{N}\,\bigg\{2\nu^{\mathrm{T}}(i)B^{-1}(i)\,\frac{\partial\nu(i)}{\partial\theta_{k}}\,-\,\nu^{\mathrm{T}}(i)B^{-1}(i)\,\frac{\partial B(i)}{\partial\theta_{k}}B^{-1}(i)\,\nu(i)\;+\;\Gamma(i)\,(\frac{\partial\nu(i)}{\partial\theta_{k}}B^{-1}(i))\,\frac{\partial^{2}\nu^{\mathrm{T}}(i)}{\partial\theta_{k}}B^{-1}(i)\bigg\}\,,

\mathrm{tr}\left[\,B^{\,\cdot\,1}(\,i\,)\;\frac{\partial B(\,i\,)}{\partial\theta_{k}}\,\right]\Bigg\}\;\;\;\;\;\;\;\;\;(\,k\;=\;1,2,\cdots,\rlap/p\,)

准则函数二阶导数

\begin{array}{c c}{{\displaystyle\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}}=\sum_{\iota=1}^{N}\left\{2\,\frac{\partial\,{\bf v}^{\intercal}(i)}{\partial\theta_{l}}B^{-1}(i)\,\frac{\partial\,{\bf v}(i)}{\partial\theta_{k}}\,-\right.}}\\ {{\displaystyle}}&{{\left.2\,{\pmb{\nu}}^{\intercal}(i)\,B^{-1}(i)\,\frac{\partial{\bf B}(i)}{\partial\theta_{l}}B^{-1}(i)\,\frac{\partial\,{\pmb{\nu}}(i)}{\partial\theta_{k}}\,-\right.}}\\ {{\displaystyle}}&{{\left.2\,{\pmb{\nu}}^{\intercal}(i)\,B^{-1}(i)\,\frac{\partial{\pmb{B}}(i)}{\partial\theta_{k}}B^{-1}(i)\,\frac{\partial\,{\pmb{\nu}}(i)}{\partial\theta_{l}}\,-\right.}}\\ {{\displaystyle}}&{{\left.\mathrm{~}}}\end{array}

{(\,l\,=\,1,2,\cdots,p\,;k\,=\,1,2,\cdots,p\,)}

待估参数矢量 \pmb{\theta} 的第 k 步的校正值 \Delta\pmb{\theta}^{(k)} 满足下列线性代数 方程组

\left(\frac{\partial^{2}J}{\partial\pmb{\theta}\partial\pmb{\theta}}\right)\Delta\pmb{\theta}^{(k)}\,=-\,\left(\frac{\partial J}{\partial\pmb{\theta}}\right)

式（5-94）～式（5-109)构成线性动力学系统最大似然辨识的全部算式。

以上给出的非线性系统和线性系统的最大似然辨识算法有普遍适用性。凡是状态方程可以用常微分方程描述的系统都可适用。更广泛地，对状态方程是常微分-积分方程组或代数方程组的系统也适用。对状态方程是偏微分方程组的分布参数系统，则需要先进行参数集中化处理，或采用差分法、有限元法，将偏微分方程组转化为常微分方程组或代数方程组，才可用上述算式。

5.3.4 修正最大似然准则

前面推导的最大似然法所取的似然函数是给定参数 \pmb{\theta} 条件下观测量 \mathbf{Y} 出现的条件概率 p(\mathbf{\Delta}Y\mid\theta) 。若将似然函数取为观测量\pmb{Y} 和待估计参数 \pmb{\theta} 出现的联合概率，则称为修正最大似然法。联合概率 {\pmb{\rho}}(\,{\bf{Y}}\,,{\pmb{\theta}}) 为

\phi\big(\,Y\,,\pmb\theta\,\big)\;=\;\rho\big(\,Y\;\mid\;\pmb\theta\,\big)\,_{\/\beta}\big(\,\pmb\theta\,\big)

修正最大似然估计是选取参数 \pmb{\hat{\theta}} ,使 \pmb{Y} 和 \pmb{\theta} 出现的联合概率达到最大值

\hat{\textbf{\textit{0}}}\mathrm{ARG}\operatorname*{max}_{\theta\in\theta}(\textbf{\textit{Y}},\theta)\,=\,\mathrm{ARG}\,\operatorname*{max}_{\theta\in\theta}(\textbf{\textit{Y}}|\textbf{\em{\theta}}\theta)\,\phi(\textbf{\theta})

给定观测系统 \pmb{Y}_{N} ，类似5.3.1节的假定和公式推导，可得\phi(\,\mathbf{Y}_{N}\,|\,\pmb{\theta}\,) 的表达式

\begin{array}{l}{{\displaystyle=\prod_{i=1}^{N}\hat{p}\big({\bf\mathfrak{y}}_{i}\mid{\bf\mathfrak{Y}}_{i-1},\pmb{\theta}\big)\~=}}\\ {{\displaystyle\frac{1}{(2\uppi)^{N m/2}\prod_{i=1}^{N}\mid B\big(i\b{\big)}\mid^{1/2}}\mathrm{exp}\Bigg\{-\displaystyle\frac{1}{2}\sum_{i=1}^{N}\big[{\bf\mathfrak{y}}_{i}-\pmb{\Bigg.}}}\\ {{\displaystyle\hat{\pmb{\mathfrak{y}}}\big(i\mid i-1\big)\big]^{\top}{\pmb{\mathfrak{B}}}^{-1}\big(i\big)\big[{\bf\mathfrak{y}}_{i}-\hat{\bf{y}}\big(i\mid i-1\big)\big]\Bigg\}}}\end{array}

设待估计参数 \pmb\theta 有先验信息，其概率分布也是正态分布，均值 E(\pmb\theta)=\pmb\theta_{0} ，方差 \pmb{P}_{\theta}(0)=E(\pmb{\theta}-\pmb{\theta}_{0})(\pmb{\theta}-\pmb{\theta}_{0})^{\mathrm{T}} ，则 p(\pmb\theta) 的表达式为

\begin{array}{l}{\displaystyle\pmb{\phi}\big(\pmb{\theta}\big)\,=\frac{1}{(2\uppi)^{\,p/2}\,\mid\,\pmb{P}_{\theta}(0)\,\mid^{\,1/2}}\,\cdot}\\ {\displaystyle\exp\[-\;\frac{1}{2}(\pmb{\theta}-\pmb{\theta}_{0})^{\mathrm{T}}\pmb{P}_{\theta}^{-1}(0)(\pmb{\theta}-\pmb{\theta}_{0})]}\end{array}

将式(5-112)、式(5-113)代入式(5-110)得 p(\boldsymbol{Y},\theta)

\rho(\,\mathbf{Y}\,,\theta)={\frac{1}{(2\pi)^{(N m+p)/2}\prod_{i=1}^{N}\;\mid\;B(i)\mid^{1/2}\mid P_{\theta}(0)\mid^{1/2}}}\mathrm{exp}\Bigg\{-{\frac{1}{2}}\sum_{i=1}^{N}\,\lbrack\,\mathbf{y}_{i}\;-\;{\frac{1}{2}}\sum_{i=1}^{N}\,\mathbf{y}_{i}\;-\;{\frac{1}{2}}\sum_{i=1}^{N}\,\mathbf{y}_{i}\;-\;{\frac{1}{2}}\sum_{i=1}^{N}\,\mathbf{y}_{i}\;-\;{\frac{1}{2}}\sum_{i=1}^{N}\,\mathbf{y}_{i}\;-\;\mathbf{y}_{i}\;{\frac{1}{2}}\sum_{i=1}^{N}\,\mathbf{y}_{i}\Bigg\}\,.

\begin{array}{l}{\hat{\mathbf{y}}\!\left(i\mathbf{\Sigma}\mid i\mathbf{\Sigma}-\mathbf{1}\right)\rceil^{\mathrm{T}}\!\!B^{-1}\!(i\mathbf{\Sigma})\left[\mathbf{y}_{i}\mathbf{\Sigma}-\hat{\mathbf{y}}\!\left(i\mathbf{\Sigma}\mid i\mathbf{\Sigma}-\mathbf{1}\right)\right]\mathbf{\Sigma}-}\\ {\mathbf{\Sigma}\displaystyle\frac{1}{2}(\mathbf{\Sigma}\!\left(\mathbf{\Sigma}\!\mathbf{\delta}-\mathbf{\delta}\mathbf{\theta}_{0}\right)^{\mathrm{T}}\!\!P_{\theta}^{-1}(0)(\mathbf{\Sigma}\!\left(\theta\mathbf{\Sigma}-\mathbf{\delta}\mathbf{\theta}_{0}\right)\right\}}\end{array}

参数的修正最大似然估计变为

\hat{\pmb{\theta}}\;=\mathrm{ARG}\operatorname*{max}_{\pmb{\theta}\in\pmb{\theta}}\bigg\{-\;\frac{1}{2}\sum_{i=1}^{N}\left[\pmb{\nu}^{\mathrm{T}}(\,i\,)\pmb{B}^{-1}(\,i\,)\,\pmb{\nu}(\,i\,)\,+\,\ln\;\mid\,\pmb{B}(\,i\,)\,\mid\,\right]

-\;\frac{1}{2}(\,\pmb{\theta}\;-\;\pmb{\theta}_{0}\,)^{\mathrm{T}}\pmb{P}_{\theta}^{-1}(\,0\,)(\,\pmb{\theta}\;-\;\pmb{\theta}_{0}\,)\;\Bigg\}

故参数的最大似然估计就是寻求参数 \hat{\boldsymbol{\theta}} ，使下列准则函数达极小值

J\,=\,\sum_{i\,=\,1}^{N}\,\{\,\pmb{\nu}^{\mathrm{T}}(\,i\,)\,\pmb{B}^{-1}(\,i\,)\,\pmb{\nu}(\,i\,)\,+\,\ln\mid\,\pmb{B}(\,i\,)\,\mid\,\nmid\,+

(\,\pmb\theta\,-\,\pmb\theta_{0}\,)^{\textup T}{\pmb P}_{\,\theta}^{\textup{-}1}(\,\pmb0\,)\,(\,\pmb\theta\,-\,\pmb\theta_{0}\,)

比较式（5-116)和式（5-64）可见,修正最大似然估计的要点在于引进参数 \pmb{\theta} 的先验知识。若没有先验知识， \pmb{P_{\theta}} (0)很大,${P}_{\theta}^{\mathrm{-}1}(0)$ 趋于零，修正最大似然法就成了最大似然法。若 \pmb{\theta} 的先验知识比较可靠， \pmb{P}_{\theta}(\mathbf{0}) 较小，则后面一项就起作用。对于测量误差很大的试验，其数据的 \pmb{{\cal B}}(\mathfrak{i}) 很大，则前面-项的作用减弱，辨识出的 \pmb{\hat{\theta}} 将靠近于 {\pmb\theta}_{0}

5.3.5 输出误差法

飞行器的飞行试验常选在晴朗天气，气动参数辨识常选取被动飞行段，这时系统的过程噪声很小，可忽略不计，即 \pmb{\eta}\left(\textbf{\em t}\right)\equiv\mathbf{0} ?$\mathbf{\Delta}P(0)!\equiv!0$ 。由式（5-78)可知齐次方程组的初值为零，其解也为零，故 \pmb{P}(\,i\mid i-1)\!\equiv\!0\,,\pmb{P}(\,i\mid i\,)\!\equiv\!0. 。由式（5-75)知卡尔曼增益 \mathbf{{K}\!\equiv\!\boldsymbol{0}}_{\circ} 新息表达式（5-74）成了输出误差

\pmb{\nu}(\,i\,)\:=\:\pmb{y}(\,i\,)\,-\,\pmb{h}\left[\pmb{x}\left(\,i\,\right),\pmb{u}\left(\,i\,\right),\pmb{\theta}\,;t_{i}\,\right]

新息协方差阵表达式（5-77）中， \pmb{{\cal B}}\left(\mathrm{\it~i~}\right)=\pmb{{\cal R}} ，似然准则函数式(5-64)变为

J\;=\;\sum_{\;i\;=\;1}^{N}\left[\;\pmb{\nu}^{\mathrm{T}}({\;i\;})\pmb{R}^{\;-1}\pmb{\nu}({\;i\;})\;+\;\ln\;|\;\pmb{R}\;\mid\;\right]

当测量噪声的统计特性已知,式(5-118)就相当于以协方差矩阵之逆作为权系数的输出误差法，也相当于以 {\pmb R}^{\mathrm{~-~}1} 为权的加权最小二乘法。

当测量噪声的统计特性未知时,常取 J 对 \pmb R 的导数为零，求R 的最佳估计，得

\hat{\pmb R}\;=\;\frac{1}{N}\sum_{i\;=\;1}^{N}{\pmb\nu}({\bf\chi}_{i}\;)\,{\pmb\nu}^{\mathrm{T}}({\bf\chi}_{i}\;)

采用上一次迭代的残差由式(5-119)求出 \hat{\pmb R}^{\mathrm{~-~}1} 作为本次选代的权矩阵,利用式(5-82)进行反复迭代,直到收敛,求得 \pmb\theta 的最优估计。在多数动力学系统试验过程中，过程噪声比较小，可以忽略。因此采用式(5-119)的 \pmb{R} 矩阵进行最大似然估计是最为普遍使用的辨识方法,也是最为实用、有效的方法。

5.3.6方程误差法

当飞行器的飞行试验可以直接测量状态的左端项时，状态方程就成了观测方程。这时对数似然函数就是 \pmb{x} 的测量值 x_{m} 与状态方程右端 f(\,x\,,u\,,\theta\,;t\,) 之差的平方和

J\,=\,\sum_{i\,=\,1}^{N}\,[\,{\pmb x}_{m}\,-\,f(\,{\pmb x}\,,{\pmb u}\,,{\pmb\theta}\,;t\,)\,]^{\mathrm{\tiny~T~}}\,.

{\pmb R}^{\,-\,1}\left[\,{\pmb x}_{m}\,-\,{\pmb f}(\,{\pmb x}\,,{\pmb u}\,,{\pmb\theta}\,;t\,)\,\right]

这样最大似然法就化成方程误差法，而权系数矩阵 {\pmb W}= {\pmb R}^{\mathrm{~-~}1} ，误差协方差矩 \pmb{R} 取为

J\,=\frac{1}{N}\Biggl\{\sum_{i\,=\,1}^{N}\left[\,{\pmb x}_{m}\left(\,i\,\right)\,-\,{\pmb f}\!\left(\,{\pmb x}\,,{\pmb u}\,,{\pmb\theta}\,;t\,\right)\,\right]\,\cdot\,\right\}}\\ {\left[\,\left[\,{\pmb x}_{m}\left(\,i\,\right)\,-\,{\pmb f}\!\left(\,{\pmb x}\,,{\pmb u}\,,{\pmb\theta}\,;t\,\right)\,\right]^{\mathrm{T}}\,}\end{array}

当飞行器动力学系统是线性系统时，方程误差法不必进行迭代计算，直接求解线性代数方程组可得待辨识参数。

线性动力学系统的状态方程可表达为

\pmb{\mathfrak{x}}\ =\ \pmb{F}(\pmb{\theta})\,\pmb{x}\ +\ \pmb{G}\,(\,\pmb{\theta}\,)\,\pmb{u}

式中 x\!-\!\!-n 维矢量；

u\!-\!-\!l 维矢量；
F{\longrightarrow}\,n\times n 维矩阵；
\scriptstyle{G\longrightarrow n\;\times\;l} 维矩阵。

设F、G矩阵元素是待辨识参数，定义下列待辨识参数矩阵 \Theta 和增广状态矢量 \pmb{x}_{a}

\Theta\;=\;\left[\begin{array}{c}{{F}}\\ {{\ldots\ldots}}\\ {{G}}\end{array}\right]\qquad x_{a}\;=\;\left[\begin{array}{c}{{x}}\\ {{\ldots\ldots}}\\ {{\ldots}}\\ {{u}}\end{array}\right]

式中 \Theta\!\!\!\!\!\cdot\!\!\!\!\!\!\!-(\,n+l\,)\times n 维矩阵；

x。-——-(n+ I)维矢量。

式(5-122)化为

{\pmb x}\;=\;{\pmb\otimes}^{\mathbb{T}}{\pmb x}_{a}

则式（5-120)可写成

\begin{array}{l}{\displaystyle{J\,=\,\sum_{i\,=\,1}^{N}\,[\,{\pmb x}_{m}\,(\,i\,)\,-\,{\pmb\Theta}^{\mathrm{T}}\:\cdot}}\\ {\displaystyle{\pmb x}_{a}(\,i\,)\,]^{\mathrm{T}}{\pmb R}^{-1}[\,{\pmb x}_{m}(\,i\,)\,-\,{\pmb\Theta}^{\mathrm{T}}{\pmb x}_{a}(\,i\,)\,]}}\end{array}

\pmb{\theta} 的最优估计 \pmb{\theta} 的必要条件为

\frac{\partial J}{\partial\pmb{\Theta}}\,=\,-\,\sum_{i\,=\,1}^{N}\pmb{x}_{a}\,(\,\pmb{x}_{m}\,-\,\pmb{\Theta}^{\mathrm{T}}\pmb{x}_{a}\,)^{\mathrm{T}}\pmb{R}^{\,-1}\,=\,\pmb{0}

式中， \frac{\partial J}{\partial\boldsymbol{\Theta}} (\,n+l\,)\times n 维矩阵。故式(5-126)是关于待辨识参数Fi、G;(i,j=1,2,…,n;k=1,2,·.,l)的(n+ l)×n 个线性代数方程,F;、G;是矩阵F、G的元素。由式(5-126)有

\sum_{i\,=\,1}^{N}\pmb{x}_{a}\pmb{x}_{a}^{\mathrm{T}}\pmb{\Theta}\pmb{R}^{\mathrm{-1}}\,=\,\sum_{i\,=\,1}^{N}\pmb{x}_{a}\pmb{x}_{\,m}^{\mathrm{T}}\pmb{R}^{\mathrm{-1}}

利用解线性代数方程的标准程序,可由式(5-127)解出待辨识参数 F_{i j}\,,G_{k j}\,,

飞行试验时，动压、质量、惯量是时变的，飞行器的动力学方程

常可简化为下列形式

\star\;=\;F(\,\pmb\theta\,)\,{\cal A}\left(\,t\,\right)x\left(\,t\,\right)\,+\;{\cal G}\left(\,\pmb\theta\,\right){\cal B}\left(\,t\,\right)u\left(\,t\,\right)

式中 \textbf{\em A(}t\textbf{)},\mathbf{\boldsymbol{B}(}t\textbf{)} 分别为 n\times n 维和 l\times l 维矩阵。

{\pmb x}_{a}\left(\,i\,\right)\;=\;\left[\begin{array}{c}{{{\bf A}\left(\,i\,\right){\pmb x}\left(\,i\,\right)}}\\ {{{\pmb B}\left(\,i\,\right){\pmb u}\left(\,i\,\right)}}\end{array}\right]\;

仍可用式(5-127)解出待辨识参数 F_{i j}\setminus G_{k j} 。

5.3.7 最大似然近似算法

计人过程噪声和观测噪声的最大似然法的计算很复杂，方程中 f,h\,,R\,,\mathcal{Q} 都与 \pmb{\theta} 有关，每次送代都要重新计算，而且协方差矩阵计算难收敛。故在实用中常作不同程度简化。下面介绍常用简化算法。

1. \pmb{B}\setminus\pmb{K} 矩阵简化为常值矩阵

设 \pmb{B} 和 \pmb{K} 为常值待辨识矩阵。将似然准则函数 J 表达式 (5-64)对 \pmb{B} 求极值,得 \pmb{B} 的最优估计 \pmb{\hat{B}}

\hat{B}\,=\,\frac{1}{N}\sum_{\substack{i\,=\,1}}^{N}\,\boldsymbol{\wp}(\,i\,)\,\boldsymbol{\nu}^{\mathrm{T}}(\,i\,)

将增益矩阵元素 K_{i j} 作为未知参数 \pmb{\theta} 的部分元素，仍用式(5-82)进行迭代求解。因 \pmb{B} 和 \pmb{K} 是常数，于是

\frac{\partial J}{\partial\pmb{\theta}_{k}}\;=\;\sum_{i\,=\,1}^{N}\,\left\{2\,\pmb{\nu}^{\sf T}\big(\,i\,\big)\,\pmb{B}^{-1}\,\frac{\partial\,\pmb{\nu}\big(\,i\,\big)}{\partial\pmb{\theta}_{k}}\,\right\}\quad(\,k\;=\,1,2,\cdots,\,\rho\,)

\frac{\partial^{2}J}{\partial\pmb{\theta_{k}}\partial\pmb{\theta_{l}}}\;=\;\sum_{i=1}^{N}\left\{2\;\frac{\partial\,\pmb{\nu}^{\mathrm{T}}(\mathbf{\Phi}_{i}\,)}{\partial\pmb{\theta_{l}}}\pmb{B}^{-1}\;\frac{\partial\,\pmb{\nu}(\mathbf{\Phi}_{i}\,)}{\partial\pmb{\theta_{k}}}\right\}\quad(\,l\,,k\;=\,1,2,\cdots,p\,)

式(5-129）和式(5-130)表明迭代求解 \pmb\theta 时，只需新息 v(i) 和新息灵敏度 \frac{\partial\,\pmb{\nu}(\,i\,)}{\partial\pmb{\theta}} ,它们可以由式(5-72)、,式(5-74),式(5-84),式(5-89)和式(5-90)求出,其中式(5-90)的 满足下式

式中 \pmb{I_{m}} 一—除 \left(\,l\,,\,m\,\right) 位置的元素为1 之外其余元素全为零的矩阵。

此法显然大大简化了计算，但是求出的 {\pmb{B}}\setminus{\pmb{K}} 与 \pmb{T},\pmb{Q} 和 \pmb R 不可能一致。当已知 \pmb{T}\times\pmb{R} 矩阵时，若采用此法会导出矛盾的结果。另-一个问题是随着状态方程和观测方程的增多， \pmb{K} 的元素迅速增多，可能导致待估计参数过多的现象。为此，可以根据系统的特性，令 \pmb{K} 矩阵中的某些元素为零，而仅对其中一小部分元素进行估计。

2）稳态线性系统的近似算法

常系数线性动力学系统的过程噪声和测量噪声的统计特性变化不大时，可假定系统在运行一段时间后趋于稳态状态，其卡尔曼滤波器的增益 \pmb{K} 、新息协方差矩阵 \pmb{B} 和状态协方差矩阵 \pmb{P}(\textit{i}|\textit{i}) P(\textit{i}|\textit{i}-1) 都是常数，从而进一步简化最大似然算法。由式(5-75)\sim 式（5-79)可得

\frac{\mathrm{d}P(\textit{t i}\textit{t}_{i-1})}{\mathrm{d}t}\,=\,F(\textit{t})P(\textit{t}\mid\textit{t}_{i-1})\,+

\pmb{P}(\pmb{t}\mid t_{i-1})\pmb{F}^{\mathrm{T}}(\pmb{t})\,+\,I Q T^{\mathrm{T}}

P(\textit{i}|\textit{i})\;=\;\left(\textit{\textbf{I}}\!-\:\kappa H\right)P(\textit{i}|\textit{i}-1)

\pmb{K}\;=\;P\big(\,i\;\mid\;i\;-\;1\,\big)\,{\pmb{H}}^{\mathrm{T}}{\pmb{B}}^{-1}

\pmb{B}\;=\;\pmb{H}\pmb{P}\big(\textit{i}\;|\;\textit{i}-1\big)\,\pmb{H}^{\mathrm{T}}+\pmb{R}

积分式(5-132),将 \boldsymbol{P}\left(\textit{i}|\textit{i}-1\right) 记为 \pmb{P} ，由于稳态假定， \pmb{P}(i) \begin{array}{r}{i\mathbf{\Pi}_{i}\left(\mathbf{\delta}_{i}-\mathbf{1}\mid i-\mathbf{1}\right),P\left(\mathbf{\delta}_{i}\mid i-\mathbf{1}\right)=P\left(\mathbf{\delta}_{i}-\mathbf{1}\mid i-\mathbf{2}\right)}\end{array} ，故有

{\pmb{{\cal P}}}\;=\;\pmb{{\cal P}}{\pmb{{\cal P}}}\left(\,i\;-\;1\;\mid\;i\;-\;1\,\right)\pmb{{\cal P}}^{\mathrm{T}}\;+\;{\pmb{{\cal Q}}}^{\prime}\;=

\pmb{\Phi}(\pmb{I}\mathrm{~-~}\pmb{K}\pmb{H})\pmb{P}\pmb{\Phi}^{\mathrm{T}}+\pmb{Q}^{\prime}

式中

\textbf{Q}^{\prime}\,=\,\int_{t_{i-1}}^{t_{i}}\mathbf{e}^{F(\,t_{i-1}\,-\,\tau)}I Q\:\!\!\!\!\!\!\!\!\!\!\!\mathbf{f}^{\intercal}\mathbf{e}^{F^{\intercal}(\,t_{i-1}\,-\,\tau)}\mathrm{d}\tau

由式(5-136)解算 \pmb{P} 比较困难,可将 \pmb{\phi} 展开作线性近似，令\pmb{Q}^{\prime}=\pmb{\mathcal{P}}\pmb{Q}^{\prime\prime}\pmb{\mathcal{P}}^{\mathrm{T}} ,则由式(5-136)有

\pmb{Q}^{\prime}=\int_{t_{i-1}}^{t_{i}}\mathbf{e}^{F(t_{i-1}-\tau)}\pmb{I}\pmb{Q}\pmb{r}^{\mathrm{T}}\mathbf{e}^{F^{\mathrm{T}}(t_{i-1}-\tau)}\mathbf{d}\tau

式(5-136)简化为

P\,=\,\Phi\big[\,(\,I\,-\,K H)\,P\,+\,Q^{\prime}\,\big]\,\Phi^{\mathrm{T}}

式(5-138)左乘 \pmb{\varPhi}^{-1} ,并右乘 (\,\pmb{\Phi}^{\intercal})^{\intercal}\,^{1} ，展开 \pmb{\mathscr{P}}^{-1}=\mathbf{e}^{-\,\pmb{F}\Delta t}= I-F\Delta t ，则得

\pmb{\phi}^{-1}\pmb{P}(\pmb{\Phi}^{\mathrm{T}})^{-1}\,=\,\pmb{P}\,-\,\pmb{K}\pmb{H}\pmb{P}\,+\,\pmb{Q}^{\prime}\,=

\pmb{P}\textnormal{-}P H^{\mathrm{T}}\pmb{B}^{-1}H P\textnormal{+}Q^{\prime\prime}

由于

\begin{array}{r}{\begin{array}{c}{\pmb{\phi}^{-1}\pmb{P}(\pmb{\phi}^{\mathrm{T}})^{-1}=(\pmb{I}-\pmb{F}\Delta t)\pmb{P}(\pmb{I}-\pmb{F}^{\mathrm{T}}\Delta t)=}\\ {\pmb{P}\rightarrow\pmb{F}\Delta t\pmb{P}\rightarrow\pmb{P}\pmb{F}^{\mathrm{T}}\Delta t}\end{array}}\end{array}

故

{\pmb F}{\pmb F}+{\pmb P}{\pmb F}^{\mathrm{T}}\,-\,{\pmb P}{\pmb H}^{\mathrm{T}}({\pmb B}\Delta t\,)^{-1}{\pmb H}{\pmb P}\,+\,\frac{{\pmb Q}^{\prime}}{\Delta t}\,=\,0

式(5-139)是连续时间黎卡堤方程形式，有成熟的算法（如Potter算法)求解。计算表明作此线性近似对于 \pmb{\theta} 的估计值没有明显误差。

由式（5-139)求得 \pmb{P} 之后，可由式（5-133）～式（5-135)分别求出 B\,,K\,,P(\,i\mid i\,) 。由式(5-136)和式(5-133)对 \theta_{k} 求导，并加以整理，可得协方差矩阵灵敏度方程

\begin{array}{r l}{\displaystyle=\Phi\big(I-K H\big)\,\frac{\partial P}{\partial\theta_{k}}\big[\,\pmb{\Phi}(I-K H)\,\big]^{\mathrm{T}}\,+}&{{}}\\ {\displaystyle\frac{\partial\pmb{\Phi}}{\partial\theta_{k}}\big(I-K H\big)P\pmb{\Phi}^{\mathrm{T}}+\,\pmb{\Phi}(I-K H)\,\pmb{P}\,\frac{\partial\pmb{\Phi}^{\mathrm{T}}}{\partial\theta_{k}}\,-}&{{}}\\ {\displaystyle\pmb{\Phi}K\,\frac{\partial H}{\partial\theta_{k}}P\pmb{\Phi}^{\mathrm{T}}+\,\frac{\partial Q^{\prime}}{\partial\theta_{k}}\,+\,\pmb{\Phi}P\bigg[-\,\frac{\partial H^{\mathrm{T}}}{\partial\theta_{k}}\pmb{B}^{-1}H\,+}&{{}}\end{array}

H^{\mathrm{T}}B^{-1}\bigg(\frac{\partial H}{\partial\theta_{k}}P H^{\mathrm{T}}\,+\,H P\;\frac{\partial H^{\mathrm{T}}}{\partial\theta_{k}}\,+\,\frac{\partial R}{\partial\theta_{k}}\bigg)B^{-1}H\bigg]P\Phi^{\mathrm{T}}

(5 -140)

式(5-140)是 的线性方程,很容易求解。由式(5-85)可求,，不需积分。虽然状态灵敏度方程仍需积分求解，但计算量已大大减少。由式(5-84)求 后,可以利用式(5-92)、式(5-83)和式（5-91)进行迭代计算，求得 \pmb{\theta} 的最大似然估计。

5.3.8 最大似然递推算法

前面讨论了最大似然基本原理、似然准则、牛顿-拉夫逊迭代算法和各种简化近似算法。选代算法是一种事后处理方法，将试验数据分组，成组地进行参数辨识。本节给出最大似然的递推近似算法，递推算法是逐点进行数据处理，观测数据每采样一次，就计算一次参数估计值，随时用新观测的数据信息来修正待估参数，不断提高参数估计准度。

系统的状态方程组和观测方程组仍然用式（5-15）和式 (5- 16）。为了导出递推型算式，将最大似然准则函数 J\left(\,k\,\right) 写成前面k\,^{\mathrm{~-~}1} 个点的似然函数 J\left(k-1\right) 和第 \pmb{k} 点新息 \nu(k) 的函数。

\begin{array}{r l}{J\left(\,k\,\right)\,=J\left(\,k\,-\,1\right)\,+\,}&{{}}\\ {\pmb{\nu}^{\mathrm{{T}}}\!\left(\,k\,\right)\pmb{B}^{-1}\!\left(\,k\,\right)\pmb{\nu}\!\left(\,k\,\right)\,+\,\ln\mid\,\pmb{B}\!\left(\,k\,\right)\,\mid}&{{}}\end{array}

设前 k-1 个数据点所求得的 \pmb\theta 的最大似然估计为 \hat{\pmb\theta}(\pmb\ k-1) 将 J\left(\,k\,^{\mathrm{~-~}}\!1\,\right),B\left(\,k\,\right),\nu\left(\,k\,\right) 绕 \hat{\pmb{\theta}}(\pmb{k}-\mathbf{1}) 作泰勒级数展开，考虑极值必要条件是一阶导数为零，故 J(k) 可表示为

\begin{array}{r l}&{J(k\,-\,1)\mid_{\beta(k-1)}+\mid\pmb\theta-\pmb\theta(k\,-\,1)\mid^{\prime}\pmb P_{\theta}^{-1}(k\,-\,1)\,\times}\\ &{\,\,\,\,[\pmb\theta-\pmb\theta(k\,-\,1)]\,+\,\pmb{\nu}^{\mathrm{T}}(k\,)\pmb B^{-1}(k\,)\,\pmb\nu(k\,)\,+\,\ln\,\mid\,\pmb B(k)\,\mid=}\\ &{\Delta\pmb\theta^{\mathrm{T}}P_{\theta}^{-1}(k\,-\,1)\Delta\pmb\theta+\Delta\pmb\theta^{\mathrm{T}}\frac{\partial\pmb\nu}{\partial\pmb\theta}B^{-1}\,\frac{\partial\,\pmb\nu^{\mathrm{T}}}{\partial\pmb\theta}\Delta\pmb\theta\,+}\end{array}

\pmb{\nu}^{\mathrm{T}}\,\frac{\partial\pmb{B}^{-\mathrm{T}}}{\partial\pmb{\theta}}\Delta\pmb{\theta}\pmb{\nu}\,+\,\pmb{\nu}^{\mathrm{T}}\pmb{B}^{-1}\,\pmb{\nu}\,+\,2\,\pmb{\nu}^{\mathrm{T}}\pmb{B}^{-1}\,\frac{\partial\pmb{\nu}^{\mathrm{T}}}{\partial\pmb{\theta}}\Delta\pmb{\theta}\,+

2\,\pmb{\nu}^{\mathrm{T}}\,\frac{\partial\pmb{B}^{\mathrm{~-~}\mathrm{T}}}{\partial\pmb{\theta}}\Delta\pmb{\theta}\,\frac{\partial\,\pmb{\nu}^{\mathrm{T}}}{\partial\pmb{\theta}}\Delta\pmb{\theta}\,+\,J\left(\,k\,-\,1\right)\,+\,\ln\,\mid\,\pmb{B}\left(\,k\,\right)\,\mid\,+

\frac{1}{\mid\mathbf{\pmb{\mathit{B}}}(\mathit{\pmb{\mathit{k}}})\mid}\left(\frac{\partial\mid\mathbf{\pmb{\mathit{B}}}(\mathit{\pmb{\mathit{k}}})\mid}{\partial\pmb{\theta}}\right)^{\sf T}\Delta\pmb{\theta}+\mathit{O}(\Delta\pmb{\theta}^{3})

式中 \mathbf{\nabla}_{\theta}^{-\mathrm{~1~\!~\!~\!~\!~\!~}}-J 对 \pmb{\theta} 的二阶导数矩阵;v-——新息；

\pmb{B} 新息协方差矩阵；

O(\Delta\theta^{3}) —与 \Delta\pmb{\theta}^{3} 同数量级的量。

忽略协方差矩阵 \pmb{B} 对 \pmb\theta 变化的影响，上式可以配成下列二次型

\begin{array}{c}{{J(k)\,=\,(\Delta\pmb{\theta}\,-\,\pmb{A}\,)^{\top}\bigg[\,{\pmb{P}}_{\pmb{\theta}}^{-1}(\,k\,-\,1)\,+\,\displaystyle\frac{\partial\pmb{\nu}}{\partial\pmb{\theta}}{\pmb{B}}^{-1}\,\frac{\partial\pmb{\nu}^{\top}}{\partial\pmb{\theta}}\bigg]\bullet}}\\ {{(\Delta\pmb{\theta}\,-\,\pmb{A}\,)+\pmb{D}\,+\,{\cal O}(\Delta\pmb{\theta}^{3})\phantom{\bigg[\,{\pmb{D}}_{\pmb{\theta}}^{-1}(\,k\,-\,1)\,+\,\displaystyle\frac{\partial\pmb{\nu}}{\partial\pmb{\theta}}{\pmb{B}}^{-1}\,\frac{\partial\pmb{\nu}^{\top}}{\partial\pmb{\theta}}\bigg].}}\end{array}

式中

\textbf{A}=-\,\left[\,P_{\theta}^{-1}\big(\,k\,-1\,\big)\,+\,\frac{\partial\,\nu}{\partial\theta}B^{-1}\,\frac{\partial\,\nu^{\mathrm{T}}}{\partial\theta}\,\right]^{-1}\,\frac{\partial\,\nu}{\partial\theta}B^{-1}\,\nu

\begin{array}{l}{{\displaystyle{D\ =\ J\big(\,k\,-\,1\big)\,+\,\nu^{\mathrm{T}}B^{-1}\nu\,+}}}\\ {{\displaystyle{\qquad\quad A^{\mathrm{\,T}}\bigg[\,P_{\theta}^{-1}\big(\,k\,-\,1\big)\,+\,\frac{\partial\,\nu}{\partial\theta}B^{-1}\,\frac{\partial\,\nu^{\mathrm{T}}}{\partial\theta}\bigg]A\,+\,\ln\,\mid\,B(\,k)\,\mid\,\,(\,5\,-\,145)}}}\end{array}

上式各项都是在 \pmb{\partial}(\pmb{k}-1) 的条件下取值， D 是 \pmb{\partial}(k-1) 的二次型函数之和,与 \Delta\pmb{\theta} 无关。由式（5-143）可知，使 \boldsymbol{J}\left(\boldsymbol{k}\right) 达极小值的必要条件是 \Delta\hat{\pmb{\theta}}-\pmb{A}=\pmb{0} ,即

\hat{\pmb\theta}(\pmb k)\:=\:\hat{\pmb\theta}(\pmb k\:-\:1)\:+\:\mathbf A

P_{\theta}^{-1}(k)\,=\,P_{\theta}^{-1}(k\,-\,1)\,+\,\frac{\partial\,{\bf v}}{\partial\theta}B^{-1}\,\frac{\partial\,{\bf v}^{\mathrm{T}}}{\partial\theta}

利用矩阵求逆运算公式

(A + BCD)-1 = A-1 - A-1B(C-1 + DA-B)-1DA -1可以导出最大似然算法的全部算式

\left\{\begin{array}{l}{\displaystyle\hat{\pmb{\theta}}(k)\,=\,\hat{\pmb{\theta}}(k\,-\,1)\,+\,K_{\theta}(k\,)\,\nu(k\,)}\\ {\displaystyle K_{\theta}(k)\,=\,P_{\theta}(k\,-\,1)\,\frac{\partial\,\nu}{\partial\theta}\bigg[{\pmb{B}}\,+\,\frac{\partial\,\nu^{\mathrm{T}}}{\partial\theta}P_{\theta}(k\,-\,1)\,\frac{\partial\,\nu}{\partial\theta}\bigg]^{-1}}\\ {\displaystyle P_{\theta}(k)\,=\,\bigg[{\pmb{I}}\,-\,K_{\theta}(k)\,\frac{\partial\,\nu^{\mathrm{T}}}{\partial\theta}\bigg]P_{\theta}(k\,-\,1)}\\ {\displaystyle\nu(k)\,=\,{\pmb{y}}(k)\,-\,h\,({\pmb{x}}\,,{\pmb{u}}\,,\theta_{k-1}\,;t_{k})}\end{array}\right.

当噪声的统计特性未知时，可取新息协方差阵 \pmb{B} 为常数权矩阵，或由式（5-128）估算。

5.4.1 线性系统参数估计的边界椭球法

当系统模型为未知参数的线性函数时，与模型、观测数据和噪声上下界相一致的未知参数可行集是凸多面体，用凸多面体本身可以精确描述参数可行集。然而,当观测数据较多或者未知参数个数较多时，参数可行集通常变得很复杂，而难以精确描述，这时一般采用近似方法。在近似方法中,边界椭球法[14],由于形式简单、计算量小、容易实时实现等优点,而被广泛使用[15]。边界椭球法首先在状态估计领域中发展起来，随后被用于参数辨识。福格尔(E.Fogel)和黄(Y.F.Huang)[16}提出了单输出线性系统参数集员辨识的最优边界椭球法（简称FH算法）。贝尔福特(G.Belforte)和博纳(B.Bona)[17]对 FH算法进行了修正,提出了修正的FH算法。克里门特（T.Clement)和真蒂(S.Gentil)[18]将最优边界椭球法扩展到输出误差模型参数的集员辨识上。文献[19]提出了多输人~多输出线性系统参数集员辨识的边界椭球法。

本小节在单输出系统参数集员辨识中综合了福格尔和黄、贝尔福特和博纳以及克里门特和真蒂的方法，并将优化算法用于多输出系统参数的集员辨识，给出了多输出系统参数集员辨识的最优边界椭球法。并在此最优边界椭球法中给出了由观测数据和噪声上界所限制的参数集 R_{k} 和前-步计算的边界椭球 \Theta_{k\,-\,1} 的交集存在的充分必要条件。

5.4.1.1 单输出系统参数集员辩识的边界椭球法

1）修正的 FH算法设单输出线性系统模型为

{y_{k}}\;=\;\pmb{\phi}_{k}^{\mathrm{T}}\pmb{\theta}\;+\;\varepsilon_{k}\;\;\;\;\left(\frac{}{}k\;=\;1\,,2\,,\cdots,N\right)

式中 \pmb\theta\in R^{p} 为待估参数矢量； \phi_{k}\in R^{\rho} 为回归矢量； y_{k}\in R^{1} 为模型输出的观测值； N 为观测数据点数; \varepsilon_{k} 为观测噪声。噪声 \varepsilon_{k} 有界,即满足

|\;\;\pmb{\varepsilon}_{k}\;\;|\;\leqslant\;\varepsilon_{k}^{M}\;\;\;\;\;\;\;\;\left(\;k\;=\;1\,,2\,,\cdots,N\right)

FH算法是一种递推算法，它在递推的每一步都计算一个尽 可能小的边界椭球 \theta_{k} ,并使 \theta_{k} 包含前一步计算的边界椭球 \theta_{k\mathrm{~-~}1} 和 R_{k} 的交集。设边界椭球 \theta_{k-1} 由下式描述

\Theta_{k-1}\:=\:\{\:\pmb{\theta}\:\:\}\:\left[\,\pmb{\theta}\:-\:\pmb{\theta}_{c}(\:\pmb{k}\:-\:1\:)\,\right]^{\mathrm{T}}\,.

P_{k-1}^{-1}[\textbf{\em\theta}-\textbf{\em\theta}_{\boldsymbol{c}}(\textbf{\em k}-1)\textbf{\em\,]}\leqslant1\}

式中 \pmb{\theta}_{c}(\pmb{k}-1)\in\cal R^{p} 是 \Theta_{k\,-\,1} 的中心;

Pk-1——p× p 的对称正定矩阵,它表征了 k-1的形状和大小。

R_{k} 与 k 时刻的观测数据。 y_{k} 、噪声上界 \pmb{\varepsilon}_{k}^{M} 和模型结构相一致的由两个平行超平面 H_{1} 和 H_{2} 所限制的区域，即由式（5-149)和式（5-150)所确定的两个不等式，定义为

R_{k}\;=\;\{\:\pmb{\theta}:\,H_{1}\,\cap\,H_{2}\,\}

式中

\begin{array}{r}{H_{1}:\phi_{k}^{\mathrm{T}}\pmb{\theta}\geqslant y_{k}\textnormal{-}\epsilon_{k}^{M}}\\ {H_{2}:\phi_{k}^{\mathrm{T}}\pmb{\theta}\leqslant y_{k}\textnormal{+}\epsilon_{k}^{M}}\end{array}

H_{1} 和 H_{2} 分别为式（5-153）和式（5-154）取等号所对应的超平面。

H_{1} 和 H_{2} 与 \Theta_{k\,-\,1} 的相对位置可能如图 5-1所示，即 H_{1} 和

图 5-1边界椭球与超平面的相对位置

H_{2} 中只有一个与 \theta_{k-1} 相交。文献【20]指出，在这种情况下，用FH算法求出的边界椭球 \theta_{k} 并不是最小的，因此FH算法不是最优算法； \theta_{k} 的体积可以通过平行移动 H_{1} 和 H_{2} 中不与 \Theta_{k-1} 相交的超平面(图 5-1 中的 H_{1} ),使之与 \theta_{k-1} 相切(图 5-1 中 H_{3} )来进一步减小。因此，在利用FH算法求 \theta_{k} 之前，可先进行下列判断和变换：

(1)设 f_{1}=y_{k}-\varepsilon_{k}^{M}\,,f_{2}=y_{k}+\varepsilon_{k}^{M} ,并计算 G=\pmb{\phi}_{k}^{\mathrm{T}}\pmb{P}_{k-1}\pmb{\phi}_{k}^{\phantom{\dagger}}. (2）如果

f_{1}\geq\phi_{k}^{\mathrm{T}}\pmb{\theta}_{c}(\,k\,-\,1\,)\,+\sqrt{\,G\,}

或者

f_{2}\leqslant\phi_{\varepsilon}^{\mathrm{T}}\theta_{c}(\,k\,-\,1\,)\,-\,\sqrt{\,G\,}

那么 \Theta_{k\mathrm{~-~}1}\bigcap R_{k}=\phi ,算法停止。

（3）否则,判断 H_{1} 是否与 \theta_{k-1} 相交,即判断 f_{1} 是否满足下列不等式

\phi_{k}^{\mathrm{T}}\pmb{\theta}_{c}\left(\textit{k}-1\right)\,-\,\sqrt{\,G}\leqslant f_{1}\leqslant\phi_{k}^{\mathrm{T}}\pmb{\theta}_{c}\left(\textit{k}-1\right)\,+\,\sqrt{\,G}

若满足,则 H_{1} 与 \Theta_{k\mathrm{~-~}1} 相交;类似地也可以判断 H_{2} 与 \Theta_{k\,-\,1} 是否相交。

（4）通过（3)的判断，有4种情况可能发生：

情况 1 H_{1} 和 H_{2} 都不与 \Theta_{k-1} 相交,则

R_{k}\supset\Theta_{k-1}\,,\Theta_{k}\;=\;\Theta_{k-1}\,\bigcap\;R_{k}\;=\;\Theta_{k-1}

情况 2 H_{1} 不与 \Theta_{k\mathrm{~-~}1} 相交,而 H_{2} 与 \Theta_{k}\ldots_{1} 相交，用平行于H_{\mathfrak{h}} 并与 \Theta_{k} 相切的 H_{3} 代替 H_{1} ,则式（5-153）相应变为

h_{\,3}:\,\pmb{\phi}_{\,k}^{\dagger}\pmb{\theta}\mathcal{P}_{\pmb{k}}^{\dagger}\pmb{\theta}_{c}(\,\pmb{k}\,-\,1\,)\,-\,\sqrt{\,G\,}

情况 3 H_{3} 不与 \Theta_{k\mathrm{~-~}1} 相交，而 H_{1} 与 \theta_{k}-1 相交，用平行于H_{2} 并与 \Theta_{k^{\mathrm{~-~}1}} 相切的 H_{4} 代替 H_{2} ,则式（5-154)相应变为

h_{\,4}:\,\pmb\phi_{\pmb\delta}^{\mathrm{T}}\pmb\theta\ll\pmb\phi_{\pmb\delta}^{\mathrm{T}}\pmb\theta_{c}\,(\,\pmb k\,-\,1\,)\,+\,\sqrt{\,G\,}

情况 4 H_{1} 和 H_{2} 都与 \Theta_{k\mathrm{~-~}1} 相交。

当出现情况2或者情况3时，用式（5-155）或者式（5-156）分别代替式（5-153)或者式（5-154），就获得了修正的FH算法。它的性能优于FH算法。

2）输出误差模型参数集员辨识的边界椭球法

考虑输出误差模型

\left\{\begin{array}{l l}{\displaystyle x_{k}\,=-\,\sum_{i\,=\,1}^{n}a_{i}x_{k\,-\,i}\,+\,\sum_{i\,=\,1}^{m}b_{i}u_{k\,-\,i}}\\ {\displaystyle y_{k}\,=\,x_{k}\,+\,\varepsilon_{k}}\end{array}\right.

式中

yx∈ R1-—模型输出的测量值;

\pmb{\theta}=(a_{1},a_{2},\cdots,a_{n}\,;b_{1}\,,b_{2}\,,\cdots,b_{m})^{\mathrm{T}}{\:\:\:\:\:\:\:\:\:\:\mathcal{K}} 知参数矢量；

εk一—观测噪声,它满足式(5-150)。

输出误差模型式(5-157)中，状态量与未知参数0有关，是未知的，不能直接用来构造回归矢量。当未知参数 a_{i}\,(\,i=1\,,2\,,\cdots, \pmb{n} ）的符号已知时，可构造如下的回归失量

\n R_{k}^{M}\,=\,\bigl(\,-\,\,y_{k\,-\,1}\,+\,\mathrm{sign}(\,a_{\,1}\,)\,\varepsilon_{k\,-\,1}^{M}\,,\cdots\,,\,-\,y_{k\,-\,n}\,\,+

\mathrm{sign}(\,\alpha_{n}\,)\,e_{k\,-\,n}^{M}\,;\,u_{k\,-\,1}\,,\cdots,u_{k\,-\,m}\,)^{\mathrm{\tiny~T}}

\n_{k}^{m}\ =\ \ n-\ y_{k-1}\,-\,\mathrm{sign}(\,a_{1})\,\varepsilon_{k-1}^{M}\,,\cdots,\ -\,y_{k-n}\ -

\mathrm{sign}(\,a_{_n}\,)\,\varepsilon_{k\,-\,n}^{M}\,;\,u_{\,k\,-\,1}\,,\cdots,u_{\,k\,-\,m}\,)^{\,\mathrm{T}}

则得到与 k 时刻观测数据 y_{k} 、模型结构式(5-149)和噪声上界式（5-150）相一致的一对不等式

(\phi_{k}^{M})^{\mathrm{T}}\pmb{\theta}\gg y_{k}\:-\:\varepsilon_{k}^{M}

(\phi_{k}^{m})^{\top}\pmb{\theta}\ll y_{k}\,+\,\varepsilon_{k}^{M}

式（5-160）和式（5-161）在参数空间定义了由两个不平行的超平面限制的子空间 R_{k} ,如图5-2所示，其中 H_{1} 和 H_{2} 分别为式(5-160）和式（5-161）取等号时对应的超平面。

图5-2 输出误差模型的最优边界椭球的确定过程

FH算法的目的就是求最小体积的边界椭球 \Theta_{k}\!\supset\!\theta_{k-1}\!\cap\!R_{k} ，但此时由两个不平行的超平面 H_{1} 和 H_{2} 所限制的子空间 R_{k} 与式（5-153）和式（5-154）定义的由两个平行的超平面所限制的子空间是不同的，而FH算法要求 R_{k} 必须为两个平行的超平面所限制的子空间，为此采用两步法来解决这个矛盾。

在图5-2中，构造与 H_{1} 平行并与 \theta_{k} -1相切的超平面 H_{\mathrm{i}}^{\prime} 。设H_{1} 和 H^{'}{}_{1} 所限制的区域为 \left[{H_{1},H_{\mathrm{~1~}}^{\prime}}\right] ，则可运用FH算法求得最小体积的边界椭球 \theta^{\prime} （见图 5-2）,使其满足

\Theta^{\prime}\supset\Theta_{k\textrm{\tiny-1}}\bigcap\;[\,H_{1}\,,H_{1}^{\prime}\,]

类似地，构造与 H_{2} 平行并与 \theta^{\prime} 相切的超平面 H_{2}^{\prime} 。设 H_{2} 和 H_{2}^{\prime} 所限制区域为 [\boldsymbol{H_{2}},\boldsymbol{H_{\Sigma}^{\prime}}] ，则再次运用FH算法，可求得最小体积的 边界椭球 \Theta_{k}^{\prime} ，使其满足

\Theta_{k}^{\prime}\supset\Theta^{\prime}\bigcap\;[\,H_{2},H_{2}^{\prime}\,]

由于

[\,H_{1}\,,H_{1}^{\prime}\,]\,\cap\,[\,H_{2}\,,H_{2}^{\prime}\,]\;=\;[\,H_{1}\,,H_{2}\,]\;=\;R_{k}

于是，由式（5-162）和式（5-163）有

\Theta_{k}^{\prime}\,\Longrightarrow\,\Theta_{k-1}\,\bigcap\,\,[\,H_{1}\,,H_{2}\,]\,=\,\Theta_{k-1}\,\bigcap\,\,R_{k}

可见, \theta_{k}^{\prime} 正是所要求的包含 \Theta_{k\mathrm{~-~}1} 和 R_{k} 交集的边界椭球 \theta_{k} 。这样便获得了输出误差模型参数集员辨识的边界椭球法。5.4.1.2 MIMO 系统参数集员辨识的最优边界椭球法

现将优化算法用于多输人多输出（MIMO）系统参数的集员辨识，给出MIMO系统参数集员辨识的最优边界椭球法。

1）集员估计问题及其递推解

由文献[19]知,MIMO线性系统可写成如下的回归形式

\mathbf{y}_{k}\;=\;{\pmb\theta}^{\mathrm{T}}{\pmb X}_{k}\;+\;{\pmb\varepsilon}_{k}

式中 y——m 维的输出；

\theta^{\mathrm{T}}\substack{\longrightarrow\,m\,\times\,n} 维的待估参数阵；
\underbrace{\mathbf{X}_{k}{\mathop{\longrightarrow}}\!\!-\!\!\!-}\!\!\!\!\!n 维的回归矢量；

&k一—m 维的动态噪声,若其功率瞬时有界,即

\|\textbf{\em{\varepsilon}}\|\mathbf{\Sigma}_{2}^{2}\leqslant\delta_{k}

k\mathfrak{-}1 时刻包含 \theta 的边界椭球 \theta_{k-1} 可写成

\begin{array}{r}{\pmb{\theta}\in\,\Theta_{k-1}=\{\pmb{\theta}\,\mid\,\mathrm{tr}[\left(\,\pmb{\theta}\,-\,\pmb{\theta}_{c}(\,k\,-\,1)\,\right)^{\mathrm{T}}\,\cdot\,}\\ {\pmb{P}_{k-1}^{-1}(\,\pmb{\theta}\,-\,\pmb{\theta}_{c}(\,k\,-\,1)\,)\,]\leqslant1\}}\end{array}

式中 \operatorname{tr}(\,\cdot\,) ——矩阵的迹;

\pmb{\theta}_{c}(\pmb{k}-1) ——椭球 \Theta_{k^{-1}} 的中心；\boldsymbol{P}_{k} 1—表征椭球 \Theta_{k\mathrm{~-~}1} 形状和大小的 \pmb{n} 维方阵。

设 \pmb{R}_{k} 是 k 时刻的观测数据 {\mathfrak{y}}_{k} 以及式(5-166)和式(5-167)所决定的参数 \pmb\theta 的集合

\pmb{\theta}\in\mathrm{~\cal~R~}=\mathrm{~\(~\pmb{\theta}~|~\mathrm{~\}~|~\pmb{\theta}_{k}~-~\pmb{\theta}^{\mathrm{T}}\pmb{X}_{k}~|\|~\llcorner~\llb{\delta}_{k}~}\end{array}

显然，在 k 时刻包含 \pmb{\theta} 的集合应该是 \theta_{k\mathrm{~-~}1} 与 R_{k} 的交集，这一交集不一定仍是椭球,为运算简便起见，取边界椭球 \Theta_{k}\!\supset\!\Theta_{k-1}\!\cap\!R_{k} 作为这个交集的近似，则 \theta_{k} 可写为

\Theta_{k}\;=\;\{\pmb\theta\;\;|\;\;\mathrm{tr}\big[\big(\pmb\theta\;-\;\pmb\theta_{c}(\:k\;-\;1)\big)^{\mathrm{T}}\pmb{P}_{k\;-\;1}^{-1}\big(\pmb\theta\;-\;\pmb\theta_{c}(\:k\;-\;1)\big)\big]\;+

q_{k}\parallel\mathbf{\boldsymbol{y}}_{k}\,-\,\mathbf{\boldsymbol{\theta}}^{\mathrm{T}}\mathbf{\boldsymbol{X}}\parallel_{2}^{2}\leqslant1\,+\,q_{k}\delta_{k}\,\!\mid

式中 q_{k}\!\stackrel{\textstyle>}{\sim}\!0 。将式(5-170)展开并进行整理可得

\Theta_{k}\;=\;\{\,{\pmb\theta}\;\;|\;\mathrm{tr}[\,(\,{\pmb\theta}\,-\,{\pmb\theta}_{c}\,(\,k\,)\,)^{\mathrm{T}}\,{\pmb P}_{k}^{\;-1}(\,{\pmb\theta}\,-\,{\pmb\theta}_{c}\,(\,k\,)\,)\,]\leqslant1\}

式中

\left\{\begin{array}{l}{\pmb{\theta}_{c}(k)\,=\,\pmb{\theta}_{c}(k\,-\,1)\,+\,\alpha_{k}\pmb{P}_{k-1}\pmb{X}_{k}[\pmb{y}_{k}^{\top}\,-\,\pmb{X}_{k}^{\top}\pmb{\theta}_{c}(k\,-\,1)]}\\ {\pmb{P}_{k}\,=\,\beta_{k}(\pmb{P}_{k-1}\,-\,\alpha_{k}\pmb{P}_{k-1}\pmb{X}_{k}\pmb{X}_{k}^{\top}\pmb{p}_{k-1})}\\ {\alpha_{k}\,=\,q_{k}/(1\,.\,0\,+\,q_{k}\pmb{X}_{k}^{\top}\pmb{P}_{k-1}\pmb{X}_{k})}\\ {\beta_{k}\,=\,1\,.\,0\,+\,q_{k}\delta_{k}\,-}\\ {\alpha_{k}\mathrm{tr}\{[\,\pmb{y}_{k}\,-\,\pmb{\theta}_{c}^{\top}(k\,-\,1)\,\pmb{X}_{k}\,][\,\pmb{y}_{k}^{\top}\,-\,\pmb{X}_{k}^{\top}\pmb{\theta}_{c}(k\,-\,1)\,]\}}\end{array}\right.

式 (\,5\!-\!171\,)\sim 式（5-172）用边界椭球法构成了参数集员估计的递推算法。当 q_{k} 恒取为1.0时，上述结果与文献[19]中由能量约束所得到的结果完全一致，椭球的中心即为 \pmb{\theta} 的最小二乘估计。当 q_{k} 按一定准则取非负实数时，椭球的中心就是以 \mathbf{\vec{q}}_{k} 为加权系数的加权最小二乘估计。但无论 q_{k} 怎样取值都能保证未知参数 \pmb\theta 总落在式（5-171)所定义的边界椭球内。 \pmb\theta_{c}\left(0\right) 可由先验信息所获得的未知参数的初始估计值给出。或取 \pmb\theta_{c}\left(0\right)=\pmb\theta\,,P_{0}=d\pmb I ,式中， d 是足够大的正数，以保证 \theta_{0} 包含参数真值。

2）优化算法

为在几何意义上表示边界椭球 \theta_{k} 的大小,给出以下定义：

定义 1 \mu_{v}(\,k\,)=\operatorname*{det}(\,P_{k}\,) 为边界椭球的体积。式中， \operatorname*{det}(P_{k}) 为 \boldsymbol{P_{k}} 的行列式值，它与边界椭球 \Theta_{k} 的体积成正比。

定义 2 \mu_{T}(\,k\,)=\mathrm{tr}(\,P_{k}\,) 为边界椭球 \theta_{k} 的迹。式中， \mathfrak{t r}(\,P_{k}\,) 为 \pmb{P}_{k} 的迹，它与边界椭球 \theta_{k} 在半轴上投影的平方和成正比。

为简便起见，记

E_{k}^{2}\;=\;\mathrm{tr}\,{\left\{\,\left[\,{\bf y}_{k}\,-\,{\pmb\theta}_{c}^{\top}({\bf\Delta}{k}\,-\,{1}\,)\,{\bf X}_{k}\,{\right]}\,{\left[\,{\bf y}_{k}^{\top}\,-\,{\bf X}_{k}^{\top}{\pmb\theta}_{c}({\bf\Delta}{k}\,-\,{1}\,)\,\right]\,{\left\}}\,{\left[\,{\bf y}_{k}\,{-}\,{\bf H}_{k}\,{\pmb\theta}_{c}({\bf~k}\,-\,{1}\,)\,{\right]}\,{\left[\,{\bf y}_{k}\,{-}\,{\bf H}_{k}\,{\bf H}_{c}({\bf~k}\,-\,{1}\,)\,{\bf H}_{k}\,{\bf H}_{c}({\bf~k}\,-\,{1}\,)\,{\bf H}_{k}({\bf y}_{k}\,{-}\,{\bf H}_{c}({\bf~k}\,-\,{1}\,))\,{\bf H}_{k}({\bf y}_{k}\,{-}\,{\bf H}_{c}({\bf~k}\,-\,{1}\,){\bf H}_{k}({\bf y}_{k}\,{-}\,{\bf H}_{c}({\bf~k}\,-\,{1}\,))\,{\bf H}_{k}({\bf y}_{k}\,{-}\,{\bf H}_{c}({\bf~k}\,-\,{1}\,){\bf H}_{k})\,{\bf H}_{k}({\bf y}_{k}\,{-}\,{\bf H}_{c}({\bf k}\,-\,{1}\,))\,{\bf H}_{k}({\bf y}_{k}\,{-}\,{1}\,){\bf H}_{k}({\bf k}\,{-}\,{1}\,){\bf H}_{k}\,

\begin{array}{r}{G_{k}\;=\;X_{k}^{\mathrm{T}}P_{k-1}X_{k}}\\ {H_{k}\;=\;X_{k}^{\mathrm{T}}P_{k-1}^{2}X_{k}}\end{array}

下面给出最小体积算法和最小迹算法。

（1）最小体积算法

最小体积算法(算法 1)就是如何选择 q_{k}\!\geqslant\!0 使 \mu_{v}\left(k\right) 最小。由式(5-172)有

P_{k}\;=\;\beta_{k}\left[\frac{}{}I\;-\;q_{k}P_{k-1}X_{k}X_{k}^{\mathrm{T}}/(1.0\;+\;q_{k}X_{k}^{\mathrm{T}}P_{k-1}X_{k}\,)\right]P_{k-1}

则

\mu_{v}(k\,)\,=\,\operatorname*{det}(\,P_{k}\,)\,=\,\,\beta_{k}^{n}\mu_{k}\,(\,k\,-\,1\,)/(\,1\,.\,0\,+\,q_{k}G_{k}\,)

式中 n\!\longrightarrow\!{\cal P}_{k} 的维数。

极小化 \mu_{v}(k) ,到得 \boldsymbol{q}_{k} 是下列方程的正实根

A_{1}q^{2}\,+\,B_{1}q\,+\,C_{1}\,=\,0

或者

A_{2}q^{2}\,+\,B_{2}q\,+\,C_{2}\,=\,0

\begin{array}{r}{\left\{A_{1}\,=\,G_{k}\delta_{k}\right.}\\ {\left.B_{1}\,=\,\delta_{k}\,+\,G_{k}\,-\,E_{k}^{2}\right.}\\ {\left.C_{1}\,=\,1\,.\,0\right.}\end{array}

\left\{B_{2}\;=\;\left(\,n\,-\,1\right)G_{k}^{2}\delta_{k}}\\ {\;}\\ {B_{2}\;=\;G_{k}\left[\,\left(2\,n\,-\,1\right)\delta_{k}\,-\,G_{k}\,+\,E_{k}^{2}\,\right]}\\ {\;}\\ {C_{2}\;=\;n\left(\delta_{k}\,-\,E_{k}^{2}\right)\,-\,G_{k}}\end{array}\right.

可以证明当 \theta_{k-1} 与 R_{k} 的交集存在时,式(5-178)无正实根；将式(5-179)的正实根代人式(5-172）,则可计算 \pmb{\theta}_{c}\left(\pmb{k}\right) 和 P_{k} 。若式(5-179)无正实根，则 q_{k}=0 ,于是 \pmb\theta_{c}\left(\pmb\ k\right)=\pmb\theta_{c}\left(\pmb\ k\right.-\left.1\right),\,P_{k}\,\,; \pmb{{\cal P}}_{k\mathrm{~-~}1} ,对应的数据 {\bf{y}}_{k} 为冗余数据。

（2）最小迹算法

最小迹算法(算法 2)就是如何选择 a_{k}\!\geqslant\!0 使 \mu_{T}(k) 最小。

\begin{array}{l}{{\it\Pi:_{T}(k\lambda)\ i=\mathrm{tr}(\{{\cal P}_{k}\}=\ }}\\ {{\ }}\\ {{\beta_{k}[\mu_{T}(k\,-\,1)\,-\,q_{k}H_{k}/(\,1.\,0\,+\,q_{k}G_{k}\,)\,]}}\end{array}

极小化 \mu_{T}(k) ,得 \pmb{q}_{k} 是下列方程的正实根

A_{3}q^{3}\,+\,B_{3}q^{2}\,+\,C_{3}q\,+\,D_{3}\,=\,0

式中

{\cal A}_{3}\,=\,G_{k}^{2}\delta_{k}\bigl[\,G_{k}\mu_{T}\bigl({\pmb k}\,-1\,\bigr)\,-\,H_{k}\,\bigr]

B_{3}\,=\,3\,G_{k}\delta_{k}\,[\,G_{k}\mu_{T}(\,k\,-\,1)\,-\,H_{k}\,]

C_{3}\,=\,G_{k}\,[\,\mu_{T}(\,k\,-\,1)(\,\delta_{k}\,-\,E_{k}^{2}\,)\,-\,H_{k}\,]\,+

2\big[\,G_{k}\mu_{T}(\,k\,-\,1)\,\delta_{k}\,-\,H_{k}\big(\,\delta_{k}\,-\,E_{k}^{2}\,\big)\,\big]

D_{3}\;=\;\mu_{T}(\,k\;-\;1\,)(\,\delta_{k}\;-\;E_{k}^{2}\,)\;-\;H_{k}

将式(5-181)的正实根代人式(5-172),则可计算 \theta_{c}\left(k\right) 和 \pmb{P}_{k} 。若式(5-181)无正实根,则 q_{k}=0 ,于是 \pmb\theta_{c}\left(\,k\,\right)=\pmb\theta_{c}\left(\,k\,-1\,\right),\pmb P_{k}= \pmb{P}_{k}\mathrm{~.~}_{1} ,对应的数据 {\mathfrak{y}}_{k} 为余数据。

3）仿真算例

本节给出了两个算例。算例1对本章的MIMO系统参数集员辨识的最优边界椭球法与文献[19的最小二乘算法作厂比较。

算例2给出了输出误差模型参数的集员辨识。

算例 1

{\binom{y_{1}(k\,)}{y_{2}(k\,)}}=\;{\binom{0.1}{-\,0.2}}\;\;\;\;\;\;0.7{\bigg[}{\begin{array}{l}{u_{1}(k\,-\,1)}\\ {u_{2}(k\,-\,2)}\end{array}}{\bigg]}+\;{\binom{\varepsilon_{1}(k\,)}{\varepsilon_{2}(k\,)}}

取 u_{\textup{l}}(\,k\,) 以 20 为周期， u_{\,1}(\,k\,)=16\,,(\,k=1\,,\cdots,10\,)\,;\,u_{\,1}(\,k\,)=\,-\,18 (\,k=11\,,\cdots,20\,) 。 u_{\,2}\left(\,k\,\right) 以10 为周期， u_{\,2}\left(\,k\,\right)=6 ， (\,k=1\,,\cdots,5\,) u_{2}(\textit{k})=\mathrm{~-~}7\,,(\,k=6\,,\cdots,10\,)_{\circ}\;\;e_{1}(\,k\,) 和 \boldsymbol{e}_{2}(\,\boldsymbol{k}\,) 分别为[-0.1,0.1]和 \left[\,-\,0\,.\,2\,,0\,.\,2\,\right] 上的不相关均匀随机噪声。取 \delta_{k}=0.05 为噪声的瞬时约束， F(\,k\,)=0.05k 为噪声的能量约束。

对算例在相同条件下，同时采用了三种算法，即文献[19]中的最小二乘算法、本节的最小体积法（算法 1)和最小迹算法（算法2）,其结果比较如表5-1所列。

从表5-1中可以看出，三种算法对参数的中心估计与参数真值都非常接近，给出的参数估计区间都包含参数真值。但优化算法（算法1和算法2)给出的参数估计区间比最小二乘算法给出的小。另外，在算法采样的200个数据点中，采用优化算法时,大约有 20\,\%\sim30\,\% 的数据为有用数据，其余为余数据，这就大大减少了参数估计更新的时间，提高了优化算法的计算效率，减少了计算量。

表5-1参数中心估计和区间估计的比较

<html>

参数真值	最小二乘法		算法1		算法 2
	中心估计	区间估计	中心估计	区间估计	中心估计	区间估计
α11 =0.10	0.099	(0.088,0.11)	0.099	(0.092,0.11)	0.099	(0.091,0.11)
a21 = -- 0.60	- 0.60	（-0.63,-0.57)	- 0.60	(-0.62,-0.59)	- 0.60	（-0.62,-0.58)
α12 = - 0.20	-0.20	-0.22,-0.18)	-0.20	(--0.21, -0.19)	- 0.19	(-0.21,-0.19)
α 22 = 0.70	0.69	(0.66,0.73)	0.69	(0.68,0.72)	0.69	(0.68,0.72)

</html>

算例 2考虑输出误差模型

\begin{array}{c}{{\left\{x_{k}\;=-\;a_{1}x_{k-1}\,+\,b_{1}\,u_{k\,-1}\right.}}\\ {{{}}}\\ {{y_{k}\;=\;x_{k}\,+\,\epsilon_{k}}}\end{array}

式中待估参数为 \pmb{\theta}=(\alpha_{1},b_{1})^{\mathrm{T}} ,它们的真值分别为0.5和1.5;输人信号 \pmb{u}_{\pmb{k}} —以6 为周期的周期信号,当 k=1,2,3 时

观测数据点取为200。

采用扩展的单输出系统参数集员辨识的最优边界椭球法辨识输出误差模型的参数。表5-2列出了最小体积算法和最小迹算法给出的未知参数的中心估计和区间估计。从表5-2可以看出，参数的估计区间都包含参数真值，而且都较小；参数的中心估计与参数真值都非常接近。因此,采用扩展的单输出系统参数集员辨识的最优边界椭球法来估计输出误差模型的参数是有效而且可行的。

表5-2输出误差模型参数的中心估计与区间估计

<html>

参数真值	最小体积算法		最小迹算法
	中心估计	区间估计	中心估计	区间估计
a, =0.50	0.5024	(0.4859,0.5191)	0.5007	(0.4821,0.5193)
b, = 1.50	1.5028	(1.4821,1.5239)	1.5001	(1.4790,1.5212)

</html>

5.4.2 线性系统参数估计的改进凸多面锥法

前-节给出了线性系统参数估计的边界椭球法，边界椭球法具有简单、计算量小、容易实现等优点，但边界椭球法仅是对参数可行集比较保守的估计。由于在噪声统计分布特性未知但有界的情况下，线性系统参数的可行集是凸多面体，用相应的凸多面体法来描述参数可行集必然是精确的。布鲁曼（Broman）和申萨(Shensa)[22］、莫(Mo)和诺顿(Norton）[23]以及皮特-拉哈涅尔(Piet-Lahanier)和沃尔特（Walter）[24]分别给出了不同的凸多面体法。

为了更方便地给出算法的初值、更有效地描述未知参数的可行集以及可以描述参数可行集在某些方向无界的情况，沃尔特和皮特-拉哈涅尔[25,26]提出了描述参数可行集的凸多面锥法。

本节以文献[25，26]中的凸多面锥算法作为基础并对它进行了改进。本节改进的多面锥法采用旧凸多面锥的边的凸组合来求新多面锥的新边，从而保证了算法的稳定性。由于输出误差模型是一种常用的模型，因此本节将凸多面锥算法扩展到输出误差模型的参数估计。

1）问题的提出设线性系统模型为

z\left(\,k\,\right)\;=\;\pmb{\Phi}_{k}^{\intercal}\pmb{\theta}\;+\;\varepsilon_{k}\;\qquad\left(\,k\;=\;1,2,\cdots,N\,\right)

式中 z\left(\,k\,\right)\in R^{1} 为 \pmb{k} 时刻系统输出的观测值;

\Phi_{k}\in R^{\mathfrak{p}} 为已知的回归矢量；

\pmb\theta\in R^{p} 为系统的未知参数矢量；

\varepsilon_{k}\in R^{1} 为 k 时刻系统的观测噪声。

假定它的统计分布特性未知，但其上界 \varepsilon_{\operatorname*{max}}\textbf{(}k\textbf{)} 和下界\varepsilon_{\operatorname*{min}}(k) 是已知的，则误差 \pmb{\xi}_{\pmb{k}} 满足

\varepsilon_{\mathrm{min}}(\,k\,)\leqslant\varepsilon_{k}\leqslant\varepsilon_{\mathrm{max}}(\,k\,)\qquad(\,k\,=\,1\,,2\,,\cdots,N\,)

由式(5-182)和式(5-183)知,未知参数 \pmb{\theta} 的可行集 S 是满足下列不等式组的集合

\pmb{\phi}_{k}^{\operatorname{T}}\pmb{\theta}\geqslant z\left(\,k\,\right)\,-\,\pmb{\varepsilon}_{\operatorname*{max}}(\,k\,)\,,\pmb{\Phi}_{k}^{\operatorname{T}}\pmb{\theta}\leqslant z\left(\,k\,\right)\,-\,\pmb{\varepsilon}_{\operatorname*{min}}(\,k\,)

(\,k\;=\;1\,,2\,,\cdots,N\,)

可行集 S 是一个凸多面体。

如果式（5-184)中未知参数 \pmb{\theta} 的下界已知，即

\theta_{i}\geqslant\theta_{i\operatorname*{min}}\qquad(\,i\;=\;1\,,2\,,\cdots,p\,)

可进行下列代换

x_{i}\;=\;\theta_{i}\;-\;\theta_{i\operatorname*{min}}\;\;\;\;(\;i\;=\;1\,,2\,,\cdots,p\,)

将式（5-186）代人式（5-184），并写成矩阵形式有

\begin{array}{r}{\textbf{A}\pmb{x}\geqslant\pmb{b}\quad(\textbf{\em x}\geqslant0)}\end{array}

式中 A\,{\overset{}{\longrightarrow}}\,2\,N\times P 的矩阵；

bE r2n. —常数项；

x\in R^{p} ——变换后的未知参数矢量。

将矢量 \pmb{x} 增加一个分量 x_{p+1}\!>\!0 ,并且矩阵相应地增加一列（其对应元素为 a_{i\,,\,p\,+\,1}=b_{i}\,,\,i=1\,,2\,,\cdots,2\,N\,) ,从而把式(5-187)转换成齐次线性不等式方程组

A x\geq\pmb{\theta}\qquad(\pmb{x}\geq0)

这种变换相当于将 \pmb{\dot{p}} 维参数空间中的凸多面体转换成 {\pmb\dot{p}}^{\mathrm{~+~}1} 维参数空间中的凸多面锥。式（5-188)就是凸多面锥法求解的标准形式。下面给出凸多面锥法的求解过程。

2）描述参数可行集的凸多面锥法

设 C^{j} 是由前 j 个不等式所获得的凸多面锥。设 \pmb{S}^{i} 是一个矩阵，它的第 k 列表示 C^{j} 的第 k 条边的方向矢量。设 R^{j} 是一个矩阵，它的行矢量为定义 C^{j} 的支撑超平面的法矢量，即 R^{j} 的行矢量为式(5-188)前 j 个不等式中与支撑超平面对应的不等式矢量。定义 \pmb{T}^{j}=\pmb{R}^{j}\pmb{S}^{j}\,,\,\pmb{T}^{j} 的元素为定义 C^{j} 的支撑超平面的行矢量与定义 C^{j} 的边的方向矢量的点乘。

如果 \pmb{T}^{j} 中位于 (\mathbf{\sigma}_{i},\mathbf{\sigma}_{k}) 的元素为0，则表示 C^{j} 的第 \pmb{k} 条边位于C^{j} 的 _i 个支撑超平面上。 T^{j}\setminus R^{j} 和 \pmb{S^{j}} 完全描绘了凸多面锥 C^{j} 。即 T^{j} 中元素的值表明了 C^{j} 的边与 C^{j} 的支撑超平面之间的关系。在算法中，要判断的是C’的某一条边是否属于C’的某一个支撑超平面，这等价于判断 \pmb{T}^{j} 中相应位置的元素是否等于0。由于 C^{j} 所有的边都是前 j 个不等式的解，因此 \pmb{T}^{j} 的所有元素都大于或等于0。这样可以用一个波利恩（Boolean)矩阵 \pmb{{\cal B}}^{j} 来代替 \pmb{T}^{j} ，它在算法中完全能起到 T的作用,并且能克服计算误差的影响。当T中的元素为0时， \pmb{{\cal B}}^{j} 中相应的元素为0；否则 \pmb{{\cal B}}^{j} 中的元素为 1\,\circ 凸多面锥算法是一种递推算法，不等式一个一个地被处理，直到处理完所有的 2N 个不等式。考虑(p+1)个对变量的非负限制,算法的初值 s^{0}\,,R^{0} 和 \pmb{{\cal B}}^{0} 都取为 \left(\,\phi+1\,\right)\times\left(\,\phi+1\,\right) 的单位矩阵。 \pmb{T}^{j} \pmb{R}^{j} 和 \pmb{S}^{j} 就完全描绘了凸多面锥 C^{j} 。

170

设第 j+1 个不等式为

a_{j+1}^{\textup T}x\geqslant0

它定义了一个新的超平面

H^{j+1}\;=\;\{\;{\pmb x}\;\mid\;{\pmb a}_{j+1}^{\,\mathrm T}{\pmb x}\;=\;{\pmb0}\}

以及两个半空间

H_{+}^{j+1}=\{\pmb{x}\ |\ \pmb{a}_{j+1}^{\mathrm{T}}\pmb{x}\geqslant0\}

和

H_{-}^{j+1}=\{\pmb{x}\ |\ \pmb{a}_{j+1}^{\mathrm{T}}\pmb{x}\leqslant0\}

显然考虑第 j^{\mathrm{~+~}1} 个不等式后的解集为 C^{j} 与 H_{+}^{j+1} 的交集。设矢量 \pmb{\beta} 定义为

\pmb{\beta}^{\mathrm{T}}\ =\ \pmb{a}_{j+1}^{\mathrm{T}}\pmb{S}^{j}

则矢量 \beta^{\gamma} 的第 _i 个分量 \beta_{i} 的符号显示 C^{j} 的第 _i 条边相对于超平面 H^{j+1} 的位置。有三种情况可能发生：

（1）所有 \pmb{\beta} 的分量都为负。即 C^{j} 所有的边都属于 \smash{\boldsymbol{H}_{\leftarrow}^{j+1}} ，该问题无解。

(2）所有 \pmb{\beta} 的分量都非负。即 C^{j} 所有的边都属于 \boldsymbol{H}_{+}^{j+1} ,因此不等式对减小C没有贡献,是余的。于是 Si+1=S,Bj+1=\boldsymbol{B}^{j}\,,\boldsymbol{R}^{j\,+\,1}=\boldsymbol{R}^{j}\,,

(3) \pmb{\beta} 的分量具有不同的符号。即超平面 F P^{j+1} 将 C^{j} 分成两部分，此时必须通过下列过程确定 C^{j\,+\,1}=C^{j}\cap H_{+}^{j\,+\,1}

首先求 \pmb{S}^{j+1} 。设 i\in N_{+}\,,k\in N\,. ,其中 N_{+}\,=\,\{\,i\mid\beta_{i}\!\ge\!0\,\} N_=kIβ<0},则 C 的第i条边S 和第k条边S 的一种合适的线性组合为

\mathbf{S}_{i\,,\,k}^{j+1}\,=\,\frac{-\,\beta_{k}}{\beta_{i}\,-\,\beta_{k}}\mathbf{S}_{i}^{j}\,+\,\frac{\beta_{i}}{\beta_{i}\,-\,\beta_{k}}\mathbf{S}_{k}^{j}

f_{k}\,=\,{\frac{-\,\beta_{k}}{\beta_{i}\,-\,\beta_{k}}}\,,\quad f_{i}\,=\,{\frac{\beta_{i}}{\beta_{i}\,-\,\beta_{k}}}

由于 0\!<\!f_{k}\!<\!1\,,0\!<\!f_{i}\!<\!1 ,且 f_{k}+f_{i}=1 ,因此 \boldsymbol{\mathcal{S}}_{i,\dot{k}}^{j+1} 是 \pmb{S}_{i}^{j} 和 \pmb{S}_{k}^{j} 的凸线性组合,并且 \boldsymbol{S}_{i\,,\,k}^{j\,+\,1} 必在 \pmb{S}_{i}^{j} 和 \pmb{S}_{k}^{j} 组成的平面上且位于 \pmb{S}_{i}^{j} 和 \pmb{S}_{k}^{j} 之间,又因

\pmb{a}_{j+1}^{\top}\cdot\,\pmb{S}_{i\,,k}^{j+1}\,=\,0

即 \boldsymbol{\mathbf{S}}_{i\,,\,k}^{j\,+\,1} 属于超平面 H^{j+1} ,故当边 _i 和边 k 相邻时， \mathbf{S}_{i,k}^{j+1} 必为 C^{j+1} 的一条新边。可见 C^{j+1} 的一条新边由两条旧边的凸组合获得。在 \pmb{S}^{j} 中去掉矢量 \pmb{\beta}^{\mathrm{T}} 中分量为负对应的边并加上所有的新边，则得到 S^{j\,+\,1}

去掉 R^{j} 中冗余的不等式所对应的行，并加上由 \pmb{a}_{j+1}^{\mathrm{T}} 组成的新行,就获得了 \pmb{R}^{j+1} 。判断一个不等式是否冗余只需判断属于该不等式对应的支撑超平面的所有边是否都属于 H_{\mathrm{~-~}}^{j+1} 。如果一个不等式对应的支撑平面上的所有边都属于 H_{\,\,\cdot}^{j^{\,+\,1}} ，则该不等式是余的， \pmb{R}^{j} 中对应的行应该去掉；反之，该不等式对应的行在 \pmb{R}^{j+1} 中应该保留。这个判断等价于，如果 \pmb{{\cal B}}^{j} 第 k 行的第 _i 列元素等于0,就有 \beta_{i}\!<\!0 ,那么 R^{j} 的第 k 行应该去掉。

在理论上,可以通过计算 R^{j+1}\cdot S^{j\ {+\ }} 来获得与此相应的波利恩矩阵 {\pmb{{\cal B}}}^{j\,+\,1} 。但实际上，由于计算误差的存在,采用这种方式计算 B^{j\,+\,1} ,往往会导致完全错误的最终结果。比如，通过精确计算\pmb{{\cal B}}^{j+1} 中应为0的元素，由于计算上的误差，使得这个元素不为0，这将会造成该元素对应的边和支撑超平面之间的错误从属关系，从而影响整个结果。因此， \pmb{{\cal B}}^{j\,+\,1} 通过 C^{j+1} 的边与支撑超平面之间的逻辑关系来获得。

重复以上过程，可以处理下一个不等式。当处理完2N个不等式后就获得了描述凸多面锥 C^{2N} 的矩阵 \pmb{S}^{2N},\pmb{R}^{2N} 和 \pmb{{\cal B}}^{2N} 。于是齐次线性不等式方程组式(5-188)的通解X可表示为

\pmb{X}^{h}\ =\ \pmb{S}^{2N}\pmb{W}\quad(\,\pmb{W}_{i}\geqslant\mathbf{0})

即凸多面锥中的每一条极线都可表示为该锥的边的线性组合。非齐次线性不等式方程组式(5-187)的通解(即相应的凸多面锥体中的任何一点）的分量可表示为

X_{k}\,=\,\frac{S_{k,\,1}^{2N}\,W_{1}\,+\,\cdots\,+\,\,S_{k,\,N S}^{2N}W_{N S}}{S_{p+1,\,1}^{2N}\,W_{1}\,+\,\cdots\,+\,\,S_{p+1,\,N S}^{2N}W_{N S}}\quad(\,k\,=\,1,2,\cdots,\,\rho\,)

式中 S_{i\,,j}^{2N}{\longrightarrow}-{\bf g}^{2N} 中位于 (\,i\,,j\,) 的元素；

NS. \mathcal{C}^{2N} 的边的条数。如果矩阵 \pmb{S}^{2N} 的第 {\phi}+1 行元素有一个为0，则式 $(5-\footnote{e m a l a d:h0000)s m a l a d d r e s s:h o776750$ 相应的凸多面体无界；反之，如果矩阵\pmb{S}^{2N} 的第 \phi+1 行元素没有一个为零，则式（5-187）相应的凸多面锥有界，并且它的第 \dot{\pmb{\tau}} 个顶点的第 \pmb{k} 个分量可表示为

V_{k}^{i}\ =\ S_{k,j}^{2N}/S_{\beta+1,\,i}^{2N}\quad(\,k\:=\:1\,,2\,,\cdots,\,p\,)

有界的凸多面锥可以表示为它的顶点凸集，因此要确定每一个参数能够达到的最大值和最小值（即参数的不确定区间）是很容易的。

3）凸多面锥法在输出误差模型参数估计的应用

由前面的分析可知，凸多面锥法适用于模型为未知参数 \pmb{\theta} 的仿射函数的情况。但输出误差模型却是未知参数 \pmb{\theta} 的非仿射函数。利用上节的思路，将凸多面锥法扩展到输出误差模型参数估计上。设输出误差模型为

\left\{x_{k}\;=\;\sum_{\stackrel{i\,=\;1}{i\,=\;1}}^{n}\,(\;-\;a_{i}x_{k\,-\,i}\;)\;+\;\sum_{i\,=\,1}^{m}\,b_{i}u_{k\,-\,i}

式中待估参数矢量 \pmb{\theta}=(\mathbf{\Phi}_{a_{1}},\cdots,\mathbf{\Phi}_{a_{n}}\,;b_{1}\,,\cdots,b_{m}\,)^{\mathrm{\scriptscriptstyleT}};

u_{k}\!\in{\!R}^{1}\!\!-\!\!\ k 时刻系统的输人;
x_{k}\in R^{1} ——系统状态；
\epsilon_{k}\!\in\!R^{1}\!\!-\!\!-\!k 时刻观测噪声；z_{k} —系统输出的测量值。

设观测噪声满足式（5-183）。

由式(5-200)和式(5-183)知

\begin{array}{r l r}{z_{k-i}\;-\;\varepsilon_{\operatorname*{max}}(\,k\,-\,i\,)\leqslant x_{k-1}\leqslant z_{k-i}\,-\,\varepsilon_{\operatorname*{min}}(\,k\,-\,i\,)}\\ {\quad}&{}&{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\\ {\quad}&{}&{(\,i\,=\,0\,,1\,,\cdots,k\,)\quad\quad\quad\quad\quad}\end{array}

当未知参数 \pmb{a}=(a_{1},\cdots,a_{n})^{\intercal} 的符号已知时,可构造回归矢量

\begin{array}{c}{\pmb{\phi}_{k}^{\mathtt{M A X}}=\textsf{\small[-}\,z_{k-1}\,-\,\mathrm{sign}\!\left(\,a_{1}\,\right)e_{\mathtt{m i n}}\!\left(\,k\,-\,1\,\right),\cdots,\,-\,z_{k-n}\,-}\\ {\mathrm{sign}\!\left(\,a_{n}\,\right)\!\,\varepsilon_{\mathtt{m i n}}\!\left(\,k\,-\,n\,\right),u_{k-1},\cdots,u_{k-m}\,\right]^{\mathtt{T}}}\end{array}

和

\begin{array}{c}{\pmb{\phi}_{k}^{\mathrm{MIN}}=\left[\mathrm{~-~}z_{k\mathrm{-}1}\mathrm{~-~}\mathrm{sign}(\,a_{1}\,)\,\varepsilon_{\mathrm{max}}(\,k\mathrm{~-~}1)\,,\cdots,\mathrm{~-~}z_{k\mathrm{-}n}\,-\right.}\\ {\left.\mathrm{sign}(\,a_{n}\,)\,\varepsilon_{\mathrm{max}}(\,k\mathrm{~-~}n\,)\,,u_{k-1},\cdots,u_{k-m}\,\right]^{\mathrm{T}}}\end{array}

使得

(\,\pmb{\varPhi}_{k}^{\mathrm{MAX}})^{\mathrm{T}}\pmb{\theta}\geqslant z_{k}\,-\,\varepsilon_{\operatorname*{max}}(\,k\,)\,,(\,\pmb{\varPhi}_{k}^{\mathrm{MIN}})^{\mathrm{T}}\pmb{\theta}\leqslant z_{k}\,-\,\varepsilon_{\operatorname*{min}}(\,k\,)

于是输出误差模型式（5-200）的参数的集员辨识问题就化成求解满足式（5-202）的参数可行集问题。通过适当的变换，式（5-202）可化为凸多面锥法求解的标准形式，从而估计出输出误差模型的未知参数 \pmb{\theta}

4）算例

用两个算例分别验证凸多面锥法对于仿射模型和输出误差模型参数估计的有效性。

算例 1 系统的模型为

z_{k}\;=\;\theta_{1}\,u\left(\,k\,\right)\;+\;\theta_{2}\,u\left(\,k\,-\,1\,\right)\,+\,\theta_{3}\,u\left(\,k\,-\,2\,\right)\,+\,\varepsilon_{k} 式中 \theta_{1}\,,\theta_{2}\,,\theta_{3} —未知参数，它们的真值分别为一0.5、2.35和

1.45;$u\left(,k,\right)$ 一一是输人信号，以6为周期的周期信号，当 k=1 2,3时， u\left(k\right)=1 ,当 k=4,5,6 时 {\pmb u}({\pmb k})=-1 ek一有界噪声,其相对误差上界F为0.02，即|\,\pm_{k}\,|\,{\leqslant}\!\,0\,.\,02\,|\,y_{k}\,|\,; yk——-k 时刻模型输出,采样数据点数为 50。

为了验证对于不同的观测噪声分布情况下凸多面锥法都是有效的，表5-3列出了在3种分布情况下相应于参数可行集的不确定区间估计以及相应于不确定区间的未知参数的中心估计。其中第1种情况， e_{k} 均值为0，标准差为 0.01\mid y_{k}\mid 的正态分布噪声；第2 种情况， \pmb{e_{k}} 为在区间 [\mathbf{\varepsilon}-\mathbf{0}\,.\,\mathbf{0}2\,|\,_{y_{k}}\,|\,,\mathbf{0}\,.\,\mathbf{0}2\,|\,_{y_{k}}\,|\,] 上的均匀分布噪声；第3种情况， \boldsymbol{e}_{k} 随机地取最大值 0.02\vert y_{k}\vert 或最小值 -\,0.02\,|\,y_{k}\,| 。

表5-3 参数的中心估计和不确定区间估计

<html>

参数	中心估计			区间估计
真值	情况 1	情况 2	情况 3	情况 1	情况 2	情况3
				0, = - 0.5|- 0.499 - 0.503 - 0.500( -0.536; -0.463)	(- 0.516; -0.490)	（-0.500: -0.500)
02 = 2.35	2.350	2.355	2.350	(2.326;2.374)	(2.342;2.367)	(2.350;2.350)
0 = 1.25	1.253	1.251	1.250	(1.237;1.268)	(1.247;1.255)	(1.250;1.250)

</html>

从表5-3中可以看出，在3种情况下凸多面锥法给出估计区间都较小，都包含参数真值，而且参数的中心估计与参数的真值都很接近，因此不论观测噪声的概率分布如何，多面锥法都是非常有效的。相比较而言，在情况3多面锥法给出的估计结果最好。这是因为集员辨识考虑的是噪声最坏的分布情况，而情况3与之最接近。

算例 2考虑输出误差模型

\begin{array}{l}{{x_{k}\,=-\,\,a_{1}x_{k-1}\,+\,b_{1}\,u_{k\,-1}}}\\ {{{}}}\\ {{z_{k}\,=\,x_{k}\,+\,\varepsilon_{k}}}\end{array}

式中 \pmb{\theta}=(a_{1},b_{1})^{\mathtt{T}}\!\!- -待估参数，它们的真值分别为0.5和

u——输人信号,它的取法与算例1同;ek———在区间[-0.02,0.02］上的均匀分布噪声；

观测数据点取为50。

采用扩展的凸多面锥法估计输出误差模型的参数。其结果是： \pmb{a}_{1} 的不确定区间估计为（0.491,0.503），中心估计的相对误差

为 1\,.21\,\%\,;b_{1} 的不确定区间估计为（1.495，1.511），中心估计的相对误差为 0.54\,\% 。参数的不确定区间包含参数真值，而且都较小，由此可见用凸多面锥法估计输出误差模型的参数是有效的。

5.4.3 非线性系统参数的集员辨识

1）问题的提出

对于非线性系统，由于未知参数的可行集往往不是凸集，甚至不连续，因此描述它非常困难。对于非线性系统参数集员辨识这个问题，前人已做了不少工作，但非线性系统参数的集员辨识问题还远未解决。米拉尼斯（Milanese)和威新诺（Vicino)[27]用直方体来近似描述FSS，解决了仅限于模型为未知参数的多项式时的集员辨识问题;乔林(Jaulin)和沃尔特(Walter)[28.29]用区间分析法较好地描述了FSS的形状，但其计算量随着未知参数的增加以及精度要求的提高而迅速增加，而且需要预先知道包含函数以及FSS的子集；随机扫描法[30]以及OMNE[31]都存在与区间分析法类似的问题。本节介绍非线性系统参数集员辨识的两步法，它与以往方法的不同之处在于，以往方法给出FSS的同时给出了参数的中心估计，两步法则分两步进行，即先用送代方法给出参数的中心估计，然后估计参数的可行集。

设系统模型输出的测量值表示为

\begin{array}{r}{\textbf{\em z}_{i}\ =\ \pmb{y}_{i}(\pmb{\theta})\ +\ \pmb{\varepsilon}_{i}\quad(\textbf{\em i}=1,2,\cdots,N)}\end{array}

式中 y_{i}\in R^{m}\;,\pmb\theta\in R^{p}\;,\pmb\varepsilon_{i}\in R^{m}\;,z_{i}\in R^{m} 一分别为系统的模型（未知参数 \pmb\theta 的可微非线性函数）、未知参数、测量噪声及测量失量。

假定测量噪声统计分布特性未知但有上界，即

|\ \pounds_{i j}\ |\leqslant\delta_{i j}\quad(j\,=\,1\,,2\,,\cdots,m\,)

0;≥0是噪声上界，e;是c；的第j个分量。

系统未知参数的集员辨识就是求参数的可行集，使其与噪声上界 \delta_{i} 模型结构 \pmb{y}_{i} 和观测数据 \pmb{z}_{i} 相容，即

176

\mathrm{FSS}\,=\,\{\,\pmb{\theta}\,\in\,\pmb{k}\,:\,\|\,\mathbf{\epsilon}_{z_{i}}\,-\,\mathbf{y}_{i}(\pmb{\theta})\,\|\,^{2}\leqslant F K\,;i\,=\,1,2,\cdots,N\,\}

式中 \pmb{k} ——验前信息所给出的未知参数 \pmb{\theta} 的集合；

F K=\pmb{\delta}_{i}^{\mathrm{T}}\pmb{\delta}_{i}\,; \|\cdot\|\longrightarrow2 范数。

2）集员辨识两步法

（1）参数的中心估计。分两步对未知参数进行集员辨识，即先求FSS的中心。用迭代法求参数的中心估计，设第 \pmb{k} 步选代后参数中心估计为 \hat{\pmb{\theta}}_{c}(\pmb{k}) ,对模型（5-203)在 \pmb{\theta}=\pmb{\hat{\theta}}_{c}\left(\pmb{\mathscr{k}}\right) 点处作线性展开,有

z_{i}\;=\;y_{i}(\,\hat{\pmb{\theta}}_{c}(\,k\,)\,)\,+\,A_{i}\Delta\pmb{\theta}_{k}\,+\,\pmb{\varepsilon}_{i}

式中

\mathbf{A}_{i}\;=\;\frac{\partial\,{\mathbf{y}}_{i}}{\partial\theta}\,\Bigg|_{\theta=\theta_{c}(\,k\,)}\;\;\;\;\;\Delta\theta_{k}\;=\;\theta\,-\,\hat{\theta}_{c}(\,k\,)

令 \pmb{e}_{i}=\pmb{z}_{i}-\pmb{y}_{i}(\hat{\pmb{\theta}}_{c}(\pmb{k})) ,则式(5-206)为

\pmb{e}_{i}\;=\;\pmb{A}_{i}\Delta\pmb{\theta}_{k}\;+\;\pmb{\varepsilon}_{i}

设 {\pmb Q} 为正定矩阵，则由对噪声的假设知

\pmb{\varepsilon}_{i}^{\mathrm{T}}\pmb{Q}\pmb{\varepsilon}_{i}\leqslant\pmb{\delta}_{i}^{\mathrm{T}}\pmb{Q}\pmb{\delta}_{i}

故有

(\pmb{e}_{i}\,-\,\pmb{A}_{i}\Delta\pmb{\theta}_{k})^{\mathrm{T}}\pmb{Q}\,(\pmb{e}_{i}\,-\,\pmb{A}_{i}\Delta\pmb{\theta}_{k})\,=\,\pmb{\varepsilon}_{i}^{\mathrm{T}}\pmb{Q}\pmb{\varepsilon}_{i}\leqslant\pmb{\delta}_{i}^{\mathrm{T}}\pmb{Q}\pmb{\delta}_{i}

则

\sum_{i\,=\,1}^{N}\,(\,e_{i}\,-\,A_{i}\Delta\pmb\theta_{k}\,)^{\mathrm T}Q\,(\,e_{i}\,-\,A_{i}\Delta\pmb\theta_{k}\,)\leqslant\,\sum_{i\,=\,1}^{N}\delta_{i}^{\mathrm T}Q\delta_{i}

令

F\;=\;\sum_{i\;=\;1}^{N}\pmb{\delta}_{i}^{T}\pmb{Q}\pmb{\delta}_{i}

对式（5-209）进行整理可得

\big(\Delta\pmb{\theta}_{k}\,+\,\Delta\hat{\pmb{\theta}}_{c}(\,k\,)\big)^{\mathrm{T}}{\pmb{P}}_{k}^{-1}\big(\Delta\pmb{\theta}_{k}\,-\,\Delta\hat{\pmb{\theta}}_{c}(\,k\,)\big)\leqslant d_{k}

式中

\left\{\begin{array}{l}{{\displaystyle\Delta\hat{\pmb{\theta}}_{k}(\,k\,)\,=\,P_{k}\sum_{i=1}^{N}{\bf A}_{i}^{\,\top}Q e_{i}}}\\ {{\displaystyle P_{k}\,=\,\Big(\sum_{i=1}^{N}{\bf A}_{i}^{\,\top}Q{\bf A}_{i}\Big)^{-1}}}\\ {{\displaystyle d_{k}\,=\,F_{n}\,-\,\sum_{i=1}^{N}e_{i}^{\top}Q e_{i}\,+\,\Delta\hat{\pmb{\theta}}_{c}^{\,\top}(\,k\,)P_{k}^{\,-1}\Delta\hat{\pmb{\theta}}_{c}(\,k\,)}}\end{array}\right.\,

第 k+1 步迭代后参数的中心估计为

\hat{\pmb{\theta}}_{c}(\,k\,+\,1\,)\,=\,\hat{\pmb{\theta}}_{c}(\,k\,)\,+\,\Delta\hat{\pmb{\theta}}_{c}(\,k\,)

Q 阵为加权阵，可根据观测噪声的大小选取,或用残差来拟合。利用式(5-210)～式(5-212)反复迭代,直到收敛,则得到参数的中心估计 \pmb{\hat{\theta}}_{c} 以及与 \pmb{P_{k}}\setminus\pmb{d_{k}} 相应的 \pmb{P} 和 \pmb{d} 。事实上式(5-210)以椭球的形式给出了参数的一个集合BES估计，即

\mathrm{BES}=\left\{\,\pmb{\theta}:(\pmb{\theta}-\hat{\pmb{\theta}}_{c})^{\mathrm{T}}\pmb{P}^{-1}(\pmb{\theta}-\hat{\pmb{\theta}}_{c})\leqslant d\,\right\}

其中 \pmb{\hat{\theta}}_{c} —边界椭球的中心;

\pmb{P} —表征其形状；
d 一表征大小。

由于由式（5-205）可推出式（5-210），显然 \mathrm{BES}\mathrm{\equivFSS} ,称BES为参数可行集FSS的一个边界椭球描述,边界椭球BES近似描述了FSS的大小，但是这种方法计算的 d 往往较大，因而BES仅是对FSS的保守估计。

（2）参数的集员估计。下面给出两种方法，构造包含FSS并且尽可能小的集合，作为参数的集员估计。

\textcircled{1} 对 d 的修正（算法A)。对 d 修正的目的是为了使边界椭球尽可能小,并且包含FSS。式（5-213)给出边界椭球的中心和形状，其大小 d 应满足由式（5-207)以及噪声的假设所给出的每一个约束条件，在数学上可表示为

\begin{array}{r l}&{\operatorname*{max}\;d}\\ &{\mathbf{s}.\mathrm{~t~}.\Delta{\pmb{\theta}}^{\mathrm{T}}{\pmb{P}}^{-1}\Delta{\pmb{\theta}}\leqslant d}\end{array}

178

-\ \delta_{i j}\leqslant e_{i j}\,-\,A_{i j}\Delta\theta\leqslant\delta_{i j}\quad(j\,=\,1\,,\cdots,m\,;i\,=\,1\,,\cdots,N)

式中 \Delta\pmb{\theta}=\pmb{\theta}-\pmb{\hat{\theta}_{c}} \mathbf{A}_{i j}\longrightarrow\_{i} 时刻时矩阵 \pmb{A} 的第 j 行元素。

图 5-3(\,\alpha\,) 和图 5\!-\!3(\,b\,) 中两条直线表示式（5-214）中某一线性约束对（对应于某个 i\,,j\,) 中不等号取等号时所定义的两个超平面，两个超平面中间的点满足这对约束条件，则在这对约束条件下求出的边界椭球如图 5{\cdot}3(6) 所示，显然式（5-214）所求的边界椭球在满足所有这些约束对的边界椭球中是最小的，这个最小的边界椭球 BESMIN(称为内边界椭球)是 FSS 的子集。BESMIN 往往很小，并且很可能不包含参数真值，因此为了求出包含FSS并且尽可能小的椭球，可对某一对约束条件求出与图 5-3(\,a\,) 情形相同的椭球，然后在所有这些椭球中取最小的椭球（即修正 \b{d} )。这样给出的边界椭球既较小又包含参数真值，从而得到了系统参数的一-个较好的集员估计。

图 5-3边界椭球与约束超平面的相对位置

\circled{2} 投影方法（算法B)。式（5-211)给出了一个由测量空间到参数空间的映射，利用这个映射可以由某时刻模型输出的变化范围,得到以参数中心估计为中心的参数变化区间。由式(5-211)构造如下映射：

\Delta\pmb{\theta}\;=\;P A_{i}^{\mathrm{~T~}}\pmb{Q}\left(\pmb{y}_{i}\;-\;\hat{\pmb{y}}_{i}\right)

式中 {\bf\underline{{\upsilon}}}_{i}\longrightarrow i 时刻模型的真实输出;

\hat{\pmb{y}}_{i}\longrightarrow\pmb{\theta}=\pmb{\hat{\theta}}_{c} 时模型的估计输出；
P_{\setminus}{\bf A}_{i} 和 Q 与式(5-211)中的定义相同。

由对噪声的假设可知， \mathbf{{y}}_{i} 满足如下约束条件

S1:z_{i}\,-\,\hat{\bf y}_{i}\,-\,\hat{\bf s}_{i}\leqslant y_{i}\,-\,\hat{\bf y}_{i}\leqslant z_{i}\,-\,\hat{\bf y}_{i}\,+\,\hat{\bf\delta}_{{\pmb\theta}_{i}}\quad(\,i\,=\,1\,,2\,,\cdots,N)

在约束条件S1下，可得

\begin{array}{r}{\Delta\pmb\theta_{i\operatorname*{max}}=\operatorname*{max}_{s_{i}\in s_{1}}\!P A_{i}^{\mathrm{\scriptscriptstyleT}}\!Q\left(\,\pmb y_{i}\ -\ \hat{\pmb y}_{i}\,\right)}\\ {\Delta\pmb\theta_{i\operatorname*{min}}=\operatorname*{min}_{s_{i}\in s_{1}}P A_{i}^{\mathrm{\scriptscriptstyleT}}\!Q\left(\,\pmb y_{i}\ -\ \hat{\pmb y}_{i}\,\right)}\end{array}

令

\begin{array}{c}{\Delta\pmb{\theta}_{\operatorname*{max}}\,=\,\operatorname*{max}(\Delta\pmb{\theta}_{i_{\operatorname*{max}}},i\,=\,1,2,\cdots,N)}\\ {\Delta\pmb{\theta}_{\operatorname*{min}}\,=\,\operatorname*{min}(\Delta\pmb{\theta}_{i_{\operatorname*{min}}},i\,=\,1,2,\cdots,N)}\end{array}

则参数的区间估计是以中心估计 \pmb{\hat{\theta}}_{c} 为中心，以 \Delta\theta_{\mathrm{max}} 和 \Delta\theta_{\mathrm{min}} 中相应参数的绝对值较大者为半径的区间。这样就以直方体的形式给出了参数的集员辨识。当未知参数的个数 \pmb{\hat{p}}\geqslant m 时，由文献[32]中的引理2可知，参数的估计区间应乘以大于 \phi/m 的系数。

3）某飞行器纵向仿真算例飞行器纵向动力学方程和运动学方程组可近似如下

\begin{array}{l}{{u\,=\,-\,{\it w q}\,+\,T/\,m\,-\,q_{\infty}\,S C_{A}/\,m\,-\,g\mathrm{sin}\theta}}\\ {{v\,=\,{\it u q}\,+\,q_{\infty}\,S C_{N}/\,m\,+\,g\mathrm{cos}\theta}}\\ {{q\,=\,q_{\infty}\,S c_{A}C_{m}/\,I_{s}}}\\ {{\theta\,=\,q}}\end{array}

式中 T —推力矢量,其沿 _x 轴方向的安装角为 \mathbf{0}_{\circ}

设飞行器的气动力模型为

\begin{array}{l}{{C_{A}\;=\;C_{A0}\,+\,A C_{N}^{2}}}\\ {{C_{N}\,=\,C_{N0}\,+\,C_{N\alpha}\alpha\,+\,C_{N_{\alpha}3}\alpha^{3}\,+\,C_{N\delta_{e}}\delta_{e}}}\end{array}

180

C_{m}\;=\;C_{m0}\,+\,C_{m\alpha}\alpha\,+\,C_{m q}q\;+\;C_{m\delta_{e}}\delta_{e}

观测量取为法向过载 n_{z} 、轴向过载 n_{x} 、俯仰速率 q 和俯仰角 \theta_{0} 设气动力系数 C_{A0\,\setminus}A\,\,,\,C_{N0\,\setminus}\,C_{N a1\,\setminus}\,C_{N a3\,\setminus}\,C_{N\delta_{e}}\,C_{m0\,\setminus}\,C_{m a\,\setminus}\,C_{m q}\,,\,C_{m\delta_{e}} 为待辨识的未知参数，观测噪声取均匀分布的白噪声，其噪声上界分别为 0.2、0.2、0.9 和 0.9,大约为峰值的 10\,\% 。观测量个数m=4 ,所以算法B中放大系数 C>\mathrm{{}}\phi/\mathrm{{}}m=2.5 ,可取 C=3 。这两种方法辨识的结果列于表 5{\cdot}4 。从表5-4中可看出，两种算法给出的参数估计区间都包含参数的真值，而且都较小，因此两种算法都是可行的。

表5-4某飞行器纵向仿真辩识结果

<html>

参数真值	中心估计	算法 A区间估计	算法B区间估计
CAo = 0.05	0.04849	(0.04260:0.05438)	(0.04369;0.05329)
A =0.06	0.05958	(0.05622;0.06296)	(0.05798;0.06118)
Cvo = 1.13	1.114	(1.078;1.150)	(1.096;1.132)
Cnc =6.0	6.057	(5.901;6.213)	(5.990;6.124)
Cn3 = - 0.10	- 0.2259	(-0.8322;0.3804)	(-0.4839; -0.0321)
Cno = 0.45	0.5503	(0.2605;0.8401)	(0.3913;0.7093)
Cmo = 0.03	0.03193	(0.02756;0.03632)	(0.02999;0.03388)
-1.0	-- 0.9973	( - 1.013; -0.9813)	(- 1.003; -0.9911)
Cmg = -2.0	-1.967	(-2.221; -1.713)	(-2.086; -1.848)
= -1.60	-1.597	(-1.627; - 1.567)	(-1.612; -1.582)

</html>

集员辨识方法同时给出了未知参数的中心估计和区间估计，参数的估计区间，反映了参数可能变化的范围，因此参数估计区间越大，则其中心估计对参数真值的估计精度越低，这一点在表5-4中可以得到验证。从表5-4中可以看出，参数 C_{N\alpha3} 和 C_{N\delta_{e}} 的估计区间较大，其中心估计与真值的误差也较大，而其余参数的估计区间较小，因而其中心估计的估计精度也较高。这与辨识经验是一致的。由此可见，新方法是可行的而且比其他点估计方法给出了

更多的有用信息。

5.5 基于广义频率响应函数(GFRF)的系统辨识

本节利用沃特拉(Volterra)泛函级数来表示非线性系统的输人输出关系，以实现基于广义频率响应函数（GFRF)的面向鲁棒控制的系统辨识。由于沃特拉泛函级数的对称核不依赖于系统输人，完全反映了非线性系统的本质特性，因此分析沃特拉泛函级数的核就能分析出其所对应的系统的许多重要特性（如谐波特性、相互调制特性、增益压缩/扩张特性等）。由于频域法实际物理意义明确，便于实验，所设计的控制器具有鲁棒性，更重要的是工程师熟悉传统的频域法。因此分析非线性系统一般是先通过获得级数的频域核（即GFRF）,然后在频域里基于GFRF来分析非线性系统，从而为非线性鲁棒控制器的设计做好准备。可见，如何获得GFRF就显得尤其重要。本节将介绍基于GFRF的系统辨识。

5.5.1 多项式类非线性连续模型的 GFRF 描述

单输人单输出多项式类非线性系统一般可用下面的非线性微分方程来描述

\sum_{n=1}^{N}\,\bigg\{\sum_{p_{1}=0}^{M}\cdots\sum_{p_{n}=0}^{M}\bigg[\,a_{n\,,\,p_{1}},\cdots,p_{n}\,\prod_{i=1}^{n}D^{\hat{p}_{i}}y(\,t\,)\,+\sum_{1\leqslant m\leqslant n-1}b_{n\,,\,m\,,\,p_{1}},\cdots,p_{n}\,\bigg\}\bigg]\bigg\}

\prod_{i=1}^{m}\prod_{k=\,m+1}^{n}D^{\beta_{i}}y\left(\,t\,\right)\,\cdot\,D^{\beta_{k}}u\left(\,t\,\right)\,+\,\,c_{n\,,\,\beta_{1}},\cdots,\L_{p_{n}}\prod_{i=1}^{n}D^{\beta_{i}}u\left(\,t\,\right)\,\right]\Bigg\}\,=\,0

式中 D —微分算子；

M 一一微分的最大阶次；
N -一微分方程的最大乘方阶次；

u\left(\footnote{I n t.18192195.22966.2882892895.E-m a i l a d d r e s s:t a n g q u a n828@s j.e d u.b r} 和 y(t) 一分别代表系统的输人和输出；

\alpha_{n} 一一系统各阶输出的系数；
c_{n} 一一一系统各阶输人的系数；
b_{n} 一—一系统各阶输出与输人的交叉系数。

若式(5-219)具有沃特拉泛函级数的解,那么其输出 y\left(\footnote{I n t.18252:\eg i s a m m a.}\right) 在时域中可表示为

y(t)=\sum\limits_{n=1}^{\infty}y_{n}(t)

式中

y_{n}(\mathbf{\xi}_{t})\,=\,\int_{-\infty}^{\infty}\cdots\int_{-\infty}^{\infty}h_{n}(\,\tau_{1},\cdots,\tau_{n}\,)\prod_{i\,=\,1}^{n}u\,(\,t\,-\,\tau_{i}\,)\,\mathsf{d}\tau_{i}

式中 h_{n} 一—沃特拉泛函级数的 \pmb{n} 阶时域核,或称为系统的 \pmb{n} 阶广义脉冲响应函数

对上式进行傅里叶变换，则有

\tilde{y}(\omega)=\sum\limits_{n=1}^{\infty}\tilde{y}_{n}(\omega)

式中

\tilde{y}_{n}(\omega)=(2\pi)^{-(n-1)}\!\!\int_{-\infty}^{\infty}\!\!\cdots\!\!\int_{-\infty}^{\infty}\!\!\tilde{h}_{n}(\omega\,-\,\omega_{2}\,-\,\cdots\,-\,\omega_{n}\,,\omega_{2},\cdots,\omega_{n})\,\times

\tilde{u}\left(\,\omega\,-\,\omega_{2}\,-\,\cdots\,-\,\omega_{n}\,\right)\tilde{u}\left(\,\omega_{2}\,\right)\cdots\tilde{u}\left(\,\omega_{n}\,\right)

这里 \tilde{y}\,,\tilde{y}_{n}\,,\tilde{u}\,- 分别代表 y\,,y_{n}\,,u 的傅里叶变换；

h,一—沃特拉泛函级数的 \pmb{n} 阶频域核(通过 h_{n} 的 \pmb{n} 维傅里叶变换获得），被称为系统的 \pmb{n} 阶广义频率响应函数GFRF，可由如下公式表示

\begin{array}{l}{{\displaystyle\tilde{h}_{n}\left(\,\omega_{1}\,,\cdots,\omega_{n}\right)\,=\,F(\,h_{n}\left(\,\tau_{1}\,,\cdots,\tau_{n}\,\right)\,)\,=\,}}\\ {{\displaystyle\int_{\,-\infty}^{\infty}\cdots\!\!\int_{\,-\infty}^{\infty}h_{n}\left(\,\tau_{1}\,,\cdots,\tau_{n}\,\right)\,\prod_{i=1}^{n}\mathrm{e}^{-j\omega_{i}\tau_{i}}\mathrm{d}\,\tau_{i}}}\end{array}

由式(5-219)和式（5-222)知， \widetilde{h}_{\,n} 和 h_{n} 都是非参数模型，它们都不依赖于系统的输人信号，是系统的固有特性。

从非线性微分方程求解GFRF最经典的方法是谐波分析法，该方法给系统作用几种不同频率的正弦输人信号，通过分析其输出响应的谐波分量，从而得到它。文献[33]在这方面取得了有意义的进展，它提出了非线性微积分方程（NIDE或NDE）与GFRF间进行变换的解析公式。下面是一种更直观、计算量更小的递推算法[ 34] 。

对于一般的多项式非线性系统式（5-219），可得其GFRF为\begin{array}{r l}&{\tilde{h}_{1}(\omega_{1})\,=-\,A_{1}^{-1}\big(j\omega_{1}\big)\,C_{1}\big(j\omega_{1}\big)}\\ &{\tilde{h}_{2}\big(\omega_{1},\omega_{2}\big)\,=-\,A_{1}^{-1}\big(j(\omega_{1}+\omega_{2})\big)\big[c_{2}\big(j\omega_{1},j\omega_{2}\big)\,+}\\ &{\qquad\,A_{2}\big(j\omega_{1},j\omega_{2}\big)\tilde{h}_{1}\big(\omega_{1}\big)\tilde{h}_{1}\big(\omega_{2}\big)\,+\,B_{2}\big(j\omega_{1},j\omega_{2}\big)\tilde{h}_{1}\big(\omega_{1}\big)\big]}\\ &{\tilde{h}_{n}\big(\omega_{1},\cdots,\omega_{n}\big)\,=-\,A_{1}^{-1}\big(j\big(\omega_{1}+\cdots+\,\omega_{n}\big)\big)\,\big\{c_{n}\big(j\omega_{1},\cdots,j\omega_{n}\big)\,+}\end{array} \begin{array}{r l}&{\displaystyle\sum_{s=2}^{a}\sum_{k_{1}+k_{2}+\cdots+k_{s}=n}^{M}\left[A_{s}(j(\omega_{1}+\cdots+\omega_{k_{1}}),j(\omega_{k_{1}+1}+\cdots+\omega_{k_{1}+k_{2}}),\right.}\\ &{\cdots,j(\omega_{n-k_{s}+1}+\cdots+\left.\omega_{n}\right))\tilde{h}_{k_{1}}(\omega_{1},\cdots,\omega_{k_{1}})\tilde{h}_{k_{2}}(\omega_{k_{1}+1},\cdots,\omega_{k_{1}+k_{2}})}\\ &{\cdots\hat{h}_{k_{s}}(\omega_{n-k_{s}+1},\cdots,\omega_{n})\right]\left.+\right.}\end{array} \begin{array}{r l}&{\displaystyle\sum_{s=1}^{\beta}\sum_{l_{1}+l_{2}+\cdots+l_{s}=n-s}^{M}\left[B_{n}(j(\omega_{1}+\cdots+\omega_{l_{1}}),j(\omega_{l_{1}+1}+\cdots+\omega_{l_{1}+l_{2}}),\cdots,}\\ &{j\big(\omega_{n-s-l_{s}+1}+\cdots+\omega_{n-s}\big),j\omega_{n-s+1},\cdots,j\omega_{n}\big)\tilde{h}_{l_{1}}\big(\omega_{1},\cdots,\omega_{l_{1}}\big)\right.}\\ &{\left.\tilde{h}_{l_{2}}\big(\omega_{l_{1}+1},\cdots,\omega_{l_{1}+l_{2}}\big)\cdots\tilde{h}_{l_{s}}\big(\omega_{n-s-l_{s}+1},\cdots,\omega_{n-s}\big)\big]\right\}}\end{array}

式中

A_{n}\left(j\omega_{1},\cdots,j\omega_{n}\right)\;=\;\sum_{p_{1}=0}^{M}\sum_{p_{n}=0}^{M}a_{n}\,,_{p_{1}},\cdots,_{p_{n}}\prod_{i=1}^{n}\left(j\omega_{i}\right)^{p_{i}} B_{n}(j\omega_{1},\cdots,j\omega_{n})\,=\,\sum_{\rho_{1}=0}^{M}\cdots\sum_{p_{n}=0}^{M}\sum_{1\leqslant m\leqslant n}b_{n,m,\rho_{1},\cdots,p_{n}}\prod_{i=1}^{m}(j\omega_{i})^{\rho_{i}}\prod_{\substack{k=\,m+1}}^{n}(j\omega_{k}) C_{n}\left(\,j\omega_{1}\,,\cdots,j\omega_{n}\,\right)\;=\;\sum_{p_{1}\,=\,0}^{M}\cdots\sum_{p_{n}\,=\,0}^{M}c_{n\,,\,p_{1},}\cdots,p_{n}\prod_{i=1}^{n}\left(\,j\omega_{i}\right)^{p_{i}} (5 - 24)

\beta\,=\,{\left\{\begin{array}{l l}{n\,/2}\\ {(\,n\,-\,1\,)/2}\\ {N}\end{array}\right.}

利用式 (\,5\!-\!223\,)\!\sim 式(5-225）,则可用解析方法直接计算式(5-219)所描述的多项式类非线性系统的GFRF。

5.5.2 多项式类非线性离散模型的GFRF描述

辨识方法经常获得的是离散的有理模型，因此本节考虑多项式系统的离散非线性有理模型，这类非线性有理模型可表示为如下的通用形式

y(\mathbf{\boldsymbol{\mathit{t}}}\,)\,=\,\frac{Y_{a}\bigl(\,t\,;\pmb{\theta}_{a}\,,y\,,u\,\bigr)}{Y_{b}\bigl(\,t\,;\pmb{\theta}_{b}\,,y\,,u\,\bigr)}

式中 Y_{a}\left(\,t\,;\theta_{a}\,,y\,,u\,\right),\,Y_{b}\left(\,t\,;\theta_{b}\,,y\,,u\,\right) —分别表示分子多项式和分母多项式；

t=1\,,2\,,\cdots 为整数序列。

分子多项式 Y_{a}\left(\,t\,;\theta_{a}\,,y\,,\,u\,\right) 和分母多项式 Y_{b}\left(\;t\;;\theta_{b}\;,y\cdot\;u\;\right) 分别定义如下：

\begin{array}{l}{{\displaystyle Y_{a}\left(\,t\,;\pmb{\theta}_{a}\,,y\,,u\,\right)\,=\,}}\\ {{\displaystyle\sum_{m=1}^{N_{a}}\bigg[\sum_{p=0}^{m}\sum_{k_{1}=1}^{k_{a}}\cdots\sum_{k_{p+q}=1}^{k_{a}}\alpha_{p,q,k_{1}},\cdots,k_{p+q}\prod_{i=1}^{p}y\big(\,t\,-\,k_{i}\big)\underset{i=\,p+1}{\prod_{i=\,p+1}^{p+q}}u\left(\,t\,-\,k_{i}\,\right)\,\bigg]}}\end{array}

\begin{array}{r l r}{\lefteqn{\zeta_{b}\left(\,t\,;\pmb{\theta}_{b}\,,y\,,u\,\right)\ =\ }}\\ &{}&{\displaystyle\sum_{m=0}^{N_{b}}\bigg[\sum_{p=0}^{m}\sum_{k_{1}=1}^{k_{b}}\cdots\sum_{k_{p+q}=1}^{k_{b}}b_{p,q\,,k_{1}},\cdots,b_{p+q}\prod_{i=1}^{n}y\left(\,t\,-\,k_{i}\right)\prod_{i=\,p+1}^{p+q}u\left(\,t\,-\,k_{i}\,\right)\,\bigg]}\end{array}

式中 N_{b} 和 N_{a} 一一分别表示分子和分母的最大非线性度；

k_{a} 和 k_{b} 一分别是输人和输出的最大滞后量；

a\left(\,\cdot\,\right) 和 b(\,\cdot\,) 一分别是分子和分母多项式不同项的系数（对应于参数集 \pmb{\theta}_{a} 和 \pmb{\theta}_{b} )；

\pmb{\dot{p}}+\pmb{q}\ =\ \pmb{m}

考虑一个非线性有理模型来说明以上概念

y(t)=\frac{0.94y(t-1)-0.5y(t-2)+0.01u^{2}(t-2)+0.3u(t-3)}{1+0.42y(t-1)u(t-2)+0.02y^{2}(t-1)}

如果设

\alpha_{0,1,3}=0.3\,,\ \ \alpha_{1,0,3}=0.94\,,\ \ \ \ \alpha_{1,0,2}=\,-\,0.5\,,\ \ \alpha_{0,2,2,2}=0.01\,,

b_{1,1,1,1,2}=0\,.\,42\,,\;\;b_{2,0,1,1}=0\,.\,02

其余为0,则利用通式，就可获得上述非线性系统的有理模型，其中， \begin{array}{r}{,k_{a}=3\,,k_{b}=2\,,N_{a}=N_{b}=2\,\circ}\end{array}

对于多项式类非线性系统的非线性有理模型（5-226），其GFRF的递推计算公式为

\Big(b_{0,0}\,-\sum_{k_{1}=1}^{k_{a}}a_{1,0,k_{1}}\mathrm{e}^{-j(\omega_{1}+\cdots+\omega_{n})\,k_{1}}\Big)H_{n}\,(j\omega_{1},\cdots,j\omega_{n})\,=

\begin{array}{r l}&{\left(b_{0,0}-\sum_{i=1}^{n}a_{1,0,i}\mathrm{e}^{-\mathrm{i}\left(n+\frac{1}{n}\right)\pi}a_{1,1}\mathrm{e}^{\mathrm{i}\left(j\omega_{1},\cdots,i,\omega_{n}\right)t}\right)H_{n}\left(j\omega_{1},\cdots,j\omega_{n}\right)=}\\ &{\qquad\times\displaystyle\sum_{i=1}^{n}\sum_{s_{i}=1}^{n}a_{0,s_{i},\nu_{i}\cdots,s_{i}}\mathrm{e}^{-\mathrm{i}\left(j\omega_{1},\cdots,j\omega_{n}\right)t}+}\\ &{\qquad\displaystyle\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}a_{0,s_{i},\nu_{i}\cdots,s_{i}}\mathrm{e}^{-\mathrm{i}\left(j\omega_{1},\cdots,j\omega_{n}\right)t}+}\\ &{\qquad\displaystyle\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}a_{0,s_{i},\nu_{i}\cdots,s_{i}}H_{n,s_{i}}\left(j\omega_{1},\cdots,j\omega_{n}\right)+}\\ &{\qquad\displaystyle\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}a_{0,s_{i},\nu_{i}\cdots,s_{i}}\mathrm{e}^{-\mathrm{i}\left(j\omega_{1},\cdots,j\omega_{n}\right)t}+}\\ &{\qquad\displaystyle\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}a_{0,s_{i},\nu_{i}\cdots,s_{i}}\mathrm{e}^{-\mathrm{i}\left(j\omega_{1},\cdots,j\omega_{n}\right)t}+}\\ &{\qquad\displaystyle\prod_{s t=1}^{n}\sum_{s_{i}=1}^{n}\left(j\omega_{1},\cdots,j\omega_{n-1,s_{i}}-j\right)-}\\ &{\qquad\displaystyle\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}\sum_{s_{i}=1}^{n}b_{0,s_{i},\nu_{i}\cdots,s_{i}}e^{-\mathrm{i}\left(j\omega_{1},\nu_{i}\cdots,j\omega

\begin{array}{l}{{\displaystyle\Bigl(\,\sum_{i=1}^{n-q-1}H_{i}(j\omega_{1},\cdots,j\omega_{i})H_{n-i,p}(j\omega_{i+1},\cdots,j\omega_{n})\,\Bigr)-}}\\ {{\displaystyle\sum_{q=1}^{n-1}\sum_{p=1}^{n-q-1}\sum_{k_{1}=1}^{k_{b}}\cdots\sum_{k_{p+q}=1}^{k_{b}}b_{p,q,k_{1},\cdots,k_{p+q}}e^{-j(\omega_{n-q+1}k_{p+1}+\cdots+\omega_{n}k_{p+q})}\:\times}}\\ {{\displaystyle\Bigl(\,\sum_{i=1}^{n-q-p}H_{i}(j\omega_{1},\cdots,j\omega_{i})H_{n-q-i,p}(j\omega_{i+1},\cdots,j\omega_{n-q})\,\Bigr)}}\end{array}

式中 H_{n\,,\,p}(\,\cdot\,) 由递推公式求得，即

H_{n,\,p}(j\omega_{1},\cdots,j\omega_{n})\;=\;\sum_{i\,=\,1}^{n-\,p+1}H_{i}(j\omega_{1},\cdots,j\omega_{i})\;\times

H_{n-i,p-1}(j\omega_{i+1},\cdots,j\omega_{n})\mathrm{e}^{-j(\omega_{1}+\cdots+\omega_{i})k}\rho

当 {\mathfrak{p}}=1 时,递推结束。而 H_{n,1}(j\omega_{1},\cdots,j\omega_{n}) 具有如下性质

H_{n,1}(j\omega_{1},\cdots,j\omega_{n})\;=\;H_{n}(j\omega_{1},\cdots,j\omega_{n})\mathrm{e}^{-j(\omega_{1}+\cdots+\omega_{n})k_{1}} (5 - 231)由式（5-229）～式（5-231）,就可用解析的方法递推地计算模型式(5-226)的 \mathrm{GFRF{\:\:\:\:\:\:\:\:\:\:}}H_{1}\left(j\omega_{1}\right),H_{2}\left(j\omega_{1},j\omega_{2}\right),\cdots_{\circ} 以上给出的算法，计算的都是相应模型的非对称核，而非对称核不是惟一的，只有对称核才是惟一的。对称核可以通过非对称核的对称化来获得,即

H_{n}^{s y m}\left(\,j\omega_{1}\,,\cdots,j\omega_{n}\,\right)\,=\,\frac{1}{n!}\sum_{\left(\,\omega_{1},\cdots,\,\omega_{n}\,\right)\,}H_{n}\left(\,j\omega_{1}\,,\cdots,j\omega_{n}\,\right)

至此，无论多项式类非线性系统是连续的微分模型还是离散的差分模型，都可通过解析的方法递推获得其GFRF。

5.5.3 GFRF 的辨识方法

用系统辨识的方法获取GFRF有两条基本的途径。第一条途径是从频域数据直接辨识沃特拉泛函级数的核（GFRF）；另一条途径是先辨识时域沃特拉泛函级数的核一一广义脉冲响应函数（GIRF），然后利用GIRF与GFRF的关系得到GFRF。本节介绍后一种途径，同时利用模型结构确定的思想，去掉时域沃特拉泛函级数中不重要的核，达到减少待辨识核数量的目的，从而避免或减轻沃特拉泛函级数辨识中存在的“维数灾难”问题。

对于离散的时间系统,其 I/O 关系可表示成如下形式的离散沃特拉泛函级数

y(\mathbf{\xi}_{n}\,)\;=\;\sum_{k\,=\,1}^{\infty}y_{k}\bigl(\,n\,\bigr)\;\;\;\;(\,n\;=\;1\,,2\,,\cdots,N\,)

式中

y_{k}\left(\,n\,\right)\ =\ \sum_{{i_{1}}=\,-\infty}^{\infty}\cdots\sum_{{i_{k}}\,=\,-\infty}^{\infty}h_{k}\left(\,i_{1}\,,\cdots,i_{k}\,\right)u\left(\,n\,-\,i_{1}\,\right)\cdots u\left(\,n\,-\,i_{k}\,\right)

式中 u\left(\,n\,\right) —输人信号；

yx(n)——第k阶级数对输出的贡献为实数序列;

h_{k}\left(\mathbf{\chi}_{i_{\textrm{l}},}\cdots,\mathbf{\chi}_{i_{k}}\right)-\hphantom{\left(\mathbf{\chi}_{i_{k}}^{+}\right)}k 阶沃特拉泛函级数的时域核（ \pmb{k} 阶 GIRF);$N$ 一一数据长度。

在频域内离散的沃特拉泛函级数可表示为

\hat{y}(\,m\,)\,=\,\sum_{k\,=\,1}^{\infty}\hat{y}_{k}(\,m\,)

式中

\tilde{y}_{k}\left(\,m\,\right)\,=\frac{1}{\left(2\pi\right)^{k-1}}\sum_{i_{1}=-\infty}^{\infty}\cdots\sum_{i_{k}=-\infty}^{\infty}H_{k}\left(\,m\,-\,i_{2}\,-\,\cdots\,-\,i_{k}\,,i_{2},\cdots,i_{k}\,\right)\,\times

\tilde{\b u}\left(\,m\,-\,i_{2}\,-\,\cdots\,-\,i_{k}\,\right)\tilde{\b u}\left(\,i_{2}\,\right)\cdots\tilde{\b u}\left(\,i_{k}\,\right)

式中 \tilde{u}\left(\,i\,\right)- 输人信号的傅里叶变换；

yk（m）——-k 阶级数对频域输出的贡献;
H_{k}(\cdot\,)\!-\!-k 阶 GFRF;$N$ —数据长度；m——输出的频率。

从频域数据中直接辨识GFRF则是利用式（5-235）和式(5-236)来构造辨识算法。本节则利用式(5-233)和式(5-234)首先辨识 h_{k} (GFRF),然后利用 h_{k} 和 H_{k} 的关系得到相应的 GFRF

H_{k}\left(\,\omega_{1}\,,\cdots,\omega_{k}\,\right)\;=\;\sum_{i_{1}=0}^{\infty}\cdots\sum_{i_{k}}^{\infty}h_{k}\left(\,i_{1}\,,\cdots,i_{k}\,\right)\mathrm{e}^{\,-j\omega_{1}\,i_{k}\,\ldots\,}\mathrm{e}^{\,-j\omega_{k}\,i_{k}\,\ldots\,}

在实际应用中,只能取截断的沃特拉泛函级数(通常取3阶)和有限的记忆长度 L 来进行辨识。基于此,利用GIRF 的对称性，并考虑测量误差，由式（5-233）有

\begin{array}{r c l}{{}}&{{=}}&{{\displaystyle{y\big(\,n\,\big)+\,\varepsilon\big(\,n\,\big)\,=\,}}}\\ {{}}&{{}}&{{\displaystyle{\sum_{i=0}^{L-1}h_{1}(\,i\,)\,u\big(\,n\,-\,i\,\big)\,+\,\sum_{i=0}^{L-1}\sum_{j=i}^{L-1}s_{2}(\,i\,,j\,)h_{2}\ ,}}}\\ {{}}&{{}}&{{}}\\ {{}}&{{}}&{{\displaystyle{\left(\,i\,,j\,\right)u\big(\,n\,-\,i\,\big)\,u\big(\,n\,-\,j\,\big)\,+\,}}}\\ {{}}&{{}}&{{\displaystyle{\sum_{i=0}^{L-1}\sum_{j=i}^{L-1}\sum_{k=j}^{L-1}s_{3}(\,i\,,j\,,k)h_{3}(\,i\,,j\,,k)\ .}}}\end{array}

u\left(\,n\,-\,i\,\right)u\left(\,n\,-\,j\,\right)u\left(\,n\,-\,k\,\right)\,+\,\varepsilon\left(\,n\,\right)

(\,{\pmb n}\,=\,1,2,\cdots,N\,)

式中 \varepsilon(\,n\,) -测量误差；
{\mathfrak{s}}_{2}({\mathfrak{i}}\,,{\mathfrak{j}}\,)\,,{\mathfrak{s}}_{3}({\mathfrak{i}}\,,{\mathfrak{j}}\,,{\mathfrak{k}}\,) 权系数。

s_{3}(\textit{i},j,k)=\left\{\begin{array}{l l}{1}&{i\,=\,j\,=\,k}\\ {\,}\\ {3}&{i\,=\,j\ne k\quad\oplus\,}\\ {\,}\\ {6}&{i<j<\,k}\end{array}\right.\quad\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,i\,<j\,=\,\pm\pm\,k}\\ {\:\quad\:=\,\frac{1}{2}(\,i\,,j\,)\,=\,\left\{\begin{array}{l l}{1}&{i\,=\,j}\\ {2}&{i\,\neq\,j}\end{array}\right.\quad\mathrm{~(~\,~}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,\!\!\!\!\!\!\,\!\!\!\!\!\!\!\!\,\!\!\!\!\!\!\,\!\!\!\!\!\!\!\,\!\!\!\!\,\!\!\!\!\!\!\!\,\!\!\!\,\!\!\!\!\!\!\!\!\,\!\!\,\!\!\!\!\!\!\!\!\,\!\!\!\,\!\!\!\!\!\!\!\!\,\!\!\!\,\!\!\!\!\!\!\!\!\,\!\!\!\!\!\!\,\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!

将GIRF当作待辨识的未知系数，利用系统辨识方法获取GIRF。为此可将式（5-238）写成适合于辨识的形式。

\begin{array}{r}{\left[\begin{array}{l}{\alpha\left(n\right)}\\ {\vdots}\\ {\vdots}\\ {\alpha\left(n-L+1\right)}\\ {\alpha\left(n\right)\alpha\left(n\right)}\\ {\vdots}\\ {\alpha\left(n\right)\alpha\left(n\right)}\\ {\vdots}\\ {\alpha\left(a\right)\alpha\left(n-L+1\right)}\\ {\alpha\left(n-1\right)\alpha\left(n-1\right)}\\ {\vdots}\\ {\alpha\left(n-L+1\right)\alpha\left(n-L+1\right)}\\ {\alpha\left(n\right)\alpha\left(n\right)\alpha\left(n\right)}\\ {\vdots}\\ {\alpha\left(n\right)\alpha\left(n\right)\alpha\left(n-L+1\right)}\\ {\alpha\left(n\right)\alpha\left(n-L+1\right)}\\ {\vdots}\\ {\alpha\left(n\right)\alpha\left(n-1\right)\left(n-1\right)}\end{array}\right]\times}\end{array}

于是，式（5-238）可表示为

{\boldsymbol{z}}\left({\bf\xi}{\bf n}\,\right)\;=\;{\pmb u}{\pmb u}^{\mathrm{\bfT}}({\bf\xi}{\bf n}\,)\,{\pmb\theta}\;+\;{\pmb\varepsilon}\left({\bf\xi}{\bf n}\,\right)\quad({\bf\xi}{\bf n}\;=\;1,2,\cdots,N) (5 - 240)式（5-240）可进-步写成矩阵形式

{\bf Z}\;=\;{\bf P}\pm\;{\bf E}

式中 \mathbf{Z}\in R^{N} —系统输出的测量值,且第 \pmb{n} 个分量 Z_{n}=z\left(\,n\,\right) P\in R^{N\times L3} -信息矩阵且 \pmb{P} 的第 \pmb{n} 行为 {\pmb u}{\pmb u}^{\textup T}(\,n\,)

E\in R^{N} 一误差矢量且 E_{n}=\varepsilon\left(\,n\,\right)

\pmb{\theta}\in R^{L3} 一一待辨识的GIRF。

求式（5-241)的最小二乘解最经济的办法是直接求解法方程，但 \pmb{P}^{\mathrm{T}}\pmb{P} 条件数较大，抗病态能力较弱；最准确的方法是将 \pmb{P} 进行正交分解

\pmb{P}\;=\;\pmb{W}\pmb{A}

式中

W\,=\,\left[\,W_{1}\,,\,W_{2}\,,\cdots,\,W_{L3}\,\right]

是列正交的 N\times L3 矩阵，满足

{\pmb W}^{\mathrm{T}}{\pmb W}\,=\,{\pmb D}

\pmb{D} 是相应维数的正对角矩阵； \pmb{A} 是 L3\times L3 的上三角矩阵。

利用模型结构确定思想估计 \pmb\theta （GIRF)的问题归结为如何选择 \pmb{P} 的子集 \pmb{P}_{s}\in R^{N\times L s} 且 L s\!\leqslant\!L3 （对应于 W_{s} 和 \boldsymbol{A}_{s} ),并估计相应的 \pmb{\theta}_{s} 使残差充分小。残差定义为

\hat{E}\;=\;{\bf Z}\,-\,{\bf P}_{s}\pmb{\theta}_{s}\;=\;{\bf Z}\,-\,(\,{\cal P}_{s}{\bf A}_{\;s}^{\,-\,1})\,(\,{\bf A}_{s}{\pmb\theta}_{s}\,)\;=\;{\bf Z}\,-\,{\bf W}_{s}\,{\bf g}_{s}

则矢量 \mathbf{Z} 各分量的平方和为

\langle z\,,{\pmb Z}\rangle\,=\,\sum_{i\,=\,1}^{L s}g_{\,i}^{2}\langle\,{\pmb W}_{i}\,,{\pmb W}_{i}\,\rangle\,+\,\langle\,\hat{\pmb E}\,,\hat{\pmb E}\,\rangle

式中 \langle\,\cdot\,\rangle —矢量点乘；

g;—矢量 g, 的第i个分量；
\pmb{W}_{i} -矩阵 {\pmb W}_{s} 的第 _i 列矢量。

由式（5-242)可见，由于 \pmb{W}_{i} 的引人残差减小的比率为

\left[\,_{e r r}\,\right]_{i}\;=\;\frac{g_{\,i}^{2}\langle\,{\bf W}_{i}\,,\,{\bf W}_{i}\,\rangle}{\left\langle\,Z\,,Z\,\right\rangle}

由式（5-243）可见，基于正交化矩阵 P 的模型结构确定的思路是每次从 \pmb{P} 中选人一列矢量 \pmb{P}_{i} 使得对应的 [\,e r r\,] ：最大。基于修正的Gram-Schmidt 的模型结构的确定过程如下。

设 P_{i}^{(0)}=P_{i}\left(\,i=1,\cdots,L3\right) {\pmb Z}^{(0)}={\pmb Z} ,则模型结构的确定过程可采用如下的步骤实现：

k=1

g_{k}(\,i\,)\,=\,\frac{\langle\,P_{i}^{(k-1)},Z^{(k-1)}\,\rangle}{\langle\,P_{i}^{(k-1)},P_{i}^{(k-1)}\,\rangle}\quad(\,i\,=\,k\,,\cdots,L3)

\left[\,e r r_{k}\,\right]_{i}\;=\;\frac{(\,g_{k}(\,i\,)\,)^{2}\langle\,{\pmb P}_{i}^{(\,k\,-1)}\,,{\pmb P}_{i}^{(\,k\,-1\,)}\,\rangle}{\langle\,{\pmb Z}\,,{\pmb Z}\,\rangle}\;\;\;\;(\,i\;=\;k\,,\cdots,L3)

\left[\,e r r_{k}\,\right]_{j}\,=\,\operatorname*{max}\left\{\,\left[\,e r r_{k}\,\right]_{j}(\,i\,\in\,\{\,k\,,L3\,\}\,)\,\right\}

则矩阵 \pmb{P}^{(k-1)} 的第 j 列与第 k 列交换,为方便起见交换后的矩阵仍记为 \pmb{P}^{(k\mathrm{~-~}1)} ,同时矩阵 \mathbf{A}_{s} 中的第 j 列和第 \pmb{k} 列的前 k\sim1 个元素交换。记 \left[\,e r r_{k}\,\right]=\left[\,e r r_{k}\,\right]_{j},

（4）用MGS方法进行正交化：

\begin{array}{r l}&{W_{k}\ =\ P_{k}^{(k-1)}}\\ &{\alpha_{k i}\ =\ \frac{\langle\,W_{k},P_{i}^{(k-1)}\rangle}{\langle\,W_{k},W_{k}\,\rangle}\qquad(i\ =\ k+1,\cdots,L3)}\\ &{P_{i}^{(k)}\ =\ P_{i}^{(k-1)}\ -\ \alpha_{k i}W_{k}\quad(i\ =\ k+1,\cdots,L3)}\\ &{g_{k}\ =\ \frac{\langle\,W_{k},Z^{(k-1)}\,\rangle}{\langle\,W_{k},W_{k}\,\rangle}}\\ &{Z^{(k)}\ =\ Z^{(k-1)}\ -\ g_{k}W_{k}}\end{array}

(5)若 k\!<\!L3\!-\!1 ,且

1\,-\,\sum_{i\,=\,1}^{k}\,[\,e r r_{i}\,]\geqslant\rho

式中 \rho-{} 允许误差。

则令 k=k+1 ，重复步骤 (2)\sim 步骤（5）；否则进行第（6）步。

(6）解方程

\pmb{A}_{s}\pmb{\theta}_{s}\;=\;\pmb{g}_{s}

由于 \mathbf{A}_{s} (其元素由 \pmb{\alpha}_{k i} 组成）为上三角阵，式（5-247)经过简单的回代即可求解。在 \pmb\theta 中被保留的Volterra泛函级数的时域核 \pmb\theta_{s} 为与 {\pmb W}_{s} 的列对应的核，其余的则被取消，相应的GFRF则可用式(5-237)获得。

取与文献[35]相同的算例，即

z(t)=-\,0.64x(t)\,+\,x(t\,-\,2)\,+\,0.9x^{2}(t)\,+\,x^{2}(t\,-\,1)\,+\,\varepsilon(t) 输人信号取伪随机信号，噪声取幅值为输人信号十分之一的高斯白噪声，数据点数取512点，沃特拉的阶取为2阶，记忆长度取为20。

本文的方法成功地辨识出了与仿真模型结构相一致的模型，与仿真模型对应的时域核分别为：-0.6362，1.0027，1.0038，1.108。

图5-4线性传递函数估计（虚线）与理论（实线）幅频特性的比较

图5-5二次传递函数的理论幅频特性

将一阶核和二阶核分别做一维和二维傅里叶变换，可得线性传递函数和二次传递函数的幅频特性，如图5-4、图5-5和图5-6所示。线性传递函数理论最高值为1.64，而估计最高为1.639；二次传递函数的理论最高值为1.90，而估计最高为2.11。该方法在有较高测量噪声的情况下仍具有较高的估计精度，而且只用了512个测量数据；文献[35]将128000个时域数据分为2000段（每段64点），再分段进行傅里叶变换，然后直接估计频域核，在未考虑测量噪声的情况下，其估计精度仍然不高。这大概就是因为有限时窗效应引起的误差，因此对于非线性差分方程模型，可以考虑用时域的沃特拉泛函级数首先求得广义脉冲响应函数，然后再用傅里叶变换获得广义频率响应函数GFRF。

图5-6二次传递函数的估计幅频特性

5.5.4基于GFRF的H辨识

前面提出了辨识GFRF的简化方法，简化方法仅给出了GFRF的一个点估计，该点估计对应于非线性系统的一个标称模型，而面向鲁棒控制系统的设计不仅需要知道标称模型，还需要知道标称模型的不确定度，即以标称模型为一个元素的模型集，该模型集应尽可能小并包含非线性系统的真实模型。

辨识的不确定性主要受两方面原因的影响：第一，未测量到的外界输人的影响（扰动、测量误差等）；第二，辨识的模型与真实模型结构间的差别（这类误差被称为结构误差）。由于所采用的数学模型不可能完全描述系统的特性，总有一部分未建模动态未包含在所辨识的模型结构内，因此结构误差总是存在的。从理论上讲，无穷阶的沃特拉泛函级数能够精确地描述连续非线性函数所表征的非线性系统，但遗憾的是，在实际中现在最多采用有限记忆长度的三阶沃特拉级数，截断的沃特拉泛函级数必然会引起结构误差。

考虑结构误差，则式（5-238）变为

z(\,n\,)\,=y(\,n\,)\,+\,y^{u}(\,n\,)\,+\,\varepsilon(\,n\,)\,=

\sum_{i=0}^{L-1}h_{1}({\it i\phi})\,u\left(\,n\,-\,{\it i\phi}\right)\,+\,\sum_{i=0}^{L-1}\sum_{j=1}^{L-1}s_{2}({\it i\phi},{\it j\phi})\,\,.

\begin{array}{l}{{\displaystyle h_{2}\big(\,i\,,j\,\big)\,u\left(\,n\,-\,i\,\right)u\left(\,n\,-\,j\,\right)\,+}}\\ {{\displaystyle\sum_{i=0}^{L-1}\sum_{j=i}^{L-1}\sum_{k=j}^{L-1}s_{3}(\,i\,,j\,,k\,)\,h_{3}(\,i\,,j\,,k\,)\ .}}\end{array}

u\left(\,n\;-\;i\,\right)u\left(\,n\;-\;j\,\right)u\left(\,n\;-\;k\,\right)\;+

y^{u}\left(\,n\,\right)\;+\;\varepsilon\left(\,n\,\right)\quad(\,n\;=\;1\,,2\,,\cdots,N\,)

式中 y^{u}\left(\,n\,\right) ——结构误差(未建模动态对输出的贡献)；

其余变量的定义与式（5-238）同。

下面分析 y^{u}\left(\,n\,\right) 的大小。设 \tilde{u} 是时域输人信号 \pmb{u} 的傅里叶变换,定义频域的 H_{P} 范数和 H_{\infty} 范数分别定义为

\begin{array}{r}{\left\|\begin{array}{l}{\bar{\textbf{\i}}\displaystyle\|_{\textbf{\em p}}=\left[\frac{1}{2\pi}\displaystyle\sum_{\omega=-\infty}^{\infty}\textbf{\ i}\,\tilde{u}\left(\omega\right)\textbf{\|}^{\rho}\right]^{1/\rho}\leqslant\infty\,;}\\ {\left\|\begin{array}{l}{\tilde{u}\,\left\|\mathbf{\omega}_{\infty}\right\|_{\infty}\,=\,\displaystyle\operatorname*{sup}_{\omega\in\,R}\textbf{\|}\,\tilde{u}\left(\omega\right)\textbf{\|}\ll\infty}\end{array}\right.}\end{array}

\pmb{n} 阶 GFRF( H_{n} )的 H_{\infty} 范数定义为

\parallel H_{n}(\,\omega_{1}\,,\cdots,\omega_{n}\,)\parallel_{\infty}\,=\,\operatorname*{sup}_{\omega_{1},\cdots,\,\omega_{n}\leqslant R}\mid H_{n}(\,\omega_{1}\,,\cdots,\omega_{n}\,)\mid\leqslant\infty

引理5.1假如二阶 \mathrm{GFRF}H_{2}(\,\omega_{1}\,,\omega_{2}) 的 H_{\infty} 范数 \|\ H_{2}(\omega_{1} \omega_{2})\parallel_{\infty} 存在,对于 \tilde{u}\in H_{1}\cap H_{2} ，且

\tilde{y}_{2}(\omega)\;=\;(2\pi)^{-1}\!\sum_{\omega_{2}=-\,\omega}^{\infty}H_{2}(\,\omega\,-\,\omega_{2}\,,\omega_{2}\,)\,\tilde{u}\,(\,\omega\,-\,\omega_{2}\,)\,\tilde{u}\,(\,\omega_{2}\,)

那么

\parallel\tilde{y}_{2}\parallel_{2}\leqslant\parallel H_{2}(\omega_{1},\omega_{2})\parallel_{\infty}\parallel\tilde{u}\parallel_{1}\parallel\tilde{u}\parallel_{2}

证明：|\tilde{\textbf{\i}}_{\partial_{2}}|^{2}\,=\,|\,\,(2\pi)^{-1}\sum_{\omega_{2}=\,-\infty}^{\infty}H_{2}(\omega\,-\,\omega_{2}\,,\omega_{2})\,\tilde{u}\,\bigl(\,\omega\,-\,\omega_{2}\,\bigr)\,\tilde{u}\,\bigl(\,\omega_{2}\,\bigr)\,\;|^{2}\leqslant \left[\,\left(2\pi\right)^{-1}\sum_{\omega_{2}=-\infty}^{\infty}\;\mid H_{2}\!\left(\omega\,-\,\omega_{2}\,,\omega_{2}\right)\tilde{u}\left(\omega\,-\,\omega_{2}\right)\tilde{u}\left(\omega_{2}\right)\,\mid\,\right]^{2}\,= \left[\,\left(2\pi\right)^{-1}\sum_{\omega_{2}=-\infty}^{\infty}\;\mid H_{2}\!\left(\omega\;-\;\omega_{2}\,,\omega_{2}\right)\,\tilde{u}\left(\omega_{2}\right)\;\mid^{1/2}\;\mid\;\tilde{u}\left(\omega\;-\;\omega_{2}\right)\;\mid\;\cdot \begin{array}{l}{{\displaystyle\mid H_{2}(\omega\,-\,\omega_{2}\,,\omega_{2})\,\tilde{u}\,(\omega_{2})\,\mid^{1/2}\right]^{2}\leqslant}}\\ {{\displaystyle\bigg\{\,(2\pi)^{-1}\bigg[\sum_{a_{2}=-\,\infty}^{\infty}\,\mid H_{2}(\omega\,-\,\omega_{2}\,,\omega_{2})\,\tilde{u}\,(\omega_{2})\,\parallel\,\tilde{u}\,(\omega\,-\,\omega_{2})\,\,\mid^{2}\bigg]^{1/2}\;.}}\\ {{\displaystyle\sum_{a_{2}=-\,\infty}^{\infty}\,\mid H_{2}(\omega\,-\,\omega_{2}\,,\omega_{2})\,\tilde{u}\,(\omega_{2})\,\mid\,\Big]^{1/2}\,\bigg\}^{2}\;=}}\\ {{\displaystyle\langle\,2\pi\rangle^{-2}\bigg[\sum_{a_{2}=-\,\infty}^{\infty}\,\mid H_{2}(\omega\,-\,\omega_{2}\,,\omega_{2})\,\tilde{u}\,(\omega_{2})\,\parallel\,\tilde{u}\,(\omega\,-\,\omega_{2})\,\mid^{2}\bigg]\;.}}\end{array} \left[\,\sum_{\omega_{2}\,=\,-\,\infty}^{\infty}\;|\;\,H_{2}(\,\omega\,-\,\omega_{2}\,,\omega_{2}\,)\,\tilde{u}\,(\,\omega_{2}\,)\,\mid\,\right]

则

\begin{array}{r l}&{\|\hat{\mathbf{y}}_{2}\|^{2}=(2\pi)^{-1}\displaystyle\sum_{s=0}^{n}\mid\hat{\mathbf{y}}_{2}\mid^{2}}\\ &{(2\pi)^{-1}\displaystyle\sum_{s=0}^{n}\left\langle(2\pi)^{-1}\left\langle\sum_{s=0}^{\infty}\mid\hat{\mathbf{H}}_{2}(u-u_{2},u_{2})\right.\cdot}\\ &{\left.\hat{u}_{1}(u_{2})\mid\hat{\mathbf{l}}_{1}(u-u_{2})\mid^{2}\right\rangle\times}\\ &{\left.\Big\langle\sum_{s=0}^{n}\mid\hat{\mathbf{H}}_{2}(u_{2}-u_{2},u_{2})\hat{\mathbf{l}}_{1}(u_{2})\mid\Big]\right\rangle\leqslant}\\ &{\left.\phantom{\sum_{s=0}^{n}}\displaystyle\sum_{s=-\infty}^{n}\hat{\big\langle}\sum_{s=0}^{(2\pi)^{-1}}\left\langle\sum_{s=0}^{n}\mid\hat{\mathbf{H}}(u-u_{2},u_{2})\hat{\mathbf{u}}(u_{2})\mid\hat{\mathbf{l}}(u-u_{2})\mid^{2}\right\rangle}\\ &{\|\hat{\mathbf{H}}_{2}(u_{2}-u_{2})\|\circ\|\hat{\mathbf{l}}_{1}\|_{1}\leqslant}\\ &{\|\hat{\mathbf{H}}_{2}(u_{1},u_{2})\|^{2}=\|\hat{\mathbf{l}}_{1}\|_{2}(2\pi)^{-1}\displaystyle\sum_{s=0}^{n}\mid\hat{\mathbf{u}}(u_{2})\mid\sum_{s=0}^{n}\mid\hat{\mathbf{u}}(u-u_{2})\mid^{2}\leqslant}\\ &{\|\hat{\mathbf{H}}_{2}(u_{2},u_{2})\|^{2},\|\hat{\mathbf{l}}\|_{1},\|\hat{\mathbf{l}}\|_{1}^{2}}\end{array}
$$H2(@1,w2) Il2HuIl 1 Hu I 1 ll u 112  

引理5.2假如n阶 GFRF H,（∞1,∞2，,∞,)的 H∞范数$\parallel\,H_{n}\left(\,\omega_{1}\,,\omega_{2}\,,\cdots,\omega_{n}\,\right)\,\parallel\,.$ 存在， $\hat{u}\in H_{1}\textrm{I}H_{2}$ ,且  

\tilde{y}{n}(\omega)=(2\pi)^{-(n-1)}\sum{\omega_{2}=-\infty}^{\infty}\cdots\sum_{\omega_{n}=-\infty}^{\infty}H_{n}(\omega,-,\omega_{2},-,\cdots,-,\omega_{n},,\omega_{2},\cdots,\omega_{n}),,\cdot

\tilde{u}\left(,\omega,-,\omega_{2},-,\cdots,-,\omega_{n},\right),{\boldsymbol{\cdot}},,\tilde{u}\left(,\omega_{2},\right),{\boldsymbol{\times}},,\cdots,{\boldsymbol{\times}},,\tilde{u}\left(,\omega_{n},\right)

\tilde{y}{n}(\omega),=(2\pi)^{-(n-1)}\sum{\omega_{2},=,-\infty}^{\infty},-,\sum_{\omega_{n},=,-\infty}^{\infty}H_{n}(\omega,-,\omega_{2},-,\cdots,-,\omega_{n},,\omega_{2},\cdots,\omega_{n}),,.

\tilde{u}\left(,\omega,-,\omega_{2},-,\cdots,-,\omega_{n},\right),\cdot,\tilde{u}\left(,\omega_{2},\right),\times,\cdots,\times,\tilde{u}\left(,\omega_{n},\right)

  

那么  

\lVert\tilde{\boldsymbol{y}}{n}\rVert{2}\leqslant\lVert,H_{n}(,\omega_{1},\omega_{2},\cdots,\omega,),\rVert_{\infty}\parallel_{\infty}\parallel\tilde{\boldsymbol{u}}\parallel_{1}^{n-1}\lVert,\tilde{\boldsymbol{u}}\rVert_{2}

  

证明：其证明过程与引理5.1的证明过程类似（略）。  

定理5.1假如非线性系统存在沃特拉级数解式(5-233）,控制输人平方可积，它的傅里叶变换 $\tilde{u}\in H_{1}\mathrm{~I~}H_{2}$ ,即存在 $L U\!>\!0$ 使得  

\parallel\tilde{\textbf{\em u}}\parallel_{2}\leqslant L U\quad\perp\tilde{\textbf{\textit{u}}}\parallel\tilde{\textbf{\em u}}\parallel_{1}\leqslant L U

  

并且假设 GFRF 的 $H_{\infty}$ 范数按指数衰减,即存在 $M{\gtrsim}0\,,\rho\!<\!1$ 且$\rho\!<\!1/L U$ ，使得  

\begin{array}{r}{\parallel H_{n}(j\omega_{1},j\omega_{2},\cdots,j\omega_{n},)\parallel_{\infty}\ll M\rho^{n}\quad(,n;=;1,\cdots,\infty,)}\end{array}

  

那么从 $_m$ 阶截断Volterra级数引l起的误差为  

\parallel y^{u}\parallel_{2}\leqslant\frac{1}{2\pi},\frac{M\rho_{1}^{m}}{1,-,\rho_{1}}

  

其中 $\rho_{1}=\rho\cdot L U$  

证明：因非线性系统存在沃特拉级数解，则  

y(,t,);=;\sum_{n,=,1}^{\infty}y_{n},(,t,);;;;;;;;;y^{u},(,t,);=;\sum_{n,=,m}^{\infty}y_{n},(,t,)

\tilde{y}^{u}(,\omega,),=,F(,y^{u}(,t,),),=,\sum_{n,=,m}^{\infty}F(,y_{n}(,t,),),=,\sum_{n,=,m}^{\infty}\tilde{y}_{n}\left(,\omega,\right)

\tilde{y}{n}(\omega),=,(2\pi)^{-(n-1)}!\sum{\omega_{2},=,-,\omega}^{\infty}\cdots!\sum_{\omega_{n},=,-,\omega}^{\infty}H_{n}(\omega,-,\omega_{2},-,\cdots,-,\omega_{n},,\omega_{2},\cdots,\omega_{n})

\tilde{u}\left(,\omega,-,\omega_{2},-,\cdots,-,\omega_{n},,\omega_{2},,^{\cdots},,\omega_{n},\right)\tilde{u}\left(,\omega_{2},\right)\cdots\tilde{u}\left(,\omega_{n},\right)

  

根据引理5.2和帕塞瓦（Parseval）公式有  

\parallel_{!!!\mathrm{!!{\caly}}}!!!^{u}\parallel_{!!!!2};=;(2\pi)^{,-1}\parallel_{!!!!\mathrm{!!y}}!!!^{u}\parallel_{!!!!2}\leqslant

(2\pi)^{-1}\sum_{n=\ m}^{\infty}\parallel\widetilde{y}{n}(\mathbf{\Sigma}\omega)\parallel{2}\leqslant

(2\pi)^{-1}\sum_{n,=,m}^{\infty}\parallel H_{n}(,\omega_{1},,\omega_{2},,\cdots,\omega_{n},)\parallel_{\infty}\parallel,\Tilde{u}\parallel_{1}^{n,-1}\parallel\Tilde{u}\parallel_{2}\leqslant

(2\pi)^{-1}\sum_{n,=,m}^{\infty}M\rho^{n},\cdot,L U^{n},=,\frac{1}{2\pi},\cdot,\frac{M\rho_{1}^{m}}{1,-,\rho_{1}}

  

证毕。  

显然，假定记忆长度足够长，式（5-248）中的截断误差为  

\parallel{\cal y}^{u}\parallel_{2}\leqslant{\varepsilon}^{u},=,\frac{1}{2\pi},\frac{M\rho_{1}^{4}}{1,-,\rho_{1}}

  

仿照式（5-241），把考虑截断误差（即结构误差）的式（5-248）写成矩阵形式有  

{\cal Z};=;P\theta;+;{\cal Y}^{u};+;{\cal E}

  

式中 ${\pmb Y}^{u}$ —一以 $y^{u}\left(\,n\,\right)$ 为分量的矢量；  

其余矢量的分量的定义与式（5-240）同。  

设观测噪声的功率是有界的，即存在 $\varepsilon^{E}{\geqslant}0$ ，使得  

\frac{1}{\sqrt{N}}\parallel\boldsymbol{E}\parallel_{2}\leqslant\epsilon^{E}

  

将式(5-256)变换为  

{\textbf{Z}}-,P\pmb{\theta};=;\pmb{Y}^{\pmb{u}},+,\pmb{E}

  

则式（5-258）两边同取 2范数，有  

\begin{array}{l}{\left|\textbf{Z}-\pmb{P}\pmb{\theta}\right|{\textnormal{2}}=\left|\textbf{Y}^{u}\right.+\pmb{E}\parallel{2}\leqslant}\ {\left|\textbf{Y}^{u}\parallel_{2}+\parallel\pmb{E}\parallel_{2}\leqslant\varepsilon^{u},+,\sqrt{N}\varepsilon^{E}}\end{array}

  

于是,集合  

F S;=;\left{,\pmb{\theta},\in,R^{L3}:;|\textbf{Z}-\pmb{P\theta},|_{;2},\right};\leqslant;\pmb{\varepsilon}^{u};+;\sqrt{N}\pmb{\varepsilon}^{E}

  

包含所有的与观测数据、测量噪声的先验信息和结构误差的先验信息相一致的沃特拉级数的时域一阶、二阶和三阶核。这个集合称为沃特拉级数的时域一阶、二阶和三阶核 $h_{1},h_{2}$ 和 $\pmb{h}_{3}$ 的可行集。  

$H_{\infty}$ 辨识误差(局部误差)定义为考虑所有可行的时域一阶、二阶和三阶核 $h_{1},h_{2}$ 和 $\pmb{h}_{3}$ ,在最差情况下的相应阶次的广义频率响应函数的误差(即误差的 $H_{\infty}$ 范数)。定义一阶GFRF的 $H_{\infty}$ 辨识误差为  

J_{1}(,\Phi,);=;\operatorname*{sup}{h{1},=,\theta^{1}\in,F!S},\left|,,H_{1}(,h_{1},,\omega,),-,H_{1}(,\Phi(,Z,),,\omega,),,\right|;_{\infty}

  

定义二阶GFRF的 $H_{\infty}$ 辨识误差为  

J_{2}(,\Phi,),=,\operatorname*{sup}{\begin{array}{c}{h{2}=\theta^{2}\in,F!!\5}},\parallel H{2}(,h_{2},,\omega_{1},,\omega_{2},),-,H_{2}(,\Phi(,Z,),,\omega_{1},,\omega_{2},),\parallel_{\infty}

  

定义三阶 GFRF 的 $H_{\infty}$ 辨识误差为  

J_{3}(,\pmb\Phi,),=,\operatorname*{sup}{\pmb{h}{3},=,\pmb\theta^{3}\in,F S},\parallel,H_{3}(,\pmb{h}{3},,\pmb{\omega}{1},,\pmb{\omega}{2},,\pmb{\omega}{3},),-

H_{3}(,\Phi(,Z),,\omega_{1},,\omega_{2},,\omega_{3},),\left|\mathbf{\Omega}_{\infty}\right.

  

最小可能达到的 $H_{\infty}$ 辨识误差 $R$ 称为信息半径  

R,=,\operatorname*{inf}_{\phi}J(\phi)

  

利用文献[36]的主要结果，最小二乘法估计  

\pmb{\theta}^{\star}\ =\ \pmb{\Phi}^{L S}(\pmb{Z})\ =\ (\pmb{P}^{\mathrm{T}}\pmb{P})^{-1}\pmb{P}^{\mathrm{T}}\pmb{Z}

  

是使 $H_{\infty}$ 辨识误差达到最小的最优辨识算法  

R,=,J\bigl(,\Phi^{L S},\bigr)\leqslant J\bigl(,\Phi,\bigr),\quad\forall,,\Phi

  

下面确定 $R$ 的值。定义  

\begin{array}{r}{F_{1}(,\omega,),=,\left[!!\begin{array}{l}{1,\mathrm{Re}{\big[\mathrm{e}^{-j\omega},\big]},,\mathrm{Re}{\big[\mathrm{e}^{-j2\omega},\big]},,\cdots,\mathrm{Re}{\big[\mathrm{e}^{-j L\omega},\big]},,0,,\cdots,0}\ {0,,\mathrm{Im}{\big[\mathrm{e}^{-j\omega},\big]},,\mathrm{Im}{\big[\mathrm{e}^{-j2\omega},\big]},,\cdots,\mathrm{Im}{\big[\mathrm{e}^{-j L\omega},\big]},,0,,\cdots,0}\end{array}!!\right]}\end{array}

\begin{array}{r l r}{\lefteqn{\hat{\tau}{2}(\omega{1},\omega_{2}),=,\left[!!\begin{array}{l}{0,\cdots,0,1,\mathrm{Re}[\mathrm{e}^{-j\omega_{2}}],\cdots,\mathrm{Re}[\mathrm{e}^{-j\omega_{2}}],\mathrm{Re}[\mathrm{e}^{-j(\omega_{1}+\omega_{2})}]\right],\ }}\ &{}\ {0,\cdots,0,0,1\mathrm{m}[\mathrm{e}^{-j\omega_{2}}],\cdots,\mathrm{Im}[\mathrm{e}^{-j L\omega_{2}}],,\mathrm{Im}[\mathrm{e}^{-j(\omega_{1}+\omega_{2})}],,\ }\ &{}\ {\cdots,\mathrm{Re}[\mathrm{e}^{-j L(\omega_{1}+\omega_{2})},],0,\cdots,0}\ &{}\ {\cdots,\mathrm{Im}[\mathrm{e}^{-j L(\omega_{1}+\omega_{2})},],0,\cdots,0}\end{array}!!\right],}&{}&{(5-268)}\end{array}

\begin{array}{r}{F_{3}(,\omega_{1},,\omega_{2},,\omega_{3},);=;\left[!!\begin{array}{c}{0,,\cdots,0,,1,,\mathrm{Re}[,\mathrm{e}^{-j\omega_{3}},],,\cdots,\mathrm{Re}[,\mathrm{e}^{-j L\omega_{3}},],,}\ {0,,\cdots,0,,0,,\mathrm{Im}[,\mathrm{e}^{-j\omega_{3}},],,\cdots,\mathrm{Im}[,\mathrm{e}^{-j L\omega_{3}},],,}\end{array}!!\right]}\end{array}

\begin{array}{r l}&{\mathrm{Re}[,\mathrm{e}^{-,j\left(\omega_{2}+\omega_{3}\right)},],,\cdots,\mathrm{Re}[,\mathrm{e}^{-,j L\left(,\omega_{1}+\omega_{2}+\omega_{3}\right)},]}\ &{\mathrm{Im}[,\mathrm{e}^{,,j\left(,\omega_{2}+\omega_{3}\right)},],,\cdots,\mathrm{Im}[,\mathrm{e}^{-,j L\left(,\omega_{1}+\omega_{2}+\omega_{3}\right)},]}\end{array}

  

下面的结果显示了怎样确定信息半径 $R$  

定理5.2对于式（5-256）的系统，信息半径分别为  

R_{1},=,J_{1}(,\Phi^{L S}),=,\operatorname*{sup}{0\leqslant\omega\leqslant\pi}\bar{r},{F{1}(,\omega,)(,P^{\mathrm{,T}}P,)^{,-1}F_{1}^{\mathrm{,T}}(,\omega,),},{,.

\sqrt{N[,(,\varepsilon^{u}/,\sqrt{,N,}+,\varepsilon^{E},)^{2},-,\varepsilon_{,r}^{2},]}

R_{2},=,J_{2}\bigl(,\Phi^{L S}\bigr),=\operatorname*{sup}{\substack{0\leqslant\omega{1},,\omega_{2}\leqslant\pi}}\bar{r},\bigl{,F_{2}\bigl(,\omega_{1},,\omega_{2}\bigr)\bigl(,P^{\top}P,\bigr)^{,-1}F_{2}^{\top}\bigl(,\omega_{1},,\omega_{2},\bigr),\bigr}

\sqrt{N[,(,\varepsilon^{u}/,\sqrt{N},+,\varepsilon^{E},)^{2},-,\varepsilon_{,r}^{2},]}

\begin{array}{r l r}{\lefteqn{R_{3}=\ J_{3}(,\Phi^{L S})}}\ &{}&{=\operatorname*{sup}{0\leqslant\omega{1},\omega_{2},\omega_{3}\leqslant\pi}\bar{r},\big{F_{3}(,\omega_{1},,\omega_{2},,\omega_{3})\big(,P^{\mathrm{T}}P,\big)^{-1}F_{3}^{\mathrm{T}}(,\omega_{1},,\omega_{2},,\omega_{3}),\big},\mathrm{.}}\end{array}

\sqrt{N[,(,\varepsilon^{u}/,\sqrt{,N,}+,\varepsilon^{E},)^{2},-,\varepsilon_{,r}^{2},]}

  

式中 $\bar{r}=\{\cdot\}-$ 对称正定矩阵最大特征值的平方根  

\pmb{\upvarepsilon}_{r}^{2};=;(1/N)(,{\bf Z},-,{\pmb P}{\pmb\theta}^{,},)^{\mathrm{T}}(,{\pmb Z},-,{\pmb P}{\pmb\theta}^{,},)

  

证明：可行集FSS(见式(5-260))可表示成[36]  

\begin{array}{r}{F S;=;\mid\pmb\theta\in;R^{L3}\mid;(\pmb\theta,-,\pmb\theta^{\star},)^{\intercal}(,{\pmb P}^{\intercal}{\pmb P},)(,\pmb\theta,-,\pmb\theta^{\star},)\leqslant;}\ {n,[,(1/,\sqrt N\pmb\varepsilon^{u},+,\pmb\varepsilon^{E},)^{2},-,\varepsilon_{r}^{2},],;\qquad\qquad\qquad(}\end{array}

  

由于  

\begin{array}{r}{\left[,\mathrm{Re}(,H_{1}(,\omega),),\right]=,F_{1}(,\omega,),{\pmb\theta}}\ {\left[,\mathrm{Im}(,H_{1}(,\omega),),\right]=,F_{1}(,\omega),{\pmb\theta}}\end{array}

\begin{array}{r}{{\small\left[\operatorname{Re}(H_{2}(,\omega_{1},,\omega_{2},),),\right]}=,F_{2}(,\omega_{1},,\omega_{2},),\theta}\ {{\small\left[\operatorname{Im}(,H_{2}(,\omega_{1},,\omega_{2},),),\right]}=,F_{2}(,\omega_{1},,\omega_{2},),\theta}\end{array}

{\Bigg[}\operatorname{Re}(,H_{3}(,\omega_{1},,\omega_{2},,\omega_{3},),){\Bigg]}=;F_{3}{\big(},\omega_{1},,\omega_{2},,\omega_{3},{\big)},\pmb{\theta}

  

于是，一阶GFRF的 $H_{\infty}$ 辨识误差为  

R_{1}(,\omega,),=,\operatorname*{sup}{\stackrel{h{1}=\theta^{1}\in\cal{F S}}{\theta^{1}\in\cal{F S}}},\mid,H_{1}(,h_{1},,\omega,),-,H_{1}(,\tilde{\phi}^{L s}(,Z,),,\omega,),\mid,=

\operatorname*{sup}{\pmb{h}{1}=\pmb{\theta}^{1}\in E S}\left|\pmb{\ F}{1}\big(\pmb{\omega}\big)\big(\pmb{\theta},-,\pmb{\theta}^{\star},\big),\right|{2}

  

二阶 GFRF 的 $H_{\infty}$ 辨识误差为  

R_{2}(\omega_{1},\omega_{2});=;\operatorname*{sup}{\stackrel{h{2}=\theta^{2}\in F\mathrm{S}}{h_{2}=\theta^{2}\in F\mathrm{S}}};\mid;H_{2}(h_{2},\omega_{1},\omega_{2});-;H_{2}(\Phi^{I S}(Z),\omega_{1},\omega_{2});\mid;=

\operatorname*{sup}{h{2}=\theta^{2}\in F S};\big|;F_{2}\big(\omega_{1},,\omega_{2}\big)\big(,\pmb\theta,-,\pmb\theta^{\mathrm{*}}\big)\big|_{2}

  

三阶 GFRF 的 $H_{\infty}$ 辨识误差为  

\begin{array}{r l r}&{\omega_{1},,\omega_{2},,\omega_{3}}\end{array}\right)\ =}&{\omega_{1},,\omega_{2},,\omega_{3}}\ &{\begin{array}{l l}{\displaystyle\operatorname*{sup}{\mathbf{\omega}{h}=\mathbf{\omega}^{3}\in\cal{\cal{F}}^{\mathrm{S}}}\ |\ {\cal{H}}{3}(\mathbf{\omega}{1},\omega_{1},\omega_{2},,\omega_{3})\ -\ {\cal{H}}{3}(\mathbf{\omega}\mathbf{\omega}^{2,,\omega}(\mathbf{\omega}^{\mathbb{Z}}),,\omega{1},,\omega_{2},,\omega_{3})\ |=}\ {\displaystyle\operatorname*{sup}{\mathbf{\omega}{h}=\mathbf{\omega}^{3}\in\cal{F}^{\mathrm{S}}}\ |\ {\cal{F}}{3}(\omega{1},,\omega_{2},,\omega_{3})(\mathbf{\omega}\theta,-,\theta^{\star})\ |{2}}&{(5,-277)}\end{array}}\ &{\begin{array}{l}{\displaystyle{h{3}=\theta^{3}!\in\cal{F}^{\mathrm{S}}}}\end{array}

  

从超椭球线性转换的标准结果有  

F_{1}(F S)={z^{1}\in C;|;(z^{1}-z^{1*},)^{\mathrm{T}}[F_{1}(\omega)(P^{\mathrm{T}}P)^{-1}F_{1}^{\mathrm{T}}(\omega)]^{-1}(z^{1}-z^{1*},)\leqslant

N[,(1/,\sqrt{N}\varepsilon^{u};+;\varepsilon^{E},)^{2};-;\varepsilon_{;r}^{2},],}

F_{2}(F\mathrm{S}),=,{,z^{2}\in,C,,\vert,(z^{2}-,z^{2}^{\ast},)^{\mathrm{T}}[,F_{2}(\omega_{1},\omega_{2})(P^{\mathrm{T}}P)^{-1}F_{2}^{\mathrm{T}}(\omega_{1},\omega_{2})}^{-1}\times

(z^{2}-,z^{2}{}^{*},)\leqslant N[(1/\sqrt{N}\varepsilon^{u},+,\varepsilon^{E})^{2},-,\varepsilon_{,r}^{2},],;

F_{3}(F S);=;{,z^{3}\in;C;\mid;(,z^{3},-,z^{3,\ast},)^{\mathrm{T}}[,F_{3}(,\omega_{1},,\omega_{2},,\omega_{3},),\cdot

(,P^{\top}P,)^{-1}\times{\cal F}{3}^{\top}(,\omega{1},,\omega_{2},,\omega_{3},),]^{-1}(,z^{3},-,z^{3,*},)\leqslant

N[,(1/,\sqrt{N}\varepsilon^{u},+,\varepsilon^{E},)^{2},-,\varepsilon_{,r}^{2},],}

  

式中  

z^{1},^{}\ =\ F_{1}(\omega)\theta,^{}\ \ \ \ z^{2},^{}\ =\ F_{2}(\omega_{1},\omega_{2})\theta,^{}\ \ \ \ z^{3},^{}\ =\ F_{3}(\omega_{1},\omega_{2},\omega_{3})\theta,^{}

  

对于每一个或一组频率,式（5-275）、式（5-276)和式（5-277)的极大化问题分别等价于寻找椭球式（5-278）、式（5-279）和式（5-280）的最大轴。由此可得其解  

R_{1}(,\omega,),=,J_{1}(,\bar{\phi}^{L S},),=,\bar{r},\Dot{|,}F_{1}(,\omega,)\big(,P^{\top}P,\big)^{-1}F_{1}^{\top}(,\omega,),\dag,,.

\sqrt{N[,(,\epsilon^{u}/,\sqrt{,N,+,\epsilon^{E},})^{2},-,\epsilon_{,r}^{2},]}

R_{2}(,\omega_{1},,\omega_{2},),=,J_{2}(,\bar{\phi}^{L S},),=,\bar{r},{,F_{2}(,\omega_{1},,\omega_{2},)(,P^{\top}P,)^{,-1}F_{2}^{\top}(,\omega_{1},,\omega_{2},),}

\sqrt{N[,(,\varepsilon^{u}/,\sqrt{,N,}+,\varepsilon^{E},)^{2},-,\varepsilon_{;r}^{2},]}

R_{3}(,\omega_{1},,\omega_{2},,\omega_{3},);=;J_{3}(,\Phi^{L S},);=;

\bar{r},!\mid!\boldsymbol{F}{3}(,\omega{1},,\omega_{2},,\omega_{3},)!\left(,\boldsymbol{P}^{\mathrm{T}}\boldsymbol{P},!\left(,\omega_{1},,\omega_{2},,\omega_{3},\right),!\left},,\right.,!,,

\sqrt{N[(,\pmb{\varepsilon}^{u}/,\sqrt{N,+,\varepsilon}^{E},)^{2},-,\varepsilon_{,r}^{2},]}

  

分别对式(5-281)、式(5-282)和式（5-283)中的频率在其变化范围内求各式的极大值，则可得式（5-270)和式（5-271）。证毕。  

取与上节相同的算例，即  

\begin{array}{r l}{\small\boldsymbol{z}\left(\ t\right),=-,0.,64x\left(,t,\right),+,x\left(,t,-,2,\right),+}&{{}}\ {0.,9x^{2}(,t,),+,x^{2}(,t,-,1),+,\varepsilon(,t,)}&{{}}\end{array}

  

输人信号取伪随机信号，噪声为在区间 $\left[\right.-0.03;0.03\right]$ 的均匀分布的白噪声，数据点数取512点，模型结构由上节方法获得。由于该模型为纯输人非线性模型，由上节方法获得的模型结构与真实结构一致，因此在该仿真算例中没有结构误差，而仅有测量噪声引起的随机误差。  

图5-7～图5-10给出了上述模型中对应时域核的区间估计的收敛过程（仅给出了前150个点的收敛过程，其余与此类同）。从图中可以看出，核的估计区间随数据点数的增加而不断缩小，且都包含核的真值。  

![](images/d52f1496152f17972b83135b657e66a949e6243e760b6b0a16fb8651984950b0.jpg)  
图 5-7 $h_{1}(\uptheta)$ 的区间收敛过程  

![](images/caeb694e95dc1f61545b7f63ecdb9130e8d7612fa44b15965f7bd7701918d52b.jpg)  
图 5-8 $h_{\mathrm{~l~}}(2)$ 的区间收敛过程  

![](images/edbeff96a2975f02a13e1c178b06f94784f16ab54466cc67e4962033b661a410.jpg)  
图 5-9 $\boldsymbol{h}_{2}(0,0)$ 的区间收敛过程  

![](images/5468d5a96f4bbaa6a50f4f9e511ec717a6c441eea52520666a1b729ac083eaff.jpg)  
图 5-10 $h_{2}(1,1)$ 的区间收敛过程  

![](images/3293c23d53a02ceaa633499035b272e1578eebd0ba306c3cb04c643b778989e1.jpg)  
图 5-11—阶频率响应  

![](images/8579dfa4616630fd17b7fd2579a7e5a9c2d8e1b6a06366f98a7e70b86d7c825e.jpg)  

图 5-12 一阶频率响应的 $H_{\infty}$ 误差界  

![](images/1c911e36cd9ded06ea6ef1d8ea05d9d4dadefefb0f6e988254c6f9358c3e764c.jpg)  
图5-13二阶频率响应  

![](images/668657d6899e6257bcd3560274a91b8c9f605c9e12dab42e41c8a77a26d784c6.jpg)  
图5-14二阶频率响应的H。误差界  

图 5-11和图5-12分别给出了一阶频率响应函数的频率响应及名义模型和实际模型在各频率点上相应的H。误差界；图5-13和图5-14分别给出了二阶频率响应函数的频率响应及名义模型和实际模型在各频率点上相应的H。误差界。由此，为H。控制器的设计提供了合适的数学模型。  

图5-15和图5-16分别给出了一阶和二阶频率响应的H。误差界的放大图。从图中可看出，在低频和高频其误差较大，而在中频较小。但从总体上看，H。辨识的最坏情况误差与频率响应的幅值相比是较小的，由此获得的 $H_{\infty}$ 辨识模型，可设计出性能较高的 $H_{\infty}$ 控制器。  

![](images/dde9972fe98895c17652115ecb4257ca28f42dbf965444eec0af91165f0da920.jpg)  
图5-15一阶频率响应误差界放大图  

![](images/29cde796793376ba23040016c2a11918bd497bb5ef75bd186df01029f6ed1272.jpg)  
图5-16二阶频率响应误差界放大图  

# 5.6 闭环系统辨识  

在工程中，有时要求辨识试验必须在闭环条件下进行，以免系统工况偏离正常值太远而发生危险或影响产品质量。比如，静不稳定飞机作飞行试验时，如果断开飞控系统，则可能造成灾难性的后果。在经济、生物等领域中，许多系统往往还存在固有的、无法断开的或隐蔽的反馈。因此，有必要对系统在闭环状态下的辨识进行研究。  

由于反馈的存在，使得输人输出数据中有关系统动态特性的信息量减少，同时引起输人输出数据相关。由此造成闭环系统的可辨识性问题变得更严重，为此本节主要讨论闭环系统的可辨识性问题，以及闭环系统的辨识方法。  

# 5.6.1 闭环系统可辨识性的基本概念  

一般说来，辨识结果的好坏与具体的辨识对象、所用的模型结构、试验条件和采用的辨识方法有关。考虑可辨识性最通用的方法是将可辨识性与参数估计 $\pmb{\hat{\theta}}^{N}$ 的一致性联系起来。如果随着观测次数 $N$ 的增加，估计值 ${\pmb\partial}^{N}$ 的序列按概率1收敛到真值 ${\pmb\theta}_{0}$ ,则称参数 0为可辨识的[37]  

为寻求模型参数的估计值，采用下列准则函数来衡量观测数据与模型之间的接近程度。  

J_{N}(,S,,M(,\pmb\theta,),,\chi,,E,),=,h,[,Q^{N}(,S,,M(,\pmb\theta,),,\chi,,E,),]

  

式中 $S$ -被辨识系统(对象）;  

$M(\pmb\theta)$ -模型类；x——试验条件;  

E——辨识方法。  

而  

$Q^{N}(\,S\,,M(\,\pmb\theta\,)\,,\chi\,,E\,)\,=\,\frac{1}{N}\sum_{k\,=\,1}^{N}\,\nu(\,k\,,\pmb\theta\,)\,\nu^{\mathrm{T}}(\,k\,,\pmb\theta\,)$ 是一个 $n_{z}\times n_{z}$ 的矩阵， ${\pmb v}({\pmb k}\,,{\pmb\theta})$ 是预报误差,即  

\pmb{\nu}(\pmb{k},,\pmb{\theta});=;\pmb{z}\left(\pmb{k},\right),-,\hat{\pmb{z}}_{m}\left(\pmb{k},\mid,\pmb{\theta}\right)

  

标量函数 $h\ [\cdot\ ]$ 一般采用矩阵的行列式或者矩阵的迹。使式（5-284）为最小的参数矢量 $\pmb\theta$ 就是 $N$ 次观测下所得的估计值 $\pmb{\hat{\theta}}$ $(N;S\,,M,\chi\,,E)$ ，简记为 ${\pmb\partial}^{N}$  

荣 $\mathbf{\Gamma}(\mathbf{L})\mathbf{u}\mathbf{n}\mathbf{g})$ 等曾经分析了 $\pmb{\partial}^{N}$ 的收敛性，并指出，在适当条件下,当 $N\!\cdots\!\infty$ ,参数估值依概率1收敛于 $D_{I}$ ,即  

\hat{\theta}(N;S,M,\chi,E)\xrightarrow[N\rightarrow\infty]{}D_{I}(S,M,\chi,E)

  

这里 $D_{I}(\,S\,,M\,,x\,,E\,)$ 是满足下列条件的 $\pmb{\theta}$ 的集合。由这些参数所形成的模型预报器的特性在下列意义下渐近地逼近真实预报器的特性  

\begin{array}{l}{{\displaystyle D_{I}({\bf\Delta}S,,{\cal M},,\chi,,E),=,}}\ {{\displaystyle{,\pmb\theta,},\operatorname*{lim}{N\rightarrow\infty},\frac{1}{N}\sum{k,=,1}^{N}E,\mid,\hat{z}{s}(k),-,\hat{\bf z}{m}(k,\mid,\pmb\theta),\mid^{2},=,{\bf0}}}\end{array}

  

式中 $\hat{z}_{s}(k)$ -—表示真实的预报值；  

$\hat{z}_{m}(\pmb{\mathscr{k}}\cdot\pmb{\theta})$ —一表示由模型 $M(\theta)$ 计算得出的输出预报值。所期望的估计值由下面的参数集合给出  

D_{I}(,S,,M,);=;{,\pmb\theta::|::G_{1\theta};=;G_{1}(,z,),,G_{3\theta};=;G_{3}(,z,),}

  

式中 $G_{1\theta}\,,\,G_{3\theta}$ —分别表示用参数矢量 $\pmb{\theta}$ 对 $\pmb{G}_{1}$ 和 $\pmb{G}_{3}$ (见图  

# 5-17)参数化的结果。  

于是这个集合所包含的参数值将使模型 $M(\pmb\theta)$ 具有于被识过程同样的传递特性和同样的噪声特性。  

下面介绍荣等人提出的可辨识性定义。  

![](images/8e213b54bf3514bc2596a4347862a54f559790b6fda5e8622087f0d740e4bae0.jpg)  
图 5-17 典型闭环系统  

定义 1  系统 $S$ 称为在 $M,\chi\,,E$ 下是系统可辨识的，只要$N{\rightarrow}\infty$ 时 $\hat{\pmb{\theta}}(N;S,M,\chi\,,E)$ 依概率1 收敛于 $D_{I}(S,M)$ ,即  

\hat{\pmb{\theta}}(N;S,,{\cal M},,\chi,,E,)\xrightarrow{\ a,.,s,.,}D_{I}(,S,,{\cal M},)

  

用符号 $S I(\boldsymbol{M},\boldsymbol{\chi}\,,E)$ 表示系统可辨识。  

定义 2  系统 $\boldsymbol{S}$ 称为在 $\chi\,,E$ 下是强系统可辨识的，只要对于所有的模型 $M$ ,它是系统可辨识的，且 $D_{I}(S,M)$ 是非空集合。用符号 $S S I(\,\pmb{\chi}\,,\pmb{E}\,)$ 表示强系统可辨识。  

定义 3  系统 $S$ 称为在 $M,\chi\,,E$ 下是参数可辨识的，只要它是系统可辨识的,而且 $D_{I}(\,S\,,M)$ 中仅包含一个元素。用符号PI$(\,M,\chi\,,E\,)$ 表示参数可辨识。  

# 5.6.2 闭环系统的辨识方法及可辨识性  

1）闭环系统的辨识方法  

闭环系统的辨识任务是：根据测量数据 $\{\textbf{z}(\textbf{\em k})\,,\,\pmb{u}\,(\textbf{\em k})\}$ 和$\{S(k)\}$ ,估计出 $G_{1}(\,z\,)\,,G_{2}(\,z\,)\,,G_{3}(\,z\,)$ 和 $G_{4}(\,z\,)$ 。其中,反馈控制回路 $G_{2}(z)$ 可能是已知的； $\{\,\pmb{S}(\,\pmb{k}\,)\,\}\,,\,\{\,\pmb{\nu}(\,\pmb{k}\,)\,\}$ 和 $\{\,\pmb{\eta}(\,k\,)\,\}$ （符号定义见图5-17)中的某一个或二个可以不存在，即可以没有外加试验信号、测量噪声或反馈噪声。闭环系统的辨识可以采用三种方案：  

（1）直接辨识法。把测量数据 $\{\,\pmb{z}\,(\,\pmb{k}\,)\,,\pmb{u}\,(\,\pmb{k}\,)\,\}$ 看成来自开环系统的观测数据一样，直接辨识出系统的参数 $\pmb{\hat{\theta}}$  

（2）间接辨识法。当已知反馈回路调节器的控制规律，同时控制规律具有线性、时不变的特性，而且无反馈噪声 $\mathbf{G}_{4}\left(\mathbf{\Sigma}_{z}\right)=0$ 时，可以先辨识出闭环系统的整体特性，例如  

\left{\begin{array}{l l}{\pmb{S}{1},=,(,{\pmb{I}},-,{\pmb{G}}{1},{\pmb{G}}{2},)^{-1},{\pmb{G}}{1}}\ {\pmb{S}{2},=,(,{\pmb{I}},-,{\pmb{G}}{1},{\pmb{G}}{2},)^{-1},{\pmb{G}}{3}}\end{array}\right.

  

然后利用已知的 $G_{2}(\,z\,)$ 把 $G_{1}(z)$ 和 $G_{3}(\,z\,)$ 求出来。这就是间接辨识法。  

（3）联合法。此法把联合数据 $\{\,\pmb{z}\left(\,k\,\right),\pmb{u}\left(\,k\,\right)\,\}$ 看成是由白噪声$\left\{\pmb{\varepsilon}(\pmb{k})\right\},\left\{\pmb{\eta}(\pmb{k})\right\}$ 激励后的输出。先辨识出整个系统的传递函数矩阵，然后利用传递函数矩阵中的分块矩阵与系统各环节传递函数的关系，求出各环节的传递函数。  

上述三种闭环系统的辨识方案，与各种参数估计方法结合起来，就形成了具体的辨识方法，但并不是每一种辨识方法都是可行的，这里存在闭环系统可辨识性问题。  

直接法是把闭环系统中的被辨识部分孤立开来，当作开环系统，直接由观测数据拟合出模型。因此，一般不能采用非因果型算法（如相关-频谱分析法）。  

联合法和间接法是把被辨识的闭环系统当作一个整体来对待，因而同开环系统一样，可以采用非因果型算法，但因果分解比较困难。另外，间接法对试验条件有较多的限制。首先，要求反馈回路是已知的且是参数化的线性系统，若反馈回路是非参数化的或非线性的，原则上不能使用间接法。其次，要求反馈回路的噪声  

等于零，或者能够测量。  

因此，在闭环系统辨识中，一般采用直接法，具体方法为因果型参数估计方法（比如预报误差法）。  

2）闭环系统的可辨识性  

闭环系统除应满足开环系统的可辨识性条件外，还存在由反馈引起的一些特殊的闭环可辨识问题，本节将就这方面作一些介绍。  

(1）绝对可辨识的充分条件。 $\pmb{S}\left(\,k\,\right)\neq0\,,\,\pmb{S}\left(\,k\,\right)\in R^{r}\,,$ $\pmb{r}$ 为 $u\left(\,k\,\right)$ 的维数,且满足充分激励条件，同时 $\pmb{S}(\pmb{k})$ 和 $\pmb{\varepsilon}(k),\pmb{\eta}(k)$ 不 相关。  

证明：由图5-17可得  

\begin{array}{r l r}{\mathrm{\boldmath~\Gamma~}}&{{}=,\psi_{z s}({\mathrm{\boldmath~\boldsymbol{z}}}),\psi_{u s}^{-1}({\mathrm{\boldmath\boldsymbol{z}}});=}\ {\mathrm{\boldmath\Gamma~}}&{{}}&{\left[,G_{1}({\mathrm{\boldmath~\boldsymbol{z}}}),\psi_{u s}({\mathrm{\boldmath\boldsymbol{z}}}),+,G_{3}({\mathrm{\boldmath\boldsymbol{z}}}),\psi_{v s}({\mathrm{\boldmath\boldsymbol{z}}}),\right],\psi_{u s}^{-1}({\mathrm{\boldmath\boldsymbol{z}}});=;{\bf G}_{1}({\mathrm{\boldmath\boldsymbol{z}}}),\mathrm{\boldmath\Gamma~}}\end{array}

  

式中 $\psi(z)$ —自相关函数或互相关函数的 $\pmb{\mathcal{Z}}$ 变换。  

由于 $\pmb{S}(\textbf{K})$ 和 $\pmb{\varepsilon}\left(\pmb{k}\right)$ 不相关，所以第二等式中 $\psi_{v s}\left(\,z\,\right)=\mathbf{0}_{\circ}$ $\mathbf{\nabla}S\left(\mathbf{\lambda}_{k}\right)$ 是外加的试验信号或外界可测量的扰动。  

这个绝对可辨识的充分条件，对于指导复杂工程系统的辨识试验是有重要实用意义的。  

（2）无反馈噪声时的可辨识条件。由绝对可辨识的充分条件可知，为了辨识前向通道的传递函数 $G_{1}(z)$ ，最好施加外部可测量的试验输人信号 $\pmb{S}(\pmb{k})$ 。但当不允许外部试验信号输人时， $\pmb{G}_{1}$ $\left(\,z\,\right)$ 的输人 $\pmb{u}\langle\pmb{k}\rangle$ 只能依靠反馈通道的扰动 $\pmb{\eta}(k)$ 来获得独立于测量噪声ε(k)的激励信号。这就给辨识造成了困难。进一步,如果反馈噪声也恒等于零，还能否辨识出前向通道的传递函数。从物理概念上看，要取得相对独立于测量噪声的激励信号，只能依靠反馈调节器来创造可辨识性的条件。下面定理给出了定量的回答。  

定理 5 .3 闭环系统可辨识性的一个充分条件是  

\operatorname{rank}\left[\begin{array}{c c c c}{{I}}&{{I}}&{{\cdots}}&{{I}}\ {{G_{2}^{(1)}}}&{{G_{2}^{(2)}}}&{{\cdots}}&{{G_{2}^{(l)}}}\end{array}\right]=;r;+;q

  

式中 r———系统的输人维数；$q$ 一系统输出维数；  

$\mathbf{G}_{2}^{\scriptscriptstyle(!)},\cdots,\mathbf{G}_{2}^{\scriptscriptstyle(!)}$ 一在试验过程中切换过的 $l$ 个不同的反馈调节器的传递函数,并且是已知的；  

证明：当使用第 $_i$ 个反馈调节器 $\pmb{G}_{2}^{(\textit{i})}$ ,即 $G_{2}=G_{2}^{({\it i})}$ 时，可得由$\{\:\pmb{\varepsilon}(\,k\,)\}\:$ 激发的以 $\{z\left(k\right)\}$ 为输出的传递函数阵  

\textbf{A}^{(i)}(,z,);=;(,I,-,G_{1}G_{2}^{(,i,)},)^{,-1}G_{3}\quad(,i,=,1,,2,,\cdots,,,l,)

  

假定 $G_{3}^{\mathrm{~-~}\mathrm{{i}}}\left(\mathrm{\mathfrak{z}}\right)$ 存在,上式可写成  

[,{\pmb A}^{(,i,)}(,z,),]^{,-1};=;{\pmb G}{3}^{,-1}(,{\pmb I},-,{\pmb G}{1}{\pmb G}_{2}^{(,i,)},)\quad(,i;=;1,,2,,\cdots,\ell,)

  

在写成矩阵形式：  

\begin{array}{r l}{\left[,\left(,\pmb{A}^{(1)},\right)^{,-1},\right.}&{{}\left.,\cdots;;;\left(,\pmb{A}^{(,\iota,)},\right)^{,-1},\right];=}\end{array}

\begin{array}{r l}{\left[,G_{3}^{,-1},\right.}&{{}\left.-,G_{3}^{,-1},G_{1},\right]\left[!!\begin{array}{l l l}{I_{q\times q}}&{\cdots}&{I_{q\times q}}\ {G_{2}^{(1)}}&{\cdots}&{G_{2}^{(l)}}\end{array}!!\right]}\end{array}

  

显然，当式(5-291)满足时，能从上式中惟一确定 $G_{3}^{\mathrm{~-~}1}$ 和$-\textbf{G}_{3}^{\cdot\downarrow}\textbf{G}_{\mathrm{l}}$ ，从而得到 $G_{\mathfrak{h}}(z)$ 和 $G_{3}(\,z\,)$ 。证毕。  

式(5-291)成立的一个必要条件是，左端矩阵的列数 $l q$ 应该不小于 $r^{\mathrm{~+~}}\boldsymbol{q}$ 。因此，定理5.3成立的一个必要条件是：切换的调节器个数满足  

l\geqslant1+\frac{r}{q}

  

当输人和输出个数相等，即 $r=q$ 时，则要求 $1\geq2$ ，即只要求两个调节器就可满足必要条件。  

定理5.3给出了用切换调节器的方法使闭环系统变成可辨识的条件。下面以单输人输出系统为例介绍用增加调节器复杂程度的方法，使系统变成可辨识的条件。  

设系统前向通道的差分方程为  

F(,z,),z\left(,k,\right);=;G(,z,),u\left(,k,\right),+,E(,z,),\pmb{\varepsilon}(,k,)

  

并设 $F(z)$ 与 $G\left(\,z\,\right),E\left(\,z\,\right)$ 之间没有公因子，且  

F(,z,),=,1,+,f_{1},z^{,-1},+,\cdots,+,f_{n_{,{1}}},z^{,-,n{,_{1}}}

G(,z,),=,g_{1},z^{,-,1},+,\cdots,+,g_{n_{1}},z^{,-,n},

E,(,z,),=,1,+,e_{1},z^{,-,1},+,\cdots,+,e_{n_{1}},z^{,-,n},_{!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!,!!!!!!!!!!!!!!!!!!!!!!!!!!,z!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

  

前向通道的最高阶次为 $n_{\textsf{l o}}$ 反馈通道的差分方程为  

H(,z,),u\left(,k,\right);=;R\left(,z,\right)z\left(,k,\right)

  

并设 $H(z)$ 与 $R\left(\,z\,\right)$ 无公因子，且  

H(,z,),=,1,+,h_{,1},z^{,-,1},+,\cdots,+,h_{n_{,2}},z^{,-,n_{,2}}

R,(,z,);=;r_{0},+,r_{1},z^{,-,1},+,\cdots,+,r_{n_{2}},z^{,-,n_{2}}

  

反馈通道的最高阶次为 $n_{2}$ 。并假设反馈闭合后，不会引起零极点相消。  

定理5.4在上述条件下系统的 $F(\,z\,)\,,G(\,z\,)$ 和 $E\left(\,z\,\right)$ 可辨识的充分条件是：反馈通道的阶次要大于前向通道的阶次，即  

n_{2}\geqslant n_{1}

  

证明：由间接法先辨识出闭环系统模型  

z(,k,),=,\frac{L(,z,)}{M(,z,)}\pmb{\varepsilon}(,k,)

  

由式(5-296)和式（5-300)可知  

M(,z,),=,H(,z,),F(,z,),-,R(,z,),G(,z,)

L\left(,z,\right);=;H(,z,),E\left(,z,\right)

  

当 $n_{2}\!\gg\!n_{\,1}$ 时,可列出式(5-305)两端前 $\pmb{n}_{1}$ 个 $\mathfrak{z}$ 的同次幂系数的等式，用矩阵可以表示为  

\begin{array}{r}{\left[\begin{array}{c c c c}{1}&{0}&{\cdots}&{0}\ {h_{1}}&{1}&{\cdots}&{0}\ {\vdots}&{\vdots}&{\ddots}&{0}\ {h_{n1-1}}&{h_{n1-2}}&{\cdots}&{1}\end{array}\right]\left[\begin{array}{c}{e_{1}}\ {e_{2}}\ {\vdots}\ {e_{n1}}\end{array}\right]=\begin{array}{c}{\left[\begin{array}{c}{l_{1}-h_{1}}\ {l_{2}-h_{2}}\end{array}\right]}\ {\vdots}\ {\left[\begin{array}{c}{h}\ {h_{n1-1}}\end{array}\right]}\end{array}

  

上式左端的矩阵显然是非奇异的，因此，由 $L\left(z\right)$ 和 $H(\,z\,)$ 可以求  

出 $E\left(\,z\,\right)$ 。  

同理可列出式(5-304)两端的 $\pmb{n}_{1}$ 的同次幂系数等式，从而由$M\!\left(\,z\,\right),H\!\left(\,z\,\right)$ 和 $R\left(\,z\,\right)$ 求出 $F(z)$ 和 $G(z)$ 。证毕。  

从式（5-300）中可以得到启示，如果采用时延调节规律  

H(,z,),u\left(,k,\right);=;R\left(,z,\right)z\left(,k,-,\tau,\right)

  

则增加 $\tau$ ，等价于增加了调节器的复杂度，相应地可降低调节器的阶次。当 $\tau$ 足够大时，即使采用低阶的调节器，也可使 $u\left(\,k\,\right)$ 中包含与当时的 $\varepsilon\left(\,k\,\right)$ 近似不相关的成分，从而使系统能辨识。  

（3）有反馈噪声时的可辨识条件。反馈通道上存在扰动信号,即 m(k)≠0,且前向通道上过程的输人输出变量是可测的。这时可利用直接辨识方法，获得前向通道的估计模型，因为反馈通道上有了扰动信号,相当于在被辨识对象的输人信号u（k）中叠加了一个与输出信号(k)不相关的扰动信号，保证了直接辨识方法的使用条件。这时系统总是可辨识的称结构可辨识，不再受定理5.3和定理5.4的限制 。  

# 5.6.3 最小二乘法在闭环辨识中的应用  

本节讨论最小二乘法在闭环直接辨识问题中的应用。辨识对象如图5-17。假定前向通道和反馈通道都受到噪声的干扰，且这二个噪声是互不相关均值为零的白噪声;没有外部输人信号输人(S(k）=0)。设前向通道的差分方程可具体写为  

z\left(,k,\right);=;-;\sum_{i,=,1}^{n_{a}}a_{i}z\left(,k,,-,,i,\right);+;\sum_{i,=,q}^{n_{b}}b_{i}u\left(,k,,-,,i,\right);+;\varepsilon\left(,k,,\right)

  

式中ε(k)}——均值为零的白噪声序列,其分布为 N(0,o²)。  

反馈通道的差分方程为  

u\left(,k,\right);=;-;\sum_{i,=,1}^{n_{c}}c_{i}u\left(,k,,-,,i,\right);+;\sum_{j,=,p}^{n_{d}}!d_{i}z\left(,k,,-,,j,\right);+;\eta(,k,)

  

式中 $\{\,\eta(k\,)\,\}$ 一均值为零的白噪声序列,其分布为 $N(0,\sigma_{\eta}^{2})$  

$\pmb{\dot{p}}$ 和 $\pmb q$ -分别是反馈通道和前向通道的滞后时间。  

前向通道的未知参数用下列矢量表示  

\pmb{\theta}^{\mathrm{T}},=,(,a_{1},,a_{2},,\cdots,a_{n_{a}},,b_{q},,\cdots,b_{n_{b}},)

  

并设回归矢量为  

\begin{array}{l}{{\pmb\varphi^{\mathrm{T}}({\pmb\mathit{k}},),=,\left[,-,z,({\pmb{k}},-,1),,\cdots,,-,z,({\pmb{k}},-,n_{a},),;,}}\ {{\pmb,u},({\pmb,k},-,{\pmb q},),,\cdots,{\pmb u},({\pmb{k}},-,n_{b},),\right]}}\end{array}

  

于是式（5-308）写为  

$z\left(k\right)\;=\;\varphi^{\mathrm{T}}(\,k\,)\,\pmb\theta\,+\,\pmb\varepsilon\left(k\,\right)\quad(\,k\;=\;1,2,\cdots)$ (5 -311)设得到 $u\left(k\right)$ 和 $z(k)$ 的 $N$ 对观测值 $(N>n_{a}+n_{b}-q+1)$ ,则有  

z=\Phi\theta+z

  

式中  

z;=;{\left[\begin{array}{l}{z(1)}\ {z(2)}\ {\vdots}\ {z(N)}\end{array}\right]}\qquad\pmb{\varepsilon};=;{\left[\begin{array}{l}{\varepsilon(1)}\ {\varepsilon(2)}\ {\vdots}\ {\varepsilon(N)}\end{array}\right]}

  

$\pmb{\phi}$ 为 $N\times(\,n_{a}+n_{b}-q+1)$ 矩阵,矩阵的第 $\pmb{k}$ 行为 $\pmb{\varphi}^{\intercal}(\pmb{k})$  

应用最小二乘法，可得 $\pmb\theta$ 的估计值  

\pmb{\hat{\theta}};=;(\pmb{\Phi}^{\mathrm{T}}\pmb{\Phi})^{-1}\pmb{\Phi}^{\mathrm{T}}\pmb{z}

  

下面将要讨论的是在闭环系统辨识中最小二乘估计在何种条件下能保证估计的一致性和惟一性。  

1）估计的一致性  

对于开环系统,如果 $\varepsilon(k)$ 是白噪声序列，则估计是一致的。但对闭环系统系统来说，还应考虑 $u\left(\,k\,\right),z\left(\,k\,\right)$ 和 $\varepsilon\left(\,k\,\right)$ 之间的依赖关系。 $\pmb{\theta}$ 的估计误差为  

\widetilde{\pmb{\theta}};=;\pmb{\theta};-;\hat{\pmb{\theta}};=-;(,\pmb{\phi}^{\mathrm{T}}\pmb{\phi},)^{-1},\pmb{\phi}^{\mathrm{T}}\pmb{\varepsilon}

\widetilde{\pmb{\theta}};=-;\left[\frac{1}{N}\pmb{\mathcal{P}}^{\intercal}\pmb{\phi}\right]^{-1}\left[\frac{1}{N}\pmb{\phi}^{\intercal}\pmb{\varepsilon}\right]

\operatorname*{lim}_{N\rightarrow\infty}\left[\frac{1}{N}\pmb{\Phi}^{\mathrm{T}}\pmb{\Phi}\right]^{-1}

  

存在。那么要求估计是一致估计，等价于要求  

\left{\begin{array}{l l}{\displaystyle\operatorname*{lim}{N\to\infty}E\left(\frac{1}{N}\pmb{\Phi}^{\mathrm{T}}\pmb{\varepsilon}\right)=\mathrm{0}}\ {\displaystyle\operatorname*{lim}{N\to\infty},\mathrm{var}\left(\frac{1}{N}\pmb{\Phi}^{\mathrm{T}}\pmb{\Phi}\right)=\mathrm{0}}\end{array}\right.

  

首先考虑 $\frac{1}{N}\pmb{\Phi}^{\mathrm{T}}\pmb{\varepsilon}$ 的数学期望。根据 $\pmb{\phi}$ 和 $\pmb{\varepsilon}$ 的定义,有  

E\left(\frac{1}{N}\Phi^{\mathsf{T}}\varepsilon\right)=\frac{1}{N}\left[\begin{array}{c}{{\displaystyle-\sum_{i=1}^{N}E\left{\varepsilon\left(i-1\right)\varepsilon\left(i\right)\right}}}\ {{\vdots}}\ {{\displaystyle\sum_{i=1}^{N}E\left{\varepsilon\left(i-n_{a}\right)\varepsilon\left(i\right)\right}}}\ {{\displaystyle\sum_{i=1}^{N}E\left{u\left(i-q\right)\varepsilon\left(i\right)\right}}}\ {{\vdots}}\ {{\displaystyle\sum_{i=1}^{N}E\left{u\left(i-n_{b}\right)\varepsilon\left(i\right)\right}}}\end{array}\right]

  

从式(5-308)和式(5-309)知,z(k)只与ε(k)及其之前的 ε(k-1),e(k－2)等有关,与噪声的将来值无关,因此在式(5-319)中}z(k)}与e(k)无关;但u（k)}是y(k)}的函数,因而也是}e$(k)!$ 的函数。在什么情况下， $\{\,{\pmb u}\left(\,{\pmb k}\,\right)\}$ 和 $\{\varepsilon(k)\}$ 无关呢？综合式(5-308)和式(5-309)知,只要 p>0 或 q >0,即不存在瞬时反馈通道或瞬时前向通道时，u（k);和}ε(k)无关。因此,只要>0或α>0,式(5-318)中第一式成立，θ为无偏估计。  

其次，讨论 $\frac{1}{N}\pmb{\Phi}^{\mathrm{T}}\pmb{\varepsilon}$ 的方差。从概率论中知道,如果四个随机变量 $.x_{1},.x_{2},.x_{3}$ 和 $x_{4}$ 均值为零，且服从正态分布，则其乘积的数学期望的计算公式为  

$E[\,x_{1}x_{2}x_{3}x_{4}\,]\;=\;R_{12}R_{34}\,+\,R_{13}R_{24}\,+\,R_{14}R_{23}$ (5 - 320)式中 $R_{i j}{\longrightarrow}x_{i}$ 与 $x_{j}$ 的互相关矩。  

对于 $\frac{1}{N}{\pmb{\phi}}^{\scriptscriptstyle\mathrm{T}}{\pmb{\varepsilon}}$ 中的某一元素 $h_{j}(1{\leqslant}j{\leqslant}n_{a})$ ,利用式(5-320)可得  

\begin{array}{l}{{\displaystyle\frac{1}{N^{2}}\displaystyle\sum_{k=1}^{N}\displaystyle\sum_{l=1}^{N}E\left{,z\left(k,-,j\right)\varepsilon\left(k\right)z\left(l-j\right)\varepsilon\left(l\right)\right}\ =}}\ {{\displaystyle\frac{1}{N^{2}}\displaystyle\sum_{k=1}^{N}\sum_{i=1}^{N}\left{R_{\bf z}^{2}\left(j\right)+R_{\bf x}(k,-,l)R_{\epsilon}(k,-,l)\right.+}}\ {{\displaystyle R_{\bf z}(j,-,k,+,l)R_{\bf z}(j,+,k,-,l)}\ =}}\ {{\displaystyle R_{\bf z}^{2}(j)+\frac{1}{N^{2}}\displaystyle\sum_{k=1}^{N}\sum_{l=1}^{N}\left{R_{\bf z}(k,-,l)R_{\epsilon}(k,-,l)\right.+}}\ {{\displaystyle R_{\bf z}(i,-,k,+,l)R_{\bf z}(j,+,k,-,l)}\ :\ \ \ \ \ \ \ \ (5-,j),=-1,}}\end{array}

  

因 $z(k-j)$ 与 $\epsilon(k)$ 不相关，故式(5-321)中的第一项为零；因 $j-k$ $+l$ 和 $j+k-l$ 中总有一项为正值，故式(5-321)中的第三项为零；式(5-321)中的第二项只有在 $k=l$ 时， $R_{\varepsilon}(0)=\sigma_{\varepsilon}^{2}$ ，因此第二项为  

\frac{1}{N}{R_{z}}(o),\sigma_{\varepsilon}^{2}

  

由于闭环系统应该稳定， $R_{z}(0)$ 为有限值，当 $N{\rightarrow}\infty$ 时，第三项为零。于是  

\mathrm{var}(,h_{j},),=,0\quad(1\leqslant j\leqslant n_{a},)

  

对于 $n_{a}\!<\!j\!\ll\!n_{a}+\,n_{b}\,-\,q+1\,,\,u\left(\,k\,\right)$ 和 $\epsilon(k)$ 之间也有同样的结果。  

因此，在线性模型中，如果测量噪声为白噪声，在前向通道或反馈通道中至少有一拍以上的延迟，并且闭环系统是稳定的，则用最小二乘法可得到前向通道参数的一致估计。  

2）估计的惟一性  

为了惟一性成立，要求矩阵  

\operatorname*{lim}{N\to\infty}\frac{1}{N}{\pmb{\phi}}^{\scriptscriptstyle\mathrm{T}}{\pmb{\phi}}\xrightarrow{\sharp\ b\ b\pmb{\phi}}R{\phi}

  

的逆矩阵存在。即要求 $\mathbf{R}_{\Phi}$ 为正定矩阵或非奇异矩阵。  

为方便起见，把式(5-308)和式(5-309)写为  

\begin{array}{r l r}{z\left(,k,\right)!!}&{{}=}&{!!\boldsymbol{x}\left(,k,\right),+,\varepsilon\left(,k,\right)}\ {u\left(,k,\right)!!}&{{}=}&{!!\boldsymbol{r}\left(,k,\right),+,\eta(,k,)}\end{array}

  

则 $R_{\Phi}$ 可用下式表示  

\pmb{R}{\pmb{\phi}}\ =\ \left[\begin{array}{c c}{\pmb{R}{x}}&{\pmb{R}{x r}}\ {\pmb{R}{r x}}&{\pmb{R}{r}}\end{array}\right]+\ \left[\begin{array}{c c}{\sigma{\epsilon}^{2},\pmb{I}}&{0}\ {0}&{\sigma_{\eta}^{2},\pmb{I}}\end{array}\right]

  

式中 $R_{x}\:,R_{r}\:,R_{x r}\:,R_{r x}\:\overset{}{\longrightarrow}$ 分别为 $n_{\alpha}\times n_{\alpha}$ $\times\ n_{a}\ ,(\ n_{b}\mathrm{~-~}q\mathrm{~+~}1)\times(\ n_{b}\mathrm{~-~}$ $q+1\,)\times(\,n_{b}\,-\,q\,+1\,)\,,n_{a}\,\times(\,n_{b}\,-\,q\,+\,1\,)$ 和 $(\,n_{b}\mathrm{~-~}q\mathrm{~+~}1\,)\times n_{a}$ 维数的相应变量的相关函数矩阵。  

（1）如果前向通道和反馈通道都存在噪声,即 $\sigma_{\varepsilon}^{2}\mathop{\neq}0$ 和 $\sigma_{\eta}^{2}\neq$ 0，由式(5-326)知,矩阵 $\pmb{R}_{\Bar{\Phi}}$ 非奇异，于是估计具有惟一性。  

(2）如果前向通道存在噪声，而反馈通道不存在噪声，即$\sigma_{\varepsilon}^{2}\neq0$ 和 $\sigma_{\,\,\eta}^{2}=0$ ，则式（5-326）变为  

{\pmb R}{\Phi}\ =\ \left[\begin{array}{c c}{{\pmb R}{x}}&{{\pmb R}{x u}}\ {{\pmb R}{u x}}&{{\pmb R}{u}}\end{array}\right]+\ \left[\begin{array}{c c}{\sigma{\varepsilon}^{2},{\pmb I}}&{0}\ {0}&{0}\end{array}\right]

  

式中 $R_{u}\ ,R_{x u}\ ,R_{u x}\,.$ 一一相应变量的相关函数矩阵，维数与 $\pmb{R}_{r}\,,$  

# $R_{x r}$ 和 $\pmb{R}_{r\pmb{x}}$ 相同。  

上式表明,矩阵的前 $\pmb{n}_{a}$ 行一定不会线性相关，如果后 $n_{b}-q$ $+\,1$ 行也不线性相关，则矩阵 $\pmb{R}_{\pmb{\phi}}$ 非奇异，估计具有唯一性。回顾$\pmb{\Phi}$ 的定义，只要矩阵  

={\begin{array}{c c c c c}{\left[{\begin{array}{c c c c c}{z(1-1)}&{\cdots}&{-,z(1-n_{a})}&{u(1-q)}&{\cdots u(1-n_{b})}\ {\vdots}&&{\vdots}&{\vdots}&{\vdots}\ {-,z(N-1)}&{\cdots}&{-,z(N-n_{a})}&{u(N-q)}&{\cdots u(N-n_{b})}\end{array}}\right]}}\end{array}}

  

后 $n_{b}\sim\textbf{q}+1$ 列线性独立，矩阵 $\pmb{\Phi}$ 列满秩。由式（5-309)可知：$u\left(\,k\,\right)$ 是 $u\left(k-1\right),\cdots,u\left(k-n_{c}\right),z\left(k-\phi\right),\cdots,z\left(k-n_{d}\right)$ 的线性函数; $u\left(\,k\,-\,q\,\right)$ 是 $u\left(k-q-1\right),\cdots,u\left(k-q-n_{c}\right),z\left(k-q-p\right)$ $z\,(\,k\,-\,q\,-\,n_{d}\,)$ 的线性函数。因而  

\left|,-,,z\left(,k,-,1,\right),\cdots,,-,z\left(,k,-,n_{a},\right),u\left(,k,-,q,\right),\cdots,u\left(,k,-,n_{b},\right),\right}

  

216  

线性相关等价于  

\begin{array}{c}{{\mathrm{Space}\left{,u\left(,k,-,q,-,1\right),\cdots,u\left(,k,-,q,-,n_{c},\right),\right},\subset}}\ {{\mathrm{Space}\left{,u\left(,k,-,q,\right),\cdots,u\left(,k,-,n_{b},\right),\right}}}\end{array}

  

或者  

\begin{array}{c}{{\mathrm{Space}{,z,(,k,-,q,-,,\phi,),,\cdots,,z,(,k,-,q,-,,n_{d},),},\subset}}\ {{\mathrm{Space}{,z,(,k,-,1,),,\cdots,,u,(,k,-,,n_{d},),}}}\end{array}

  

即  

q;+;n_{c}\leqslant n_{b};;;;;\frac{\oplus}{x};;;;;q;+;n_{d}\leqslant n_{a}

  

反之，如果  

n_{c}>,n_{b},-,q,,,,,,,,,\frac{\pi}{x}!!!!!/,,,,,,,,,,,n_{d},>,n_{a},-,q

  

则是线性独立的，最小二乘估计存在唯一解。  

（3）如果前向通道不存在噪声，而反馈通道存在噪声，即$\sigma_{\epsilon}^{2}=0$ 和 $\sigma_{\eta}^{2}\not=0$ ，则式（5-326）变为  

R_{\oplus}\ =\ {\left[\begin{array}{l l}{R_{x}}&{R_{x u}}\ &{}\ {R_{u x}}&{R_{u}}\end{array}\right]}+{\left[\begin{array}{l l}{0}&{0}\ &{}\ {0}&{\sigma_{\eta}^{2},I}\end{array}\right]}

  

和第（2）种情况一样，可得最小二乘具有惟一解的条件是  

n_{a},+,1,>,n_{a},,,,,,,,\frac{\pi}{x}!!!!!\slash,,,,,,,,,,n_{b},+,1,>,n_{b}

  

显然这个条件一定成立。  

综上所述，在最小二乘意义下，闭环系统前向通道模型参数估计有惟一解的条件是反馈通道上存在噪声；如果反馈通道上不存在噪声，则要求反馈通道的模型阶次不能底于前向通道的模型阶次。  

# 5.6.4 辅助变量法在闭环辨识中的应用  

本节讨论辅助变量法在闭环直接辨识问题中的应用，辨识对象如图 5-17 所示。假定反馈噪声 $\eta(k)$ 为零，前向通道的噪声$\varepsilon(k)$ 是均值为零的有色噪声。对此不能像上节那样用最小二乘法获得模型参数的无偏一致估计，因为这种情况卜， $u\left(k\right)$ 不仪与$\varepsilon(k)$ 的现在值有关，而且与它的过去值有关。为了获得好的估计值，必须设法解除这种 $u\left(k\right)$ 与 $\varepsilon(k)$ 的相关性。 如给系统加上外部激励信号，即 $S(k)$ 不等于零，那么可将系统的输人输出变量分解为  

\left{\begin{array}{l}{{\pmb u\left(\pmb{k}\right);=;{\pmb u}{v}(\pmb{k});+;{\pmb u}{S}(\pmb{k})}}\ {{\pmb\varepsilon(\pmb{k});=;{\pmb z}{\pmb{\varepsilon}}(\pmb{k});+;{\pmb z}{S}(\pmb{k})}}\end{array}\right.

  

下标“e"和“S"表示相应变量由ε(k)和 S(k)激励产生。显然us(k)和 zs(k)与ε(k)是不相关的,若用 us(k)和 zs(k)代替$u\left(k\right)$ 和 $z(k)$ 构成辅助矩阵，记作  

\pmb{\phi}{s}^{\mathrm{T}},=,\left[,\pmb{\varphi}{s}(1),,\pmb{\varphi}{s}(2),,\cdots,\pmb{\varphi}{s}(N),\right]

  

式中  

\begin{array}{l}{{\pmb{\varphi}{S}^{\mathrm{T}}({\pmb{k}},),=,\left[,-,z{S}({\pmb{k}},-,1),,\cdots,,-,z_{S}({\pmb{k}},-,n_{a}),,\right.}}\ {{\ }}\ {{\left.u_{S}({\pmb{k}},-,{\pmb{q}},),,\cdots,u_{S}({\pmb{k}},-,n_{b}),\right]}}\end{array}

  

那么利用辅助变量法，可得参数估计值为  

\pmb{\hat{\theta}}{I V};=;(,\pmb{\mathcal{P}}{S}^{\mathrm{T}}\pmb{\mathcal{P}},)^{-1},\pmb{\mathcal{P}}_{S}^{\mathrm{T}},\pmb{z}

  

(5 - 334)  

由于 Φs与∈(k)无关,故用辅助变量法可望得到无偏一致估计值。但辅助矩阵 Φs 中的元素us(k)和 zs(k)是不可测的,只能用迭代的方法逐步逼近。  

# 参考文献  

1  liff K W, Maine R E. A Bibliography for Aircraft Parameter Estimation. NASA TM86804，1986  

2  Iliff K W. Parameter Estimation for Flight Vehicle. J. Guidance and Control, 1989, 12 (5): $609\!\sim\!662$   
3  Fisher R A. On the Mathematical Foundation of Theoretical Statistics. Phil. Trans., 1921,A-222: 309   
4李惕碚.实验的数学处理.北京：科学出版社，1983   
5南京大学数学系计算数学专业.最优化方法.北京：科学出版社，1978   
6  Tayior L W Jr, liff K W. Systems Identification Using a Modified Newton-Raphson Method-A Fortran Program. NASA TND-6734, 1972   
7  Balakrishnan A V. Stochastic Differential System I: Filtering and Control-A Function Space Approach. Berlin: Springer Verlag, 1973   
8 Taylor L W Jr, Iliff K W. A Comparison of Newton-Raphson and Other Method for Determining Stability Derivatives from Flight Data. AIAA 69-315, 1969   
9 Maine R E, Iliff K W. Formulation and Implementation of a Practical Algorithm for Parameter Estimation with Process and Measurement Noise. SIAM. J. of Aplli. Math., 1981, 41(3): 558\~579   
10 Gertler J, etc. A Recursive ( $\mathrm{On}$ - Line) Maximum Likelihood Identification Method. IEEE Trans., 1974, AC-19: 816 \~ 820   
11吴广玉等.系统辨识与自适应控制.哈尔滨：哈尔滨工业大学出版社，1987   
12张金槐，常兆诚．飞行器试验统计学（下册）.长沙：国防科技大学出版社，1984   
13蔡金狮.动力学系统辨识与建模.北京：国防工业出版社，1991   
14 Schweppe F C. Recursive State Estimation: Unknown but Bounded Errors and System Inputs. IEEE Transactions on Automatic Control, 1968, 13: 22\~ 28   
15 Milanese M, Vicino A. Optimal Estimation Theory for Dynamic Systems with Set Membership Uncertainty: An Overview. Automatica, 1991, 27: 997\~ 1009   
16 Fogel E, Huang Y F. On the Value of Information in System Identification Bounded Noise Case. Automatica, 1982, 18: 229\~238   
17 Belforte G, Bona B. An Improved Parameter Identification Algorithm for Signals with Unknown but Bounded Errors. Prep. 7th IFAC/IFORS Symposium on Identification and System Parameter Estimation, 1985, 1507\~ 1512   
18  Clement T, Gentil S. Recursive Membership Set for Output Eror Models. Mathematics and Computers in Simulation, 1990, 32 : 505 -- 513   
19袁震东，徐桥南．多输人多输出系统参数的集员辨识．控制理论与应用，1994， 11(4): 404\~412   
20  Smith R S, Doyle J C. Model Validation--——-A Collection between Robust Control and Identification. IEEE Trans. Automatic Control, 1992, 37: 942\~ 952   
21  Broman V, Shensa M J. Polytopes: A Novel Approach to Tracking. Proceedings 25th IEEE Lonierence on Decision ana Lontrol, AInens, 17o0, 1/4>- 113   
22  Broman V, Shensa M J. A Compact Algorithm for Intersection and Approximation of N- dimensional Polytopes. Mathematics and Computers in Simulation, 1990, 32: 469 \~ 480   
23 Mo S H, Norton J P. Fast and Robust Algorithm to Compute Exact Polytope Parameter Bounds. Mathematics and Computers in Simulation, 1990, 32: 481 \~ 493   
24 Piet-Lahanier H, Waiter E. Further Results on Recursive Polyhedral Description of Parameter Uncertainty in the Bounded Error Context. Proceedings 28th IEEE Conference on Decision and Control, Tampa, 1989, 1964 \~ 1966   
25 Walter E, Piet-Lahanier H. Exact and Recursive Description of the Feasible Parameter Set for Bounded Error Models. Proceedings 26th IEEE Conference on Decision and Control, Los Angeles, 1987, 1921 \~ 1922   
26  Walter E, Piet- Lahanier H. Exact Recursive Polyhedral Description of the Feasible Parameter Set for Bounded Error Models. IEEE Transactions on Automatic Control, 1989, 34: 911\~915   
27  Milanese M, and Vicino A. Estimation Theory for Nonlinear Models and Set Membership Uncertainty. Automatica, 1991, 27: 403\~ 408   
28 Jaulin L, Walter E.Guaranteed Nonlinear Parameter Estimation from Bounded Error Data via Interval Analysis. Mathematics and Computers in Simulation, 1993, 35: 123 \~127   
29 Jaulin L, Walter E. Set Inversion via Interval Analysis for Nonlinear Bounded Error Estimation. Automatica, 1993, 29(4) : 1053\~1064   
30 Falk T E. Global Solutions of Signomial Programs. Technical Report T-274, George Washington University, Washington D. C., 1973   
31  Walter E, Piet-Lahanier H. Robust Nonlinear Parameter Estimation in the Bounded Noise Case. Proceedings of 25th Conference on Decision and Control, Athens, Greece , 1986, 1037\~ 1042   
32  Milanese M, and Belforte G. Estimation Theory and Uncertainty Intervals Evaluation in Presence of Unknown but Bounded Errors: Linear Families of Models and Estimators. IEEE Transactions on Automatic Control, 1982, 27: 408\~414   
33 Billings S A, Peyton J C. Mapping Nonlinear Integro-Differential Equation in the Frequency Domain. Int. J. Control, 1990, 52: 863 \~-879   
34 Han C. A General Formula of Generalized Frequency Response Functions for Nonlinear Differential Equations. Research Report of Xi'an Jiaotong University, 1992   
35 Kim K I , Powers E J, A Digital Method of Modeling Quadratically Nonlinear Systems with a General Random Input. IEEE Trans. Acoustics, Speech, and Signal  

# 220  

Processing, 1988, 36(11): 1758\~1769  

36 Milanese M. Properties of Least-Squares Estimates in Set Membership Identification. Automatica, 1995, 31: 327\~ 332  

37 Ljung L, Gustavsson I, Soderstrom T. Identification of Liner Multivariable Systems Operating under Liner Feedback Control. IEEE Trans. Auto. Control, 1974, AC-19: 836\~840  

38 Gustavsson I, Ljung L, Soderstrom, T. Identification of Processes in Closed Loop Identifiability and Accuracy Aspects. Automatica, 1977, 13: 59\~ 75  

39徐南荣,宋文忠,夏安帮.系统辨识.南京：东南大学出版社,1991  

40方崇志，萧得云.过程辨识.北京：清华大学出版社，1994  

# 第6章 频域辨识算法  

6.1概述  

自从17世纪牛顿力学出现以来，动力学系统研究通常采用状态参数法在时域进行。20世纪40年代 $\sim\!50$ 年代，工程控制论初兴，频率响应、传递函数成了控制系统分析和设计的主要工具，工程界盛行频域法。此时动力学系统动态特性研究也引进了频域法，相继提出了一系列应用频域法、频率响应曲线以研究动力学系统振动特性和从试验数据提取系统中待定参数的方法，频域法也成了动力学系统参数估计的重要手段之一[1,2] O  

20世纪60年代数字电子计算机出现后，适用于数字计算和非线性系统分析的状态参数法进人控制论领域，促使滤波、预测和估计理论蓬勃发展，时域法逐渐取代频域法而成为系统辨识的主要方法和途径。1965 年库利-图基（Cooley-Tukey）3发明了快速傅里叶变换（FFT），大大提高了在数字计算机上进行傅里叶变换的速度，使频域算法在工程上得到更迅速发展和广泛应用。三十多年来，时域的输出误差法、最大似然法、卡尔曼滤波法在动力学系统辨识，特别是气动参数辨识中得到广泛的应用。目前，时域法是动力学系统辨识的主要方法。  

20世纪70 年代初，梅拉（R.K.Mehra）重新研究了频域法[4]，最初他只给出了一般的频域回归公式,后来又给出了最大似然法[5]、方程误差法[6]和辅助变量法[7的频域公式,不过他是着眼于最优输人设计。克莱因（V．Klein)从参数估计的角度，给出了从频率响应曲线求飞机传递函数的复变量回归法，并总结了频域中参数估计的最大似然法、输出误差法和方程误差法，进行了较为严谨的数学推导，使之可用于多种数据形式一—实验数据时间历程的傅里叶变换、频率响应曲线、谱或互谱密度等，从而使在时域中应用广泛的统计学辨识方法推广到了频域[8]  

频域法虽然只能用于线性系统，但在处理弹性动力学系统和非定常线性动力学系统的参数辨识方面有独特优点，正在得到应用和开发。  

# 6.2 频域分析的基础知识  

试验数据和动力学系统数学模型从时域转到频域，必须应用傅里叶变换和有关公式。本节给出频域分析中常用的傅里叶变换的基本概念和公式。  

# 6.2.1 傅里叶变换  

任何单值复函数 $x(t)$ ，在给定区间若只有有限个间断点且绝对可积,则 $x(t)$ 可以表示为整个连续的频率区间的积分，此积分称为傅里叶积分。定义如下  

x\left(,t,\right),=,\frac{1}{2\pi}!!\int_{,-\infty}^{+\infty}!!!\tilde{x}\left(,\omega,\right)!\mathrm{e}^{\mathrm{i}\omega t}\mathrm{d}\omega\equiv F T^{-1}!\left{!!\tilde{x}\left(,\omega,\right)\right}

  

上式称为 $\tilde{x}^{(\omega)}$ 的傅里叶反变换  

\tilde{\boldsymbol{x}}\left(\omega\right),=,\int_{,-\infty}^{+\infty}\boldsymbol{x}\left(,t,\right)\mathrm{e}^{-\mathrm{i}\omega t}\mathrm{d}t,\equiv,F T\left{,\boldsymbol{x}\left(,t,\right),\right}

  

上式称为 $x(t)$ 的傅里叶变换。  

$x(t)$ 和 $\tilde{x}^{(\omega)}$ 称为傅里叶变换对，可表示为  

x(\mathbf{\Delta}t){\leftrightarrow}\tilde{x}(\mathbf{\Delta}\omega)

  

傅里叶变换满足下列运算规则  

x(t)\pm y(t){\leftrightarrow}\tilde{x}(\omega)\pm\tilde{y}(\omega)

  

(2）数乘: $a x\,(\,t\,){\leftrightarrow}\,a{\bar{x}}\,(\,\omega\,)$  

(3）比例伸缩: $x(a t){\leftrightarrow}{\frac{1}{\left|\,a\,\right|}}{\tilde{x}}\left({\frac{\omega}{a}}\right)$  

（4）时延： $x\left(\iota\pm\iota_{0}\right)\leftrightarrow\mathrm{e}^{\pm\ i\omega_{0}\ell\tilde{\mathbf{\alpha}}}\acute{x}\left(\omega\right)$  

(5)频移： $\cdot\,\mathrm{e}^{\,\pm\,\mathrm{i}\omega_{0}t}x\left(\,t\,\right){\leftrightarrow}\,\tilde{x}\left(\,\omega\mu\omega_{0}\,\right)$  

(6）面积: $\int_{\mathbb{-\infty}}^{+\,\infty}x\left(\,t\,\right)\mathrm{d}t\;=\;\tilde{x}\left(0\right)$  

\left.\frac{1}{2\pi}\right\lbrack\stackrel{\scriptscriptstyle+,\infty}{\ldots}!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

  

（7）能量: $\int_{\textrm{\tiny\infty}}^{+\infty}\mid x\left(\textit{t}\right)\mid^{2}\mathrm{d}t\;=\;\frac{1}{2\uppi}\!\!\int_{-\infty}^{+\infty}\mid\tilde{x}\left(\textit{\omega}\right)\mid^{2}\mathrm{d}\omega$  

（8）微分： $\frac{\mathrm{d}^{n}x\left(\,t\,\right)}{\mathrm{d}t^{n}}\mathrm{\leftrightarrow}(\mathrm{i}\omega)\,^{n}\widetilde{x}\left(\,\omega\,\right)$  

(-\mathrm{~i}t,)^{n}x(,t,){\leftrightarrow},\frac{\mathrm{d}^{n}\widetilde{x}\left(,\omega,\right)}{\mathrm{d}\omega^{n}}

  

(9）矩:时域函数的 $\pmb{n}$ 次矩正比于频域函数的 $\pmb{n}$ 次微商在原点的值。表示为  

=,\int_{-\infty}^{+\infty}t^{n}x\left(,t,\right)\mathrm{d}t;=;\mathrm{i}^{n}\left[\frac{\mathrm{d}^{n}\widetilde{x}\left(,\omega\right)}{\mathrm{d}\omega^{n}}\right]_{\omega,=,0}

\frac{1}{2\uppi}!!\left{!!\begin{array}{l}{{\displaystyle{^+\infty}}}\ {{\displaystyle{^-\infty}}}\end{array}!!\omega^{\eta}!!\widetilde{x}\left(\omega\right)!!\right}!!\mathrm{d}\omega;=;\left[\frac{\mathrm{d}^{n}x\left(!!\mathrm{\Delta}t,\right)}{\mathrm{d}t^{n}}\right]_{t,=,0}

  

（10）乘积与卷积：两个时域函数的卷积等效于频域的乘法运算，反之亦然。表示为  

\begin{array}{r}{x(t)y(t){\leftrightarrow}\hat{x}(\omega)\tilde{y}(\omega)}\ {x(t)y(t){\leftrightarrow}\tilde{x}(\omega)\tilde{y}(\omega)}\end{array}

  

式中 一卷积符号，定义为  

A\left(,t,\right),*,B\left(,t,\right);=,\int_{-\infty}^{+\infty}!A\left(,\tau,\right)B\left(,t,-,\tau,\right)\mathrm{d}\tau

  

# 6.2.2 离散傅里叶变换  

通常，试验数据是有限长度的离散采样数据序列，为建立离散信号的时域和频域关系式，必须应用离散傅里叶变换。 $x\left(\mathbf{\chi}_{i}\right)\left(\mathbf{\chi}_{i}=\right.$ $0\,,1\,,\cdots,N-1\,)$ 为 $N$ 点离散数据系列,其离散傅里叶变换对定义  

为  

x\left(j\right)\mathrm{=}\frac{1}{N}\sum_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\hat{x}\left(n\right)\mathrm{e}^{\mathrm{i}n\left(\frac{2\pi}{N}\right)j}

\tilde{\chi}\left(,n,\right)\ =\ \sum_{,j,=,0}^{N-1}x\left(j,\right)\mathrm{e}^{-,\mathrm{i}n,\left(\frac{2\pi}{N}\right)j}

  

离散型“傅里叶变换对”用下列符号表示  

x(j){\leftrightarrow}{\tilde{x}}(,n,)

  

长度为 $N$ 的有限序列数据 $x\left(\,i\,\right)$ ，可被认为是从以 $N$ 为周期的周期性序列数据 $x_{\mathfrak{p}}(\,i\,)$ 中截取一个周期的样本序列。周期函数$x_{\hat{p}}(\,i\,)$ 有相应的傅里叶级数,其傅里叶系数 $\tilde{x}_{\mathnormal{p}}\left(\mathnormal{n}\right)$ 也是一个以 $N$ 为周期的周期性频谱序列。抽出一个周期的谱线序列可构成$\tilde{x}\left(\,n\,\right)$ ，即  

\tilde{x}\left(,n,\right),=,\left{!!!{\tilde{x}}_{\phi}(,n,)\quad-,\frac{N}{2}!\ll n\ll\frac{N}{2}-1\right.

x(i),=,{\left{\begin{array}{l l}{x_{\rho}({,i,})}&{0\leqslant i\leqslant N;-;1}\ {0}&{i;{\ast}i\mathbb{H}\mathbb{H}\mathbb{H}\mathbb{H}{\mathbb H}{\mathbb H}}\end{array}\right.}

  

因此,离散傅里叶变换也满足与上节傅里叶变换相对应的运算法则。  

x(i)\pm y(i){\leftrightarrow}\tilde{x}(n)\pm\tilde{y}(n)

  

$x(j)\mathrm{e}^{\pm\mathrm{i}\,\left(\frac{2\pi}{N}\right)m j}\mathrm{\leftrightarrow}\,\tilde{x}\,(\,n\,\mp\,m\,)$  

(6)序列总和 ： $\sum_{\stackrel{i}{i}\,=\,0}^{N-1}x\left(\,i\,\right)\,=\,\stackrel{\sim}{x}\left(0\right)$  

x(0),=,\frac{1}{N}\sum_{n,=,-\frac{N}{2}}^{\frac{N}{2}-1}\bar{x},(,n,)

\sum_{i,=,0}^{N-1},\mid x\left(,i,\right),\mid^{2},=,\frac{1}{N}\sum_{n,-,-,\frac{N}{2}}^{-\frac{N}{2}-1},\mid\tilde{x}\left(,n,\right),\mid^{2}

  

(8）圆周卷积: $x(\mathbf{\psi}_{i})\star\mathbf{\psi}_{y}(\mathbf{\psi}_{i}){\leftrightarrow}\tilde{\mathbf{\psi}}(\mathbf{\psi}_{n})\tilde{\mathbf{\psi}}(\mathbf{\psi}_{n})$  

x(\mathbf{\Psi}{i}\mathbf{\Psi})y(\mathbf{\Psi}{i}\mathbf{\Psi})\leftrightarrow\frac{1}{N}\widetilde{x}\left(\mathbf{\Psi}{n}\right)\ast\widetilde{y}\left(\mathbf{\Psi}{n}\right)

  

圆周卷积即周期性卷积，以 $N$ 为周期，则  

\begin{array}{l}{\displaystyle{\boldsymbol x}\left({,i,}\right)\ast{\boldsymbol y}\left({,i,}\right),=,\sum_{r,-,0}^{N-1}\boldsymbol x\left({,r,}\right){\boldsymbol y}\left({,i,-,}r,\right)}\ {\displaystyle\tilde{\boldsymbol x}\left({,n,}\right)\ast\tilde{\boldsymbol y}\left({,n,}\right),=,\sum_{r,=,-,\frac{N}{2}}^{\frac{N}{2}-1}\tilde{\boldsymbol x}\left({,r,}\right)\tilde{\boldsymbol y}\left({,n,-,}r,\right)}\end{array}

  

离散傅里叶变换在线性系统、光学、电学、声学、量子力学等诸多领域得到广泛应用，但由于在数字计算机进行变换计算时，其计算量随数据样点数 $N$ 成 $N^{2}$ 倍增长，当 $N$ 很大时,极费机时，难于实用。1965年库利-图基利用变换运算过程中原始变换矩阵运算的多余性，发明了快速傅里叶变换（FFT），其计算量正比于$N\log_{2}N$ ,计算速度提高了 $N/\log_{2}N$ 倍,大大降低了计算成本，使数字系统远优于模拟系统而得到厂泛实际应用，快速傅里叶变换不仅有了成熟的应用软件并且发展了专用硬件和专用处理机。采用频域辨识算法时，可直接采用FFT进行离散傅里叶变换。  

# 6.2.3 复随机变量  

傅里叶变换的运算公式利用复数形式推导比较简捷，复随机变量的统计特性便于推广到多维矢量，因此在频域法中常用到复随机变量。本节简要介绍复随机变量及其概率分布的定义。  

（1）复随机变量 $x=x_{R}+\mathrm{i}x_{I}$ 的期望值、方差定义为 (2) $r$ 维复随机变量的协方差矩阵、相关函数定义为 协方差矩阵 $\operatorname{cov}(\,x_{k}\,,x_{l}\,)\equiv E\,|\,[\,x_{k}\,-\,E\,(\,x_{k}\,)\,][\,x_{\,l}^{\mathrm{~*~}}\,-\,E\,(\,x_{\,l}^{\mathrm{~*~}})\,]\,\}$  

相关函数： $r\left(\,x_{k}\,,x_{l}\,\right)\equiv E\left\{\,x_{k}x\,\right\}^{*}\,\right\}$ 式中 $x\,_{l}^{\star}\longrightarrow x_{l}$ 的共轭复数。  

若复随机变量 $z_{1},z_{2},\cdots,z_{n}$ 满足下式,则是不相关的$r\,(\,x_{k}\,,x_{l}\,)\;=\;E\,\{\,x_{k}x_{l}^{\,*}\,\}\;=\;E\,\{\,x_{k}\,\}\,E\,\{\,x_{l}^{\,*}\,\}\;\;\;\;\;(\,k\,,l\;=\;1,2,\cdots,n\,)$  

（3）复变量正态分布函数:若复随机变量 $x=x_{R}+\mathrm{i}x_{\mathrm{~I~}}$ 的实部和虚部都是均值为零、方差为 $\left(\mathfrak{t}/2\right)\sigma_{x}^{2}$ 的高斯分布，且实部和虚部统计独立,那么复随机变量 $_x$ 的分布函数定义为独立变量 $x_{R}$ 和 $\boldsymbol{x}_{I}$ 的联合分布，即  

\begin{array}{r l r}{\lefteqn{\int_{\mathbb{\Gamma}}^{}\left[\frac{\d H}{\d x_{R}}\right]f\left[\frac{\d x_{I}}{\d x_{I}}\right],=,}}\ &{}&{\frac{1}{\sqrt{\pi\sigma_{x}^{2}}}\mathrm{exp}[\left(,-,x_{R},\right)^{2}/\sigma_{x}^{2},],\frac{1}{\sqrt{\pi\sigma_{x}^{2}}}\mathrm{exp}[\left(,-,x_{I},\right)^{2}/\sigma_{x}^{2},],=,}\ &{}&{\left(\frac{1}{\pi\sigma_{x}^{2}}\right)\mathrm{exp}(-,x^{\ast},x/\sigma_{x}^{2}),}\end{array}

  

(4) $^r$ 维复矢量正态分布函数：若 $x_{r}$ 为 $^r$ 维复矢量，其正态分布函数 $\phi(x_{r})$ 定义为  

\phi(,{\pmb x}{r},),=,,\bigg(\frac{1}{\pi^{r},|{\pmb B},|}\bigg)\mathrm{exp}(,-,{\pmb x},{r}^{\star},{\pmb B}^{-1}{\pmb x}_{r},)

  

式中 $\scriptstyle B\longrightarrow\pmb{x},$ 的 $\pmb{r}$ 维协方差矩阵。若 $x_{r}$ 的元素统计独立,则 $\pmb{B}$ 是对角矩阵。  

# 6.2.4 随机过程  

以 $t$ 为参数的随机变量 $x(t)$ ，称为随机过程。对于给定的 $\pmb{t}$ $x\left(\footnote{I n t}\right)$ 取值是随机的；而沿时轴 $t\,,x\left(\,t\,\right)$ 又是随机变量 $\pmb{x}$ 随时间的变化过程。描述随机过程的概率密度是多层次的：一维概率密度$\ p_{\,1}(\,,x\,;t\,)$ 是以 $t$ 为参数， $_x$ 的概率密度分布；二维概率 $\phi_{2}(\,x_{1}\,,x_{2}\,;$ $t_{\tiny{1}},t_{2})$ 是 $\boldsymbol{x}$ 在 $\pmb{\tau}_{1}$ 时刻取 $x_{1}$ ，而在 $t_{2}$ 时刻取 $x_{2}$ 的概率密度··.···在工程应用中，通常只用下列几个特征参量：  

(1）均值 $\mu_{x}$  

\mu_{x}\equiv E\left{,x\left(,t,\right),\right};=;\int_{-\infty}^{+\infty}x/p_{1}(,x,,t,)\mathrm{d}x

  

(2）均方值 $\psi_{x}^{2}$  

\psi_{x}^{2}\equiv E,{,x^{2}(,t,),};=;\int_{-\infty}^{+\infty}x^{2},/p_{1}(,x,,t,),\mathrm{d}x

  

(3) 方差 $\sigma_{x}^{2}(\ t)$  

\begin{array}{l}{\sigma_{x}^{2}(t)\equiv!E!\mid![,x(t),-,\mu_{x}(,t,),]^{2}!\mid,=}\ {\displaystyle\int_{,-\infty}^{+,\infty}!!!\Big[,x(,t),-,\mu_{x}(,t,),]^{2},\phi_{1}(,x,,t,)\mathrm{d}x}\end{array}

  

（4）自相关函数 $r_{x x}(\,t_{1}\,,t_{2}\,)$  

\begin{array}{l}{r_{x x}\equiv E\left\vert\left.x\left(t_{1}\right)x\left(t_{2}\right)\right}\right.=}\ {\quad\left.\int_{-\infty}^{+\infty}!!!\int_{-\infty}^{+\infty}!!!x(t_{1})x(t_{2}),!,!p_{2}(x_{1},x_{2};t_{1},t_{2})\mathrm{d}x_{1}\mathrm{d}x_{2}\right.}\end{array}

  

式中  

\begin{array}{r}{{x_{1}=x\left(,{t_{1}},\right);\ }}\ {{x_{2}=x\left(,{t_{2}},\right)_{\circ}}}\end{array}

  

(5）互相关函数 $r_{x y}$  

\begin{array}{l}{r_{x y}\equiv E\left{,x\left(,t_{1}\right)y!\left(,t_{2}\right),\right};=}\ {\displaystyle\int_{,-\infty}^{+\infty}!!\int_{,-\infty}^{+\infty}!!x!\left(,t_{1}\right)y!\left(,t_{2}\right)\phi_{2}!\left(,x_{1},y_{2};t_{1},,t_{2}\right)!\mathrm{d}x_{1}\mathrm{d}y_{2}}\end{array}

  

（6）协方差函数 $P_{x x}(\,t_{1}\,,t_{2}\,)$  

\begin{array}{l}{\displaystyle\equiv E\left{\left[,x_{1},-,\mu_{x}(,t_{1})\right]\left[,x_{2},-,\mu_{x}(,t_{2}),\right],\right}\ =}\ {\displaystyle\int_{,-\infty}^{+,\infty}!!!\int_{,-\infty}^{+,\infty}!\left[,x_{1},-,\mu_{x}(,t_{1}),\right]\left[,x_{2},-,\mu_{x}(,t_{2}),\right],\times}\ {\displaystyle\qquad\qquad\qquad\quad\int_{,2}^{}!\left(,x_{1},x_{2},;t_{1},t_{2}\right)!\mathrm{d}x_{1}\mathrm{d}x_{2}}\end{array}

  

（7）互协方差函数 $P_{x y}(\,t_{1}\,,t_{2})$  

P_{x y},=!\int_{-\infty}^{+\infty}!!\int_{-\infty}^{+\infty}!\left[,x_{1},-,\mu_{x}(,t_{1},),\right]\left[,y_{2},-,\mu_{y}(,t_{2},),\right],\times

\phi_{2}\big(,x_{1},,y_{2},;t_{1},,t_{2},\big)\mathrm{d}x_{1}\mathrm{d}y_{2}

  

（8）特征参数的基本关系  

\begin{array}{r l}&{\psi_{x}^{2}(,t,),=,r_{x x}(,t,,t,)}\ &{\sigma_{x}^{2}(,t,),=,,\psi_{x}^{2}(,t,),-,\mu_{x}^{2}(,t,),=,r_{x x}(,t,,t,),-,\mu_{x}^{2}(,t,)}\ &{P_{x x}(,t_{1},,t_{2},),=,,r_{x x}(,t_{1},,t_{2},),-,\mu_{x}(,t_{1},),\mu_{x}(,t_{2},)}\end{array}

  

# 6.2.5 平稳随机过程  

统计特性不随时间变化的随机过程称为平稳随机过程。二阶以下矩函数不随时间变化的随机过程称为弱平稳随机过程，或宽平稳随机过程。通常讨论平稳随机过程皆指弱平稳随机过程。  

# 1）平稳随机过程  

特征参数的基本关系为  

{\begin{array}{r l}&{\mu_{x}(t)=\mu_{x}(0)}\ &{r_{x x}(\tau)=\left.E\right{x(t),x(t+\tau)\right}=\left.r_{x x}(-\tau)}\ &{{\dot{\phi}}{x}^{2}=r{x x}(0)\geqslant0}\ &{{\dot{\sigma}}{x}^{2}=\operatorname{var}{x(t)}=\left.r{x x}(0)-\mu_{x}^{2}\right.}\ &{\left.P_{x x}(\tau)=\operatorname{cov}{x(t)}=\left.r_{x x}(\tau)-\mu_{x}^{2}\right.}\ &{\left.|r_{x x}(\tau)|\leqslant r_{x x}(0)\right.}\ &{r_{x y}(\tau)=\left.r_{y x}(-\tau)\right.}\ &{\left.|r_{x y}(\tau)|\leqslant r_{x x}(0),r_{y y}(0)\right.}\ &{\left.|r_{x y}(\tau)=r_{x y}(\tau)-\mu_{x}\mu_{y}\right.}\end{array}}

  

# 2）各态历经平稳随机过程  

若平稳随机过程 $x(t)$ 的各特征参数的期望值等于相对应的时间平均值，则称为各态历经平稳随机过程。故各态历经随机过程的全部统计特性都可以由任意的一个样本过程来确定。  

自相关函数:  

r_{x x}(,\tau);=;\operatorname*{lim}{T\rightarrow\infty},\frac{1}{2,T}{\int{-,T}^{T}}x(,t,)x(,t,+,\tau,)\mathrm{d}t

  

互相关函数：  

r_{x y}(,\tau);=;\operatorname*{lim}{T\rightarrow\infty},\frac{1}{2,T}{\biggr\lbrack}{-T}^{T}x(,t,),y(,t,+,\tau,){\mathrm{d}}t

  

互协方差函数：  

P_{x y}(,\tau,),=,\operatorname*{lim}{T\rightarrow\infty},\frac{1}{2,T}{\biggr\lbrack}{-T}^{T}[,x(,t,),-,\mu_{x},]{,\bigl\lbrack},y(,t,+,\tau,),-,\mu_{y}{\bigr\rbrack}{,\mathrm{d}}t

  

3）统计特征参数估计  

在系统辨识中经常要估计各随机过程的均值、相关函数等。对于各态历经平稳随机过程，这些统计特征参数可以由随机过程的有限个测量值来估计。  

\mu_{x},=,\frac{1}{N}\sum_{i,=,1}^{N}{x,(,i,)}

  

自相关函数： $r_{x x}(\,\tau)\equiv r_{x x}(\,l\,)\,=\,\frac{1}{N}\sum_{i\,=\,1}^{N}x\,(\,i\,)\,x\,(\,i\,+\,l\,)$  

(l,=,0,,,\pm,1,,,\pm,2,,\cdots,,\pm,(,N,-,1,),)

  

互相关函数： $r_{x y}(\,\tau)\equiv r_{x y}(\,l\,)\,=\,\frac{1}{N}\sum_{i\,=\,1}^{N}x(\,i\,)y(\,i\,+\,l\,)$  

(l;=;0,,;\pm;1,,;\pm;2,,\cdots,;\pm;(,N,-,1,),)

  

互协方差函数：  

P_{x y}(,\tau)\equiv P_{x y}(,l,),=,\frac{1}{N}\sum_{i,-1}^{N},[,x,(,i,),-,\mu_{x},],[,y,(,i,+,l,),-,\mu_{y},]

\left(,l;=;0,,,\pm,1,,,\pm,2,,\cdots,,\pm,\left(,N,-,1,\right),\right)

  

# 6.2.6 随机过程的傅里叶变换  

随机过程在均方意义下是周期性时，可以展成傅里叶级数，对有限长度的随机序列可以进行离散傅里叶变换。随机过程从时域转换到频域时，其中某些统计特性将保持不变。  

1）随机过程离散傅里叶变换  

设x(i)(i=0,1，"·,N-1)是有限长度为 N 的实随机序列,  

且 $E\left\{\,x\left(\,i\,\right)\,\right\}=0\,,E\left\{\,x\left(\,i\,\right)x\left(\,k\,\right)\,\right\}\,=r_{x x}\left(\,i\,-\,k\,\right)$ ,则其傅里叶变换对为  

\begin{array}{c}{{\left|x\big(j\big)\right.=\displaystyle\frac{1}{N}\sum_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\tilde{x}\big(n\big)\mathrm{e}^{\mathrm{i}n\big(\frac{N}{2}\big)j}\quad\mathrm{(}j,=,0,1,\cdots,N,-1\big)}}\ {{\left.\tilde{x}\big(,n,\big),=,\displaystyle\sum_{\prime,=,0}^{N-1}x\big(j,\mathrm{e}^{-\mathrm{i}n\big(\frac{2\pi}{N}\big)j}\quad\quad\quad\big(,n,=,-,\frac{N}{2},,-,\frac{N}{2},+,1,\cdots,\frac{N}{2},-,1\big)\right|}}\end{array}

  

且  

$\begin{array}{l}{{\displaystyle E\left\{\,\tilde{x}\left(\,n\,\right)\right\}\,=\,0}}\\ {{\displaystyle E\left\{\,\tilde{x}\left(\,m\right)\tilde{x}^{\,\ast}\left(\,n\,\right)\right\}\,=\,N\,\tilde{r}_{x x}(\,n)\delta_{m n}\big(\,m\,,n\,=-\,\frac{N}{2},\,-\,\frac{N}{2}+1,\cdots,\frac{N}{2}\,-\,1\big)}}\end{array}$ 式中  

\begin{array}{c}{{\displaystyle{\tilde{r}{x x}(\mathbf{\bar{\mu}}{n})\ =\ \sum_{j\mathop{=}0}^{N-1}r_{x x}(\mathbf{\bar{\mu}}{j})\mathrm{e}^{-\mathrm{i}n\left(\frac{2\pi}{N}\right)j}}}}\ {{\displaystyle{\tilde{r}{x x}(j\mathbf{\bar{\mu}})\ =-\ \frac{1}{N}\sum_{n\mathop{=}-\frac{N}{2}}^{\frac{N}{2}-1}r_{x x}(\mathbf{\mu}_{n})\mathrm{e}^{-\mathrm{i}n\left(\frac{2\pi}{N}\right)j}}}}\end{array}

  

2）高斯分布随机过程的傅里叶变换也是高斯分布  

设 $x\left(\,i\,\right)\left(\,i=0\,,1\,,\Lambda,N-1\,\right)$ 是统计独立的高斯分布实随机序列,且 $E\left\{\,x\,(\,i\,)\,\right\}=0\,,E\left\{\,x^{2}(\,i\,)\,\right\}=\sigma^{2}$ ,则其傅里叶变换也是一个统计独立的复数高斯分布随机变量序列，而且  

E,{,\tilde{x}{R},(,n,),};=;0;;;;E,{,\tilde{x}{I},(,n,),};=;0

E\Biggl{\Biggl[\tilde{\bar{x}}{R}(\ m)\Biggr]\Biggl[\tilde{\bar{x}}{R}(\ m)\Biggr]^{\mathrm{T}}\Biggr}=\ N\Biggl[\tilde{\bar{r}}{x x};;;;;0\atop;;\tilde{r}{x x}\Biggr]\delta_{m n};;.

  

# 6.2.7 随机过程的谱密度  

1）帕塞瓦尔定理  

对于确定性过程，帕塞瓦尔的总能量谱定理以频谱积分形式  

给出过程 $x\left(\,t\,\right)$ 总能量的表达式  

\int_{-\infty}^{+\infty}x^{2}(\mathbf{\Psi}{t}\mathbf{\Psi})\mathrm{d}t\ =\ \frac{1}{2\pi}{\int{-\infty}^{+\infty}\parallel\hat{\mathbf{\Psi}}{x}(\mathbf{\Psi}{\omega})\parallel^{2}\mathrm{d}\omega}

  

式中 $\bar{\boldsymbol{x}}\left(\omega\right)\!-\!\!\longrightarrow\!\!\left(\,t\,\right)$ 的傅里叶变换。  

当过程的总能量不是有限值时,过程的平均功率满足  

\operatorname*{lim}{T\to\infty}\frac{1}{2,T}{\int{;\ldots;T}^{T}}x^{2}(,t,)\mathrm{d}t,=,\frac{1}{2\pi}{\int_{;\ldots;\infty}^{+\infty}}S_{x}\left(,\omega,\right)\mathrm{d}\omega

  

式中  

S_{x}(,\omega,);=;\operatorname*{lim}_{T\to\infty},\frac{1}{2,T}:\Vert\mathbf{\Sigma}\tilde{\boldsymbol{x}}\left(,\omega,\right),\Vert^{,2}

  

将上述结果推广到随机过程，可建立随机过程 $x\left(\,i\,\right)$ 的均方值$\boldsymbol{\psi}_{x}^{2}$ 与功率谱的关系式  

\psi_{x}^{2},=,\frac{1}{2\uppi}\overset{\textstyle+,\infty}{\textstyle\int_{\stackrel{\scriptstyle-\infty}{\scriptstyle-\infty}}}S_{x}(,\omega,)\mathrm{d}\omega

  

式中  

S_{x}(,\omega,);=;\operatorname*{lim}_{T\to\infty},\frac{1}{2,T}E,{,\parallel,\tilde{x},(,\omega,),\parallel^{,2},}

  

$S_{x}(\,\omega\,)$ 称为随机过程 $x\left(\mathit{t}\right)$ 的平均功率谱密度，简称功率谱或谱密度。它反映功率在不同频域的分布，是 $x\left(\,t\,\right)$ 的重要统计特性。  

# 2）维纳-辛钦定理  

维纳-辛钦定理证明，平稳随机过程 $x\left(\,t\,\right)$ 的谱密度等于自相关函数的傅里叶变换  

\left{\begin{array}{l}{\displaystyle S_{x}(,\omega,),=,\tilde{r}{x x}(,\omega,),=,\int{-\infty}^{+\infty}r_{x x}(,\tau,)\mathrm{e}^{-\mathrm{i}\omega t}\mathrm{d}\tau}\ {\displaystyle r_{x x}(,\tau),=,\frac{1}{2\pi}!!\int_{-\infty}^{+\infty}!!\tilde{r}_{x x}(,\omega,),\mathrm{e}^{-\mathrm{i}\omega\tau}\mathrm{d}\tau}\end{array}\right.,

  

对于离散系统  

r_{x,r}(\mathbf{\chi}{i}){\leftrightarrow}\tilde{r}{x,\tau}(\mathbf{\chi}_{n})

\hat{\mathrm{\boldmath~\mu~}}{x x}(;i;);=;E\left{,x(;k;)x(;k;+;i;),\right};=;\operatorname*{lim}{N\to\infty},\frac{1}{N,-,\left|,i;\right|}\sum_{k;=;1}^{N-\left|,i;\right|},x(;k;)x(;k;+;i;)

\tilde{r}_{x x}(,n,);=;\frac{1}{N}E,{,\tilde{x}^{\mathrm{!\star~}}(,n,),\tilde{x},(,n,),}

  

对于互相关函数,可建立互功率谱 $\tilde{r}_{x y}(\r_{n})$  

r_{x y}({\bf\chi}{i}){\leftrightarrow},\bar{r}{x y}({\bf\chi}_{n})

\tilde{r}_{x y}(,n,);=;\frac{1}{N}E,{,\tilde{x}^{\mathrm{\star}}(,n,),\tilde{y}(,n,),}

  

# 6.3 最大似然法  

最大似然法是目前最实用和有效的参数估计方法。本节将导出似然函数的频域表达式、频域中的最大似然法辨识算式以及作为其特殊情况的输出误差法和方程误差法的算式。  

频域法主要用于常系数线性系统，也能用于研究可进行傅里叶变换的变系数线性系统。常系数线性系统的数学模型可表述如下。  

状态方程：  

\begin{array}{r}{\left{\dot{\pmb{x}}\left(,t,\right),=,\pmb{F}(,\pmb{\theta},),\pmb{x}(,t,),+,\pmb{G}(,\pmb{\theta},),\pmb{u}\left(,t,\right),+,\pmb{T}(,\pmb{\theta},),\pmb{\eta}(,t,)\right.}\ {\left.\pmb{E}\left{,\pmb{x},(0),\right},=,\pmb{x}{0},,\pmb{E}\left{,\pmb{x},(0),\pmb{x}^{\mathrm{T}}(0),\right},=,\pmb{P}{0}\quad(,t,\in,\left[0,T\right])}\end{array}

  

观测方程：  

\begin{array}{c}{{\pmb{y}(,i,),=,\pmb{H}(,\pmb{\theta},),\pmb{x},(,i,),+,\pmb{D}(,\pmb{\theta},),\pmb{u},(,i,),+,\pmb{\varepsilon},(,i,)}}\ {{(,i,=,0,,1,,2,,\cdots,N,-,1,)}}\end{array}

  

式中 $\pmb{x}\left(\begin{array}{r}{t}\end{array}\right)$ -状态矢量；  

$\pmb{u}\left(\pmb{t}\right)$ 一 一控制矢量；$\pmb\theta$ 一待估计参数；  
$\pmb{x}\left(\,i\,\right)-\$ 时刻的状态矢量；  
$\mathbf{y}\left(\mathbf{\chi}_{i}\right)$ --观测矢量；$N$ 偶数；  

${\cal F}\,,G\,,{\cal T}\,,{\cal H}\,,{\cal D}^{\prime}$ —常系数矩阵；  

$\pmb{\eta}(\pmb{t})$ 和 $\pmb{\varepsilon}(\mathbf{\sigma}_{i})$ 一一分别为过程噪声和观测噪声，是平稳高斯序  

列，互不相关，且满足下述关系  

E,{,\pmb{\eta}(,t,),},=,\pmb{0},,E,{,\pmb{\eta}(,t,),\pmb{\eta}^{\mathrm{T}}(,\tau,),},=,Q\left(,\pmb{\theta},\right)\delta_{t,,\tau}

E,{,\pmb{\varepsilon},(,i,),};=;0,,E,{,\pmb{\varepsilon},(,i,),\pmb{\varepsilon}^{\mathrm{T}}(,k,),};=;\pmb{R},(,\pmb{\theta},),\delta_{i,,k}

  

频域中参数最大似然估计的基本思想与时域中的最大似然估计相同,就是对给定观测数据序列 $Y_{N}=\left\{\,y_{0}\,,\,{\mathbf{y}}_{1}\,,\cdots,\,{\mathbf{y}}_{N-1}\,\right\}$ ，在满足状态方程和观测方程的条件下，寻求参数 $\pmb{\theta}$ 使 $\pmb{Y}_{N}$ 出现的条件概率达最大值；只是它是在频域中进行。下面给出频域中的似然函数表达式和最大似然估计算式。  

# 6.3.1 似然准则推导  

假定观测数据序列 $\pmb{Y}_{\mathbb{N}}$ 的各观测是互相独立的，似然函数 $L$ 在观测量的概率密度分布为高斯分布的条件下，在时域可表示为  

\begin{array}{l}{{\displaystyle{\cal L}\left(,\pmb{\theta},\big|,{\pmb Y}{N}\right),=\ln,!\hat{p}\left(,{\pmb Y}{N},\big|,\pmb{\theta}\right),=}}\ {{\displaystyle\quad-,\frac{1}{2}\sum_{t,=,0}^{N-1},{\pmb{\nu}!\left(,t,\right)^{\mathrm{T}}{\pmb B}^{-1}(,t,),\pmb{\nu}!\left(,t,\right),+,\ln,\big|,{\pmb B}\left(,t,\right),\big|,}}}\end{array}

  

在频域中， $\pmb{Y}_{N}$ 的离散傅里叶变换为 $\tilde{\bf Y}_{N/2\mathrm{~-~}1}\;=\;\langle\tilde{\bf\Delta y}_{\mathrm{~-~}N/2}\,,$ $\tilde{\textbf{y}}_{\dots N/2+1},\cdots,\tilde{\textbf{y}}_{N/2-1})$ 。离散傅里叶变换对定义为  

\left{\begin{array}{l}{\displaystyle\mathbf{y}{t}\equiv\mathbf{y}(\mathbf{\boldsymbol{\mathit{t}}}),=,\frac{1}{N}\sum{n,=,-\frac{N}{2}}^{\frac{N}{2}-1}\tilde{\mathbf{y}}(\mathbf{\boldsymbol{\mathit{n}}})\mathrm{e}^{\mathrm{i}n\omega_{0}t}\big(\mathbf{\boldsymbol{\mathit{t}}},=,0,1,\cdots,N-1\big)}\ {\displaystyle\tilde{\mathbf{y}}{n}\equiv\tilde{\mathbf{y}}(n),=,\frac{1}{N}\sum{\iota=0}^{N-1}\mathbf{y}(t)\mathrm{e}^{-\mathrm{i}n\omega_{0}t}}&{\displaystyle\big(,n,=-,\frac{N}{2},,-,\frac{N}{2}+1,\cdots,\frac{N}{2},-1\big)}\end{array}\right.,

  

式中 $\omega_{0}=2\pi/N_{\mathrm{\circ}}$  

在频域,可以假定 $\widetilde{\pmb Y}_{n}$ 的概率分布密度为 $\phi(\,\widetilde{Y}_{n}\,|\,\theta\,)$ ，则由条件概率定义，推得  

\begin{array}{r l}{\quad_{\mathcal{P}}(\left.\widetilde{\mathbf{Y}}{\frac{N}{2}-1}\right|\pmb{\theta})\equiv{\mathcal{P}}(\widetilde{\mathbf{y}}{\frac{N}{2}}\mathbf{\Phi}{1},\widetilde{\mathbf{Y}}{\frac{N}{2}-2}|\pmb{\theta}),=}&{}\ {\quad}&{\qquad\qquad\qquad\quad,{\mathcal{P}}(\widetilde{\mathbf{y}}{\frac{N}{2}-1}|\wedge{\widetilde{\mathbf{Y}}{\frac{N}{2}-2}}\pmb{\theta}),{\mathcal{P}}(\widetilde{\mathbf{Y}}{\frac{N}{2}-2}|\pmb{\theta}),=}\ {\quad}&{\qquad\qquad\qquad\quad,{\mathcal{P}}(\widetilde{\mathbf{y}}{\frac{N}{2}-1}|,\widetilde{\mathbf{Y}}{\frac{N}{2}-2},\pmb{\theta}),{\mathcal{P}}(\widetilde{\mathbf{y}}{\frac{N}{2}-2}|,\widetilde{\mathbf{Y}}{\frac{N}{2}-3},\pmb{\theta}),{\mathcal{P}}(\widetilde{\mathbf{Y}}_{\frac{N}{2}-3}|,\partial),=,\cdots,=}\end{array}

\prod_{n=-\frac{N}{2}}^{\frac{N}{2}-1}\phi\left(\stackrel{.}{{\bf y}}{n}\mid\stackrel{.}{{\bf Y}}{n}{\bf\Phi}_{1},\bullet\right)

  

据6.2.6节所述,若 $\pmb{Y}_{N}$ 是正态分布,则 $\widetilde{Y}_{N/2\;-\;1}$ 的概率分布密度也是正态分布。即  

\phi\left(,\mathbf{\widetilde{y}}{n}\mid\mathbf{Y}{n-1},,,\pmb\theta,\right);=;\frac{\exp!\left(,-,,\mathbf{\widetilde{v}}^{,\star}\left(,n,\right)\widetilde{\pmb B}^{,-1}!\left(,n,\right)\widetilde{\pmb v}\left(,n,\right),\right)}{\pi^{m},\left|\widetilde{\pmb B}\left(,n,\right),\right|}

\widetilde{\pmb{B}}\left(,n,\right);=;E\left{,\widetilde{\pmb{\nu}}\left(,n,\right),\widetilde{\pmb{\nu}}^{,\ast}\left(,n,\right),\right};=;\widetilde{N r_{v v}}

  

式中 $\scriptstyle m\,{\overset{\underset{\star}{}}{\longrightarrow}}{\tilde{\mathbf{y}}}_{n}$ 的维数；  

$\widetilde{B}\,(\mathbf{\Sigma}_{n}\,)\longrightarrow\,\widetilde{\mathbf{y}}_{n}$ 的协方差矩阵;  

$\tilde{\pmb{\nu}}(\,n\,)$ ——新息的傅里叶变换；$\bar{r}_{v v}\longrightarrow\bar{v}$ 的功率谱。  

取似然函数 $L$ 为给定 $\pmb{\theta}$ 下 $\widetilde{Y}_{N/2\,\cdots\,1}$ 的条件概率之对数,则  

L(,\pmb\theta,|,\widetilde{\mathbfcal Y}_{\frac{N}{2}-1},):=:\ln{:!!!!!!!!!\int!!!!!!!!\frac{}{}\frac{}{}\frac{}{}\dots{},|!!!!!\nabla!!!!!!\theta,\rangle}:=

\sum_{n,=,-\frac{N}{2}}^{\frac{N}{2}-1},\bigl[,\tilde{\pmb{\nu}}^{\star},\bigl(,n,\bigr),\tilde{\pmb{B}}^{,-1}\bigl(,n,\bigr),\tilde{\pmb{\nu}},\bigl(,n,\bigr),+,\ln,\big|,\tilde{\pmb{B}},\bigl(,n,\bigr),\big|,\bigr]

  

因此,在频域的最大似然判剧 $\tilde{\boldsymbol{J}}\left(\boldsymbol{\theta}\right)$ 为  

\bar{J}\left(,\pmb\theta,\right);=;\sum_{n,=,-\frac{N}{2}}^{\frac{N}{2}-1}\left[\frac{1}{N}\tilde{\pmb v}^{\mathrm{*}}(,\pmb\ n,),\tilde{\pmb r}{,\pmb v\pmb v}^{-1}\tilde{\pmb v}\left(,n,\right),+,\ln,\lvert,\tilde{\pmb r}{\pmb v\pmb v},\rvert,\right]

  

式中 $\dot{\boldsymbol{r}}_{v v}$ ——新息 $\tilde{\pmb{\nu}}(t)$ 的相关函数 $r_{w}\left(\,t\,\right)$ 的傅里叶变换,称为$\pmb{\nu}(t)$ 的功率谱密度；  

至此，已导出了频域的最大似然准则 $\tilde{\boldsymbol{J}}\left(\,\theta\,\right)$ ，下面将证明频域的最大似然准则与时域的最大似然准则是等价的。  

根据帕塞瓦尔定理，自相关函数和功率谱密度有下列关系  

B\left(,t,\right),=,E\left{,\pmb{\nu}\left(,t,\right)\pmb{\nu}^{\mathrm{T}},\right},=,\frac{1}{N}E\left{,\tilde{\pmb{\nu}}\left(,\pmb{n},\right),\tilde{\pmb{\nu}}^{\star}\left(,\pmb{n},\right),\right}

  

将式(6-84)代人式(6-87)可得  

\pmb{{\cal B}}\left(\mathit{\Pi}{t}\right);=;\pmb{{\Pi}}{r_{V}};=;-b{{\dot{r}}}_{\nu\nu}

  

将式(6-88)和式(6-84)代人式(6-86）,可证明时域准则与频域准则的等价性  

\begin{array}{l}{{\displaystyle:\frac{1}{N}{\sum}{n}\tilde{\mathbf{\upnu}}^{*}\left(\mathbf{\mu}\right)\tilde{r}{\mathbf{\L{v}}^{*}}^{-1}\left(\mathbf{\mu}\right)\tilde{\mathbf{\upnu}}(n)\left.+\left.N\mathrm{ln}\right|\tilde{r}{\mathbf{\L{v}}^{\nu}}\right|~=}}\ {{\displaystyle\frac{1}{N}{\sum}{n}{\sum}{\nu}\mathrm{P}^{\mathrm{T}}(t)\mathrm{e}^{\mathrm{i}n\omega{0}t}B^{-1}{\sum}{\tau}\mathrm{\L{v}}(\tau)\mathrm{e}^{-\mathrm{i}n\omega{0}\tau}+\left.N\mathrm{ln}\right|B\right|=}}\ {{\displaystyle\frac{1}{N}{\sum}{\nu}{\sum}{\nu}\mathrm{P}^{\mathrm{T}}(t),B^{-1}\nu(\tau){\sum}{n}\mathrm{e}^{\mathrm{i}n\omega{0}t}+\left.N\mathrm{ln}\right|B\right|=}}\ {{\displaystyle\sum_{i}\nu^{\top}B^{-1}\nu+\left.N\mathrm{ln}\right|B\right|~=~J\left(\pmb{\theta}\right)}}\end{array}

  

$\sum_{n}=\sum_{n\,=\,-\,N/2}^{N/2\,-\,1};$  

\sum_{t}=\sum_{t=0}^{N-1}\circ

  

推导中利用了下式  

\sum_{n}\mathrm{e}^{-\mathrm{i}n\omega_{0}t}\ =\ \left{{N\quad(\exists\ q\ t=\tau)}\right.

  

# 6.3.2 最大似然算法  

对常系数线性系统通用表达式（6-79)和式（6-80）,在第5章已给出时域的状态参数 $x(t\mid t)$ 和协方差矩阵 $\pmb{P}(t\mid t)$ 的最佳滤波方程组。  

状态最佳滤波方程  

\begin{array}{r}{\left{\frac{\mathrm{d}\hat{\mathbf{x}}\left(,t,\mathbf{\nabla}\mid,t,\right)}{\mathrm{d}t}\right.=\left.F!\left(,\pmb{\theta},\right)\hat{\mathbf{x}}\left(,t,\mathbf{\nabla}\mid,t,\right),+,\mathbf{G}\left(,\pmb{\theta},\right)u\left(,t,\right),+,\mathbf{K}\left(,t,\right)\pmb{\nu}\left(,t,\right),}\ {E!\left\mid,\pmb{x}\left(,0,\right),\right},=,\mathbf{x}_{0}}\end{array}

  

协方差矩阵方程  

\left{\begin{array}{l l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\pmb{P}(t,|,t),=,\pmb{F}(\pmb{\theta})\pmb{P}(t,|,t),+,\pmb{P}(t,|,t)\pmb{F}^{\mathrm{T}}(\pmb{\theta})+,\pmb{\cal{\Gamma}}\pmb{Q}\pmb{T}^{\mathrm{T}},-}\ {\pmb{P}(t,|,t,)\pmb{H}^{\mathrm{T}}(\pmb{\theta})\pmb{R}^{-1}(t)\pmb{H}(\pmb{\theta})\pmb{P}(t,|,t)}\ {\pmb{P}(t_{0},|,t_{0}),=,\pmb{P}_{0}(\pmb{\theta})}&{\quad\mathrm{(6.4)}}\end{array}\right.

  

式中  

\pmb{\nu}(,t,);=;\pmb{y}(,t,),-,\pmb{H}(,\pmb{\theta},),\pmb{x}\left(,t,\mid,t,\right),-,\pmb{D}(,\pmb{\theta},),\pmb{u}\left(,t,\right)

\pmb{K}(\pmb{t}):=:\pmb{P}(\pmb{t}:\mid:t:),\pmb{H}^{\mathrm{T}}(\pmb{\theta}),\pmb{R}^{-1}(\pmb{t}:)

  

式(6-90)可化为初始条件为零的方程组，只需做下列变量替换 $\pmb{x}_{1}(\,t\mid t\,)=\pmb{x}\left(\,t\mid t\,\right)-\pmb{x}_{0}\,$ ，对式(6-90)和式(6-92)进行上述变换（略去下标1）后可得  

\begin{array}{l}{\displaystyle\left{\frac{\mathrm{d}\hat{\mathbf{x}}\left(\ t\ |\ t\right)}{\mathrm{d}t},=,{\pmb F}(\pmb\theta)\left[\hat{\mathbf{x}}\left(\ t\ |\ t\right),+,{\pmb x}_{0}\right],+,{\pmb G}(,\pmb\theta),{\pmb u}(,t,),+,{\pmb K}(,t,),{\pmb\nu}(,t,)}\ {\displaystyle E\left{,{\pmb x}(0),\right},=,0}\end{array}

\pmb{\nu}(,t,);=;\pmb{y}(,t,),-,\pmb{H}(,\pmb{\theta},),[,\pmb{x},(,t,|,t,),+,\pmb{x}_{0},],-,\pmb{D}(,\pmb{\theta},),\pmb{u},(,t,)

  

从上述方程组可看出，卡尔曼增益项 $\pmb{K}(\pmb{t})\pmb{\nu}(\pmb{t})$ 是非线性项，如不进行简化，直接对此方程组进行傅里叶变换将出现 $\pmb{K}$ 和 $\pmb{y}$ 的卷积，难于求解。对常系数性系统，运行足够长时间以后，可认为卡尔曼滤波趋于稳态，即 $\pmb{K}(\,t\,),\pmb{R}(\,t\,),\pmb{P}(\,t\,|\,\,t\,)$ 趋于常数而简化计算。此时可以从式(6-91)右端为零来计算 $P(t\mid t)$ 的稳态值，再由式(6-93)计算 $\dot{\pmb{{\kappa}}}(t)$ ,但计算 $\pmb{P}(t\mid t)$ 稳态值还比较复杂；另一种较简化的算法,即将 $\pmb{K}$ 值作为待估计参数矩阵与待估计参数一起进行估计,求出 $\pmb{K}$ 值后再由式(6-93)求 $\textstyle P(t\mid t)$ 。  

对式(6-90)和式(6-92)进行傅里叶变换,可得出它们在频域的表达式，为了书写简便，取 ${\pmb x}_{0}\,{=}\,0$  

\mathrm{i}\omega\tilde{\cal I}!\tilde{!\mathbf{x}}\left(,\omega,\right);=;{\cal F}(,\theta,),\tilde{!\mathbf{x}}\left(,\omega,\right),+,{\cal G}\left(,\theta,\right),\tilde{!u}\left(,\omega,\right),+,{\cal K}\left(,\theta,\right),\tilde{!\mathbf{\Omega}}!\left(,\omega,\right)

\tilde{\pmb{\nu}}\left(,\omega,\right);=;\tilde{\pmb{y}}\left(,\omega,\right);-;\pmb{H}\left(,\pmb{\theta},\right)\tilde{\pmb{x}}\left(,\omega,\right);-;\pmb{D}\left(,\pmb{\theta},\right)\tilde{\pmb{u}}\left(,\omega,\right)

  

式中【——单位矩阵；  

K(0)——卡尔曼增益矩阵。  

由式(6-96)解出 $\tilde{\pmb{x}}(\omega)$ ,并代人式(6-97)可得  

\tilde{\pmb{x}}\left(,\omega,\right);=;\left[,\mathrm{i}\omega\pmb{I},-,\pmb{F}(,\pmb{\theta},),\right]^{-1}\left[,\pmb{G}\left(,\pmb{\theta},\right)\tilde{\pmb{u}}\left(,\omega,\right),+,\pmb{K}\left(,\pmb{\theta},\right)\tilde{\pmb{\nu}}\left(,\omega,\right),\right]

\begin{array}{r l r}&{\ddot{\pmb{\nu}}\big(\omega\big)+\pmb{{\cal D}}\big(\pmb{\theta}\big)\ddot{\pmb{u}}\left(\omega\right)+\pmb{{\cal H}}\big(\pmb{\theta}\big)\big[\ddot{\pmb{x}}\left(\omega\right)\big],=}&\ &{\ddot{\left|\pmb{\cal H}\big(\pmb{\theta}\big)\right[\mathrm{i}\omega\pmb{I},-,F\big(\pmb{\theta}\big)\big]^{-1}}\pmb{\cal G}\left(\pmb{\theta}\right)+\pmb{{\cal D}}\left(\pmb{\theta}\right)\ddot{\left|\pmb{u}\left(\omega\right)\right.}+}&\ &{\ddot{\left|\pmb{\cal H}\big(\pmb{\theta}\big)\right[\mathrm{i}\omega\pmb{I},-,F\big(\pmb{\theta}\big)\big]^{-1}}\pmb{\cal K}\left(\pmb{\theta}\right),+\pmb{{\cal I}},\right|,\ddot{\pmb{\nu}}\left(\omega\right)\equiv}&\ &{\pmb{{\cal T}}{1}\big(\omega,,\pmb{\theta}\big),\ddot{\pmb{u}}\left(\omega\right)+\left.\pmb{{\cal T}}{2}\big(\omega,,\pmb{\theta}\big),\ddot{\pmb{\nu}}\left(\omega\right)}&{\left(\pmb{\theta}\right)}\end{array}

  

式中  

\pmb{T}_{1}\equiv\pmb{H}(\pmb{\theta})\left[\mathrm{i}\omega\pmb{I}\rightarrow\pmb{F}(\pmb{\theta})\right]^{-1}\pmb{G}(\pmb{\theta})\rightarrow\pmb{D}(\pmb{\theta})

{\cal T}_{2}\equiv{\cal H}(,\pmb{\theta})[,\mathrm{i}\omega{\pmb I},-,{\pmb F}(,\pmb{\theta}),]^{-1}{\pmb K}(,\pmb{\theta}),+,{\pmb I}

  

通常 $T_{2}$ 是非退化矩阵,从式(6-99)可解出 $\tilde{\pmb{\nu}}(\omega)$  

\tilde{\bullet}\left(,\omega,\right);=;\left.T_{2}^{-1},\tilde{,}\tilde{,}\left(,\omega,\right);-;T_{2}^{-1},T_{1},\tilde{,}\tilde{,}\left(,\omega,\right),

  

对连续模型，频域的最大似然准则式(6-86)可写成  

\tilde{J}\left(\theta\right);=;\frac{1}{N}\sum_{n}\tilde{\nu}^{\mathrm{\scriptsize~*~}}\left(\omega_{n}\right)r_{;\nu\nu}^{-1}\tilde{\nu}\left(\omega_{n}\right);+;N\mathrm{ln}\left|\tilde{,r}{\nu\nu}\right|;\left(\omega{n}\right);,

  

频域中参数估计就是在式(6-98）～式(6-102)的约束下选取$\pmb{\theta}$ 值使 $\tilde{\boldsymbol{J}}\left(\boldsymbol{\theta}\right)$ 达极小值,这实质上是优化计算。经验表明，牛顿-拉夫逊迭代算法对解决这类问题最有效。待估计参数包括 ${\pmb F}\setminus{\pmb G}\setminus$ $D\setminus H\setminus K$ 和 $\tilde{r}_{w}$ 中的未知元素。下面给出进行未知参数估计的具体算式。  

首先估算 $\bar{r}_{w}$ 。对于稳态系统， $\bar{r}_{w}$ 是常值，可以通过取 $\tilde{\boldsymbol J}\left(\boldsymbol\theta\right)$ 对 $\bar{r}_{v v}$ 的导数等于零，直接得出 $\tilde{r}_{w}$ 的最佳估计值  

\tilde{r}{v v};=;\frac{1}{N^{2}}\sum{n}\tilde{\pmb{\nu}}\left(,\omega_{n},\right)\tilde{\pmb{\nu}}^{\star}\left(,\omega_{n},\right)

  

式中， $\tilde{\pmb{\nu}}$ 由式 $(6^{-}100)\sim$ 式(6-102)计算。其中 $\pmb{\theta}$ 的和 $\pmb{K}$ 取预测值，或上次迭代所得估计值。未知量 $\pmb{\theta}$ 的最优估计 $\pmb{\hat{\theta}}$ 必须满足下列方程  

\left.\frac{\partial\tilde{J}\langle\theta\rangle}{\partial\theta}\right|_{\theta=\theta},=,0

  

注意上式中的 $\pmb{\theta}$ 包括 $F,G\,,D\,,H$ 中的未知参数和增益值 $\pmb{K}$ 。通常采用牛顿-拉夫逊迭代算法求解上述方程。先给-一个 $\pmb{\theta}$ 的预估值，再由下式求其校正值，直到 $\tilde{\boldsymbol{J}}$ 收敛到最小值时，所对应的参数值 $\pmb{\theta}$ 即为参数的最优估计 $\pmb{\hat{\theta}}$  

{\pmb\theta}^{(k+1)};=;{\pmb\theta}^{(k)},-,\widetilde{\pmb M}^{,-1},\left{\frac{\partial\widetilde J}{\partial{\pmb\theta}},\right}_{k}

\widetilde{\pmb{M}},=,E\left{\frac{\partial^{2}\tilde{\pmb{J}}}{\partial\pmb{\theta}\partial\pmb{\theta}^{\mathrm{T}}}\right}^{(k}

  

式中 ${\partial\bar{J}}/{\partial\theta}$ 准则函数 $\tilde{J}$ 对于待估计参数 $\pmb{\theta}$ 的灵敏度；  

$\widetilde{M}$ —费希尔信息矩阵。  

下面给出 $\partial\tilde{\boldsymbol{J}}/\partial\boldsymbol{\theta}$ 和 $\widetilde{M}$ 的表达式。待估计参数是实数， $\tilde{\boldsymbol{J}}$ 也是实数,所以 $\widetilde{M}$ 和 $\partial{\tilde{J}}/\partial\pmb\theta$ 是实数。由式(6-103)可得  

\frac{\partial\tilde{J}}{\partial\theta_{k}},=,\frac{2}{N}\mathrm{Re}\sum_{n}\left{\frac{\partial\tilde{\pmb{\nu}}^{\ast}}{\partial\theta_{k}}\tilde{r}_{\nu\nu}^{-1}\right}

  

对式(6-9)求 $\theta_{k}$ 的偏导数，考虑到 $\tilde{\mathbf{y}}\left(\omega\right)$ 是频域的观测量，与 $\theta_{k}$ 无关，可得  

\frac{\partial\tilde{\pmb{\nu}}^{\ast}}{\partial\theta_{k}};=-;\left(,T_{2}^{-1};\frac{\partial,{\bf T}{2}}{\partial\theta{k}}\tilde{\pmb{\nu}};+;T_{2}^{-1};\frac{\partial,{\bf T}{1}}{\partial\theta{k}}\tilde{\pmb{u}},\right)^{\ast}

  

将式(6-109)和式(6-102)代入式(6-108),可推导出  

\begin{array}{r}{\frac{\partial\tilde{J}(\pmb{\theta})}{\partial\theta_{k}}=-;2\mathrm{Re}\sum_{n}\Bigg{\mathrm{tr}\Bigg[\frac{\partial\mathbf{T}{1}^{*}}{\partial\theta{k}}(\mathbf{\calT}{2}^{*},)^{-1}\tilde{r}{v v}^{-1}\mathbf{\calT}{2}^{-1}(\tilde{r}{s u},-,{\cal T}{1}\tilde{r}{u u})\Bigg]\Bigg}+}\ {\mathrm{tr}\Bigg[\frac{\partial\mathbf{\calT}{2}^{*}}{\partial\theta{k}}(\mathbf{\calT}_{2}^{*},)^{-1}\Bigg]\qquad\qquad\qquad\qquad(6-1)}\end{array}

  

推导中利用了下列近似公式  

\left{\begin{array}{l l}{\displaystyle E\left{\right.\tilde{\pmb{\nu}}\tilde{\pmb{\nu}}^{\star}\left}\ =\ N\tilde{\pmb{r}}{{\pmb{\nu}}{\pmb{\nu}}}}\ {\displaystyle E\left{\right.\tilde{\bf y}\tilde{\pmb{u}}^{\star}\left}\ =\ N\tilde{\pmb{r}}{{\pmb{y}}{\pmb{u}}}}\ {\displaystyle E\left{\right.\tilde{\pmb{u}}\tilde{\pmb{u}}^{\star}\left}\ =\ N\tilde{\pmb{r}}_{{\pmb{u}}{\pmb{u}}}}\end{array}\right.,

  

下面推导 $\widetilde{M}$ 的表达式。利用式(6-109)和式（6-111),经过简  

单运算可得  

\begin{array}{r}{E\left{\frac{\partial,\tilde{\pmb{\nu}}}{\partial,\theta_{k}},\frac{\partial,\tilde{\pmb{\nu}}}{\partial\theta_{l}},\right}=N\left{,{\pmb{T}}{2}^{-1},\frac{\partial,{\pmb{T}}{2^{-}}}{\partial,\theta_{k}}\frac{\partial,{\pmb{T}}{2}^{\star}}{\partial,\theta{l}}(,{\pmb{T}}{2}^{\star},)^{,-1},+}\ {{\pmb{T}}{2}^{-1},\frac{\partial,{\pmb{T}}{1}}{\partial,\theta{k}}\tilde{\pmb{r}}{u u},\frac{\partial,{\pmb{T}}{1}^{\star}}{\partial,\theta_{l}}(,{\pmb{T}}_{2}^{\star},)^{,-1},\right}}\end{array}

  

推导中利用了下列式子  

\left{\begin{array}{l}{{E,{,\tilde{\mathbf{y}}\tilde{\mathbf{y}}^{\star},},=,N,{\lvert,T_{1}\tilde{r}{u u}T{1}^{\star},+,T_{2}\tilde{r}{v v}T{2}^{\star},}}}\ {{E,{\lvert,\tilde{\mathbf{y}}\tilde{\mathbf{u}}^{\star},},=,N\mathbf{T}{1}\tilde{r}{u u}}}\ {{E,{\lvert,\tilde{\mathbf{y}}\tilde{\mathbf{y}}^{\star},},=,N r_{u u}T_{1}^{\star}}}\end{array}\right.

  

由式(6-112)和式(6-113)可推导出信息矩阵 $\widetilde{M}$ 的元素表达式  

\begin{array}{r l}&{\mathrm{\boldmath\sigma~}{\mathrm{{N}}}^{2}\mathrm{Re}E\left{\sum{s}\frac{\partial^{s}\tilde{\gamma}{s}^{+}+\frac{1}{2}\tilde{\partial}{s}^{0}}{\partial\beta_{s}^{+}\partial\beta_{s}^{-}}\right}=}\ &{\frac{2}{N}\mathrm{Re}\sum_{s}w\Biggl{E\left{\frac{\partial}{\partial s}\frac{\partial}{\partial\beta_{s}^{+}}\frac{\partial}{\partial\beta_{s}^{+}}\left[\tilde{\gamma}{s}^{-1}\right]^{2}=\right}}\ &{2\mathrm{Re}\sum{s}\Biggl{w\left[\mathrm{Tr}{{2}}^{-1}\frac{\partial^{s}}{\partial\beta{s}^{-}}\frac{\partial^{s}}{\partial\beta_{s}^{-}}({\bf T}{2}^{+})^{-1}e^{-\frac{s}{2}\tilde{\gamma}{s}^{-}}\right]+}\ &{\mathrm{\boldmath\sigma~}{\mathrm{{U}}}^{\prime}\sum{s}\frac{\partial^{s}\Gamma_{\mathrm{r}{s}^{-}}}{\partial\beta{s}^{+}}\Bigl(\frac{\partial{\bf T}{\mathrm{r}{1}}^{-1}}{\partial\beta_{s}^{+}}\bigl(\mathrm{Tr}{{2}}^{+}\bigr)^{-1}e^{-\frac{s}{2}\tilde{\gamma}{s}^{-}}\Bigr)\Biggr|;=}\ &{2\mathrm{Re}\sum_{s}\Biggl{w\left(\frac{\partial T_{\mathrm{r}{1}}^{-2}}{\partial\beta{s}^{+}}({\bf T}{2}^{+})^{-1}\tau{s}^{-}\right)\frac{\partial^{s}\Gamma_{\mathrm{r}{s}^{-}}}{\partial\beta{s}^{-}}\Biggr}+}\ &{\mathrm{\boldmath\sigma~}{\mathrm{{N}}}^{\prime}\Biggl{\frac{\partial T{\mathrm{r}{1}}^{-1}}{\partial\beta{s}^{+}}({\bf T}{2}^{+})^{-1}+\frac{\partial^{s}}{\partial\beta{s}^{-}}\frac{\partial{\bf T}{\mathrm{r}{1}}^{-1}}{\partial\beta_{s}^{+}}\Biggr}\

  

至此，已 以用来求得未知参数 算流程是,对于给定的一组观测数据 ${\bf y}\left(\,i\,\right)$ 和控制历程 $\pmb{u}\left(\begin{array}{c}{\end{array}}_{i}\right)$ ,由式(6-82)求得其傅里叶变换 $\bar{\mathbf{y}}\left(\,n\,\right)$ 和 $\tilde{\pmb{u}}\left(\,n\,\right)$ 。对于给定的 $\pmb{\theta}$ 初估值 $\theta^{(k)}$ （包括增益 $\pmb{K}$ 在内),由式(6-102)和式(6-104)求出 $\tilde{\pmb{\nu}}(\,n\,)$ 和 $\tilde{r}_{w}$ ,并利用式(6-103)计算似然准则函数 $J(\theta^{(k)})$ 。利用 ${\bf\boldsymbol{y}}({\boldsymbol{i}})$ 和 $\pmb{u}\left(\begin{array}{c}{\end{array}}\end{array}\right)$ 计算互相关函数 $r_{u u}\,,\,r_{y u}\,,\,r_{y y}$ ,进行傅里叶变换得 $\tilde{r}_{u u}\,,\tilde{r}_{y u}\,,\tilde{r}_{y y\,\circ}$ 由式(6-110)和式(6-114)计算似然准则函数的灵敏度 $(\partial\tilde{J}/\partial\pmb{\theta})^{(k)}$ 和信息矩阵 $\widetilde{M}^{(k)}$ ，求 $(\widetilde{\pmb{M}})^{\widetilde{-1}})^{(\widetilde{\pmb{k}})}$ 代人式(6-106)算出 ${\theta}^{(k+1)}$ ，以 ${\theta}^{(k+1)}$ 代替上面的 $\theta^{(k)}$ ,重复上述计算,直至 $|\,\,[\,J\,(\,\theta^{(\,k\,+\,1)}\,)\,-\,J\,(\,\theta^{(\,k\,)}\,)\,]/$ $J(\theta^{(k)})\left\{<\varepsilon\right.$ 为止,所得之 ${\boldsymbol{\theta}}^{(k+1)}$ 就是待估计参数和增益系数的最优估计。当需要估计初始状态 $x_{0}$ 时,观测方程(6-99)应增加与$H(\pmb\theta)\left[\mathrm{i}\omega\pmb{I}-\pmb{F}(\pmb\theta)\right]^{-1}\times\pmb{x}_{0}\delta(\omega)$ 项,相应地式(6-110)和式(6-114)也增加与 $\pmb{x}_{0}$ 有关的项，推导方法同上，公式形式类同，但更复杂些。  

# 6.3.3 离散型最大似然算法  

常系数线性系统的数学模型表达式（6-79)和式（6-80），可利用状态转移矩阵改写成离散型的方程式。  

状态方程  

\left{\begin{array}{l}{\pmb{x}\big(\textit{i}+1\big):=:\pmb{\Phi}\big(\textit{i}+1,\textit{i}\big),\pmb{x}\big(\textit{i}\big),+,\pmb{G}\big(\pmb{\theta}\big),\pmb{u}\big(\textit{i}\big),+,\pmb{T}(\pmb{\theta}),\pmb{\eta}\big(\textit{i}\big)}\ {\pmb{E}\big{\textit{x}(0)\big},=,\pmb{x}_{0}\qquad\textnormal{(}\textit{i}=0,1,2,\cdots,N\mathrm{-}1\big)}\end{array}\right.

  

观测方程  

\begin{array}{r}{\textbf{y}!\left(,i,\right),=,\pmb{H}!\left(,\pmb{\theta},\right)\pmb{x}\left(,i,\right),+,\pmb{D}\left(,\pmb{\theta},\right)\pmb{u}\left(,i,\right),+,\pmb{\varepsilon}\left(,i,\right)}\end{array}

  

式中 $\pmb{\Phi}$ -——转移矩阵，并满足式（4-11）；  

$\pmb{\eta}(\mathbf{\sigma}_{i})\,,\pmb{\varepsilon}(\mathbf{\sigma}_{i})$ ——过程噪声和观测噪声。  

满足式(5-71)。 常系数线性系统方程组(6-115)和式(6-116)的状态参数 $\pmb{x}$ 和协方差矩阵 $\pmb{P}$ 的无偏估计可以近似地由下列稳态卡尔曼滤波公式给出（参阅4.2节）。  

状态预测方程  

\pmb{x}\left(,i\mid i,-,1,\right);=;\pmb{\phi}\pmb{x}\left(,i,-,1\mid i,-,1,\right),+,\pmb{G}\left(,\pmb{\theta},\right)\pmb{u}\left(,i,-,1,\right)

  

状态校正方程  

\pmb{x}\left(,i\mid i,\right);=;\pmb{x}\left(,i\mid i,-,1,\right),+,\pmb{K}\pmb{\nu}\left(,i,\right)

  

协方差预测方程  

{\pmb{P}};=;\pmb{\Phi}[,{\pmb I},-,K{\pmb H}!\left(,i,\right),],{\pmb P}\pmb{\Phi}^{\mathrm{T}},+,{\pmb I}\pmb{Q}{\pmb r}^{\mathrm{T}}

  

式中  

\begin{array}{c}{\pmb{K};=;\pmb{P}\pmb{H}^{\top}\pmb{B}^{-1},,\pmb{B};=;\pmb{H}\pmb{P}\pmb{H}^{\top},+,\pmb{R}}\ {\pmb{\nu}(,i,);=;\pmb{y}(,i,),-,\pmb{H}(,\pmb{\theta},),\pmb{x},(,i,|,i,-,1),-,\pmb{D},(,\pmb{\theta},),\pmb{u},(,i,)}\end{array}

  

(6 - 120)  

考虑初始条件的影响,在变换到频域之前,先做变换 $\hat{\pmb{x}}_{1}(\,i\,|\,\,i\,)=$ $\hat{\mathbf{x}}\left(\mathbf{\chi}_{i}\mid i\right)-\mathbf{\chi}_{0}$ ,将状态初始条件化为零，上述方程就变成了（下式已将 $x_{1}$ 的下标1省略）  

\hat{\textbf{x}}(,i,+,1\mid i,),=

\pmb{\mathcal{P}}\big[\hat{\pmb{x}},\big(,i\mid i,-,1,\big),+,{\pmb{K}}\pmb{\nu},\big(,i,\big),+,{\pmb{x}}_{0},\big],+,{\pmb{G}},\big(,\pmb{\theta},\big),\pmb{u},\big(,i,\big)

\pmb{y}(\mathbf{\sigma}_{i})\pmb{H}(\pmb{\theta})=

\left[,\hat{\pmb{x}}\left(,i,\left|,i,-1\right.\right),+,{\pmb{x}}_{0},\right],+,{\pmb{D}}\left(,\pmb{\theta},\right)\pmb{u}\left(,i,\right),+,\pmb{\nu}\left(,i,\right)

  

对式（6-121)和式（6-122）进行离散傅里叶变换，得到它们在频域的表达式（为书写简便，取 $\pmb{x}_{0}=\mathbf{0}$  

\begin{array}{r l r}{\lefteqn{\sum_{n}\hat{\pmb{x}}\left(,n,\right),=,\pmb{\Phi}\pmb{\tilde{x}}\left(,n,\right),+,\pmb{\Phi}\pmb{K}\tilde{\nu}\left(,n,\right),+,\pmb{G}\left(,\pmb{\theta},\right)\tilde{\pmb{u}}\left(,n,\right)}}\ &{}&{\tilde{\pmb{\nu}}\left(,n,\right),=,\tilde{\pmb{y}}\left(,n,\right),-,\pmb{H}\left(,\pmb{\theta},\right)\tilde{\pmb{x}}\left(,n,\right),-,\pmb{D}\left(,\pmb{\theta},\right)\tilde{\pmb{u}}\left(,n,\right)}\end{array}

  

式中 $Z_{n}=\exp(\mathrm{i}\,n\omega_{0})$  

由式(6-123)解出 $\tilde{\boldsymbol{x}}\left(\,n\,\right)$ 代人式(6-124)可得  

\begin{array}{c}{{\displaystyle{\bf\tilde{y}}\left({\bf\Phi}{n}\right);=;{\bf\Phi}{\cal T}{1}\left({\bf\Phi}{n},,{\pmb\theta}\right){\bf\tilde{u}}\left({\bf\Phi}{n}\right);+;{\bf\Phi}{\cal T}{2}\left({\bf\Phi}{n},,{\pmb\theta}\right){\bf\tilde{\nu}}({\bf\Phi}{n}\right)},}\ {{\displaystyle{\bf\tilde{\nu}}\left({\bf\Phi}{n}\right);=;{\bf\Phi}{\cal T}{2}^{{\bf\Phi}{1}}{\bf\tilde{y}}\left({\bf\Phi}{n}\right);-;{\bf\Phi}{\cal T}{2}^{{-}1}{\bf\Phi}{\cal T}{1},{\tilde{\pmb u}}\left({\bf\Phi}{n}\right)}}\end{array}

  

式中  

{\pmb T}{1}({\bf\Psi},{\pmb\theta});=;{\pmb H}({\pmb\theta}),(,Z{n}{\pmb I},-,{\pmb\Phi})^{-1},G^{,(},{\pmb\dot{\theta}},),+,{\pmb D}({\pmb\theta},)

{\cal T}{2}(\mathbf{\Gamma},\theta\mathbf{\Gamma});=;{\cal H}(\theta)\left(,Z{n}{\cal I},-,\Phi,\right)^{-1}\Phi{\cal K};+;{\cal I}

  

对稳态系统，卡尔曼增益 $\pmb{K}$ 是常数，系统的未知参数 $\pmb{\theta}$ 包括$\Phi\,,G\,,D\,,H\,,K$ 的系数。参数估计的最大似然法就是在方程式（6-123）～式（6-128)的约束条件下选择参数值 $\pmb\theta$ ，使下列最大似然判据 $\tilde{\pmb J}(\pmb\theta)$ 取最小值  

\tilde{J}\left(,\pmb{\theta},\right);=;\frac{1}{N}\sum_{n}{\mid\tilde{\pmb{v}}^{\mathrm{*}}\left(,n,\right)\tilde{\pmb{r}}{v v}\tilde{\pmb{v}}\left(,n,\right),};+;N\mathrm{ln}\mid\tilde{\pmb{r}}{v v}\mid

  

具体算法:预先给出 $\pmb{\theta}$ 的预估计值 $\theta^{(k)}$ ,由实测的 ${\bf y}\left(\mathbf{\boldsymbol{\mathit{i}}}\right),{\bf\boldsymbol{\mathit{u}}}\left(\mathbf{\boldsymbol{\mathit{i}}}\right)$ 计算其傅里叶变换 $\tilde{\mathbf{y}}\left(\mathbf{\bar{\kappa}}_{n}\right),\tilde{\mathbf{u}}\left(\mathbf{\bar{\kappa}}_{n}\right)$ ，由式(6-124)算出 $\tilde{\pmb{\nu}}^{\,(\,n\,)}$ ,并计算它们的功率谱密度和互谱密度 $\overset{\cdot}{r}_{y y},\overset{\sim}{r}_{v\nu},\overset{\cdot}{r}_{y u}$ 等,由式(6-114)计算$\widetilde{M}_{k l}$ ,由式(6-110)计算 $\partial J/\partial\theta_{k}$ ,由式(6-106)计算 $\theta^{(k+1)}$ 。用 ${\theta}^{(k+1)}$ 代替 $\theta^{(k)}$ ,重复上述过程,直到 $\tilde{\boldsymbol{J}}\left(\,\theta\,\right)$ 达到最小值为止的 $\theta^{(k)}$ 就是参数的最优估计 $\pmb{\hat{\theta}}$ 。  

# 6.3.4 输出误差法  

当系统的过程噪声很小，以致可忽略不计时，系统的状态协方差矩阵近似为零，卡尔曼增益 ${\cal K}\!\stackrel{\equiv=}{=}\!0\,,\,T_{2}\!\equiv\!{\cal I}$ ,这时新息简化为输出误差，最大似然法简化成输出误差法。上面最大似然算式表达为功率谱和互谱密度形式。对于输出误差法，除可用谱密度算式，也可不计算功率谱和互谱，而直接用观测量和控制变量的傅里叶变换 $\bar{\mathbf{y}}\left(\,n\,\right)$ 和 $\tilde{\pmb{u}}\left(\,n\,\right)$ 进行参数估计，甚至可以直接采用传递函数进行参数辨识。下面给出输出误差法的几种表达形式。  

# 1）谱密度形式  

上节给出了用功率谱和互谱形式的信息矩阵 $\widetilde{M}$ 和似然函数导数 ${\partial\bar{J}}/{\partial{\pmb\theta}}$ 的表达式。在此简化情况，系统的观测量 $\tilde{\bf y}$ 、信息矩阵$\widetilde{M}$ 和似然函数导数的表达式（6-125）式（6-114）和式（6-110）等可写为  

\tilde{\textbf{y}}(\mathbf{\Delta}n\mathbf{\Delta});=;\mathbf{T}_{1}(\mathbf{\Delta}n\mathbf{\Delta},\pmb{\theta}),\tilde{\textbf{u}}(\mathbf{\Delta}n\mathbf{\Delta}),+,\tilde{\textbf{"{v}}}(\mathbf{\Delta}n\mathbf{\Delta})

\tilde{\dot{r}}{y y};=;\frac{1}{N^{2}}\sum{\eta}\tilde{\pmb{\nu}}\left(\mathbf{\mu}{n}\right)\tilde{\pmb{\nu}}^{;*}\left(\mathbf{\mu}{n}\right)

\widetilde{M}{k l};=;2\mathrm{Re}\sum{n}\mathrm{tr}\left[\frac{\partial,{\bf T}{1}^{;*}}{\partial\theta{l}}\hat{\pmb{r}}{\nu\nu},\frac{\partial,{\cal T}{1}}{\partial\theta_{k}}\tilde{\pmb{r}}_{u u}\right]

\frac{\partial\tilde{J}\left(\mathbf{\nabla}\theta\right)}{\partial\theta_{k}},=-,2\mathrm{Re}\sum_{n}\mathrm{tr}\Bigg[\frac{\partial,T_{1}^{*}}{\partial\theta_{k}}\tilde{r}{v v}^{-1}\big(\tilde{r}{y u},-,T_{1}\tilde{r}_{u u}\big)\Bigg]

  

2）傅里叶变换形式  

系统也可直接由 ${\pmb u}\left({\pmb\ell}\right),{\pmb y}\left({\pmb\ell}\right)$ 的傅里叶变换 $\hat{\pmb{u}}\left(\begin{array}{l}{n}\end{array}\right)$ 和 $\tilde{\mathbf{y}}\left(\mathbf{\Lambda}n\right)$ 进行参数估计,此时 $\widetilde{\pmb{\nu}}\,.\widetilde{\pmb{r}}_{v v}\,.\widetilde{\pmb{M}}\,.\widetilde{\partial}\widetilde{\pmb{J}}/\partial\pmb{\theta}$ 可化为下列形式  

\begin{array}{c}{{\displaystyle{\widetilde{\pmb{\nu}}}\left({\bf\Lambda}{\boldsymbol{n}}\right)={\widetilde{\bf y}}\left({\bf\Lambda}{\boldsymbol{n}}\right)-{\bf T}{1}({\bf\Lambda}{\boldsymbol{n}},,\pmb{\theta}){\widetilde{\pmb{u}}}\left({\bf\Lambda}{\boldsymbol{n}}\right)}}\ {{\displaystyle{\widetilde{\pmb{r}}}{{\pmb{\nu}}{\pmb{\nu}}}=\frac{1}{N^{2}}\sum_{n}{\widetilde{\pmb{\nu}}}\left({\bf\Lambda}{\boldsymbol{n}}\right){\widetilde{\pmb{\nu}}}^{\ast}\left({\bf\Lambda}{\boldsymbol{n}}\right)}}\end{array}

\widetilde{M}{k l};=;\frac{2}{N}\mathrm{Re}\sum{n}\frac{\partial(,{\bf T}{1}\tilde{\pmb u},),^{*}}{\partial\theta{k}}\tilde{\pmb r}{w}^{-1},\frac{\partial(,{\bf T}{1}\tilde{\pmb u},)}{\partial\theta_{l}}

\frac{\partial J\left(\mathbf{\delta}\pmb{\theta}\right)}{\partial\theta_{k}},=-,\frac{2}{N}\mathrm{Re}\sum_{n},\frac{\partial\left(,T_{1}\tilde{\pmb{u}},\right)^{\ast}}{\partial\theta_{k}}\tilde{r}_{{\pmb{v}}{\pmb{v}}}^{,-1}\tilde{\pmb{v}}\left(,n,\right)

  

# 3）传递函数形式  

在某些试验中,采用频率扫描法直接测量系统传递函数，这时可以用传递函数的输出误差作为估计准则函数  

\tilde{J}\left(,\pmb\theta,\right);=;\frac{1}{N}\sum_{n},[;T_{E}(,n,);-;T_{1}(,n,,\pmb\theta,),]^{\mathrm{*}};.

\tilde{r}{,\nu\nu}^{,-1}[;T{E}(,n,);-;T_{1}(,n,,\pmb\theta,),]

{\pmb T}_{1}({\bf\pmb\alpha},{\pmb\theta}),=,{\pmb H}({\pmb\theta}),[,{\mathrm{i}}\omega{\pmb I},-,{\pmb F}({\pmb\theta}),]^{,-,1},{\pmb G}({\pmb\theta}),+,{\pmb D}({\pmb\theta})

  

式中 $T_{E}(\,n\,)$ -—测量的传递函数。  

仍然采用牛顿-拉夫逊迭代算法求解。这时，信息矩阵和似然函数的灵敏度导数为  

\widetilde{M}{k l};=;\frac{2}{N}\mathrm{Re}\sum{n},\frac{\partial,{\bf T}{1}^{\star}}{\partial,\theta{k}}{\bf r}{v v}^{;-1},\frac{\partial,{\bf T}{1}}{\partial,\theta_{l}}

\frac{\partial\tilde{J}\left(\pmb{\theta}\right)}{\partial\theta_{k}},=-,\frac{2}{N}\mathrm{Re}\sum_{n},\frac{\partial,{T_{1}^{\star}}}{\partial\theta_{k}}r_{\nu\nu}^{-1}\bigl[,T_{E}(,n,),-,T_{1}(,n,,\pmb{\theta}),\bigr]

  

利用上面给出的 $\widetilde{M}$ 和 $\displaystyle{\left(\partial\mathbf{\tilde{{J}}}/\partial\pmb{\theta}\right)}$ 等三种算式，同式（6-112)可以迭代求解 $\pmb{\theta}$ 的最优估计。处理的试验数据可以是由时域观测量转换到频域的傅里叶变换；也可以是功率谱和互谱密度或者系统的传递函数等。  

# 6.3.5方程误差法  

当系统没有测量噪声而存在过程噪声时，状态方程含有过程噪声且状态测量是准确的。此时,对数似然函数最好取为以 $\pmb{x}$ 为  

观测量的新息的函数,即  

\tilde{J};=;\sum_{n}\mid\mathrm{i},\omega\tilde{I}!!!\mid,\omega\left(\frac{}{}\omega,\right),-,\tilde{F}!!!\tilde{\mathbf{x}}\left(,\omega,\right),-,G!!!\tilde{\mathbf{u}}\left(,n,\right),\mid,^{2}

  

最大似然法即简化为方程误差法。假设待估计参数 $\pmb{\theta}$ 为 ${\pmb F}\,,{\pmb G}$ 的元素,令  

\pmb{\theta};=;\left[\begin{array}{l l l}{F}\ {G}\end{array}\right];;;;;;;;\tilde{\pmb{x}}_{a}\left(,\omega,\right);=;\left[\begin{array}{l}{\tilde{x}\left(,\omega,\right)}\ {\tilde{u}\left(,\omega,\right)}\end{array}\right]

  

则式(6-139)化成  

\tilde{J};=;\sum_{n}\left[\mathrm{i}\omega\tilde{\cal I}\tilde{\mathbf{x}}{a}!\left(\omega\right);-;\pmb{\theta}^{\top}\tilde{\mathbf{x}}{a}!\left(\omega\right)\right]^{\mathrm{\normalsize~*~}};.

  

将式(6-141)对 $\pmb\theta$ 求导，令 $\frac{\partial\bar{J}}{\partial\pmb{\theta}}=\mathbf{0}$ ,则有  

\frac{\partial\tilde{J}}{\partial\theta};=;2\mathrm{Re}\sum_{n}\tilde{\bf x}{a}\left(,\omega,\right)\left[,\mathrm{i}\omega\tilde{\bf I}\tilde{\bf x}{a},^{\ast}\left(,\omega,\right),-,\tilde{\bf x}_{,a}^{,\ast}\left(,\omega,\right)\theta,\right];=;0

  

所以  

\hat{\pmb{\theta}},=,\frac{\mathrm{Re}[\sum_{n}\mathrm{i}\omega\tilde{I}\tilde{\mathbf{x}}{a}\left(\omega\right)\tilde{\mathbf{x}}{a}^{\mathrm{*}}(\omega)]}{\mathrm{Re}[\sum_{n}\tilde{\mathbf{x}}{a}^{\mathrm{*}}(\omega)\tilde{\mathbf{x}}{a}(\omega)]}

  

式（6-143)的右端项与 $\pmb\theta$ 无关，仅是状态参量和控制矢量的傅里叶变换的函数，都是已知值。求 $\pmb{\hat{\theta}}$ 无需迭代计算。这实际上是最小二乘法。当然也很容易写出加权最小二乘算式。权矩阵取为新息协方差最优估计之逆。式(6-143)是算子运算写法，对于实际问题，需列出具体算式，解算线性代数方程组，才能求得参数0的估计值0。  

# 6.3.6 零添补技术  

上节的离散傅里叶变换对式（6-82）的变元都写成整数形式，实际应用时试验数据的采样时刻不是整数，此时离散傅里叶变换对可写成  

\left{\begin{array}{l}{\displaystyle g(,k\Delta t,),=,\frac{1}{N}\sum_{n,=,-\frac{N}{2}}^{\frac{N}{2}-1},\widetilde{y}\big(,n,\Delta\omega\big),\mathrm{e}^{\mathrm{i}n\Delta\omega k\Delta t}}\ {\displaystyle\widetilde{y}\big(,n,\Delta\omega\big),=,\sum_{k,=,0}^{N-1},y\big(,k,\Delta t,\big),\mathrm{e}^{-\mathrm{i}n\Delta\omega k\Delta t}}\end{array}\right.

  

式中 $\Delta\omega=\omega_{0}/\Delta t=2\pi/(\mathbf{\Omega}N\Delta t\mathbf{\Omega})$ $\Delta t=T\backslash N:$  

$T$ —实验总时间； $N$ 为采样总点数。  

由式（6-144)可见，在频域中连续两个谱线的间隔 $\Delta\omega$ 为$2\pi/\;T$ ,它是基波的角频率。实测数据经过变换，在频域的 $-\,\pi/\Delta t$ 到 $\pi/\Delta t$ 之间有 $N$ 条谱线。但实际上，对于低频振荡的动力学系统，变换所得谱线在高频区的幅值几乎为零，例如民航机的短周期小扰动运动在圆频率6rad/s以上的谱线的幅值几乎为零。这导致实测数据在频域中的谱线很少。频域的最大似然法对于有足够多谱线的测量数据，其估计是一致收敛和无偏的；当测量数据的谱线过少时，将降低辨识准度，导致有偏估计。  

显然，可以通过选择采样步长 $\Delta t$ 来使得利用式(6-144)进行变换时,所得到的谱线条数与时域的数据采样总点数相等。若 $\omega_{p}$ 为数据实际的频带宽,只须取 $\Delta t=2\pi/\omega_{p}$ 。但这样选定的 $\Delta t$ ，将导致时域中实测数据在每个主要振荡周期（例如飞机纵向运动的俯仰短周期振荡)内的采样点太少。为适应实测数据在时域的分析和辨识的需求，对于主要振荡模态，至少每周应有十多个采样数据。这样的采样速率将导致在时域的采样数据很多，而变换到频域后，其所得谱线过少的现象，除非测量时刻 $T$ 很大。为了克服此缺陷，以提高频域的辨识准度,可以采用“零添补技术"9]  

零添补技术的基本思想是，对给定的实测数据，不改变 $\Delta t$ 而增大 $N$ 和 $T$ 。显然当 $T$ 加大1倍，其谱线也增加1倍。具体作法是在实测数据之后添加零均值和常值协方差的随机序列，直至获得足够多的频域中的谱线。容易证明，零添补数据不会使实测数据原来频谱发生畸变，而只是加密谱线而已。若 $N$ 增大1倍，则在原有频谱的每两谱线之间增添了一条谱线，使频谱的谱线增加1 倍。  

零添补技术已用于飞行器气动参数辨识，结果表明可以明显改善在频域中的稳定导数和控制导数的辨识准度。  

# 参考文献  

1  Donegan J J. Determination of Lateral-Stability Derivative and Transfer- Function Coefficients from Frequency-Response Data for Lateral Motion. NACA TR 1225, 1955   
2 Milliken W F Jr. Progress in Dynamic Stability and Control Research. J. A. S. , 1947, 14(9): 493\~ 519   
3  Cooley J W, Tukey J W. An Algorithm for the Machine Calculation of Complex Fourier Series. Mathematics of computation, 1965, 19(90) : 297 \~ 301   
4  Mehra R K. Frequency-Domain Synthesis of Optimal Inputs for Linear System Parameter Estimation. Div. Eng. Apple. phys. Harvard Univ., TR 645, 1973   
5  Mehra R K. Synthesis of Optimal Input for Multinput-Multioutput( MiMO) System with Process Noise. System Identification--Advances and Case Studies, Academic Press, 1976, 211\~ 249   
6  Gupta N K. New Frequency Domain Method for System Identification. 1977 Joint Autom. Contr. Conf. ,1977, 2: 804-808   
7 Gupta N K, Bohn J G. A Technique for Measuring Rotorcraft Dynamic Stability in the 40-by-80-Foot Wind Tunnel. NASA CR-151955, 1977   
8  Klein V. Maximum Likelihood Method for Estimating Airplane Stability and Control Parameters from Flight Data in Frequency Domain. NASA TP 1637, 1980   
9Wells W R, Banda S S. Analysis of Flight Data in the Frequency Domain. Proc. of the 27th Inteina. Instrumentation Symposium, Indiana, 1981, 18(1): 357— 367  

# 第7章 试验设计和最优输人  

系统辨识是利用系统的试验数据，建立系统数学模型的技术科学。试验设计是系统辨识的基础，直接关系辨识结果的优劣和成败。试验设计包括拟定试验和测试方案；确定输人参数和输出参数；选定数据采集系统及其相应参数；制定试验大纲并组织实施。在上述诸多因素中，对辨识结果影响最大的是输人设计，系统输出的传感器和数据采集速率的选定也是重要的。最优输人设计是系统辨识的一个重要课题。  

# 7.1 输人设计  

动力学系统参数的辨识准度固然与模型辨识和参数估计方法有关，但更重要的是试验数据所含待估计参数的信息量和试验数据的测量准度。不同的控制输人激发出动力学系统的不同运动模态，试验数据所含动力学系统待估计参数的信息量也就不同，例如当飞机做稳态水平飞行时，给飞机升降舵一个扰动，则飞机在铅垂平面做俯仰运动，此时记录下的试验数据只能用于辨识与纵向俯仰运动有关的气动参数，因为飞机没有激发横侧向运动模态，也就无法辨识与横侧向运动有关的滚转、偏航的气动参数。由此可见，控制输人决定了系统的输出特性，从而决定了系统参数的可辨识性和辨识准度。从这个意义上讲，输人信号的设计是系统辨识的基础。诚然，不同的动力学系统对输人信号的设计有不同的要求。  

飞行器的运动历程（动态响应）取决于其控制部件的运动规律。飞行运动取决于升降舵、副翼和方向舵的运动；导弹运动取决于舵面的偏转角和推力作用方向的变化规律。飞行器动力学系统的动态响应特性就是指飞行器对控制部件运动的响应特性。  

飞行器输人设计的目的，就是设计飞行器控制部件的运动规律，使飞行试验过程可以激发出与待辨识参数相关的运动模态，提供辨识所需的足够的信息量。常用的输人信号有以下几种形式[1。  

1）阶跃输人  

阶跃输人信号（图7-1）是最简单的信号，但它只在低频区域含有能量，不能用于激发高频振荡模态的响应，而且阶跃输人常使飞行器偏向某方向运动而离开线性区域。阶跃输人的数学模型为  

\delta,=,\binom{0}{\alpha}\quad(,t,\in,[,0,,t_{1},),)}\ {\delta,=,\binom{0}{\alpha}\quad(,t,\in,[,t_{1},,,+,\infty,),)}\end{array}

  

![](images/498d3b0f57d308bdc6eb2e3a882a45bcb19e374f4ca81498ed0d36d1dd60c734.jpg)  
图 7-1各种输人信号的功率频谱  
标准频率0△!  

2）方波输人、偶极方波输人  

方波输人和偶极方波输人的频谱密度较宽，在高频区域也含有能量（见图 7-1),适当调整 △t 可以在感兴趣的模态的频率段含有足够的能量，而且克服了阶跃输人使飞行器运动向某一方向偏离的缺点，是个简单而有效的输人信号，在飞机飞行试验中常被米用，其数学模型为  

方波  

\delta,=,\left{\begin{array}{l l}{0}&{\left(,t,\in,\left[,0,,t_{1}\right),t,\in,\left[,t_{1},+,\Delta t,,,+,\infty,\right)\right)}\ {\alpha}&{\left(,t,\in,\left[,t_{1},t_{1}+,\Delta t,\right]\right)}\end{array}\right.

  

偶极方波  

\delta,=,\left{\begin{array}{r l}{0\quad(,t,\in,[,0,,t_{1}),,t,\in,[,t_{1},+,2\Delta t,,,+,\infty,),)}\ {\alpha\quad(,t,\in,[,t_{1},,t_{1},+,\Delta t,),)}\ {-,\alpha\quad(,t,\in,[,t_{1},+,\Delta t,,t_{1},+,2\Delta t,),)}\end{array}\right.

  

3）“3211"输人  

“3211"多级方波输人是个频带相当宽的信号，通过调整 $\Delta{\mathfrak{t}}$ 可以将频带移到试验所希望激发的频带上去（见图7"1)。“3211"输人的数学模型为  

\delta,=,\left{\begin{array}{r l}{0}&{\left(\iota\in[0,t_{1}),\iota\in[\iota_{1}+7\Delta t,,+,\infty,)\right)}\ {,\alpha}&{\left(\iota\in[\iota_{1},\iota_{1}+3\Delta\iota)\right)}\ {-,\alpha}&{\left(\iota\in[,t_{1}+3\Delta t,,t_{1}+5\Delta t,)\right)}\ {,\alpha}&{\left(\iota\in[,t_{1}+5\Delta t,,t_{1}+6\Delta t,)\right)}\ {-,\alpha}&{\left(\iota\in[,t_{1}+6\Delta t,,t_{1}+7\Delta t,)\right)}\end{array}\right.

  

4）振荡型输人  

振荡型输人是一个比较容易实现的输人型式,但频谱单一，只当振荡频率与被辨识模态的频率比较相近时才能激发。振荡型输人的数学模型为  

\begin{array}{r}{\delta,=,\left{\begin{array}{l l}{0}&{(,t,\in,[0,t_{1}),,t,\in,[,t_{1}+\Delta t,,,+,\infty,))}\ {\quad}&{\quad}\ {\alpha\mathbf{e}^{-\lambda t}\sin(\omega t,+,\varphi)}&{(,t,\in,[,t_{1},t_{1}+\Delta t,))}\end{array}\right.}\end{array}

  

# 5）闭环控制输人  

对于某些动力学系统，在试验状态下控制系统与动力学系统无法断开，控制输人是系统状态参数的函数，故输人历程难以预先给定，这给参数辨识带来一些困难，可能出现不可辨识。闭环控制输人的数学模型为  

\mathbf{\dot{\theta}}=\mathbf{\nabla}\mathbf{A}\dot{\mathbf{x}},+,B x,+,C\delta

  

250  

式中—控制矢量；  

$\pmb{x}$ —系统状态参数矢量；  

$A\,,B\,,C^{\prime}$ 控制系统的增益系数矩阵。  

我国导弹飞行试验极少作开环飞行试验，在导弹闭环飞行试验的气动参数辨识舵偏规律设计中，要注意上述 $\Delta t$ 的选取和幅值的确定。特别是导弹飞行速度变化较大，在跨声速区，如果 $\Delta t$ 选取过大，就无法辨识出气动参数在跨声速区的变化规律。  

设计输人信号要考虑实现的可能性，必须根据控制装置的结构，对控制面运动的振幅、频率、坡度做适当限制，同时考虑控制机构实现的可能性和测试设备的动态特性以及试验场所等客观条件。  

正如第1章所论述的，系统辨识是通过系统输人和输出信息来确定系统的数学模型。在飞行试验之前必须很好设计输人信号，在飞行试验中还必须准确测得输人信号。因此，必须很好设计输人信号的测量装置，以获得准确的输人信号。例如飞机纵向气动参数辨识，必须设计好升降舵的变化规律，要求驾驶员或自动驾驶仪按此规律动作。在飞行试验时，在升降舵的转轴必须安装电位计以准确测定升降舵的实际舵偏角变化历程,绝不可以用舵偏指令代替舵偏角实测历程。  

# 7.2输出设计  

飞行器动力学系统满足牛顿第二定律，当系统控制输人的时间历程选定后，系统输出（系统的动态响应）的时间历程是确定的，无法选择。系统输出设计是指输出参数测量量的选择、传感器型式和量程的选择、传感器精度要求的确定以及安装位置的选定等等。  

# 7.2.1 输出信号测量要求  

输出信号是参数辨识的基本数据和依据，直接关系参数可辨识性及辨识准度。输出信号应含有待辨识参数的足够的信息量，这不仅要求有正确的输人设计，还要求提出正确的测量要求。  

对于飞行器动力学系统，反映系统动态特性的参数有：线位移、线位移速度、线位移加速度、角位移、角速率和角加速率等。线位移和线位移速度无法在运动物体上测量，通常用电影经纬仪或雷达进行遥测。线加速度、角位移、角速率、角加速度的测量传感器通常安装在运动物体上，测量所得数据经过数据采集系统记录在磁带上，或发送到实验控制台的接收机上。  

每次系统辨识试验之前，要先选择好测量的参数和相应的传感器及测量设备。确保试验能提供与待辨识参数相关的振动模态的动态响应。选择测量参数还应注意以下几点。  

1）传感器安装位置确定  

对于飞行器动力学系统，测量过载（加速度）的传感器应尽量安装在质心附近，并准确测量出其安装位置。利用各过载传感器的安装位置与质心位置的偏差量和角速率数据可以修正由于飞行器绕质心旋转运动所引起的附加过载，求得质心处的过载值。  

对于弹性体动力学系统，为获取足够的信息，必须沿振型方向布置足够的过载传感器，测量各点的位移加速度；必要时，还用角度传感器测量角位移（如弯曲角、扭转角等）。例如，进行飞机机翼弯扭振型的参数辨识时，就必须沿展向（弯曲方向）和弦向（扭转方向）布置足够的过载传感器，测量各点加速度的时间历程。要求确定振型的阶数越高，则布置的传感器也越多。  

流向角传感器（如攻角传感器、侧滑角传感器）的安装位置，要尽量不受物体运动的扰动的影响，而且事先应在风洞中做好角度标定试验。  

对于含流体的动力学系统，测量特定位置的压力、温度和流动速度是必要的。对于工程湍流辨识，必须测量流速剖面、压力场、湍动能场、雷诺应力场或者表面摩阻力系数等。液体晃动力学参数的辨识，通常是测量贮箱的加速度。  

传感器安装方位应与物体固连坐标系一致。安装方位角误差直接影响测量数据准度，从而影响辨识准度。方位角安装精度的要求对于不同辨识问题是不同的，通常角度误差应控制在几分的量级。  

2）传感器量程确定  

制定试验方案时，应按动力学系统的先验知识，应用动力学系统基本方程,预测试验过程中观测量的最大值 $y_{\tt m a x}$ 和最小值 $y_{\mathbf{min}}$ 作为选择传感器型号和量程的依据。这是一项至关重要的工作，传感器量程选择不好，可能由于量程太小而使试验过程中传感器一直处于满量程状态，无法提供信息；也可能由于量程太大而使实测只是总量的百分之几，无法提供准确的试验数据。  

# 3）传感器精度要求  

对于不同试验目的，不同动力学系统对传感器的测量精度要求是不同的。对于特定问题，可以利用飞行器动力学系统的辨识仿真软件进行各种测量误差条件下的辨识仿真统计试验运算，利用辩识仿真所得辨识结果的误差来确定对传感器的测量精度要求[2.3]。对于飞行器动力学系统辨识,传感器的测量精度应控制在 $1\,\%$ 左右，包括信号传输误差在内。有些传感器零位漂移较大，应在参数估计过程中将漂移量辨识出来，并加以清除。  

根据试验目的要求选择合适的传感器并确定其量程和精度要求是输出设计的重要内容。有关传感器的结构和性质已超出本书范围，读者可参阅有关专著[4]。  

# 7.2.2 运动轨迹的测量  

飞行器在空中、海面的运动轨迹可以采用雷达、照相经纬仪和方位定向器三种方法测定。测量的主要仪器都布置在地面上。  

# 1）雷达测量  

雷达以一定的重复频率将窄带宽的无线电脉冲发送到空中，并接受物体反射回的脉冲或应答信号，以此确定物体的方位角、高低角 θ 以及从发送波至收到回波的时间间隔。利用 和无线电波传播速度c可求得物体与雷达站的距离D=（rc/2)。由D、y1 可以确定物体的位置。为提高测量精度,常采用两台精测雷达测量，同时配备一台环视雷达帮助精测雷达捕捉目标。  

# 2）照相经纬仪测量  

用两台已知距离 $L$ 的照相经纬仪同时对物体拍照，记录下物体相对于照相机的两个方向角和两个高低角，从而确定出物体的空间位置。为提高测量精度，常采用三台照相经纬仪进行交会拍照。  

# 3）方位定向测量  

由地面两台无线电接收站利用方位定向器接收由物体上的振荡器和天线所发射的-定频率的无线电波，确定物体相对于接收站的两个方向余弦。利用这四个方向弦就可以确定物体在空间的位置。这种方法对于低空飞行物体的测量误差较大。  

# 7.2.3 数据采集系统  

飞行器动力学系统辨识试验的输人信号和输出信号，通常采用顺序控制数据采集系统进行采集。数据采集系统的主要任务是对试验中各个传感器测得的物理量电信号进行采样，并将大量单路的模拟信号综合成多路脉冲编码数字信号，然后发送到测控中心或进行磁记录（见图7-2）。记录的信号经过解调重发后，可得  

![](images/35d5aa3f0be1de4a1ade55dd8992962d73563f6bea21ae9a2a65ec5c8fe4d0bb.jpg)  
图 7-2 数据采集系统示意图  

试验的测量数据。  

研制飞行器动力学系统辨识所用的数据采集系统时，应注意选好两个参数一一采样速率和电码分层数。对于有振荡周期的飞行状态，采样速率应满足每个待辨识参数所对应的振型的振动周期内有10个 $\sim\!15$ 个测量数据,至少不能少于5个测量数据。当数据中混有高频信号时，为了滤去高频信号，采样速率要提高一个数量级[5]。电码分层数通常取为 $2^{8}$ 是足够的。  

# 7.3几何、物理和环境参数测量  

飞行器动力学系统辨识不仅需要测量系统试验时的输人和输出数据，还必须测量系统本身的几何、物理参数。例如在飞机气动参数辨识中，需要飞机的质量、惯量矩和质心位置。为了获取无量纲气动参数还必须给出飞机的特征长度、特征面积。动力学系统辨识的状态方程中还含有试验的环境参数。例如，飞机飞行试验时的大气密度、风速和风向，直接影响系统的输出，是必须测量的。  

# 7.3.1 几何、物理参数的测定  

物体质量的测定。对于常质量物体（如再人体），质量可以在产品出厂时测量；对于飞行试验过程中质量变化较大的物体（如飞机），可以在试验前和试验后进行测量，试验过程中的瞬时质量可以用内插法求出。对于火箭飞行中的质量就只能由每秒消耗的燃料进行估算。物体的质心可以用多台地秤称重，算出质心；也可以用点悬挂法，由几条垂线的交点确定质心。试验过程中质心的变化可以根据燃料消耗进行估算。物体主轴惯量矩可以进行多线悬挂振荡试验，由振荡频率来确定 $I_{x x}\setminus I_{y y}\setminus I_{z z}$ 。惯量积 $I_{x z}$ 等参数较难于测定，通常采用理论计算。对于大型物体，主轴惯量矩也难于测定，通常是根据设计图中各质量块的质量和位置算得。物体的特征长度、特征面积可以直接采用设计数据，无需直接测量。  

# 7.3.2 环境参数测量  

环境参数测量涉及面较广，这里只介绍与参数辨识有关的几种主要参数测量。  

# 1）大气密度测量  

对于飞行试验,通常在试验前、试验中、试验后进行三次测量。采用放气球或发射探空火箭的办法，将测量温度、压力和湿度的传感器送上天，同时采用光测的办法(如电影经纬仪)确定仪器运动的时间历程。温度、压力、湿度等数据经模数变换、编码、调制后，由无线电发送回地面接收站。利用温度、压力、湿度和气球轨迹可以求出试验时的大气密度随高度的变化曲线。气球只能测量$30\,\mathrm{km}$ 以下数据，高空数据常采用标准大气密度并进行适当修正，或用探空火箭测量。  

# 2）风速测量  

在地面，采用风标和风速计测量风速和风向。高空风用气球测定，认为气球的水平方向运动是风引起的，只能测量水平风速和风向；垂直风的测量要有专门设备。在参数辨识中，常忽略垂直风，只计人水平风效应。  

# 7.4 最优输人设计  

最优输人设计就是设计飞行器动力学系统控制面的运动规律，使试验能获得与待辨识参数有关动态响应的最大信息量。诚然，最优输人有多种意义，本章只讨论参数辨识的最优输人。  

最早研究动态系统最优输人问题的是莱文(M.J．Levin)(6],之后加莱克(P．H．Garlach)[7研究了飞行器参数辨识的最优输人。20世纪70年代,梅拉(R.K．Mehra)[8\~10]进行了系统的理论研究，给出了最优输人判据的各种表达形式，证明它们的等价性并给出在时域和频域的具体算法。当然参数辨识的优化设计还处于基础研究阶段，离实际应用还有一段距离，不论是准则、算式、算法和应用都有待进一步研究。  

# 256  

# 7.4.1 最优输入设计准则  

参数估计总是要求辨识出的参数的数学期望值与真值之间的偏差尽可能小，两者间的协方差也尽可能小。迄今，已研究出一系列无偏估计器。例如最大似然法、卡尔曼滤波器等,其估计值渐近趋于真值，即是说估计偏差的期望值为零。对无偏估计器，最优输人设计就是要求设计输人信号使得参数估计的误差协方差为最小值。根据克拉马-劳（Cramer-Rao)不等式[11],可推知信息矩阵之逆矩阵可用于估算参数估计的误差协方差。因此，信息矩阵的各种不同范数就可用作为最优输人设计准则。当然对输出误差法，也可用输出量的误差协方差或系统传递函数的误差协方差作为最优输人准则。  

# 1）基本假设  

最优输人设计通常做如下假设：  

（1）估计器是无偏而有效的，可以用信息矩阵作为协方差矩阵的估计值。  

（2）已知待估计参数 $\pmb\theta$ 的预估值 $\theta_{0}$ 和协方差阵的预估值 $\pmb{P_{0}}$ 。在优化计算中以 $\theta_{0}$ 代替 $\pmb{\theta}$ 。  

(3）输人 $\pmb{u}$ 具有能量约束或幅值约束。  

能量约束 ： $\Omega_{\!\;\!u}\;=\;\{\:{\pmb u}:{\pmb u}^{\mathrm{T}}{\pmb u}\leqslant{\pmb b}\}$ (7-7)  

幅值约束： $\Omega_{u}\ =\ \{\,u\,:\,a_{t}\leqslant u\,(\,t\,)\leqslant b_{t}\,\}$ (7-8)  

在优化计算中要求已知 $\pmb{\theta}$ 值，通常以参数预估值 $\pmb{\theta}_{0}$ 代替 $\hat{\pmb{\theta}}$ 进行计算，这会给最优输入设计带来误差，下面分析一下在什么条件下用 $\pmb{\theta}_{0}$ 代替 $\pmb{\hat{\theta}}$ 是允许的。信息矩阵 $M$ 可绕 ${\pmb\theta}_{0}$ 展开：  

{\bf\cal M}(,\widehat{\pmb{\theta}},),=,E_{\theta}{\pmb{\cal M}}(,{\pmb{\theta}},),=,E_{\theta},\bigg\lbrace,{\pmb{\cal M}}(,{\pmb{\theta}}{0},),+,\frac{\partial{\pmb{\cal M}}}{\partial{\pmb{\theta}}},\bigg\vert{,{\pmb{\theta}}{0}},(,{\pmb{\theta}},-,{\pmb{\theta}}{0},),+

\begin{array}{l}{{\displaystyle\frac{1}{2}(,{\pmb\theta},-,{\pmb\theta}{0}){\mathrm{tr}}\frac{\partial^{2}{\pmb M}}{\partial{\pmb\theta}^{2}},\bigg\vert_{,{\pmb\theta}{0}}(,{\pmb\theta},-,{\pmb\theta}{0}),+,\cdots\bigg\vert_{\infty}}}\ {{\displaystyle M(,{\pmb\theta}{0}),+,\frac{1}{2}\mathrm{tr}\bigg[\frac{\partial^{2}{\pmb M}}{\partial{\pmb\theta}^{2}},\bigg\vert{,{\pmb\theta}{0}}P{0}\bigg]}}\end{array}

P_{0},=,\int_{\Omega_{0}}\left(,\pmb{\theta},-,\pmb{\theta}{0},\right)\left(,\pmb{\theta},-,\pmb{\theta}{0},\right)^{\mathrm{T}},!!\rho\left(,\pmb{\theta},\right)\mathrm{d},\pmb{\theta}_{0}

  

当式(7-9)中的第二项远小于第一项 $\left(\mathbf{\nabla}P_{0}\right)$ 很小，也即 ${\pmb\theta}_{0}$ 估计值较准确；或者信息矩阵 $M$ 对 $\pmb{\theta}$ 不很敏感）时，就可以基于预估值$\pmb\theta_{0}$ 来进行输人的优化设计。能量约束反映控制能量限制,要求控制量的平方和限制在特定数值之内，如喷气控制系统。幅值约束反映飞机操纵系统的机械约束，如舵的最大正负偏转角。当然也可以通过能量限制来达到幅值限制。从实用观点，还需要考虑输人的频率，过高的舵偏振动频率是无法实现的。舵的偏转速率也应限制在操纵机构的可行范围内，过陡的梯度可能超过作动筒的可用功率。对于由驾驶员操纵的动力学系统，还要求控制输人的动作要比较简单，容易实现。  

整个优化输人设计应包括：给出系统的状态方程、观测方程和信息矩阵表达式；定义输人的限定集和准则泛函；由准则泛函推导出最优输人的必要条件，并推导出优化计算的具体公式，然后编制程序上机计算。最后还必须分析计算结果的正确性与工程实现的可能性。  

# 2）优化准则  

对动态系统，当试验的采样数据点足够多时，可以证明动态系统的最大似然估计是渐近有效的，其估计值与真值的误差协方差矩阵渐近趋于信息矩阵之逆，所以可用信息矩阵代替协方差矩阵来研究最优输人。信息矩阵在第5章已定义过，式（5-91）给出信息矩阵元素的一般表达式。下面利用信息矩阵的不同范数给出时域最优输人准则的几种表达式。  

（1）参数平均方差达极小。信息矩阵逆矩阵的迹反映参数的平均方差，可取之为优化准则。据此准则的优化设计结果是参数平均方差达极小的最优输人：  

J_{1};=;{\sf t r}(,{\pmb M}^{-1})

{\pmb u}{o p t};=;\mathrm{ARG}{;{\pmb u}\in;\Omega_{!!u}!!\mathrm{Ir}}(,{\pmb M}^{\mathrm{-}1})

  

（2）信息矩阵逆矩阵的最大特征值达极小。此特征值反映参数估计的不确定度椭球的主轴方向和大小，最大特征值达极小的物理意义是，参数估计的最大偏差量达极小值，也相当于协方差达极小。  

J_{2},=,\lambda_{\mathrm{\scriptsize{nax}}}(,M^{-1})

  

即  

\pmb{u}{o p t};=;\mathrm{ARG}:\operatorname*{min}{u,\in;\Omega_{u}}\lambda_{\operatorname*{max}}(,\pmb{M}^{-1},)

  

式中 $\lambda_{\operatorname*{max}}(A)\!\!-\!\!\!-A$ 矩阵的最大特征根。  

（3）不确定度椭球的体积达极小。协方差矩阵的行列式等子不确定性椭球的体积，此椭球体积越小，参数的辨识准度越高。故可取信息矩阵的逆矩阵行列式为优化准则  

J_{3};=;\mid M^{-1}\mid

  

即  

{\pmb u}{o p t};=;\mathrm{ARG}:\operatorname*{min}{{\pmb u},\in;{\pmb\Omega}_{!!\star}}|{\pmb M}^{-1}|

  

如果参数辨识的目的是估计输出量 y(t,0),可直接采用系统输出的协方差矩阵作为估计准则。优选输人u,使输出 y(t,θ)的协方差矩阵某范数的极大值达极小  

\pmb{u}{o p t};=;\mathrm{ARG}:\operatorname*{min}{\mathfrak{u}\in;\Omega_{\pmb{u}}}\operatorname*{max};\phi\left[,\mathrm{cov}(,\pmb{y}(,t,,\hat{\pmb{\theta}}),),\right]

  

式中 $\phi(\mathbf{{A}}){\longrightarrow}\mathbf{{A}}$ 的某范数（例如特征根、行列式值等）。  

# 7.4.2  最优输入算法  

本节根据输人设计的最优准则,先给出线性系统参数辨识的最优输人设计在时域的具休算式和解算方法。对于非线性系统，其参数辨识的最优输人设计可以采用类似于5.3.2节“非线性动力学系统最大似然算法”的办法进行近似处理。也即状态方程和观测方程保持为非线线性方程，而信息矩阵的表达式与线性系统相同。  

1）最优输人设计基本方程  

本节给出线性系统用于参数辨识的最优输人设计的基本方程。略去过程噪声，系统状态方程和观测方程可写成  

状态方程： $\dot{\boldsymbol{x}}\;=\;\boldsymbol{F}(\,\pmb{\theta}\,)\,\pmb{x}\;+\;\boldsymbol{G}\left(\,\pmb{\theta}\,\right)\pmb{u}\;\;\;\;\left(0\leqslant t\leqslant T\;\right)$ (7-14)观测方程： ${\bf y}\left(\,i\,\right)\;=\;H(\,\pmb\theta\,)\,{\pmb x}\left(\,i\,\right)\;+\;{\pmb\varepsilon}\left(\,i\,\right)\quad(\,i\;=\;1\,,2\,,\cdots,N\,)$  

能量约束： $\mathbf{\Psi}^{\int_{0}^{T}}\pmb{u}^{\mathrm{~T~}}\pmb{u}\,\mathrm{d}t\;=\;E$ 式中 $\pmb{x}(\,t\,)-\$ 维状态矢量；  

${\pmb u}\left({\bf\Phi}_{t}\right)\!-\!{\bf\Phi}\!-\!{\bf\Phi}\!\left({\pmb u}\left({\bf\Lambda}_{t}\right)\!-\!{\bf\Phi}\!\right)$ 维控制矢量；${\wp}{\rule{0ex}{2ex}}{\rule{0ex}{0ex}}{\rule{0ex}{0ex}}$ 维待估计参数矢量；  
$\mathbf{y}\left(\,i\,\right)\longrightarrow m$ 维观测矢量；$i\!-\!-\!t_{i}$ 时刻的值；  

$\pmb{\varepsilon}(\,i\,)-$ 观测噪声，为零均值高斯白噪声。  

E\left[,\pmb{\varepsilon},\right];=;\pmb{0};;;;E\left[,\pmb{\varepsilon},(,t,),\pmb{\varepsilon}^{\mathrm{T}}(,\tau,),\right];=;\pmb{R}\delta\left(,t,-,\tau,\right)

  

能量约束方程（7-16)可用来通过调整 $E$ 值以限制 $\pmb{u}$ 的最大幅值和状态参数 $\pmb{x}$ 的最大值，使解出的最优输人在实际上可实现。  

第5章式（5-91)给出了信息矩阵元素 $M_{k l}$ 的一般表达式。忽略过程噪声，有 $\pmb{{\cal B}}\left(\mathbf{\Lambda}_{i}\right)=\pmb{{\cal R}}\left(\mathbf{\Lambda}_{i}\right)$ 且 $\partial\,{\pmb R}\,(\,_{i}\,)/\partial\,{\pmb\theta}={\bf0}$ ,故信息矩阵 $M$ 的元素 $M_{k l}$ 简化成  

M_{k\ell};{=}\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{\ell}};=;\sum_{i;{\textrm{--}}1}^{N}2;\frac{\partial,{\pmb{\nu}}^{\mathrm{T}}(,i,)}{\partial\theta_{\ell}}{\pmb{R}}^{;{\scriptscriptstyle{-1}}}(,i,);\frac{\partial,{\pmb{\nu}}(,i,)}{\partial\theta_{k}};{=}

2\sum_{i;;-1}^{N};\frac{\partial\pmb{x}^{\top}({\bf\Xi}{i},)}{\partial\theta{l}}\pmb{H}^{\mathrm{T}}({\bf\Xi}{i},),{\pmb{R}}^{\mathrm{\tiny~\textit~{l}~}}({\bf\Xi}{i},);{\pmb{H}}({\bf\Xi}{i},);\frac{\partial\pmb{x}({\bf\Xi}{i},)}{\partial\theta_{k}}

(,\iota,,k;=;1,,2,,\cdots,p,)

  

系统的待估计参数 $\pmb{\theta}=[\:\theta_{1}\:,\theta_{2}\:,\cdots,\theta_{\rho}\:]^{\mathrm{T}}$ 考虑到各个参数对系统响应的影响不同，每次试验不一定对所有参数都感兴趣，这里引进权系数矩阵 $\pmb{W}$ ,其对角线元素为 $\boldsymbol{W}_{1}\,,\,\boldsymbol{W}_{2}\,,\cdots,\,\boldsymbol{W}_{p}$ ，其余为零元素，$\boldsymbol{W}_{i}$ 为常数， $\pmb{W}$ 为 ${\boldsymbol{p}}\times{\boldsymbol{p}}$ 维矩阵。为了计算简便，以信息矩阵 $M$ 代替 $M^{-1}$ ,最优输人的准则式（7-10)变成  

{J_{1};=;\o{\operatorname{tr}}{(\boldsymbol{W}\boldsymbol{M}\boldsymbol{W})}}

  

即  

u_{o p t};=;\mathrm{ARGmaxtr}(:W M W)

  

将式(7-17)代人式（7-18)得  

J_{1},=,\operatorname{tr}\sum_{i,=,1}^{N}\left(,\pmb{\nabla}{\pmb{\theta}}\pmb{x},(,i,),\pmb{W},\right)^{\mathrm{T}}\pmb{H}^{\mathrm{T}}\pmb{R},^{-1}\pmb{H}\big(,\pmb{\nabla}{\pmb{\theta}}\pmb{x},(,i,),\pmb{W}\big)

\pmb{\nabla}{\pmb{\theta}}\pmb{x}\left(\mathbf{\Delta}{i}\mathbf{\Lambda}{j}\right)\pmb{W}=\left[\pmb{W}{1}\ \frac{\partial\pmb{x}\left(\mathbf{\Delta}{i}\mathbf{\Lambda}{j}\right)}{\partial\theta_{1}},\pmb{W}{2}\ \frac{\partial\pmb{x}\left(\mathbf{\Delta}{i}\mathbf{\Lambda}{j}\right)}{\partial\theta{2}},\cdots,\pmb{W}{p}\ \frac{\partial\pmb{x}\left(\mathbf{\Delta}{i}\mathbf{\Lambda}{j}\right)}{\partial\theta{p}}\right]^{\mathrm{T}}

  

$n\times\,p$ 维矩阵。为了便于书写和应用优化算法,将状态的灵敏度系数 增广到状态矢量。  

定义下列状态参数矢量 $x_{A}$  

\begin{array}{r l}&{\pmb{x}{\Lambda}^{\mathrm{T}}\equiv\left[\pmb{x},,\pmb{W}{1},\frac{\partial\pmb{x}}{\partial\theta_{1}},\cdots,\pmb{W}{P},\frac{\partial\pmb{x}}{\partial\theta{p}}\right]}\ &{\pmb{G}{\Lambda}^{\mathrm{T}}\equiv\left[\pmb{G},,\pmb{W}{1},\frac{\partial\pmb{G}}{\partial\theta_{1}},\cdots,\pmb{W}{P},\frac{\partial\pmb{G}}{\partial\theta{p}}\right]}\end{array}

F_{A}\equiv\left(\begin{array}{c c c c}{{F}}&{{0}}&{{\cdots}}&{{0}}\ {{W_{1},\frac{\partial\mathit{F}}{\partial\theta_{1}}}}&{{F}}&{{\cdots}}&{{0}}\ {{\vdots}}&{{\vdots}}&{{\ddots}}&{{\vdots}}\ {{W_{\rho},\frac{\partial\mathit{F}}{\partial\theta_{\rho}}}}&{{0}}&{{\cdots}}&{{F}}\end{array}\right)\quad{\cal H}_{A};=;\left(\begin{array}{c c c c c}{{0}}&{{{\cal H}}}&{{0}}&{{\cdots}}&{{0}}\ {{0}}&{{0}}&{{{\cal H}}}&{{\cdots}}&{{0}}\ {{\vdots}}&{{\vdots}}&{{\vdots}}&{{\ddots}}&{{\vdots}}\ {{0}}&{{0}}&{{0}}&{{\cdots}}&{{{\cal H}}}\end{array}\right)

R_{A}={\left(\begin{array}{l l l l}{R}&{0}&{\cdots}&{0}\ {0}&{R}&{\cdots}&{0}\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\ {0}&{0}&{\cdots}&{R}\end{array}\right)}

  

式中 $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\pmb{x}_{A}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! $ 维矢量；  

$\mathbf{{G}}_{A}-(\mathbf{{\Sigma}}_{P}+1)\mathbf{{\Sigma}}_{n}\times\cal{l}$ 维矩阵；  
$\boldsymbol{F_{A}}\mathrm{-}\mathrm{-}\bigl(\,\boldsymbol{p}+1\,\bigr)\,\boldsymbol{n}\times\bigl(\,\boldsymbol{p}+1\,\bigr)\,\boldsymbol{n}$ 维矩阵；  
$H_{A}\mathrm{-}\mathrm{-}\,\rho m\times\left(\,\rho+1\,\right)n$ 维矩阵；  
${\cal R}_{A}{\ \ \ \ \ \ \ \ \ \ \dot{p}m\times\dot{p}m}$ 维矩阵；$u\!\longrightarrow\!\langle\;\times\;1$ 维矢量。  

将式(7-14)对 $\theta_{i}$ 求导，得灵敏度方程组,将其增广到状态方程式（7-14)中，求得增广状态方程，利用式 $(7-20)\sim$ 式（7-23)的定义式，可得增广状态方程  

\dot{\pmb{x}}{A};=;{\pmb{F}}{A}{\pmb{x}}{A};+;{\pmb{G}}{A}{\pmb{u}}

  

利用式 $(7-20)\sim$ 式(7-23）,准则函数表达式(7-19)可改写成  

J_{1},=,,\sum_{i,=,1}^{N}\pmb{x}{A}^{\intercal}({,i,}),\pmb{H}{A}^{\intercal}({,i,}),\pmb{R}{A}^{\intercal}\pmb{H}{A}({,i,}),\pmb{x}_{A}({,i,})

  

式（7-25）也可采用积分形式  

J_{1},=,\int_{,0}^{,T}\pmb{x}{A}^{\mathrm{T}}\pmb{H}{A}^{\mathrm{T}}\pmb{R}{A}^{,-1}\pmb{H}{A}\pmb{x}_{A},\mathrm{d}t

  

满足能量约束方程式(7-23)的 $J_{\updownarrow}$ 条件极大值问题，可通过引！进常数乘子 $\mu$ 而化为下列 $J$ 的极小值问题  

J;=;\frac{1}{2}{\displaystyle\int_{0}^{\tau}}\big[-;x_{A}^{\top}{\pmb H}{A}^{\top}{\pmb R}{A}^{-1}{\pmb H}{A}{\pmb x}{A};+;\mu\left(,{\pmb u}^{,T}{\pmb u};-;E/T,\right),\big],\mathrm{d}t

  

线性系统（7-14）的参数辨识的最优输人设计问题变为在满足状态方程式（7-24）的条件下，寻求 $\pmb{u}\left(\begin{array}{r}{t}\end{array}\right)$ 使式（7-27)的 $J$ 达极小值。这是个有约束条件的最优化问题，有各种解法，下节给出一种具体解法。  

# 2）参数辨识最优输人算法  

应用邦特列雅金（J.C.IoHTparáH)I11的极大值原理可推导出最优化输人 $u\left(\t\right)$ 必须满足的必要条件，从而导出求解 $\pmb{u}\left(\pmb{\ell}\right)$ 的算式。增广状态方程式（7-24)和准则函数表达式（7-27)的哈密顿函数 $H_{m}$ 为  

\begin{array}{l}{{\displaystyle{\cal H}{m};=\frac{1}{2}\bigg[-;x{\Lambda}^{\mathrm{T}}{\cal H}{A}^{\mathrm{T}}{\cal R}{\Lambda}^{-1}{\cal H}{A}x{A};+;\mu\left(\frac{}{}\boldsymbol{u}^{\mathrm{T}}\boldsymbol{u};-\frac{\boldsymbol{E}}{T}\right)\bigg]+}}\ {{\displaystyle\qquad;\lambda^{\mathrm{T}}\left[,F_{A}x_{a},+,G_{A}\boldsymbol{u},\right]}}\end{array}

  

式中 $\lambda\left(\,t\,\right){\mathrm{-}}{\mathit{\underline{{x}}}}_{A}\left(\,t\,\right)$ 的协态变量,是 $\left(\,\phi+1\,\right)n$ 维矢量。  

$\lambda\left(\,t\,\right)$ 和 $\pmb{x}_{A}\left(\pmb{\tau}\right)$ 满足下列哈密顿方程  

\begin{array}{r l}&{\frac{\mathrm{d}\ensuremath{\mathbf{x}}{A}}{\mathrm{d}t},=,\left(\frac{\partial H{m}}{\partial\ensuremath{\mathbf{\lambda}}}\right)^{\mathrm{T}}\Bigg}}\ &{\frac{\mathrm{d}\ensuremath{\mathbf{\lambda}}}{\mathrm{d}t},=,\left(\frac{\partial H_{m}}{\partial\ensuremath{\mathbf{\lambda}}_{A}}\right)^{\mathrm{T}},\Bigg}}\end{array}

  

最优输人的必要条件为  

{\frac{\partial H_{m}}{\partial u}};=;0

  

将式（7-28）代人式（7-29）和式（7-30），得出最优输人相对应的$\lambda\left(\,t\,\right)$ 和 $\pmb{u}\left(t\right)$ 满足下式  

\pmb{\lambda};=;-;\pmb{F}{\pmb{A}}^{\mathrm{T}}\pmb{\lambda};+;\pmb{H}{\pmb{A}}^{\mathrm{T}}\pmb{R}{\pmb{A}}^{;-;1}\pmb{H}{\pmb{A}}\pmb{x}_{A}

\pmb{u};=;-;\frac{1}{\mu}\pmb{G}_{A}^{\mathrm{T}}\pmb{\lambda}

  

将式（7-32)代人式（7-29）和式（7-30），得出最优控制必须满足的方程组  

\left{\begin{array}{l}{{{\displaystyle\frac{\mathrm{d}{\bf x}{A}}{\mathrm{d}t}}{=}{\displaystyle{\cal F}{A}{\bf x}{A}{-}{\displaystyle\frac{1}{\mu}}{\cal G}{A}{\bf G}{A}^{\mathrm{T}}\lambda}}}\ {{{\displaystyle\frac{\mathrm{d}\lambda}{\mathrm{d}t}}{=}{\displaystyle H{A}^{\mathrm{T}}{\cal R}{A}^{-1}H{A}{\varepsilon}{A}{-}{\displaystyle{\cal F}{A}^{\mathrm{T}}\lambda}}}\ {{{\displaystyle{\cal x}{A}(0){=}{\displaystyle{\cal x}{A0}}}}}\ {{{\displaystyle\lambda(T)~{=}~0}}}\end{array}\right.

  

最优输人设计转化成求解上面的线性方程组的两点边值问题。因为系统的最优输人与状态初始值无关，令 $\pmb{x}_{A0}=\mathbf{0}$ ，则上式成了边条件为零的线性齐次方程组，只当 $\pmb{\mu}$ 取特定值时才有非平凡解。问题成了求解 $\pmb{\mu}$ 的特征值。常系数线性齐次方程组有通解，可以用转移矩阵型式表示，假设 $\pmb{\phi}(\mathbf{\nabla}_{t},\mathbf{0};\pmb{u})$ 为转移矩阵，由转移矩阵方程（参见式（5-136））可得下列表达式  

\pmb{\mathcal{P}}(\ t,,0,;\mu);=;\exp\left[\begin{array}{c c}{F_{\mathrm{A}}}&{-;\frac{1}{\mu}\mathbf{G}{\mathrm{A}}^{\mathrm{T}}\mathbf{G}{\mathrm{A}}}\ {\quad}&{\quad}\end{array}\right]t

  

将 $\pmb{\Phi}$ 按 $x_{A}$ 和 $\lambda$ 两部分分割开来,取 $t=T$ ，得下式  

\begin{array}{r}{\left[\pmb{x}{A}\left(\begin{array}{l}{T}\end{array}\right)\right]=\pmb{\Phi}\left[\pmb{x}{A}\left(0\right)\right]=}\ {\pmb{\lambda}\left(\begin{array}{l}{T}\end{array}\right),\right]=\pmb{\Phi}\left[\pmb{\lambda}\left(0\right)\right]=}\end{array}

\begin{array}{r l}{\left[\pmb{\Phi}{x x}(\mathrm{~}T,0;\mu)\right.}&{{}\pmb{\Phi}{x\lambda}(\mathrm{}T,0;\mu)\right]\cdot\left[\pmb{x}{A}(0)\right]}\ {\pmb{\Phi}{\lambda x}(\mathrm{}T,0;\mu)}&{{}\pmb{\Phi}_{\lambda\lambda}(\mathrm{~}T,0;\mu)\right]\cdot\left[\pmb{\lambda}(0)\right]}\end{array}

  

将 $\lambda\left(\,T\,\right)=0$ 代人式(7-35)的第二方程，由于 $\pmb{x}_{A}(0)=\mathbf{0}$ ，得  

\lambda\left(,T,\right);=;\pmb{\Phi}_{\lambda\lambda}\left(,T,,0,;\mu,\right)\lambda\left(0,\right);=;0

  

对于非平凡解， $\mu$ 必须满足下列行列式  

\vert;\Phi_{\lambda\lambda},(;T,,0,;\mu,);\vert;=,0

  

方程式（7-37）是式（7-32）、式（7-33）哈密顿系统的特征值方程,是 $\pmb{\mu}$ 的非线性代数方程，可以用牛顿-拉夫逊选代算法或共轭梯度等算法求解。通常 $\mu$ 有许多特征值,其中最大值 $\mu_{\mathrm{\,max}}$ 相应于$J$ 的极小值。 $\pmb{\mu}$ 是 $T$ 的函数，对给定的时间区间 $T$ ，由式(7-37)求最大特征值 $\mu_{\mathrm{\,max}}$ 比较因难且费机时,难于判断 $\pmb{\mu}$ 值是最大值。这里给出另一种算法一——黎卡堤方程法。定义黎卡堤矩阵 $\pmb{P}(t)$ 为  

\pmb{x}_{A}(\pmb{\mathscr{s}});=;\pmb{P}(\pmb{\mathscr{s}})\pmb{\mathscr{\lambda}}(\pmb{\mathscr{s}})

  

对式（7-38）求导，并利用式（7-33），可得 $\textbf{\emph{P}}$ 的一阶微分方程  

\begin{array}{r l}&{\left{\dot{\pmb{P}};=;\pmb{F}{A}\pmb{P},+,\pmb{P}\pmb{F}{A}^{\mathrm{T}},-,\pmb{P}\pmb{H}{A}^{\mathrm{T}}\pmb{R}{\dot{A}}^{-1}\pmb{H}{A}\pmb{P};-;\frac{1}{\mu}\pmb{G}{A}\pmb{G}_{A}^{\mathrm{T}}\right.}\ &{\left.\quad\pmb{P}!\left(0\right);=;0}\end{array}

  

由式(7-38)和式(7-39）,可知当 $P^{-1}$ 存在时，有  

{\bf p}\sp{\scriptscriptstyle-1}(,T),=,0

  

从式(7-40)可知,对于给定的 $\pmb{\mu}$ ，从 $\boldsymbol{t}=\mathbf{0}$ 积分式（7-39），当出现 $P\{\ t\}$ 变得很大，则表明此时刻是对应于给定 $\pmb{\mu}$ 值的 $T$ 值，因为积分是从 $t=0$ 开始，所以第一次出现很大 $\pmb{P}(t)$ 值的时刻是对应于给定μ值的最小T值。可以证明,最小T值相应于最大的特征值 $\mu_{\textup{m a x0}}$ 所以,用这种算法,对给定 $\pmb{\mu}$ ,积分式(7-39),所得的第一个 $T$ 就构成 $(\,T,\mu_{\tt m a x}\,)$ 。改变 $\pmb{\mu}$ 就可以得 $\mu_{\mathrm{{max}}}$ 随 $T$ 的函数关系$\mu_{\operatorname*{max}}=\mu_{\operatorname*{max}}(\,T)$ 。计算经验表明,确定 $T$ 的重要标志是黎卡堤矩阵的对角线元素变号。一步一步积分黎卡堤矩阵时，当突然出现变号，也即从一个方向（例如 $-\infty$ )变到另一个方向(例如 $+\infty$ ),此时刻即为对应于给定 $\mu$ 值的 $T$ 值。将此 $\mu,T$ 值代人式(7-37),可求得对应的特征矢量  (0),并由能量约束式(7-16)确定其幅值。确定了 (0)就可积分式(7-32)和式(7-33)。 $\lambda\left(\,T\,\right)=0$ 是自动满足的，因为 $\mu,T$ 满足式(7-38)。至此，线性系统优化输入设计的公式已完备，本节还给出了具体解算方法。  

3）含过程噪声系统的最优输人算法  

含过程噪声的线性系统的通式见式（5-34）和式（5-35），对线性常系数系统为  

\begin{array}{r}{\left{\dot{\pmb{x}};=;\pmb{F}(\pmb{\theta}),\pmb{x};+;\mathbf{G}\left(,\pmb{\theta},\right)\pmb{u};+;\pmb{F}(,\pmb{\theta},),\pmb{\eta}\right.}\ {\left.\pmb{y};=;\pmb{H}\left(,\pmb{\theta},\right)\pmb{x};+;\pmb{D}\left(,\pmb{\theta},\right)\pmb{u};+;\pmb{\varepsilon}\right.}\end{array}

  

对式(7-41)表达的线性常系数系统,其信息矩阵 $\pmb{M}$ 的表达式见式(5-33）。比式(7-17)增加了 项,使公式复杂多了。当忽略新息方差 $\pmb{B}$ 随 $\pmb{\theta}$ 的变化,其信息矩阵 $M$ 仍以式（7-17)表达。但状态方程式（7-14)应改为（参见式（3-113）～式（3-117））  

\begin{array}{r l}&{\dot{\hat{\pmb{x}}}\ \ {-}\ \ \hat{\pmb{F}}\acute{\pmb{x}}\ +\ \pmb{G}{\pmb u}\ +\ {\pmb{K}}\left(,\mathbf{y}\ -\ \pmb{H}\dot{\mathbf{x}}\ -\ \pmb{D}{\pmb u},\right)}\ &{\mathbf{\hat{K}}\ =\ ,p\pmb{H}^{\mathrm{T}}{\pmb{R}}^{-1}}\ &{\dot{\pmb{P}}\ =\ \pmb{F}{\pmb{P}}\ +\ \pmb{P}\pmb{F}^{\mathrm{T}}\ +\ \pmb{T}\pmb{Q}\pmb{F}^{\mathrm{T}}\ -\ \pmb{P}\pmb{H}^{\mathrm{T}}{\pmb{R}}^{-1},\pmb{H}\pmb{P}}\end{array}

  

因此 $\nabla_{\theta}\textbf{\em x}$ 的计算比不考虑过程噪声的情况复杂多了。对具体问题还须做进一步简化才能求得有用结果，有待进一步研究。这里给出一种特殊情况的算法。对于待估计参数·仅含于 $\pmb{G}$ 的特殊情况，因为 $\mathbf{\deltaK}$ 和 $\pmb{P}$ 与 $\pmb{G}$ 无关，灵敏度方程有下列简单公式  

\widehat{\textbf{\textit{v}},},\widehat{\textbf{\textit{x}}}=\textbf{\textit{(F-K H)}},\nabla_{\theta}\widehat{\mathbf{\textit{x}}},+,\nabla_{\theta}G u

  

式中， $\pmb{K}$ 通常是时变的，但是若系统是完全可控和可观测的， $\pmb{K}$ 口司趋向某常数的稳态值。这时式（7-45）与式（7-14)类同。前面对于无过程噪声情况所推导的全部公式都可用于此情况。  

# 7.4.3 应用实例  

最优化输人设计是一门新课题，目前还在开发研究中，在飞行器参数辨识中应用并不广泛。下面给出几个常用输人信号和最优输人信号的实例，并做简单评述。  

在飞行试验中最常采用的是阶跃、方波、偶极方波等形式的舵偏规律（见图 7-1)来激发飞行器的响应。凯勒(R.Koehler)Li2}采用多级方波型求得一个在频域内功率谱分布比较均匀的输人，称为“3211"信号（即三个时间单位的正方波，两个时间单位的负方波,接着再一个时间单位的正方波，一个时间单位的负方波）。从图7-1的功率谱曲线可看出，“3211"信号是个频带相当宽的信号，通过调整 $\Delta t$ ，可以将频谱移到飞行试验所希望激发的频带去。  

图7-1还显示阶跃输人信号只在低频时含有能量，故它不能用来激发高频响应，而且阶跃输人常使飞机偏向一方而飞离线性区域。由图还可看出偶极方波也有较宽的频带，通过调整 $\Delta t$ 可使在高频带含有足够的能量。  

这里给出3个用最优输人设计求出的输人信号。舒尔茨（G.Schulz)[13] 以信息矩阵的迹达最大求出离散的单输入信号,用此法分别计算辨识纵、横向气动导数的输人信号。图7-3给出辨识纵向气动导数的最佳升降舵输人的频谱和时间历程。荷兰德佛特技术大学(DUT)[14]以误差协方差矩阵之逆达极小设计出由相等频率间隔的正弦波总合而成的最佳输人，由最优条件确定各频率正弦波的幅值。图7-4给出用此法设计的最佳升降舵输人。梅拉[15)给出使信息矩阵行列式达极大值的最佳输人的频域算法,所得最佳升降舵输人历程和频谱分布见图7-5。  

为了验证上述5种输人信号（图7-6）的优劣，德国飞行试验研究所和荷兰德佛特技术大学各自独立地应用上述输人信号激发“海狸”飞机的动态响应，进行气动参数辨识。其结果示于图7-7和图7-8。图7-7给出各种输入所辨识气动导数的相对标准偏差，可以看出梅拉、“3211”和德佛特技术大学的辨识精度相当。用5种输人信号激发的飞机响应所辨识的纵、横向气动导数的结果列$\left(\,a\,\right)$ 图的纵坐标为振幅值； $(\,b\,)$ 舵偏时间历程。  

![](images/8390e57e5c9fc5fdeaa89f77df37bc31139388acd23c7e46ea10b63f5fc9ece4.jpg)  
图 7-3舒尔蒋最佳升降舵输人  

![](images/3908f93ce5bb6e737a722bcd58aeb9ea25d0fd625b3e3e6950e61c47c1118743.jpg)  
图 7-4德佛特技术大学最佳升降舵输人$\left(a\right)$ 图的纵坐标为10倍振幅值平方； $\left(\,\delta\,\right)$ 舵偏时间历程。  

![](images/4437efee0e66cf722192e18995a44df9ebda62d1f348da17298ed89da84f8702.jpg)  
图 7-5梅拉最佳升降舵输人$\mathbf{\lambda}(\,a\,)$ 频谱分析； $(b)$ 舵偏时间历程。  

于图 $7-8^{[14]}$ 。其中，德国飞行试验研究所采用最大似然法；荷兰德佛特技术大学采用建模前估计法，先用卡尔曼滤波再用逐步回归法。辨识的标准偏差是由 $(9\sim10)$ 次飞行试验辨识结果求出的。由此图可见，纵向导数的差异主要是两种辨识方法和模型不同所致，输人信号不同对辨识结果影响甚微。横向导数受输人信号的影响较大，从图7-8可见，“3211”、偶极方波和德佛特技术大学的结果较好，而梅拉的横向结果比纵向结果差些，这是因为应用梅拉方法时，是将副翼和方向舵分别作为单输人进行优化，然后叠加在一起，因此所得结果不是最优输人，仅为次优输人。舒尔茨信号的结果较差，这说明采用信息矩阵的迹达最大比以信息矩阵行列式达极大作为优化准则要差些。  

美国对F-8飞机也曾采用9种不同输人做过类似试验[16]。结论是静稳定导数对输人方式不敏感，而控制导数对输人比较敏感。横向导数对输人信号的型式也较敏感。经验表明，飞机在一个副翼动作之后，紧接着一个舵动作就较充分地激发横向运动模态。  

268  

![](images/cbc0e6e6e8c89b19882e67d0fc287b45400988a0bf8f1ab0d0785754929c4ef8.jpg)  
图 7-6用于飞行试验的5个最佳升降舵输人$\left(\,a\,\right)$ 偶极方波输人； $(\,b\,)~^{\ast}3211^{\ast}$ 输人； $(c)$ 梅拉输人；$(d)$ 舒尔茨输人； $\left(\,e\,\right)$ 德佛特技术大学输人。  

上述飞机参数辨识研究的结果，对于其他动力学系统，特别是飞行器动力学系统，也是有参考价值的。当然，目前参数辨识的最优化输人研究基本上只局限于线性系统，而且实用和有效的方法还有待进一步开发。目前国内飞机、导弹飞行试验的输人都采用多重方波形式，只是在方波幅值和作用时间 $\Delta t$ 之中进行优化选择。  

![](images/8d0f03c078b7e8589b33623a9819218cf9eb63f79d7cb901bbbfdd91b4444835.jpg)  
图 7-7输人信号对导数辨识准度的影响  

（每组数据从左至右依次是：偶极方波输人、“3211”输人、梅拉输人、舒尔茨输人、德佛特技术大学输人）  

![](images/bce28b6946f0504fa8d9b58b45dacf02026e0c11357f440530d7b30f76583eaf.jpg)  
图 7-8从 $9\!\sim\!10$ 次机动飞行中辨识出的导数的平均值和标准偏差（横坐标 $1\!\sim\!5$ 依次是：偶极方波输人、3211"输人、梅拉输人、舒尔茨输人、德佛特技术大学输人）  

# 参考文献  

1蔡金狮．动力学系统辨识与建模．北京：国防工业出版社，1991   
2 Bryant W H, Hodge W F. Effects of Instrumentation Errors on the Estimation of Aircraft Stability and Control Derivatives. NASA TND-7647, 1974, 261 \~ 280   
3  Bryant W H, Hodge W F. A Monte Carlo Analysis of the Effects of Instrumentation Error on Aircraft Parameter Identification. AGARD CP-172, paper 5, 1975   
4李楚，郑宏才．传感技术大全．武汉：湖北科学技术出版社，1986   
5  Maine R E. Aerodynamic Derivatives for an Oblique Wing Aircraft Estimated from Flight Data by Using a Maximum Likelihood Technique. NASA TP-1336, 1978   
6 Levin M J. Optimal Estimation of Impulse Response in the Presence of Noise. IRE Trans. , 1960, CT-7(1): 50\~ 56   
7  Gerlach P H. Analyse van een Mogelijke Method voor Het Meten van Prestaties en Stabilitietsen Besturingseigenschappen van een Vliegtuig in Niet-Stationaire, Symmetrische Vluchten. Delft Uni. of Techno. Report, UTH-117, 1964   
8 Mehra R K, Gupta N K. Status of Input Design for Parameter Identification. AGARD CP-172, paper 12, 1975   
9 Mehra R K. Optimal Inputs for Linear System Identification. IEEE Trans. , 1974, AC-19(3) : 192 \~ 200   
10  Mehra R K. Optimal Inputs Signais for Parameter Estimation in Dynamic System Survey and New Results. IEEE Trans. , 1974, AC-19(6): 753\~768   
11 HaHTprHH JI C. MareMaTHueCKaa TeopH9 OnTHMaJbHbIx HIpoueccOB. ΦH3HaTJM3, 1961.   
12  Koehler R, Wilhelm K. Auslegung von Eingangsignalen fuer die Kennwerter-mittlung. DFVLR Institute fuer Flugemechanik, IB 154-77/40, 1977   
13  Schulz G. Entwurf Optimaler Eingangssignale fuer die Systermidentifizierung under Beruecksichtigung Von mef-und System Rauschen. Regalungstechnik, 1977 , Heft 10 : 324 \~ 330   
14 Plaetschke E, Schulz G. Practical Input Signal Design. AGARD LS-104, paper3, 1979   
15 Mehra R K. Frequency-Domain Synthesis of Optimal Inputs Linear System Parameter Estimation. Div. of Engine. & Appl. Phs. Harvard Univ., TR645, 1973   
16   Shafer A. Flight Investigation of Various Control Inputs Intended for Parameter Estimation. AIAA 84-2073, 1984  

# 第8章 辨识准度与系统验证  

8.1概述  

参数估计准度取决于参数辨识所用的数学模型、估计方法、输人信号、过程噪声和测量系统的精确度等多个方面。系统模型结构确定准则、估计算法、输人信号设计方法等都是针对一定的系统在一定的假设条件及工程近似下导出的；测量及过程噪声常常被假设为零均值高斯白噪声；对于飞行器这类复杂的非线性系统的辨识，不可避免地会存在一些工程近似，假设条件也只能近似满足；通过有限的试验数据对未知参数进行估计时，得到的辨识结果只能是真值的近似。辨识所建立的数学模型的精确度将直接影响控制系统设计、系统仿真的正确性和置信度，因此，确定估计值的准确度与参数估计本身是同等重要的。辨识难度评价与系统验证是系统辨识中极其重要的一环。  

本章对已有的准度评价准则进行比较，讨论其优缺点及适用范围。  

# 8.2 参数估计准度评价准则  

# 8.2.1 估计偏差  

偏差定义为在统计意义下的一致性或重复性误差，记为$\pmb{b}\left(\pmb{\theta}_{\mathfrak{n}\mathfrak{r}}\right)$ 。且  

\pmb{b}\left(\pmb{\theta}{\mathrm{tr}}\right);=;E\left{\pmb{\theta}\mid\right.};-;\pmb{\theta}{\mathrm{tr}}

  

272  

若 $b\left(\,\pmb\theta_{\mathrm{tr}}\right)=0$ ,则估计是无偏的。  

理论上讲，只要试验数据足够多，极大似然参数估计就是渐近无偏的,但其无偏性是在下列假设下证明的[1]:  

（1）动力学系统的数学模型是精确的；  

（2）噪声为高斯白噪声；  

（3）似然函数的表达式是精确的。  

飞行器及其测量系统极其复杂，常常难以满足上述假设，因而其参数估计总是有偏的。  

估计的偏差给出了估计值离真值的大小,但没有给出随机的分散度，而且由于真值未知，偏差很难计算，因此很少采用偏差作为准度的量度。  

# 8.2.2 估计分散度  

分散度定义为在相同的试验条件下，重复多次试验，所得参数估计结果的分散程度，记为 $S(\,\pmb\theta_{\mathrm{tr}})$ 。且  

S(,\pmb\theta_{\mathrm{tr}}),=,\frac{1}{N}\sum_{i,=,1}^{N},(,\hat{\pmb\theta}{i},-,\frac{1}{N}\sum{j,=,1}^{N}\hat{\pmb\theta}_{j},)^{2}

  

用分散度来衡量估计准度有许多优点，因为它来自多次试验，反映了系统的实际特性。但它要求做多次试验，当试验次数较少时无法确定哪次试验的辨识准度更高些。此外,分散度没有考虑估计的偏差，许多情况可能导致围绕不正确估计值而有小的分散度。例如当飞机惯量有偏差时，多次飞行试验求得气动参数的均值就不是正确值，试验所得之分散度是围绕不正确值散布的。  

分散度计算简单，只要有足够的试验数据，就可用来估计辨识准度。  

# 8.2.3 克拉马-罗不等式  

克拉马-罗（Cramer-Rao)不等式是准度估计理论中最重要的结果，它给出参数估计准度可达到的理论极限。在某种意义上，克拉马-罗不等式给出了数据中所含信息量的度量。对于有偏估计  

克拉马-罗不等式为  

\begin{array}{r}{E,{(\hat{\pmb{\theta}},-,\pmb{\theta}{\mathrm{tr}})(\hat{\pmb{\theta}},-,\pmb{\theta}{\mathrm{tr}})^{\mathrm{T}}}\gg\lbrack\pmb{I},+,\pmb{\nabla}{\theta{\mathrm{tr}}}b(\pmb{\theta}{\mathrm{tr}})\rbrack\pmb{M}^{-1}(\pmb{\theta}{\mathrm{tr}})\times}\ {\lbrack\pmb{I},+,\pmb{\nabla}{\theta{\mathrm{tr}}}b(\pmb{\theta}_{\mathrm{tr}})\rbrack^{\mathrm{T}}\qquad\qquad(8\

  

式中 $\nabla_{\theta_{\mathfrak{n}}}\pmb{b}(\pmb{\theta}_{\mathfrak{n}_{\tau}})$ ——估计的偏差对参数真值的一阶梯度；  

$M$ ——信息矩阵。  

对于无偏估计， $b\left(\,\pmb\theta_{\mathrm{tr}}\right)=0$ ,式(8-3)化成  

E\left{(\hat{\pmb{\theta}}-\pmb{\theta}{\mathrm{tr}})(\hat{\pmb{\theta}}-\pmb{\theta}{\mathrm{tr}})^{\mathrm{T}}\right}\gg\pmb{M}^{-1}(\pmb{\theta}_{\mathrm{tr}})

  

式（8-4)表明，参数估计值与真值之方差总是大于信息矩阵之逆，只当信息阵无穷大时，才可能充分接近真值。还可以定义使式(8-4)的等号成立的估计器为有效估计器,并证明了若有效估计存在的话,此估计器即为最大似然估计。可以证明,在某些条件下，最大似然估计对于动力学系统是渐近有效的，也就是说，当试验的数据足够多时，式（8-4）的等式成立。经验证明，只要数据含有系统的最大固有周期的几倍长的数据，式(8-4)的等号就接近成立。因此式（8-4)是最大似然参数估计准度的最好度量。在参数估计时， $\pmb\theta_{\mathrm{r}}$ 是未知的，故以 $\hat{\pmb{\theta}}$ 代替 $\pmb\theta_{\mathrm{{tr}}}$  

信息矩阵 $M$ 可由下式计算  

M(,\pmb{\theta}{\mathrm{tr}}),=E,{,[,\pmb{\nabla},{\pmb{\theta}{\mathrm{tr}}}\ln\hat{p},(,\pmb{y}{1},,\pmb{y}{2},,\cdots,\pmb{y}{N},|,\pmb{\theta}),],\times

\big[;\nabla_{\theta_{\mathrm{tr}}}^{\mathrm{T}}!\ln\rho,(,\pmb{y}{1},,\pmb{y}{2},,\cdots,\pmb{y}_{N},|,\pmb{\theta},\big],\big}

  

式中 $\boldsymbol{\rho}\left(\,y_{1}\,,y_{2}\,,\cdots,y_{N}\,|\,\pmb{\theta}\,\right).$ -条件概率密度。  

由式(8-5)给出的信息矩阵的形式不便于计算,在 $\phi\left(\,\mathbf{y}_{1}\,,\,\mathbf{y}_{2}\,,\,$ $\cdots,y_{N}\left|\,\pmb\theta\,\right>$ 充分光滑的假设下，可导出  

{\pmb{M}}(,{\pmb\theta}{\mathrm{tr}});=-;E,{,{\pmb\nabla}{,{\pmb\theta}{\mathrm{tr}}}^{,2}\ln\phi,(,{\pmb y}{1},,{\pmb y}{2},,\cdots,{\pmb y}{N},|,{\pmb\theta},),}

  

对于飞行器非线性系统模型（见第5章），信息矩阵 $\pmb{M}$ 可由下式 $\pmb{H}$ 近似  

\pmb{H}\ =\ \sum_{i=1}^{N}\left(\frac{\partial\pmb{\nu}}{\partial\pmb{\theta}}\right)^{\top}\pmb{B}{i}^{-1}\left(\frac{\partial\pmb{\nu}}{\partial\pmb{\theta}}\right)\approx\ \pmb{\nabla}{\pmb{\theta}{\mathrm{tr}}}^{2}J\left(\pmb{\theta}{\mathrm{tr}}\right)

  

当系统的过程噪声分布矩阵为零，观测噪声分布阵已知时， $\pmb{H}$ 是信息矩阵的 $M$ 的精确表达，否则 $\pmb{H}$ 是信息矩阵 $M$ 的很好的近似。  

# 8.2.4 不确定度椭球  

不确定度椭球是基于克拉马-罗不等式所导出的参数的置信度区间,定义为  

(,\pmb\theta,-,\hat{\pmb\theta},)^{\intercal}{\pmb M}(,\hat{\pmb\theta},)(,\pmb\theta,-,\hat{\pmb\theta},),=,1

  

或由 $\pmb{H}$ 近似 $M$ ，有  

(,\pmb\theta,-,\hat{\pmb\theta},)^{\mathrm{T}}{\cal H}(,\pmb\theta,-,\hat{\pmb\theta},),=,1

  

此椭球基于一一次试验数据给出了参数估计分散度区域的形式和大小的理论预测，不需做大量重复性试验，是辨识准度很好的预测方法。一维及二维不确定度椭球可较直观地显示参数估计可能的散布形式。  

# 8.3 估计准度评价的简化算法  

不确定度椭球是估计准度的良好预测方法，但对于多参数估计，椭球维数高，无法直观显示。为了评价各个参数的估计准度，基于不确定椭球，导出了几种准度评价的简化算法。  

# 8.3.1 灵敏度  

灵敏度表示判据函数 $J$ 相对于待估参数变化的敏感程度，因为 $\partial J(\partial)/\partial\pmb{\theta}=\mathbf{0}$ ,故以 $\partial^{2}J/\partial\pmb{\theta}^{2}$ 度量之。灵敏度的倒数称为不灵敏度。不灵敏度代表当系统的参数中仅有一个参数变化时， $J$ 对该参数变化的不敏感区域。从不确定度椭球的定义可知，当参数在不确定度椭球内变化时， $J$ 是不敏感的。当 $\pmb\theta_{i}$ 变化时，只要 $\pmb\theta_{i}$ 是在不确定度椭球与 $\pmb{\theta}_{i}$ 轴的截距内， $J$ 是不敏感的。不确定度椭球与$\pmb\theta_{i}$ 轴的截距为 $(\sqrt{M_{i i}})^{-1}$ ,或近似为 $(\sqrt{H_{i i}})^{-1}$ ，故不灵敏度 $S_{i}$ 为  

S_{i};=;\theta_{i};-;\hat{\theta}{i}\leqslant(\sqrt{M{i i}},)^{,-,1}

  

或  

S_{i};=;\theta_{i};-;\hat{\theta}{i}\leqslant(\sqrt{:H{i i}},)^{,-1}

  

其几何解释如图8-1所示， $C$ 表示常数， $J\left(\theta\right)$ 为极大似然准则函数。当同时估计多个参数时，参数间的相关性使不灵敏度不能再作为精度评价的指标。它通常只适用于一维系统。  

![](images/7421820d7bf17e33f7967a97e9b1cc276a678e404fe244666cd925e34901940c.jpg)  
图 8-1 不灵敏度的几何解释  

# 8.3.2 相关性  

两个待估参数 $\theta_{i}$ 和 $\theta_{j}$ 间的相关性定义为  

r_{i j},=,\frac{E,{,(\hat{\theta}{i},-,\theta{\mathrm{tr}}),(\hat{\theta}{i},-,\theta{\mathrm{tr}})}{\sqrt{E,{,(\hat{\theta}{i},-,\theta{\mathrm{tr}})^{2},},E,{,(\hat{\theta}{j},-,\theta{\mathrm{tr}})^{2},}}}

  

它是协方差矩阵的非对角元由相应的对角元正则化的结果。对极大似然参数估计，可近似用下式计算  

r_{i j};=;(M^{-1}){i j}\big/,\sqrt{(M^{-1}){i i}(M^{-1})_{j j}}

  

或  

r_{i j};=;\big(,H^{-1},\big){i j}\big/,\sqrt{\big(,H^{-1},\big){i i}\big(,H^{-1},\big)_{j j}}

  

若将各未知参数的灵敏度缩尺变换到数值相等，则相关性就相当于不确定椭球的偏心率。相关性 $r_{i j}$ 越接近1,缩尺后的不确定椭球越扁平。两个参数相关性越接近1，它们的相关性越大，就越难将它们同时分别辨识出，所以相关性是衡量辨识准度的一个指标。但相关性却存在下列缺点：  

（1）相关性只反映了两个参数间的相关程度，而不能显示多个参数间同时存在高相关的情况，多个参数同时存在高相关时，相应参数是不可同时单独辨识的。  

(2）相关性只反映了不确定度椭球的形状，而没有反映其大小。  

（3）参数的相关性难以直观地显示。  

（4）在某些情况下，好的估计可能有高相关。而坏的估计可以有低相关。  

例如当某不确定度椭球全部位于另一不确定度圆球之内时（见图8-2），就出现了相关性大的反而辨识准度高的情况。所以相关性可作为辅助精度评价指标。  

![](images/b090c20947747c085cd05cfe1ad492dd0a98acee5ae74538a819acc2a4124fd9.jpg)  
图 8-2相关性的几何解释  

# 8.3.3 克拉马-罗界  

克拉马-罗界是基于不确定度椭球导出的。第 $_i$ 个参数的克拉马-罗界定义为  

C_{i},=,\sqrt{(,M^{-1},){,i i}},\leqslant,\theta{i},-,\hat{\theta}_{i}

  

或  

C_{i};=;\sqrt{;(,H^{-1},){,i i}^{\phantom{-1}}},\leqslant,\theta{i};-;\hat{\theta}_{i}

  

此准度评价准则也可定义为标准偏差或估计方差（它是克拉马-罗界的平方）。克拉马-罗界与不灵敏度有些相似，就计算而言，克拉马-罗界是 $\sqrt{(M^{\cdots1})_{i i}}$ ,不灵敏度是 $\sqrt{\,(M_{i i})\:-1}$ ;就几何关系而言，不灵敏度 $\sqrt{(M_{i i})\textsuperscript{-1}}$ 是保持其他参数不变的条件下,求椭球的最大 $\mid\theta_{i}-\hat{\theta}_{i}\mid$ ；而克拉马-罗界却对其他参数不做其他限制，求不确定椭球的最大 $\{\,\theta_{i}\,-\,\hat{\theta}_{i}\,\}$ 。两者间的差异见图8-3， $C$ 表示常数：  

![](images/ab914594c2dbd3afce096b24b0a6a62ecef7d78fb5085dffeee567d26ba09a4c.jpg)  
图8-3克拉马-罗界与不灵敏度的差别  

克拉马-罗界可同时反映不确定度椭球的形状和大小，对每一个待估参数只用一个参数来描述其估计准度，且对每一次试验都可预测其辨识准度。所以它是参数辨识准度的最好的理论预测。通常在参数估计时，同时给出估计值及其对应的克拉马-罗界，以表示估计值的可信度。应注意的是灵敏度及相关性判据在分析辨识准度时也是有用的。  

# 8.3.4 修正的克拉马-罗界  

克拉马-罗界是准度预测的方法，这已为飞行器参数辨识的大量数字仿真所证实。但是对飞行试验实测数据的参数辨识实践却表明[2\~5},重复多次飞行试验所得参数估计结果的方差却比克拉马-罗界高5倍 $\sim\!10$ 倍。究其原因，主要是由于估算克拉马-罗界时假定了噪声是平均分布于直至奈奎斯特频率的白色噪声，而对飞行器参数辩识有重要影响的噪声却是局限于低频区域的有色噪  

278  

声。噪声特性之差导致 $\pmb{\hat{\theta}}$ 的真实方差与克拉马-罗界之比值为奈奎斯频率与系统截止频率之比，约为 $5\!\sim\!10$  

鉴于上述分析，引出修正克拉马-罗界为  

C_{i};=;k;\sqrt{(,M^{-1},){,i i}};\leqslant;\theta{i};-;\hat{\theta}_{i}

  

或  

C_{i};=;k;\sqrt{(,H^{-1},){;i i}};{\leqslant;\theta{i};-;\hat{\theta}_{i}

  

式中 $k$ ——修正因子。  

修正因子可以凭经验取为 $5\!\sim\!10$ 间的一个常数；或者严格地通过残差的谱分析确定系统的截止频率 $B$ 。折中的办法是选用截止频率2倍 $\sim3$ 倍于系统自然频率的简单的单极点滤波器，以滤波残差的功率除以滤波器的截止频率，求得接近和低于系统自然频率区域的平均功率谱密度,以获取修正因子[2]。修正因子计算含有人为因素，只是真实克拉马-罗界的近似。  

# 8.4 参数的置信区间估计  

参数置信区间是参数估计准度的一种统计评价方法。参数的估计值是-个统计量，其准度估计也是个统计量。若被估参数的真值为 $\pmb\theta_{\mathrm{tr}}$ ，它落人估计值 $\pmb{\hat{\theta}}$ 邻域 $\left[\,\hat{\pmb{\theta}}-\Delta\pmb{\theta}_{1}\,,\hat{\pmb{\theta}}+\Delta\pmb{\theta}_{2}\,\right]$ 的概率为 $\xi$ 则定义 $[\,\hat{\pmb{\theta}}-\Delta\pmb{\theta}_{1}\,,\hat{\pmb{\theta}}+\Delta\pmb{\theta}_{2}\,]$ 为置信水平 $\xi$ 条件下，估计值 $\pmb{\hat{\theta}}$ 的置信区间。其数学表达式可记为  

p\left(,\hat{\pmb{\theta}};-;\Delta\pmb{\theta}{1},\ll,\pmb{\theta}{\mathrm{tr}}\ll,\hat{\pmb{\theta}};+;\Delta\pmb{\theta}_{2},\right);=;\pmb{\xi}

  

式(8-19)的物理意义是:参数真值 $\pmb\theta_{\mathrm{tr}}$ 落于随机区间 $\{\,\hat{\pmb{\theta}}\mathrm{~-~}\Delta\pmb{\theta}_{1}\,,\,\hat{\pmb{\theta}}\mathrm{~+~}$ $\Delta\pmb{\theta}_{2}\rbrace$ 的概率为 $\xi$  

置信区间估计综合了方差和置信水平的信息，可提供完整的参数估计准度的描述，是参数估计精度与可靠性的很好的度量方法[6)。区间估计给出了参数估计的精度,而置信度(水平)则表明了估计的可靠性[7]。根据置信区间(或置信区域)的定义,对于复合假设检验，似然率是一个很有用的统计量。  

# 8.4.1 线性系统置信区间估计  

以单输出线性回归方程为例推导置信区间估算公式，结果可推广用于一般线性系统。线性回归模型可表示为  

\pmb{y}=\pmb{X}\pmb{\theta}+\pmb{\varepsilon}

  

式中 $\theta\mathrm{\longrightarrow}\,\theta$ 维矢量；  

$\mathbf{y}\longrightarrow N$ 维矢量，代表变量 $y$ 的 $\boldsymbol{\cdot}$ 个采样值；  
$X{\mathrm{--}}\,N\times\,p$ 维回归矩阵。  

若 $\pmb{y}$ 服从正态分布 $N(\,{\cal X}\theta\,,I\sigma^{2})$ ，考虑假设检验为  

\begin{array}{r}{\pmb{H}{0}:\pmb{\theta}{\mathrm{tr}};=;\pmb{\theta}}\ {\pmb{H}{1}:\pmb{\theta}{\mathrm{tr}};\neq\pmb{\theta}}\end{array}

  

按输出误差法， $\pmb\theta$ 和 $\hat{\pmb\theta}$ 的似然准则函数 $J(\pmb\theta)\setminus J(\hat{\pmb\theta})$ 为  

\begin{array}{r}{J(\pmb\theta),=,(,\pmb y,-,\pmb X\pmb\theta)^{\mathrm{T}}(,\pmb y,-,\pmb X\pmb\theta)}\ {J(\pmb\theta),=,(,\pmb y,-,\pmb X\hat{\pmb\theta},)^{\mathrm{T}}(,\pmb y,-,\pmb X\hat{\pmb\theta},)}\end{array}

  

由式（8-23）和式（8-24）可得  

J\left(,\pmb\theta,\right);-;J\left(,\hat{\pmb\theta},\right);=;\left(,\pmb\theta;-;\hat{\pmb\theta},\right)^{\intercal}\pmb X^{\intercal}\pmb X(,\pmb\theta;-;\hat{\pmb\theta},)

  

定义似然率 $\lambda$ 为  

\lambda;=;\exp\bigg{-;\frac{1}{2\sigma^{2}}\big[J(\pmb\theta);-;J(\pmb\theta);\bigg}

  

可以证明[8],若 ${\pmb\varepsilon}\!\simeq\!N(0,I\sigma^{2})$ ,则有  

\hat{\pmb{\theta}}\simeq\cal{N}(\pmb{\theta},\pmb{X}^{\mathrm{T}}\pmb{X}\sigma^{2})

J(\hat{\pmb{\theta}})\simeq\sigma^{2}\chi_{,N-\hat{p}}^{2}

J(,\pmb\theta,),-,J(,\pmb\theta,)\simeq,\sigma^{2},\chi_{,p}^{2}

  

（4）当 $\boldsymbol{{J}}(\hat{\pmb{\theta}})$ 与 $J(\pmb\theta)-J(\hat{\pmb\theta})$ 相互独立时，有  

\frac{J(\pmb\theta),-,J(\pmb\theta)}{J(\pmb\theta)},\frac{N,-,\phi}{\phi}\simeq F_{\alpha_{p}}(,\rho,,N,-,\rho,)

  

故置信区间可由下式给出  

J(,\pmb\theta,),-,J(,\hat{\pmb\theta},)\leqslant\beta S^{2}F_{a_{\rho}}(,\rho,,N,-,\rho,)

  

式中 $S^{2}=J(\hat{\pmb{\theta}}\,)/(\,N-\,p\,)$  

$\alpha_{\hat{\rho}}$ 一一置信水平。  

将式（8-24）代人式（8-31）得置信度椭球  

(,\pmb\theta,-,\hat{\pmb\theta},)^{\mathrm{T}}(,{\pmb X}^{\mathrm{T}}{\pmb X},)(,{\pmb\theta},-,\hat{\pmb\theta},)\leqslant,\beta S^{2},F_{a_{p}}(,{\pmb\phi},,N,-,\hat{p},)

  

式(8-32)在 $\pmb{\hat{p}}$ 维参数空间定义了一个以 $\hat{\pmb{\theta}}$ 为中心的椭球,真值 $\pmb\theta_{\mathfrak{v}}$ 含于该椭球的概率为 $1-\alpha_{\rho}$ 。  

史卫普(F.C.Schweppe)还进一步证明了[9,当且仅当参数的真值处于椭圆的平行切平面的所有切点之间时，参数的真值才处于椭球内。这意味着参数真值 $\boldsymbol{\theta}_{\mathrm{tr}}$ 处于下列置信区间的概率为$1^{\mathrm{~-~}}\alpha_{\phi}$  

\pmb{\hat{\theta}}\mid-\sqrt{k}\pmb{\sigma}{\theta}<\pmb{\theta}{\mathrm{tr}}<\pmb{\hat{\theta}}\mid+\sqrt{k}\pmb{\sigma}_{\theta}

  

式中  

\begin{array}{c}{{k;=;\displaystyle{\beta F_{\alpha_{\beta}}(,\rho,,N\mathrm{\boldmath~-~},!!!p,)}}}\ {{\sigma_{\vartheta_{i}};=;\displaystyle{\cal S,}\sqrt{(,H^{-1},)_{,i i}}}}\end{array}

  

或  

\sigma_{\theta_{i}},=,S,\sqrt{(,M^{-1},)_{,i i}}

  

比较式（8-33）与式（8-35）可见，参数估计的置信区间与克拉马-罗界都与信息矩阵之逆的平方根成正比。两者仅相差比例因子 $S\,\sqrt{k}$  

# 8.4.2 非线性系统置信区间估计  

非线性系统可以通过线性化，而直接应用式（8-31）来近似确定局部置信区间  

\begin{array}{c}{{J(\pmb{\theta})-J(\pmb{\hat{\theta}})\approx(\pmb{\theta}-\pmb{\hat{\theta}})^{\mathrm{T}}\bigg(\frac{\partial^{\mathrm{T}}\pmb{\nu}}{\partial\pmb{\theta}^{\mathrm{T}}}\frac{\partial\pmb{\nu}}{\partial\pmb{\theta}}\bigg)(\pmb{\theta}-\pmb{\hat{\theta}})\leqslant}}\ {{p S^{2}F_{a_{\rho}}(\pmb{\rho},N-\pmb{\rho})}}\end{array}

  

式中 $\frac{24}{36}-$ 灵敏度矩阵。  

但实际应用表明式（8-37）的置信区间估计并不理想。比尔  

(E.M.L.Beale){10]提出非线性修正因子的算法，令  

J\left(,\pmb\theta,\right),-,J\left(,\hat{\pmb\theta},\right),=,,\beta S^{2},F_{{a{p}}}!\left(,\hat{,p},,N,-,\hat{,p},\right)\left(,1,+,\frac{N\left(,\hat{,p},+,2\right)}{\left(,N,-,\hat{,p},\right),\hat{p}}N_{\varphi}\right)

  

对于多输出情况，有  

J\left(,\pmb\theta,\right);-;J\left(,\hat{\pmb\theta},\right);=;\rho S^{2},F_{\alpha_{\rho}}^{\phantom{2}}\left(,\rho,,N m,-,\rho,\right)\left(1,+,\frac{N m\left(,\rho,+,2\right)}{\left(N m,-,\rho,\right),\hat{p}}N_{\varphi}\right)

  

式中 m—输出矢量的维数；  

$N$ 一一一数据采样总点数；$S^{2}=J(\hat{\pmb{\theta}})/(\,N m\,-\,p\,)_{\circ}$  

非线性修正因子 $N_{\varphi}$ 是对接近 $J\left(\hat{\pmb{\theta}}\right)$ 的解轨迹的非线性度量， 下节给出具体算式。  

由式（8-38）所定义的置信轮廓不能像线性情形那样清晰地确定，因为它的形状不一定是椭球，可能是极不规则的，而且可能有几个局部和全局极小点。  

# 8.4.3 非线性因子估计算法  

本节给出非线性因子 $N_{\varphi}$ 的估计算法，对于多变量的飞行器动力学系统辨识，它是一个非线性的经验度量方法，但也是个有效算法。  

设 $P(\pmb\theta)$ 代表样本空间的一解轨迹，当 $\pmb{\hat{\theta}}$ 是参数空间中使似然准则函数 $J$ 取极小值的点时， $P(\hat{\pmb{\theta}})$ 是解轨迹上最接近测量点$Y(\,\pmb{y}_{1}\,,\pmb{y}_{2}\,,\cdots,\pmb{y}_{N}\,)$ 的点。对于线性估计问题，样本空间的解轨迹是个平面；对于非线性估计问题，解轨迹是个曲面。定义 $T(\pmb\theta)$ 为在$P(\pmb\partial)$ 处 $P(\pmb\theta)$ 的切平面，显然 $P(\theta)$ 与 $T(\pmb\theta)$ 的距离是系统非线性程度的度量。粗略地,取 $\hat{\pmb{\theta}}$ 邻域 $\pmb{W}$ 个 $\pmb\theta$ 值的 $P(\theta)$ 与 $T(\pmb\theta)$ 的距离平方和作为非线性度量  

Q_{\varphi};=;\sum_{\omega;=;1}^{\Psi};|;P(;\pmb\theta_{\omega},);-;T(;\pmb\theta_{\omega},);|;^{2}

  

$Q_{\varphi}$ 随W值加大而加大,且与 $\pmb\theta_{\omega}$ 的位置选取有关,不反映非线性固有特性。为消除此影响,比尔(E.M.L.Beale)建议用 $P\left(\,\pmb\theta_{\omega}\,\right)$ 到$P(\hat{\pmb\theta})$ 的平方距离的平方和 $D$ 加以正则化。  

D;=;\sum_{\omega;=;1}^{w};\vert;P(;\pmb\theta_{\omega};);-;P(;\hat{\pmb\theta};);\vert^{;4}

  

正则化后的 $Q_{\varphi}$ 记为 $N_{\varphi}$  

N_{\varphi};=;\rho S^{2}Q_{\varphi}/D

  

$N_{\varphi}$ 虽然排除了采样点数 $\pmb{W}$ 和 $P(\pmb\theta_{\omega})$ 与 $P(\pmb\{\hat{\theta}})$ 的距离的影响，但仍然依赖于 $\pmb{\theta}_{\omega}$ 的取值。 $P(\pmb\theta_{\omega})$ 与 $T\left(\,\pmb\theta_{\omega}\right)$ 的联线并不垂直于切平面 $T(\pmb\theta)$ 。为获得固有非线性,计算 $Q_{\varphi}$ 时应取 $P(\pmb\theta_{\omega})$ 与其垂足$T(\pmb{\theta}_{\omega_{1}})$ 的距离,它相应于 $Q_{\varphi}$ 的极小值记为 $Q_{\varphi}$ ,故反映系统固有非线性特性的非线性因子可取为 $\hat{N}_{\varphi}$ 。  

\hat{N}{\varphi};=;\rho S^{2}\hat{Q}{\varphi}/D

  

对于飞行器非线性动力学系统参数辨识，在样本空间的切平面 $T(\pmb\theta)$ 上有  

\small\textbf{y}(\pmb{\theta}{\omega{1}});=;\pmb{y}(\hat{\pmb{\theta}}),+,\frac{\partial,\mathbf{y}}{\partial\pmb{\theta}}(\pmb{\theta}{\omega{1}}-\hat{\pmb{\theta}})

  

当系统数学模型和试验数据给定时， $\hat{\mathbf{Q}}_{\varphi}$ 可近似表示为  

\begin{array}{c}{{\displaystyle\hat{Q}{\varphi},=,\sum{\omega^{=1}}^{\overline{{\nu}}},\sum_{i=1}^{N},[,y_{i}(,\pmb{\theta}{\omega}),-,y{i}(,\pmb{\theta}{\omega{1}},),]^{\mathrm{T}}{\pmb{B}}^{-1},[,y_{i}(,\pmb{\theta}{\omega}),-,y{i}(,\pmb{\theta}{\omega{1}},),],=}}\ {{\displaystyle\sum_{\omega^{=1}}^{\overline{{\nu}}},\sum_{i=1}^{N},\Big[,\delta y_{i},-,\frac{\partial,y_{i}}{\partial\pmb{\theta}}(,\pmb{\theta}{\omega},-,\hat{\pmb{\theta}},),\Big]^{\mathrm{T}}{\pmb{B}}^{-1},\Big[,\delta y{i},-,\frac{\partial,y_{i}}{\partial\pmb{\theta}}(,\pmb{\theta}_{\omega},-,\hat{\pmb{\theta}},),\Big]}}\end{array}

  

式中  

\delta\mathbf{y}{i};=;y{i}\left(,\pmb{\theta}{\omega},\right);-;y{i}\left(,\pmb{\hat{\theta}},\right)

  

对于给定的 $\pmb{\hat{\theta}}$ 和 $\pmb{\theta}_{\omega}$ ,式(8-45)仅有W个未知量 $\pmb{\theta}_{\omega_{1}}$ ，它们满足 使 ${\hat{Q}}_{\varphi}$ 达极小值的条件  

\partial,\hat{\bf Q}{\varphi}/\partial,\pmb{\theta}{\omega_{1}},=,0\qquad(,\omega;=;1,,2,,\cdots,W,)

  

求解式（8-47）得  

\pmb\theta_{\pmb\omega_{1}};=;\hat{\pmb\theta};+;\biggl(,\sum_{i=1}^{N};\frac{\partial^{\top}{\pmb y}{i}}{\partial\pmb\theta}\pmb B^{-1};\frac{\partial{\pmb y}{i}}{\partial\pmb\theta}\biggr)^{-1},\biggl(,\sum_{i=1}^{N};\frac{\partial^{\top}{\pmb y}{i}}{\partial\pmb\theta}\pmb B^{-1},\delta{\pmb y}{i},\biggr)

  

相应地， $D$ 可由下式算得  

D;=;\sum_{\omega,=,1}^{\cal W},|,\sum_{i,=,1}^{\cal N},[,y_{i},(,\pmb\theta_{\omega},),-,y_{i},(,\hat{\pmb\theta},),]^{\mathrm{T}}\pmb{B},^{-1}[,y_{i},(,\pmb\theta_{\omega},),-,y_{i},(,\hat{\pmb\theta},),],}^{2}

  

以上给出了近似计算系统非线性因子的全部算式。具体计算步骤为：  

（1）在动力学系统辨识求得参数估计值 $\pmb{\hat{\theta}}$ 之后，在 $\pmb{\hat{\theta}}$ 邻域选取W个 $\pmb{\theta}_{\omega}$ 值；  

(2）由式(8-46)计算8yi 取参数辨识收敛时的灵敏度计算结果， $B$ 为辨识收敛时的新息协方差矩阵；  

(3）利用式(8-48)求出0; (4）由式(8-49)计算 $D$ ： (5）由式(8-45)计算 $\hat{Q}_{\varphi}$ (6）用式(8-43)计算非线性因子 $N_{\varphi}\,.$  

非线性因子 $N_{\varphi}$ 的大小表明了估计问题非线性的强弱，也表明了对 $J$ 做二次近似的好坏。若 $N_{\varphi}$ 的值较小，表明估计问题的非线性较弱，则对损失函数 $J$ 做二次近似是充分的，克拉马-罗界是较好的准度评价方法；否则克拉马-罗界不能作为准度评价方法，必须计算估计问题的置信区间。  

# 8.5 准度的工程判断  

工程判断是最古老的估计可靠性的评价方法，尽管前面述及的理论精度评价方法已经存在，但由于飞行器非线性系统的复杂性及试验条件、外界环境的非理想性，任何理论的评价方法都必须经过基于经验及实践的工程判断的检验，否则所得结果的可靠性仍难于保证。  

判断估计精度的最基本因素是先验知识。研究者根据以往的经验、参数相对重要性的程度、线性相关性、获取数据的质量等因素，可以预期参数估计的准度。通常根据地面试验及理论计算，可以确定待估参数应处于某一范围内，若估计结果严重偏离这一范围，则估计结果就可能是不正确的。此外，建模误差可能导致估计算法和理论精度评价方法无效。  

测量和估计时间历程的拟合程度也是工程判断的重要组成部分。建模误差、传感器故障以及数据处理误差等都可通过拟合曲线显示出来。  

总之，工程判断必须依据所有的理论预测及经验信息，综合地对估计结果加以判断，以便获取正确的参数准度估计。  

# 8.6系统验证  

由前面几节的讨论可见，飞行器系统是一个极其复杂的非线性系统，受多种因素的影响，目前就飞行器参数辨识的准度评价来说，任何单一的准度评价方法都难以对估计结果的准度进行精确评价，必须同时采取多条途径，多个准度评价方法的综合比较和验证，才能得到可信的结果。  

工程判断、估计的分散度、克拉马-罗界或置信区间估计是较好的准度评价方法，只要条件允许，就应同时采用这些方法进行参数的准度评价，而且准度评价结果不应有大的差异，古则结果是不可信的。  

不论是动力学系统参数辨识，还是系统结构参数辨识，都应将理论计算结果、估计结果和实物试验结果综合在一起进行分析，只有当参数辨识结果、理论计算结果和地面缩比直接测量结果相一致时，才可确认辨识所得模型和参数估计值是正确的。  

理论计算、系统辨识和实物缩比模型直接试验各有其局限性，  

# 不可偏信任何一一方，只有三大手段较为一致的综合分析结果才是可信的结果[1]  

# 参考文献  

1 Balakrishnan A V. Communication Theory. Mc Graw-Hil Book Co., 1968   
2 Maine R E, Iliff K W. The Theory and Practice of Estimating the Accuracy of Dynamic Flight-Determined Coefficients. NASA RP-1077, 1981   
3  Klevin V. Determination of Stability and Control Parameter of a Light Airplane from Flight Data Using Two Estimation Methods. NASA TP-1306, 1979   
4  Iliff K W, Maine R E. Practical Aspects of Using a Maximum Likelihood Estimation Method to Extract Stability and Control Derivatives from Flight Data. NASA TND8209,1976   
5 Maine R E, lliff K W. Use of Cramer-Rao Bounds on Flight Data with Colored Residuals. J. Guidance, Control and Dynamics, 1981, 4(2): 207\~213   
6  Murphy P C, Klein V. Maximum Likelihood Algorithm Using an Efficient Scheme for Computing Sensitivities and Parameter Confidence Intervals. AIAA 84-2084, 1984   
7李惕碚．实验的数学处理．北京：科学出版社，1980   
8  Draper N R, Smith H. Applied Regression Analysis. John Wiley & Sons, Inc. , Second Edition, 1981   
9  Schweppe F C. Uncertainty Dynamic Systems. Prentice-Hall, Inc. , 1973   
10  Beale E M L. Confidence Regions in Nonlinear Estimation. J. of Royal Statistical Society, Ser. B, 1960, 22(1): 41\~88   
11蔡金狮．飞行器系统辨识．北京：宇航出版社，1994  

# 第9章试验数据预处理及相容性检验  

9.1概述  

飞行器系统本身及飞行环境条件的复杂性，传感器和数据采集系统的非理想性，飞行试验设计的不完善等众多因素的影响，不可避免地使飞行实测数据中含有确定性误差和随机误差,这些误差将使参数估计有一定的偏差，甚至使估计过程发散或收敛到错误值。因此在采用飞行实测数据辨识前，必须对实测数据进行预处理和数据相容性检验，目的在于尽可能消除实测数据中的各种噪声和系统误差，以提高辨识结果的准确度。  

数据预处理包括：数据从电量到物理量的转换；数据野值的识别、剔除与补正；数据加密与采样时刻校正；传感器安装位置校正；数据平滑与微分平滑；数据时间迟后修正；滤除高频噪声等。  

数据相容性检验主要功能是将数据中的常值误差，特别是零位漂移误差，辨识出来并重新建立没有常值误差的试验数据。  

试验数据预处理的另一重要内容，就是要根据先验知识和理论方法对候选数学模型中的各待辨识系数进行可辨识性分析，同时给出待估参数的初估值。  

# 9.2 飞行试验数据的预处理  

飞行试验数据测量是个复杂的遥测过程。首先需将传感器所敏感的被测状态参数从物理量转化为电量，冉经过放大、编码记录、调制、发射、接收、解调以及由电量转化为物理量。整个过程的各个环节都可能引进测量误差。例如，传感器的动态误差，机电转换过程中的零位误差、摩擦、分辨率，数字传输过程的高频线路干扰、间歇工作、噪声、模/数变换器的串行采样、各参数采样速率和采样时刻的差别等等。因此，飞行试验数据用于参数辨识之前，应进行数据误差修正，尽可能消除各种测量误差是很必要的。  

数据预处理主要包括以下几个方面：数据分组与提取，数据从电量到物理量的转换，野值的识别、剔除和补正，数据加密与采样时刻校正，传感器安装位置校正，数据平滑，数据时间延迟修正，滤除高频噪声等等；还可进行动力学系统参数的信息量和可辨识性分析；对飞行试验数据进行数值微分，为参数辨识做好准备。  

# 9.2.1 测量数据由电码到物理量的转换  

无线电遥测设备将被测量的电信号以相对电压的形式发送到地面，或记录于机（弹）上磁记录装置并回收，经地面接收设备解调以相对电压的形式输出，相对电压转换到物理量是根据事先测定的校准曲线及标定电平进行的，在换算时应考虑各种因素的变化，作必要的修正。通式如下  

\mathrm{\boldmath~\Psi~}^{\prime},=,P_{0},+,a,+,b K_{c}V_{P}(,\mathcal{K},),+,b V_{s0},-,b K_{c0},V_{P_{0}}(,\mathcal{K},)

  

式中  

$P$ ——测量量的物理量；$P_{0}$ ——测量量的初值；$\alpha\,,b$ 一校准曲线公式化的系数；K-一一因供电方式及校准方法不同而引人的修正系数；$K_{c0}$ 一—零位记录时的修正值；$V_{s0}$ -—校准曲线的电位零位；  

Vp(%），Vp（%)——飞行记录、零位记录的判读值。  

设某物理量 $\omega$ 的最大正值为 $\omega_{\mathrm{\,max}}$ ,最小负值为 $\omega_{\mathrm{min}}$ 。在地面标定时， $\omega_{\textrm{\tiny m a x}}$ 对应的电压为 $V_{\operatorname*{max}},\omega_{\operatorname*{min}}$ 对应的电压为 $V_{\mathrm{min}}$ ,零值时对应的电压为Vo;而飞行时wmax对应的电压为Vmmax,零值时对应的电压为 $V_{m0}\,,\omega_{\mathrm{min}}$ 对应的电压为 $V_{m\operatorname*{min}}$ ,那么飞行测得的电压$V_{m}$ 相应于地面标定曲线上的 $V$ 应该是  

V,=,\left{\begin{array}{l l}{\displaystyle{\frac{V_{\mathrm{max}},-,V_{0}}{V_{m\mathrm{max}},-,V_{m0}}}(,V_{m},-,V_{m0}),+,V_{0}}&{(,V\geqslant V_{0})}\ {\displaystyle{\frac{V_{\mathrm{min}},-,V_{0}}{V_{m\mathrm{min}},-,V_{m0}}}(,V_{m},-,V_{m0}),+,V_{0}}&{(,V<V_{0})}\end{array}\right.

  

由于磁带上串行数码给出的是该测量量所对应的电码分层数，故还需要做线性变换，将电码分层数转换成对应的电压。设$V_{m\,\mathrm{nux}}$ 的电码分层数为 $m_{\operatorname*{max}},V_{m0}$ 对应的电码分层数为 $m_{0}$ ，那 $V_{m}$ 对应的电码分层数 $m_{m}$ 满足下式  

\frac{V_{m};-;V_{m0}}{V_{m,\mathrm{max}}};=;\frac{m_{m};-;m_{0}}{m_{,\mathrm{max}}}

  

将式(9-3)代人式(9-2）,求得相应于观测量的电码分层数 $m_{m}$ 的电压值 $V$  

\begin{array}{r l}&{V,=,\frac{{\cal V}{\mathrm{max}},-,{\cal V}{0}}{{\cal V}{m\mathrm{max}},-,{\cal V}{m0}},\cdot,\frac{{\cal V}{m\mathrm{max}}}{m{\mathrm{max}}}(,m_{m},-,m_{0},),+,{\cal V}{0}\quad(,V\geqslant V{0}),\Bigg[}\ &{V,=,\frac{{\cal V}{\mathrm{min}},-,{\cal V}{0}}{{\cal V}{m\mathrm{min}},-,{\cal V}{m0}},\cdot,\frac{{\cal V}{m\mathrm{max}}}{m{\mathrm{max}}}(,m_{m},-,m_{0},),+,{\cal V}{0}\quad(,V<,V{0}),\Bigg]}\end{array}

  

式中 $V_{\mathrm{max}}\,,V_{0}\,,V_{\mathrm{min}}-$ -一从地面标定曲线取值；  
$V_{m\operatorname*{max}}\,,V_{m\operatorname*{min}}\,,m_{0}$ 和 $m_{m}$ 从飞行试验数据获取；  

电码最大分层数 $m_{\operatorname*{max}}$ 已知值。  

由式(9-4)求出 $V$ 值后，可以从标定曲线或相应标定数据表插值求出对应的物理量 $\omega$ 的实测值。  

# 9.2.2 零位修正  

对于倾斜发射的战术导弹，发射角 $\theta_{0}$ 用姿态陀螺测量，因姿态角陀螺开始工作时，陀螺的输出信号为零，故发射角6影响0  

的零位。陀螺输出应为  

\theta_{T};=;\theta_{m};+;\theta_{0}

  

式中 $\theta_{m}$ 测量值；$\theta_{T}$ —修正值。  

# 9.2.3 野值的识别、剔除与补正  

飞行试验过程中，外界干扰和仪器偶然跳动，可能使测量结果出现很不合理的跳点，称之为野值。如果不将野值从试验数据中排除掉，必将歪曲试验结果，用它辨识出来的结果就不正确；但如果将测量数据必然存在的一定的分散度视为野值加以剔除，那辨识出来的结果似乎精度很高，但不真实。所以，需要建立一个正确的准则，剔除真正的野值并加以补正。从统计原理上讲，只要给一个置信度水平（置信概率）和置信区间，凡某点的误差超过这一区间就认为不是随机误差，该点即为野值，应予以剔除。  

对于稳态试验，当试验的采样点足够多时，可以将残差 $v(i)$ 大于三倍标准偏差 $\pmb{\sigma}$ 的值视为野值。当采样点较少时，这个条件太苛刻。曹维尼特（Chauvenet）、格鲁布斯（Grubbs）等提出修正准则，认为残差(i)满足(i)>K（N,α)的测量数据为野值。式中的K$\left(\,N,\alpha\,\right)$ 是采样总点数 $N$ 和置信度 $\alpha$ 的函数，可以查表？得到。  

飞行试验数据是时变数据，观测值的数学期望不能用均值表示，无法直接应用上述修正准则。对于动力学系统的试验数据，可以从动力学系统的状态方程组出发，米用厂义卡尔曼滤波、分割递推算法或最大似然递推算法，根据已有的信息预测卜一个观测值的数学期望，求得其残差来识别野值并加以剔除。这是较理想的方法，但是太复杂，不适用于数据预处理。最简单的方法是采用低阶多项式滑动拟合法来判断和剔除野值。  

为避免后面的野值逆传而误将正常值判断为野值，不能以平均值作为数学期望，只能采用前推差分算式。下列七点二阶算式是合适的。当然如果每个振荡周期有几十个采样点，也可采用更多点的二阶算式来预测下-点的期望值。  

\left{\begin{array}{l l}{\hat{y}{1}=(32y{1}+15y_{2}+3y_{3}-4y_{4}-6y_{5}-3y_{6}+5y_{7})/42}\ {\hat{y}{2}=(5y{1}+4y_{2}+3y_{3}+2y_{4}+y_{5}-y_{7})/14}\ {\hat{y}{3}=(y{1}+3y_{2}+4y_{3}+4y_{4}+3y_{5}+y_{6}-2y_{7})/14}\ {\hat{y}{4}=(-\mathbf{\sigma}{1}+3y_{2}+6y_{3}+7y_{4}+6y_{5}+3y_{6}-2y_{7})/21}\ {\hat{y}{5}=(-2y{1}+y_{2}+3y_{3}+4y_{4}+4y_{5}+3y_{6}+y_{7})/14}\ {\hat{y}{6}=(-\mathbf{\sigma}{1}+y_{2}+2y_{4}+3y_{5}+4y_{6}+5y_{7})/14}\ {\hat{y}{4}=(5y{i-6}-3y_{i-5}-6y_{i-4}-4y_{i-3}+3y_{i-2}+15y_{i-1}+}\ {;32y_{i})/42;;;;;;(i=7,8,9,\cdots,N)}\end{array}\right.

  

按时间顺序逐点计算 ${\hat{y}}_{i}$ 及新息 $v_{i}=y_{i}\leftarrow\hat{y}_{i}\,,$ 。对于野值，其 $\boldsymbol{v}_{i}$ 值远大于正常值。可以采用下列准则，满足下式者为野值  

\mid y_{k},-,\hat{y}{k}\mid>,2,.,2\sqrt{\sum{i,=,k,-,6}^{k}(y_{i},-,\hat{y}_{i})^{2}/6}\equiv E

  

试验数据中可能出现连续跳点，通常连续跳点的值比较靠近，因此，可用下式判断连续跳点。当 $k$ 点是野值，则满足下式的点也是野值  

\vert;y_{k,+,i},-,y_{k},\vert,<,E,\qquad(,i,=,1,,2,,\cdots,m,)

  

为避免将阶跃信号误作为野值剔除，可以取 $m=3$ ，当满足式(9-6)的 $k+\,i>k+3$ 时，则认为 $y_{k}\,,y_{k}+1\,,\cdots,y_{k}+m$ ,都是正常值。  

若已判定 $y_{k}\,,y_{k}+1\,,\cdots,y_{k}+m$ 是野值,则将它们剔除,并采用以yk-3,yk-2,yk-1,yk+m+1,yk+m+2，yk+m+3为已知值的拉格朗日插值公式,求出 $y_{k}\cdot y_{k}+1\cdot\cdots,y_{k}+m$ 的补正值  

y_{l},=,\sum_{\stackrel{j=k-3}{(i,j\ne k,k+1,\cdots,k+m,}}^{k+m+3}!!!\prod_{i,j=k,i\ne j)}^{k+m+3}!!!!!\frac{t_{l},-,t_{i}}{t_{j},-,t_{i}}y_{i},\quad(,l,=,k,,k,+,1,\cdots,k,+,m,)

  

图9-1给出试验数据剔除野值的算例。图中实线是飞行试验的仿真数据，采用式（9-5）～式（9-7）剔除数据中的野值，开用式（9-8）补正，虚线是补正后的数据。  

![](images/a3009c2ec35f0338c47f1d6caea6338e0411c2d435337ff0697dc9669f5e61a6.jpg)  
图 9-1 试验数据野值剔除与补正  

在工程应用上,最简单又实用的剔除野值的办法是将试验数据的时间历程曲线作出来，从曲线图中～目了然地找出野值并加以剔除，然后用拉格朗日内插公式补正之。  

# 9.2.4 试验数据加密与采样时刻校正  

飞行实测数据由于受飞行条件、测量设备及技术上的限制,采样率不可能太高，而气动参数辨识常常要求较高的采样率，有时甚至高达500点/s，因此需要对实测数据进行加密处理。  

地面的光测、雷测和气象测量数据的采样速率，通常远低于飞行器上的测量数据的采样速率，进行参数估计之前可先用拉格朗日插值求出各数据点的速度、高度和密度。通常密度测量较疏,因此插值最好用高度的指数函数进行，会准确些。对于某些动力学系统的试验数据，由于系统的固有频率很高，若采样速度不高，可能出现一个周期只测几个点的现象，这时也可用内插值加密。对于某些情况下的试验数据，由于观测量的幅值相对于峰值很小，可能出现数据的峰值只相应2个～3个电码分层数，从而形成阶梯状数据，这时为改善数据，可以按阶梯上角点数据进行内插，求得各采样点的相应数据。  

稳态风是在地面坐标系测量的，须用下式转换到物体固连坐标系  

\begin{array}{r}{\begin{array}{r l}{u_{w}=}&{u_{w0}{\cos}\phi{\cos}\theta+,v_{w0}{\sin}\phi{\cos}\theta\ -,w_{w0}{\sin}\theta}\ &{v_{w}=\ u_{w0}\big(-,{\sin}\phi{\cos}\phi,+,\cos\phi{\sin}\theta{\sin}\phi,\big),+,v_{w0}\big(\cos\phi\cos\phi,+,\vartriangle}\ &{\qquad,{\sin}\phi{\sin}\theta{\sin}\phi,\big),+,w_{w0}{\cos}\theta{\sin}\phi}\ &{w_{w}=\ u_{w0}\big(\mathrm{sin},\phi{\sin}\phi,+,\cos\phi{\sin}\theta{\cos}\phi,\big),+,\vartriangle_{w0}\big(-,{\cos}\phi{\sin}\phi,+,\vline}\ &{\qquad,{\sin}\phi{\sin}\theta{\cos}\phi,\big),+,\vline}&{w_{w0}{\cos}\theta{\cos}\phi}\end{array}}\end{array}

  

由于记录器的交换子对试验数据是串行采样，每个数据的采样时刻是不词的，两个相邻数据采样的时间差 $\Delta t_{s}$ 为  

\Delta t_{s};=;T_{s}/N_{s}

  

式中 $N_{s}$ --交换子采样数据的总个数：  

$T_{s}$ —一交换子采样所有数据一退所需时间。  

以某数据为中心，以其采样时刻为标准时刻，将周围的数据用拉格朗日插值标准程序插值，求得在统一的采样时刻的测量数值。  

# 9.2.5 传感器安装位置校正  

刚体运动由质心平移运动和绕质心旋转运动两部分组成，在动力学系统状态方程组中的过载是质心处过载，但是过载传感器不可能总装在质心处，安装在非质心处的过载传感器除敏感系统的平移运动，同时还敏感由于刚体旋转运动所引起的附加过载。  

因此，必须将测量的过载数据换算到质心处  

\begin{array}{r}{\left{{n_{x c\theta},=,n_{x m},+,\left[,l_{x x}(,q^{2},+,r^{2}),-,l_{x y}(,p q,+,r^{}),-,l_{x z}(,p r,+,q,)\right]/g,}\right.}\ {\left.{n_{y x\theta},=,n_{y m},-,\left[,l_{y x}(,p q,+,r^{}),-,l_{y y}(,p^{2},+,r^{2}),+,l_{y z}(,q r,-,\bar{p},),]/g,}\right.}\ {\left.{n_{z c\theta},=,n_{z m},+,\left[,l_{z x}(,p r,-,q,),+,l_{z y}(,q r,+,\bar{p},),-,l_{z z}(,\bar{p}^{2},+,q^{2}),]/g,}\right.}\end{array}

  

攻角、侧滑角是物体平移速度与物体纵轴的夹角。攻角、侧滑角传感器通常安装于物体的端点处，它不仅敏感物体的平移速度，同时还敏感由于刚体旋转而产生的附加的局部速度。因此攻角、侧滑角的实测数据必须做旋转效应校正，换算到质心处  

\begin{array}{r}{\left{\alpha_{c g};=;\alpha_{m};+;\left(\left.q x_{a};-;\beta y_{a}\right)\right/V\right.;;}\ {\left.\beta_{c g};=;\beta_{m};+;\left(;-;r x_{\beta};+;\beta z_{\beta}\right)\right/V}\end{array}

  

式中 标“ $c g$ ”—质心处数据；  

下标“ $\pmb{m}$ ” 一实测数据；  

lrrxy、lr—过载传感器 n,安装位置在物体固连坐标系的三个分量， $n_{y}\setminus n_{z}$ 的安装位置由 $l_{y x}\setminus l_{y y}\setminus l_{y z}$ 和$l_{z x}\setminus l_{z y}\setminus l_{z z}$ 表示；$x_{\alpha}\setminus z_{\alpha}$ ——攻角传感器安装位置在 $x\sim z$ 轴的分量；yg、β——侧滑角传感器安装位置在 y、轴的分量;g——引力常数。  

通常过载传感器安装位置与质心位置的纵向偏差远小于 $1\mathrm{m}$ 横向偏差在 $0\,.\,1\mathfrak{m}$ 左右，故多数情况下，此修正量是比较小的，可忽略不计。  

攻角、侧滑角传感器通常安装在机（弹）体的头部，与质心的距离较大，所以攻角、侧滑角的测量数据在运动速度比较低而角速率较高时必须做位置修正。  

# 9.2.6 数据平滑和微分平滑  

在式（9-10）中，过载的质心修正项里含有角加速率。目前，在我国还没有研制出较好的角加速率传感器，角加速率通常由角速  

率数据经数值微分求出。  

研究表明,对含噪声的信号直接微分，一般将导致更高的噪声水平，随着微分阶数的增加，信号的质量变得更差。下列几种方法可以控制误差，保持合理的信噪比：  

（1）使用最小二乘法在感兴趣的点周围用多项式拟合，然后微分多项式。  

（2）采用样条函数拟合数据，之后微分此样条函数。  

（3）对测量数据进行傅里叶变换,如欲计算 $\pmb{n}$ 阶导数，则将变换后数据乘以 $(\}\omega)^{\,n}$ ,去掉高于感兴趣的频率的系数,然后施加逆傅里叶变换，就得到了 $\pmb{n}$ 阶导数。  

（4）采用多项式中心平滑公式来获取微分数据。  

上述 4种方法中的(1)、(2)两种方法较费时间，且要求选择多项式阶数和数据点，较少采用；傅里叶变换具有一定的滤波作用，且易于实现，是很有效的；方法（4）由于简单，因而在实际中常被采用。下面给出多项式中心平滑公式。  

多项式中心平滑公式是最简单和常用的微分平滑公式。所谓中心平滑就是采用奇数点进行平滑，以平滑点为中心点；多项式平滑就是以 $\pmb{n}$ 阶多项式用最小二乘法拟合这些点，然后用拟合所得的多项式求出中心点的平滑值和微分平滑值。首先给出较常用的二、三阶多项式的中心平滑公式。  

三点二阶公式  

\begin{array}{r}{\left{\hat{y}{i}=y{i}\right.}\ {\left.\hat{y}{i}=[\mathbf{\epsilon}-0.5y{i-1}+0.5y_{i+1}]/\Delta t\right.}\end{array}

  

五点二阶公式  

\begin{array}{r}{\left{\hat{y}{i};=;\big[-3\big(y{i-2},+,y_{i+2}\big),+,12\big(,y_{i-1},+,y_{i+1}\big),+,17y_{i}\big]/35\right.}\ {\quad\hat{y}{i};=;\big[2\big(,y{i+2},-,y_{i-2},\big),+,1\big(,y_{i+1},-,y_{i-1}\big),\big]/\big(10\Delta t,\big)}\end{array}

  

五点三阶公式  

\begin{array}{r}{\left{\hat{y}{i};=;\big[-;3\big(,y{i-2},+,y_{i+2},\big),+,12\big(,y_{i-1},+,y_{i+1},\big),+,17y_{i},\big]/35\right.}\ {\quad\hat{y}{i};=;\big[,-,\big(,y{i+2},-,y_{i-2},\big),+,8\big(,y_{i+1},-,y_{i-1},\big),\big]/(12\Delta t,)}\end{array}

  

七点二阶公式  

\left{\begin{array}{l}{\hat{y}{i}=\big[-2\big(y{i-3}+y_{i+3}\big)+3\big(y_{i-2}+y_{i+2}\big),+}\ {\qquad\quad6\big(y_{i-1}+y_{i+1}\big)+7y_{i}\big]/21}\ {\hat{y}{i}=\big[3\big(y{i+3}-y_{i-3}\big)+2\big(y_{i+2}-y_{i-2}\big),+}\ {\qquad\quad(y_{i+1}-y_{i-1})\big]/(28\Delta t)}\end{array}\right.

  

七点三阶公式  

\left{\begin{array}{l}{\dot{y}{i}=\mathrm{[-}2(y{i-3}+y_{i+3})+3(y_{i-2}+y_{i+2})\mathrm{}+}\ {\qquad6(y_{i-1}+y_{i+1})+7y_{i}]/21}\ {\qquad\qquad\mathrm{}}\ {\dot{y}{i}=\mathrm{[-~}22(y{i+3}-y_{i-3})+67(y_{i+2}-y_{i-2})\mathrm{}+}\ {\qquad58(y_{i+1}-y_{i-1})]/(252\Delta t\mathrm{})}\end{array}\right.

  

由于式（9-10)中角加速率项不是主要项,通常利用式（9-12)计算角加速率已足够了。如果采用第3章的模型辨识方法进行气动力建模和参数预估计，则需要较准确的角加速率，可根据实测数据的特性选取点数较多的平滑公式。下面给出任意点数、任意阶数的正交多项式平滑公式。  

设 $\pmb{Y}_{M}=(\,y_{0}\,,y_{1}\,,\cdots,y_{M}\,)^{\mathrm{T}}$ 是一组等间隔观测数据。数据平滑问题是将 $\mathbf{Y}_{M}$ 展成 $\boldsymbol{n}$ 阶正交多项式 $\xi_{l}\left(\,i\,\right)$ 的线性组合，使其方差$J$ 达极小。  

J;=;\sum_{\stackrel{i;=;0}{i;=;0}}^{M};\Big(,y_{i};-;\sum_{l;=;0}^{\eta}a_{l}\xi_{l},(;i;),\Big)^{2};

  

由 $\left(\partial J/\partial a_{l}\right)=\mathbf{0}$ 和 $\xi_{l}\left(\,i\,\right)$ 的正交性可求得 $a_{l}$ 的表达式为  

a_{l};=;\Big{\sum_{\stackrel{i}{i};=;0}^{M}y_{i}\pmb{\xi}_{l}\big(i,\big),\Big}\big/,S(,l,,M)

S(\mathit{l},,{\cal M});=;\sum_{i,=,0}^{M}\xi_{\mathit{l}}^{2}(\mathit{l},)

  

故 $\mathbf{\Delta}Y_{M}$ 的各分量 $y_{i}$ 的平滑公式为  

y_{M+j};=;\sum_{\tiny l;=;0}^{n}a_{l}\pmb{\xi}{l}\left(,M,+,j,\right);=;\sum{\tiny l;=;0}^{M}b_{i j}y_{i}

  

式中 $b_{i j}\;=\;\sum_{l\,=\,0}^{n}\left[\,\xi_{l}(\,i\,)\,\xi_{l}(\,M\,+\,j\,)\,\right]/S(\,l\,,M)$  

对式(9-20)求 $\pmb{k}$ 次导数，得 $\pmb{Y}_{M}$ 的 $k$ 阶微分 $\pmb{Y}_{M}^{(\pmb{k})}$ 的平滑公式，其各分量的表达式为  

y_{M+j}^{(k)}=\sum_{i=0}^{M}c_{i j}^{(k)}y_{i}

  

式中 $c_{i j}^{(k)}\,=\,\sum_{l\,=\,k}^{n}\,\bigl[\,\pmb{\xi}_{l}(\,i\,)\,\pmb{\xi}_{l}^{(k)}(\,M+j\,)\,\bigr]/S(\,l\,,M)\,;M\mathrm{-}\,$ 奇整数。  

$j$ 取为 $0\,,\,-\,1\,,\,-\,2\,,\cdots,1\,-\,M$ 的不同值时，所得的公式相当于对不同点的平滑公式； $j=(1-M)/2$ 时为中心平滑。对于 $M$ 个观测数据，根据 $\xi_{l}\left(\,i\,\right)$ 的正交性，可以求出其解析表达式  

式中  

\begin{array}{c}{{\displaystyle\xi_{l}(,i,),=,\sum_{\jmath,=,0}^{n},(-,1)^{j}C_{n}^{l}C_{n+1}^{l},A_{n}^{l}/A_{M}^{i}}}\ {{\displaystyle C_{n}^{l}=,n!/\big[,(,n-l,)!/l!,\big],;}}\ {{\displaystyle A_{n}^{l}=n!/(,n-l,)!_{,0}}}\end{array}

  

当选定数据平滑的点数 $M$ 、多项式的阶数 $_{n}$ 之后，可以由式（9-20）～式(9-22)求出数据的平滑值、一阶微分平滑直至 $\pmb{k}$ 阶微分平滑的具体算式。  

# 9.2.7 数据的低通数字滤波  

飞行器动力学系统的运动频率比较低，通常小于 $10\mathrm{Hz}$ 。由于各种干扰因素的影响，飞行试验数据中常含有高频成分，为此应对实测数据作频谱分析，分析出不合理的高频成分，从而设计低通滤波器将其滤除。  

为了使设计的低通数字滤波器具有对不同型号飞行器及不同采样率的飞行实测数据均有处理能力，滤波器设计成可变带宽及可变采样率。  

设计通带截止频率为 $\omega_{\rho}$ 、阻带截止频率为 $\omega_{q}$ ,采样周期为 $T$ 的数字低通滤波器的过程如下[5}：  

（1）求出  

\bar{\omega}{\dot{p}};=;\tan\frac{\omega{\dot{p}}T}{2};;;;;;;;;\bar{\omega}{q};=;\tan\frac{\omega{q}T}{2}

  

(2）设计通带截止频率为 $\overline{{\omega}}_{\rho}$ ,阻带截止频率为 $\ddot{\omega}_{q}$ 的模拟低通滤波器 $H(\mathbf{\varepsilon}_{s})$ 。  

(3)将 $H\left(\mathbf{\nabla}_{s}\right)$ 中 $\boldsymbol{s}$ 代之以 $\frac{z-1}{z+1}$ ，即进行双线性变换，得到$H(z)_{\ast}$  

（4）表达成适用于计算机处理的差分格式。  

按照以上步骤,下面给出设计举例。选定技术指标∞。=3且 $\omega>\omega_{q}$ 时阻带衰减的技术指标分别为三倍频衰减20dB,30dB,40dB,设计了如下二阶、三阶及四阶低通数字滤波器。  

二阶低通数字滤波器：  

传递函数  

H(z)=

\frac{\bar{\omega}{p}^{2}(,z^{2},+,2z,+,1)}{\big(1,+,1.414\bar{\omega}{p},+,\bar{\omega}{p}^{2}\big),z^{2},+,2\big(\bar{\omega}{p}^{2},-,1\big),z,+,\big(1,-,1.414\bar{\omega}{p},+,\bar{\omega}{p}^{2}\big)}

  

表达成差分格式  

\bar{y}^{(},n,)=,\frac{1}{A},\lbrace,\bar{\omega}_{\rho}^{2},[,y(,n,),+,2y(,n,-,1),+,y(,n,-,2,),],-,

\left[:C!!!!:\right(\left.,n:-:1,\right):+:B!!!!:\bar{y}!\left(\left.,n:-:2,\right),\right]\big}

  

式中 $y$ —实测数据;  

$\bar{y}$ 一—滤波后的数据(以下同)。  

\begin{array}{r l}&{A=,1+1.414\bar{\omega}{\rho},+,\bar{\omega}{\dot{\rho}}^{2}}\ &{B=,1,-,1,.414\bar{\omega}{\rho},+,\bar{\omega}{\dot{\rho}}^{2}}\ &{C=,2\big(\bar{\omega}_{\dot{\rho}}^{2},-,1\big)}\end{array}

  

三阶低通数字滤波器：  

298  

H(z),=,\frac{\bar{\omega}_{p}^{3}(z^{3}+2z^{2}+3z+1)}{A C z^{3}+(2C^{2}D+A D),z^{2},+,(B C+2C D^{2}),z,+,B D}

  

表达成差分格式  

\begin{array}{c}{{\displaystyle\frac{1}{A C}{\bar{\omega}_{p}^{3}{y(,n,),+,3y(,n,-,1),+,3y(,n,-,2)}}}\ {{\displaystyle y(,n,-,3),],-,\bigl[,(2C^{2}D,+,A D)\bar{y}(,n,-,1),\times}}\ {{\displaystyle(B C,+,2C D^{2})\bar{y}(,n,-,2),+,B D\bar{y}(,n,-,3),],;}}\end{array}

  

式中  

\begin{array}{l l}{{A;=;1,+,\bar{\omega}{P},+,\bar{\omega}{P}^{2};;;;}}&{{B;=;1,-,\bar{\omega}{\dot{p}},+,\bar{\omega}{\dot{p}}^{2}}}\ {{C;=;\bar{\omega}{\dot{\rho}},+,1;;;}}&{{D;=;\bar{\omega}{\dot{\rho}};-,1}}\end{array}

  

四阶低通字滤波器：  

传递函数  

H(,z,),=,\frac{\tilde{\omega}_{,p}^{4}(,z,+,1,)^{4}}{(,A z^{2},+,B z,+,C,)(,D z^{2},+,B z,+,C,)}

  

表达成差分格式  

\begin{array}{l}{{(\displaystyle n~)=\frac{1}{A C}{\bar{\omega}_{p}^{4}[y(n)+4y(n-1)+6y(n-2)+}}\ {{4y(n~-3)+y(n~-4)]{-}[(A B~+B D)\bar{y}(n-1)+}}\ {{(A E~+C D+B^{2})\bar{y}(n-2)+(B E+C B)\bar{y}(n-3)\times}}\ {{(C E\bar{y}(n-4)]}{\qquad\qquad\qquad\qquad(9-1)}}\end{array}

  

式中  

\begin{array}{l l}{{A;=;1,+,0.7653\bar{\omega}{\rho},+,\bar{\omega}{\rho}^{2}}}&{{\qquad B,=-,2,+,2\bar{\omega}{\rho}^{2}}}\ {{C,=,1,-,0.7653\bar{\omega}{\rho},+,\bar{\omega}{\rho}^{2}}}&{{\qquad D,=,1,+,1.8477\bar{\omega}{\rho},+,\bar{\omega}{\rho}^{2}}}\ {{E,=,1,-,1.8477\bar{\omega}{\rho},+,\bar{\omega}_{\rho}^{2}}}\end{array}

  

选用上述滤波器进行数据处理时，需注意下列问题：  

（1）所选滤波器的阶数愈高，则阻带衰减愈快,但滤波初始段的过冲也愈大,因此要在二者间根据需要权衡。  

(2）在使用此滤波器前,必须给出通带截止频率 $\omega_{\hat{p}}$ 及采样周期 $T$ ,这一般要采用快速傅里叶变换对飞行数据作频谱分析来确定，而通常飞行器的被测参量不具备周期性，为了防止泄漏效应，消除“旁瓣”，还需加窗处理。  

（3）在具体选定了滤波器的阶数后，进行应用之前，需进一步的仿真，以确定过冲时间，再配以滤波前后曲线的比较，以便确定选用某一一段进行参数辨识是十分必要的。  

（4）数字滤波会引人时间延迟，为此可对所有参数采用同-滤波器进行处理，或滤波后进行时延修正。滤波还有一个稳定过程，在滤波的最初几点结果不好，可采用向前和向后滤波来解决这个问题。  

例:截止频率 $10\hbar{z}$ 的四阶CB型低通滤波器为 $\Gamma\,3\,!$  

\begin{array}{c}{{\breve{y}{i}=\ a{0}y_{i},+,a_{1}y_{i-1},+,a_{2}y_{i-2},+,a_{3}y_{i-3},+,a_{4}y_{i-4},-}}\ {{{}}}\ {{b_{1}{\breve{y}}{i\ 1},-,b{2}{\breve{y}}{i-2},-,b{3}{\breve{y}}{i-3},-,b{4}{\breve{y}}_{i-4}}}\end{array}

\begin{array}{l}{{a_{1}=a_{3}=0.009912;}}\ {{,}}\ {{a_{2}=0.01487;}}\ {{,}}\ {{b_{1}=-2.914;}}\ {{,}}\ {{b_{2}=3.52;}}\ {{,}}\ {{b_{3}=-2.035;}}\ {{,}}\ {{b_{4}=0.4729;}}\end{array}

  

图 $9{-}2\!\left(\,a\,\right)$ 给出了混有高频噪声的角速率数据，图 $9^{-2(\,b\,)}$ 给出了滤去高频噪声后的角速率数据与精确值的比较，其中虚线是角速率的精确值，实线为通过滤波器并做时间延迟修正的角速率值。由图9-2可看出，采用上述公式可滤去高频噪声，而且滤波后的角速率数据与精确数值很一致。  

![](images/f7a0f337468363704cd522369d14760d8172797e62ca764fbc5e4382bba444f0.jpg)  
$\left(\fint\alpha\right)$ 混有高频噪声的试验数据； $(\,\pmb{\ b}\,)$ 滤波后的试验数据。  
图 9-2低通滤波结果  

# 9.2.8 数据的时间迟后修正  

试验数据中各个测量量的时间坐标如果不一致，将给参数辨识结果带来误差。造成各试验数据时间不一致的主要原因有三个：遥测时统与外测(雷测、光测等)时统不一致；传感器的时间响应不同；数据采集和传输过程中，传导时间不同，采样时刻不同；以及滤波器引起的时间延迟等等。  

滤波器时间延迟、采样时刻差以及传导时刻差，通常是在设计测量系统时就已知，只需用下式进行时间修正即可：  

\omega_{i}\left(\textit{t}+\textit{t}{i}\right);=;\omega{i}\left(\textit{t}\right)

  

对于空域不大的试验（如飞机和战术弹等），遥测与外测的时间系统是同一的。对于空域很大的试验，例如战略导弹飞行试验，发射点与落点相距几兆米，遥测和外测的时间测量系统通常不是一个系统,这将导致遥测参数(过载与角速率)与外测参数(速度、高度以及气象测量的密度）的相应时间不-致。从而使得气动参数辨识中的动压数据有误差，影响辨识准度。战略导弹的弹头飞行速度很快且弹道较陡，在飞行试验时应将两个时统的偏差控制在 $20\mathrm{ms}\!\sim\!30\mathrm{ms}$ 以下，否则它将影响辨识出的气动参数的准度。  

飞行器动力学系统试验中最主要的传感器一一速率陀螺、姿态陀螺、过载传感器、角加速率传感器、风标传感器等，都是振荡系统,可采用二阶振荡系统描述之[6]。角速率和过载传感器的运动微分方程可写成  

\begin{array}{r l r}{I\Ddot{\theta}{i},+,C{\omega}\dot{\theta}{i},+,K{\omega}\theta_{i},=,H\omega_{i}\quad}&{\left(,i,=,x,,y,,z,\right)}\ {m\Dot{x}{i},+,C{n}\Dot{x}{i},+,K{n}x_{i},=,-,m n_{i}\quad}&{\left(,i,=,x,,y,,z,\right)}\end{array}

  

式中 $\omega_{i}$ ——代表角速率 $\pmb{\hat{P}}\setminus\pmb{q}\setminus\pmb{r}$ $\theta_{i}$ —相应于 ${\pmb{\hat{p}}}\setminus{\pmb q}\setminus{\pmb r}$ 的陀螺输出角位移；$I$ —陀螺转子和内框的惯量矩；$C_{\omega}$ —陀螺粘性阻尼系数;K一——陀螺应变弹簧常数;$H^{\prime}$ -陀螺角动量；m—过载传感器重块的标准质量；$C_{n}$ ———过载传感器阻尼系数；$K_{n}$ -—过载传感器应变弹簧常数。  

严格地说，要考虑迟后效应，应将式（9-31）和式（9-32）加人观测方程组，同时还要给出 $\theta_{i}$ 与输出电压 $V_{i}$ 的关系，以及 $\mathbf{{V}}_{i}$ 与 $\pmb{\omega}_{i}$ 之间的标定曲线。利用这关系式，可以通过仿真计算求出各传感器的时间响应,求得各数据的时间迟后修正量。但这样做的计算工作量太大,不适用于预处理。通常采用二阶振荡系统的时间延迟进行估算。二阶振荡系统对外作用的动态响应的时间延迟与传感器的固有频率 $\pmb{\omega}_{s}$ 、固有阻尼 $\pmb{n}_{s}$ 及外作用的频率 $\omega_{f}$ 有关，其表达  

式为  

\tau,=,\frac{1}{\omega_{f}}\mathtt{a r c t a n}\left(\frac{2,n_{s}\omega_{f}}{\omega_{f}^{2},-,\omega_{s}^{,2}}\right)

  

式中 $\omega_{s}^{2}=K_{\omega}/I:$  

2\pi_{s}=C_{\omega}/I_{\circ}

  

由式(9-33)可见,当 $\omega_{s}\gg\omega_{f}$ 时， $\tau\!\approx\!0$ 。若传感器固有频率$\omega_{s}\!>\!2.5\omega_{f}$ ,则时间迟后可以忽略不计。  

图9-3给出时间延迟仿真计算结果,取外作用圆频率 $\omega_{f}=$ 20；传感器的圆频率为 $\omega_{s}=40$ ,阻尼值为圆频率的0.4倍。实线为带有阻尼的谐振运动，是角速率（或过载）的仿真数据，虚线为在角速率作用下传感器（二阶振荡系统）输出的仿真数据，显然传感器输出是有时间延迟的。表 9-1 列出由式(9-31)数值积分求出时间延迟精确值和用式(9-33)估计时间延迟的结果比较。  

由表9-1可见式（9-33）可以很好地估计传感器的时间延迟。  

![](images/16d6f2e3b06c8de88508827cd184815c98c6bc79b9c25425b405f377a7b9ae51.jpg)  
图 9-3时间迟后仿真计算  

表 9-1  传感器时间延迟计算结果  


<html><body><table><tr><td>外作用 频率</td><td>传感器 频率</td><td>传感器 阻尼</td><td>时间延迟 精确值/s</td><td>时间延迟 近似值/s</td><td colspan="2">误差</td></tr><tr><td rowspan="4">w= 20</td><td rowspan="2">w, = 40</td><td></td><td></td><td>0.0130</td><td>绝对误差/s</td><td>相对误差/%</td></tr><tr><td>0.2ws</td><td>0.0121</td><td>0.0245</td><td>0.0009 0.0019</td><td>7.4 9.4</td></tr><tr><td rowspan="2">w, = 60</td><td>0.4ws 0.2w,</td><td>0.0226 0.00672</td><td>0.0074</td><td>0.00072</td><td>9.6</td></tr><tr><td>0.4ws</td><td>0.0134</td><td>0.0146</td><td>0.0012</td><td>8</td></tr></table></body></html>  

当知道角速率陀螺的固有频率 $\pmb{\omega}_{\pmb{\omega}}$ 和阻尼 $n_{\omega}$ 以及过载传感器的固有频率 $\omega_{n}$ 和阻尼 $\pmb{n}_{n}$ 、外作用力固有频率 $\omega_{f}$ ,则可用下式进行两个传感器之间的时间延迟修正  

\Delta t,=,\frac{1}{\omega_{f}}\bigg[\arctan\left(\frac{2,n_{\omega}\omega_{f}}{\omega_{f}^{2},-,\omega_{{\omega}}^{2}}\right)-\arctan\left(\frac{2,n{n}\omega_{f}}{\omega_{f}^{2},-,\omega_{_{n}}^{2}}\right)\bigg]

  

在工程应用中，也可以根据实测数据的各参数物理意义进行时间延迟修正。例如当飞机做纵向运动时，角速率 $\pmb q$ 和姿态角 $\theta$ 的相位正好相差 $90^{\circ}$ ，也即一个参数的蜂值正好对应于另一参数的零点。如果实测数据不满足这个条件，可以将数据沿时间轴做平移加以修正。  

# 9.3 数据相容性检验和数据重建  

辨识理论已证明，当试验的观测噪声和过程噪声是零均值随机噪声时，最大似然辨识法给出参数的无偏、有效估计。但是当观测量含有常值误差时，估计将是有偏的。通常，观测误差包含常值误差和零均值随机误差（或称系统误差和偶然误差）两部分，飞行器动力学系统试验数据也是如此。具有常值误差的试验数据不满足系统动力学方程组，这将导致参数辨识结果是有偏的。  

飞行器动力学系统试验的测量数据常含有零位漂移（偏置）或比例因子等常值误差造成各实测数据互不协调（不相容）。所谓不相容是指各状态参数不满足运动方程组。数据相容性检验的目的是辨识出观测量中的常值误差并加以修正，使试验数据在统计意义上满足动力学方程组，以提高气动参数辨识准度。  

数据相容性检验的必要条件是，试验有多余的测量。也即某观测量已经直接测量了，同时它又可以根据其他观测量通过某运动方程或者运动关系式求出。如果此试验直接测量的量与间接求出的量相同，则此试验数据是相容的；否则此试验的各观测量是不相容的。造成数据不相容的原因是测量误差，只需利用该运动方程式把测量误差辨识出来，就可以重新构出相容的观测量。由于测量总有误差，所以试验时应尽可能采用不同途径进行测量，以便从中辨识出常值测量误差，加以排除，以提高辨识准度。  

格洛克（O.H.Gerlach）最早研究飞行试验数据的相容性检验[7,之后克莱茵(V.Klein)采用广义卡尔曼滤波和最大似然法给出了飞行试验数据相容性检验和数据重建的一般算法[8,9],各国航空研究部门也取得了一些应用成果[10\~17]  

对于飞行器动力学系统，数据相容性检验通常采用运动速度、角速率、攻角、侧滑角、姿态角（欧拉角）和高度等参数的测量数据，借助线速度、欧拉角和线位移等三组运动方程组，采用参数估计算法,辨识出测量数据的常值偏差、比例因子误差等。估计算法可采用广义卡尔曼滤波法[8,9,18,19] 、最大似然法[20] 、最小二乘法等[21,22]  

数据相容性检验实质上是一项状态重建技术，它还可用于事故分析。通常飞行器失事时，遥测参数测量不全，这时可采用与数据相容性检验类同的方法，将雷达、飞行记录等不同来源的数据组合起来,估计失事时飞行器的运动状态[23] 。常用广义卡尔曼滤波，也可用变分法[24] 、解析法[25,26]  

# 9.3.1 相容性检验基本方程及算法  

飞行器飞行试验数据相容性检验的基本思想是，以飞行器动力学方程组作为状态方程组，将常值测量误差作为待估计参数，用系统辨识方法估计出常值测量误差，将实测数据扣除常值误差，就得到了相容的试验数据。  

在飞行试验中，外力可以用加速度计测量，因此在动量方程中可以不出现未知参数；而目前还没有直接测量飞行器所承受的力矩的传感器,动量矩方程含有外作用的未知参数。所以在数据相容性检验的状态方程中，只包含动量方程组和姿态运动方程组，而不包含动量矩方程组。  

在数据相容性检验的状态方程中含有角速率、过载、攻角、侧滑角和姿态角,不包含舵偏、大气密度等,因此相容性检验无法辨识舵偏和大气密度等的测量误差。角速率、过载等传感器的常值测量误差，通常可以分解为比例因子误差、零位偏置误差、安装方位误差、安装位置误差等。在正常情况下，安装方位误差和安装位置误差是比较小的。零位偏置误差是最主要的常值误差，对于某些传感器（如攻角、侧滑角传感器），比例因子误差也是重要的。因此，用于辨识传感器常值误差的数学模型取为  

z\left(,t,\right);=;\left(1,+,\epsilon_{y},\right)y(,t,),+,\Delta y,+,\epsilon,(,t,)

  

式中 $z\left(t\right)$ —实测值；  

$y\left(\footnote{I n t h:/4}\right)$ 理想测量值； Ey 比例因子误差； $\Delta y$ 零位偏置；   
$\varepsilon\left(\,t\,\right)$ 随机噪声，且满足 $E\left\{\,\varepsilon\left(\,t\,\right)\,\right\}=0\,,E\left\{\,\varepsilon\left(\,t\,\right)\varepsilon\left(\,\tau\,\right)\,\right\}\,=$ $R\delta(\,t\,-\,\tau\,)_{\circ}$  

$\Delta y$ 和 $\varepsilon_{y}$ 实际上是由传感器的零位漂移及工作不稳定而引人的误差。  

现建立飞行器动力学系统常值测量误差的辨识数学模型。飞行器飞行试验数据相容性检验以动量方程组和姿态角方程组作为系统的状态方程组（参见2.1.2节）。  

1）状态方程组  

\dot{u}~=v r-w q+g\left(n_{x}-\sin\theta\right)

\begin{array}{l}{{\dot{v}\ =\ w p\ -\ u r\ +\ g\big(,n_{y},+,\mathrm{cos}\theta\mathrm{sin},\phi,\big)}}\ {{\dot{\omega}\ =\ u q,-\ v p,+,g\big(,n_{z},+,\mathrm{cos}\theta\mathrm{cos}\phi,\big)}}\end{array}

\dot{\psi},=,\frac{1}{\mathrm{cos}\theta}(,q\sin\phi,+,r\cos\phi,)

\dot{\theta}\ =\ q\cos\phi\ -\ r\sin\phi

\pmb{\dot{\phi}}=\pmb{\dot{p}}+\tan\theta\big(,q\sin\phi~+~r\cos\phi,\big)

\dot{h}~=u\sin\theta-v\cos\theta\sin\phi-~w\cos\theta\cos\phi

  

式中  

\dot{p};=;\lambda_{\dot{p}}\dot{p}{m};-;a{\dot{p}};\sqrt{q_{m}^{2};+;r_{m}^{2}};-;\Delta\dot{p}

\begin{array}{r}{q;=;\lambda_{q}q_{m};-;a_{q},\sqrt{\dot{p}{m}^{2};+;r{m}^{2}};-;\Delta q}\ {r;=;\lambda_{r}r_{m};-;a_{r},\sqrt{\dot{p}{m}^{2};+;q{m}^{2}};-;\Delta r}\end{array}

\begin{array}{r l}&{n_{x},=,n_{x m},-,\Delta n_{x}}\ &{}\ &{n_{y},=,n_{y m},-,\Delta n_{y}}\ &{}\ &{n_{z},=,n_{z m},-,\Delta n_{z}}\end{array}

  

2）观测方程组  

V_{m};=;\left(1,+,\varepsilon_{V}\right),\sqrt{,u^{,2},+,v^{,2},+,w^{,2},},+,\Delta V,+,\epsilon_{1}

\alpha_{m};=;\big(1,+,,\varepsilon_{\alpha}\big)\mathrm{arctan}\bigg(\frac{w,-,q x_{\alpha},+,,\dot{p}y_{\alpha}}{u}\bigg)+,\Delta\alpha,+,\varepsilon_{2}

\beta_{m};=;(1:+:\epsilon_{\beta})\arcsin\left(\frac{\displaystyle v:+:r x_{\beta}:-:\hat{p}z_{\beta}}{V}\right)+,\Delta\beta:+:\epsilon_{3};

\begin{array}{r l}&{\phi_{m},=,\left(1,+,\varepsilon_{\phi}\right)\phi,+,\Delta\psi,+,\varepsilon_{4}}\ &{\theta_{m},=,\left(1,+,\varepsilon_{\theta}\right)\theta,+,\Delta\theta,+,\varepsilon_{5}}\ &{\phi_{m},=,\left(1,+,\varepsilon_{\phi}\right)\phi,+,\Delta\phi,+,\varepsilon_{6}}\ &{h_{m},=,\left(1,+,\varepsilon_{h}\right)h,+,\Delta h,+,\varepsilon_{7}}\end{array}

  

式中 $\mathsf{\pmb{\varepsilon}}_{i}(\,i=1\,,2\,,\cdots,7)$ —测量噪声。  

3）待估计参数0  

\pmb{\theta};=;\left(,\varepsilon_{V},,\Delta V,,\varepsilon_{\alpha},,\Delta\alpha,,\varepsilon_{\beta},,\Delta\beta,,\lambda_{\beta},,a_{\beta},,\Delta\phi,,\right.

\lambda_{q},,a_{q},,\Delta q,,\lambda_{r},,a_{r},,\Delta r,,\Delta n_{x},,\Delta n_{y},,

\Delta n_{z},,\epsilon_{\phi},,\Delta\psi,,\epsilon_{\theta},,\Delta\theta,,\epsilon_{\phi},,\Delta\phi,,\epsilon_{h},,\Delta h,)^{\textup{T}}

  

根据上述状态方程组和观测方程组，可以采用5.3节最大似然法辩识出待估计参数 $\pmb{\theta}$ ，辨识过程中所需的灵敏度 $\partial\,{\bf y}/\partial\,{\pmb\theta}$ 可由下列灵敏度方程组积分求得。  

# 4）灵敏度方程组  

状态变量对待估计参数的灵敏度满足下列方程组  

\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial,u}{\partial\theta_{k}}\right)=;r;\frac{\partial,v}{\partial\theta_{k}},-,q;\frac{\partial,w}{\partial\theta_{k}},-,g\mathrm{cos}\theta;\frac{\partial,\theta}{\partial\theta_{k}},+,U_{1,k}

{\frac{\mathrm{d}}{\mathrm{d}t}}\left({\frac{\partial,v}{\partial\theta_{k}}}\right)=;{\boldsymbol{\beta}};{\frac{\partial,w}{\partial\theta_{k}}},-,r;{\frac{\partial,u}{\partial\theta_{k}}},-,g\mathrm{sin}\theta\mathrm{sin}\phi;{\frac{\partial,\theta}{\partial\theta_{k}}},+

g\mathrm{cos}\theta\mathrm{cos}\phi;\frac{\partial\phi}{\partial\theta_{k}},+,U_{2,{\pmb k}}

\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial,w}{\partial\theta_{k}}\right)=,q;\frac{\partial,u}{\partial\theta_{k}},-,\phi;\frac{\partial,v}{\partial\theta_{k}},-,g,\mathrm{sin}\theta\mathrm{cos}\phi;\frac{\partial,\theta}{\partial\theta_{k}},-

g\mathrm{cos}\theta\mathrm{sin}\phi;\frac{\partial\phi}{\partial\theta_{k}}+;U_{3,k}

\begin{array}{c}{{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial\psi}{\partial\theta_{k}}\right)=,\frac{1}{\cos\theta}(,q\cos\phi,-,r\sin\phi,);\frac{\partial,\phi}{\partial\theta_{k}},+}}\ {{\displaystyle\frac{1}{\cos^{2}\theta}(,q\sin\phi,+,r\cos\phi,)\sin\theta;\frac{\partial,\theta}{\partial\theta_{k}},+,U_{4,k}}}\end{array}

\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial\theta}{\partial\theta_{k}}\right)=\mathrm{\left(-~,}q\sin\phi,-,r\cos\phi,\right),\frac{\partial\phi}{\partial\theta_{k}},+,U_{5,k}

\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial\phi}{\partial\theta_{k}}\right)=,\tan\theta(,q\cos\phi,-,r\sin\phi,),\frac{\partial\phi}{\partial\theta_{k}},+

\frac{1}{\cos^{2}!\theta}(,q\sin!\phi,+,r\cos!\phi,);\frac{\partial\theta}{\partial\theta_{k}},+,U_{6,k}

\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial h}{\partial\theta_{k}}\right)=,\frac{\partial,u}{\partial\theta_{k}}\mathrm{sin}\theta:+:u,\mathrm{cos}\theta:\frac{\partial\theta}{\partial\theta_{k}}:-:\frac{\partial,v}{\partial\theta_{k}}\mathrm{cos}\theta\mathrm{sin}\phi:+

v\sin\theta\sin\phi\ {\frac{\partial\theta}{\partial\theta_{k}}},-,v\cos\theta\cos\phi\ {\frac{\partial\phi}{\partial\theta_{k}}},-,{\frac{\partial w}{\partial\theta_{k}}}\mathrm{cos}\theta\mathrm{cos}\phi\ +

w s i n\theta\mathrm{cos}\phi~{\frac{\partial\theta}{\partial\theta_{k}}}+w\mathrm{cos}\theta\mathrm{sin}\phi{\frac{\partial\phi}{\partial\theta_{k}}}

  

灵敏度方程的积分初值皆取为零。 $U_{i}$ .项为  

![](images/579d10d6c0a3a9d05108cb48d550ecb39091e5c397369716203be69268207bb4.jpg)  

U_{3,11};=;-;u;\sqrt{\dot{p}{;m}^{2};+;r{;m}^{2}};;;;;;;;;;;;;U_{3,12};=-;u

\begin{array}{r l}{\varepsilon_{\mathrm{4},\mathrm{n}}^{-\dagger}}&{=\frac{1}{\cos\theta}\sin\theta;}\ {U_{\mathrm{4},\mathrm{n}}=\frac{1}{\cos\theta}\sin^{2}\theta;}&{U_{\mathrm{4},\mathrm{n}}=-\frac{1}{\cos\theta}\sin^{2}\theta;{\sqrt{\gamma_{\mathrm{+}}}}+;}\ {U_{\mathrm{4},\mathrm{n}}=-\frac{1}{\cos\theta}\sin\theta;}&{U_{\mathrm{4},\mathrm{n}}=\frac{1}{\cos\theta}\sin^{2}\theta;}\ {U_{\mathrm{4},\mathrm{n}}=-\frac{1}{\cos\theta}\cos^{4}\sqrt{\gamma_{\mathrm{-}}+\theta_{\mathrm{4},\mathrm{n}}^{2}};}&{U_{\mathrm{4},\mathrm{n}}=-\frac{1}{\cos\theta}\cos^{4}\theta}\ {U_{\mathrm{5},\mathrm{n}}=\ q_{\mathrm{\infty}}\cos^{4}\theta;}&{U_{\mathrm{5},\mathrm{n}}=-\cos^{6}\sqrt{\gamma_{\mathrm{-}}+\gamma_{\mathrm{\infty}}^{2}}}\ {U_{\mathrm{5},\mathrm{n}}=-\cos^{6}\theta;}&{U_{\mathrm{5},\mathrm{n}}=-;r_{\mathrm{{sa}}}\sin^{4}\theta}\ {U_{\mathrm{5},\mathrm{n}}=\sin\sqrt{\gamma_{\mathrm{-}}+\gamma_{\mathrm{\infty}}^{2}};}&{U_{\mathrm{5},\mathrm{n}}=\sin^{4}\theta}\ {U_{\mathrm{6},\mathrm{n}}=\frac{1}{\sin\theta}\sin^{2}\theta;}&{U_{\mathrm{6},\mathrm{n}}=-\sqrt{\gamma_{\mathrm{-}}^{2}+\gamma_{\mathrm{\infty}}^{2}}}\ {U_{\mathrm{6},\mathrm{n}}=-1,;U_{\mathrm{6},\mathrm{n}}=q_{\mathrm{\infty}}\sin\theta;}&{U_{\mathrm{4},\mathrm{n}}=-\sqrt{\gamma_{\mathrm{-}}+\gamma_{\mathrm{\infty}}^{2}}\sin\theta;}\ {U_{\mathrm{6},\mathrm{n}}=-\sin\theta\sin\theta;}&{U_{\mathrm{6},\mathrm{n}}=\frac{r_{\mathrm{{sa}}}\sin\theta;}{r

0  

观测量对待估计参数的灵敏度为  

\frac{\partial,V_{m}}{\partial\theta_{k}};=;\left(1,+,\varepsilon_{V}\right),\frac{\partial,V}{\partial\theta_{k}};+;W_{1,k}

\frac{\partial\alpha_{m}}{\partial\theta_{k}};=;\frac{1,+,\varepsilon_{\alpha}}{u^{2};+;(;w;-;q x_{\alpha};+;\rho y_{\alpha},)^{2}}\left(,u;\frac{\partial w}{\partial C_{k}};-;w;\frac{\partial u}{\partial C_{k}}\right)+;{\cal W}_{2,k}

\frac{\partial\beta_{m}}{\partial\theta_{k}},=,\frac{1,+,\varepsilon_{\beta}}{V,\sqrt{V^{2},-,(,v,+,r x_{\beta},-,,\rho z_{\beta},)^{2}}}\bigg(,V,\frac{\partial,v}{\partial,\theta_{k}},-,v,\frac{\partial,V}{\partial,\theta_{k}}\bigg),+,W_{3,k}

\begin{array}{r l}&{\displaystyle\frac{\partial,\psi_{m}}{\partial,\theta_{k}},=,\left(1,+,\varepsilon_{\phi}\right),\frac{\partial,\psi}{\partial,\theta_{k}},+,W_{4,k}}\ &{\displaystyle\frac{\partial,\theta_{m}}{\partial,\theta_{k}},=,\left(1,+,\varepsilon_{\theta}\right),\frac{\partial,\theta}{\partial,\theta_{k}},+,W_{5,k}}\end{array}

\begin{array}{r l}&{\displaystyle\frac{\partial\phi_{m}}{\partial\theta_{k}},=,\left(1,+,\epsilon_{\phi}\right),\frac{\partial,\phi}{\partial\theta_{k}},+,W_{6,k}}\ &{\displaystyle\frac{\partial,h_{m}}{\partial\theta_{k}},=,\left(1,+,\epsilon_{h}\right),\frac{\partial,h}{\partial\theta_{k}},+,W_{7,k}}\end{array}

  

式中  

\begin{array}{r l}{\displaystyle\frac{\partial V}{\partial\theta_{k}}=}&{\displaystyle\frac{1}{V}!\left(u,\frac{\partial u}{\partial\theta_{k}}+v,\frac{\partial v}{\partial\theta_{k}}+w,\frac{\partial w}{\partial\theta_{k}}\right)}\ {\displaystyle W_{1,1}=V}&{\displaystyle W_{1,2}=1}\ {\displaystyle w_{2,3}=\arctan\frac{w}{u}-(,q x_{}-p y_{})/V}&{\displaystyle W_{2,4}=1}\ {\displaystyle V_{2,7}=(1+\varepsilon_{})p_{}/V}&{\displaystyle W_{2,8}=-,(1+\varepsilon_{})\sqrt{q^{2}+r^{2}}y_{}/V}\ {\displaystyle V_{2,9}-(,1+\varepsilon_{})y_{}/V}&{\displaystyle W_{2,10}=-,(1+\varepsilon_{}),q x_{}/V}\ {\displaystyle w_{2,11}=(1+\varepsilon_{})\sqrt{p^{2}+r^{2}}x_{}/V}&{\displaystyle W_{2,12}=(1+\varepsilon_{}),x_{}/V}\ {\displaystyle W_{3,5}=\arctan\frac{w}{u}-(,-r x_{\ell}+p z_{\ell})/V,W_{3,6}=1}\end{array}

T  

\begin{array}{r l r l}&{\quad_{<,t}}&{\sim_{->t}\operatorname{c.c.}\quad}&{\sim_{->t}\operatorname{c.c.}\quad,}\ &{v_{2,\eta}=-\left(1+\epsilon_{\mu}\right){>\mu{1}}V}&{\quad_{\mathcal{U}{2,10}}=-\left(1+\epsilon{\mu}\right){\mathcal{U}{s}}f V}\ &{v_{2,11}=\left(1+\epsilon_{\mu}\right)\sqrt{\beta^{2}+r^{2}},x_{\mu}/V}&{\quad W_{2,12}=\left(1+\epsilon_{\mu}\right)x_{\alpha}/V}\ &{v_{3,S}=\arctan\frac{w}{\mu}-\left(-r x_{\beta}+\rho\varepsilon_{\beta}\right)/V,W_{3,6}=1}\ &{v_{3,7}=-\left(1+\epsilon_{\beta}\right)p_{\alpha\beta}/V}&{\quad W_{3,8}=\left(1+\varepsilon_{\mu}\right)\sqrt{q^{2}+r^{2}},z_{\mu}/V}\ &{v_{3,9}=\left(1+\epsilon_{\mu}\right)z_{\mu}/V}&{\quad W_{3,13}=\left(1+\epsilon_{\mu}\right)r x_{\beta}/V}\ &{v_{3,14}=-\left(1+\epsilon_{\mu}\right)\sqrt{\beta^{2}+q^{2}},x_{\mu}/V}&{\quad W_{3,15}=-\left(1+\varepsilon_{\mu}\right)x_{\mu}/V}\ &{v_{4,19}=\phi}&{\quad W_{4,20}=1}\ &{v_{5,21}=\theta}&{\quad W_{5,22}=1}\end{array}

  

甘全  

利用上述状态方程组、观测方程组和灵敏度方程组，由最大似然法求得0值后，可用下式重建相容的飞行试验数据。  

5）数据重建方程  

\begin{array}{c}{{V,=,(,V_{m},-,\Delta V)/(1,+,\varepsilon_{V})}}\ {{\phantom{,=,},\alpha,=,\left(,\alpha_{m},-,\Delta\alpha,\right)/(1,+,\varepsilon_{a})}}\end{array}

  

310  

\begin{array}{r l}&{\qquad\beta=(\beta_{m}-\Delta\beta)/(1+,\varepsilon_{\beta})}\ &{\qquad\beta,=,\lambda_{\rho}\dot{p}{m},-,\alpha{\rho},\sqrt{q_{m}^{2},+,r_{m}^{2}},-,\Delta\rho}\ &{\qquad q,=,\lambda_{q}q_{m},-,\alpha_{q},\sqrt{\dot{p}{m}^{2},+,r{m}^{2}},-,\Delta q}\ &{\qquad r,=,\lambda_{r}r_{m},-,\alpha_{r},\sqrt{\dot{p}{m}^{2},+,q{m}^{2}},-,\Delta r}\end{array}

\begin{array}{r l}&{n_{x};=;n_{x m};-;\Delta n_{x}}\ &{n_{y};=;n_{y m};-;\Delta n_{y}}\ &{n_{z};=;n_{z m};-;\Delta n_{z}}\end{array}

\begin{array}{r l}&{\emph{\phi}=,(,\phi_{m},-,\Delta\psi,)/(1,+,\varepsilon_{\phi},)}\ &{\emph{\theta}=,(,\theta_{m},-,\Delta\theta,)/(1,+,\varepsilon_{\theta},)}\ &{\emph{\phi}=,(,\phi_{m},-,\Delta\phi,)/(1,+,\varepsilon_{\phi},)}\ &{\emph{h}=,(,h_{m},-,\Delta h,)/(1,+,\varepsilon_{h},)}\end{array}

  

上面给出了数据相容性检验的基本方程和算法。在应用上述算法解决实际问题时，应注意到参数矢量 $\pmb\theta$ 中的各个参数并不都是独立无关的。例如从式（9-38）、式（9-40）式（9-50)、式（9-53)可看出，对于纵向小扰动运动， $\phi{\ll}1\,,g n_{z}/u{\ll}q$ ,这时 $\epsilon_{\alpha}$ 和 $\epsilon_{\theta}$ 是相关的,无法同时辨识 $\epsilon_{\alpha}$ 和 $\epsilon_{\theta}$ 。因此,进行数据相容性检验时,要根据各传感器测量参数的物理意义和传感器的物理特性，选定合适的数学模型。例如角速率、姿态角传感器由陀螺或压电晶体构成，其比例因子误差较小，主要常值误差是零位漂移；过载传感器也主要是零位漂移；攻角、侧滑角传感器安装在物体上，物体对流场的影响造成攻角、侧滑角传感器有较大的比例因子误差和零位偏置。再者，每次试验中测量的参数不同，需要辨识的常值误差也不同。为适用于多种情况，编制计算程序时，应能灵活选择待辨识参数。  

图9-4给出数据相容性检验和数据重建计算结果。图 $9{-}4(\alpha)$ 是相容性检验前的不相容数据，实线是测量的攻角 $\pmb{\alpha}$ 值，虚线是角速率积分得到的 $\pmb{\alpha}$ 值,两者相差较大。图 $9{-}4(b)$ 是经过数据相容性检验，辨识出角速率的零位偏置值,进行数据重建的结果。这时实线和虚线很一致，说明数据重建后的角速率数据和攻角数据  

![](images/bbd6d4662c29a316baff33a13098ff0d725450a8a76de22ee1b764f81a168fd6.jpg)  
图 9-4数据相容性检验和数据重建计算结果$(\fint\alpha)$ 相容性检验前； $\left(\,b\,\right)$ 相容性检验并数据重建后。  

是相容的。  

# 9.3.2 四元素相容性检验模型  

航天飞行器的角运动、飞机进人尾旋运动状态都可能出现俯仰角 $\theta=90^{\circ}$ 的状态，此时式（9-39）和式（9-41)出现奇异性，相应地,式(9-60)和式(9-62)也出现奇异性，上述算法无法进行。这一奇异性并非物理奇异性，而是由欧拉角的数学定义所致，只需采用不同的角度定义即可消除奇异性，常用的办法是四元素法。美国阿波罗计划就成功地采用四元素进行姿态控制。  

四元素也称超复数，由一个标量和三维矢量构成  

e;=;e_{1}:+:e;=;e_{1}:+:e_{2}:\dot{\iota};+;e_{3}\dot{J}:+:e_{4}:k

  

四元素有自己的加法、减法、乘法和除法运算法则，构成四元素数域。四元素可以代替欧拉角来表示刚体绕定点的旋转运动。四元素和欧拉角的关系可写成  

\left{\begin{array}{l}{\displaystyle e_{1},=,\cos{\frac{\phi}{2}}\cos{\frac{\theta}{2}}\cos{\frac{\phi}{2}},-,\sin{\frac{\phi}{2}}\sin{\frac{\theta}{2}}\sin{\frac{\phi}{2}}}\ {\displaystyle e_{2},=,\cos{\frac{\phi}{2}}\cos{\frac{\theta}{2}}\sin{\frac{\phi}{2}},+,\sin{\frac{\phi}{2}}\sin{\frac{\theta}{2}}\cos{\frac{\phi}{2}}}\ {\displaystyle e_{3},=,\cos{\frac{\phi}{2}}\sin{\frac{\theta}{2}}\sin{\frac{\phi}{2}},+,\sin{\frac{\phi}{2}}\cos{\frac{\theta}{2}}\cos{\frac{\phi}{2}}}\ {\displaystyle e_{4},=,\cos{\frac{\phi}{2}}\sin{\frac{\theta}{2}}\cos{\frac{\phi}{2}},-,\sin{\frac{\phi}{2}}\cos{\frac{\theta}{2}}\sin{\frac{\phi}{2}}}\end{array}\right.

  

利用式（9-85），经过简单代数运算得  

\left{\begin{array}{l}{{\sin\theta,,=,2(e_{1}e_{4},+,e_{2}e_{3})}}\ {{\cos\theta\mathrm{cos}\phi,=,e_{1}^{2},-,e_{2}^{2},+,e_{3}^{2},-,e_{4}^{2}}}\ {{\mathrm{cos}\theta\mathrm{sin}\phi,=,2(e_{1}e_{2},-,e_{3}e_{4})}}\ {{\mathrm{cos}\theta\mathrm{sin}\phi,=,2(e_{1}e_{3},-,e_{2}e_{4})}}\end{array}\right.

  

由角速率和四元素定义出发，还可以导出  

\begin{array}{r}{\left{\begin{array}{l}{\Dot{e}{1}=-\big(e{2}\phi,-,e_{3}r,+,e_{4}q,\big)/2}\ {\Dot{e}{2}=\big(e{1}\phi,+,e_{4}r,+,e_{3}q\big)/2}\ {\Dot{e}{3}=\big(e{4}\phi,-,e_{1}r,-,e_{2}q,\big)/2}\ {\Dot{e}{4}=\big(-,e{3}\phi,-,e_{2}r,+,e_{1}q,\big)/2}\end{array}\right.}\end{array}

  

将式（9-86）和式（9-87）用于式（9-36）～式（9-55）可得采用四元素法的常值测量误差辨识数学模型：  

1）状态方程组  

\begin{array}{r l}{u}&{=v r-w q+g(n_{x}-2e_{1}e_{4}-2e_{2}e_{3})}\ &{v}&{=w\hbar-u r+g(n_{x}+2e_{1}e_{2}-2e_{3}e_{4})}\ &{w}&{=u q-p v-g(n_{y}+e_{1}^{2}-e_{2}^{2}+e_{3}^{2}-e_{4}^{2})}\ &{\quad\quad e_{1}=-(e_{2}\beta-e_{3}r+e_{4}q)/2}\ &{\quad\quad e_{2}=(e_{1}\beta+e_{4}r+e_{3}q)/2}\ &{\quad\quad e_{3}=(e_{4}\beta-e_{1}r-e_{2}q)/2}\ &{\quad\quad e_{4}=(-e_{3}\beta-e_{2}r+e_{1}q)/2}\ &{\dot{h}=2u(e_{1}e_{4}+e_{2}e_{3})-2v(e_{1}e_{2}-e_{3}e_{4})-}\end{array}

\boldsymbol{w}\big(,e_{1}^{2},-,e_{2}^{2},+,e_{3}^{2},-,e_{4}^{2}\big)

  

式中,p、qr、nn、n与式(9-43)～式(9-48)同。虽然角速度传感器输出的是欧拉角,但经过式(9-85),可以得到é1、é2、é3、é4的实测值。e；的主要常值误差是零位漂移，所以观测方程组变为下列形式。  

2）观测方程组  

V_{m};=;\left(1,+,\epsilon_{V}\right),\sqrt{,u^{2},+,v^{2},+,w^{2},},+,\Delta V,+,\epsilon_{1}

\begin{array}{r}{\alpha_{m}\ =\ \left(1,+\ \varepsilon_{\alpha}\right)\arctan\left(\frac{w\ -\ q x_{\alpha}\ +\ \phi y_{\alpha}}{u}\right)+\ \Delta\alpha\ +\ \varepsilon_{2}\ \left(9\ -97\right)}\ {\beta_{m}\ =\ \left(1\ +\ \varepsilon_{\beta}\right)\arcsin\left(\frac{v\ +\ r x_{\beta}\ -\ \phi z_{\beta}}{V}\right)+\ \Delta\beta\ +\ \varepsilon_{3}\ \left(9\ -98\right)}\end{array}

\begin{array}{r}{e_{1m},=,e_{1}+\Delta e_{1},+,\varepsilon_{4}}\ {e_{2m},=,e_{2}+,\Delta e_{2},+,\varepsilon_{5}}\ {e_{3m},=,e_{3}+,\Delta e_{3},+,\varepsilon_{6}}\ {e_{4m},=,e_{4}+,\Delta e_{4},+,\varepsilon_{7}}\end{array}

h_{m};=;\left(1,+,\varepsilon_{h},\right)h;+;\Delta h;+;\varepsilon_{8}

  

3）待估计参数 ${\pmb\theta}$  

\pmb{\theta}=\left(\pmb{\varepsilon}{V},\Delta V,\pmb{\varepsilon}{a},\Delta\alpha,,\pmb{\varepsilon}{\beta},\Delta\beta,\lambda{\beta},,\alpha_{\beta},,\Delta\phi,,\lambda_{q},,\alpha_{q},,\Delta q,,\lambda_{r},,\alpha_{r},,\Delta r,,\pmb{\varepsilon}_{\beta}\right)

\Delta n_{x},,\Delta n_{y},,\Delta n_{z},,\Delta e_{1},,\Delta e_{2},,\Delta e_{3},,\Delta e_{4},,\varepsilon_{h},,\Delta h,)^{\mathrm{T}}

  

根据上述状态方程组和观测方程组，可以采用最大似然法辨识出待估计参数 $\pmb{\theta}$ 。辨识过程中所需的灵敏度可以通过对式（9-88）～式(9-103)求导而得。结果类似于式(9-57)～式(9-70),这里不再赘述。  

# 9.3.3 飞行数据相容性检验实用算法  

在相容性检验的一般算式中，待辨识参数0（见式（9\~56））的各个分量并不都是相互独立的，不可能都同时辨识出正确结果，必须针对实际情况简化模型，给出实用算法。下面介绍两种简化模型的实用算法。  

# 1）战术导弹飞行数据相容性检验  

小型战术导弹因容积小，有时飞行试验时仅装有角速率传感器和用于控制的姿态角陀螺，而由光测提供飞行轨迹，这时观测数据仅有  

\textbf{y}=,(,\pmb{\phi}{m},,\pmb{q}{m},,r_{m},,\pmb{\psi}{m},,\pmb{\theta}{m},,\pmb{\phi}{m},,x{,g}^{'},,y_{g}^{'},,z_{g}^{'},)^{,\mathrm{T}}

  

式中，下标“ $\mathbf{\nabla}m$ ”代表实测值。这时可采用三步法进行数据相容性检验和重建[27]  

（1）利用姿态角方程辨识陀螺漂移。状态方程为  

\begin{array}{c}{{\dot{\phi},=,\frac{1}{\mathrm{cos}\theta}[,(q,+,\Delta q,)\mathrm{sin}\phi,+,(,r,+,\Delta r,)\mathrm{cos}\phi,]\quad0}}\ {{\dot{\theta},=,\left(,q,+,\Delta q,)\mathrm{cos}\phi,-,(,r,+,\Delta r,)\mathrm{sin}\phi,\qquad0}}\ {{\dot{p},+,\Delta\phi,),+,\mathrm{tan}\theta[,(q,+,\Delta q,)\mathrm{sin}\phi,+,\left(,r,+,\Delta r,)\mathrm{cos}\phi,]\quad0}}\end{array}

  

观测方程为  

\begin{array}{r c l}{{\theta_{m}!!!}}&{{=}}&{{!!!\left(1,+,\varepsilon_{\theta}\right)\theta,+,\Delta\theta,+,\varepsilon_{5}}}\ {{\phi_{m}!!!}}&{{=}}&{{!!!\left(1,+,\varepsilon_{\phi}\right)\phi,+,\Delta\phi,+,\varepsilon_{6}}}\end{array}

  

待估参数  

\pmb{\theta},=,(\Delta\phi,,\Delta q,,\Delta r,,\Delta\theta,,\Delta\phi)^{\mathrm{T}}

  

经过上述处理,利用前述的辨识方法即可获得剔除偏差后精确的 $\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\,\!\!\,\!\,\!\,\!\,\!\,\!\!\,\!\,\!\,\!\,\!\,\!\!\,\!\,\!\,\!\,\!\!\,\!\,\!\,\!\!\,\!\,\!\,\!\!{\!\!\!\,\!\,\!\,\!\!\,\!\,\!\!\,\!\,\!\,\!\!{\!\!\!\,\!\!\,\!\,\!\!\,\!\,\!\!\,\!{\!\!\!\!\,\!\,\!\!\,\!\!\,\!\$ 和 $\phi\,,\theta\,,\phi$ 的时间历程。通常 $\Delta\phi$ 没有冗余测量,无法辨识,以 $\psi_{m}$ 代替 $\phi_{0}$  

(2)由 $x_{g}^{\prime},y_{g}^{\prime},z_{g}^{\prime}$ 计算 $V,\psi_{k}\,,\theta_{k}\,,\alpha\,,\beta_{\0}$ ，利用光测的铅垂地面坐标系位置 $x_{g}^{\prime},y_{g}^{\prime},z_{g}^{\prime}$ ,经数值运算可得速度 $\pmb{V}$ 、航迹方位角 $\psi_{k}$ 及爬升角 $\theta_{k}$  

\left{{\begin{array}{l}{u_{g},=,{\dot{x}}{g},,,v{g},=,{\dot{y}}{g},,w{g},=,{\dot{z}}{g}}\ {V,=,{\sqrt{,u{g}^{2},+,v_{g}^{2},+,w_{g}^{2}}}}\ {\phi_{k},=,\arctan(,v_{g}/u_{g},)}\ {\theta_{k},=,\arcsin(,-,,w_{g}/V)}\end{array}}\right.

  

进一步由 $V,\psi,\theta\,,\psi_{k}\,,\theta_{k}$ 可获得较精确的速度在弹体坐标系的三个分量  

\left[{\bf\Psi}{v}\right]=\mathbf{\Phi}{L_{b g}L_{g k}}\left[{\bf\Psi}_{0}^{V}\right]

  

式中  

\begin{array}{r}{\pmb{L}{g k}=\left[\cos\psi{k}\cos\theta_{k}\quad-\ \sin\psi_{k}\quad\cos\psi_{a}\sin\theta_{k}\right]}\ {\pmb{\sin\psi_{k}}\cos\theta_{k}\quad\cos\psi_{k}\quad\ \sin\psi_{k}\sin\theta_{k}}\ {-\ \sin\theta_{k}\quad\quad0\quad\quad\cos\theta_{k}}\end{array}

\mathbf{L}_{b g}=\left[\begin{array}{c c c}{\cos\phi\cos\theta}&{-;\cos\theta\sin\phi}&{\sin\theta}\ {\cos\psi\sin\theta\sin\phi}&{-;\sin\psi\sin\theta\sin\phi}&{-;\cos\theta\sin\phi}\ {+;\sin\psi\cos\phi}&{+;\cos\phi\cos\phi}&{}\ {-;\cos\phi\sin\theta\cos\phi}&{\sin\psi\sin\theta\cos\phi}&{\cos\theta\cos\phi}\ {+;\sin\psi\cos\phi}&{+;\cos\phi\sin\phi}&{}\end{array}\right]

  

从而有  

\left.\begin{array}{l}{{\alpha;=;\arctan(,w/,u,)}}\ {{\beta;=;\arcsin(,v/,V)}}\end{array}\right}

  

至此,完成了 $V\,,\psi_{k}\,,\theta_{k}\,,\alpha\,,\beta$ 的数据重构。  

（3）由弹道参数求过载。先求航迹坐标系的过载  

\left{\begin{array}{l}{n_{x k};=;V\mathrm{cos}\phi_{k}\mathrm{cos}\theta_{k}/g;+;\mathrm{sin}\theta_{k}}\ {n_{y k};=;V\mathrm{sin}\phi_{k}\mathrm{cos}\theta_{k}/g}\ {n_{z k};=;-;V\mathrm{sin}\theta_{k}/g;-;\mathrm{cos}\theta_{k}}\end{array}\right.

  

再类似于式(9-112）,利用 $L_{\delta g}\pmb{L}_{g k}$ 将 $n_{x\dot{\sf R}}\,,\,n_{y\dot{\sf R}}\,,\,n_{z\dot{\sf R}}$ 转换到弹体坐标系，求得 $\begin{array}{r}{\pmb{n}_{x}\mathrm{~,~}\pmb{n}_{y}\mathrm{~,~}\pmb{n}_{z\mathrm{~\circ~}}}\end{array}$  

上面给出了从角速率、姿态角和弹道测量数据重构角速率、过载、姿态角、攻角、侧滑角的方法。过载数据是由弹道参数数值微分得到的,故对弹道测量精度要求较高。攻角和侧滑角是由航迹角、姿态角和速度信息求取的，要求姿态角测量准确。为验证计算结果，还可用下列几何关系进行验算  

\left{\begin{array}{l}{\sin\alpha=\left[\sin\theta\cos\phi\cos\theta_{k}\cos(\psi\mathrm{-}\phi_{k})\mathrm{-}\right.}\ {\left.\qquad\sin\phi\cos\theta_{k}\sin(\psi\mathrm{-}\phi_{k})\mathrm{-}\cos\theta\cos\phi\sin\theta_{k}\right]/\cos\beta}\ {\sin\beta=\cos\phi\cos\theta_{k}\sin(\psi\mathrm{-}\phi_{k})\mathrm{+}}\ {\left.\sin\phi\sin\theta\cos\theta_{k}\cos(\psi\mathrm{-}\phi_{k})\mathrm{-}\sin\theta\sin\phi\sin\theta_{k}\right.}\end{array}\right.

  

# 2）再人体数据相容性检验  

再入体飞行试验常常仅测量过载和角速率，没有安装姿态角传感器，也没有攻角和侧滑角实测数据，严格地说测量没有余  

量，无法进行相容性检验。但实际飞行试验数据确实存在过载与角速率数据不协调的现象。  

鉴于再人体的过载与攻角、侧滑角成正比这一特点，利用法向力导数的先验知识，可以近似求得攻角和侧滑角的模拟观测值为  

\left{\begin{array}{l l}{\alpha_{m},=,-,,n_{z}m g/(,q,!\infty,S C_{N\alpha})}\ {\beta_{m},=,,n_{y}m g/(,q,!\infty,S C_{Y\beta})}\end{array}\right.

  

式中  

\begin{array}{r}{n_{y},=,n_{y m},-,\Delta n_{y}}\ {n_{z},=,n_{z m},-,\Delta n_{z}}\end{array}

  

$n_{\mathrm{{ym}}}$ 和 $\pmb{n}_{z m}$ 为质心处的过载测量值。  

再人体速度很高，致使在速度分量方程组中过载和重力项是小量，因此数据相容性检验主要是确定角速率漂移量。取状态方程组和观测方程组如下：  

状态方程组  

\frac{\mathrm{d}u}{\mathrm{d}t},=,v\bigl(,r_{m},-,\Delta r,\bigr),-,w\bigl(,q_{m},-,\Delta q,\bigr),+

g(,n_{x m},-,\Delta n_{x},-,\mathrm{sin}\theta,)

\frac{\mathrm{d},v}{\mathrm{d}t},=,w\big(,p_{m},-,\Delta\dot{p},\big),-,u,\big(,r_{m},-,\Delta r,\big),+

g(,n_{y},-,\Delta n_{y},+,\mathrm{cos}\theta\mathrm{sin}\phi,)

\frac{\mathrm{d}w}{\mathrm{d}t},=u\left(,q_{m},-,\Delta q,\right),-,v\left(,\phi_{m},-,\Delta\phi,\right),+

g\big(,n_{z m},-,\Delta n_{z},+,\mathrm{cos}\theta,\mathrm{cos}\phi,\big)

\frac{\mathrm{d}\theta}{\mathrm{d}t}=;\langle,q_{m},-,\Delta q,\rangle\mathrm{cos}\phi,-,\langle,r_{m},-,\Delta r,\rangle\mathrm{sin}\phi

\frac{\mathrm{d}\phi}{\mathrm{d}t}=\ p_{m}\ -\ \Delta\phi\ +\ \mathrm{tan}\theta\big[,\big(,q_{m}\ -\ \Delta q,\big)\mathrm{sin}\phi\ +

(,r_{m},-,\Delta r,)\cos\phi,]

  

观测方程组  

\alpha_{m};=;\arctan(,\w/,u,);+;\varepsilon_{1}

\beta_{m};=;\arcsin(;v/;\sqrt{{{u}^{2}},+,{{v}^{2}},+,{{w}^{2}}},);+;{\epsilon}_{2}

  

待估计参数 $\pmb{\theta}=(\Delta\phi\,,\Delta q\,,\Delta r\,,\Delta n_{x}\,,\Delta n_{y}\,,\Delta n_{z}\,)^{\mathrm{T}},$ 采用5.3节的最大似然法可以辨识出0,进而重构出相容的角速率和过载数据。  

对于正常式布局的某些战术导弹，舵面升力远小于总升力，仍可近似假定过载与攻角、侧滑角成正比，利用上述数学模型进行数据相容性检验。  

# 9.4 气动参数可辨识性分析和预估计  

气动参数可辨识性问题早在20世纪70年代初就已引起了研究者的高度重视，导致气动参数不可辨识的原因大致有以下一些：输人序列不能充分激发飞行器的某些模态；飞行器增稳系统的作用抑制了某些运动模态；测试设备及传感器的测量误差过大；待估参数之间多重相关；数学模型选择不合适；数据样本长度不够及参数初值选择不当等。这些因素都可能导致估计结果没有物理意义或估计误差协方差过大。因此,在气动参数辨识前，应进行参数的可辨识性分析，以确定哪些参数有可能进行参数估计，哪些参数因为信息量太少或信噪比太小而无法估计。对于可能进行参数估计的参数，还应根据先验知识或采用参数预估计方法给出待估计参数的初值。  

# 9.4.1 参数可辨识性分析  

判定系统可辨识性是个没有完全解决的理论问题。特别是对于非线性系统,从理论上判定可辨识性十分困难。这里只是从实用的角度，讨论飞行器气动参数可辨识性的实用分析方法。它实质上是一种基于参数数量级分析和相关性分析的工程方法。  

1）力系数的可辨识性分析  

气动力系数主要通过过载、攻角、舵偏角测量进行辨识,以纵  

318  

向气动力为例，采用线性气动力模型，其观测方程可写成  

\begin{array}{c}{{n_{z}\ =-\ \bigg[,R\sin\phi_{T},+,q,{\infty},S,\bigg(C{N0},+,C_{N\alpha},+,}}\ {{\phantom{\bigg|}}}\ {{C_{N\delta_{e}}\delta_{e},+,C_{N q},\frac{q c_{A}}{2,v}\bigg),\bigg],/,m g}}\end{array}

  

或  

-\ n_{z}m g\ -\ R\sin\phi_{T}\ =\ q,\infty,S\left(C_{N0},+,C_{N\alpha}\alpha\ +\right.

C_{N\delta_{\epsilon}}\sigma_{e},+,C_{N q},\frac{q c_{A}}{2,v}\Big)\equiv\sum_{i,=,1}^{4}C_{i}

  

式(9-125)左端是观测量，右端有 4个待估计参数,分为 4项。众所周知观测量是有误差的。设左端观测量的标准偏差为 $\sigma$ ，那么当式(9-125)右端某一项 $C_{i}$ 的值小于 $\pmb{\sigma}$ 时，表明此项对观测量的影响小于观测量的测量误差。换言之，此项提供的有用信息将湮没在测量的随机噪声之中。显然,在这种情况下， $C_{i}$ 项对应的气动参数是不可辨识的。  

对于飞机飞行试验，试验仪器的量程是按最大机动飞行时设计的，对于一般稳定、控制导数参数辨识的飞行试验，观测量通常只达总量程的 $1/10$ 左右。飞机飞行试验仪器的精度约为 $1\%\sim$ $2\%$ ，故观测量的误差约为 $10\%$ 。若式（9-125）中右端某项小于左端项的 $10\%$ ，则该项的气动系数无法辨识。即使参加辨识，其辨识出的结果是不可信的。  

若式(9-125)左端的值接近零，而右端有 $\pmb{\dot{p}}$ 项观测量的量级超过总量程的 $10\%$ ,那么可以辨识出 ${\mathfrak{p}}-1$ 个系数，也即只能辨识出气动系数的比值。当然，右端各项要有不同的时间历程，否则也无法辨识。例如,在某一飞行段中， $\delta_{e}\left(\,t\,\right)$ 等于常数,那么 $C_{N\hat{\delta}_{\!\varepsilon}}\delta_{e}\left(\mathbf{\Delta}t\right)$ 和 $C_{\mathrm{N0}}$ 是线性相关的，就无法分别辨识 $C_{N\hat{\sigma}_{e}}$ 和 $C_{N0}$ ,而只能辨识CNo。（t）+CNo。在这种情况下，如两项分别辨识，可能导致一项是很大的正值，另一项是绝对值很大的负值，都不可信，而两者之和却是合理的。  

图9-5给出一个算例。用风洞实验和理论估算所给的气动参数先验值计算式(9-125)各项的数值。由图可见,法向力项 $C_{N\alpha}\alpha$ 起主要作用，控制力项 $C_{N\delta_{e}}\delta_{e}(\mathbf{\Psi}_{t})$ 仅有法向力项的 $10\,\%$ 左右。由此可见，法向力静导数可以辨识，而控制导数虽可辨识，但误差会比较大。法向力的非线性项和法向力阻尼都很小，无法辨识。  

![](images/a30c778fce13eab07895520ab44811cb8f0965fd824e99ad300ffaf923cd3029.jpg)  
图9-5法向力参数数量级比较  

2）力矩系数可辨识性分析  

气动力矩系数主要由动量矩方程组进行辨识。以纵向气动力矩系数为例，采用布莱恩线性模型，其状态方程组为  

\frac{\mathrm{d}q}{\mathrm{d}t}=;\frac{I_{z},-,I_{x}}{I_{y}}p r,+,\frac{I_{x z}}{I_{y}}\bigl(,r^{2},-,\phi^{2},\bigr),+,\frac{q_{\infty},S c_{A}}{I_{y}}\Bigl(C_{m0},+,,C_{m a},+,\phi,\Bigr)

C_{m\hat{\delta}{\varepsilon}}\hat{\partial}{e},+,C_{m d}\ \frac{d c_{A}}{2,V},+,C_{m q}\ \frac{q c_{A}}{2,V}\Bigg)

  

应用攻角的微分方程，即体轴系的动量方程，代人式（9-126），略去高阶小量，稍加整理可得  

\frac{\mathrm{d}q}{\mathrm{d}t},-,\frac{I_{z},-,I_{x}}{I_{y}}\rho r,-,\langle,{r}^{2},-,{\rho}^{2},\rangle;\frac{I_{x z}}{I_{y}},=

  

320  

\frac{q_{\infty},S c_{A}}{I_{y}},\biggl[,C_{m0},+,C_{m a}a,+,C_{m\delta_{e}}\delta_{e},+,\bigl(,C_{m d},+,C_{m q},\bigr),\frac{q c_{A}}{2,V},\biggr]

  

(9 - 127)  

式（9-127)左端为观测量，右端五项是待估计参数项。类似于上节分析，若右端某一项远小于左端，则该项是不可辨识的。若左端接近于零,那么也只能辨识气动导数的比值。式(9-127)中的 $C_{m d}$ 和$C_{m q}$ 以相同形式出现于方程中，故这两个系数也无法分别辨识，只能辨识 $C_{m d}+C_{m q}$ ,除非对飞行试验做特殊的设计。  

图9-6给出又一算例。用风洞实验和理论估算所给的气动力矩系数的先验值计算式（9-127）的各项数值。由图可见，恢复力矩项 $C_{m a}\alpha$ 和控制力矩项 $C_{m\delta_{e}}\delta_{e}$ 的量级相当，且符号相反，它们是主要项。阻尼力矩 $(\,C_{m d}\,+\,C_{m q}\,)\,q c_{A}/2\,V$ 项虽然量级较小,仅有上述主要项的百分之十几,但因恢复力矩项 $C_{m a}\alpha$ 和控制力矩项 $C_{m\delta_{e}}\delta_{e}$ 符号相反，互相抵消。故阻尼力矩项对观测量有明显影响，可辨识。恢复力矩的非线性项比较小，不可辨识。  

![](images/fc703f98b56ebdeff8b9572b6fdcff1271493f19d7f5f0c07350bafce2460ad8.jpg)  
图9-6力矩系数各气动参数的数量级比较  

\begin{array}{r c l}{{}}&{{}}&{{\longleftarrow\left(\left.I_{z}\right/q_{\infty},S c_{A}\right)\left(\mathrm{d}q/\mathrm{d}t\right);;;-\cdots-\cdots-;C_{m\partial_{e}}\delta_{e};}}\ {{}}&{{}}&{{}}\ {{}}&{{---;-;;C_{m d}\alpha,;;\cdots\cdots\cdots;C_{m q}q c_{A}/,V_{\circ}}}\end{array}

  

# 9.4.2 参数预估计  

第5章讨论的参数估计方法都要给出待估参数的初值。通常初值离真值越近,则辨识计算收敛就越快。特别是参数估计最有效的最大似然法通常是采用牛顿一拉夫逊迭代算法，该算法忽略了待估计参数增量 $\Delta\pmb{\theta}$ 的平方项，这就要求 $\Delta\pmb{\theta}$ 是个小量，也就要求0的初值位于真值附近。  

待估计参数的初值通常是利用先验知识给出；也可以依据动力学系统的状态方程组，采用简化算法求得。下面以飞行器气动参数辨识为例，讨论参数预估计方法。一般情况下，气动参数辨识可以采用理论计算或风洞实验的气动数据作为选代初值。但有时由于理论计算或风洞实验的气动数据与飞行中的气动数据有较大差别，或者某些参数在风洞中测量不准，因而影响辨识准度，有时甚至引起迭代发散。这时，需要采用近似算法对气动系数进行预估计。以下所述的建模前估计法是一个简易有效的方法。  

# 1）力系数和力矩系数估计  

建模前估计法的第一步是利用观测数据确定气动力系数和力矩系数。由飞行器运动六自由度动力学方程，可以求出力和力矩系数的表达式  

C_{A};=;(:X_{T}:-:n_{x}m g:)/q_{\infty},S

C_{\Upsilon};=;n_{\mathrm{y}}m g/q_{\infty},S

C_{N};=;-;\left.n_{z}m g\right/q\infty S

\begin{array}{l}{{C_{l},=,\displaystyle\frac{1}{D}\bigg(,C_{l1},-,\displaystyle\frac{I_{x z}}{I_{z}}C_{n1}\bigg)}}\ {{\phantom{\bigg(}}}\ {{C_{n},=,\displaystyle\frac{1}{D}\bigg(,C_{n1},-,\displaystyle\frac{I_{x z}}{I_{x}}C_{l1}\bigg)}}\end{array}

C_{m};=;\frac{1}{q_{\infty},S c_{A}}\big[,I_{s}q:-:\big(,I_{z}:-:I_{x},\big),\phi r:-:I_{x z},(:r^{2}:-:\phi^{2}),\big]

  

式中  

D;=;1:-:I_{{x z}}^{2}/(:I_{x}I_{z})

\begin{array}{l}{{C_{I1},=,\displaystyle\frac{1}{q_{\infty},S l}\bigg[,I_{x}D!!!/,p,-,\left(\frac{I_{x},-,I_{y}}{I_{z}},+,1\right)I_{x z}p q,-,\left(,I_{y},-,I_{z},-,\frac{I_{x z}^{2}}{I_{z}},\right)!!q r,\bigg],,}}\ {{C_{n1},=,\displaystyle\frac{1}{q_{\infty},S l}\bigg[,I_{z}D!!!r,-,\left(,I_{x},-,I_{y},+,\frac{I_{x z}^{2}}{I_{x}},\right)!!p q,-,\left(\frac{I_{y},-,I_{z}}{I_{x}},-,1\right)I_{x z}q r,\bigg],.}}\end{array}

  

将实测的 $n_{x}\setminus n_{y}\setminus n_{z}\setminus{p}\setminus{q}\setminus r$ 及其微分平滑 $\pmb{\mathscr{p}}\setminus\pmb{\mathscr{q}}\setminus\pmb{\mathscr{r}}$ 代人式$(9\mathrm{-}128)\mathrm{\sim}$ 式(9-133)可求出力系数和力矩系数 $C_{A}\left(\,t\,\right),C_{Y}\left(\,t\,\right)$ $C_{\vee}(\,t\,)\,,C_{l}(\,t\,)\,,C_{n}(\,t\,)\,,C_{m}(\,t\,)$ 的时间历程。  

# 2）待辨识参数初值的预估计  

建模前估计法的第二步是由力系数和力矩系数确定待辨识的未知参数。若力系数和力矩系数是系统状态参数的已知模型，那么采用加权最小二乘法即可求得待估计参数的预估值。例如，已知空气动力和力矩系数 $C_{A}\left(\,t\,\right),C_{Y}\left(\,t\,\right),\,C_{N}\left(\,t\,\right),\,C_{l}\left(\,t\,\right),\,C_{n}\left(\,t\,\right)$ $C_{m}\left(t\right)$ 和状态参数 $\alpha(\,t\,)\,,\beta(\,t\,)\,,\phi^{\prime}(\,t\,)\,,q(\,t\,)\,,r(\,t\,)$ ，控制参数 $\delta_{a}\left(t\right)$ $\delta_{e}(\,t\,)\,,\delta_{r}(\,t\,)$ 。而气动力数学模型是布莱恩线性模型  

C_{A}(,t,),=,C_{A0},+,C_{A B}\bigl(,\alpha^{2}(,t,),+,\beta^{2}(,t,),\bigr)

C_{Y}(,t,),=,,C_{Y0},+,C_{Y\beta}\beta(,t,),+,C_{Y\delta_{\gamma}}\delta_{r}(,t,),+,C_{Y r},\frac{r,(,t,),l}{2,V}

C_{N}(,t,),=,C_{N0},+,C_{N\alpha},a\left(,t,\right),+,C_{\delta,}\delta_{e}(,t,),+,C_{N q},\frac{q\left(,t,\right)c_{A}}{2,V}

C_{l}(,t,),=,C_{l0},+,C_{l\beta}\beta(,t,),+,C_{l\delta_{a}}\delta_{a}(,t,),+,C_{l\beta},\frac{\beta(,t,),l}{2,V}

C_{m}\left(,t,\right);=;C_{m0},+,C_{m a},\alpha\left(,t,\right),+,C_{m\delta_{e}}\delta_{e}(,t,);+;C_{m q};\frac{q\left(,t,\right)c_{A}}{2,V}

C_{n}(,t,),=,C_{n0},+,C_{n\beta}\beta(,t,),+,C_{n\delta,}\delta_{r}(,t,),+,C_{n r},\frac{r,(,t,),l}{2,V}

  

则利用式（9-134）～式（9-139）,采用加权最小二乘法可以很快求出 $C_{A0}\ldots C_{A B}\ldots C_{N0}\,,C_{N a}\ldots\ldots C_{n\delta_{r}}$ $C_{n r}$ 等待估计参数的初值。若力系数、力矩系数与系统状态参数的关系式（即数学模型）没有确定，则需要采用第3章的模型辨识方法确定模型形式，然后冉确定参数初值。  

# 参考文献  

1蔡金狮．飞行器系统辨识．北京：宇航出版社,1995   
2蔡金狮．动力学系统辨识与建模．北京:国防工业出版社,1991   
3何国伟，误差分析方法,北京：国防工业出版社，1978   
4肖明耀．误差理论及应用．北京：计量出版社，1985   
5陈启宗．一级数字信号处理.北京：高等教育出版社，1987   
6  Williamson W E Jr. Instrument Modeling for Aerodynamic Coefficient Identification from Flight Test Data.J.Guidance and Control,1980,3(3) :225 \~ 279   
7 Gerlach O H. Measurement of Performance, Stability and Control Characteristics in Nonsteady Flight with a High Accuracy Instrumentation System. Rep. VTH - 136, Dept. Aeronaut . Eng. Technol. Univ. Delft, Netherlands, 1976   
8  Klein V,Schiess J R. Compatibility Check of Measured Aircraft Responses Using Kinematic Equations and Extended Kalman Filter. NASA TND-8514,1997   
9  Klein V,Mogan D R.Estimation of Bias Errors in Measured Airplane Responses Using Maximum Likelihood Method, NASA TM-89059,1987   
10  Evans R J, Goodwin G C,Feik R A,et al. Aircraft Flight Data Compatibility Checking Using Maximum Likelihood and Extended Kalman Filter Estimation . 7th IFAC Identification and System Parameter Estimation, York, UK,1985   
11 Keskar D A, Klein V.Determination of Instrumentation Errors from Measured Data Using Maximum Likelihood Method. AIAA 80-1602,1980   
12 2 Martin C A. Estimation of Aircraft Dynamic States and Instrument Systematic Erors from Flight Test Measurements Using the Carlson Square- Root Formulation of the Kalman Filter. ARL-Aero-Note-399,1981   
13  Feik R A.A Maximum Likelihood Program for Nonlinear System Identification with Application to Aircraft Flight Data Compatibility Checking. ARL-Aero-Note-411 , 1983   
14  Feik R A. On the Applica1:ion of Compatibility Checking Techniques to Dynamic Flight Test Data. ARL-Aero-R-161,1985   
15  Feik R A. Determination of Instrument Errors by Compatibility Checking-Results from Dynamic Flight Test Data. ARL-Aero-R-162,1985   
16 Poskawetz K O, Brockhaus R.Flight Path Reconstruction-A Powerful Tool for Data Compatibility Check. ICAS-86-5.4.4,1986   
17  Verhaegen M H. Robust Adaptive Flight Path Reconstruction Technique for Nonsteady Longitudinal Flight Test Maneuvers. J. Guidance, Control and Dynamics, 1988,11(1) : 72 \~ 79   
18  Trankle T L, Rabin U H. Filtering Flight Data prior to Aerodynamic System Identifica tion . AIAA 83-2098,1983   
19 Bierman G J. Factorization Methods for Discrete Sequential Estimation.New York: Academic Press,1977   
20  Keskar D A, Klein V.Determination of Instrumentation Errors from Measured Data Using Maximum Likelihood Method. AIAA 80-1602,1980   
21 Heck M L,Findlay J T,Compton H R.Calibration of the Aerodynamic Coefficient Identification Package Measurements from the Shuttle Entry Flights Using Inertial Measurement Unit Data.AIAA 83-2100,1983   
22  Heck M, Findlay J T ,Kelly G M. The Adaptation of a Strap down Formulation for Processing Inertial Platform Data.AIAA 82-1332,1982   
23 Wingrove R C,Bach R E Jr.Analysis of General Aviation Accidents Using ATC Radar Records.AIAA 82-1310,1982   
24  Bach R E Jr.A Variational Technique for Smoothing Flight- Test and Accident Data. AIAA 80-1601,1980   
25 Wingrove R C,etc . Aircraft Motion Analysis Using Limited Flight and Radar Data. $10^{\circ}$ Annual Symposium of the Society of Flight Test Engineers, Las Vegas, 1979   
26  Bach R E, Wingrove R C.Equation for Determining Aircraft Motion from Accident Data . NASA TM-78609,1930   
27李乃宏,吴瑶华,黄文虎．飞行实测数据相容性检验的三步法．宇航学报，1993，  

(4)  

# 第10章 气动力参数辨识  

10.1概述  

本教材前8章着重论述了系统辨识的基本理论和实用算法。从本章开始讨论系统辨识在飞行器研制实践中的应用。其中，气动力参数辨识是飞行器系统辨识中应用最早、发展最快、解决问题最成功的领域。  

飞行器气动参数辨识自华纳（Warner）等的先导性工作以来，至今已有八十余年的历史。早期的气动参数辨识是从稳态飞行和长周期振荡数据获取飞行特性。20 世纪 40 年代至50年代，一方面，飞机性能的提高使短周期模态对纵向飞行品质的影响开始突出,另一方面，频域法和回归技术在工程界普及，气动参数辨识主要采用频域法、回归技术、图形技术、模拟匹配技术。随着现代控制理论、统计数学和电子计算机技术的迅速发展，系统辨识理论不断丰富和完善。它在飞行试验数据分析中的应用，促使气动参数辨识在60年代末特别是70年代获得了飞跃发展，并在飞行器研制中发挥着越来越重要的作用[1]  

气动参数辨识的目的是建立空气动力系数的数学模型，亦即建立气动力系数与飞行状态参数的关系式。这个关系式可以是代数方程、积分方程或微分方程形式。最早建立的气动力数学模型是线性代数方程式，模型参数为稳定导数和操纵导数，它仅适用小攻角飞行状态。线性模型在飞行器研制中得到广泛应用，至今仍是飞行器运动稳定性、飞行品质和飞行性能分析的基础。线性气动参数辩识已发展得很成熟，各国主要飞行器研制单位都备有自己的线性气动参数辨识软件包。当飞行器处于大攻角飞行状态时，例如飞机的失速/尾旋区和过失速机动状态、战术导弹的大机动状态等，线性气动力模型不再适用，为此，已提出了多项式模型、样条函数模型、阶跃响应函数模型、状态空间模型、微分方程模型等各种形式的非线性气动力数学模型。目前，气动参数辨识研究工作的重点是非线性气动参数、大攻角非定常效应、非线性闭环系统的辨识方法和应用。  

本章针对各类不同飞行器的不同试验方法和输出信息，建立不同的气动参数辨识方程组，并采用不同的辨识方法进行参数估计。目的在于，帮助读者掌握和灵活应用参数辨识技术，解决飞行器研制中提出的气动参数辨识问题。  

# 10.2 固定翼飞行器气动参数辨识  

固定翼飞行器是指飞机、飞航导弹、地空导弹、空空导弹等具有较大升力面的飞行器。这类飞行器的共同特点是：始终在稠密的大气层内飞行，由升力面产生升力来平衡自身的重力，而由舵面产生控制力矩作必要的机动动作。本节首先给出固定翼飞行器刚体6自由度非线性动力学系统的气动参数辨识最大似然算法，然后分别给出纵向和横侧向小扰动运动的气动参数辨识增厂厂义卡尔曼滤波算法，最后阐述静不稳定飞行器气动参数辨识的方程解耦技术。  

# 10.2.1 6 自由度模型气动参数辨识  

当飞机和战术弹作大机动飞行时，纵横向运动互相耦合，必须采用6自由度动力学方程。由于飞行试验的大气环境通常较好，可忽略过程噪声。因此,这里给出以6自由度动力学方程组作为状态方程组、不考虑过程噪声的气动参数辨识最大似然法和具体算式[2,3]。算式适用于面对称飞行器的一般形式。采用这套算式编制的软件，既可用于面对称飞行器6自由度飞行状态的气动参数辨识，也可用于轴对称型或纵向、横侧向运动等简化情况的气动参数辩识。  

1）空气动力数学模型  

用最大似然法进行气动参数辨识，首先要求给出空气动力的数学模型。这里采用多项式模型，其中气动静导数取至三阶或五阶项以反映非线性特性，舵面效率和动导数只取线性项。体轴系6分量气动力系数的数学模型和相应的气动参数的具体形式如下  

\begin{array}{l}{{C_{A},=C_{A0},+,C_{A B}(,\alpha^{2},+,\beta^{2})}}\ {{\ }}\ {{C_{Y},=C_{Y0},+,C_{Y\beta}\beta,+,C_{Y\beta}{}^{3}\beta^{3},+,C_{\gamma\delta_{r}}\hat{\partial}{r}}}\ {{\ }}\ {{C{N},=C_{N0},+,C_{N a}\alpha,+,,C_{N a}{}^{3}\alpha^{3},+,C_{N\partial_{\epsilon}}\hat{\partial}{e}}}\ {{\ }}\ {{C{l},=C_{l0},+,C_{l a}\alpha,+,C_{l\beta}\beta,+,C_{l\delta_{a}}\hat{\partial}{a},+,C{l\delta_{r}}\hat{\partial}_{r}\ +}}\end{array}

C_{l\phi}!!!!!/,\frac{l}{2,V},+,C_{l q}q,\frac{c_{A}}{2,V},+,C_{l r}r,\frac{l}{2,V}

C_{m};=C_{m{\bf0}},+,C_{m{\alpha}}{\alpha},+,C_{m a}{}^{3},\alpha^{3},+,C_{m a}{}^{5},\alpha^{5},+,C_{m{\delta}{e}}{\delta}{e};+

C_{m\dot{0}}\dot{\delta}{e};\frac{c{A}}{2,V},+,C_{m q}q;\frac{c_{A}}{2,V},+,C_{m p}\dot{p};\frac{l}{2,V}

C_{n};=C_{n0};+;C_{n\beta}\beta;+;C_{n\beta}^{;;;3}\beta^{3};+;C_{n\beta}^{;;;;5}\beta^{5};+;C_{n\delta_{r}}^{;;;;;;;};

C_{n\delta_{r}}\dot{\delta}{r}\ \frac{l}{2,V},+,C{n r}r\ \frac{l}{2,V},+,C_{n\phi}p\ \frac{l}{2,V}

  

式中 CA——平均空气动力弦长；  

$l$ 横侧向参考长度，通常取为机（弹）翼展长；  

a、0、,一——-分别为滚转、俯仰、偏航操纵器的偏度。  

面对称飞行器的 $I_{x z}$ 不为零，角速率 $\pmb{\dot{p}}$ 和 $r$ 满足下列方程  

\begin{array}{c}{{\dot{p}\ =\displaystyle\frac{1}{D}\bigg[\left[\frac{I_{s},-,I_{z}}{I_{x}},-,\frac{I_{x z}^{2}}{I_{x}I_{z}}\right]q r,+,\left(\frac{I_{x},-,I_{y}}{I_{z}},+,1\right)\frac{I_{x z}}{I_{x}}\dot{p}q\ +}}\ {{\frac{q_{\infty},S l}{I_{x}}\bigg(C_{l},+,\frac{I_{x z}}{I_{z}}C_{n}\bigg)\bigg]}}\end{array}

  

328  

\begin{array}{l}{\dot{r},=\displaystyle\frac{1}{D}\bigg[\left(\displaystyle\frac{I_{x},-,I_{y}}{I_{z}},+,\displaystyle\frac{I_{x z}^{2}}{I_{x}I_{z}}\right)+,\left(\displaystyle\frac{I_{y},-,I_{z}}{I_{x}},-,1\right)\displaystyle\frac{I_{x z}}{I_{z}}q r,,+}\ {\displaystyle\frac{q_{\infty},S l}{I_{z}}\Big(C_{n},+,\displaystyle\frac{I_{x z}}{I_{x}}C_{l}\Big)\bigg]}\end{array}

  

式中 $D=1-{I_{x z}}/{(\,I_{x}I_{z}\,)}$  

为了简化气动参数辨识方程，令  

\begin{array}{r}{C_{l1}\equiv C_{l}+\frac{I_{x z}}{I_{z}}C_{n}}\ {C_{n1}\equiv C_{n}+\frac{I_{x z}}{I_{x}}C_{l}}\end{array}

  

取 $C_{l1}$ 和 $C_{n1}$ 的数学模型与 $C_{l}$ 和 $C_{n}$ 相同。在下面的气动参数辨识方程组中,辨识的气动参数均为与 $C_{l1}$ 和 $C_{n1}$ 相应的气动参数，但为了书写方便，下标“1”都已略去。  

对 $C_{l1}$ 和 $C_{n1}$ 进行参数辨识得到相应的气动参数 $C_{l10}\,,C_{l1\beta}\,,\cdots$ 和 $C_{n\,10}\,,C_{n\,1\,\beta}\,,\cdots$ 后,再利用式(10-7)和式(10-8)求出 $C_{l0}\,,C_{l\beta}\,,\cdots$ 和 $C_{n0}\ldots C_{n\beta}\ldots\ldots_{\circ}$ 例如  

\begin{array}{l}{{C_{l\beta},=,\displaystyle\frac{1}{D}\bigg(C_{l,1\beta},-,\displaystyle\frac{I_{z x}}{I_{z}}C_{n,1\beta}\bigg)}}\ {{\mathrm{}}}\ {{C_{n\beta},=,\displaystyle\frac{1}{D}\bigg(C_{n,1\beta},-,\displaystyle\frac{I_{z x}}{I_{z}}C_{l,1\beta}\bigg)}}\end{array}

  

2）气动参数辨识方程组  

飞行器6自由度动力学系统包括3个速度分量、3个角速率分量、3个欧拉角和3个位置坐标，共12个状态变量。由于偏航角 $\psi$ 和位置坐标 $x_{g}^{\prime},y_{g}^{\prime}$ 对各气动参数和其他状态变量没有影响，在气动参数辨识的状态方程组中可以略去。位置坐标 $\boldsymbol{z}_{g}^{\prime}$ 或高度$h$ 通过大气密度值影响气动力和气动力矩，在状态方程组中应予保留。当高度有测量值 $h\left(t\right)$ ,且密度也有测量值 $\rho(h)$ 时,可以直接采用测量值，而略去状态方程组中的高度方程。  

由于状态变量的初值是未知的，它对最大似然参数辨识结果的影响又较大，因此，通常将状态变量的初值作为未知参数参加辨识。  

飞行器气动参数辨识的状态变量、观测变量和待辨识参数分别为  

状态变量： $x\left(\,t\,\right)=\left(\,u\,,v\,,w\,,\phi\,,q\,,r\,,\theta\,,\phi\,,h\,\right)^{T}$ 观测变量: $y(\mathbf{\xi}_{t})=(\mathbf{\xi}_{\hat{P}}\,,q\,,r\,,a_{x}\,,a_{y}\,,a_{z}\,,\alpha\,,\beta,\theta\,,\phi\,,h\,)^{\textup{T}}$  

待辨识参数： $\theta=(\,C_{l0}\,,\,C_{l a}\,,\,C_{l\beta}\,,\,C_{l\delta_{a}}\,,\,C_{l\delta_{r}}\,,\,C_{l\beta}\,,\,C_{l q}\,,\,C_{l r}\,,\,C_{m0}\,,\,C_{l\delta_{r}}\,,$ $\begin{array}{r}{\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\sum_{m\alpha}\,,C_{m a}^{\phantom{\dagger}}\,,\,C_{m a}^{\phantom{\dagger}}\,^{\phantom{\dagger}}\,,C_{m{\hat{\theta}}_{\epsilon}}^{\phantom{\dagger}}\,^{\phantom{\dagger}},\,C_{m{\hat{\theta}}_{\epsilon}}^{\phantom{\dagger}}\,^{\phantom{\dagger}},C_{m q}^{\phantom{\dagger}}\,^{\phantom{\dagger}},C_{m{\hat{\theta}}}^{\phantom{\dagger}}\,^{\phantom{\dagger}}\,C_{n{\hat{\theta}}}^{\phantom{\dagger}}\,^{\phantom{\dagger}}\,^{\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,\,C_{m a}^{\dagger}\,\!,}\,C_{m{\hat{\theta}}_{\epsilon}}^{\phantom{\dagger}}\,^{\phantom{\dagger}}\,^{\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,\!\!\!\!\!\!\!\!\!\!\!\!\!\!\,\!\!\!\!\!\!\!\!\!\!\!\!\,C_{m{\hat{\theta} $ $\begin{array}{l}{{{\nonumber\,o r a\!\!\!}\,{\bf\Gamma}_{m a}\!{\bf\Gamma},{\bf\Gamma}_{m a}\!{\bf\Gamma},{\bf\Gamma}_{{m a}}\!{\bf\Gamma},{\bf\Gamma}_{{m a}}\!{\bf\Gamma},{\bf\Gamma}_{{m a}}\!{\bf\Gamma},-m{\bf{e}}_{\!\!\!},{\bf\Gamma}_{{m}}\!{\bf\Gamma}_{{m}}\!{\bf\Gamma},-m{\bf{e}}\,{\bf{\Gamma}}_{{m}}\!{\bf\Gamma},{\bf\Gamma}_{{m}}\!{\bf\Gamma},{\bf\Gamma}_{{m}}\!{\bf\Gamma}_{{m}}\!{\bf\Gamma},\!\!\!}}}\\ {{\nonumber\,C_{n\delta_{r}}\!{\bf\Gamma},C_{n r}\,,{\bf{\Gamma}}_{{C_{{n}}}\!{\bf{\Gamma}},C_{{A0}}}\,,\,C_{{A B}}\,,\,C_{{X0}}\,,\,C_{Y0}\,,\,C_{Y\beta},\,C_{Y\beta^{3}}\,,\,C_{Y\delta_{r}}\,,\,C_{N0}\,,\,C_{N a}\,,\,C_{N a}\,,\,C_{N a}}}\\ {{\nonumber\,C_{N\delta_{r}}\,,{\bf{\Gamma}}_{{u\bf{\Gamma}}}_{0}\,,\upsilon_{0}\,,\upsilon_{0}\,,\beta_{0}\,,q_{0}\,,r_{0}\,,\beta_{0}\,,\beta_{0}\,,h_{0}\}^{T}}}\end{array}$ 3下面给出气动参数辨识最大似然法的具体算式：  

（1）状态方程组。  

\begin{array}{r l}&{\dot{u};=-;q w,+,r v,+,g,(,n_{x},-,\mathrm{sin}\theta,)}\ &{\dot{v};=-;r u;+;\rho w,+,g,(,n_{y},+,\mathrm{cos}\theta\mathrm{sin}\phi,)}\ &{\dot{w};=-;\rho v;+;q u;+;g,(,n_{z},+,\mathrm{cos}\theta\mathrm{cos}\phi,)}\end{array}

\dot{p}\ =\frac{1}{D}\Bigg[\left[\frac{I_{y},-,I_{z}}{I_{x}},-,\frac{I_{x z}^{2}}{I_{x}I_{z}}\right]q r;+;\left[\frac{I_{x},-,I_{y}}{I_{z}},+,1\right]\frac{I_{x z}}{I_{x}}p q\ +

\begin{array}{c c}{{\displaystyle{\frac{q_{\infty}{I_{x}}}{I_{x}}\biggl(C_{l0}+C_{l a}a\ +\ C_{l i j}\beta+C_{l i}\hat{a}{a}+C{l i k}\hat{a}{r}+}}\ {{\displaystyle{\cal C}{l i j}{\hat{\cal D}}\ {\hat{\cal U}}+C_{l i j}q\ \frac{c_{A}}{2V}+\ C_{l\ell}r\ \frac{l}{2V}\biggr)\ \biggr]}}}&{{(10}}\ {{\dot{q}}\ {=}\frac{I_{\tau}-I_{x}}{I_{y}}p r-\frac{I_{x x}}{I_{y}}(\hat{p}^{2}-r^{2})\ +}}\ {{\displaystyle{\frac{q_{\infty}{\cal S}}{I_{y}}}\biggl(C_{m0}\ +\ C_{m a}a\ +\ C_{m a}a^{3}+C_{m a}a^{5}+C_{m b}\hat{a}{e}\ +}}\ {{\displaystyle{\cal U}{\ m}{\cal S}\ +\ }}\end{array}

C_{m\dot{\delta}}\dot{\delta}{e};\frac{c{A}}{2,V},+,,C_{m q}q;\frac{c_{A}}{2,V},+,,C_{m\dot{p}}\dot{p};\frac{l}{2,V}\Bigg)

\dot{r};=\frac{1}{D}\Bigg[;\Bigg[\frac{I_{x};-;I_{y}}{I_{z}},+;\frac{I_{x z}^{2}}{I_{x}I_{z}}\Bigg]\beta q;+;\Bigg(\frac{I_{y};-;I_{z}}{I_{x}},-,1\Bigg)\frac{I_{x z}}{I_{z}}q r;+

\begin{array}{l}{{{\displaystyle\frac{q_{\infty}S l}{I_{z}}\biggl(C_{n0}+,C_{n\beta}\vartheta+,C_{n\beta}\mathrm{}^{3},\beta^{3},+,C_{n\beta}\mathrm{}^{5},\beta^{5},+,C_{n\delta_{r}}\hat{\delta}{r},+,}}}\ {{~~}}\ {{C{n\beta}\hat{\delta}{r},\frac{l}{2,V},+,C{n r},\frac{l}{2,V},+,C_{n\beta}\dot{p},\frac{l}{2,V},\biggr)}}\ {{}}\ {{{\displaystyle\dot{\vartheta}~}=q\cos\phi,-,r\sin\phi}}\ {{}}\ {{{\displaystyle\dot{\phi}=\phi~+,\tan\theta,(q\sin\phi,+,r\cos\phi)}}}\ {{~~}}\ {{{\displaystyle\dot{h}~}=,u\sin\theta,-,v\cos\theta\sin\phi,-,w\cos\theta\cos\phi}}\end{array}\qquad

  

式中  

\begin{array}{l}{{n_{x},=\displaystyle\frac{1}{m g}(,T\mathrm{cos}\phi_{T}\mathrm{cos}\varphi_{T},-,q_{\infty},S C_{A},)}}\ {{,}}\ {{n_{y},=\displaystyle\frac{1}{m g}(,T\mathrm{sin}\phi_{T},+,q_{\infty},S C_{Y},)}}\ {{,}}\ {{n_{z},=\displaystyle\frac{1}{m g}(,T\mathrm{cos}\phi_{T}\mathrm{sin}\varphi_{T},-,q_{\infty},S C_{N})}}\end{array}

  

为3个体轴方向的过载；  

$S$ ——参考面积；  

$T$ 发动机推力；  

$\psi_{T}$ -推力作用线与 $\boldsymbol{O x z}$ 平面的夹角；  

$\varphi_{T}$ 一—推力作用线在 $O x z$ 平面上的投影与 $O x$ 轴的夹角。  

推力作用线偏离质心通常较小,且难以准确测定，它所形成的力矩可并人气动力矩的常数项中。  

状态方程组的积分初值可先取实测值，再迭代校正。取实测值时,速度分量由速度、攻角和侧滑角计算获得；若攻角和侧滑角无实测值，可根据式（10-19)和式（10-20），由过载和舵偏角的实测值以及横向力和法向力参数的先验知识估算出 $\alpha\left(0\right)$ 和 $\beta(0)$ ，再计算 $u\left(0\right),v(0),w(0),$  

（2）观测方程组。  

\begin{array}{l}{{\phi,=,\phi,+,\varepsilon_{,1}}}\ {{{}}}\ {{q,=,q,+,\varepsilon_{,2}}}\end{array}

\begin{array}{c}{{\cdot\lefteqn.\qquad\cdot\ s}}\ {{\quad n_{x},=\displaystyle\frac1{m g}\big[\ T\cos!\phi_{T}!\cos!\phi_{T},-,}}\ {{\quad\quad q_{\infty},S(,C_{A0},+,C_{A B}(,\alpha^{2},-,\beta^{2}),),\big],+,\varepsilon_{4}}}\ {{\quad n_{y},=\displaystyle\frac1{m g}\big[\ T\sin!\phi_{T},+,q_{\infty},S(,C_{Y0},+,}}\end{array}

C_{Y\beta},\beta,+,C_{{\scriptscriptstyle Y!\beta}^{3}}\beta^{3},+,C_{{\scriptscriptstyle Y!\delta}{r}}\delta{r},),],+,\varepsilon_{5}

n_{z}\ =\frac{1}{m g}[\ T\mathrm{cos}\psi_{T}\mathrm{sin}}\phi_{T}\ -\ q,\infty,S(,C_{N0}\ +

C_{N!\alpha}!\alpha:+:C_{N!\alpha^{3}}!\alpha^{3}:+:C_{N!\delta_{e}}!\delta_{e}!\right)\mathrm{]+~}!\epsilon_{6}

\begin{array}{r l}&{\alpha,=\arctan\frac{w,-,w_{w}}{u,-,u_{w}},+,\epsilon_{7}}\ &{\beta,=\arcsin\frac{v,-,v_{w}}{V},+,\epsilon_{8}}\ &{\theta,=\theta,+,\epsilon_{9}}\ &{\phi,=\phi,+,\epsilon_{10}}\ &{h,=\ h,+,\epsilon_{11}}\end{array}

  

# 式中 e;——零均值随机观测噪声；  

$u_{w}\setminus v_{w}\setminus w_{w}$ 稳态风在体轴系上的投影；  

V=\sqrt{,(\mathrm{\boldmath~\boldsymbol{\mu}}!-!\mathrm{\boldmath\boldsymbol{\mu}}_{w}\mathrm{\boldmath})^{2}+(\mathrm{\boldmath~\boldsymbol{\sigma}}!-!\mathrm{\boldmath\boldsymbol{v}}_{w},)^{2}+(\mathrm{\boldmath\boldsymbol{w}}!-!\mathrm{\boldmath\boldsymbol{w}~}_{w},)^{2}}

  

# （3）灵敏度方程组。  

\begin{array}{c}{{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial{\bf\it\Psi}}{\partial\theta_{l}},=,v,\frac{\partial{r}}{\partial\theta_{l}},+,r,\frac{\partial{v}}{\partial\theta_{l}},-,w,\frac{\partial{q}}{\partial\theta_{l}},-,q,\frac{\partial{w}}{\partial\theta_{l}},+}}\ {{\displaystyle g\left(\frac{\partial{n_{x}}}{\partial\theta_{l}},-,\cos\theta,\frac{\partial{\theta}}{\partial\theta_{l}}\right)}}\ {{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial{v}}{\partial\theta_{l}},=,w,\frac{\partial{p}}{\partial\theta_{l}},+,\phi,\frac{\partial{w}}{\partial\theta_{l}},-,u,\frac{\partial{r}}{\partial\theta_{l}},-,r,\frac{\partial{u}}{\partial\theta_{l}},+}}\end{array}

g\left{\frac{\partial,n_{y}}{\partial\theta_{l}},-,\sin\theta\mathrm{sin}\phi;\frac{\partial,\theta}{\partial\theta_{l}},+,\mathrm{cos}\theta\mathrm{cos}\phi;\frac{\partial,\phi}{\partial\theta_{l}}\right}

\begin{array}{r l}{\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial w}{\partial\theta_{i}}=u,\frac{\partial q}{\partial\theta_{i}}+\ q,\frac{\partial u}{\partial\theta_{i}}-v,\frac{\partial p}{\partial\theta_{i}}-\ p,\frac{\partial v}{\partial\theta_{i}}+}&{}\ &{\quad\quad\quad\quad\quad\quad\varepsilon\Big(\frac{\partial n_{s}}{\partial\theta_{i}}-\sin\theta\cos\phi,\frac{\partial\theta}{\partial\theta_{i}}-\cos\theta\sin\phi,\frac{\partial\phi}{\partial\theta_{j}}\Big)}\ {\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial p}{\partial\theta_{i}}=\frac{1}{D}\Big[\left[\frac{I_{s}-I_{s}}{I_{s}}-\frac{I_{s}^{2}}{I_{s}I_{s}}\right]\Big(\frac{\partial}{\partial\theta_{i}}+\nu\frac{\partial q}{\partial\theta_{i}}\Big)+}\ &{\quad\quad\quad\quad\quad\Big[\frac{I_{s}-I_{s}}{I_{s}}+1\Big]\frac{I_{s}}{I_{s}}\Big(\nu\frac{\partial q}{\partial\theta_{i}}+\frac{\partial p}{\partial\theta_{i}}\Big)+}\ &{\quad\quad\quad\quad\quad\frac{q=S_{i}}{I_{s}}\Big(C_{s},\frac{\partial\alpha}{\partial\theta_{i}}+C_{s},\frac{\partial\beta}{\partial\theta_{i}}+}\ &{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad C_{s},\frac{I}{2}\frac{\partial p}{\partial\theta_{i}}+C_{s},\frac{c_{s}}{2}\frac{\partial q}{\partial V}\Big)}\ &{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\end{array}

\begin{array}{r l}&{\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial q}{\partial\theta_{l}}=\frac{I_{z},-,I_{x}}{I_{y}}\bigg(\hbar,\frac{\partial,r}{\partial\theta_{l}}+,r,\frac{\partial,\phi}{\partial\theta_{l}}\bigg)-2,\frac{I_{x z}}{I_{y}}\bigg(\hbar,\frac{\partial,\phi}{\partial\theta_{l}}-,r,\frac{\partial,r}{\partial\theta_{l}}\bigg)+}\ &{\quad\quad\quad\quad\quad\frac{q_{\infty},S l}{I_{y}}\bigg(C_{m,\alpha},\frac{\partial,\alpha}{\partial\theta_{l}}+3{C_{m,\alpha}}^{,\alpha}^{2},\frac{\partial,\alpha}{\partial\theta_{l}},+}\ &{\quad\quad\quad\quad\quad5C_{m,\alpha},{^3,\alpha},\frac{\partial,\alpha}{\partial\theta_{l}},+,C_{m,q},\frac{C_{A}}{2,V},\frac{\partial,q}{\partial\theta_{l}},+,C_{m,\rho},\frac{l}{2,V},\frac{\partial,\phi}{\partial\theta_{l}}\bigg)+,U_{2,l}}\end{array}

\begin{array}{l}{{\displaystyle\frac{r}{\bar{\jmath}{\ell}}=\frac{1}{D}\bigg[\left(\frac{{\cal I}{s}-{\cal I}{y}}{{\cal I}{\ell}}+\frac{{\cal I}{x z}^{2}}{{\cal I}{x}{\cal I}{\ell}}\right)\left(\dot{p},\frac{\partial q}{\partial\theta{\ell}}+q,\frac{\partial\dot{p}}{\partial\theta_{\ell}}\right)+}}\ {{\displaystyle~~}}\ {{\displaystyle~\left(\frac{{\cal I}{y}-{\cal I}{\tau}}{{\cal I}{x}}-1\right)\frac{{\cal I}{x z}}{{\cal I}{z}}\bigg(q,\frac{\partial\dot{r}}{\partial\theta{\ell}}+,r,\frac{\partial q}{\partial\theta_{\ell}}\bigg)+}}\ {{\displaystyle~\frac{q_{\infty}{\cal S}{\cal I}{\ell}}{{\cal I}{z}}\bigg(C_{n\beta},\frac{\partial\beta}{\partial\theta_{\ell}}+3C_{n\beta}\beta^{2},\frac{\partial\beta}{\partial\theta_{\ell}},+}}\ {{\displaystyle~~}}\ {{\displaystyle~~~}}\end{\cal S}{\displaystyle C}{n\beta}\dot{\beta}^{4},\frac{\partial\dot{\beta}}{\partial\theta{\ell}}+,C_{n r},\frac{1}{2,{\cal V}},\frac{\partial\dot{r}}{\partial\theta_{\ell}}+,C_{n\beta},\frac{\dot{\cal I}}{2,{\cal V}},\frac{\partial\dot{p}}{\partial\theta_{\ell}}\bigg)\bigg]+,\cal U_{3,\ell}\quad\mathrm{(onon)},.}}\end{array}

\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial\theta}{\partial\theta_{l}},=\frac{\partial q}{\partial\theta_{l}}\mathrm{cos}\phi,-,q,\mathrm{sin}\phi,\frac{\partial\phi}{\partial\theta_{l}},-,\frac{\partial r}{\partial\theta_{l}}\mathrm{sin}\phi,-,r\mathrm{cos}\phi,\frac{\partial\phi}{\partial\theta_{l}}

\begin{array}{r l}&{\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial^{4}}{\partial\theta_{i}}-\frac{\partial^{3}}{\partial\theta_{i}}+\tan\theta\Big(\frac{\partial\theta}{\partial\theta_{i}}\mathrm{sin}^{+}+\mathrm{\ros}\frac{\partial^{2}\phi}{\partial\theta_{i}}+}\ &{\frac{\partial^{2}\mathrm{recos}}{\partial\theta_{i}}\mathrm{s}-r\mathrm{sin}^{\frac{\partial}{\partial\theta_{i}}}\Big)+}\ &{-\frac{1}{\mathrm{cos}^{2}}\varphi(\mathrm{sin}^{+}+\mathrm{recos}^{\frac{\partial\theta}{\partial\theta_{i}}})\frac{\partial^{2}}{\partial\theta_{i}}}\ &{\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial\phi}{\partial\theta_{i}}-\frac{\partial^{3}}{\partial\theta_{i}}\mathrm{sin}^{\frac{\partial}{\partial\theta}}+\nu\mathrm{cos}\frac{\partial^{3}\theta}{\partial\theta_{i}}-}\ &{\frac{\partial^{1}\mathrm{recos}}{\partial\theta_{i}}\mathrm{sin}^{\frac{\partial}{\partial\theta}}+\nu\mathrm{sin}^{\partial}\mathrm{sin}^{\frac{\partial}{\partial\theta}}\frac{\partial^{\theta}}{\partial\theta_{i}}-}\ &{\mathrm{vesin}\partial\phi\frac{\partial^{2}}{\partial\theta_{i}}-\frac{\partial^{3}}{\partial\theta_{i}}\mathrm{cos}\theta\mathrm{cos}^{\phi}\mathrm{sin}^{\phi}+}\ &{\mathrm{win}\partial\phi\mathrm{cos}\frac{\partial^{4}}{\partial\theta_{i}}+\nu\mathrm{cos}\delta\mathrm{sin}\frac{\partial^{3}\phi}{\partial\theta_{i}}}\end{array}

\begin{array}{r l}{\displaystyle\theta\boldsymbol{\ell}{l}}&{!-!\cdots!\cdots\cdots!\cdots\cdots!\cdots!}\ &{w\sin\theta\cos\phi,\frac{\partial\theta}{\partial\theta{l}}+w\cos\theta\sin\phi,\frac{\partial\phi}{\partial\theta_{l}}\qquad\quad(11\pm\frac{\partial\boldsymbol{\ell}{1}}{\partial\theta{1}}),,}\ {\displaystyle\frac{\partial\boldsymbol{n}{x}}{\partial\theta{l}}=-,\frac{2}{m\boldsymbol{g}}q_{\infty},S C_{A B}\bigg(\alpha,\frac{\partial\alpha}{\partial\theta_{l}}+,\beta,\frac{\partial\beta}{\partial\theta_{l}}\bigg)+,U_{4,l}\quad(11\pm\frac{\partial\boldsymbol{g}{y}}{\partial\theta{1}}),,}\ {\displaystyle\frac{\partial\boldsymbol{n}{y}}{\partial\theta{l}}=\frac{1}{m\boldsymbol{g}}q_{\infty},S\bigg(C_{Y_{\beta}},\frac{\partial\beta}{\partial\theta_{l}}+3,C_{Y^{\beta}}\beta^{2},\frac{\partial\beta}{\partial\theta_{l}}\bigg)+,U_{5,l}\quad(11\pm\frac{\partial\boldsymbol{g}{y}}{\partial\theta{1}}),,}\ {\displaystyle\frac{\partial\boldsymbol{n}{z}}{\partial\theta{l}}=-,\frac{1}{m\boldsymbol{g}}q_{\infty},S\bigg(C_{N_{\alpha}},\frac{\partial\alpha}{\partial\theta_{l}}+3,C_{N_{\alpha}}\mathrm{s}^{\alpha},\frac{\partial\alpha}{\partial\theta_{l}}\bigg)+,U_{6,l}\quad(11\pm\frac{\partial\boldsymbol{g}{z}}{\partial\theta{l}})}\end{array}

\frac{\partial\alpha}{\partial\theta_{l}},=\frac{\left(,u,-,u_{w}\right),\frac{\partial,w}{\partial\theta_{l}},-,\left(,w,-,w_{w}\right),\frac{\partial,u}{\partial\theta_{l}}}{\left(,u,-,u_{w}\right)^{2},+,\left(,w,-,w_{w}\right)^{2}}

\frac{\partial\beta}{\partial\theta_{\iota}}=\frac{1}{V!\cos\beta},\frac{\partial,v}{\partial\theta_{\iota}}

  

式中 $U_{i\,,j}\big(\,i=1\,,2\,,\cdots,6\,;j=1\,,2\,,\cdots,43\,\big)$ 项为  

$\begin{array}{r l}{U_{1,n}=U_{1,n}\frac{q_{1}}{2\sqrt{\pi}}}&{U_{1,n}=U_{1,n},\frac{q_{1}}{2\sqrt{\pi}}}\\ {U_{2,n}=\frac{q_{2}}{L}}&{U_{2,n}=U_{2,n},\quad U_{2,n}=U_{2,n},\frac{q_{1}}{2\sqrt{\pi}}}\\ {U_{1,n}=U_{2,n}\nearrow}&{U_{2,n}=U_{2,n},\quad U_{2,n}=U_{2,n}\frac{q_{2}}{2\sqrt{\pi}}}\\ {U_{2,n}=U_{1,n}\frac{q_{1}}{2\sqrt{\pi}}}&{U_{2,n}=U_{2,n}\frac{p_{2}}{2\sqrt{\pi}}}\\ {U_{3,n}=U_{2,n}\quad}&{U_{3,n}=U_{3,n}\beta}&{U_{3,n}=U_{3,n}\beta^{3}}\\ {U_{3,n}=U_{3,n}\beta^{3}}&{U_{3,n}=U_{3,n}\beta,\quad U_{3,n}=U_{3,n}\beta,\quad\frac{q_{1}}{2\sqrt{\pi}}}\\ {U_{3,n}=U_{3,n}\tau\frac{q_{1}}{2\sqrt{\pi}}}&{U_{3,n}=U_{3,n}\beta\frac{q_{1}}{2\sqrt{\pi}}}\\ {U_{4,n}=-\frac{1}{m}q_{1}}&{U_{4,n}=U_{4,n}(\alpha^{2}+\beta^{2})}\\ {U_{5,n}=U_{5,n}\beta}&{U_{6,n}=U_{5,n}\beta^{3}}&{U_{8,n}=U_{3,n}\beta^{3}}\\ {U_{5,n}=U_{4,n}\beta}&{U_{8,n}=U_{3,n}\beta^{3}}\end{array}$ $\begin{array}{r l}&{U_{1,1}=\displaystyle\frac{q_{\infty}S^{i}}{D I_{x}}\qquad U_{1,2}=U_{1,1}\alpha\qquad U_{1,3}=U_{1,1}\beta}\\ &{U_{1,4}=U_{1,1}\delta_{a}\quad U_{1,5}=U_{1,1}\delta,\qquad U_{1,6}=U_{1,1}\beta\;\frac{L}{2V}}\\ &{U_{1,7}=U_{1,1}\underline{{\sigma}}\;\frac{c_{\mathrm{A}}}{2V}\quad U_{1,8}=U_{1,1}r\;\frac{I}{2V}}\\ &{U_{2,9}=\displaystyle\frac{q_{\infty}S^{i}}{I_{y}}\qquad U_{2,10}=U_{2,9}\alpha\quad U_{2,11}=U_{2,9}\alpha^{3}}\\ &{U_{2,12}=U_{2,9}\alpha^{5}\quad U_{2,13}=U_{2,9}\delta,\quad U_{2,14}=U_{2,9}\delta_{c}\;\frac{c_{\mathrm{A}}}{2V}}\\ &{U_{2,15}=U_{2,9}\underline{{\sigma}}\;\frac{c_{\mathrm{A}}}{2V}\quad U_{2,16}=U_{2,9}\beta\;\frac{I}{2V}}\end{array}$ U6,31 = U4.25 U6,32 = U6,31α U6,33 = U6,31α U6.34 =U6,31  

其余的 $U_{i,j}=\mathbf{0}$  

灵敏度方程的积分初值为  

$\frac{\partial u\left(0\right)}{\partial\theta_{35}}\:=\frac{\partial v\left(0\right)}{\partial\theta_{36}}\:=\:\frac{\partial w\left(0\right)}{\partial\theta_{37}}\:=\:\frac{\partial\phi\left(0\right)}{\partial\theta_{38}}\:=\:\frac{\partial q\left(0\right)}{\partial\theta_{39}}\:=$ $\frac{\partial r(0)}{\partial\theta_{40}}\,=\,\frac{\partial\theta(0)}{\partial\theta_{41}}\,=\,\frac{\partial\phi(0)}{\partial\theta_{42}}\,=\,\frac{\partial h(0)}{\partial\theta_{43}}\,=\,1$  

（4）最大似然准则。  

J\left(,\theta,\right);=;\sum_{i,=,1}^{N}\left[,\pmb{\nu}^{\mathrm{T}}(,i,),\pmb{R}^{,-1}\pmb{\nu}(,i,),+,\ln,\mid,\pmb{R},\mid,\right]

  

式中 $\pmb{\nu}(i)$ 输出误差  

\pmb{\nu}(,i,);=;\hat{\pmb{y}}(,i,):-:\pmb{y}_{m}(,i,)

  

${\hat{\mathbf{y}}}\left(\,i\,\right)$ ——由观测方程(10-21)～式(10-31)计算得到的观测量；  

$\boldsymbol{y}_{m}\left(\textit{i}\right)$ ———观测量的实测值。  

$\pmb{R}$ -一测量噪声的协方差矩阵，当测量噪声的统计特性未知时，采用 $\pmb{R}$ 的最优估计  

\hat{\pmb{R}};=;\frac{1}{N}\sum_{i,=,1}^{N}{\pmb{\nu}}\big({,i,}\big),{\pmb{\nu}}^{\mathrm{T}}\big({,i,}\big)

  

（5）牛顿-拉夫逊迭代修正公式  

\Delta\pmb{\theta}:=:\left(\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}}\right){43\times43}^{-1}\left(\frac{\partial J}{\partial\theta{k}}\right)_{43\times1}

  

式中  

\frac{\partial J}{\partial\theta_{k}},=,2\sum_{i,=,1}^{N}\pmb{\nu}^{\mathrm{T}}(,i,)\pmb{R}^{-1},\frac{\partial\hat{\pmb{y}}(,i,)}{\partial\theta_{k}}

\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}};=;2\sum_{i,=,1}^{N},\frac{\partial\hat{\mathbf{y}}^{\mathrm{T}}(\mathbf{\nabla}i,)}{\partial\theta_{k}}\pmb{R}^{-1},\frac{\partial\hat{\mathbf{y}}(\mathbf{\nabla}i,)}{\partial\theta_{l}}

  

$\frac{\partial\hat{\mathbf{y}}\left(\mathbf{\nabla}i\mathbf{\eta}\right)}{\partial\theta_{k}}$ 是由灵敏度方程式（10-32）～式（10-45)计算得到的观测量对待辨识参数的灵敏度。  

用上述算式编制计算程序，可以从飞行器飞行试验数据或动态响应仿真数据辨识气动参数。此方法收敛较快，一般迭代3次 ${\sim}4$ 次即可收敛。  

在最大似然辨识方法中，气动参数是常数。为了反映气动参数随时间的变化，可以每次处理飞行试验数据中的 $N$ 个数据，每处理一段后就向前推进 $N_{f}$ 个点， $N_{f}{\ll}N$ 。这样，相邻的两段数据有 $(N-N_{f})$ 个点是重复的。随着数据向前推进，由每段数据辨识  

![](images/a3864472a9d4006ff317134150aeea8280bff98b46d1ea8bb9f5a9a65bc9977d.jpg)  

![](images/c55c45f4e7952dcf3fc6737516d92cbcd9bcb29653a652e3bbc8a9a3db97af9e.jpg)  

1-01  

![](images/a3f3460c30fcd9d2c0b2c8f1e803564134bea77ec3286b45be174993b1159992.jpg)  

![](images/0350c7c316e541c5cbdb6a54fe5e662271bbea5082869aa1551a049887557d90.jpg)  

![](images/b31a1253b3be9e10affe5669908be3ba30d30652d49fd750b3479f4ec7c569ec.jpg)  

![](images/fa855e47e5e4145bfdefbe351424548408f0fc07ddfc2a2c815ecf175f74a96c.jpg)  

![](images/57eb09420eec7c32b5c6971307b3dd907ec788fa0f3fd5b60bafe24c7b24f063.jpg)  

-O 国  

获得的气动参数是不同的，可以近似反映出气动参数随马赫数、雷诺数等参数的变化规律。  

# 3）算例  

取某典型导弹的物理几何参数、气动参数和控制输人进行气动参数辨识仿真计算。表10-1给出无噪声条件下理想观测量的非线性气动参数辨识结果。结果表明，辨识值与准确值符合较好。由于非线性项很小,其辨识误差较大,但总的气动系数的准确值与辨识结果是非常一致的，参见图10-1。  

表10-1无噪声非线性气动参数辨识结果  


<html><body><table><tr><td>气动参数</td><td>准确值</td><td>辨识值</td><td>相对误差</td><td>气动参数</td><td>准确值</td><td>辨识值</td><td>相对误差</td></tr><tr><td>Cio</td><td>0.01</td><td>0.01005</td><td>0.005</td><td>C</td><td>-- 15.74</td><td>- 15.09</td><td>0.041</td></tr><tr><td>Cia</td><td>0.08</td><td>0.0799</td><td>0.0013</td><td>CnB</td><td>- 52.0</td><td>4 90.4</td><td>0 0.73</td></tr><tr><td>Cip</td><td>0.12</td><td>-0.1188</td><td>0.01</td><td></td><td>250.0</td><td>271.3</td><td>0.085</td></tr><tr><td>Ci</td><td>-6.0</td><td>- 5.996</td><td>0.0007</td><td>Cnb</td><td>-- 15.47</td><td>- 15.30</td><td>0.011</td></tr><tr><td>C6,</td><td>-- 4.0</td><td></td><td></td><td></td><td>2.0</td><td></td><td></td></tr><tr><td>Cip</td><td>- 20.0</td><td>- 20.36</td><td>0.018</td><td>Cn</td><td>- 300.0</td><td>- 244.3</td><td>18.6</td></tr><tr><td>Ctr</td><td>10.0 一</td><td>7.686</td><td>0.23</td><td></td><td>-50.0</td><td>1 21.65</td><td>0 57</td></tr><tr><td>Cia</td><td>- 15.0</td><td>-- 14.08</td><td>0.061</td><td>CAO</td><td>0.5</td><td>0.5138</td><td>0.028</td></tr><tr><td></td><td>0.03</td><td>0.044</td><td>0.47</td><td>CAB</td><td>-2.0</td><td>-3.13</td><td>565</td></tr><tr><td>ma</td><td>- 15.74</td><td>一 15.85</td><td>0.007</td><td>Cyo</td><td>0.02</td><td>0.044</td><td>1.2</td></tr><tr><td></td><td>52.0 一</td><td>- 37.21</td><td>0.28</td><td>Cyβ</td><td>- 18.0</td><td>17.64</td><td>0.02</td></tr><tr><td>Cma?</td><td>250.0</td><td>203.3</td><td>0.19</td><td>CyB3</td><td>- 60.0</td><td>77.52</td><td>0.292</td></tr><tr><td>Cm8,</td><td>- 15.74</td><td>- 15.84</td><td>0.024</td><td>Cy8,</td><td>-5.0</td><td>-5.0</td><td>0</td></tr><tr><td>Cmo</td><td>2.0</td><td></td><td></td><td>CNO</td><td>0.01</td><td>0.012</td><td>0.20</td></tr><tr><td>Cmg </td><td>- 300.0</td><td>- 290.0</td><td>0.033</td><td>CNa</td><td>18.0</td><td>17.77</td><td>0.013</td></tr><tr><td>Cmp</td><td>50.0 一</td><td>-43.21</td><td>0.136</td><td>CNa3</td><td>- 60.0</td><td>47.45 一</td><td>0.21</td></tr><tr><td>Cno</td><td>0.02</td><td>0.0867</td><td>3.34</td><td>CN8,</td><td>5.0</td><td>5.018</td><td>0.004</td></tr></table></body></html>  

图 10-2和图10-3分别给出方波型输人并有标准偏差为观测量峰值 $5\,\%$ 的随机噪声和大气风暴湍流过程噪声的气动参数辨识仿真结果与精确值的比较。结果表明，在较大的观测噪声和过程噪声的情况下，最大似然法仍能给出工程上有价值的辨识结果。  

图10-4给出某地空导弹的闭环飞行试验的气动参数辨识结果与风洞试验、理论计算结果的比较，气动静导数比较一致，动导数相差较大，舵面效率的风洞试验结果偏大。  

![](images/77a4cd6e0b4eb91dcf692127750a2e65ee417e2baf2db9f62ff387c513f0c2f3.jpg)  
图10-4某地空导弹飞行试验的辨识结果与风洞试验、理论计算结果的比较  
风洞试验结果： $\Delta\!\cdots\!\Delta$ 计算结果： $\circ$ 飞行辨识结果。  

表 10-2气动参数真值及其仿真结果  


<html><body><table><tr><td>气动参数</td><td>C10</td><td>Cβ</td><td>CIp</td><td>C ma</td><td>Cm8</td><td>C mq</td><td>nf3</td><td>Cno r</td></tr><tr><td>精确值</td><td>0.01</td><td>-1.0</td><td>- 20.0</td><td>- 15.74</td><td>-15.47</td><td>- 300.0</td><td>- 15.74</td><td>- 15.47</td></tr><tr><td>辨识结果</td><td>0.0045</td><td></td><td>0.9923 -20.73</td><td>-15.71</td><td>- 14.26</td><td>- 304.8</td><td>- 15.49</td><td>-15.57</td></tr><tr><td>气动参数</td><td></td><td>CAO</td><td>CAB</td><td>Cyβ</td><td>Cy8,</td><td>CNα</td><td>CN8,</td><td></td></tr><tr><td>精确值</td><td>- 300.0</td><td>0.50</td><td>-2.0</td><td>- 18.04</td><td>-2.58</td><td>18.04</td><td>2.58</td><td></td></tr><tr><td>辨识结果</td><td>-- 280.9</td><td>0.4885</td><td>-2.03</td><td>- 17.51</td><td>- 1.898</td><td>17.15</td><td>1.567</td><td></td></tr></table></body></html>  

表 10-3气动参数真值及其仿真结果  


<html><body><table><tr><td>气动参数</td><td>Cio</td><td>Ciβ</td><td>CIP</td><td>Cma</td><td>hu)</td><td>CnB</td></tr><tr><td>精确值</td><td>0.01</td><td>- 1.0</td><td>- 20.0</td><td>- 15.74</td><td>- 300.0</td><td>- 15.74</td></tr><tr><td>辨识结果</td><td>0.0055</td><td>-1.132</td><td>30.97</td><td>- 15.26</td><td>- 143.1</td><td>- 17.78</td></tr><tr><td>气动参数</td><td>Cnr</td><td>CAO</td><td>CAB</td><td>Cyβ</td><td>CNa</td><td></td></tr><tr><td>精确值</td><td>300.0</td><td>0.50</td><td>- 2.0</td><td>- 18.04</td><td>18.04</td><td></td></tr><tr><td>辨识结果</td><td>- 384.4</td><td>0.5064</td><td>-- 2.742</td><td>- 18.58</td><td>18.44</td><td></td></tr></table></body></html>  

# 10.2.2 纵向气动参数辨识  

当飞行器在铅垂平面内飞行时，可以用 $(\,u\,,w\,,q\,)3$ 个自由度描述之。研究飞行器稳定性和操纵性的小扰动线化方程组，也可以解耦成两组独立无关的方程组，即纵向小扰动方程组和横侧向小扰动方程组。本节给出应用增广的广义卡尔曼算法进行气动参数辩识的具体算式，其中气动力采用线性模型。  

对于纵向机动和纵向小扰动，飞行器运动的状态参数简化为${\pmb x}=(\,{\pmb u}\,,{\pmb w}\,,{\pmb q}\,)^{\mathrm{~T~}}$ ，状态方程组为  

\begin{array}{r l}{\dot{u};=-;q w;+;g(;n_{x};-;\mathrm{sin}\theta,)}&{{}}\ {\dot{w};=;q u;+;g(;n_{z};-;\mathrm{cos}\theta)}&{{}}\end{array}

\dot{q};=;\frac{q_{\infty},S l}{I_{y}},\bigg(C_{m0},+,C_{m a}\alpha,+,C_{m\delta_{e}}\delta_{e},+,C_{m q}q,\frac{c_{A}}{2,V}\bigg)

\begin{array}{r c l}{{n_{x}!!}}&{{!=\displaystyle\frac{1}{m g}\big[,T\mathrm{cos}\phi_{T},-,q_{\infty},S C_{A},\big]}}\ {{}}&{{}}&{{}}\ {{n_{z}!!}}&{{!=!\displaystyle\frac{1}{m g}\big[,T\mathrm{sin}\phi_{T},-,q_{\infty},S\big(,C_{N!a}\alpha,+,C_{N!\delta_{e}}\delta_{e}\big),\big]}}\ {{}}&{{}}&{{}}\ {{\alpha:=\arctan\displaystyle\frac{w,-,w_{w}}{u,-,u_{w}}}}\end{array}

  

待辨识的气动参数为  

\begin{array}{r l}&{\pmb{\theta}=(\boldsymbol{C}{A},,\boldsymbol{C}{N_{a}},,\boldsymbol{C}{\mathrm{N}\delta{\epsilon}},,\boldsymbol{C}{m0},,\boldsymbol{C}{m a},,\boldsymbol{C}{m q},,C{m\delta_{\epsilon}})^{\mathrm{T}}\equiv}\ &{\qquad(,\theta_{1},,\theta_{2},,\cdots,\theta_{7},)^{\mathrm{T}}}\end{array}

  

满足  

\theta_{i};=;0\qquad(;i;=;1,,2,,\cdots,,7,)

  

定义增广的状态矢量x。为  

\begin{array}{c}{{{\pmb x}{a},=(,u,,w,,q,,\theta{1},,\theta_{2},,\cdots,\theta_{7},)^{\mathrm{T}}=}}\ {{\ }}\ {{(,x_{1},,x_{2},,\cdots,x_{10},)^{\mathrm{T}}}}\end{array}

  

观测矢量 $\pmb{y}$ 取为  

{\bf y},=,(,q,,n_{x},,n_{z},)^{\textup T}

  

根据 4.2.4节有关状态矩阵 F 和观测矩阵H 的定义，由式(10-48）～式（10-53)可推导出  

\begin{array}{r l}&{F_{1,1}=\displaystyle\frac{1}{m}\delta\mathrm{S}\alpha\mathrm{C}{A}}\ &{F{1,2}=-,q}\ &{F_{1,3}=-,w}\ &{F_{2,1}=q-\displaystyle\frac{1}{m^{\beta}}\delta\bigg[u,\mathrm{C}{N}-\frac{1}{2},(w-w{w}),{\cal C}{N{a}}\bigg]}\ &{F_{2,2}=-\displaystyle\frac{1}{m^{\beta}}\delta\bigg[w,\mathrm{C}{N}+\frac{1}{2},(u-u{w}),{\cal C}{N{a}}\bigg]}\ &{F_{2,3}=u}\ &{F_{3,1}=\displaystyle\frac{1}{2}\beta\bigg[u,\mathrm{C}{m}-\frac{1}{2},(w-w{w}),{\cal C}{m}\bigg]}\ &{F{3,2}=\displaystyle\frac{1}{2}\beta\bigg[w,\mathrm{C}{m}-\frac{1}{2},(u-u{w}),{\cal C}_{m}\bigg]}\end{array}

\begin{array}{l}{{F_{3,3}\displaystyle=\frac{1}{I_{y}}q\infty S l C_{m q}\ \frac{c_{A}}{2,V}}}\ {{{\cal F}_{4,3}\displaystyle=1}}\end{array}

  

其余 $F_{i,j}\;=\;0(\;i\;=\;1,2,\cdots,10\,;j\;=\;1,2,\cdots,10)$ (10 - 58)$\begin{array}{l}{{\displaystyle{H_{1,3}=1}}}\\ {{\displaystyle{H_{2,1}=-\frac{1}{m g}\rho S u C_{A}}}}\\ {{\displaystyle{H_{2,2}=-\frac{1}{m g}\rho S w C_{A}}}}\\ {{\displaystyle{H_{3,1}=-\frac{1}{m g}\rho S\Big[u C_{N}-\frac{1}{2}(w-w_{w})C_{N_{a}}\Big]}}}\\ {{\displaystyle{H_{3,2}=-\frac{1}{m g}\rho S\Big[w C_{N}+\frac{1}{2}(u-u_{w})C_{N_{a}}\Big]}}}\end{array}$ 其余 $H_{i,j}\,=\,0(\,i\,=\,1\,,2\,,3\,;j\,=\,1\,,2\,,\cdots,10)$ (10 - 59)  

忽略过程噪声的影响， $\pmb{T}\!=\!0$ 。利用式(10-48)～式（10-59)，可采用增广的广义卡尔曼算法辨识飞行器纵向气动参数，具体步骤如下 :  

（1）输人数据。舵偏输人 $\delta_{e}(\,t\,)$ ,速度 $V(t)$ ,高度 $h\left(t\right)$ ,密度$\rho(t)$ ，风速 ${\pmb u}_{{\pmb w}}({\pmb\ t})$ 和 $w_{w}(t)$ ,质量 $m\left(t\right)$ ,惯量矩 $\boldsymbol{I}_{\boldsymbol{y}}(\boldsymbol{\tau})$ ,参考面积S,参考长度 $l$ ，过载传感器 $\pmb{n}_{x}$ 和 ${\pmb n}_{\pmb z}$ 的安装位置， $n_{z}$ 和 $\pmb q$ 传感器的固有频率和阻尼,气动参数 $C_{A}\ 、C_{N a}\ 、C_{N\bar{o}_{e}}\ 、,C_{m0}\ 、C_{m a}\ 、C_{m q}\ 、C_{m\bar{o}_{e}}$ 的预估值,遥测数据 $q\left(\,i\,\right),n_{x}\left(\,i\,\right),n_{z}\left(\,i\,\right)$ ，等等。  

(2）数据预处理。剔除和补正跳点、错点，滤去高频噪声，进行时延修正等。  

(3）状态初值确定。利用式(10-51）一式(10-53),由过载初值 估算出攻角初值，再估算出 ${\pmb u}\left({\bf0}\right)$ 和 ${\boldsymbol{w}}(0)$  

(4）状态参数预测。利用式(10-48）～式(10-50)和式（10-55），从 $u\left(0\right),w(0),q\left(0\right)$ 和气动参数初值积分出 $u\left(1\,|\,0\,\right),w\left(1\,|\,0\,\right).$ $q\left(1\mid0\right)$ ，得 $\pmb{x}_{a}(1\,|\,\mathbf{0})$  

（5）误差协方差阵初值确定。根据验前信息确定 $10\times10$ 维误差协方差矩阵 ${\cal P}(0\,|\,0)$ ，可取为对角矩阵。  

(6）误差协方差阵预测。由式(10-59)和下式积分 $\pmb{P}$ (1/0)  

\frac{\mathrm{d}}{\mathrm{d}t}p(\textit{t}|\textit{t}{k-1}),=,{\cal F}(\textit{t}){\cal P}(\textit{t},|\textit{t}{k-1}),+

\mathbf{\cal{P}}(\mathbf{\lambda}{t}\mid t{k-1})\mathbf{\cal{F}}^{\mathrm{{T}}}(\mathbf{\lambda}_{t}),+,P Q P^{\mathrm{{T}}}

\begin{array}{r}{P\left(,t_{k-1}\mid t_{k-1},\right);=;P\left(,k,-,1,\mid,k,-,1,\right)\quad(,t_{k-1}\leqslant t\leqslant t_{k},)}\end{array}

  

从 $\pmb{P}(\pmb{k}-1\mid\pmb{k}-1)$ 积分出 $\pmb{{\cal P}}(\pmb{\mathscr{k}}\mid\pmb{\mathscr{k}}-1)$  

(7）增益矩阵 $\kappa(k)$ 的计算。由式(10-59)和下式计算 $10\times3$ 维增益矩阵 $\kappa(k)$  

\pmb{K}(\pmb{k}),=,\pmb{P}(\pmb{k}\mid\pmb{k},-,1)\pmb{H}^{\operatorname{T}}(\pmb{k})\big[\pmb{H}(\pmb{k})\pmb{P}(\pmb{k}\mid\pmb{k},-,1),\times

\pmb{H}^{\mathrm{T}}(,\pmb{k},),+,\pmb{R}(,\pmb{k},),]^{-1}

  

（8）误差协方差阵校正。由下式计算 $\pmb{P}$ (1 1)  

\pmb{P}(\pmb{k}\mid\pmb{k}),=,\left[\pmb{I},-,\pmb{K}(,\pmb{k},),\pmb{H}(,\pmb{k},),\right]\pmb{P}(,\pmb{k},\mid,\pmb{k},-,1)

  

（9）状态参数和气动参数校正值计算。由下式计算校正值$\pmb{x}_{a}$ (1/ 1)  

\pmb{x}{a}\left(,k,\mid,k,\right);=;\pmb{x}{a}\left(,k,\mid,k,-1,\right),+,K\left(,k,\right)\pmb{\nu}\left(,k,\right)

\psi\left(k\right);=;\left(,q,-,q_{m},,n_{x},-,n_{x m},,n_{z};-;n_{z m},\right)^{\mathrm{T}}

  

从而得到利用新的实测信息对气动参数初估值的校正。重复 $(4)\sim$ （9）的计算步骤，就可以递推估计出气动参数。  

# 10.2.3 横侧问气动参数辨识  

当飞行器作小扰动飞行时，横侧向运动可与纵向运动解耦。从而，在横侧向运动方程中，纵向运动变量作为已知的时间历程而出现。本节给出应用增广的广义卡尔曼滤波法进行气动参数辨识的具体算式，其中气动力采用线性模型。  

飞行器横侧向气动参数辩识的状态变量、观测变量和待辨识 参数为  

状态变量： ${\pmb x}\,(\,t\,)=(\,{\pmb\,\nu}\,,\,{\pmb\,\phi}\,,\,{\pmb\,r}\,,\,\phi\,)^{\textup T}$ 观测变量： $\mathbf{y}(\,t\,)=(\,\beta,\rho\,,r\,,\phi\,,a_{y}\,)^{\mathrm{T}}$  

待辨识参数：  

\boldsymbol{\theta}=(,C_{Y\beta},,C_{Y\hat{\sigma}{r}},,C{l\beta},,C_{l\beta},,C_{l r},,C_{l\delta_{a}},,C_{l\delta_{r}},,C_{n\beta},,C_{n\beta},,C_{n r},,C_{n\delta_{a}},,C_{n\delta_{r}},)^{\mathrm{T}}

  

1）状态方程组  

\begin{array}{c}{{\dot{v}=-\dot{r},\tilde{u},+,\beta\dot{w}+,g,(n_{y}+\cos\bar{\theta}\sin\phi)\qquad\qquad\qquad(10-66)}}\ {{\dot{p}={\frac{1}{D}}\Bigg[\left({\frac{I_{y}-I_{z}}{I_{x}}}-{\frac{I_{x}^{2}\dot{\mathbf{z}}}{I_{x}I_{z}}}\right)!\bar{q}r+\left({\frac{I_{x}-I_{y}}{I_{z}}}+{1}\right)!{\frac{I_{x}}{I_{x}}}\hat{p}\bar{q}\dot{\mathrm{\Delta}}+}}\ {{\frac{q_{\infty}S l}{I_{x}}}\Big(C_{t}+{\frac{I_{x}\dot{\mathbf{z}}}{I_{x}}}C_{n}\Big)\Bigg]}\ {{\dot{r}={\frac{1}{D}}\Bigg[\left({\frac{I_{x}-I_{y}}{I_{z}}}+{\frac{I_{x}^{2}}{I_{x}I_{z}}}\right)!\bar{p}!!!+\left({\frac{I_{y}-I_{z}}{I_{x}}}-1\right)!{\frac{I_{x}\hat{q}\cdot r}{I_{z}}}+}}\ {{\frac{q_{\infty}S l}{I_{z}}\Big(C_{n}+{\frac{I_{x}\dot{\mathbf{z}}}{I_{x}}}C_{l}\Big)\Bigg]}}\end{array}\ \ \left(10-68\right)

\dot{\phi}=\phi,+,\tan!\tilde{\theta}(,\tilde{q}\sin\phi,+,r\cos\phi,)

\dot{\theta}_{i},=0\qquad(,i,=,1,,2,,\cdots,12,)

  

式中 $\:\tilde{u}\;,\tilde{w}\;,\tilde{q}\;,\tilde{\theta}-\:$ 已知的时间历程。  

\begin{array}{l}{{\displaystyle{D,=1,-,\frac{I_{x z}}{I_{x}I_{z}}}}}\ {{\displaystyle{n_{y},=\frac{1}{m g}(,T\mathrm{cos}\psi_{T}\mathrm{sin},\phi_{T},+,q_{,\infty},S C_{Y},)}}}\end{array}

  

气动力模型为  

C_{Y};=;C_{Y\beta}\beta:+:C_{Y\hat{\delta}{r}}\delta{r}

C_{l};=C_{l\beta},\beta;+;C_{l\phi},\dot{\rho};\frac{l}{2,V},+;C_{l r}r;\frac{l}{2,V},+;C_{l\delta_{a}}\delta_{a};+;C_{l\delta_{r}}\delta_{r}

C_{n}\ =C_{n\beta},\beta,+,C_{n\beta},\frac{l}{2,V},+,C_{n r}r,\frac{l}{2,V},+,C_{n\delta_{a}}\delta_{a},+,C_{n\delta_{r}}\delta_{r}

  

为简化参数辨识方程组，令  

C_{l1}\equiv C_{l}+\frac{I_{x x}}{I_{z}}C_{n};=

C_{l1\beta}\beta,+,C_{l1\beta}\dot{P}\ {\frac{l}{2,V}},+,C_{l1r}r,{\frac{l}{2,V}},+,C_{l1\delta_{a}}\delta_{a},+,C_{l1\delta_{r}}\delta_{r}

\begin{array}{l}{{\displaystyle C_{n1}\equiv C_{n},+,\frac{I_{x z}}{I_{x}}C_{l},=}}\ {{\displaystyle C_{n1\beta},{\beta},+,C_{n1\beta}{\beta},\frac{l}{2,V},+,C_{n1r}r,\frac{l}{2,V},+,C_{n1\delta_{a}}\delta_{a},+,C_{n1\delta_{r}}\delta_{r},}}\end{array}

  

将 $C_{l1}$ 和 $C_{n\,1}$ 代人状态方程(10-67)和式(10-68),从而,待辨识参数中的力矩导数变为 $C_{l1\beta}\setminus C_{l1\beta}\setminus C_{l1r}\setminus C_{l1\delta_{a}}\setminus C_{l1\delta},$ 和 $C_{n\,1\,\beta}\,,C_{n\,1\,\beta}\,,C_{n\,1\,r}\,\,,$ $C_{n\,1\,\delta_{a}}\setminus C_{n\,1\,\delta_{r}}\circ$ 辨识得到上述参数之后，可利用下式求出飞行器的气动参数 $C_{l\beta}\,,C_{l\dot{p}}\,,C_{l r}\,,C_{l\delta_{a}}\,,C_{l\delta},$ 和 $C_{n\beta\setminus C_{n\beta}\setminus C_{n r}\setminus C_{n\delta_{a}}},C_{n\delta_{r}}$ 。  

\begin{array}{l}{{\displaystyle C_{l x_{i}}\ {=}\frac{1}{D}\bigg(C_{l1x_{i}}\ {-}\ \frac{I_{z x}}{I_{z}}C_{n1x_{i}}\bigg)}}\ {{\displaystyle C_{n x_{i}}\ {=}\frac{1}{D}\bigg(C_{n1x_{i}}\ {-}\ \frac{I_{x z}}{I_{z}}C_{l1x_{i}}\bigg)}}\end{array}

(,x_{i},=,\beta,/,r,,\delta_{a},,\delta_{r},)

  

状态方程组的积分初值中， $\phi\left(0\right),r(0),\phi(0)$ 取实测值， $\pmb{\tau}$ (0)由下式计算  

v(0);=;V(0)\mathrm{sin}\beta(0);+;v_{w}(0)

  

2）观测方程组  

\begin{array}{l}{\displaystyle\beta=\arcsin\frac{\upsilon,-,\upsilon_{w}}{V},+,\epsilon_{1}}\ {\displaystyle\phi,=,\phi,+,\epsilon_{2}}\ {\displaystyle r,=,r,+,\epsilon_{3}}\ {\displaystyle\phi,=,\phi,+,\epsilon_{4}}\end{array}

n_{y},={\frac{1}{m g}}\bigl[,T\mathrm{cos}\phi_{T}\mathrm{sin}\phi_{T},+,q_{,\infty},S(,C_{Y!\beta},{\beta},+

C_{Y\delta_{\gamma}}\delta_{r},),],+,\varepsilon_{5}

  

式中 $\boldsymbol{\varepsilon}_{i}^{\prime}$ —零均值随机观测噪声；  

V,{=},\sqrt{,(\tilde{,u},-,u_{w},)^{2}+(,v,-,v_{w},)^{2}+(,\varpi,-,w_{w},)^{2}}

  

3）系数矩阵 $\pmb{F}$ 和 $\pmb{H}$  

应用广义卡尔曼滤波算法,必须给出状态方程组和观测方程 组线化后的系数矩阵 $\pmb{F}$ 和 $\pmb{H}$  

矩阵 $\pmb{F}$ 的元素为  

\begin{array}{r l}&{F_{\mathrm{1,3}}=w}\ &{F_{\mathrm{1,3}}=-\bar{u}}\ &{F_{\mathrm{1,4}}=z\cos\Phi\cos\phi}\ &{F_{\mathrm{2,4}}=\frac{1}{D_{\mathrm{1}}\bar{f}}\delta\mathrm{S}^{\mathrm{T}}\Bigl[({\mathrm{\boldmath~\Psi~}}-{\mathrm{\boldmath~\Psi~}}{\mathrm{v}})C{\mathrm{1}}+\frac{1}{2},C_{\mathrm{0}}y,\sqrt{v^{2}-({\mathrm{\boldmath~\Psi~}}-v_{\mathrm{0}})^{2}}\Bigr]}\ &{F_{\mathrm{2,1}}=\frac{1}{D_{\mathrm{1}}\bar{f}}\left[\frac{L_{\mathrm{2}}-L_{z}}{1_{z}}+\mathrm{1}\bigg]\frac{L_{\mathrm{2}}-\mathrm{e}}{L_{\mathrm{1}}\bar{f}}+\frac{1}{4L_{\mathrm{2}}}V\mathrm{S}^{\mathrm{T}}\Bigl[\frac{1}{C_{\mathrm{1}}z}\Bigr]}\ &{F_{\mathrm{2,3}}=\frac{1}{D}\biggl[\bigg[\frac{L_{\mathrm{2}}-L_{z}}{L_{\mathrm{1}}}-\frac{L_{\mathrm{2}}}{L_{\mathrm{L}}\bar{f}}\Bigr]\bar{\phi}+\frac{1}{4L_{\mathrm{2}}}V\mathrm{S}^{\mathrm{T}}\bar{z}c_{\mathrm{1}}\biggr]}\ &{F_{\mathrm{3,1}}=\frac{1}{D_{\mathrm{1}}\bar{f}}\frac{\partial\mathrm{S}}{\partial L}\Bigl[\Bigl({\mathrm{\boldmath~\Psi~}}!!!C_{\mathrm{3}}+\mathrm{\boldmath~\H~}!!\sum_{\mathrm{4}}\exp\Bigl\langle{\mathrm{\boldmath~\Psi~}}!!!\nabla^{2}-{\mathrm{\boldmath~\Psi~}}!!!\Bigr\rangle\Bigr\Bigr)}\ &{F_{\mathrm{3,2}}=\frac{1}{D}\biggl[\bigg(\frac{L_{\mathrm{2}}-L_{z}}{L_{\mathrm{1}}}+\frac{L_{\mathrm{2}}}{L_{\mathrm{1}}}\bigg)\bar{\phi}+\frac{1}{4L_{\mathrm{2}}}V\mathrm{S}^{\mathrm{T}}\bar{z}c_{\mathrm{1}}\biggr]}\ &{,}\end{array}

\begin{array}{r l}&{F_{1,2}=\frac{1}{B}\left[\left{\frac{U_{e}-I}{L_{t}}+1\right}\frac{I_{e}\omega_{e}^{2}}{I_{e}^{2}}+\frac{4I_{e}\omega V\sin^{2}C_{0}n_{e}}{4I_{e}^{2}}\right]}\ &{F_{2,3}=\frac{1}{B}\left[\left{\frac{I_{e}-I}{L_{t}}-\frac{I_{e}n_{e}^{2}}{I_{e}L_{t}}\right}\frac{1}{e^{4}}+\frac{1}{4I_{e}^{2}}V\mathrm{S}^{2}\mathrm{S}^{2}\mathrm{I}{0}\right]}\ &{F{3,1}=\frac{1}{B L_{t}}\omega\tilde{S}\left(\kappa_{3}+\frac{1}{2}C_{0},\sqrt{\kappa_{3}}\right)}\ &{F_{3,2}=\frac{1}{B}\left[\left{\frac{I_{e}-I}{L_{t}}+\frac{I_{e}n_{e}^{2}}{I_{e}L_{t}}\right}\frac{1}{e^{4}}+\frac{1}{4I_{e}}\theta\mathrm{S}^{2}\mathrm{S}^{2}\mathrm{I}{0}\right]}\ &{F{3,3}=\frac{1}{B}\left[\left{\frac{I_{e}-I}{L_{t}}-1\right}\frac{I_{e}n_{e}^{2}}{I_{e}^{2}}+\frac{1}{4I_{e}^{2}}\nu\mathrm{S}^{2}\mathrm{S}^{2}\mathrm{C}{0}\right.,}\ &{F{4,2}=1}\ &{F_{4,3}=\tan\mathrm{for}\omega^{2}}\ &{F_{4,4}=\tan\mathrm{for}\omega\epsilon-r\sin\phi.}\end{array}

  

其余 $F_{i\,,j}=0\qquad\mathrm{~}(\,i=1\,,2\,,\cdots,16\,;\,j=1\,,2\,,\cdots,16$  

矩阵 $\pmb{H}$ 的元素为  

\begin{array}{r l}&{H_{1,1}=\cfrac{\sqrt{V^{2}-\left(\nu-v_{w}\right)^{2}}}{V^{2}}}\ &{H_{2,2}=1}\ &{H_{3,3}=1}\ &{H_{4,4}=1}\ &{H_{5,1}=\cfrac{1}{m_{g}\epsilon}\delta\left[\left(\nu-v_{w}\right)C_{Y}+\frac{1}{2}C_{Y\beta}\sqrt{V^{2}-\left(\nu-v_{w}\right)^{2}}\right]}\ &{H_{5,5}=\cfrac{1}{m_{g}\epsilon}\alpha_{0}\delta}\ &{H_{5,6}=\cfrac{1}{m_{g}\epsilon}\alpha_{0}S,}\end{array}

  

$H_{i,j}\,=\,0\qquad(\,i\,=\,1\,,2\,,\cdots,5\,;j\,=\,1\,,2\,,\cdots,16\,)$  

4）噪声特性矩阵  

卡尔曼滤波算法还要求给出描述过程噪声和观测噪声特性的矩阵 $\pmb{T}$ 和 ${\pmb Q}\setminus{\pmb R}$ 。可以认为，飞行器的过程噪声主要是由风和舵偏角的测量误差引起的，即 $\pmb{\{w=(\Delta\beta,\Delta\delta_{a}\,,\Delta\delta_{r}\,)^{\mathrm{T}}}}$ ,从而过程噪声的分布矩阵 $\pmb{T}$ 为  

\boldsymbol{T}=\left[\begin{array}{c c c}{\frac{1}{m}q_{\infty}\boldsymbol{S}C_{\gamma\beta}}&{0}&{\frac{1}{m}q_{\infty}\boldsymbol{S}C_{\gamma\beta}}\ {\frac{1}{D I_{x}}q_{\infty}\boldsymbol{S}[C_{\boldsymbol{1}\beta}}&{\frac{1}{D I_{x}}q_{\infty}\boldsymbol{S}[C_{\boldsymbol{1}\beta}}&{\frac{1}{D I_{x}}q_{\infty}\boldsymbol{S}[C_{\boldsymbol{1}\beta}}\ {0}&{\frac{1}{D I_{x}}q_{\infty}\boldsymbol{S}[C_{\boldsymbol{1}\beta}}&{\frac{1}{D I_{x}}q_{\infty}\boldsymbol{S}[C_{\boldsymbol{1}\beta}}&{\frac{1}{D I_{x}}q_{\infty}\boldsymbol{S}[C_{\boldsymbol{1}\beta}}\ {0}&{0}&{0}&{0}\ {0}&{0}&{0}\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\ {0}&{0}&{0}\end{array}\right]

  

过程噪声协方差阵 $\pmb{Q}$ 应由实测数据确定。当缺乏实测数据时,可根据实际环境参数和舵偏电位计的测量精度估计 $\Delta\beta,\Delta\delta_{\alpha}$ $\Delta\delta_{r}$ 的大小，取其平方值作为 $\pmb{Q}$ 阵的对角线元素，在辨识过程中  

352  

再作适当调整。  

观测噪声协方差阵 $\pmb R$ 在广义卡尔曼滤波中起着重要的作用，但要确切地确定其数值是比较困难的。通常，侧滑角测量的标准误差约为 $0.1^{\circ}$ ,可取 $R_{1,1}=R_{4,4}\,{=}\,0.01(\,^{\circ}\,)^{2}$ ;速率陀螺测量的标准误差约为 $0.2(^{\circ})/\mathrm{s}$ ,可取 $R_{2,2}=R_{3,3}=0.05(^{\circ})^{2}/\mathrm{s}^{2}$ ；过载传感器测量的标准误差与其量程有关，对于小量程过载传感器，若标准误差为0.01,则 $R_{5,5}=0.0001$ ；对角线以外的元素取为 $0_{\circ}\textbf{\textit{R}}$ 阵的选取有很大自由度，与各观测量的量级有关，对给定的实测数据，可根据实际情况灵活选取。  

有了上述基本公式，就可以利用4.2.4节所阐述的增广的广义卡尔曼滤波算法估计横侧向气动导数。  

# 10.2.4静不稳定飞行器气动参数辩识  

众所周知，输出误差法是飞行器气动参数辨识最厂泛采用的方法，并且，为了避免飞行控制系统引起的复杂性，通常将闭环系统当做开环来处理，即直接取操纵面偏转角作为状态方程的控制输人。然而，对于静不稳定的飞行器，在采用输出误差法进行气动参数辨识时，状态方程组和灵敏度方程组都是不稳定的，由于下述几方面的原因，其积分往往迅速发散，辨识算法无法进行：  

（1）状态变量的初值有偏差；  

（2）气动参数值有偏差；  

（3）运动方程和气动力模型存在模型误差；  

（4）飞行试验中包含有过程噪声。  

频域辨识方法适用于静不稳定的飞行器。在时域中，方程误差法、滤波误差法、多重打靶方法也可直接用于静不稳定飞行器的气动参数辨识。针对采用输出误差法进行静不稳定飞行器气动参数辨识所遇到的数值困难，还发展了基于方程解耦的输出误差法和带人工稳定的输出误差法。各种方法的比较可参说参考文献[4]。这里仅阐述方程解耦技术i5}，它是克服不稳定系统状态方程组和灵敏度方程组积分发散的一种有效方法。  

# 1）方程解耦技术  

对于线性和非线性系统，方程解耦技术都是非常有用的。为方便起见，用下列线性系统为例来阐述方程解耦技术：  

\dot{\pmb{x}}\left(,t,\right);=;\pmb{F}(,\pmb{\theta},),\pmb{x}\left(,t,\right),+,\pmb{G}\left(,\pmb{\theta},\right)\pmb{u}\left(,t,\right)

\mathbf{y}\left(\mathbf{\Omega}{t}\right)\ =\ H\left(\pmb{\theta}\right)\pmb{x}\left(\mathbf{\Omega}{t}\right)\ +\ \pmb{\varepsilon}\left(\mathbf{\Omega}_{t}\right)

  

方程解耦技术的基本思想是，引人两个 $n\,\times\,n$ 矩阵 $\kappa o$ 和KOI，其元素满足下列两个约束条件：  

条件1  

\begin{array}{l l}{{K O(,i,,i,),=,1,}}&{{i,=,1,,2,,\cdots,n}}\ {{\nonumber,}}&{{\K O(,i,,j,),=,0,,1,}}&{{i,,j,=,1,,2,,\cdots,n}}\end{array}

  

且当 $K O(\,i\,,\,j\,)=K O(\,i\,,\pmb{k}\,)=1$ 时， $K O(j\,,k\,)=1\,,\,i\,,j=1\,,2\,,\cdots,n\,_{\circ}$  

条件2  

K O I(,i,,j,),=,1,-,K O(,i,,j,),\qquad i,,j,=,1,,2,,\cdots,n

  

利用矩阵 $\kappa\mathbf{o}$ 和K01，将式（10-81）改写为  

\pmb{x}(\pmb{t});=;(\pmb{F}(\pmb{\theta})\star\pmb{K}\pmb{O})\pmb{x}(\pmb{t})\ +

\left(,{\pmb F}(,{\pmb\theta},)\star{\pmb K}O I,\right){\bf y}(,t,),+,{\pmb G}(,{\pmb\theta},),{\pmb u}\left(,t,\right)

  

式中，算子“￥”表示两个矩阵对应的元素相乘。  

适当选取矩阵 $\pmb{K0}$ 和KO1，可使状态方程组部分解耦或完全解耦。例如，当K0为单位矩阵时，方程完全解耦，即对于每一个状态变量，其微分方程中包含的其他状态变量均以观测数据代替，这样，每一个状态方程都可以独立地进行积分。  

方程解耦能够改变系统的稳定性。即使是在解耦系统仍不稳定的情况下，通过矩阵KOI将状态变量的观测数据引人状态方程组，也能够有效地阻止状态方程组积分的迅速发散。  

2）基于方程解耦的输出误差法  

在静不稳定飞行器的气动参数辨识问题中，由于 $C_{m a}>0\,,q$ 方程不稳定，从而导致系统的不稳定性。为此，可以采用前述的方程解耦技术。为了尽量减少由方程解耦引人的过程噪声，通常仪对寸 $q$ 方程进行解耦。  

基于 $\pmb q$ 方程解耦的输出误差法,与10.2.1节给出的6自由度模型气动参数辨识算法是完全类似的，只需作如下修改。  

（1）将状态方程组中的 $\pmb q$ 方程修改为  

\begin{array}{l}{{\displaystyle{\frac{I_{z},-,I_{x}}{I_{y}}}\tilde{p}\tilde{r},-,{\frac{I_{z x}}{I_{y}}}(\tilde{\rho}^{2},-,\tilde{r}^{2}),+}}\ {{\displaystyle{\frac{1}{I_{y}}}q_{\infty},S l\left(C_{m0},+,C_{m a}\tilde{\alpha},+,C_{m a}^{,}\tilde{\alpha}^{3},+,C_{m a}^{,}\tilde{\alpha}^{5},+,C_{m\delta}\delta_{e}\right.+}}\ {{\displaystyle{\vphantom{\bigg)}}}}\ {{\displaystyle C_{m\delta_{e}}\delta_{e},{\frac{c_{A}}{2,V}},+,C_{m q}q,{\frac{c_{A}}{2,V}},+,C_{m\beta}\tilde{\rho},{\frac{l}{2,V}},\bigg),}}\end{array}

  

式中 $\tilde{p}\,,\tilde{r}\,,\tilde{\alpha}-$ 实测值。  

(2) 将 $\pmb q$ 对待估计参数的灵敏度方程修改为  

\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial q}{\partial\theta_{l}},=,\frac{1}{I_{y}}q_{\infty},S l C_{m q},,\frac{c_{A}}{2,V},\frac{\partial q}{\partial\theta_{l}},+,U_{2,l}

  

相应的 $U_{2,\iota}(\,l=1\,,2\,,\cdots,43\,)$ 项为  

U_{2,9},=,\frac{1}{I_{y}}q_{\infty},S l\qquad U_{2,10},=,U_{2,9}\tilde{\alpha}\qquad U_{2,11},=,U_{2,9}\tilde{\alpha}^{3},

  

# 3）仿真辨识算例  

对某鸭式布局飞机进行纵向运动的辨识仿真计算。开始时，飞机处于平飞状态。采用“3211”形式的杆力输人，仿真得到的鸭翼偏转 $\mathfrak{F}_{c}$ 和升降舵偏转 $\delta_{e}$ 如图10-5所示。 由于 $\pmb{\delta}_{c}$ 和 $\delta_{e}$ 近似相关，相关的操纵导数不能同时辨识。  

取待辨识气动参数的初值与真值偏差 $\pm\,70\,\%$ 。用这一初值积分状态方程组，由状态量计算得到的观测量与仿真数据的比较示于图10-6。由于状态方程组积分发散较严重，辨识算法因计算过程中产生浮点溢出而无法进行。  

为此，采用基于 $\pmb q$ 方程解耦的输出误差法进行气动参数辨识。图10-7示出了辨识拟合结果与含测量噪声的仿真数据的比较，两者符合得很好。表10-4列出了所有气动参数的真值及其辨识结果,其中“”号表示对应的气动参数不参加辨识,而取其真值。由于鸭翼偏转对法向力系数影响很小,在运动方程中, $C_{N\delta_{c}}\delta_{c}$ 项被测量噪声淹没，因此， $C_{N\delta_{c}}$ 的辨识结果与真值偏差较大。其余参数的辨识结果接近其真值。  

![](images/524bc61800a2d5066144992d2d5540b6f629d7b098eecd0f55e0328a2f9362c0.jpg)  
图 10-5 操纵输人和鸭翼、升降舵偏响应  

![](images/4fce9c33bd90335987a7a40e9a4188e3c62c3bc49ec8666c026284cc42a8a36b.jpg)  
图 10-6 方程耦合的积分结果  

![](images/45353d51ced1a9c3e6c03d467c6dbbb77915be5c3c7531da0b4b4295698dfb12.jpg)  
图 10-7 辨识拟合结果  

表 10-4气动参数真值及其辨识结果  


<html><body><table><tr><td>气动参数</td><td>CAO</td><td>CAM</td><td>CAa</td><td>CAC</td><td>Cn</td><td></td><td></td></tr><tr><td>真值</td><td>0.0160</td><td>- 0.0080</td><td>0.0630</td><td>0.0894</td><td>0.1272</td><td></td><td></td></tr><tr><td>辨识结果</td><td>0.0161</td><td></td><td></td><td>*</td><td></td><td></td><td></td></tr><tr><td>气动参数</td><td>CNO</td><td>CNM</td><td>CNa</td><td></td><td>CN8</td><td></td><td></td></tr><tr><td>真值</td><td>-0.0227</td><td>0.0190</td><td>2.9336</td><td>0.1432</td><td>1.1345</td><td></td><td></td></tr><tr><td>辨识结果</td><td>-0.0263</td><td></td><td>3.0183</td><td>0.2997</td><td></td><td></td><td></td></tr><tr><td>气动参数</td><td>Cmo</td><td>CmM</td><td>Cma</td><td>Cmoc</td><td>Cme</td><td>Cmg </td><td>Cma</td></tr><tr><td>真值</td><td>0.0063</td><td>0.0010</td><td>0.2229</td><td>0.2292</td><td>-0.5546</td><td>- 0.8140</td><td>-0.0341</td></tr><tr><td>辨识结果</td><td>0.0064</td><td>￥</td><td>0.2219</td><td>0.2265</td><td>￥</td><td>- 0.8216</td><td></td></tr></table></body></html>  

可见，方程解耦技术提供了将输出误差法扩展应用于静不稳定飞行器气动参数辨识的一种有效工具。基于方程解耦的输出误差法较好地克服了不稳定系统状态方程组和灵敏度方程组积分发散的问题，是静不稳定飞行器气动参数辨识的一种实用方法。  

# 10.3 旋翼飞行器气动参数辨识  

在过去30年中，人们在进行固定翼飞行器气动参数辨识的同时，也开展了旋翼飞行器气动参数辨识研究工作。但由于旋翼飞行器固有的复杂性，其进展远落后于固定翼飞行器。与固定翼飞行器相比，旋翼飞行器气动参数辨识的困难在于：  

（1）模型的高度耦合导致描述旋翼飞行器动力学特性的数学模型阶次较高，未知参数较多。  

（2）旋翼飞行器的不稳定性限制了试验的持续时间。  

（3）较高的振动水平降低了测量精度，并且有些变量很难测量，例如低速和悬停状态下的速度分量、旋翼叶片动态特性等。  

AGARD飞行力学组于1987年专门成立了一个由各成员国的研究专家和工业界人士组成的研究小组（FMPWG18）,开展旋翼飞行器系统辨识方法和应用研究[6]。WG18的研究工作极大地促进了这一研究领域的发展。  

旋翼飞行器除机身6个刚体自由度外，还有旋翼挥舞自由度。因此，在进行气动参数辨识时，首先应根据实际需要选择不同复杂程度的动力学系统数学模型。这里着重阐述6自由度模型和含旋翼自由度模型的气动参数辨识方法。  

# 10.3.1 6 自由度模型气动参数辨识  

旋翼动态特性的频率远高于机身模型的频率。对于操稳特性分析和驾驶仿真等应用领域，只需考虑飞行器低到中等频率范围(约 $10\mathrm{rad/s}$ 以内)的动态特性，可以采用刚体6自由度模型。  

刚体6自由度模型的状态方程组为  

{\dot{\pmb x}};=;{\bf A}{\pmb x};+;{\bf B}{\pmb u};+;{\pmb f}{1},+,{\pmb f}{2}

  

观测方程组为  

\mathbf{y}\ =\ C x\ +\ D u\ +\ \pmb{\varepsilon}

  

式中x一—状态矢量;  

y-—观测矢量；  

$\pmb{u}$ ——控制矢量;  

$\mathbf{A}\ ,\mathbf{B}\cdot$ —状态矩阵；  

C,D-—-观测矩阵；  

$f_{1},f_{2}$ 运动项和重力项；ε———观测噪声。  

各个量的表达式为  

\begin{array}{r l}&{\pmb{x},=(,u,,\pmb{v},,\pmb{w},,\pmb{\phi},,\pmb{q},,r,,\theta,,\pmb{\phi},)^{\mathrm{T}}}\ &{\pmb{y},=(,u_{m},,v_{m},,w_{m},,\beta_{m},,q_{m},,r_{m},,\theta_{m},,\phi_{m},,n_{x m},,n_{y m},,n_{z m},)^{\mathrm{T}}}\ &{\pmb{u},=(,\delta_{\log},,\delta_{\log},,\delta_{\mathrm{ped}},,\delta_{\mathrm{col}},)^{\mathrm{T}}}\end{array}

\begin{array}{r}{\overrightarrow{A}=\left[\begin{array}{c}{\overrightarrow{X}{\ast},,\Tilde{X}{\ast},,\Tilde{X}{\ast},,\Tilde{X}{\ast},,\Tilde{X}{\ast},,\Tilde{X}{\ast},,,0,,0}\ {\bigg|,\widetilde{Y}{\ast},,\widetilde{Y}{\ast},,\widetilde{Y}{\ast},,\widetilde{Y}{\ast},,\widetilde{Y}{\ast},,\Tilde{Y}{\ast},,0,,0}\ {\int_{\mathcal{K}},\widetilde{Z}{\ast},,\Tilde{Z}{\ast},,\Tilde{Z}{\ast},,\Tilde{Z}{\ast},,\Tilde{Z}{\ast},,0}\ {\int{\mathcal{K}},\hat{L}{\ast},\hat{L}{\ast},\hat{L}{\ast},\hat{L}{\ast},,\hat{L}{\ast},,\hat{L}{\ast},,0}\ {\widetilde{M}{\ast},\widetilde{M}{\ast},\widetilde{M}{\ast},\widetilde{M}{\ast},\mathcal{M}{\ast},,,0,,0}\ {\widetilde{N}{\ast},\widetilde{N}{\ast},\widetilde{N}{\ast},\widetilde{N}{\ast},\widetilde{N}{\ast},,0,,0}\ {0\quad0\quad0\quad0\quad0\quad0\quad0\quad0\quad0\quad0}\ {0\quad0\quad0\quad0\quad0\quad0\quad0\quad0\quad0\quad0\quad0}\end{array}\right]}\end{array}

f_{1}=\left[\begin{array}{c}{-q w-r w}\ {-r w-p w}\ {-p w+q w}\ {\left(I_{x}-I_{y}+I_{z}\right)I_{x}}\ {I_{z}I_{z}-I_{z}^{2}}\ {I_{x}-I_{z}-I_{y}}\ {\frac{I_{z}-I_{z}}{I_{y}}p-\frac{I_{x}}{I_{y}}(p^{2}-r^{2})}\ {\vdots}\ {\frac{I_{z}-I_{z})I_{z}+I_{z}^{2}}{I_{x}I_{z}-I_{x}^{2}}p+\frac{\left(I_{y}-I_{z}-I_{z}\right)I_{x}}{I_{x}I_{z}-I_{x}^{2}}q r}\ {q c s^{6}-r s\sin\theta}\ {\vdots}\ {\frac{p+\mathrm{\hbar}\tan\theta}{\left(q\sin\phi+r\cos\phi\right)}}\end{array}\right]f_{2}=\left[\begin{array}{c}{-\frac{v\sin\theta}{\sin\theta}}\ {g\cos\theta\sin\theta}\ {g\cos\theta\cos\theta}\ {0}\ {0}\ {0}\ {0}\ {0}\ {0}\end{array}\right]

  

$\widetilde{X}\,,\widetilde{Y}\,,\widetilde{Z}\,,\widetilde{L}\,,\widetilde{M}\,,\widetilde{N}$ 为规范力和力矩,其表达式为  

\begin{array}{l l l}{\widetilde{X};=;X/,m}&{\widetilde{Y};=;Y/,m}&{\widetilde{Z};=;Z/,m}\ {\widetilde{L};=;\displaystyle\frac{I_{z}L,+,I_{x z}N}{I_{x}I_{z},-,I_{x z}^{2}}}&{\widetilde{M};=;\displaystyle\frac{M}{I_{y}}}&{\widetilde{N};=;\displaystyle\frac{I_{x z}L,+,I_{x}N}{I_{x}I_{z},-,I_{x z}^{2}}}\end{array}

  

式(10-86)前两个主项是线性的，但运动项和重力项保持非线性形式。  

待辨识参数为气动稳定导数 $A_{i j}\l(\l_{i}\,,\l_{j}=1\,,2\,,\cdots\,,6\l)$ 和操纵导数  

$B_{i j}\,({\it i}=1\,,2\,,\cdots,6\,;{\it j}=1\,,2\,,3\,,4\,)$ ，即  

\begin{array}{r l}&{=(\widetilde{X}{u},\widetilde{X}{v},\widetilde{X}{w},\widetilde{X}{p},\widetilde{X}{q},\widetilde{X}{r},\widetilde{Y}{u},\widetilde{Y}{v},\widetilde{Y}{w},\widetilde{Y}{p},\widetilde{Y}{q},\widetilde{Y}{r},:}\ &{\quad\widetilde{Z}{u},\widetilde{Z}{v},\widetilde{Z}{w},\widetilde{Z}{p},\widetilde{Z}{q},\widetilde{Z}{r},\widetilde{L}{u},\widetilde{L}{v},\widetilde{L}{w},\widetilde{L}{p},\widetilde{L}{q},\widetilde{L}{r},,}\ &{\quad\widetilde{M}{u},\widetilde{M}{v},\widetilde{M}{w},\widetilde{M}{p},\widetilde{M}{q},\widetilde{M}{r},\widetilde{N}{u},\widetilde{N}{v},\widetilde{N}{w},\widetilde{N}{p},\widetilde{N}{q},\widetilde{N}{r},,}\ &{\quad\widetilde{X}{\delta{\mathrm{k}{u}}},\widetilde{X}{\delta_{\mathrm{k}{u}}},\widetilde{X}{\delta_{\mathrm{p}\omega^{\perp}}},\widetilde{X}{\delta{\mathrm{k}{u}}},\widetilde{Y}{\delta_{\mathrm{k}{u}}},\widetilde{Y}{\delta_{\mathrm{k}{u}}},\widetilde{Y}{\delta_{\mathrm{el}}},\widetilde{Y}{\delta{\mathrm{el}}},}\ &{\quad\widetilde{Z}{\delta{\mathrm{k}{u}}},\widetilde{Z}{\delta_{\mathrm{k}{u}}},\widetilde{Z}{\delta_{\mathrm{el}}},\widetilde{Z}{\delta{\mathrm{el}}},\widetilde{L}{\delta{\mathrm{k}{u}}},\widetilde{L}{\delta_{\mathrm{k}{u}}},\widetilde{L}{\delta_{\mathrm{el}}},\widetilde{L}{\delta{\mathrm{el}}},,}\ &{\quad\widetilde{M}{\delta{\mathrm{k}{\mathrm{k}}}},\widetilde{M}{\delta_{\mathrm{k}{u}}},\widetilde{M}{\delta_{\mathrm{en}}},\widetilde{M}{\delta{\mathrm{el}}},\widetilde{N}{\delta{\mathrm{k}{u}}},\widetilde{N}{\delta_{\mathrm{k}_{u

  

采用最大似然法进行气动参数辨识。似然判据取为负对数似然函数，即  

\pmb{J}(\pmb{\theta}):=:\sum_{i,=,1}^{N}\pmb{\nu}^{\mathbb{T}}!\left(,i,\right)\pmb{R}^{,-1}\pmb{\nu}!\left(,i,\right)

  

式中 $\pmb{\nu}(\mathbf{\chi}_{i})$ ——残差矢量  

\pmb{\nu}(,i,);=;\pmb{y}(,i,);-;\pmb{y}_{m}\left(,i,\right)

  

$\pmb{R}$ —误差协方差阵，当 $\pmb{R}$ 未知时，可用下式进行估计  

\pmb{R}\ =\ \sum_{\stackrel{i}{i}=1}^{N}\pmb{\nu}(,i,),\pmb{\nu}^{\mathrm{T}}(,i,)

  

气动参数辨识过程，就是在参数空间中寻求参数 $\pmb{\hat{\theta}}$ ，使似然判据 $J$ 达极小值。为此，可采用牛顿-拉夫逊迭代算法，第 $\pmb{k}$ 步的参数修正公式为  

\pmb{\theta}^{(k)};=;\pmb{\theta}^{(k,-,1)},-,(,\pmb{\nabla}{\theta}^{2}\pmb{J},)^{,-,1},\pmb{\nabla}{\theta},J

  

式中  

\nabla,{\theta}J;=;\left(\frac{\partial J}{\partial\theta{k}}\right){60\times1}\qquad\qquad\qquad\nabla,{\theta}^{2}J;=;\left(\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}}\right)_{60\times60}

\frac{\partial J}{\partial\pmb{\theta}{k}};=;2\sum{i=1}^{N},\frac{\partial\pmb{y}^{\sf T}(\it i\phi)}{\partial\theta_{k}}\pmb{R}^{-1}\pmb{\nu}(\it i\phi),;\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}};=;2\sum_{i=1}^{N},\frac{\partial\pmb{y}^{\sf T}(\it i\phi)}{\partial\theta_{k}}\pmb{R}^{-1},\frac{\partial\pmb{y}(\it i\phi)}{\partial\theta_{l}}

  

观测量对待辨识参数的灵敏度为  

\frac{\partial\mathbf{y}}{\partial A_{i j}}\ =\ \left{\begin{array}{l l}{\displaystyle C\ \frac{\partial\mathbf{x}}{\partial A_{i j}},+,I_{i+8,j}^{(11\times8)}u\quad(\ i,=,1,,2,,3,;j,=,1,,2,,\cdots,6)}\ {\displaystyle C\ \frac{\partial x}{\partial A_{i j}}\ }&{(\ i,=,4,,5,,6,;j,=,1,,2,,\cdots,6)}\end{array}\right.

\frac{\partial\textbf{y}}{\partial B_{i j}},=,\left{\begin{array}{l l}{!C,\frac{\partial\textbf{x}}{\partial B_{i j}},+,I_{i+8,j}^{(11\times4)}!u,}&{!(,i,=,1,,2,,3,;j,=,1,,2,,3,,4)}\ {!}&{!(,j,=,4,,5,,6,;j,=,1,,2,,3,,4)}\end{array}\right.

  

状态量对待辨识参数的灵敏度由下述灵敏度方程组积分获得  

\frac{\mathrm{d}}{\mathrm{d}t}\ \frac{\partial\pmb{x}}{\partial A_{i j}}\ =\ \pmb{A}\ \frac{\partial\pmb{x}}{\partial A_{i j}}\ +\ \pmb{I}_{i,.,j}^{(8\times8)}\pmb{x}\quad(,i\ =\ 1,2,\cdots,6,;j\ =\ 1,2,\cdots,6)

\frac{\mathrm{d}}{\mathrm{d}t}\ \frac{\partial\pmb{x}}{\partial B_{i j}}\ =\ \pmb{A}\ \frac{\partial\pmb{x}}{\partial B_{i j}}\ +\ \pmb{I}_{i,j}^{(8\times4)}\pmb{u}\quad(\mathrm{}i\mathrm{=}1,2,\cdots,6\backslash j\mathrm{=~}1,2,3,4)

  

$I_{\textit{i,j}}^{(\textit{m}\times\textit{n})}$ 为 $\left(\mathbf{\nabla}m\times n\right)$ 矩阵，它的第 $(\,i\,,j\,)$ 个元素为1,其余元素为 0。  

6自由度模型式（10-86)对操纵输人立即产生响应。但事实上，由于旋翼和液压系统动态特性的影响，旋翼飞行器对操纵输人的响应有迟后。通常用等价时间延迟来近似这一效应。某些重要导数的估计对时间延迟很敏感，因此，准确地确定等价时间延迟是十分重要的[7]  

图10-8给出了采用相关性分析的方法，确定B0-105滚转加速率响应等价时间延迟的过程[7]。图 10-9 给出了 BO-105 纵向操纵输人、横向操纵输人、总距输人、尾桨输人四个机动的气动参数辨识拟合结果与实测数据的比较[7]  

# 10.3.2 含旋翼自由度模型气动参数辨识  

对于高带宽的控制系统设计，要求模型能够准确描述直至$(\,18\!\sim\!20\,)\,\mathrm{rad/s}$ 的频率范围的旋翼飞行器动态特性，超出了6目由度模型的能力范围。因此，必须扩展6自由度模型，以包含旋翼目由度[8]。  

![](images/0b931033cb2c76c883ca93111b4c5a599bf86a05843f438c7f76199df0e8b348.jpg)  
图10-8 滚转加速率等价时间延迟的确定—测量数据；--辨识结果  

对于含旋翼自由度模型的气动参数辨识，需要在体轴系建立旋翼挥舞运动方程，而旋翼测量是在旋转系统进行的，必须进行转换。考虑 4 片桨叶的旋翼，分别以 1、2、3、4来标记，旋翼的桨尖轨迹平面测量数据为旋翼的方位角（叶片1朝后方位角定义为零）各叶片的挥舞角 $\beta_{1}\,,\beta_{2}\,,\beta_{3}\,,\beta_{4}$ ，由下式可计算旋翼的锥度 $\alpha_{0\setminus}$ 纵向挥舞 $\boldsymbol{a}_{1s}$ 和横向挥舞 $b_{1s}$  

a_{0},=0,.,25(,\beta_{1},+,\beta_{2},+,\beta_{3},+,\beta_{4})

  

![](images/886b6f36982ed900ff3d9a644ddea3562e21935365d4df26c7d01d10bb0dccfa.jpg)  
图 10-96自由度模型辨识拟合结果与实测数据的比较测量数据；----辨识结果。  

a_{1s},=0,.,5[,\beta_{1}\mathrm{cos}\psi,+,\beta_{2}\mathrm{cos}(,\psi,+,0,.,5\pi),,+

\beta_{3}\mathrm{cos}(,\psi,+,\pi),+,\beta_{4}\mathrm{cos}(,\psi,+,1.,5\pi),]

b_{1s},=0,.5[,\beta_{1}\sin\phi,+,\beta_{2}\sin(,\psi,+,0,.5\pi),,+

\beta_{3}\mathrm{sin}(,\psi,+,\pi),+,\beta_{4}\mathrm{sin}(,\psi,+,1,.,5\pi),]

  

含旋翼自由度模型的状态方程组为  

{\dot{\pmb x}};=;{\pmb A}{\pmb x};+;{\pmb B}{\pmb u};+;{\pmb f}{1};+;{\pmb f}{2}

  

观测方程组为  

\mathbf{y}\ =\ C x\ +\ D u\ +\ \pmb{\varepsilon}

{\begin{array}{r l r l}{x\ =\ {\left[!!{\begin{array}{l}{x_{1}}\ {x_{2}}\end{array}}\right]}}&{\ A\ =\ {\left[!!{\begin{array}{l l}{A_{11}}&{A_{12}}\ {A_{21}}&{A_{22}}\end{array}}\right]}}&{\ B\ =\ {\left[!!{\begin{array}{l}{B_{1}}\ {B_{2}}\end{array}}\right]}}\ {y\ =\ {\left[!!{\begin{array}{l}{y_{1}}\ {y_{2}}\end{array}}\right]}}&{\ C\ =\ {\left[!!{\begin{array}{l l}{C_{11}}&{C_{12}}\ {C_{21}}&{C_{22}}\end{array}}\right]}}&{\ D\ =\ {\left[!!{\begin{array}{l}{D_{1}}\ {D_{2}}\end{array}}\right]}}\ {f\ =\ {\left[!!{\begin{array}{l}{f_{11}}\ {f_{12}}\end{array}}\right]}}&{\ f_{2}\ =\ {\left[!!{\begin{array}{l}{f_{21}}\ {f_{22}}\end{array}}\right]}}&{\ g\ =\ {\left[!!{\begin{array}{l}{\varepsilon_{1}}\ {\varepsilon_{2}}\end{array}}\right]}}\end{array}}

  

式中 $x_{1}$ -—机体模型的状态矢量；  

$\pmb{x}_{2}$ —旋翼模型的状态矢量,可取 $\pmb{x}_{2}=(a_{1s}\,,b_{1s})^{\mathrm{T}}$ 或 $\pmb{x}_{2}$ ${\bf{\tau}}=(\,a_{1s}\,,b_{1s}\,,a_{0}\,,\dot{a}_{1s}\,,\dot{b}_{1s}\,,\dot{a}_{0}\,)^{\mathrm{T}}{\bf{\Psi}};$   
$\pmb{A}_{11}$ 一一机体模型的状态矩阵；  
$\pmb{A}_{22}$ 一旋翼模型的状态矩阵；  

${\bf A}_{12}$ 和 $\pmb{A}_{21}$ —反映机体与旋翼的交叉耦合；  

$\pmb{{\cal B}}_{1}$ —-机体模型的控制矩阵；${\pmb{{\cal B}}}_{2}$ —一旋翼模型的控制矩阵；$\pmb{f}_{1}$ ——运动项；$f_{2}$ —重力项；y1-—机体模型的观测矢量;${\mathfrak{y}}_{2}$ 一—旋翼模型的观测矢量， $\mathbf{y}_{2}=(a_{1s}\,,b_{1s}\,,a_{0}\,)^{\mathrm{T}}$ C、D-——扩展模型的观测矩阵；观测噪声矢量。  

与6自由度模型相比,扩展的含旋翼自由度模型在结构上的主要变化是：  

（1）扩展机体动力学方程组，使其包含旋翼运动方程，以反应机体与旋翼的交叉耦合。  

(2）在机体方程中忽略滚转阻尼导数 $L_{p}$ 和俯仰阻尼导数$M_{q}\,.$  

（3）从机体方程中删除纵向、横侧、总距操纵导数,这些操纵导数仅用于旋翼方程。  

利用旋翼的对称性，可将旋翼方程中的某些参数强制取相同的值，例如旋翼的挥舞阻尼等。  

扩展的含旋翼自由度模型中，待辨识的未知参数较多，在参数辨识之前还应对参数之间的相关性和各参数的“鲁棒性”进行详细的分析，尽可能减少待辨识参数的数量。  

含旋翼自由度模型的状态方程组和观测方程组确定之后，就可以采用与6自由度模型相同的方法进行气动参数辨识。  

图 10-10 给出了 B0-105 纵向操纵输人、横向操纵输人、总距输人三个机动的旋翼测量数据与含旋翼自由度模型辨识结果的比较[8]。扩展模型包含旋翼状态变量 $a_{1s},b_{1s},a_{0},\dot{a}_{1s},\dot{b}_{1s},\dot{a}_{0}$ ,为9自由度的 14阶模型。  

![](images/6cd67729753781399edff2c392121ca92d3fe0248a2bbeba6074970497cb4e96.jpg)  
图 10-10含旋翼自由度模型辨识拟合结果与实测数据的比较测量数据；---辨识结果。  

# 10.4 自旋飞行器气动参数辨识  

自旋飞行器是指采用自旋滚转稳定和继电式舵机进行控制的一类小型导弹,如反坦克导弹、肩扛发射对空导弹等。早期的自旋导弹由于采用肩扛发射，体积很小,要求控制系统简单,通常采用单通道的脉冲调宽指令操纵继电式舵机，使舵面按特定规律作阶跃式周期运动,形成俯仰和偏航方向的操纵力矩，使导弹获得所需方向的气动力，将导弹引向目标。随着这类导弹从肩扛、手携式转向装甲机动发射，弹体容积加大，已从单通道控制转向滚转稳定和俯仰、偏航操纵。射手将光学瞄准具光轴对准目标，让导弹在电视测角装置的视场中飞行，测角器测出导弹相对于目标的高低角和方位角偏差，此角偏差信息通过制导装置转化为俯仰、偏航控制信号操纵舵机，将导弹引向目标。  

就气动参数辨识而言，两种控制方式的自旋导弹的主要区别在于，等效舵偏的表达式不同，气动力模型略有差别。考虑到自旋导弹的现状和发展趋势，这里仅阐述后一种控制方式的自旋导弹的气动参数辨识方法。  

# 10.4.1 等效舵偏角和气动力数学模型  

对于多通道控制的自旋导弹，弹体的 $O x z$ 平面上装有上下舵$\delta_{1}$ 和 $\delta_{2}\,,O x y$ 平面上装有左右舵 $\delta_{3}$ 和 $\delta_{4}$ 。飞行试验时测量 $\delta_{1}$ $\delta_{2},\delta_{3},\delta_{4}$ ，由下式换算出 $\mathbf{\mathcal{x}}\setminus\mathbf{\mathcal{y}}\setminus\mathbf{\mathcal{z}}$ 方向的等效舵偏  

\begin{array}{r l}&{\delta_{z}=-\ c_{1}(\delta_{2}-\ \delta_{1})/2}\ &{}\ &{\delta_{y}=c_{2}+\ c_{3}(\ \delta_{4}-\ \delta_{3})/2}\ &{}\ &{\delta_{x_{z}}=c_{1}(\ \delta_{1}+\ \delta_{2})/2}\ &{}\ &{\delta_{x_{y}}=c_{3}(\ \delta_{3}+\ \delta_{4})/2}\ &{}\ &{\delta_{D}=(\mid\delta_{1}\mid+\mid\delta_{2}\mid+\mid\delta_{3}\mid+\mid\delta_{4}\mid)/4}\end{array}

  

式中 $c_{1\setminus c_{2}\setminus c_{3}}$ 舵机设计已确定的参数，相当于舵的幅值和配平角。  

自旋导弹的飞行攻角和侧滑角较小，可以采用线性气动力数学模型。取气流坐标系的气动力模型为  

\begin{array}{r l}&{C_{D},=C_{D0},+,C_{D2},(,\alpha^{2},+,\beta^{2}),+,C_{D\delta_{D}}\delta_{D}}\ &{C_{C},=C_{C0},+,C_{C\beta},\beta,-,C_{C\delta_{z}}\delta_{z}}\ &{C_{L},=C_{L0},+,C_{L a}\alpha,-,C_{L\delta_{y}}\delta_{y}}\end{array}

  

弹体坐标系的气动力矩数学模型为  

C_{l};=C_{l0};-;c_{l\phi}\dot{p};\frac{l}{2,V},-;\bar{C}{1\delta{y}}\delta_{x_{y}}\mathrm{cos}\beta,-,C_{l\delta_{z}}\delta_{x_{z}}\mathrm{cos}\alpha

C_{m};=C_{m0},-,(,C_{D}\mathrm{sin}\alpha,\mathrm{cos}\beta,+,C_{L}\mathrm{cos}\alpha,),\eta,-,C_{m q}q,\frac{c_{A}^{2}}{V l};-

C_{m\hat{\delta}{y}}\hat{\partial}{y};-;C_{l\hat{\delta}{y}}\hat{\partial}{x_{y}}\mathrm{sin}\beta:+:C_{n\hat{\delta}{D}}\hat{\partial}{D}\mathrm{sin}\alpha,\mathrm{cos}\beta

C_{n};=C_{n0},-,\left(,C_{C}\mathrm{cos}\beta,-,C_{L}\sin\beta,\right)\eta,-,C_{n r},\frac{c_{A}^{2}}{V l},+,C_{n\hat{\sigma}{z}}\hat{\partial}{z},-,

C_{1,\delta_{z}}\delta_{x}\mathrm{sin}\alpha:-:C_{n\delta_{D}}\delta_{D}\mathrm{sin}\beta

  

式中——静稳定裕度; $\pmb{\eta}=(\,x_{c p}-x_{c g}\,)/l_{\ c}$  

# 10.4.2 气动参数辨识数学模型  

自旋导弹的状态方程组建立在弹体固连坐标系和气流坐标系上。导弹的推力偏心角和攻角、侧滑角均为小量，略去高阶小量，状态方程组为  

{\frac{\mathrm{d}V}{\mathrm{d}t}},={\frac{1}{m}},(,T,\mathrm{cos}\phi_{T}\mathrm{cos}\alpha,\mathrm{cos}\beta,-,,m g,\mathrm{sin}\theta_{k},-,q,{\infty},S C{D},)

\frac{\mathrm{d}\theta_{k}}{\mathrm{d}t},=\frac{1}{m V}[,T\mathrm{cos}\psi_{T}\mathrm{sin}\alpha\mathrm{cos}\phi_{k},+,T\mathrm{sin}\phi_{T}\mathrm{cos}\varphi_{T}\mathrm{cos}\alpha\mathrm{cos}\phi_{k},-,\

\begin{array}{r l}&{\begin{array}{c c c c}{\mathrm{d}t}&{m V^{\star,-,}\cdots\cdots\cdots\cdots}&{\cdots}&{\cdots}\ &{m g\cos\theta_{k}+q_{\infty}S(C_{L}\mathrm{cos}\phi_{k}-,C_{C}\mathrm{sin}\phi_{k})]}&{(10,-,\mathrm{odd};\phi_{k})}\end{array}}\ &{\begin{array}{c c c c}{\frac{\mathrm{d}\phi_{k}}{\mathrm{d}t}=\frac{1}{m V\cos\theta_{k}^{\star}}[,T\mathrm{cos}\phi_{T}\mathrm{sin}\alpha,\mathrm{sin}\phi_{k}+}&&\ {T,\mathrm{sin}\phi_{T}\mathrm{cos}\varphi_{T}\mathrm{cos}\alpha,\mathrm{sin}\phi_{k}-T\mathrm{cos}\phi_{T}\mathrm{cos}\alpha,\mathrm{sin}\beta\mathrm{cos}\phi_{k}+}&&\ {q_{\infty},S(C_{L}\mathrm{sin}\phi_{k}+C_{C}\mathrm{cos}\phi_{k})]}&&{(10,-,\mathrm{~odd};\phi_{k})}\end{array}}\ &{\frac{\mathrm{d}\phi}{\mathrm{d}t}=\frac{q_{\infty},S(C_{L})}{I_{\mathrm{r}}}C_{l}}&&{(10,-,\mathrm{~odd};\phi_{k})}\end{array}}\end{array}

\begin{array}{r l}&{\frac{\mathrm{d}q}{\mathrm{d}t}=\frac{I_{s}-I_{s}}{I_{s}}p_{r}+\frac{q_{\infty}S l}{I_{s}}C_{\infty}}\ &{\frac{\mathrm{d}r}{\mathrm{d}t}=\frac{I_{s}-I_{s}}{I_{s}}p_{d}+\frac{q_{\infty}S l}{I_{s}}C_{\infty},}\ &{\frac{\mathrm{d}\phi}{\mathrm{d}t}=\frac{1}{\cos\theta}(q\sin\phi+\ r\cos\phi)}\ &{\frac{\mathrm{d}\theta}{\mathrm{d}t}=q\cos\phi-r\sin\phi}\ &{\frac{\mathrm{d}\phi}{\mathrm{d}t}=p+\tan\theta(q\sin\phi+r\cos\phi)}\ &{\mathrm{~}}\end{array}

\begin{array}{r l}&{\frac{\mathrm{d}u_{F}}{\mathrm{d}t}=-\frac{1}{\cos\theta}\left(\sin\theta+r\cos\phi\right)}\ &{\frac{\mathrm{d}B_{\theta}}{\mathrm{d}t}=\cos\phi-r\sin\theta}\ &{\frac{\mathrm{d}B_{\phi}}{\mathrm{d}t}=p_{0}\sin\theta(\sin\phi+r\cos\phi)}\ &{\frac{\mathrm{d}B_{z}^{\prime}}{\mathrm{d}t}=p_{0}\sin\theta(\cos\phi-r\cos\phi)}\ &{\frac{\mathrm{d}B_{z}^{\prime}}{\mathrm{d}t}=\cos\theta_{0}\cos\phi_{\mathrm{th}}}\ &{\frac{\mathrm{d}B_{\phi}^{\prime}}{\mathrm{d}t}=\cos\theta_{0}\sin\phi_{\mathrm{th}}}\ &{\frac{\mathrm{d}B_{z}^{\prime}}{\mathrm{d}t}=-\nabla\sin\theta_{0}\sin\phi_{\mathrm{th}}}\ &{\frac{\mathrm{d}B_{z}^{\prime}}{\mathrm{d}t}=-\nabla\sin\theta_{0}\sin\phi_{\mathrm{th}}}\ &{\frac{\mathrm{d}B_{\phi}^{\prime}}{\mathrm{d}t}=-T_{\mathrm{fain}}^{2}.}\end{array}

  

式中 $\psi_{T}$ 和 $\varphi_{T}$ 一推力偏心角；  

和θ一—航迹方位角和爬升角；$\phi_{k}$ 一绕速度矢量的滚转角；  

$x_{g}^{\prime},y_{g}^{\prime},z_{g}^{\prime}$ 导弹质心在铅垂地面坐标系中的坐标  

\begin{array}{l}{{\alpha\approx\theta,-,\theta_{k}}}\ {{\ }}\ {{\beta\approx\psi\mathrm{cos}\theta,-,\phi_{k}\mathrm{cos}\theta_{k}}}\ {{\ }}\ {{\phi_{k}\approx(\beta\mathrm{sin}\theta,+,\phi,\mathrm{cos}\theta)/\mathrm{cos}\theta_{k}}}\end{array}

  

式（10-123)表示 $_{m}$ 为有效比冲 $I_{\mathrm{eff}}$ 的函数，也可采用下式来近似  

\frac{\mathrm{d}m}{\mathrm{d}t},=,\left{\begin{array}{l r}{0}&{t\leqslant t_{s}}\ {-,c_{4}/\big[,(,t_{h},-,t_{s},),\times,9.81,\big]}&{t_{s}<,t\leqslant t_{h}}\ {-,,c_{5}/\big[,(,t_{k},-,t_{k},),\times,9.81,\big]}&{t_{h}<,t\leqslant t_{k}}\ {0}&{t\geqslant t_{k}}\end{array}\right.

  

式中， $c_{4},c_{5}$ 由发动机的地面点火试验确定。  

自旋导弹飞行试验时因体积小，通常不装角速率陀螺和过载传感器，而仅装偏航、俯仰、倾斜三个陀螺仪，同时采用光学测量装置测量导弹质心的运动历程。因此,气动参数辨识的观测矢量 $\pmb{y}$ $=(\,\psi\,,\theta\,,\phi\,,x_{\,g}^{\prime}\,,y_{\,g}^{\prime}\,,z_{\,g}^{\prime}\,)$ ，观测方程组可取为  

\begin{array}{r l}{\phi_{m},=,\psi,+,\varepsilon_{1}}&{}\ {\theta_{m},=,\theta,+,\varepsilon_{2}}\ {\phi_{m},=,\phi,+,\varepsilon_{3}}&{}\ {x_{g m}^{\prime},=,x_{g}^{\prime},+,\varepsilon_{4}}&{}\ {y_{g m}^{\prime},=,y_{g}^{\prime},+,\varepsilon_{5}}&{}\ {z_{g m}^{\prime},=,z_{g}^{\prime},+,\varepsilon_{6}}&{}\end{array}

  

以式（10-111）一式（10-122）为状态方程组，式（10-125）～式（10-130）为观测方程组，适当设计控制输人使输出含有足够的气动信息，可以辨识下列气动参数  

\pmb{\theta},=(,C_{l0},,C_{l p},,C_{l\hat{\delta}{y}},,C{l\hat{\delta}{z}},,C{m0},,C_{m q},,C_{m\hat{\delta}{y}},,C{n0},,

C_{n r},,C_{n\delta_{z}},,C_{n\delta_{D}},,,\eta,,C_{D0},,C_{D2},,C_{D\delta_{D}},,C_{C0},,C_{C\beta},,C_{C\delta_{z}},,

C_{L0},,C_{L a},,C_{L\delta_{y}})^{\mathrm{T}},=,(,\theta_{1},,\theta_{2},,\cdots,\theta_{21},)^{\mathrm{T}}

  

下面给出采用最大似然递推估计的具体算法。为此，先列出灵敏度满足的微分方程组  

\begin{array}{r l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial,V}{\partial,\theta_{l}},=\frac{1}{m},\bigg[-,T\mathrm{cos}\phi_{T}\mathrm{sin}\alpha,\mathrm{cos}\beta,\frac{\partial,\alpha}{\partial,\theta_{l}}\ -}&{{}}\ {T\mathrm{cos}\phi_{T}\mathrm{cos}\alpha,\mathrm{sin}\beta,\frac{\partial,\beta}{\partial,\theta_{l}},-,m g\mathrm{cos}\theta_{k},\frac{\partial,\theta_{k}}{\partial,\theta_{l}}\ -}\end{array}

\begin{array}{r l}&{\quad q_{\infty}\ S\frac{\partial C_{D}}{\partial\theta_{i}}\ -\ \rho V S C_{D}\frac{\partial V}{\partial\theta_{i}}\Biggr]}\ &{\stackrel{\mathrm{d}}{=}\frac{\partial\theta_{k}}{\partial\theta_{i}}\ \frac{1}{\partial\theta_{i}}=\frac{1}{m}\Biggl[T(\cos\phi_{T}\cos\alpha-}\ &{\sin\phi_{T}\cos\varphi_{T}\sin\alpha)\cos\phi_{k}\ \frac{\partial\alpha}{\partial\theta_{i}}\ -}\ &{\quad m g\sin\theta_{k}\ \frac{\partial\theta_{k}}{\partial\theta_{i}}\ +\ q_{\infty}S\left(\frac{\partial C_{L}}{\partial\theta_{i}}\cos\phi_{k}-\frac{\partial C_{C}}{\partial\theta_{i}}\sin\phi_{k}\right)-}\ &{\quad(T\cos\phi_{T}\sin\alpha\sin\phi_{k}-\ T\sin\phi_{T}\cos\varphi_{\mathrm{r}}\cos\alpha\sin\phi_{k}+}\ &{\quad q_{\infty}S C_{L}\sin\phi_{k}\ -\ q_{\infty}S C_{C}\cos\phi_{k})\ \frac{\partial\phi_{k}}{\partial\theta_{i}}\Biggr]\qquad(10-9)}\end{array}

\begin{array}{l}{{\displaystyle\cdots\cos\cdots\beta\eta_{l}\ \ \cdots\ \cdots\ \cdots\ \cdot\ \partial\eta_{l}\ \ \cdots\ \cdots\ \cdots\ \partial\eta_{l}\ \ \cdots\ \cdots\ \cdots\ \cdots\ \rho\sigma_{l}\ }}\ {{\displaystyle\ (T\cos\varphi_{\mathrm{rimin}}\sin\varphi_{\mathrm{rims}}\ -\ T\sin\varphi_{\mathrm{ress}})\cos\varphi_{\mathrm{ress}}\ \sin\psi_{\mathrm{t}}\ +\ \cdots\ }}\ {{\displaystyle\ (q=S c_{l}\sin\dot{\kappa}{k}-q{\mathrm{s}}S c_{l}\cos\dot{\kappa}{k})\ \frac{\partial\dot{\theta}{k}}{\partial\theta_{l}}\Big[\ (10\ \cdot\ \left(\mathrm{~se~~~~~~~~~~~~~~~~~~~~~~\right.}}\ {{\displaystyle\frac{\mathrm{d}}{d t}\ \frac{\partial\dot{\phi}{k}}{\partial\dot{\theta}{l}}=\frac{1}{m\mathrm{Vess}\dot{\theta}{k}}\Big[T\cos\psi{\mathrm{ress}}\cos\dot{\kappa}\dot{\bf n}\dot{\theta}{k}\ -\ }}\ {{\displaystyle\ \ \ \sin\dot{\gamma}{l}\cos\varphi_{\mathrm{rimin}}\sin\dot{\gamma}{k}+\ \cos\dot{\gamma}{l}\sin\dot{\alpha}\dot{\bf n}\dot{\theta}{l}\cos\dot{\phi}{k}\ \Big]\ \frac{\partial\dot{\theta}{l}}{\partial\theta{l}}-}}\ {{\displaystyle\ \ }T\cos\dot{\gamma}{l}\cos\cos\varphi{\mathrm{d}}\cos\dot{\theta}{k}\ \dot{\theta}{l}\ }}\ {{\displaystyle\ }T(\cos\dot{\gamma}{\mathrm{rimin}}\cos\theta{k}+\ \sin\dot{\gamma}{\mathrm{ress}}\cos\varphi{\mathrm{ress}}\cos\varphi_{\mathrm{rim}}\ +\ \cdots\ \dot{\gamma}{\mathrm{ress}})\ \dot{\theta}{k}\ }}\ {{\displaystyle\ \cos\dot{\gamma}{\mathrm{ress}}\cos\theta{\mathrm{d}}\dot{\gamma}{\mathrm{ab}}\dot{\theta}{l}\ }}\end{array}

\begin{array}{r l}&{\quad_{1}=-\cdots\quad,\quad_{r}\quad,\quad-\quad-\quad\cdot\quad-\quad\cdot\quad\cdot\quad\cdot\quad\sigma_{0,r},,}\ &{\quad\quad-\quad\frac{1}{r}\sec[1+\cos\theta\cos\theta\sin^{2}\theta-1\sec^{2}\theta]}\ &{\quad\quad\sin\theta\cos\psi(\cos\psi-\sin\theta\sin\theta)\cos\phi,,}\ &{\quad\quad\cos\psi\cos\psi\cos\theta\sin\theta,,}\ &{\quad\quad T\cos\psi\cos\alpha\cos\theta\cos\phi,\quad\frac{\partial\theta}{\partial\theta},,}\ &{\quad\quad T(\cos\psi\cos\theta\cos\theta\sin\theta,+,\sin\psi\cos\psi\cos\theta\cos\phi,,,+,}\ &{\quad\quad\cos\theta\cos\psi\sin\theta)\sin\frac{\partial\theta}{\partial\theta},,}\ &{\quad\quad\cos\theta\cos\psi\cos\theta\sin\theta,+,\quad\frac{\partial\theta}{\partial\theta},,}\ &{\quad\quad\cos\theta\cos\psi\sin\theta,+,\quad C_{1}\cos\theta\sin^{2}\theta,,}\ &{\quad\quad\sin^{2}\theta\cos\psi\cos\theta\sin\frac{\partial\theta}{\partial\phi}\Big]\quad\quad\quad(10,\textrm{m i n})\in\mathbb{Z}\times[0,10\pi],,}\ &{\quad\quad\sin\theta\cos\psi\cos\theta\sin\theta,\quad\quad(10,\textrm{m i n})\in\mathbb{Z}\times[0,20\pi],.}\end{array}

\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial,\dot{p}}{\partial\theta_{l}},=\frac{q_{\infty},S l}{I_{x}},\bigg(-,C_{l\dot{p}},\frac{\partial,\dot{p}}{\partial\theta_{l}},\frac{l}{2,V},+,C_{l\dot{\alpha}{!!{y}}}\delta_{x_{!!{y}}}\mathrm{sin}\beta,\frac{\partial\beta}{\partial\theta{l}},+

C_{l\delta_{z}}\delta_{x_{z}}\sin\alpha\ \frac{\partial\alpha}{\partial\theta_{l}}\Biggr)+\ U_{4,l}

\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial,q}{\partial\theta_{l}},=\frac{I_{z},-,I_{x}}{I_{y}}\left(,r,,\frac{\partial,\rlap/p}{\partial\theta_{l}},+,\rlap/p,\frac{\partial,r}{\partial\theta_{l}}\right)+

\begin{array}{l}{{\displaystyle{\frac{q_{\infty}{\cal S}l}{{\cal I}{y}}}\Bigg[-;\left({\frac{\partial{\cal C}{D}}{\partial\theta_{l}}}\mathrm{sin}\alpha\mathrm{cos}\beta+{\frac{\partial{\cal C}{L}}{\partial\theta{l}}}\mathrm{cos}\alpha\right)!\eta;+}}\ {{\displaystyle(;-;{\cal C}{D}\eta\mathrm{cos}\alpha\mathrm{cos}\beta+;{\cal C}{L}\eta\mathrm{sin}\alpha;+}}\ {{\displaystyle{\cal C}{n\delta{D}}\delta_{D}\mathrm{cos}\alpha\mathrm{cos}\beta\left.{\frac{\partial\alpha}{\partial\theta_{l}}};+;({\cal C}{D}\eta\mathrm{sin}\alpha\mathrm{sin}\beta-;{\frac{\partial\alpha}{\partial\theta{l}}}\right)!;+}}\end{array}

C_{n\hat{\sigma}{D}}\delta{D}\mathrm{sin}\alpha\sin\beta\ {\frac{\partial\beta}{\partial\theta_{l}}},-,C_{m q}\ {\frac{\partial q}{\partial\theta_{l}}},{\frac{c_{A}^{2}}{V l}}\Biggr]+\ U_{5,l}

\frac{q_{\infty},S l}{I_{z}}\bigg[\Big(-\frac{\partial C_{C}}{\partial\theta_{l}}\mathrm{cos}\beta+\frac{\partial C_{L}}{\partial\theta_{l}}\mathrm{sin}\beta\Big)\eta,+

(,C_{C}\eta\mathrm{sin}\beta,+,C_{L}\eta\mathrm{cos}\beta,-,C_{n\delta_{D}}\delta_{D}\mathrm{cos}\beta,)~\frac{\partial\beta}{\partial\theta_{i}}~-

C_{l\hat{\sigma}{z}}\hat{\delta}{x_{z}}\mathrm{cos}\alpha\ \frac{\partial\alpha}{\partial\theta_{l}},-,C_{n r}\ \frac{\partial r}{\partial\theta_{l}},\frac{c_{A}^{2}}{V l}\Biggr]+\ U_{6,l}

  

.d a4 sinp + 3r COsp dt a01 cosθ [ 301 301  

(10 - 138)  

\frac{\mathrm{d}}{\mathrm{d}t};\frac{\partial\theta}{\partial\theta_{l}};=;\left(\frac{\partial q}{\partial\theta_{l}}\mathrm{cos}\phi;-;\frac{\partial r}{\partial\theta_{l}}\mathrm{sin}\phi\right)-;\left(\frac{}{}q\mathrm{sin}\phi;+;r\mathrm{cos}\phi;\right);\frac{\partial\phi}{\partial\theta_{l}}

  

(10 - 139)  

\begin{array}{l}{{\displaystyle{\frac{\mathrm{d}}{\mathrm{d}t}}\ {\frac{\partial\phi}{\partial\theta_{l}}}\ {}={\frac{\partial,\rlap/}{\partial\theta_{l}}}\ +\ \tan\theta\left[,\left({\frac{\partial,q}{\partial\theta_{l}}}{}\mathrm{sin}\phi,+,{\frac{\partial,r}{\partial\theta_{l}}}{}\mathrm{cos}\phi,\right),+,\right.}}\ {{\displaystyle{}\left.\left(,q,\mathrm{cos}\phi,-,r\mathrm{sin}\phi,\right),{\frac{\partial,\phi}{\partial\theta_{l}}},\right]+,{\frac{1}{\mathrm{cos}^{2},\theta}}(,q,\mathrm{sin}\phi,+,r\mathrm{sin}\phi,)\ {\frac{\partial,\theta}{\partial\theta_{l}}}}}\end{array}

  

(10 - 140)  

\begin{array}{r l}&{\frac{\mathrm{t}}{t}\frac{\partial x_{e}^{}}{\partial\theta_{i}}=-\nu\frac{\partial\theta_{i+1}}{\partial\theta_{i}}\boldsymbol{\partial\phi}{i}\boldsymbol{\cos}\phi{}-V\frac{\partial\phi_{\boldsymbol{\phi}{\boldsymbol{\phi}{\boldsymbol{\phi}}}}}{\partial\theta_{i}}\boldsymbol{\cos}\theta_{i}\boldsymbol{\sin}\phi_{}}\ &{\frac{\mathrm{t}}{t}\frac{\partial y_{e}^{}}{\partial\theta_{i}}=-\nu\frac{\partial\phi_{\boldsymbol{\phi}{\boldsymbol{\phi}}}}{\partial\theta{i}}\boldsymbol{\sin}\theta_{i}\boldsymbol{\sin}\phi_{}+V\frac{\partial\phi_{\boldsymbol{\phi}{\boldsymbol{\phi}}}}{\partial\theta{i}}\boldsymbol{\cos}\phi_{}}\ &{\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial z_{e}^{*}}{\partial\theta_{i}}=-\nu\frac{\partial\theta_{i}}{\partial\theta_{i}}\boldsymbol{\cos}\theta_{i}}\ &{\frac{\partial C_{D}}{\partial\theta_{i}}=2C_{D\theta}\bigg(\alpha\frac{\partial\theta_{i}}{\partial\phi_{i}}+\beta\frac{\partial\beta}{\partial\theta_{i}}\bigg)+U_{1,i}}\ &{\frac{\partial C_{C}}{\partial\theta_{i}}=C_{\phi}\frac{\partial\beta}{\partial\theta_{i}}+U_{2,i}}\ &{\frac{\partial C_{\boldsymbol{\phi}}}{\partial\phi_{i}}=C_{L}\frac{\partial\alpha}{\partial\theta_{i}}+U_{3,i}}\ &{\partial\alpha_{\boldsymbol{\phi}}=\frac{\partial\beta}{\partial\phi_{i}}.}\end{array}

\begin{array}{r l}&{\begin{array}{r l}&{-\cdots}\ &{\frac{\partial\hat{\sigma}{i j}}{\partial\hat{\sigma}{i j}}=2C_{i}\omega_{i}\left(\frac{\partial\hat{\sigma}{i j}}{\partial\hat{\sigma}{i j}}+\beta\frac{\partial\hat{\beta}}{\partial\hat{\theta}{i}}\right)+U{1,i},}\ &{\frac{\partial C_{i}}{\partial\hat{\sigma}{i j}}=C{0}\frac{\partial\hat{\beta}}{\partial\hat{\theta}{i j}}+U{2,i},}\ &{\frac{\partial C_{i}}{\partial\hat{\sigma}{i j}}=C{i}\frac{\partial\hat{\beta}}{\partial\hat{\theta}{i j}}+U{3,i},}\ &{\frac{\partial C_{i}}{\partial\hat{\sigma}{i j}}=2\hat{\sigma}{i j}\frac{\partial\hat{\sigma}{i j}}{\partial\hat{\theta}{i j}}}\ &{\frac{\partial\hat{\sigma}{i j}}{\partial\hat{\theta}{i j}}=\frac{\partial\hat{\beta}}{\partial\hat{\theta}{i j}}-\frac{\partial\hat{\beta}{i j}}{\partial\hat{\theta}{i j}}}\ &{\frac{\partial\hat{\beta}{i j}}{\partial\hat{\theta}{i j}}=\frac{\partial\hat{\beta}{i j}}{\partial\hat{\theta}{i j}}\frac{\partial\hat{\beta}{i j}}{\partial\hat{\theta}{i j}}-\frac{\partial\hat{\beta}{i k}}{\partial\hat{\beta}{i j}}\cos\theta{i}\cdot}\ &{\hat{\beta}{i j}\sinh\hat{\alpha}{i j}\frac{\partial\hat{\beta}{i j}}{\partial\hat{\theta}{j}}}\ &{\frac{\partial\hat{\beta}{i k}}{\partial\hat{\theta}{i j}}=\frac{1}{2}\left[\left(\frac{\partial\hat{\beta}{i j}}{\partial\hat{\beta}{k}\partial\hat{\theta}{i j}}+\frac{\partial\hat{\beta}{i j}}{\partial\hat{\beta}{k}\partial\hat{\theta}{i j}}\right)+\right.}\end{array}}\end{array}

  

301  

(10 - 149)  

式中  

\begin{array}{l l l}{{U_{1,13}=1\quad}}&{{;;U_{1,14}=\alpha^{2}+\beta^{2}\quad}}&{{U_{1,15}=\delta_{D}}}\ {{\displaystyle U_{2,16}=1\quad}}&{{\phantom{\frac{1}{\alpha}}U_{2,17}=\beta\quad}}&{{\phantom{\frac{1}{\alpha}}U_{2,18}=,-,}}\ {{\displaystyle U_{3,19}=1\quad}}&{{\phantom{\frac{1}{\alpha}}U_{3,20}=\alpha\quad}}&{{\phantom{\frac{1}{\alpha}}U_{3,21}=,-,}}\ {{\displaystyle U_{4,1}=\frac{q_{\infty},S l}{I_{x}}}}&{{\phantom{\frac{1}{\alpha}}U_{4,2}=,-,}U_{4,1},\rho,\frac{l}{2,V}}}\end{array}

  

$\begin{array}{l l}{{U_{4,3}={\displaystyle U_{4,1}\delta_{x,}{\cos\beta}}}}&{{U_{4,4}={\displaystyle U_{4,1}\delta_{x,}{\cos\alpha}}}}\\ {{\displaystyle U_{5,5}={\displaystyle\frac{q_{\infty}S l}{I_{5}}}}}&{{U_{5,6}={\displaystyle U_{5,5}q}\displaystyle\frac{c_{A}^{2}}{V l}}}\\ {{\displaystyle U_{5,7}={\displaystyle U_{5,5}\delta_{y}}}}&{{U_{5,3}=-\ {U_{5,5}\delta_{x,}\sin\beta}}}\\ {{\displaystyle U_{5,11}=U_{5,5}\delta_{x,}{\sin}{\cos\beta}}}&{{\displaystyle\alpha}}\\ {{\displaystyle U_{5,12}=-\ {U_{5,5}(C_{D}{\sin}\alpha{\cos\beta}+C_{L}{\cos\alpha})}}}\\ {{\displaystyle U_{6,8}=\displaystyle\frac{q_{\infty}S l}{I}}}&{{U_{6,9}=-\ {U_{6,8}r\displaystyle\frac{c_{A}^{2}}{V l}}}}\end{array}$ U6.10 =—U 6.8 02 U6,11 = -U6.8 ODsinβ U6.4=-U6.8_sinα U6,12 = - U6,8(Cccosβ - CL sinβ) 其余 $U_{i\,,\,j}=\mathbf{0}$ $(\,i=1,2,\cdots,6\,;j=1\,,2\,,\cdots,21\,)$  

初值取为零，由式（10-132）一式（10-149)可以积分求得灵敏度系数。  

利用5.3.6节的最大似然递推算法可以估计未知参数。首先，根据风洞试验或理论计算的验前信息给出某时刻导弹的气动参数估计值 $\pmb\theta(k-1)$ 和参数的协方差阵 $P_{\theta}(\,k\,-\,1\,)\,_{\circ}\quad P_{\theta}$ 可以取为对角线矩阵，对本模型 $\pmb\theta$ 是21维矢量， $\scriptstyle P_{\theta}$ 是 $21\times21$ 维矩阵。根据飞行试验测量数据确定出 $(k-1)$ 时刻的状态参数初值（当状态参数初值未知时，取状态方程前一个积分结果），由式（10-111）～式（10-122）积分出 $\pmb{k}$ 时刻的状态值，并得到 $\phi(\,k\,),\theta(\,k\,),\phi(\,k\,)\,.$ $x_{g}^{\prime}(\,k\,)\,,y_{g}^{\prime}(\,k\,)\,,z_{g}^{\prime}(\,k\,)\,_{c}$ ，由下式计算新息 $v(k)$  

\pmb{\nu}(,k,),=,\bigl[,\psi(,k,),-,\psi_{m}(,k,),,\theta(,k,),-,\theta_{m}(,k,),,\phi(,k,),-,\phi_{m}(,k,),,

x_{,g}^{,\prime}(,k,),-,x_{,g m}^{,\prime}(,k,),,y_{,g}^{,\prime}(,k,),-,y_{,g m}^{,\prime}(,k,),,z_{,g}^{,\prime}(,k,),-,z_{,g m}^{,\prime}(,k,),]^{\intercal}

  

下标 $_m$ 表示实测值。 $\psi(k)$ 为6维矢量，由(10-132)～式(10-149)积分出 $\partial\,{\pmb v}/\partial\,{\pmb\theta}$ ，是 $21\times6$ 维矩阵。根据系统得噪声统计特性，选取新息协方差矩阵 $\pmb{{\cal B}}$ ，可以取为对角线矩阵，也可以由下式计算  

\hat{\pmb{B}};=;\frac{1}{k,-,1}\sum_{\substack{i,-,1}}^{k,-,1}\pmb{\nu}(,i,),\pmb{\nu}^{\mathrm{\tiny~T}}(,i,)

  

然后，由下式计算得到 $\hat{\pmb{\theta}}(\,k\,)\,,\pmb{K}_{\theta}(\,k\,)\,,\pmb{P}_{\theta}(\,k\,)$  

\hat{\pmb\theta}(,k,);=;\hat{\pmb\theta}(,k,-,1,),+,{\bf K}_{\beta}(,k,),{\pmb\nu}(,k,)

\mathbf{\hat{K}}{\theta}(,k,),=,-,,P{\theta}(,k,-,1,),{\frac{\partial,\nu}{\partial\theta}}\bigg[,{\hat{B}},+,{\frac{\partial,\nu}{\partial\theta}}{\pmb{P}}_{\theta}(,k,-,1,),{\frac{\partial,\nu}{\partial\theta}},\bigg]^{,-,1}

{\bf P}{\theta}(,k,);=;\left[\frac{}{}I,+,K{\theta}(,k,);\frac{\partial,\pmb{\nu}}{\partial\theta}\right]!!{\bf P}_{\theta}(,k,-,1,)

  

式（10-152）～式（10-154)给出了气动参数辨识的新估计值及下次迭代所需的协方差矩阵 $\boldsymbol{P}_{\theta}\left(\,k\,\right)$ 。这样，就可以递推估计出气动参数。  

# 10.5 再人体气动参数辨识  

再人体是专指以极高速度重返大气层的物体，包括洲际弹头、卫星、飞船等，多数是没有控制面的飞行器。再人体最关心的气动力参数是静稳定裕度、动稳定性导数和小不对称气动力。这些气动参数决定了再人体的运动稳定性，从而决定了其生存概率。再人体以 $4\mathbf{km}/\mathbf{s}\!\sim\!8\mathbf{km}/\mathbf{s}$ 的飞行速度进人大气层，所形成的高温气体鞘高达几千度，无法安装攻角传感器，所以攻角估计也是再人体气动参数估计的重要问题。本节给出利用飞行试验记录的角速率和过载遥测数据以及弹道实测数据辨识再人体静稳定裕度、动稳定性导数、小不对称气动力以及估算攻角的算法和具体算式。  

# 10.5.1 再入体气动力矩导数辨识  

再人体气动参数可以采用10.2.1节介绍的6自由度动力学方程作为状态方程组进行参数辨识，也可针对无控再人体的特点，对状态方程组作简化,给出简化算法[11]  

对于无控再人体， $\delta_{e}=\delta_{r}=\delta_{a}\!\equiv\!0$ ,采用气动力和力矩的线性  

模型，对式（10-13）～式（10-14)求导，并将式 $(\mathfrak{i}0^{-10})\sim$ 式（10-11) 代人，消去 $\alpha\cdot\beta$ 等,略去小量,经简单整理可得下列方程组  

\begin{array}{c}{{\displaystyle\frac{\mathrm{d}{q}}{\mathrm{d}t},=,\dot{q}}}\ {{\displaystyle\frac{\mathrm{d}\dot{q}}{\mathrm{d}t},=,\frac{q_{\infty},S l^{2}}{2,V I_{y}}\bigg(,C_{m q},+,C_{m\dot{a}},+,\frac{2,C_{N a}I_{y}}{m l^{2}}\bigg),\dot{q},+,\frac{q_{\infty},S l}{I_{y}}C_{m a}q,,+}}\ {{\displaystyle\quad\cdot,\frac{I_{y},-,I_{x}}{I_{y}}p_{m}^{2}q,+,\frac{2,I_{z},-,I_{x}}{I_{y}}p_{m}\dot{r},+,\frac{I_{z},-,I_{x}}{I_{y}}\dot{p}_{m}r,-,}}\end{array}

\begin{array}{r l r}&{}&{\frac{\mathrm{e}^{-1}}{2,\mathrm{V}I_{y}}^{2},}\ &{}&{\frac{q_{\mathrm{s}},S L^{2}}{2,\mathrm{V}I_{y}}\bigg(C_{w}-C_{w}+C_{w}\mu_{\mathrm{s}}+\frac{I_{z}-I_{z}}{m^{2}}C_{w}\ln\bigg)p_{w},r\cdot}\ &{}&{C_{w},\beta_{m},\frac{q_{\mathrm{s}},S L}{I_{y}}+\frac{q_{\mathrm{s}}}{q_{\mathrm{s}}^{2}},\dot{q}-\frac{\dot{q}{\mathrm{s}}}{q{\mathrm{s}}},\frac{I_{z}-I_{z}}{I_{y}}p_{w}r\quad(1)}\ &{}&{\frac{\mathrm{d}r}{\mathrm{d}t}=\dot{r}}\ &{}&{\frac{\mathrm{d}\dot{\mathrm{p}}}{\mathrm{d}t}=\frac{q_{\mathrm{s}},S L^{2}}{2,\mathrm{V}I_{\mathrm{s}}},\bigg[C_{w}-C_{w}+\frac{2C_{w}p_{z}L}{m^{2}}\bigg],\dot{r}+\frac{q_{\mathrm{s}},S L}{I_{z}}C_{w},+}\ &{}&{\frac{I_{z}-I_{z}}{I_{z}},p_{w}^{2}r-\frac{2,I_{z}-I_{z}}{I_{z}},\dot{p}{w}\dot{q}-\frac{I{z}-I_{z}}{I_{z}},\dot{p}{w}\dot{q}+}\ &{}&{q{\mathrm{s}},S L^{2},\bigg[\int_{z}}&{\dots\quad z,,}\end{array}

{\frac{q_{\infty},S l^{2}}{2,V I_{z}}}\left[C_{m q},+,C_{m\dot{\alpha}},-,C_{n\hat{\rho}\alpha},+,{\frac{I_{y},-,I_{x}}{m l^{2}}},C_{Y!\beta}\right]!\hat{p}_{m}q,,-

C_{m0},\rlap/p_{m};\frac{q_{\infty},S l}{I_{z}},+,\frac{\dot{q}{\infty}}{q{\infty}}\dot{r},+,\frac{\dot{q}{\infty}}{q{\infty}};\frac{I_{y},-,I_{x}}{I_{z}}\ p_{m}q

  

式中 Pm——直接用角速率 p 的测量值。  

再人体基本外形是轴对称体，参考长度统-取为 $l$ ，动导数用 $(2V)$ $l)$ 无量纲化。以式（10-155）～式（10-158)作为状态方程组，仅利用角速率和动压的测量数据就可以辨识再人体的气动力矩导数。待估计参数0取为  

\pmb{\theta};=;\left(C_{m q};+;C_{m\dot{\alpha}};+;\frac{2,C_{N_{\alpha}}I_{y}}{m l^{2}},,C_{m\alpha},,C_{n r};-;C_{n\dot{\beta}};+\right.

C_{m\beta\beta},+,\frac{I_{z},-,I_{x}}{m l^{2}}C_{N\alpha},,C_{m0},,C_{n r},-,C_{n\beta},+,\frac{2C_{Y\beta}I_{z}}{m l^{2}},,C_{n\beta},,C_{m q},+,

  

观测方程组为  

\begin{array}{l}{{q_{m};=;q,+,\varepsilon_{1}}}\ {{{}}}\ {{r_{m};=;r,+,\varepsilon_{2}}}\end{array}

  

采用最大似然法由式（10-155）～式（10-161)辨识再人体气动 力矩导数,还必须给出灵敏度方程组。记  

Q_{l},=,\partial q/\partial\theta_{l}\qquad R_{l},=,\partial r/\partial\theta_{l}

  

则灵敏度方程组为  

\begin{array}{c}{{\displaystyle{\ddot{Q}}{\iota}\ =\frac{q{\infty}S l^{2}}{2,V I_{y}}\dot{Q_{1}}\ {\dot{Q_{\iota}}}{\iota}\ +\ \frac{q{\infty}S l}{I_{y}}\theta_{2}Q_{l}\ +\ \frac{I_{y}\ -\ I_{x}}{I_{y}}p_{m}^{2}Q_{l}\ +}}\ {{\displaystyle\ \ \ \frac{2I_{z}\ -\ I_{x}}{I_{y}}\rho_{m}{\dot{R}}{l}\ +\ \frac{I{z}\ -\ I_{x}}{I_{y}}{\dot{p}}{m}R{l}\ -\ \frac{q_{\infty}S l^{2}}{2,V I_{y}}\theta_{3},\rho_{m}R_{l}\ +}}\ {{\displaystyle\ \ \ \frac{\dot{q}{\infty}}{q{\infty}}\biggl(\dot{Q}{\iota}\ -\frac{I{z}\ -\ I_{x}}{I_{y}}\rho_{m}R_{l}\ \biggr)+\ {U}_{q,\iota}}\end{array}

\ddot{R}{l},=\frac{q{\infty},S l^{2}}{2,V I_{z}}\theta_{5}\dot{R}{l},+,\frac{q{\infty},S l}{I_{z}}\theta_{6}R_{l},+,\frac{I_{z},-,I_{x}}{I_{z}}\phi_{{!m}}^{2}R_{l},-,

\begin{array}{l}{{{\displaystyle\frac{2,I_{y},-,I_{x}}{I_{z}}{{\cal p}}{m},\dot{Q{l}}{l},-,\displaystyle\frac{I{y},-,I_{x}}{I_{z}}{{\cal\dot{p}}}{m}Q{l}+\displaystyle\frac{q_{\infty},S l^{2}}{2,V I_{z}}\theta_{7},{\cal\dot{p}}{m}Q{l},+,}}\ {{{\displaystyle\frac{\dot{q}{\infty}}{q{\infty}}\left[\dot{R}{l},+,\displaystyle\frac{I{y},-,I_{x}}{I_{z}}\phi_{m}Q_{l}\right]+,U_{r,l}}}}\end{array}

\begin{array}{l l}{{U_{q,1}={\frac{q_{\infty}{\cal S}l^{2}}{2,{\cal V}{p}}}\displaystyle\phi(~~~~~}}&{{~~~~U{q,2}={\frac{q_{\infty}{\cal S}l}{I_{y}}}q}}\ {{{\cal U}{q,3}=-{\frac{q{\infty}{\cal S}l^{2}}{2,{\cal V}{p}}}\displaystyle\phi{m}r~~~~}}&{{~~~~U_{q,4}={\frac{q_{\infty}{\cal S}l}{I_{y}}}\displaystyle\hat{p}{m}}}\ {{{\cal U}{r,5}={\frac{q_{\infty}{\cal S}l^{2}}{2,{\cal V}{q{\infty}}}}\displaystyle\hat{r}~~~~}}&{{~~~~{\cal U}{r,6}={\frac{q{\infty}{\cal S}l}{I_{z}}}\displaystyle\hat{r}}}\ {{{\cal U}{r,7}={\frac{q{\infty}{\cal S}l^{2}}{2,{\cal V}{q{\infty}}}}\displaystyle\hat{p}{m}q{\infty}~~~}}&{{~~~{\cal U}{r,8}=-{\frac{q{\infty}{\cal S}l}{I_{z}}}\displaystyle\hat{p}_{m}}}\end{array}

  

灵敏度方程组的积分初值为  

Q_{9}(0);=;\dot{Q}{10}(0);=;R{11}(0);=;\dot{R}_{12}(0);=;1

  

$Q_{l}(0)\;=\;\dot{Q}_{l}(0)\;=\;R_{l}(0)\;=\;\dot{R}_{l}(0)\;=\;0$  

(,\iota,=,1,,2,,\cdots,12,)

  

再人体飞行速度很高，大气湍流的影响相对而言很小，可忽略，故可采用输出误差法进行参数估计。令辨识准则函数 $J$ 为  

J;=;\frac{1}{N}\sum_{i;=;1}^{N},[;W_{1}(,q;-;q_{m},)^{2}:+;W_{2}(,r:-:r_{m},)^{2},]

  

式中， $W_{1}\,,\,W_{2}$ 由验前信息确定，或选为使式中两项的数量级相近，也可采用误差协方差阵的最优估计。选取 $\pmb{\theta}$ 使 $J$ 达极小是最小二乘问题，易于求解。  

$\pmb\theta$ 的最优估计给出了静稳定导数 $C_{m a}$ 和 $C_{n\beta}$ ，小不对称气动参数 $C_{m0}$ 和 $C_{n0}$ ；动稳定导数和马格斯导数可由下式求得  

C_{m q};+;C_{m\dot{\alpha}};=;\theta_{1};-;\frac{2C_{N\alpha}I_{y}}{m l^{2}}

C_{n r};-;C_{n\dot{\beta}};=;\theta_{5};-;\frac{2,C_{Y\beta}I_{z}}{m l^{2}};

C_{m p\beta}:=:\theta_{3}:-:\theta_{5}:+:\frac{2,C_{Y\beta}I_{z}}{m l^{2}}:-:\frac{I_{z}:-:I_{x}}{m l^{2}},C_{N a}

C_{n\dot{p}\alpha};=;\theta_{7}:-:\theta_{1}:-:\frac{2,C_{N_{\alpha}}I_{y}}{m l^{2}}:+:\frac{I_{y}:-:I_{x}}{m l^{2}},C_{Y\beta}

  

利用上述简化辨识数学模型，对某典型再人体参数进行辨识仿真计算。表10-5给出了部分辨识仿真结果，可见辨识误差较小，表明此简化数学模型可以用来辨识再人体的静、动俯仰力矩导数。但对小不对称气动参数的辨识误差较大，因此下一小节给出小不对称参数的另一种辨识算法。  

表 10-5 再入体简化模型的辨识准度  


<html><body><table><tr><td>气动导数</td><td>Cma,- Cnβ</td><td>Cmg + Cma</td><td>Cn - Cp</td><td>Cmg + Cm=Cnr - Cn</td></tr><tr><td>准确值</td><td>-0.3</td><td>-2.0</td><td>-2.0</td><td>-2.0</td></tr><tr><td>辨识结果</td><td>- 0.29</td><td>-1.72</td><td>-2.16</td><td>-1.9</td></tr><tr><td>相对误差/%</td><td>3</td><td>14</td><td>8</td><td>5</td></tr></table></body></html>  

# 10.5.2 小不对称气动参数辨识  

再人体设计，特别是小型再人体设计，最关心的气动力参数是静稳定裕度和小不对称气动参数。设计的静稳定裕度太小，可能导致再人体出现静不稳定，从而攻角发散；小不对称气动参数太大,可能导致再人体出现低空滚转共振,使配平攻角过大[10]。这两种现象都可能导致再人体因过载太大而解体，这是再人体设计时非常关心的关键气动问题。  

轴对称再人体是否出现低空滚转共振，主要取决于再人体的质量不对称、惯量不对称和气动力不对称。这些不对称量来源于设计、加工和安装过程的初始不对称，再人过程中的烧蚀、侵蚀和边界层不对称转护等又使这些不对称量不断变化，难以预先确定。由于小不对称外形无法预先确定，使得通过风洞试验和理论计算获取再人体小不对称气动力极为困难，从飞行试验数据辨识这些小不对称参数成了主要研究手段。  

再人体旋转角速率的时间历程主要取决于静稳定裕度 $\pmb{\eta}$ ,动稳定导数 $C_{l\rho}\,,C_{m q}\,,C_{n r}$ ,小不对称气动参数 $C_{l0}\,,C_{m0}\,,C_{n0}$ ,压心和质心的横向偏移 $y_{\pmb{\rho}\pmb{g}}\setminus z_{\pmb{\rho}\pmb{g}}$ ，以及惯量不对称参数 $I_{x y}\setminus I_{x z}$ 等。下面建立从飞行试验数据辨识这些参数的简化数学模型。  

再人体角运动服从下列方程组  

\frac{\mathrm{d},\dot{p}}{\mathrm{d}t},=\frac{L}{I_{x}},+,\frac{I_{y},-,I_{z}}{I_{x}}q r,+,\frac{I_{x y}}{I_{x}}\left(\frac{\mathrm{d}q}{\mathrm{d}t},-,\dot{p}r\right)+

\frac{I_{x z}}{I_{x}}\bigg(\frac{\mathrm{d}r}{\mathrm{d}t},+,\dot{p}q\bigg)+\frac{I_{y z}}{I_{x}}(,q^{2},-,r^{2})

\frac{\mathrm{d}q}{\mathrm{d}t},=\frac{M}{I_{y}},+,\frac{I_{z},-,I_{x}}{I_{Y}}p r,+,\frac{I_{y z}}{I_{y}}\Bigl(\frac{\mathrm{d}r}{\mathrm{d}t},-,p q\Bigr),+

\frac{I_{x y}}{I_{y}}\left(\frac{\mathrm{d},\rho}{\mathrm{d}t},-,q r,\right)+,\frac{I_{x z}}{I_{y}}(,r^{2},-,\rlap/p^{2})

\frac{\mathrm{d}r}{\mathrm{d}t},=\frac{N}{I_{z}},+,\frac{I_{x},-,I_{y}}{I_{z}}p q,+,\frac{I_{x z}}{I_{x}}\biggl(\frac{\mathrm{d}\phi}{\mathrm{d}t},-,q r\biggr),+

\frac{I_{y z}}{I_{x}}\left(\frac{\mathrm{d}q}{\mathrm{d}t},+,p r,\right)+,\frac{I_{x y}}{I_{x}}(,\rho^{2},-,q^{2})

  

式中 $L\,,M\,,N\cdot$ 一—气动力矩在体轴的投影,它是攻角、侧滑角、角速率、速度和高度的函数。  

为使运动方程组封闭，必须引进体轴的速度方程组 $(\,u\,,v\,,w$ 或 $V\,,\pmb{\alpha}\,,\pmb{\beta})$ 和姿态角方程组。通常高度取实测值，故角速率、线速度和姿态角的九个方程构成参数辨识的状态方程组。10.2.1节给出了采用上述状态方程组进行气动参数辨识的最大似然法。本节采用过载实测值表达气动力矩，建立辨识静稳定裕度和小不对称参数的简化数学模型。  

气动力矩可表达为  

L\ =,q_{\infty},S l\left(,C_{l0},+,C_{l p},\frac{;\rlap/{p l}}{2,V}\right)+,,m g\left(,n_{z}y_{\rlap/{p g}},-,n_{y}z_{\rlap/{p g}}\right)

  

380  

\begin{array}{l}{{{\cal M},=,q_{\infty},S l\left(,C_{m0},+,C_{m q},\displaystyle{\frac{q l}{2,V}}\right)+,m g n_{z}l,\eta}}\ {{{\cal N},=,q_{\infty},S l\left(,C_{n0},+,C_{n r},\displaystyle{\frac{r l}{2,V}}\right)-,m g n_{\mathrm{s}}l,\eta}}\end{array}

  

式中 n——稳定裕度；  

$n_{\textrm{y}},n_{z}$ —横向过载。  

式(10-172)～式(10-174)不出现攻角和侧滑角,因此可仅用式(10-169)～式(10-171)作为状态方程组，略去速度方程组和姿态角方程组。静稳定裕度 $\pmb{\eta}$ 定义为气动力合力作用线与再人体纵轴的交点与质心的距离除以参考长度 $\iota$ ,且 $\eta\!>\!0$  

根据再人体运动特性,式（10-169）～式（10-171）可进一步简化。为减小再人落点散布，再入体在再人过程中常具有 $1\tau/\mathrm{s}\!\sim\!3\mathrm{r}/\mathrm{s}$ 的滚转角速率 $\pmb{\hat{p}}$ ,其数值比 $\pmb q$ 和 $\pmb{r}$ 高一个数量级。再人体角加速率 $\pmb q$ 和 $\pmb{r}$ 的幅值分别为角速率 $\pmb q$ 和 $\pmb{r}$ 的幅值与气动固有振荡圆频率的乘积。对于再人体，在稠密大气层的气动圆频率大于10，故角速率的量级为  

\begin{array}{l}{\displaystyle\dot{p},=,O,(10\mathrm{rad}/\mathrm{s}),;\quad q,,r,=,O,(1\mathrm{rad}/\mathrm{s})}\ {\displaystyle}\ {\displaystyle\dot{p},=,O,(1\mathrm{rad}/\mathrm{s}^{2}),;\quad q,,r,=,O,(10\mathrm{rad}/\mathrm{s}^{2})}\end{array}

  

式中 $O(\,\cdot\,)$ 表示同数量级。  

以 $\pmb q\setminus r$ 为基准量级， $\pmb{\varepsilon}$ 代表一阶小量，则再人体各角运动参数、惯量矩和气动力矩的数量级如表10-6所列。  

表 10-6各参数的数量级  


<html><body><table><tr><td>参数</td><td>(1,- I,)/1x</td><td>Ix/ Ix</td><td>Ire/ I.</td><td>Ix/ 1</td><td>I/1,、I/1,</td><td>b</td></tr><tr><td>数量级</td><td></td><td>E</td><td>E</td><td>E</td><td>E</td><td>1</td></tr><tr><td>参数</td><td>p</td><td>L/1r</td><td>p</td><td>~b</td><td>M11,</td><td>N/ Ix</td></tr><tr><td>数量级</td><td>1</td><td>1</td><td>1/e</td><td>1/e</td><td>1/e</td><td>1/e</td></tr></table></body></html>  

按上述各参数的数量级分析方程式（10-169）～式（10-171)的  

各项,各项的数量级如表10-7所列。  

表 10-7 各项的数量级  


<html><body><table><tr><td colspan="2"></td><td>左式</td><td>右式1项</td><td>2项</td><td>3项</td><td>4项</td><td>5 项</td></tr><tr><td rowspan="3">数 量 级</td><td>式(10-169)</td><td>1</td><td>1</td><td>e2</td><td>1</td><td>1</td><td>E</td></tr><tr><td>式(10-170)</td><td>1/e</td><td>1/e</td><td>1</td><td></td><td>W</td><td>1</td></tr><tr><td>式(10-171)</td><td>1/e</td><td>1/e</td><td>1</td><td>E</td><td>E</td><td>1</td></tr></table></body></html>  

略去方程中的 $\pmb{\varepsilon}$ 量级的项,根据式(10-169)～式(10-174),再入体的状态方程组可以简化为  

\begin{array}{l}{{\displaystyle\frac{\mathrm{d}{\phi}}{\mathrm{d}t}=\frac{q_{\infty}S l}{I_{x}}\biggl(C_{l0}+C_{l\dot{p}}\frac{\dot{p}l}{2V}\biggr)+\frac{m g}{I_{x}}(,n_{z}y_{p\dot{z}},-,n_{y}z_{p\dot{z}},),+}}\ {{\displaystyle\qquad\frac{I_{x y}}{I_{x}}\biggl(\frac{\mathrm{d}q}{\mathrm{d}t},-,\dot{p}r\biggr)+\frac{I_{x z}}{I_{x}}\biggl(\frac{\mathrm{d}r}{\mathrm{d}t},-,\dot{p}q\biggr)}}\ {{\displaystyle\frac{\mathrm{d}q}{\mathrm{d}t}=\frac{q_{\infty}S l}{I_{y}}\biggl(C_{m0}+C_{m q},\frac{q l}{2V}\biggr)+\frac{m g l}{I_{y}}n_{z}\eta,+}}\ {{\displaystyle\qquad\frac{I_{z},-,I_{x}}{I_{y}}\dot{p}r+\frac{I_{x z}}{I_{y}}(r^{2},-,\dot{p}^{2})}}\end{array}\qquad\qquad(10)

\frac{\mathrm{d}r}{\mathrm{d}t},=\frac{q_{\infty},S l}{I_{z}}\bigg(C_{n0},+,C_{n r},\frac{r l}{2,V}\bigg)-\frac{,m g l}{I_{z}}n_{y}\eta,+

\frac{I_{x};-;I_{y}}{I_{z}}!p q,+,\frac{I_{x y}}{I_{z}}(,\rho^{2},-,q^{2})

  

实际上，上述方程式(10-175)仅保留同阶量，而式（10-176)及式（10-177）保留一阶小量，这样的简化方程可适用于高空飞行段。在高空飞行段，气动力项很小,式(10-176)及式(10-177)中 $I_{x y}\,,I_{x z}$ 起主导作用。  

取式（10-175）～式（10-177)为状态方程组，观测方程组为  

\begin{array}{r}{\pmb{\hat{p}{m}},=,\pmb{\hat{p}},+,\pmb{\varepsilon}{1}}\ {\pmb{q_{m}},=,\pmb{q},+,\pmb{\varepsilon_{2}}}\ {\pmb{r_{m}},=,\pmb{r},+,\pmb{\varepsilon_{3}}}\end{array}

  

待辨识参数为  

382  

\begin{array}{c}{\textbf{\em{\theta}}=(,C_{l0},,C_{l\beta},,C_{m0},,C_{m q},,C_{n0},,C_{n r},,y_{p g},,z_{p g},,I_{x y},,I_{x z},,\eta,,}\ {\qquad\beta_{0},,q_{0},,r_{0},)^{\mathrm{T}},=,(,\theta_{1},,\theta_{2},,\cdots,,\theta_{14},)^{\mathrm{T}}\qquad\qquad\qquad(10,\cdot20)}\end{array}

  

灵敏度方程组由式(10-175）～式（10-177)对 $\theta_{l}$ 求偏导数,交换 $\frac{\partial}{\partial\theta_{l}}\#\mathbb{1}\frac{\mathrm{d}}{\mathrm{d}t}$ 的次序得到。其初值除 $\frac{\partial\phi(\mathbf{0})}{\partial\phi_{0}}=\frac{\partial q\left(\mathbf{0}\right)}{\partial q_{0}}=\frac{\partial r(\mathbf{0})}{\partial r_{0}}=1$ 其余全为零。  

基于上述数学模型，采用牛顿-拉夫逊迭代算法，可以辨识出未知参数 $\pmb{\theta}$  

状态方程组（10-175）～式（10-177）是非线性系统，但对于待辨识参数 $\pmb{\theta}$ 而言，却是线性的。仅当状态方程中相应于各个待辨识参数的项线性无关时，才可能分别辨识出各个未知参数。利用回归分析的概念，将各方程中未知参数 $\theta_{i}$ 所相对应的乘积项称为其预报因子 $X_{i}$ 。显然，若方程中有两个预报因子 $X_{i}$ 和 $X_{j}$ 是线性相关的,则参数辨识只能估计出 $\dot{\theta}_{i}$ 和 $\theta_{j}$ 的加权和，而无法分别辨识出参数 $\theta_{i}$ 和 $\theta_{j}$ 。各预报因子的相关性因子可以用 $\boldsymbol{r}_{i,j}$ 表示  

r_{i,j},=,\frac{\displaystyle\sum_{k=1}^{N}X_{i}(k),X_{j}(k,)}{\displaystyle\sqrt{\sum_{k=1}^{N}X_{i}^{2}(k,)},\sqrt{\sum_{k=1}^{N}X_{j}^{2}(k,)}}

  

$r_{i}$ .,元素构成相关性矩阵 $R$ ，在利用飞行试验数据进行小不对称参数辨识时，应先计算相关性矩阵 $R$ ，分析各参数的可辨识性。由于式(10-176)和式(10-177)中的 $C_{m0}$ 和 $C_{n0}$ 对应于长周期项，而$\pmb{\eta}$ 对应的是短周期项，故三个参数可分别辨识；式（10-175）中的$C_{\ell0}$ 对应于长周期项,而 $y_{\hat{p}g}\setminus z_{\hat{p}g}$ 对应于短周期项,故这三个参数也可分别辨识; $I_{x y}\,,I_{y z}$ 和 $y_{\dot{p}g}\setminus z_{\dot{p}g}$ 的相应项都是短周期项,难以分别辨识,可以利用高空飞行试验数据先忽略气动力作用,辨识出 $I_{x y}$ 和 $I_{y z}$ ,再利用低空飞行试验数据辨识 $y_{\pmb{p}\pmb{g}}$ 和 $z_{\phi g}$ 。当然，若某参数的对应项太小，其有用信息小于测量噪声时，则该参数也无法辨识。  

对于典型再人体的飞行状态参数，采用上述简化数学模型，辨识小不对称参数，辨识结果与真值的偏差值列于表10-8。通常再人体的纯滚转力矩系数 $C_{l0}$ 约为 $10^{\,^{-\,5}}\!\sim\!10^{\,^{-\,6}}$ ，俯仰小不对称力矩系数 $C_{m0}\setminus C_{n0}$ 约为 $10^{\,-\,3}\!\sim\!10^{\,-\,4}$ （以再人体总长为参考长度）;压心和质心的横向偏移 $y_{p g}\,\setminus z_{p g}$ 约为 $\mathbf{0.001m\!\sim\!0.01m}$ 。由表可知,就工程应用而言，此辨识结果的误差是可以接受的，简化数学模型可实用。由于小不对称参数量级很小，对飞行试验的测量准度也要求比较高，在实用时应根据实际情况进行大量辨识数字仿真，提出对遥测传感器的测量精度要求。  

表10-8小不对称参数仿真辩识结果与  

真值的偏差随高度的变化  


<html><body><table><tr><td>h /km</td><td>Cro</td><td>Cm0</td><td>Cno</td><td>yp</td><td>84z</td></tr><tr><td>2</td><td>1E-9</td><td>1E-6</td><td>1E-6</td><td>8E-6</td><td>7E-6</td></tr><tr><td>10</td><td>3E-9</td><td>3E-6</td><td>2E-6</td><td>6E-6</td><td>1E-6</td></tr><tr><td>20</td><td>4E-8</td><td>4E-6</td><td>3E-6</td><td>2E-6</td><td>3E-6</td></tr><tr><td>30</td><td>7E-8</td><td>1E-5</td><td>4E-6</td><td>4E-6</td><td>8E-7</td></tr><tr><td>40</td><td>7E-7</td><td>1E-5</td><td>1E-5</td><td>2E-5</td><td>2E-5</td></tr><tr><td>50</td><td>5E-5</td><td>2E-8</td><td>3E-6</td><td>3E-4</td><td>4E-6</td></tr></table></body></html>  

# 10.5.3 再入攻角和气动力导数估计  

攻角、侧滑角是与飞行器气动性能和飞行性能密切相关的参数，是飞行试验结果分析的重要参数。再人体高速飞行形成的高温气体使其无法外装攻角传感器，如何从飞行试验遥测参数估计再人攻角是个重要问题。本节给出由角速率和过载估计攻角的实用算法。  

角速率数据反映再人体相对于惯性空间运动的姿态角变化率,而攻角、侧滑角是飞行速度与再人体体轴的夹角。从物理机理看，要获得攻角、侧滑角，除角速率和过载信息外还需要弹道信息和初始条件。由于再人体飞行速度很高，在飞行过程中轨道角和偏航角变化很小,利用这一特性可以导出由角速率和过载或仅由角速率估计攻角和侧滑角的算法。  

攻角 $\pmb{\alpha}$ 、侧滑角 $\beta$ 和总攻角 $\sigma$ 通常由体轴系速度分量 ${\pmb u}\setminus{\pmb v}\setminus{\pmb w}$ 定义  

\begin{array}{r l r}{\mathrm{tan}\alpha!!!}&{{}=}&{!!!w/,u}\ {\mathrm{sin}\beta!!!}&{{}=}&{!!!v/,V}\end{array}

\cos\sigma:=:\cos\alpha\cos\beta

  

式(10-183）～式(10-185)对时间 $t$ 求导，将式（10-9）～式（10-11)的加速度分量代入，并利用气流坐标系到铅垂地面固定坐标系、气流坐标系到弹体坐标系、弹体轴系到铅垂地面固定坐标系的变换矩阵以及铅垂地面固定坐标系的速度分量微分方程组，可以推导出下列方程组  

\frac{\mathrm{d}\alpha}{\mathrm{d}t},=q,-,\gamma\tan\beta\mathrm{cos}\alpha,-,r\mathrm{sin}\alpha\tan\beta,-,g\left(,n_{x}\mathrm{sin}\alpha,-,n_{y}\mathrm{~sin}\alpha,\right.

n_{z}\mathrm{cos}\alpha,-,\mathrm{cos}\theta_{a},\mathrm{cos}\phi_{a},)/,V\mathrm{cos}\beta

\frac{\mathrm{d}\beta}{\mathrm{d}t},=,-,,r\cos\beta,+,,\dot{p}\sin\alpha,+,,g,\big(,-,,n_{z}\sin\alpha\sin\beta,+,\

n_{s}\mathrm{cos}\beta,-,n_{x}\mathrm{cos}\alpha,\mathrm{sin}\beta,+,\mathrm{cos}\theta_{a},\mathrm{sin}\phi_{a},)/,V

\sin\sigma~{\frac{\mathrm{d}\sigma}{\mathrm{d}t}},=\sin\alpha\cos\beta~{\frac{\mathrm{d}\alpha}{\mathrm{d}t}},+,\cos\alpha\sin\beta~{\frac{\mathrm{d}\beta}{\mathrm{d}t}}

  

通常再人体角速率是 $O(1)$ ，过载也是 $O(1)\!\sim O(10)$ ,而 $V$ 是 $4000\!\sim\!8000$ ,故 $g/V$ 是 $O(1/100)$ 。由此可见，只要积分时间不很长,式(10-186)一式(10-187)的最后一项可以忽略,从而  

\begin{array}{l}{{{\displaystyle\frac{\mathrm{d}\alpha}{\mathrm{d}t}}{=}q{-}p\tan\beta\mathrm{cos}\alpha{-}r\sin\alpha\tan\beta}}\ {{{\displaystyle\frac{\mathrm{d}\beta}{\mathrm{d}t}}{=}{-}r\cos\beta+\rho\mathrm{sin}\alpha}}\ {{{\displaystyle\frac{\mathrm{d}\sigma}{\mathrm{d}t}}{=}(q\sin\alpha\cos\beta~{-}~r\sin\beta)/\mathrm{sin}\sigma}}\end{array}

  

在式（10-189）～式（10-191)的整个推导过程中都没有用到小攻角的假定,故这些公式对大攻角也是适用的。利用式(10-189)～式(10-170)和角速率、过载的实测值,可以辨识气动力导数,同时估计攻角和侧滑角。下面给出采用最大似然法辨识气动力导数和估计攻角、侧滑角的具体算式。  

1）状态方程组  

\begin{array}{l}{{{\displaystyle\frac{\mathrm{d}\alpha}{\mathrm{d}t}},=q,-,,p\tan\beta\mathrm{cos}\alpha,-,r\sin\alpha,\mathrm{tan}\beta}}\ {{{\displaystyle\frac{\mathrm{d}\beta}{\mathrm{d}t}},=-,,r\mathrm{cos}\alpha,+,,\rho\sin\alpha}}\end{array}

  

积分初值为待估计参数,迭代开始点可用理论计算或风洞试验的 $C_{N_{a}}$ 和 $C_{Y\beta}$ 算出  

\displaystyle\alpha\left(0\right)\equiv,\alpha_{0},=,\frac{-\ n_{z m}\left(0\right)m g}{q,\infty,S,-,C_{N\alpha}}\quad\beta(0)\equiv\beta_{0},=,\frac{n_{y m}\left(0\right)m g}{q,\infty,S C_{Y\beta}}

  

2）观察方程组  

\begin{array}{l}{{N_{x m}\ ={\displaystyle\frac{q,\infty,S}{m g}}(,C_{A0},+,C_{A2}\sigma^{2},),+,\varepsilon_{1},;;;;;}}\ {{;n_{y m};={\displaystyle\frac{q,\infty,S}{m g}}(,C_{Y0},+,C_{Y\beta},\beta,+,C_{Y\beta}{}^{3}\beta^{3},),+,,\varepsilon_{2},;;;;}}\end{array}

n_{z m};=-;\frac{q_{\infty},S}{m g}(,C_{N0},+,C_{N\alpha}\alpha,+,C_{N\alpha}{}^{3},\alpha^{3},);+;\epsilon_{3}

  

对于轴对称再入体,可以用 $n_{y z m}=\sqrt{\,n_{y m}^{2}+n_{z m}^{2}}$ 作为观测量，而以下式代替式（10-194)和式(10-195）：  

n_{y z m};=;{\frac{q_{\infty},S}{m g}}(,C_{N0},+,C_{N!\alpha},+,C_{N!\alpha}{}^{3}\sigma^{3},);+;\varepsilon_{4}

  

3）待估计参数  

\begin{array}{r l r}&{\pmb{\theta}=(\ a_{0},\beta_{0},C_{A0},,C_{A2},,C_{Y0},,C_{Y\beta},C_{Y\beta}^{\phantom{\beta}},C_{N0},,C_{N\alpha},,C_{N\alpha}^{\phantom{\beta}})^{\mathrm{T}}\equiv}&\ &{\qquad(\ \theta_{1}^{\phantom{\dagger}},\theta_{2}^{\phantom{\dagger}},\cdots,\theta_{10}^{\phantom{\dagger}})^{\mathrm{T}}\qquad\qquad\qquad\qquad\qquad(10^{-1})^{\dagger}}&{}\end{array}

  

4）灵敏度方程组  

\begin{array}{r}{\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial\alpha}{\partial\theta_{l}},=,\gamma\tan\beta\mathrm{sin}\alpha,,\frac{\partial\alpha}{\partial\theta_{l}},-,\gamma,\frac{\cos\alpha}{\cos^{2}\beta},\frac{\partial\beta}{\partial\theta_{l}},-,}\ {r\cos\alpha\tan\beta,\frac{\partial\alpha}{\partial\theta_{l}},-,r,\frac{\sin\alpha}{\cos^{2}\beta},\frac{\partial\beta}{\partial\theta_{l}}}\end{array}

{\frac{\mathrm{d}}{\mathrm{d}t}};{\frac{\partial\beta}{\partial\theta_{l}}},=r\sin\alpha;{\frac{\partial\alpha}{\partial\theta_{l}}},+,p\cos\alpha;{\frac{\partial\alpha}{\partial\theta_{l}}}

\frac{\partial,n_{x m}}{\partial,\theta_{l}};=\frac{2,q_{\infty},S\sigma}{m g}C_{A2};\frac{\partial,\sigma}{\partial,\theta_{l}};+;U_{1,l}

\frac{\partial,n_{s m}}{\partial,\theta_{\iota}}:=\frac{q_{\infty},S}{m g}(,C_{Y!\beta}:+:3,C_{Y!\beta}^{~}\beta^{2}):\frac{\partial\beta}{\partial,\theta_{\iota}}:+:U_{2,\iota}

\frac{\partial,n_{z m}}{\partial,\theta_{l}},=-,\frac{q_{\infty},S}{m g}(,C_{N a},+,3,C_{N a}{}^{3},\alpha^{2},),,\frac{\partial,\alpha}{\partial\theta_{l}},+,U_{3,l}

  

式中  

\begin{array}{l l l}{{U_{1,3},=,\displaystyle{\frac{q_{\infty},S}{m g}}}}&{{,U_{1,4},=,U_{1,3}\sigma^{2}}}\ {{,}}&{{,}}\ {{U_{2,5},=,U_{1,3}}}&{{,U_{2,6},=,U_{1,3}\beta}}&{{,U_{2,7},=,U_{1,3}\beta^{3}}}\ {{,}}&{{,}}\ {{U_{3,8},=,-,,U_{1,3}}}&{{,U_{3,9},=,-,,U_{1,3}\alpha}}&{{,U_{3,10},=,-,,U_{1,3}\alpha^{3}}}\ {{,}}&{{,}}\ {{,\Re,\widehat{,},\widehat{,}{\mathfrak{F}},,U_{i j},=,0,}}&{{,(,i,,j,=,1,2,,\cdots,10,)}}\end{array}

  

积分初值为  

\frac{\partial\alpha(0)}{\partial\theta_{1}}:=:\frac{\partial\beta(0)}{\partial\theta_{2}}:=:1,,\qquad:\sharp\hat{\ltimes}\frac{\partial\alpha(0)}{\partial\theta_{i}}:=:\frac{\partial\beta(0)}{\partial\theta_{j}}:=:0

  

采用5.3节所述最大似然算式，由式（10-189）～式（10-202） $\sim$ 可求出待估计参数0。辨识迭代收敛后，式（10-169）和式（10- 170)积分所得的攻角和侧滑角即为最优估计值。  

# 10.6 弹丸气动参数辩识  

弹丸系指由炮管发射的无翼、无动力飞行器，其气动外形是静不稳定的。为提高落点精度，通常由炮管的来福线使弹丸以极高速自旋而保持运动稳定性。弹丸体积很小，飞行试验时体内无法安装遥测系统，其质心的运动特性是通过雷达系统或光学观测系统提供其质心位置的时间历程；绕质心的姿态运动难以准确地由光学摄影系统确定。早期的弹丸飞行试验是通过弹丸穿过纸靶时留下的孔迹来粗糙地确定其飞行姿态角，从而获取弹丸的气动力矩特性。20世纪60年代以来，人们通过在弹丸上开狭缝安装太阳方位角传感器以获取弹丸飞行姿态信息，用来辨识弹丸的气动力矩特性。  

本节给出利用雷达测量弹丸太阳方位角等实测数据辨识弹丸气动参数的算法和具体算式。  

# 10.6.1 太阳方位计的姿态测定  

太阳方位计又称偏航计，是在弹体上开两个平行于弹轴的狭缝，每个狭缝确定一个平面视场，两狭缝与弹轴形成固定的夹角$2\beta$ 。狭缝内装有太阳光敏感元件，弹丸滚转到狭缝对准阳光时，就接受了光信号。同一狭缝的相继两次接受阳光的时间间隔即为滚转运动周期；不同狭缝所获相邻的时间间隔反应太阳光线与弹轴的夹角 $\sigma$ 。因此,太阳方位计可以测得弹丸的 $\sigma(\,t\,)$ 和 ${\boldsymbol{\dot{p}}}\left({\boldsymbol{t}}\right)$  

太阳方位计仅提供弹丸相对太阳的一元角运动规律，必须建立此信息与弹丸三维角运动的关系式。令 $\pmb{p}$ 为弹丸纵轴单位矢量， $\pmb{s}$ 为太阳与铅垂地面固定坐标系原点连线的单位矢量（见图10-11),则有  

\begin{array}{r l r}{\pmb{p}{\pmb{\eta}}=}&{\left[\cos\theta\cos\psi\right]}&{\quad\pmb{s}{\pmb{\eta}}=;\left[\cos\theta_{s}\cos\psi_{s}\right]}\ {\pmb{p}{\pmb{\eta}}=}&{\left[\cos\theta\sin\psi\right]}&{\quad\pmb{s}{\pmb{\eta}}=;\left[\cos\theta_{s}\sin\psi_{s}\right]}\ &{\quad-;\sin\theta}&{\quad\quad-;\sin\theta_{s}}\end{array}

  

从而  

\cos\sigma;=;,p s;=;,\cos\theta\mathrm{cos}\theta_{s}\mathrm{cos}(,\psi_{s};-;\psi,);+;\mathrm{sin}\theta\mathrm{sin}\theta_{s}

  

弹丸的位置由雷达测定的斜距 $R$ 、方位角 $A$ 和仰角 $E$ 确定，  

388  

![](images/e69ff60c01e4145a2d08abbb57ba6d52ce51b5d1eab1ec37faaf9a6eb624d55b.jpg)  
图10-11太阳方位角示意图  

用弹丸质心在铅垂地面固定坐标系的坐标表示为  

\begin{array}{r l}&{R,=,\sqrt{,x_{,g}^{2},+,y_{,g}^{2},+,z_{,g}^{2}}}\ &{A,=,\arctan(,y_{g}^{'}/x_{,g}^{'})}\ &{E,=,\arcsin(,-,z_{g}^{'}/R,)}\end{array}

  

# 10.6.2 弹丸气动参数辨识数学模型  

弹丸气动参数辨识的坐标系取在铅垂地面固定坐标系Oxg,以发射点为坐标原点，x轴指向正北，2轴铅垂向下，y轴构成右手坐标系。由于弹丸射程较短,而且参数辨识时仅截取一小段弹道参数,因此可以忽略地球旋转和地球曲率效应,将铅垂地面固定坐标系作为惯性坐标系。弹丸是无控的高速自旋飞行器，其参数辨识的状态方程组与10.4节类同。质心运动和绕质心旋转运动的动力学方程组建立在不随弹丸自旋的准弹体坐标系。状态参数矢量x=(uA，UA,WA,PA，qA,rA，山，θ，中，xy，)T。  

1）状态方程组  

\begin{array}{l}{\displaystyle\frac{\mathrm{d}u_{A}}{\mathrm{d}t},=-,,q_{A}w_{A},+,r_{A}v_{A},+,g,(,n_{x},-,\mathrm{sin}\theta,)}\ {\displaystyle}\ {\displaystyle\frac{\mathrm{d}v_{A}}{\mathrm{d}t},=-,,r_{A}u_{A},+,\big(,\beta_{A},-,\dot{\phi},\big),w_{A},+,g n_{y}}\end{array}

\frac{\mathrm{d}w_{A}}{\mathrm{d}t},=-,\left(,\phi_{A},-,\dot{\phi},\right)v_{A},+,q_{A}u_{A},+,g\bigl(,n_{z},+,\cos\theta\bigr)

\begin{array}{r l}{d t}&{\quad k_{\perp}\ f}\ {d t}&{=\left(1-\frac{L_{\perp}}{L_{\perp}}\right)\rho_{0,k_{\perp}}+q_{\perp}\dot{\phi}+\frac{N_{\perp}}{L_{\perp}}}\ &{\quad+\frac{d\phi}{d t}=\frac{f}{2}\kappa_{\perp}}\ {d t}&{=\cfrac{m_{e}^{2}}{c^{2}+\mathrm{Re}^{2}\phi}}\ &{\quad+\frac{d\phi}{d t}=q_{\perp}}\ &{\quad+\frac{d\phi}{d t}=\rho_{\mathrm{A}}+r_{\perp}\mathrm{cus}\theta}\ &{\quad\frac{d\phi}{d t}=\rho_{\mathrm{A}}+r_{\perp}\mathrm{cus}\theta}\ &{\quad\frac{d\phi_{r}^{2}}{d t}}&{=\alpha_{\mathrm{A}}\cos\phi\cos\theta-v_{\mathrm{A}}\sin\phi+\pi_{\mathrm{A}}\cos\phi\sin\theta}\ &{\quad\frac{d\phi_{r}^{2}}{d t}}&{=\alpha_{\mathrm{A}}\sin\phi\cos\theta+\pi_{\mathrm{A}}\cos\phi+\pi_{\mathrm{A}}\sin\phi\sin\theta}\ &{\quad\frac{d\phi_{r}^{2}}{d t}}&{=\alpha_{\mathrm{A}}\sin\theta+\pi_{\mathrm{A}}\cos\theta}\ &{\quad\frac{d\phi_{r}^{2}}{d t}=-\pi_{\mathrm{A}}\sin\theta+\pi_{\mathrm{A}}\cos\theta}\end{array}

  

式中  

\begin{array}{r l}&{n_{x}=(-\mathrm{\ḊcosḌ}\eta_{\mathrm{A}}+\mathrm{\calL}\sin\eta_{\mathrm{A}})/m g}\ &{n_{y}=\left[\ -\mathrm{\ensuremath{\ḊsinḌ}}\beta_{\mathrm{A}}\ -\mathrm{\small\displaystyleL}\frac{\cos\eta_{\mathrm{A}}\sin\beta_{\mathrm{A}}}{\sin\eta_{\mathrm{A}}}\ +\mathrm{\ensuremath{\skew~\Biggl1}}\right]}\ &{\phantom{n_{x}=\ ;}\ C;\frac{\cos\beta_{\mathrm{A}}\sin\alpha_{\mathrm{A}}}{\sin\eta_{\mathrm{A}}}\bigg/m g}\ &{n_{x}=\left[\ -\mathrm{\ensuremath{\ḊsinḌ}}\beta_{\mathrm{A}}\sin\alpha_{\mathrm{A}}\ -\mathrm{\ensuremath{\calL}}\cos\eta_{\mathrm{A}};\frac{\cos\beta_{\mathrm{A}}\sin\alpha_{\mathrm{A}}}{\sin\eta_{\mathrm{A}}}\ +\mathrm{\ensuremath{\skew~\Biggl1}}\right]}\end{array}

C\left.\frac{\mathrm{cos}\beta_{A},\mathrm{sin},\alpha_{A}}{\sin\eta_{A}}\right}/m g

\begin{array}{c}{{{\bf\sin\eta_{\alpha}}}}\ {{{\bf\sin\eta_{\alpha}}}}\ {{{\bf\sin\eta_{\alpha}}}}\ {{{\cal L\ }=q_{\infty},S({\cal C}{D0}+{\cal C}{D2},\eta_{\alpha}^{2})}}\ {{{\cal L\ }=q_{\infty},S({\cal C}{L\alpha}\eta{A}}}\ {{{\cal C}=q_{\infty},S{\cal C}{C\beta}\eta{A}\eta_{A},\frac{d}{2{\cal V}}}}\ {{{\cal L}{A}\ =q{\infty},S l C_{l\beta}\hbar_{A},\frac{d}{2{\cal V}}}}\ {{{\cal N}{A}\ =q{\infty},S l\left[\ -\ {\cal C}{m\alpha}\eta{A},\frac{\sin\beta_{A}}{\sin\eta_{A}}},+,{\cal C}{m\beta}r{A},\frac{d}{2{\cal V}}+\dots\right]}}\end{array}

C_{n p a}!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

M_{A},=,q,{\infty},S l,\left{,C{m\alpha}\eta_{A}\ {\frac{\cos\beta_{A}\sin\alpha_{A}}{\sin\eta_{A}}},+,C_{m q}q_{A}\ {\frac{d}{2,V}},-,

C_{n p\alpha}\phi_{A}\eta_{A};\frac{d}{2,V},\frac{\sin\beta_{A}}{\sin\eta_{A}},;

\begin{array}{l}{{\cos{\eta_{A}}\ =\cos{\alpha_{A}}\cos{\beta_{A}}}}\ {{{\tan}{\alpha_{A}}\ =,{w_{A}}/,{u_{A}}}}\ {{{\sin}{\beta_{A}}\ =,{v_{A}}/,V}}\end{array}

  

上述式中 $C_{D}$ ——阻力系数；  

$C_{L_{a}}$ -升力导数；   
$C_{C\beta\alpha}$ 马格努斯力导数；   
$C_{\ell\ p}$ 极阻尼力矩导数；   
$C_{m\alpha}$ 翻转力矩导数；   
$C_{m q}$ 翻转阻尼力矩导数；   
$C_{n\rho\alpha}$ 马格努斯力矩导数；   
7A—总攻角。  

弹丸出炮口时受膛内高压气流扰动较大，之后扰动量就比较 小,故飞行的总攻角比较小。式（10-222）～式（10-227)给出轴对  

称弹丸气动力的线性模型。  

2）待辨识参数  

\begin{array}{r l}&{\pmb{\theta}\simeq\left(,C_{D0},,C_{D2},,C_{L\alpha},,C_{C\beta\alpha},,C_{l\beta},,C_{m\alpha},,C_{m q},,C_{n\beta\alpha},,\right.}\ &{\quad\quad\left.u_{A0},,v_{A0},,w_{A0},,\phi_{A0},,q_{A0},,r_{A0},\right)^{\mathrm{T}}}\end{array}

  

3）观测方程组  

\sigma_{m};=;\operatorname{arccos}[,\cos!\theta\cos\theta_{s}\cos(,\phi_{s},-,\phi,),+,\sin\theta_{s}\sin\theta,],+,\varepsilon_{1}

\begin{array}{r l}&{\phi_{m},=,\phi,+,\epsilon_{2}}\ &{R_{m},=\sqrt{{x_{,g}^{\prime},+,{y_{,g}^{'},+,z_{,g}^{'},+,\varepsilon_{3}}}}}\ &{E_{m},=\arcsin({-,z_{,g}^{\prime}/,\sqrt{{x_{,g}^{'},+,{y_{,g}^{'},+,z_{,g}^{'}}}}}),+,\varepsilon_{4}}\ &{A_{m},=\arctan({y_{,g}^{\prime}/{x_{,g}^{'}}}),+,\varepsilon_{5}}\end{array}

  

式中 $\theta_{s}$ —太阳仰角；  

$\psi_{s}$ 一—太阳相对正北的方位角。  

两者均取飞行试验时的当地值，为常数。  

# 4）判据函数  

J;=;\frac{1}{N}\sum_{i,=,1}^{N},[;\pmb{\nu}^{\top}({;i,}),\pmb{R}^{,-,1},\pmb{\nu}({;i,});+;\ln;|;\pmb{R};|;]

  

式中  

\pmb{\nu},=,(,\sigma_{m},\mathrm{-},\sigma,,\phi_{m},\mathrm{-},\phi,,R{m},-,R,,E{m},-,E,,A{_m},-,A,)^{\intercal}

\pmb{R}\ =\frac{1}{N}\sum_{\substack{i,=,1}}^{N}\pmb{\nu}(,i,),\pmb{\nu}^{\mathrm{T}}(,i,)

  

采用牛顿-拉夫逊代算法，给定 $\pmb\theta$ 的初估值 $\pmb{\theta}_{0}$ ，用下式进行迭代计 算,直至收敛  

\pmb\theta_{k,+,1}=\pmb\theta_{k}-\left(\frac{\partial^{2}J}{\partial\pmb\theta\partial\pmb\theta}\right)^{-1}\left(\frac{\partial J}{\partial\pmb\theta}\right)

  

式中 ,矩阵 $\left(\frac{\partial^{2}J}{\partial\pmb{\theta}\partial\pmb{\theta}}\right)$ 和矢量 $\left(\frac{\partial J}{\partial\pmb{\theta}}\right)$ 是观测灵敏度 $\frac{\partial\,{\mathbf y}}{\partial\,\pmb\theta}$ $\frac{\partial\,\mathbf{y}}{\partial\,\theta}$ 由式（10-207)～式（10-236)对 $\pmb\theta$ 求偏导数得到的常微分方程组积  

分而获得，具体算式可以参考10.2.1节。  

# 10.6.3 气动参数辨识对测试准度的要求  

采用上述弹丸气动参数辨识数学模型，对某典型炮弹进行辨识仿真计算,验证辨识软件的正确性并对太阳方位计和雷达测量精度提出要求。弹丸的物理几何参数和气动参数列于表10-9。  

表10-9弹丸的物理几何参数和气动参数  


<html><body><table><tr><td colspan="3">物理几何参数</td><td colspan="2">气动力参数</td></tr><tr><td>弹丸质量/kg</td><td>m</td><td>16</td><td>Cia</td><td>2.8</td></tr><tr><td>极转动惯量/(kg·m²）</td><td>Ix</td><td>0.002</td><td>Cma</td><td>3.0</td></tr><tr><td>赤道转动惯量/（kg·m²）</td><td>Iz</td><td>0.02</td><td>CDo</td><td>0.15</td></tr><tr><td>参考长度/m</td><td>d,l .</td><td>0.1</td><td></td><td>- 0.34</td></tr><tr><td>参考面积/m2</td><td>S</td><td>0.008</td><td>Cmta</td><td>-0.1</td></tr><tr><td>太阳方位角/(°)</td><td>业.</td><td>- 90</td><td>Cip</td><td>0.05</td></tr><tr><td>太阳仰角/(°)</td><td>0s</td><td>10</td><td>Cmg</td><td>- 0.0001</td></tr></table></body></html>  

辨识仿真取轨道初始段和轨道顶段两组典型参数列于表10-10。  

表 10-10 两组典型的轨道参数  


<html><body><table><tr><td>初始条件</td><td>轨道初始段</td><td>轨道顶段</td></tr><tr><td>V(0)/(m/s)</td><td>900</td><td>250</td></tr><tr><td>p(0)/(rad/s)</td><td>1900</td><td>1200</td></tr><tr><td>xs(0)/m</td><td>0</td><td>12000</td></tr><tr><td>z′(0)/m</td><td>0</td><td>16000</td></tr></table></body></html>  

对式（10-207）～式（10-236）计算所得观测仿真数据，加上不同方差的零均值正态分布随机噪声作为观测量 $\sigma_{m}\setminus R_{m}$ 等，进行气动参数辨识仿真计算。雷达所测的斜距、仰角和方位角主要提供气动力的信息，其中阻力主要由 $R$ 数据确定，升力和侧力主要由 $E$ 和 $\pmb{A}$ 确定。太阳方位角数据提供气动力矩信息。在辨识仿真计算中，观测误差的标准差对于气动力矩辨识是指太阳方位角测量误差，对于阻力系数是指斜距测量误差，对升力和马格努斯力系数是指弹丸仰角和方位角测量误差。气动参数辨识仿真的典型结果列于表10-11。  

表 10-11弹丸气动参数辨识仿真结果  


<html><body><table><tr><td colspan="4">初 始段</td><td colspan="3">轨道 顶 段</td></tr><tr><td></td><td>标准差</td><td>辨识结果</td><td>相对误差/%</td><td>标准差</td><td>辨识结果</td><td>相对误差/ %</td></tr><tr><td rowspan="4">Cma</td><td>0</td><td>2.98</td><td>0.5</td><td>0</td><td>3.36</td><td>12</td></tr><tr><td>0.3°</td><td>2.99</td><td>0.3</td><td>0.016*</td><td>3.61</td><td>20.3</td></tr><tr><td>0.4°</td><td>2.78</td><td>7.3</td><td>0.032*</td><td>3.85</td><td>28.2</td></tr><tr><td>1.0'</td><td>2.50</td><td>16.7</td><td>0.064*</td><td>4.20</td><td>40</td></tr><tr><td rowspan="4"></td><td>0</td><td>0.0435</td><td>13</td><td>0</td><td>0.0435</td><td>13</td></tr><tr><td>100((°)/s)</td><td>0.046</td><td>8</td><td>2((°)/s)</td><td>0.046</td><td>8</td></tr><tr><td>200((°)/s)</td><td>0.049</td><td>2.0</td><td>5((°)/s)</td><td>0.05</td><td>0</td></tr><tr><td>300((°)/s)</td><td>0.051</td><td>2.0</td><td>10((°)/s)</td><td>0.056</td><td>12</td></tr><tr><td rowspan="4">Cpo</td><td>0</td><td>0.154</td><td>2.7</td><td>0</td><td>0.132</td><td>12</td></tr><tr><td>1m</td><td>0.152</td><td>1.3</td><td>0.025m</td><td>0.149</td><td>0.7</td></tr><tr><td>3m</td><td>0.146</td><td>2.7</td><td>0.05m</td><td>0.165</td><td>10</td></tr><tr><td>5m</td><td>0.141</td><td>6.0</td><td>0.075m</td><td>0.179</td><td>19</td></tr><tr><td rowspan="4">CLa</td><td>0</td><td>2.76</td><td>1.4</td><td>0</td><td>1.32</td><td>54</td></tr><tr><td>0.006°</td><td>2.89</td><td>3.2</td><td>0.0012*</td><td>1.36</td><td>51</td></tr><tr><td>0.012'</td><td>3.02</td><td>7.9</td><td>0.0018°</td><td>1.43</td><td>48</td></tr><tr><td>0.03°</td><td>3.41</td><td>21.8</td><td>0.006*</td><td>1.68</td><td>40</td></tr><tr><td rowspan="4"></td><td>0</td><td>- 0.528</td><td>55</td><td>0</td><td>- 25.821</td><td>7500</td></tr><tr><td>0.001'</td><td>- 0.558</td><td>64</td><td></td><td></td><td></td></tr><tr><td>0.003*</td><td>- 0.619</td><td>82</td><td></td><td></td><td></td></tr><tr><td>0.006°</td><td>-0.71</td><td>109</td><td></td><td></td><td></td></tr></table></body></html>  

由表10-11可知，轨道顶段参数辨识要求的测量精度远远高于发射初始段。实际上，上表表明，由于对测量要求过高，利用轨道顶段的测量数据进行气动力参数辨识是不现实的。结果还表明，利用初始轨道段的太阳方位计测量数据辨识气动力参数，在目前测量精度条件下, $C_{m a}$ 误差约为 $10\,\%$ $C_{l p}$ 误差约为 $10\,\%$ ，马格努斯力矩系数仅能给出数量级。  

# 10.7 鱼雷水动力参数辨识  

鱼雷在水中运动承受的水动力与飞行器在空气中飞行所承受的气动力的作用是相似的，均满足牛顿第二定律，可用6自由度动力学方程组精确描述。本节在鱼雷动力学系统数学模型的基础上，建立鱼雷水动力参数辨识的基本方程组，并给出辨识算法和部分仿真计算结果。  

# 10.7.1 鱼雷动力学系统基本方程  

目前鱼雷有两种动力装置，一种是电机驱动螺旋桨推进的，另一种是液体燃料的燃气体驱动螺旋桨推进的。电动鱼雷的质量分布和惯量是轴对称的，而且是定常的。液体燃料鱼雷在运动中不断消耗燃料，是变质量的，其质量分布和惯量不是轴对称的，剩余燃料在重力和惯性力作用下基本上成面对称分布，可以近似假定其惯量特性是面对称的。  

鱼雷与导弹动力学方程的主要区别是附加质量与浮力。水的密度是地面空气密度的800倍，鱼雷在水中运动时带动周围液体一起运动所消耗的能量是不可忽略的。计人此效应，鱼雷动力学方程组中的质量和惯量矩矩阵都需要加上附加质量和附加惯量矩。在大气中，空气对导弹的浮力相对于重力是可以忽略的，但水对鱼雷的浮力与重力是相当的，鱼雷动力学方程必须计人浮力的作用。鱼雷浮力作用中心（浮心）仅与鱼雷儿何外形有关，在航行过程中是不变的，而质心与鱼雷质量分布有关，随燃料消耗而不断移动，因此鱼雷动力学方程组通常建立在以浮心为原点的坐标系上。  

在以浮心为原点的体轴坐标系上，鱼雷6自由度动力学方程  

组为  

\left(;m;+;\lambda_{11},\right),\frac{\mathrm{d}u}{\mathrm{d}t};-;m y_{c};\frac{\mathrm{d}r}{\mathrm{d}t};+;m z_{c};\frac{\mathrm{d}q}{\mathrm{d}t};-;\left(;m;+;\lambda_{22},\right)v r;+

m z_{c}\ p r\ =\ T,-,C_{A}q_{\infty},S,-,\Delta G\sin\theta

  

$\left(~m~+~\lambda_{22}~\right)~\frac{\mathrm{d}v}{\mathrm{d}t}~-~m z_{c}~\frac{\mathrm{d}\,\phi}{\mathrm{d}t}~-~\left(~\lambda_{26}~-~m x_{c}\right)~\frac{\mathrm{d}\,r}{\mathrm{d}t}~-~\left(~m~+~\lambda_{33}\right)\,\phi w~-~m x_{c}^{2}\,\mathrm{d}\,r,$ $m y_{c}\dot{p}^{2}\;+\;\left(\,\lambda_{35}\;+\;m x_{c}\,\right)\dot{p}q\;+\;\left(\;m\;+\;\lambda_{11}\,\right)r u\;-\;m y_{c}r^{2}\;-\;m z_{c}r q\;=$  

C_{Y}q\infty,S,+,\Delta G\cos\theta\sin\phi

  

$\left(\,m\;+\;\lambda_{33}\,\right)\,\frac{\mathrm{d}w}{\mathrm{d}t}\;+\;m y_{c}\;\frac{\mathrm{d}\,\phi}{\mathrm{d}t}\;-\;\left(\,\lambda_{35}\,+\;m x_{c}\,\right)\,\frac{\mathrm{d}\,q}{\mathrm{d}t}\;-\;\left(\,m\;+\;\lambda_{11}\,\right)q u\;+$ $\begin{array}{r l r}&{}&{m y_{c}r q\;-\;m z_{c}q^{2}\;+\;\left(\;m\;+\;\lambda_{22}\right)\phi v\;+\;m z_{c}\beta^{2}\;+\;\left(\;\lambda_{26}\;-\;m x_{c}\,\right)\beta r\;=}\\ &{}&{-\;\;C_{\mathrm{}^{N}}q_{\infty}\,S\;+\;\Delta G\mathrm{cos}\theta\mathrm{cos}\phi\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\end{array}$  

\mathrm{(}I_{x}\mathrm{+}\lambda_{44}\mathrm{)}\frac{\mathrm{d}\phi}{\mathrm{d}t},-,I_{x z},\frac{\mathrm{d}r}{\mathrm{d}t},-,I_{x y},\frac{\mathrm{d}q}{\mathrm{d}t},+,m y_{c},\frac{\mathrm{d}w}{\mathrm{d}t},-,m z_{c},\frac{\mathrm{d}v}{\mathrm{d}t},-,

  

$\left(~m~+~\lambda_{22}\right)v w~+~m z_{c}\beta v w~+~\left(~\lambda_{26}~-~m x_{c}\right)r w~+~\left(~m~+~\lambda_{33}\right)v w~-~m x_{c}^{2}w~+~\left(~m~+~\lambda_{33}\right)v w~-~\left(~m~+~\lambda_{33}\right)v w~+~\left(~m~+~\lambda_{33}\right)v w$ $m y_{c}p v\:+\:\left(\lambda_{35}\:+\:m x_{c}\right)q v\:-\:I_{x z}p q\:-\:I_{y z}q^{2}\:-\:m y_{c}q u\:+\:$ $(\,\lambda_{26}\mathrm{~-~}m x_{c}\,)\,q v\mathrm{~+~}(\,I_{z}\mathrm{~+~}\lambda_{66}\,)\,r q\mathrm{~-~}m z_{c}r u\mathrm{~+~}$ $\left(\,\lambda_{35}\,+\,m x_{c}\,\right)r w\,+\,I_{x y}\beta r\,+\,I_{y z}r^{2}\,-\,\left(\,I_{y}\,+\,\lambda_{55}\,\right)r q\;=$ $q_{\infty}\,S l C_{m}\;+\;m g\,(\,y_{c}\mathrm{cos}\theta\mathrm{cos}\phi\:-\:z_{c}\mathrm{cos}\theta\mathrm{sin}\phi\,)$ (10 -244)  

$:I_{y}\,+\,\lambda_{55}\ )\ \frac{\mathrm{d}q}{\mathrm{d}t}\,-\,I_{x y}\,\frac{\mathrm{d}\phi}{\mathrm{d}t}\,-\,I_{y z}\,\frac{\mathrm{d}r}{\mathrm{d}t}\,+\,m z_{c}\,\frac{\mathrm{d}u}{\mathrm{d}t}\,-\,\left(\lambda_{35}\,+\,m x_{c}\right)\,\frac{\mathrm{d}w}{\mathrm{d}t}\,-\,\overline{{\frac{\mathrm{d}\phi}{\mathrm{d}t}}}\,-\,\overline{{\frac{\mathrm{d}\phi}{\mathrm{d}t}}}\,\overline{{\frac{\mathrm{d}\phi}{\mathrm{d}t}}}\,+\,\overline{{\frac{\mathrm{d}\phi}{\mathrm{d}t}}}\,.$ $\left(~m~+~\lambda_{33}~\right)u w~-~m y_{c}\rho u~+~\left(~\lambda_{35}~+~m x_{c}~\right)q u~+~\left(~m~+~\lambda_{11}~\right)u w~-~m x_{c}~+~\left(~m~+~\lambda_{33}~\right)p\left(~m~+~\left(~m~+~\lambda_{33}~\right)u w~-~m x_{c}~\right)q u~+~\left(~m~+~\lambda_{33}~\right)q u~+~\left(~m~+~\lambda_{33}~\right)q u~-~m x_{c}{I}~.$ myrw - mzqw + mycpu + (A26 - mr)pu + Izp² - $\left(\;I_{z}\;+\;\lambda_{66}\right)\phi r\;+\;I_{y z}\phi q\;+\;m y_{c}r w\;-\;m z_{c}r v\;+\;\left(\;I_{x}\;+\;\lambda_{44}\right)p r\;-$  

\scriptstyle I_{x z}r^{2};-;I_{x y}r q;=

q_{\infty},S l C_{m};-;m g,(,z_{C}\mathrm{sin}\theta:+:x_{c}\mathrm{cos}\theta\mathrm{cos}\phi,)

  

$\mathit{\Pi}_{\mathit{\Pi}_{\mathrm{2}}}^{\mathrm{~\,~}}\left(\mathit{\Pi}_{\mathit{\delta}_{\mathrm{1}}\mathrm{~+~}\lambda_{66}}\right)\frac{\mathrm{d}\mathit{\Pi}_{\mathrm{\Pi}}}{\mathrm{d}t}\;-\;I_{x z}\;\frac{\mathrm{d}\mathit{\Pi}_{\mathrm{1}}}{\mathrm{d}t}\;-\;I_{y z}\;\frac{\mathrm{d}q}{\mathrm{d}t}\;-\;m y_{c}\;\frac{\mathrm{d}u}{\mathrm{d}t}\;-\;\left(\lambda_{26}\;-\;m x_{c}\right)\frac{\mathrm{d}v}{\mathrm{d}t}\;-\;\left(\lambda_{36}\;-\;m y_{c}\right)\frac{\mathrm{d}\mathit{\Pi}_{\mathrm{1}}}{\mathrm{d}t}\;-\;\left(\lambda_{36}\;-\;m y_{c}\right)\frac{\mathrm{d}\mathit{\Pi}_{\mathrm{1}}}{\mathrm{d}t}\;,$ $\left(\,m\;+\;\lambda_{11}\,\right)u r\;+\;m y_{c}r v\;-\;m z_{c}q v\;+\;\left(\,m\;+\;\lambda_{22}\,\right)u v\;-\;m z_{c}\dot{p}u\;-$  

\begin{array}{r l r}&{}&{\big(\lambda_{26},-,m x_{c}\big),r u,+,m z_{c}q v,-,m y_{c}q w,-,\big(,I_{x},+,\lambda_{44}\big),\dot{p}q,+}\ &{}&{\big I_{x z}q r,+,I_{x y}q^{2},+,m z_{c}\dot{p}u,-,\big(\lambda_{35},+,m x_{c}\big),\dot{p}w,-,I_{x y}\dot{p}^{2},-}\ &{}&{\big I_{y z}\dot{p}r,+,\big(,I_{y},+,\lambda_{55}\big),\dot{p}q,=,\qquad\qquad}\ &{}&{q_{\infty},S l C_{n},+,m g\big(,y_{c}\mathrm{sin}\theta,+,x_{c}\mathrm{cos}\theta\mathrm{sin}\dot{\phi},\big)\qquad\quad(10)}\end{array}

  

式中  

\begin{array}{r l}&{C_{A}=C_{A0}+C_{A2}(\alpha^{2}+\beta^{2})}\ &{C_{Y}=-,(C_{Y\beta}\beta+C_{Y},r\frac{l}{2V}+C_{Y\beta},\hat{\alpha}{r})}\ &{C{N}=C_{N\alpha}+,C_{N\beta}q,\frac{l}{2V}+,C_{N\beta}\hat{\alpha}{e}}\ &{C{l}=C_{l0}+,C_{\ell\beta}\hat{\alpha}{\alpha}+,C{l\beta}\frac{l}{2V}}\ &{C_{m}=C_{m\alpha}\alpha\ +,C_{m\beta}q,\frac{l}{2V}+,C_{m\beta}\hat{\alpha}{e}}\ &{C{n}=C_{n\beta}\beta\ +,C_{n},r\frac{l}{2V}+,C_{n\beta}\hat{\alpha}_{e}}\end{array}

  

式中  

$\lambda_{i j}$ —附加质量；$x_{c}\,,y_{c}\,,z_{c}$ 质心坐标；m 质量；$I_{i j}$ 惯量矩；  

# $\boldsymbol{\theta}$ 和 $\phi$ -一鱼雷的俯仰角和滚转角；  

C;（i=A，Y,N,l,m，n）—体轴系气动力和气动力矩系数。  

以上各式推导过程中忽略了质量变化形成的惯性力和力矩，此惯性力和力矩很小。式(10-241）～式(10-246)是 $u\;,\,v\;,\,w\;,\,\phi\;,$ $q\,,r$ 的线性代数方程组，令 $\begin{array}{r}{\pmb{x}=(\,x_{1},x_{2},\cdots,x_{6}\,)^{\mathrm{T}}\mathbf{\equiv}(\,u\,,v\,,w\,,\phi\,,}\end{array}$ $_{q\mathrm{~},\mathrm{~}r})^{\mathrm{~T~}}$ ，可得一阶常微分方程组，写成状态方程组的一般表达形式,为  

\begin{array}{r l}{x_{i},=c_{i1},u v,+,c_{i2},u w,+,c_{i3},v w,+,c_{i4},q u,+,c_{15},r u,+,}&{{}}\ {c_{i6},f v,+,c_{i7},r v,+,c_{i8},f w,+,c_{i9},q w,+,c_{i10},\dot{p}^{2},+,}&{{}}\ {c_{i1},f q,+,c_{i12},\dot{p}r,+,c_{i13},q^{2},+,c_{i14},q r,+,c_{i15},r^{2},+,}&{{}}\end{array}

\begin{array}{c}{{\displaystyle\sum_{j\mathop{=}1}^{3},(,m,+,\lambda_{j j}^{\phantom{}}),g b_{i j}^{\phantom{}}(,n_{j}^{\phantom{}},+,G_{j}^{},),+}}\ {{\displaystyle\sum_{j\mathop{=}4}^{6},(,q,\infty,S l b_{i j}C_{j}^{\phantom{}},+,m g b_{i j}G_{j}^{\phantom{}},)\quad(,i,=,1,2,\cdots,6)}}\end{array}

  

(10 - 253)  

$\begin{array}{r l}{G_{2}}&{=m\cos\beta h\sin\beta(l(m+\lambda_{2}))}\\ &{G_{3}=m\cos\beta h\cos\beta}\\ &{\quad G_{4}=y\cos\alpha h\cos\beta,}\\ &{\quad G_{5}=y\cos\beta h\sin\beta-\cos\beta h\sin\beta}\\ &{\quad G_{6}=y\sin\beta+\chi_{2}\cos\beta\cos\beta}\\ &{\quad G_{7}=y\sin\beta+\chi_{3}\cos\beta\sin\beta}\\ &{\quad G_{8}=\beta h(\lambda_{1}-\lambda_{2})}\\ &{\quad G_{9}=b_{x}(\lambda_{3}-\lambda_{3})}\\ &{\quad\therefore}\\ &{\quad\;\;\;\cos\beta=\lambda_{3}(\lambda_{3}-\lambda_{2})}\\ &{\quad\;\;\;\beta_{4}=b_{y}(\lambda_{1}+\lambda_{1})+m_{y}b_{x}-b_{z}(\lambda_{3}+\mu_{\mathrm{X}})}\\ &{\quad\;\;\varepsilon_{6}=-b_{z}(\mu+\lambda_{11})+m_{z}b_{y}+b_{z}(\lambda_{3}+m_{x})}\\ &{\quad\;\;\varepsilon_{8}=-b_{z}(\mu+\lambda_{2})+b_{z}\sin\beta\;+b_{y}(\lambda_{3}+m_{x})}\\ &{\quad\;\;\varepsilon_{9}=b_{z}(\mu+\lambda_{2})+b_{z}\sin\alpha\;+b_{z}\sin\beta}\\ &{\quad\;\;\varepsilon_{10}=b_{z}(\mu+\lambda_{1})+b_{z}\sin\alpha\;+b_{z}(\lambda_{1}+m_{x})}\\ &{\quad\;\;\varepsilon_{1}=b_{z}(\mu+\lambda_{2})+b_{z}\sin\alpha\;+b_{z}(\lambda_{1}+\lambda_{2})}\end{array}$ $\begin{array}{l}{n_{1}=n_{2}=(\mathrm{\Gamma}-q_{\mathrm{\Gamma}}\circ S C_{4}+\mathrm{\Gamma},\mathrm{a}\sin\theta)/(m+\mathrm{\Gamma}_{31})g}\\ {n_{2}=n_{3},}\\ {n_{3}=n_{4},}\\ {n_{4}=n_{5}-(\mathrm{\Gamma},q_{\mathrm{\Gamma}}\circ S C_{30}\sin\theta)/(m+\mathrm{\Gamma}_{22})g}\\ {n_{3}=n_{4},\ (\mathrm{\Gamma}-q_{\mathrm{\Gamma}}\circ S C_{30}-\mathrm{Bov}\circ\cos\theta)/(m+\mathrm{\Gamma}_{33})g}\\ {\mathrm{\Gamma}}\\ {G_{1}=-m\sin\theta/(m+\mathrm{\Gamma}_{11})}\\ {G_{2}=m\cos\theta\sin\theta/(m+\mathrm{\Gamma}_{22})}\\ {G_{3}=m\cos\theta\cos\theta/(m+\mathrm{\Gamma}_{33})}\\ {G_{4}=\mathrm{\Gamma},}\\ {G_{5}=-\mathrm{\Gamma},\sin\theta-\mathrm{\Gamma}_{\kappa0}\cos\theta\cos\theta}\\ {G_{6}=\mathrm{\Gamma}_{5}\sin\theta+\mathrm{\Gamma}_{\kappa0}\sin\theta}\\ {G_{8}=b_{6}(\lambda_{1}-\lambda_{2})}\\ {c_{4}=b_{8}(\lambda_{3}-\lambda_{11})}\\ {c_{6}=b_{6}(\lambda_{3}-\lambda_{2})}\end{array}$ $\begin{array}{r l}{c_{4}}&{=b_{4}(\lambda_{3}-\lambda_{2})}\\ {c_{4}}&{=b_{3}((\ m+\lambda_{11})+m)y_{4}-b_{4}(\lambda_{3}+m x_{1})}\\ {c_{5}}&{=-b_{2}(m+\lambda_{11})+m z_{3}b_{4}-b_{6}(\lambda_{3}+m x_{1})}\\ {c_{6}}&{=-b_{3}(m+\lambda_{2})+b_{4}m y_{5}+b_{8}(\lambda_{3}+m x_{1})}\\ {c_{7}}&{=b_{4}(m+\lambda_{2})+b_{6}m z_{7}-b_{4}m y_{6}}\\ {c_{8}}&{=b_{4}(m+\lambda_{3})-b_{4}m\pi_{2}+b_{8}(\lambda_{3}+m x_{1})}\\ {c_{9}}&{=-b_{1}(m+\lambda_{3})+b_{3}m x_{7}+b_{4}m y_{6}}\\ {c_{10}}&{=b_{2}m y_{8}-b_{3}m x_{7}-b_{8}I_{4}+b_{4}T_{9}}\\ {c_{11}}&{=b_{1}m y_{5}-b_{2}(\lambda_{3}+m x_{1})+b_{1}d x_{1}-b_{3}I_{9}+b_{10}}\\ {b_{6}(I_{4}+\lambda_{4}-I_{7}-\lambda_{3})}\\ {c_{11}}&{=-b_{1}m z_{4}+b_{3}(\lambda_{3}+m x_{1})-b_{4}I_{10}+b_{6}I_{1_{0}}}\\ {b_{8}(I_{4}+\lambda_{4}-I_{1}-\lambda_{6})}\end{array}$  

$\begin{array}{r l}{c_{i13}\:=\:-\:b_{i1}(\:\lambda_{35}\:+\:m x_{c}\:)\:+\:b_{i2}\:m z_{c}\:+\:b_{i4}\:I_{y z}\:-\:b_{i6}\:I_{x y}}&{}\\ {c_{i14}\:=\:b_{i2}\:m z_{c}\:-\:b_{i3}\:m y_{c}\:+\:b_{i4}(\:I_{y}\:+\:\lambda_{55}\:-\:I_{z}\:-\:\lambda_{66}\:)\:+}&{}\end{array}$ $b_{i5}\,I_{x y}\,-\,b_{i6}\,I_{x z}$  

\begin{array}{r l}&{c_{i15},=b_{i1}(,\lambda_{35},+,m x_{c},),+,b_{i2},m y_{c},-,b_{i4},I_{y z},+,b_{i5},I_{x z}}\ &{}\ &{b_{11},=\big[,(,m,+,\lambda_{11},),+,m y_{c},(,a_{33},m y_{c},-,a_{23},m z_{c},),-,}\end{array}

m z_{c},(,a_{23},m y_{c}:-:a_{22},m z_{c},),]/(Ⓜ️+:\lambda_{11},)^{2}

b_{12};=b_{21};=;\left[;m y_{c}\left(,a_{13},m z_{c},-,a_{33}!\left(,\lambda_{35},+,m x_{c},\right)\right);-

  

$m z_{c}(\,a_{12}\,m z_{c}\,-\,a_{23}(\,\lambda_{35}\,+\,m x_{c}\,)\,)\,]/(\,m\,+\,\lambda_{11}\,)\,(\,m\,\cdot$ +入22) $b_{13}\;=b_{31}\;=\;\left[\;m y_{c}\(\,\alpha_{23}(\,\lambda_{35}\,+\,m x_{c}\,)\,-\,\alpha_{13}\,m y_{c}\,)\;-\right.$  

$m z_{c}(\,a_{22}(\,\lambda_{35}\,+\,m x_{c}\,)\,-\,a_{12}\,m y_{c}\,)\,]/(\,m\;+\,\lambda_{11}\,)(\,m\;+\,\lambda_{33})$ $\begin{array}{r l}&{b_{14}\ =b_{41}\ =\ \big(\ a_{13}\,m y_{c}\,-\,a_{12}\,m z_{c}\big)/\big(\,m\,+\,\lambda_{11}\,\big)}\\ &{b_{15}\,=b_{51}\ =\ \big(\,a_{23}\,m y_{c}\,-\,a_{22}\,m z_{c}\big)/\big(\,m\,+\,\lambda_{11}\,\big)}\\ &{b_{16}\,=b_{61}\ =\ \big(\,a_{33}\,m y_{c}\,-\,a_{23}\,m z_{c}\big)/\big(\,m\,+\,\lambda_{11}\,\big)}\\ &{b_{22}\,=\big[\,\big(\,m\,+\,\lambda_{22}\,\big)\,+\,m z_{c}\big(\,a_{11}\,m z_{c}\,-\,a_{13}\,\big(\lambda_{35}\,+\,m x_{c}\,\big)\,\big)\,-}\\ &{\qquad\big(\,\lambda_{22}\,+\,m x\,\big)\,\big(\,a_{23}\,m z\,-\,a_{23}\,\big(\,\lambda_{24}\,+\,m x\,\big)\,\big)\,\big]/\big(\,m\,+\,\lambda_{23}\,)^{2}}\end{array}$ (A3s + mxc)(a13mzc - a33(A3s + mxc))]/(m + A22)2  

b23 = b32 = [(mzc(a12(A3s + mxc) - a11 myc) - (入3s + mxc)(a23(A3s + mxc) - a13myc)]/(m + 入22)(m + 入33)  

\begin{array}{r l}&{b_{24},=b_{42},=,\left[,\alpha_{11}m z_{c},-,\alpha_{13}(\lambda_{35},+,m x_{c}),\right]/(,m,+,\lambda_{22})}\ &{b_{35},=b_{52},=,\left[,\alpha_{12}m z_{c},-,\alpha_{23}(\lambda_{35},+,m x_{c}),\right]/(,m,+,\lambda_{22})}\ &{b_{26},=b_{62},=,\left[,\alpha_{13}m z_{c},-,\alpha_{33}(\lambda_{35},+,m x_{c}),\right]/(,m,+,\lambda_{22})}\ &{b_{33},=\left[,\left(,m,+,\lambda_{32}\right),+,\left(\lambda_{35},+,m x_{c},\right)\left(,\alpha_{22}(\lambda_{35},+,m x_{c}),\right.\right.}\end{array}

  

$\alpha_{12}\,m y_{c}\,)\,-\,m y_{c}\,(\,\alpha_{12}(\,\lambda_{35}\,+\,m x_{c}\,)\,-\,\lambda_{11}\,m y_{c}\,)\,]/(\,m\,+\,\lambda_{33}\,)^{2}$ $\begin{array}{r l}&{b_{34}\,=\,b_{43}\,=\,\bigl[\,\alpha_{12}(\lambda_{35}\,+\,m x_{c})\,-\,a_{11}\,m y_{c}\bigr]/(\,m\,+\,\lambda_{33})}\\ &{b_{35}\,=\,b_{53}\,=\,\bigl[\,\alpha_{22}(\lambda_{35}\,+\,m x_{c})\,-\,a_{12}\,m y_{c}\bigr]/\bigl(\,m\,+\,\lambda_{33})}\\ &{b_{36}\,=\,b_{63}\,=\,\bigl[\,\alpha_{23}(\lambda_{35}\,+\,m x_{c})\,-\,\alpha_{13}\,m y_{c}\bigr]/\bigl(\,m\,+\,\lambda_{33}\bigr)}\\ &{b_{44}\,=\,a_{11}}\end{array}$  

\begin{array}{r l}{{b}{4s}}&{={b}{4};=;{a}{12}}\ {~}&{}\ {{b}{4s}}&{={b}{64};=;{a}{13}}\ {}&{}\ {{b}{5s}}&{={a}{22}}\ {{b}{6s}}&{={b}{6s}=;{a}{23}}\ {{b}{6*}}&{={a}{33}}\ {{a}{11}}&{=\displaystyle\frac{1}{d}\Bigg{\left[;(I_{y}+\lambda_{53})-\frac{\left(m z_{6}\right)^{2}}{m+\lambda_{11}}-\frac{\left(\lambda_{33}+m x_{6}\right)^{2}}{m+\lambda_{33}}\right];\cdot}\ {}&{~~~\left[;{a}{4*}\ldots;,;;;;(m y{})^{2};;;(\lambda_{33}+m x_{})^{2}\right];;;\left[;;m^{2}y_{4};\right]}\end{array}

\begin{array}{r l}{\alpha_{11}}&{!=!\frac{1}{d}\Bigg\langle\Bigg[(I_{y}+\lambda_{5}s)-\frac{\big(m z_{\epsilon}\big)^{2}}{m+\lambda_{11}}-\frac{\big(\lambda_{35}+\ m x_{\epsilon}\big)^{2}}{m+\lambda_{33}}\Bigg]!\cdot!}\ &{!!!!!!!!!!!!!\Bigg\lbrack(I_{z}+\lambda_{66})-\frac{\big(m y_{\epsilon}\big)^{2}}{m+\lambda_{11}}-\frac{\big(\lambda_{35}+m x_{\epsilon}\big)^{2}}{m+\lambda_{22}}\Bigg\rbrack!-!\left[\frac{m^{2}y_{\epsilon}z_{\epsilon}}{m+\lambda_{11}}-I_{y z}\right]!\cdot!}\ {!!!!!!!!!!!!\alpha_{22}=\frac{1}{d}\Bigg\langle\Bigg[(I_{x}+\lambda_{44})-\frac{\big(m z_{\epsilon}\big)^{2}}{m+\lambda_{44}}-\frac{\big(m y_{\epsilon}\big)^{2}}{m+\lambda_{33}}\Bigg]}\ {!!!!!!!!!!!!!!!!!!!!!!!!!!\left[(I_{z}+\lambda_{66})-\frac{\big(m y_{\epsilon}\big)^{2}}{m+\lambda_{11}}-\frac{\big(\lambda_{35}+m x_{\epsilon}\big)^{2}}{m+\lambda_{22}}\right]!-!\Bigg[\frac{m}{m+\lambda_{12}}\Bigg]^{2}}\end{array}

  

$\left[\frac{m z_{c}\left(\lambda_{35}\,+\,m x_{c}\right)}{m\,+\,\lambda_{22}}\,-\,I_{x z}\right]^{2}\right\}$  

\begin{array}{r l}{\cdot}&{\quad\cdot}\ {a_{3}=\frac{1}{d}\Bigg[\Big{U_{y}+\lambda_{44}\mathrm{-}\frac{\big(m\varepsilon_{y}\big)^{2}}{m}-\frac{\big(m\varepsilon_{y}\big)^{2}}{m}\Big}\frac{\mathrm{(\rhoox)~}{y}}{n}\Bigg]}\ &{\quad\times\Bigg[\big(I{y}+\lambda_{8}\big)-\frac{\big(m\varepsilon_{x}\big)^{2}}{m}-\frac{\big(\lambda_{8}+m\varepsilon_{x}\big)^{2}}{m+\lambda_{1}}\Bigg]-}\ &{\quad\times\Bigg[\frac{m\varepsilon_{y}\big(\lambda_{8}+m\varepsilon_{x}\big)}{m+\lambda_{3}}-I_{z}\Bigg]^{2}\Bigg}}\ {a_{12}=\frac{1}{d}\Bigg{\Bigg[\frac{m\varepsilon_{x}\big(\lambda_{3}+m\varepsilon_{x}\big)}{m+\lambda_{2}}-I_{x}\Bigg]\Big[\frac{m^{2}\mathrm{Pr}{z}\varepsilon{x}}{m+\lambda_{1}}-I_{y}\Bigg]-}\ &{\quad\Big[\frac{m\varepsilon_{y}\big(\lambda_{8}+m\varepsilon_{x}\big)}{m+\lambda_{3}}-I_{z}\Bigg]\Big[\big(I_{z}+\lambda_{6}\big)-\frac{\big(m\varepsilon_{y}\big)^{2}}{m+\lambda_{1}}\Bigg]}\ &{\quad\times\Bigg(\frac{\lambda_{8}+m\varepsilon_{x}\big)^{2}}{m+\lambda_{1}}\Bigg[\lambda_{1}}\end{array}

\left.\frac{(,\lambda_{35},+,m x_{c},)^{2}}{m,+,\lambda_{22}},\right]\Biggr}

  

400  

$a_{13}\,=\frac{1}{d}\Biggl\{\left[\frac{m y_{c}\,(\,\lambda_{35}\,+\,m x_{c}\,)}{m\,+\,\lambda_{33}}\,-\,I_{x y}\,\right]\left[\frac{m^{2}y_{c}z_{c}}{m\,+\,\lambda_{11}}\,-\,I_{y z}\,\right]-$ $\biggl[{\frac{m z_{c}(\lambda_{35}+\,m x_{c}\,)}{m\,+\,\lambda_{22}}}\,-\,I_{x z}\biggr]\biggl[\,(\,I_{y}\,+\,\lambda_{55}\,)\,-\,{\frac{(\,m z_{c}\,)^{2}}{m\,+\,\lambda_{11}}}\,-\,\frac{1}{2\,+\,\lambda_{35}}\,\biggr]\,\,,$ $\frac{(\,\lambda_{35}\,+\,m x_{c}\,)^{2}}{m\,+\,\lambda_{33}}\biggr]\Biggr\}$  

$a_{23}\,=\frac{1}{d}\Biggl\{\left[\frac{m z_{c}(\lambda_{35}+\,m x_{c})}{m\,+\,\lambda_{22}}\,-\,I_{x z}\right]\left[\frac{m y_{c}(\lambda_{35}+\,m x_{c})}{m\,+\,\lambda_{33}}\,-\,I_{x y}\right]-\,\Biggr\}\,\,.$ $\biggl[\frac{m^{2}y_{c}z_{c}}{m\,+\,\lambda_{11}}\,-\,I_{y z}\,\biggr]\biggl[\,(\,I_{x}\,+\,\lambda_{44}\,)\,-\,\frac{(\,m z_{c})^{2}}{m\,+\,\lambda_{22}}\,-\,\frac{(\,m y_{c}\,)^{2}}{m\,+\,\lambda_{33}}\,\biggr]\Biggr\}$ $d\ =\left[\,\big(\,I_{x}\,+\,\lambda_{44}\,\big)\,-\,\frac{(\,m z_{c})^{2}}{m\,+\,\lambda_{22}}\,-\,\frac{(\,m y_{c})^{2}}{m\,+\,\lambda_{33}}\,\right]\left[\,\big(\,I_{y}\,+\,\lambda_{55}\,\big)\,-\,\frac{(\,m z_{c})^{2}}{m\,+\,\lambda_{11}}\,\right]^{2}\,,$ $\frac{(\lambda_{35}+\ m x_{c})^{2}}{m\ +\ \lambda_{33}}\left]\left[\,(\,I_{z}\,+\,\lambda_{66}\,)\,-\,\frac{(\,m y_{c})^{2}}{m\ +\ \lambda_{11}}\,-\,\frac{(\,\lambda_{35}\,+\,m x_{c})^{2}}{m\ +\ \lambda_{22}}\right]+\right.$ $\begin{array}{r l}&{\quad_{m}:_{*=3,0}\quad_{*=1}}\\ &{\geq\left[\frac{m_{\Re}\left(\lambda_{3,3}+m_{\Im}x\right)}{m}-I_{\Re}\right]\left[\frac{m_{\Re}y\cdot x_{\Re}}{m}-I_{\Re}\right]}\\ &{\quad_{\_{m}}\geq\left(\lambda_{3,1}-m_{\Re}\right)-I_{\Re}\right]\left[\frac{m_{\Re}y\cdot x_{\Re}}{m}-I_{\Re}\right]}\\ &{\quad_{\left[\frac{m_{\Re}\left(\lambda_{3,3}+m_{\Im}x\right)}{m}-I_{\Re}\right]-\left[\frac{m_{\Re}y\cdot x_{\Im}}{m}+\lambda_{3,3}\right]}-I_{\Re}\right]^{2}}\\ &{\quad\left[(I_{\Re}+\lambda_{\Re})-\frac{\left(m_{\Re}y\right)^{2}}{m+\lambda_{11}}-\frac{\left(\lambda_{\Re}+m_{\Re}x\right)^{2}}{m}\right]-}\\ &{\quad\left[\frac{m^{2}y\cdot x_{\Re}}{m+\lambda_{11}}-I_{\Re}\right]^{2}\left[(I_{\Im}+\lambda_{\Im})-\frac{\left(m_{\Re}y\right)^{2}}{m+\lambda_{21}}-\frac{\left(m_{\Re}y\right)^{2}}{m+\lambda_{31}}\right]-}\\ &{\quad\left[(I_{\Re}+\lambda_{\Re})-\frac{\left(m_{\Re}z\right)^{2}}{m+\lambda_{11}}-\frac{\left(\lambda_{\Re}+m_{\Im}x\right)^{2}}{m+\lambda_{31}}\right]}\\ &{\quad\left[\frac{m_{\Re}\left(\lambda_{3,3}+m_{\Re}x\right)}{m}-I_{\Im}\right]^{2}}\end{array}$ $q\infty\ ={\frac{1}{2}}\rho V^{2}$  

\begin{array}{l}{{V,=\sqrt{,u^{2},+,v^{2},+,w^{2}}}}\ {{,}}\ {{\alpha,=\arctan(,w/u,)}}\ {{,}}\ {{\beta,=\arcsin(,v/V)}}\end{array}

  

为形成封闭方程组，还需补充姿态角方程组  

\begin{array}{l}{\displaystyle\phi,=\frac1{\cos\theta}(,q\sin\phi,+,r\cos\phi,)}\ {\displaystyle\theta,=q\cos\phi,-,r\sin\phi}\ {\displaystyle\phi,=,\phi,+,\tan\theta(,q\sin\phi,+,r\cos\phi,)}\ {\displaystyle h,=,u\sin\theta,-,v\cos\theta\sin\phi,+,w\cos\theta\cos\phi}\end{array}

\Delta G;=;m g:-:B

  

式中 $B$ 浮力；  

$\Delta G$ -称为负浮力。  

式(10-253）～式(10-257)给出了鱼雷精确的6自由度动力学方程组。  

# 10.7.2 水动力参数辨识基本方程  

本节给出采用最大似然法进行鱼雷水动力参数辨识的基本方程组。  

状态方程组取6自由度精确动力学方程组（10-253）～式（10-257)。状态参数矢量为  

\pmb{x};=;(;u,,v,,w,,\phi,,q,,r,,\phi,,\theta,,\phi,,h,)^{\intercal}

  

由式(10-253)可见,鱼雷的水动力学参数都与 $b_{i j}$ 以乘积形式出现,而 $b_{i j}$ 中含有附加质量 $\lambda_{i j}$ ,亦即水动力参数与附加质量在状态方程中以乘积形式出现。因此，若以式（10-253）作为状态方程组,是无法同时辨识水动力参数和附加质量 $\lambda_{i j}$ 的。 $\lambda_{i j}$ 必须由鱼雷在水洞中的试验另行确定。当 $\lambda_{i j}$ 和质心位置、质量和惯量矩已知时,则式(10-253)中的 $c_{i j}\,,b_{i j}$ 都可算出,系数中的未知量就只剩水动力学参数了，待估计参数成了  

\pmb{\theta},=,(,C_{l0},,C_{l\hat{\partial}{q}},,C{l p},,C_{m a},,C_{m q},,C_{m\hat{\partial}{e}},,C{n\beta},,C_{n r},,C_{n\hat{\partial}_{r}},,

C_{A0},,,C_{A2},,,C_{Y\beta},,,C_{Y r},,,C_{Y\hat{\sigma}{r}},,,C{N\alpha},,,C_{N q},,,C_{N\hat{\sigma}{\epsilon}},,,u{0},,,v_{0},,

w_{0},,,\beta_{0},,q_{0},,,r_{0},,\theta_{0},,\phi_{0},,h_{0})^{\mathrm{T}}\equiv(\theta_{1},,\theta_{2},,\cdots,\theta_{26})^{\mathrm{T}}

  

观测矢量 ${\bf y}=(\,\phi\,,\,q\,,\,r\,,\,\phi\,,\,\theta\,,\,\phi\,,\,n_{x}\,,\,n_{y}\,,\,n_{z}\,,\,h\,)^{\textup T}$ ,观测方程组为  

\begin{array}{r l}{\dot{\rho}{m}=\dot{\rho}+\varepsilon{1}}&{}\ {q_{m}=q+\varepsilon_{2}}&{}\ {r_{m}=r+\varepsilon_{3}}&{}\ {\dot{\varphi}{m}=\dot{\varphi}+\varepsilon{4}}&{}\ {\dot{\theta}{m}=\dot{\theta}+\varepsilon{5}}&{}\ {\dot{\varphi}{m}=\dot{\phi}+\varepsilon{6}}&{}\ {n_{x m}=n_{x}+\varepsilon_{7}}&{}\ {n_{y m}=n_{y}+\varepsilon_{8}}&{}\ {n_{x m}=n_{x}+\varepsilon_{9}}&{}\ {h_{\mathbf{\dot{\theta}}{1}}=h{\mathbf{\dot{\theta}}{1}}+\varepsilon{10}}&{}\ {h_{\mathbf{\dot{\theta}}{2}}=h{\mathbf{\dot{\theta}}}+\varepsilon_{10}}&{}\end{array}

  

似然判据 $J$ 为  

J;=;\frac{1}{N}\sum_{i;=;1}^{N}\left[,(,{\pmb y}{m},(,i,),-,{\pmb y},(,i,),)^{\mathrm{T}}{\pmb R}^{,-1}\big(,{\pmb y}{m},(,i,),-,{\pmb y}(,i,),\big),+,\ln;|,{\pmb\ R},\mid,\right]

  

式中  

\pmb{R};=;\frac{1}{N}\sum_{i,=,1}^{N}\left(,\pmb{y}{m}\left(,i,\right),-,\pmb{y}\left(,i,\right),\right)\left(,\pmb{y}{m}\left(,i,\right),-,\pmb{y}\left(,i,\right),\right)^{\intercal}

  

采用牛顿-拉夫逊迭代算法，给出未知数 $\pmb{\theta}$ 的初估值 $\pmb{\theta}_{0}$ ，用下列线性代数方程组（10-273）求 $\Delta\pmb{\theta}$ ，再用 $(\,\pmb{\theta}_{0}+\Delta\pmb{\theta}\,)$ 重复上述过程，直至 $J$ 收敛为止，所得 $\pmb\theta_{k}$ 就是 $\tilde{\pmb{v}}$ 的最佳估计。  

\sum_{l=1}^{26};\sum_{i=1}^{N};\left(;\sum_{j,=1}^{10};\sum_{\boldsymbol{k},=1}^{10};\frac{\partial,y_{j}\left(,i,\right)}{\partial,\theta_{l}}(,\boldsymbol{R}^{-1},){,i k};\frac{\partial,y{k}\left(,i,\right)}{\partial,\theta_{m}}\right)\Delta\theta_{l};=

\sum_{i=1}^{N};\left(;\sum_{j,=,1}^{10};\sum_{k,=,1}^{10};(,y_{m j}\left(,i,\right),-,y_{j}\left(,i,\right),);{\frac{\partial,y_{k}\left(,i,\right)}{\partial\theta_{m}}}\right)

(,m,=,1,,2,,\cdots,26,)

  

式中 $\frac{\partial y_{j}(\mathbf{\chi}_{i})}{\partial\theta_{l}}-$ 由下列灵敏度方程组积分求得，或用差分法近似计算。  

灵敏度方程组为  

\begin{array}{r l}&{\varepsilon_{\mathrm{\varepsilon}\mathrm{A}}\left(v,\frac{\partial u}{\partial\theta_{i}}+u,\frac{\partial y}{\partial\theta_{i}}\right)+c_{i2}\left(w,\frac{\partial u}{\partial\theta_{i}}+u,\frac{\partial w}{\partial\theta_{i}}\right)+}\ &{\varepsilon_{\mathrm{\varepsilon}\mathrm{A}}\left(w,\frac{\partial v}{\partial\theta_{i}}+v,\frac{\partial w}{\partial\theta_{i}}\right)+c_{i4}\left(q,\frac{\partial u}{\partial\theta_{i}}+u,\frac{\partial q}{\partial\theta_{i}}\right)+c_{i5}\left(r,\frac{\partial u}{\partial\theta_{i}}+u,\frac{\partial r}{\partial\theta_{i}}\right)+}\ &{c_{\mathrm{\varepsilon}\mathrm{A}}\left(p,\frac{\partial v}{\partial\theta_{i}}+v,\frac{\partial p}{\partial\theta_{i}}\right)+c_{i7}\left(r,\frac{\partial v}{\partial\theta_{i}}+v,\frac{\partial r}{\partial\theta_{i}}\right)+c_{N}\left(p,\frac{\partial w}{\partial\theta_{i}}+w,\frac{\partial p}{\partial\theta_{i}}\right)+}\ &{c_{\mathrm{\varepsilon}\mathrm{O}}\left(q,\frac{\partial w}{\partial\theta_{i}}+w,\frac{\partial q}{\partial\theta_{i}}\right)+2c_{\mathrm{\varepsilon}\mathrm{A}}\eta,\frac{\partial p}{\partial\theta_{i}}+c_{\mathrm{\varepsilon}\mathrm{A}}\left(q,\frac{\partial q}{\partial\theta_{i}}+p,\frac{\partial q}{\partial\theta_{i}}\right)+}\ &{c_{\mathrm{\varepsilon}\mathrm{A}}\left(r,\frac{\partial p}{\partial\theta_{i}}+p,\frac{\partial r}{\partial\theta_{i}}\right)+2c_{\mathrm{\varepsilon}\mathrm{A}}\eta,\frac{\partial q}{\partial\theta_{i}}+c_{\mathrm{\varepsilon}\mathrm{Ai}}\left(r,\frac{\partial q}{\partial\theta_{i}}+q,\frac{\partial r}{\partial\theta_{i}}\right)+}\ &{2c_{\mathrm{\varepsilon}\mathrm{A}}r,\frac{\partial r}{\partial\theta_{i}}+\left[\left(m+\lambda_{1}\right)g,\frac{\partial n}{\partial\theta_{i}}-m\mathrm{g},\frac{\partial\theta}{\partial\theta_{i}}\right]b_{\mathrm{\varepsilon}\mathrm{A}},.}\end{array}

\begin{array}{r l}&{\mathrm{tot:}{\rho}{\mathcal{H}{j}}\cdots{\rho_{\mathcal{H}{j}}}^{\mathcal{H}{j}}\cdots{\sigma_{\mathcal{H}{j}}}^{\mathcal{H}{j}}\cdots\quad\mathcal{O}{\mathcal{H}{j}}\cdots\cdots\mathcal{O}{\mathcal{H}{j}}\cdots\mathcal{O}{\mathcal{H}{j}}\cdots\mathcal{O}{\mathcal{H}{j}}\cdots\mathcal{O}{\mathcal{H}{j}}}^{\mathcal{H}_{j}},}\ &{\mathrm{tot}{\frac{\partial\hat{\mathcal{H}}{\mathcal{H}}}{\partial\hat{\mathcal{H}}{j}}+\boldsymbol{w}\frac{\partial}{\partial\hat{\mathcal{H}}{j}}}+2\epsilon{\mathcal{W}}\beta_{\hat{\mathcal{H}}{j}}\dot{\mathcal{H}}{\mathcal{H}}\cdots\mathrm{tot}\left(\frac{\partial}{\partial\hat{\mathcal{H}}{j}}+\beta\frac{\partial}{\partial\hat{\mathcal{H}}{j}}\right)+}\ &{\mathrm{tot~}{r_{\mathcal{W}{j}}^{\hat{\mathcal{H}}{j}}+\beta\frac{\partial}{\partial\hat{\mathcal{H}}{j}}}+2\epsilon{\mathcal{W}}\eta\frac{\partial}{\partial\hat{\mathcal{H}}{j}}\dot{\mathcal{H}}{\ell}\cdots\mathrm{tot}\left(r\frac{\partial}{\partial\hat{\mathcal{H}}{\ell}}+\frac{\partial}{\partial\hat{\mathcal{H}}{\ell}}\right)+}\ &{2\epsilon_{\mathcal{W}{j}}r\frac{\partial}{\partial\hat{\mathcal{H}}{j}}+\left[(\ln+\lambda_{11}),g\frac{\partial_{\mathcal{W}{j}}}{\partial\hat{\mathcal{H}}{j}}-\mathrm{mgcos},\frac{\partial}{\partial\hat{\mathcal{H}}{j}}\right]{\mathcal{H}{1}}+}\ &{\left[\left(,m+\lambda{22}\right)g\frac{\partial_{\mathcal{W}{j}}}{\partial\hat{\mathcal{H}}{j}}+m g\left(-\frac{\partial}{\partial\hat{\mathcal{H}}{j}}\mathrm{signisin}+\frac{\partial}{\partial\hat{\mathcal{H}}{\ell}}\mathrm{cosfcos},\phi\right)\right]b_{2}+}\ &{\left[\left(,m+\lambda_{33

\begin{array}{l}{{\displaystyle z_{c}\left(,-,\frac{\partial\theta}{\partial\theta_{l}}\mathrm{sin}\theta\mathrm{sin}\phi,+,\frac{\partial\phi}{\partial\theta_{l}}\mathrm{cos}\theta\mathrm{cos}\phi,\right),\bigg\vert b_{i4},+,U_{4,,l}b_{i4},+,}}\ {{\displaystyle q_{\infty},S l\left(,C_{m a},\frac{\partial\alpha}{\partial\theta_{l}},+,C_{m q},\frac{\partial q}{\partial\theta_{l}},\frac[2,V,\right]b_{i5},+,m g\left[-,,z_{c},\frac{\partial\theta}{\partial\theta_{l}}\mathrm{cos}\theta,-,\right]b_{i5},+,}}\ {{\displaystyle x_{c}\left(,-,\frac{\partial\theta}{\partial\theta_{l}}\mathrm{sin}\theta\mathrm{cos}\phi,-,\frac{\partial\phi}{\partial\theta_{l}}\mathrm{cos}\theta\mathrm{sin}\phi,\right),\bigg\vert b_{i5},+,U_{5,,l}b_{i5},+,}}\end{array}

\begin{array}{r l}&{q_{\infty}S l\left(C_{n\beta}\frac{\partial\beta}{\partial\theta_{l}}+C_{n r}\frac{\partial r}{\partial\theta_{l}}\frac{l}{2\nabla}\right)!b_{i\delta}+,m g\left[y_{c},\frac{\partial\theta}{\partial\theta_{l}}\mathrm{cos}\theta\right.}\ &{x_{c}\Bigg(-\frac{\partial\theta}{\partial\theta_{l}}\mathrm{sin}\theta\mathrm{sin}\phi+\frac{\partial\phi}{\partial\theta_{l}}\mathrm{cos}\theta\mathrm{cos}\phi\Bigg)\Bigg]b_{i\delta}+,U_{6,l}b_{i\delta}+}\ &{!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

  

$\frac{\partial\psi}{\partial\theta_{l}}\,=\frac{1}{\cos\!\theta}\left(q\cos\!\phi\;\frac{\partial\phi}{\partial\theta_{l}}\,+\,\sin\!\phi\;\frac{\partial q}{\partial\theta_{l}}\,-\,r\sin\!\phi\;\frac{\partial\phi}{\partial\theta_{l}}\;+\;$ $\cos\phi\;\frac{\partial r}{\partial\theta_{l}}\Biggr)+\;\left(\,q\sin\phi\;+\;r\cos\phi\,\right)\;\frac{\sin\theta}{\cos^{2}\!\theta}\;\frac{\partial\theta}{\partial\theta_{l}}$  

\frac{\partial\theta}{\partial\theta_{l}},=-,,q\sin\phi,\frac{\partial\phi}{\partial\theta_{l}},+,\cos\phi,\frac{\partial q}{\partial\theta_{l}},-,r\cos\phi,\frac{\partial\phi}{\partial\theta_{l}},-,\sin\phi,\frac{\partial r}{\partial\theta_{l}}

\frac{\partial\phi}{\partial\theta_{l}},=\frac{\partial\phi}{\partial\theta_{l}},+,\tan\theta\left(,q\cos\phi;\frac{\partial\phi}{\partial\theta_{l}},+,\sin\phi;\frac{\partial q}{\partial\theta_{l}},-,r\sin\phi;\frac{\partial\phi}{\partial\theta_{l}};+,\right.

\cos\phi;{\frac{\partial r}{\partial\theta_{l}}}\left)+;\left(,q\sin\phi;+;r\cos\phi,\right);{\frac{1}{\cos^{2}!\theta}};{\frac{\partial\theta}{\partial\theta_{l}}}

\frac{\partial h}{\partial\theta_{l}},=u,\mathrm{cos}\theta:\frac{\partial\theta}{\partial\theta_{l}},+,\mathrm{sin}\theta:\frac{\partial u}{\partial\theta_{l}},-,\mathrm{vcos}\theta\mathrm{cos}\phi:\frac{\partial\phi}{\partial\theta_{l}},+

{\begin{array}{r l r}&{v\sin\theta\sin\phi\ {\frac{\partial\theta}{\partial\theta_{l}}}-\cos\theta\sin\phi\ {\frac{\partial,v}{\partial\theta_{l}}}-\ w\cos\theta\sin\phi\ {\frac{\partial,\phi}{\partial\theta_{l}}}\ -}\ &{w\sin\theta\cos\phi\ {\frac{\partial,\theta}{\partial\theta_{l}}}+\cos\theta\cos\phi\ {\frac{\partial,w}{\partial\theta_{l}}}\ }&{(10)}\end{array}}

  

式中  

\frac{\partial n_{1}}{\partial\theta_{1}},=-,\frac{\rho V S}{\left(,m,+,\lambda_{11}\right)g}\big(,C_{A0},+,C_{A2}\big(,\alpha^{2},+,\beta^{2},\big),\big);\frac{\partial V}{\partial\theta_{l}},+

\begin{array}{r l}&{\frac{B}{\left(\m|m\ +\lambda_{11}\right)g}\mathrm{cos}\theta,\frac{\partial\theta}{\partial\theta_{l}},-,\frac{q_{\infty},S}{\left(\ m\ +\lambda_{11}\right)g}\left(2\alpha\ \frac{\partial\alpha}{\partial\theta_{l}}\ +\ \right.}\ &{\left.2\beta,\frac{\partial\beta}{\partial\theta_{l}}\right)+\ {U}_{1,l}}\end{array}

\frac{\partial,n_{2}}{\partial\theta_{l}},=\frac{1}{\left(,m,+,\lambda_{22},\right)g},\left{,q,\mathrm{o},S\left(,C_{Y\beta},\frac{\partial,\beta}{\partial\theta_{l}},+,C_{Y r},\frac{\partial,r}{\partial\theta_{l}},\frac{l}{2,V}\right)-\right.

\begin{array}{r l}{\partial\theta_{i}}&{:=\langle\mathbf{1}{2}\mathbf{1}\rangle\mathbb{E}\left{\mathbf{1}^{\rho}\cdots\nabla\right}^{-1}\gamma^{-1}\gamma^{-1}\partial\theta{i}\quad\cdot\mathbf{1}^{\rho}\approx\partial\mathbf{1}{\theta{i}}\mathcal{L}^{2}V_{f}}\ &{\quad\quad\quad\quad\theta_{i}\simeq\sin\beta\hbar_{i}^{2}+\hbar_{0}^{2}\cos\theta_{i}\frac{\partial\theta_{f}}{\partial\theta_{i}}\Biggr}+}\ &{\quad\quad\quad\quad\mu\times\bigg(\nabla\pi_{\theta}\frac{\partial\theta_{i}}{\partial\theta_{i}}+c_{\nabla\theta}p+c_{\nabla\theta}^{2}\frac{\partial\theta_{f}}{\partial\theta_{i}}\bigg)\frac{\partial\theta_{i}}{\partial\theta_{i}}\bigg}:\cdot\mathbf{1}^{\rho}:,}\ &{\quad\quad\quad\frac{\partial\theta_{i}}{\partial\theta_{i}}=\frac{1}{(m+\lambda_{\mathrm{B}}){\mathrm{S}}}\bigg[\bigg\langle\theta{i}\frac{\partial\theta_{i}}{\partial\theta_{i}}+c_{\nabla\theta}\frac{\partial\theta_{i}}{\partial\theta_{i}}\bigg\rangle\frac{\partial\theta_{i}}{\partial\theta_{i}}\bigg]-}\ &{\quad\quad\quad\quad;;\mathbf{D}\bigg\langle-i\sin\theta\cos\theta_{i}\frac{\partial\theta_{f}}{\partial\theta_{i}}:\cos\theta_{\mathrm{sh}}\bigg\rangle\frac{\partial\theta_{i}}{\partial\theta_{i}}\bigg\rangle+}\ &{\quad\quad\quad\quad\rho\times\bigg\langle\mathbf{C}\left(\mathbf{1}{\theta{i}}+c_{\nabla\theta}+c_{\nabla\theta}q_{\frac{\partial\theta_{i}}{2}}^{\frac{1}{2}}\right)\frac{\partial\theta_{i}}{\partial\theta_{i}}\bigg\rangle:\otimes_{\theta_{i},\mathbf{1}}}\ &{\quad\quad\quad\frac{\partial\theta_{i}}{\partial\theta_{i}}=\frac{1}{\tau^{-1}}\frac{1}{\hbar_{0}^{2}}\bigg\langle\mathbf{1}{\theta{i}}^{\rho}u_{\theta}^{\rho}-\frac{u_{\nabla\theta_{i}}^{\theta}}{\partial\theta_{i}}\bigg\rangle}\ &{\quad\quad\quad

  

qα S U1.10 = - U1,11 = U1,10(α² + β²) (m +A11)g  

U2,12 =m +22 $U_{2,13}\,=\,\frac{q_{\infty}\,S}{m\,+\,\lambda_{22}}\,\frac{r l}{2\,V}$  

Y∞S $U_{3,15}\,=\,-\,\frac{q\,\infty\,S}{m\,+\,\lambda_{33}}\alpha$ U2,14 =m + 入22 2 V  

406  

U_{3,16},=,-,{\frac{q,\infty,S}{m,+,\lambda_{33}}},{\frac{q l}{2,V}}\qquad U_{3,17},=,-,{\frac{q,\infty,S}{m,+,\lambda_{33}}}\delta_{e}

\begin{array}{c c c}{{}}&{{\cdots}}&{{\cdots}}\ {{}}&{{}}&{{}}\ {{U_{4,1},=,q_{\infty},S l}}&{{U_{4,2},=,U_{4,1}\delta_{a}}}&{{U_{4,3},=,U_{4,1},{\frac{\displaystyle p l}{\displaystyle2,V}}}}\ {{}}&{{}}&{{}}\ {{U_{5,4},=,U_{4,1}\alpha}}&{{U_{5,5},=,U_{4,1},{\frac{\displaystyle q l}{\displaystyle2,V}}}}&{{U_{5,6},=,U_{4,1}\delta_{e}}}\ {{}}&{{}}&{{}}\ {{U_{6,7},=,U_{4,1}\beta}}&{{U_{6,8},=,U_{4,1},{\frac{\displaystyle r l}{\displaystyle2,V}}}}&{{U_{6,9},=,U_{4,1}\delta_{r}}}\end{array}

U_{i,j},=,0;;;;;;;;;;;;(,i,=,1,2,\cdots,6,;j,=,1,,2,\cdots,26)

  

灵敏度方程组的积分初值为  

\frac{\partial u}{\partial u_{0}},=,\frac{\partial v}{\partial v_{0}},=,\frac{\partial w}{\partial w_{0}},=,\frac{\partial,\dot{p}}{\partial,\dot{p}{0}},=,\frac{\partial q}{\partial q{0}},=,\frac{\partial,r}{\partial,r_{0}},=

\frac{\partial\theta}{\partial\theta_{0}},=,\frac{\partial,\psi}{\partial,\psi_{0}},=,\frac{\partial,\pmb{\phi}}{\partial,\pmb{\phi}{0}},=,\frac{\partial,h}{\partial,h{0}},=,1

  

其余为零。  

# 10.7.3 辨识仿真算例  

给定某鱼雷的典型物理、几何参数、附加质量、负浮力和水动力参数，由式（10-253）可以积分出鱼雷运动的状态参数。利用伪随机数发生器由式（10-261）～式（10-270）产生观测量的仿真数据，利用上一小节算式可以进行辨识仿真计算。表10-12给出水动力参数部分辨识仿真结果。结果表明，只要试验数据含有足够的信息量，测量噪声比较小，则上述辨识数学模型可以辨识出工程上可实用的水动力学参数。  

上述模型采用6自由度动力学方程组作为参数辨识的状态方程组，待辨识的水动力参数有26个，它要求鱼雷的俯仰、偏航、滚转和三个方向位移都有测量数据。而鱼雷试验时，常常先在铅垂平面作爬高试验，或在同一高度上作盘旋运动等等。这时观测失量的某些参数没有信息，因而与它相对应的水动力学参数就无法辨识。为了使水动力参数辨识软件适用于各种情况，在编程时要设计成可以针对各种不同的试验状态和输人控制参数，使软件不仅可以在信息充足时辨识所有水动力参数，而且可以适应各种不同信息量条件下，只辨识其中某些参数。为了节省机时，矩阵运算要采用稀疏矩阵运算。由于鱼雷试验弹可以反复使用，设计解耦运动模式的试验方案，以增加试验次数为代价换取辨识准度的提高，是提高水动力学参数辨识准度的重要手段。  

表 10-12鱼雷水动力参数辨识仿真结果  


<html><body><table><tr><td>水动力参数</td><td>精确值</td><td colspan="2">理想观测数据</td><td colspan="2">含标准差为1%峰值 的观测噪声的数据</td></tr><tr><td>Cma</td><td>0.586</td><td>0.5854</td><td>0.1%</td><td>0.5607</td><td>4.3%</td></tr><tr><td>Cmq</td><td>-0.60</td><td>- 0.5995</td><td>0.8%</td><td>- 0.5759</td><td>4%</td></tr><tr><td>Cnβ</td><td>- 0.576</td><td>-- 0.5664</td><td>1.7%</td><td>-0.5424</td><td>6%</td></tr><tr><td>Cnr</td><td>-0.60</td><td>- 0.5996</td><td>0.7%</td><td>-- 0.5934</td><td>1.1%</td></tr><tr><td>CAO</td><td>0.003</td><td>0.00301</td><td>0.3%</td><td>0.0026</td><td>13%</td></tr><tr><td>CNa</td><td>2.15</td><td>2.152</td><td>0.1%</td><td>2.222</td><td>3.3%</td></tr><tr><td>Cyβ</td><td>-2.20</td><td>- 2.199</td><td>0.1%</td><td>-2.235</td><td>1.6%</td></tr></table></body></html>  

# 10.8地面试验气动参数辨识  

气动参数辩识方法不仅可用于从飞行器的飞行试验数据辨识气动参数，而且可用于露天模型自由飞试验、风洞和弹道靶模型自由飞试验、风洞模型自由振荡试验等的试验数据处理，获取气动参数，还可用于处理大振幅强迫振荡等动态风洞试验数据，建立非线性非定常气动力数学模型，等等。本节给出几种典型地面试验的气动参数辨识数学模型。  

# 10.8.1 弹道靶自由飞试验气动参数辨识  

弹道靶模型自由飞试验采用非接触测量方法，通过气动参数辨识不仅可得到模型静态气动参数,而且同时可得到动态气动参数。与常规风洞动导数试验相比,弹道靶模型自由飞试验由于没有支架干扰,对动态气动力试验更具吸引力。  

早期的弹道靶模型自由飞气动参数辨识，采用双自由度线性动力学方程组作为状态方程组[11],或直接拟合其近似的三周期解，气动力采用线性模型。近年来，弹道靶常用于大攻角气动力试验，必须采用非线性气动力模型，相应地，状态方程组需采用6自由度非线性动力学方程组[12]  

气流坐标系和体轴系的6自由度非线性动力学方程组为  

\begin{array}{l}{{\displaystyle{\frac{\mathrm{d}V}{\mathrm{d}t}},={\frac{1}{m}}(-,m g\mathrm{sin}\theta_{k},-,q_{\infty},S C_{D})}}\ {{\displaystyle{\frac{\mathrm{d}\theta_{k}}{\mathrm{d}t}},={\frac{1}{m V}}[-,m g\mathrm{cos}\theta_{k},+,q_{\infty},S(,C_{L}\mathrm{cos}\phi_{k},-,C_{C}\mathrm{sin}\phi_{k})]}}\end{array}

\begin{array}{r l}&{\frac{d\phi_{k}}{d t}=\frac{q_{k}-L_{p}}{\gamma\cos\theta_{k}}(C_{k}\sin\phi_{k}+C_{q}\cos\phi_{k})}\ &{\frac{d\phi_{k}}{d t}=\frac{q_{k}-M_{p}}{L_{p}}C_{k}}\ &{\frac{d\phi_{q}}{d t}=\frac{I_{s}-I_{p}}{I_{s}}\rho_{r}+\frac{q_{s}-S_{p}}{I_{s}}C_{s}}\ &{\frac{d\phi_{r}}{d t}=\frac{I_{s}-L_{p}}{I_{s}}\rho_{r}+\frac{q_{s}-S_{p}}{I_{s}}C_{s}}\ &{\frac{d\phi_{q}}{d t}=\frac{q_{k}-L_{p}}{\gamma\sin\phi_{k}}+\frac{q_{s}-S_{p}}{I_{s}}C_{s}}\ &{\frac{d\phi_{q}}{d t}=\frac{q_{k}-S_{p}}{\cos\phi_{k}}(\cos\phi+\cos\phi)}\ &{\frac{d\theta}{d t}=q_{k}\cos\phi-r\sin\phi}\ &{\frac{d\phi_{k}}{d t}=p_{k}+\tan\theta(\phi\sin+r\cos\phi)}\end{array}

\begin{array}{l}{{\displaystyle\frac{\mathrm{d}x_{g}^{'}}{\mathrm{d}t}{=}V\mathrm{cos}\theta_{k}\mathrm{cos}\phi_{k}}}\ {{\displaystyle\frac{\mathrm{d}y_{g}^{'}}{\mathrm{d}t}{=}V\mathrm{cos}\theta_{k}\mathrm{sin}\phi_{k}}}\ {{\displaystyle\frac{\mathrm{d}z_{g}^{'}}{\mathrm{d}t}{=}-~V\mathrm{sin}\theta_{k}}}\end{array}

  

式中  

\begin{array}{r l}{\tan\alpha}&{={\cos\phi[\sin\theta\cos\theta_{k}\cos(\phi\ -\ \phi_{k})\ -\ \cos\theta\sin\theta_{k}]\ -}\ &{}\ &{\cdot\ \cos\theta_{k}\sin(\phi\ -\ \phi_{k})\sin\phi}/[[\cos\theta\cos\theta_{k}\cos(\phi\ -\ \phi_{k})\ +}\ &{\ \ \ \ \ \ \sin\theta\sin\theta_{k}]}\ &{\ \ \ \ \ \ \sin\theta\sin\theta_{k}]}\ &{\sin\beta=\cos\theta_{k}\sin(\phi\ -\ \phi_{k})\cos\phi\ +\ [\sin\theta\cos\theta_{k}\cos(\phi\ -\ \phi_{k})\ -}\ &{\ \ \ \ \ \ \cos\theta\sin\theta,\ ]\sin\phi}\end{array}

\begin{array}{r l}&{\sin\beta=\cos\theta_{k}\sin(\phi-\phi_{k})\cos\phi+[\sin\theta\cos\theta_{k}\cos(\phi-\phi_{k})-}\ &{\qquad\qquad\cos\theta\sin\theta_{k}]\sin\phi}\ &{\sin\phi_{k}=(\sin\theta\cos\alpha\sin\beta-\cos\theta\cos\phi\sin\alpha\sin\beta+}\ &{\cos\theta\sin\phi\cos\beta)/\cos\theta_{k}}\end{array}

  

气动力可以采用两种模型形式。一种是采用多项式形式的气动力模型  

C_{D};=;C_{D0},+,C_{D2}\sigma^{2}

\begin{array}{l}{{C_{C},=,C_{C0},+,C_{C\beta},\beta,+,C_{C\beta}^{\phantom{-}3},\beta^{3}}}\ {{{}}}\ {{C_{L},=,C_{L0},+,C_{L a}\alpha,+,C_{L a}^{\phantom{-}3},\alpha^{3}}}\end{array}

C_{l};=;C_{l0},+,C_{l a}\alpha,+,C_{l\beta},\beta,+,C_{l\beta}\dot{p};\frac{l}{2,V}

C_{m};=C_{m0},+,C_{m\alpha}\alpha,+,C_{{m\alpha}^{3}}\alpha^{3},+,C_{m{\alpha}^{5}}{\alpha}^{5},+,C_{m q}q;\frac{l}{2,V}

C_{n}\ =\ C_{n0},+,C_{n\beta},\beta,+,C_{n\beta}{^3}\beta^{3},+,C_{n\beta}{^5}\beta^{5},+,C_{n r}r,{\frac{l}{2,V}}

  

待辨识气动参数为  

\begin{array}{r}{\pmb{\theta},=,(,C_{D0},,C_{D2},,C_{C0},,C_{C\beta},,C_{C\beta}^{\phantom{\dagger}},,C_{L0},,C_{L a},,C_{L a}^{\phantom{\dagger}},,}\end{array}

C_{l0},,C_{l a},,C_{l\beta},,C_{l\beta},,C_{m0},,C_{m a},,C_{m a}{}^{3},,C_{m a}{}^{5},,C_{m q},,

C_{n0},,C_{n\beta},,C_{n\beta}{^3,C_{n\beta}}{^5,C_{n r}})^{\mathrm{T}}

  

另一种气动力模型是假定弹道靶试验的气动特性与风洞试验相似，成线性关系，即  

\begin{array}{l}{{C_{D},=C_{D0},+,K_{D}C_{D w}(,{\alpha},,\beta)}}\ {{{}}}\ {{C_{C},=C_{C0},+,K_{C}C_{C w}(,{\alpha},,\beta)}}\ {{{}}}\ {{C_{L},=C_{L0},+,K_{L}C_{L w}(,{\alpha},,\beta)}}\ {{{}}}\ {{C_{l},=C_{l0},+,K_{l}C_{l w}(,{\alpha},,\beta),+,,C_{l p}{\beta},\frac{l}{2,V}}}\end{array}

C_{m};=C_{m0},+,K_{m}C_{m w}(,\alpha,,\beta),+,C_{m q}q;{\frac{l}{2,V}}

C_{n},=C_{n0},+,K_{n}C_{n w}(,\alpha,,\beta),+,C_{n r}r,{\frac{l}{2,V}}

  

式中 $C_{D w}({\tiny\alpha}\,,\beta)\,,{\cal C}_{C w}({\tiny\alpha}\,,\beta)\,,C_{L w}({\tiny\alpha}\,,\beta)\,,C_{l w}({\tiny\alpha}\,,\beta)\,,C_{m w}({\tiny\alpha}\,,\beta)\,,$   
Cnu（α,β)—风洞试验测得的6 分量气动力随α和β 的非线性变化规律。  
待辨识的气动参数为  

\begin{array}{c}{\pmb{\theta}=(,C_{D0},,K_{D},,C_{C0},,K_{C},,C_{L0},,K_{L},,C_{l0},,K_{l},,C_{l p},,}\ {\pmb{\theta}=(,C_{m0},,K_{m},,C_{m q},,C_{n0},,K_{n},,C_{n r},)^{\mathrm{T}},}\end{array}

  

弹道靶模型自由飞试验的观测数据为三个姿态角和三个方向的位移。姿态角的测量是在模型飞行时，通过水平方向和铅垂方向的闪光拍照，获得其投影的底片，借助光学仪器、电子仪器或人工判读求得模型的俯仰角 $\theta$ 和偏航角 $\psi$ ,而滚转角 $\phi$ 则是利用安装在模型底部的长短两根针在底片上的投影进行判读的。位移测量通常采用激光测距进行基准标定，再由底片判读质心和基准的距离,从而确定位移距离 $x_{g}^{\prime},y_{g}^{\prime},z_{g}^{\prime}$ 。因此,观测方程组取为  

\begin{array}{r l}{x_{s m}^{\prime}}&{=x_{s}^{\prime}+\varepsilon_{1}}\ &{}\ {y_{s m}^{\prime}}&{=y_{s}^{\prime}+\varepsilon_{2}}\ &{}\ {z_{s m}^{\prime}}&{=z_{s}^{\prime}+\varepsilon_{3}}\ &{}\ {\phi_{m}}&{=\phi+\varepsilon_{4}}\ &{}\ {\theta_{m}}&{=\theta+\varepsilon_{5}}\ &{}\ {\phi_{m}}&{=\phi+\varepsilon_{6}}\end{array}

  

有了上述状态方程组和观测方程组，就可以采用5.3节所述最大似然法进行气动参数辨识。  

表10-13和表10-14给出某典型再人飞行器弹道靶气动参数辨识结果，飞行马赫数处于 $1.1\!\sim\!1.2$ 之间，其中表10-13为采用多项式形式非线性气动力模型的辨识结果，表10-14为采用风洞试验气动力模型的辨识结果。从全部辨识拟合曲线来看，采用前一种气动力模型的拟合程度比后一种气动力模型好。下面以多项式形式气动力模型的辨识结果为依据作一简要分析。  

弹道靶试验所得配平攻角为 $-\ 19^{\circ}.65$ ；风洞试验配平攻角在$M\!a=1\,.1$ 时为 $-\,19^{\circ}.604\$ ，在 $M\!a=1\,.2$ 时为－19°.758；工程计算所得配平攻角在 $M\!a=1.2$ 时为一20°.105，三者比较接近。 弹道靶试验中，配平特性不受靶场空气密度测量误差的影响，姿态角测量误差影响也较小，因此所得配平特性是比较准确、可信的。  

对于阻力系数和升力系数，各次试验的辨识结果分散度较大，约 $10\,\%\sim15\,\%$ ,辨识结果的均值比风洞试验结果低，其中阻力：数低 $8\,\%$ ，升力系数低 $18\,\%$ 。阻力系数和升力系数的辨识误差靶场空气密度的测量误差成反比。  

果结数参动气靶道弹的型模气式项多用采1-01表  


<html><body><table><tr><td></td><td>-17.627</td><td>- 20.500</td><td>- 20.250</td><td>- 20.167</td><td>- 20.530</td><td></td><td>- 18.938 - 19.082</td><td>- 20.170</td><td>- 19.213</td><td>- 20.574</td><td></td><td>-18.365</td><td>- 19.270</td><td>- 20.503</td><td>-19.932 -19.652</td></tr><tr><td></td><td>-0.5161</td><td>-0.0495</td><td>- 1.7520</td><td>-0.4759</td><td>0.3281</td><td>1.4250</td><td>- 0.2941</td><td>1.4710 -1.</td><td>2.9830</td><td>- 0.3192</td><td>- 4.1320</td><td>0.2914</td><td>- 0.1083</td><td>-0.6721</td><td>-0.3402</td></tr><tr><td>5 DU C</td><td>0.7142</td><td>0.6989</td><td>.7002 0</td><td>0.7000</td><td>0.6539</td><td>0.6999</td><td>0.6992</td><td>.7002 0</td><td>0.7000 0</td><td>.7000 0</td><td>.7000</td><td>0.7000</td><td>0.7000</td><td>0.7000</td><td>0.6976</td></tr><tr><td></td><td>- 0.3448</td><td>-0.3961</td><td>- 0.4000</td><td>-0.4000</td><td>-- 0.3756</td><td>- 0.4000</td><td>-- 0.4002</td><td>- 0.3951</td><td>- 0.4000</td><td>- 0.4000</td><td>- 0.4000</td><td>- 0.4000</td><td>- 0.4001</td><td>- 0.4000</td><td>- 0.3937</td></tr><tr><td></td><td>- 0.09138</td><td>- 0.08764</td><td>- 0.05415</td><td>- 0.04844</td><td>- 0.06746</td><td>-0.08660</td><td>- 0.08290</td><td>- 0.10060</td><td>- 0.13260</td><td>- 0.05426</td><td>-0.2305</td><td></td><td>- 0.10090 - 0.08160</td><td></td><td>- 0.10530 - 0.07977</td></tr><tr><td></td><td>-0.03617</td><td>- 0.04489</td><td>-0.03282</td><td>-0.03065</td><td>-0.03760</td><td>-0.04035</td><td>~0.03957</td><td>-0.05019</td><td>-0.05704</td><td>-0.03385</td><td>-0.01822</td><td>-0.04618</td><td>-0.04345</td><td></td><td>- 0.04651 -0.03978</td></tr><tr><td></td><td>2.533</td><td>2.379</td><td>2.400</td><td>2.400</td><td>2.423</td><td>2.378</td><td>1.972</td><td>2.400</td><td>2.400</td><td>2.400</td><td>2.400</td><td>2.400</td><td>2.398</td><td>2.400</td><td>2.377</td></tr><tr><td>CLa</td><td>.378 -1.</td><td>.309 -</td><td>- 1.157</td><td>- 1.164</td><td>- 1.312</td><td>-1.093</td><td>.214</td><td>-1.291</td><td>.200 -1.</td><td>.203 -1.</td><td>-1.148</td><td>- 1.191</td><td>- 1.356</td><td>-1.355</td><td>- 1.234</td></tr><tr><td>Cp2</td><td>-0.030</td><td>-0.050</td><td>-0.300</td><td>- 0.300</td><td>-0.300</td><td>-0.100</td><td>- 0.298</td><td>- 0.500</td><td>-0.300</td><td>- 0.300</td><td>- 0.300</td><td>.300 '0-</td><td>.300 :0-</td><td>.300 -0.</td><td>.253 'o-</td></tr><tr><td></td><td>1.196</td><td>1.310</td><td>1.200</td><td>1.200</td><td>.200</td><td>1.050</td><td>.180</td><td>.400</td><td>1.100</td><td>1.120</td><td>1.200</td><td>1.290</td><td>.250</td><td>0.980</td><td>.200</td></tr><tr><td></td><td>206</td><td>313</td><td>401</td><td>408</td><td>415</td><td>417</td><td>410</td><td>304</td><td>327</td><td>308</td><td>319</td><td>324</td><td>314</td><td>411</td><td>均值</td></tr></table></body></html>  

# 表 10-14采用风洞试验气动力模型的弹道靶气动参数辩识结果  

<html><body><table><tr><td>序号</td><td>KD</td><td>Kc</td><td>KL</td><td>Cm0</td><td>Km</td><td>Cn0</td><td>Kn</td></tr><tr><td>206</td><td>1.091</td><td>0.984</td><td>1.041</td><td>-- 0.03053</td><td>1.034</td><td>0.0030</td><td>1.147</td></tr><tr><td>313</td><td>950</td><td>.460</td><td>1. 196</td><td>- 0.02803</td><td>1 .046</td><td>-0.01518</td><td>1.232</td></tr><tr><td>401</td><td>940 0</td><td>847 0</td><td>1 032</td><td>- 0.04200</td><td>177</td><td>0.0020</td><td>0.9126</td></tr><tr><td>408</td><td>0 890</td><td>4 535</td><td>604</td><td>- 0.02161</td><td>006</td><td>-0.02475</td><td>0.9129</td></tr><tr><td>415</td><td>0 930</td><td>0. 7905</td><td>052</td><td>-0.03999</td><td>353</td><td>0.001454</td><td>0.9082</td></tr><tr><td>410</td><td>920 0</td><td>520</td><td>1 350</td><td>-0.03970</td><td>1 300</td><td>0.003808</td><td>0.9029</td></tr><tr><td>417</td><td>0.910 0</td><td>0. 4246</td><td>0.8313</td><td>-0.04056</td><td>303</td><td>-0.000427</td><td>0.9137</td></tr><tr><td>304</td><td>一 100</td><td>-0.00226</td><td>0.7428</td><td>0.05761 一</td><td>569 1</td><td>- 0.0079</td><td>1.251</td></tr><tr><td>327</td><td>.900</td><td>1.000</td><td>1.000</td><td>-0.04404</td><td>400</td><td>0.008034</td><td>105</td></tr><tr><td>308</td><td>900 0</td><td>0.7471</td><td>170</td><td>0.03382 一</td><td>.067</td><td>0.01304</td><td>0 .8977</td></tr><tr><td>319</td><td>0.900</td><td>0.2 2624 2</td><td>1.127</td><td>- 0.03425</td><td>.210</td><td>- 0.009801</td><td>1 452</td></tr><tr><td>324</td><td>990</td><td>9106 0 9</td><td>0. 9 9702</td><td>- 0.03811</td><td>1 299</td><td>0.005779</td><td>222</td></tr><tr><td>314</td><td>100</td><td>.019</td><td>0.8 8836</td><td>- 0.04350</td><td>538</td><td>0.009751</td><td>0. .9205</td></tr><tr><td>411</td><td>0.700</td><td>0.3311</td><td>.824 1</td><td>- 0.02337</td><td>1.300</td><td>0.007259</td><td>0.9351</td></tr><tr><td>均值</td><td>0.944</td><td>1.1306</td><td>1.1303</td><td>-0.03694</td><td>1.2573</td><td>- 0.000281</td><td>1.0509</td></tr></table></body></html>  

![](images/b0775873ac9f635f551f6b6b20507dfbd9dc1aa51e46171094dbde45f85c3215.jpg)  
图 10-12 升阻比的弹道靶辨识结果与风洞试验、工程计算结果的比较  

图10-13给出升阻比的弹道靶辨识结果与风洞试验结果的比较。由图可见,弹道靶辨识所得升阻比比风洞试验值低8%左右。弹道靶辨识所得升阻比不受靶场空气密度测量误差的影响，其试验精确度比升力系数和阻力系数高。  

图 10-13给出俯仰力矩系数辨识结果与风洞试验结果的比较,可见辨识结果的均值与风洞试验结果比较一致，而且分散度也是可以接受的，表明辨识结果是可信的。  

![](images/bb254e434228bcb7fda86602ad47a6f55bcca9c0359626a0bba9333018bc46a9.jpg)  
图 10-13俯仰力矩系数的弹道靶辨识结果与风洞试验、工程计算结果的比较  

辨识仿真计算表明，对于弹道靶这类数据采样点稀少且有测量误差的试验设备，为获得正确的阻尼导数，试验数据应有 $(1.8\sim$ 2.3）个周期。而本次弹道靶试验数据的振荡周期处于 $(\,1\,.\,3\!\sim\!1\,.\,5\,)$ 个周期，这就给动导数辨识带来较大困难。由表10-13可见，动导数辨识结果散布度较大。  

由于滚转角测量误差很大，无法用来辨识滚转气动力矩系数，在辨识过程中滚转角实测值作为已知量代人状态方程组进行处理。  

# 10.8.2 风洞自由振荡试验气动参数辨识  

地面试验研究飞行器的动稳定性主要是采用自由振荡和强迫振荡两种方法。自由振荡试验通常是采用液体或气浮轴承，将模型支撑在风洞中作单自由度的自由振荡运动。试验过程中，利用传感器测试系统测量振荡的角位移信号，而不直接测量气动力和力矩。  

从角位移信号获取动稳定导数，通常是根据振幅的衰减来进行近似估算。这种估算方法对静态力矩系数作了线性假设，在大振幅振荡时，静态力矩系数非线性会对估算结果产生较大的影响。并且，由于测量数据的振幅直接受各种测量误差和噪声的影响，在阻尼较小和小振幅的情况下，估算结果对测量误差和噪声很敏感。因此，这里阐述采用系统辨识技术从角位移测量数据获取动稳定导数的方法。  

# 1）状态方程组  

对于俯仰方向的自由振荡试验，模型的运动方程为  

\frac{\mathrm{d}q}{\mathrm{d}t};=;\frac{1}{I_{y}}q_{\infty},S l\left[,C_{m s t};+;\left(,\overline{{C}}{m q},+,\overline{{C}}{m\dot{\alpha}},\right)q;\frac{l}{2,V},\right]+,\frac{1}{I_{y}}M_{f}

{\frac{\mathrm{d}\alpha}{\mathrm{d}t}},=,q

  

式中 $C_{m s t}$ 一——静态俯仰力矩系数；  

$(\,\bar{C}_{m q}+\,\bar{C}_{m i}\,)$ 一—辨识时间段的平均动稳定导数；  

$M_{f}$ ——机构的摩擦阻尼力矩。  

状态方程组的积分初值为 $q_{0}$ 和 $\alpha_{\parallel\mathrm{0}\,^{\mathrm{0}}}$  

静态俯仰力矩系数 $C_{m s t}$ 可采用静态风洞试验结果。静态俯仰力矩系数主要影响振荡周期，而动稳定导数决定振幅的衰减，因此，当没有静态俯仰力矩系数风洞试验结果时，可采用五次多项式来近似  

C_{m s t};=;C_{m0},+,C_{m a}\alpha,+,C_{m a}^{~~~3},+,C_{m a}^{~~~5},\alpha^{5}

  

2）观测方程  

\alpha_{m};=;\alpha;+;\alpha_{B};+;\varepsilon_{1}

  

式中 αm\~——-攻角的测量值;  

$\alpha_{B}$ ——角位移传感器的零位漂移；  

$\varepsilon_{1}$ --服从零均值正态分布 $N(\mathbf{0}\,,\sigma^{2})$ 的随机噪声。  

3）待辨识的未知参数  

\begin{array}{r l r}&{\pmb{\theta}=(,\alpha_{B},,,C_{m0},,,C_{m\alpha},,C_{m a}{}^{,3},,C_{m a}{}^{,s},,(,\bar{C}{m q},+,\bar{C}{m\dot{a}},),,q_{0},,\alpha_{0},)^{\mathrm{T}}\equiv}&{}\ &{\qquad(,\theta_{1},,\theta_{2},,\cdots,,\theta_{8},)^{\mathrm{T}}}&{(10-3,\alpha_{0})^{\mathrm{T}}}\end{array}

  

4）判据函数  

由于只有一个观测量，最大似然判据等价于最小二乘判据  

J;=;\sum_{\mathrm{\scriptsize\textit{i}=1}}^{N}\left[,\alpha\left(,{i},\right),+,\alpha{B};-;\alpha_{m}\left(,_{i},\right),\right]^{2}

  

5）迭代算法  

采用牛顿-拉夫逊算法，其送代公式为  

\pmb{\theta}^{(,n,+1,)};=;\pmb{\theta}^{(,n,)};+;\Delta\pmb{\theta}^{(,n,)}

\Delta\pmb{\theta};=-;\left(\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}}\right){7\times7}^{-1}\left(\frac{\partial J}{\partial\theta{k}}\right)_{7\times1}

  

式中 ${\pmb\theta}^{(\,n\,)}$ 第 $\pmb{n}$ 次迭代的参数值；  

\frac{\partial J}{\partial\theta_{k}}:=\left{\begin{array}{l l}{\displaystyle2\sum_{i=1}^{N}\left[,\alpha\left(,i,\right):+:\alpha_{B}:-:\alpha_{m}\left(,i,\right)\right]\left[\frac{\partial\alpha\left(,i,\right)}{\partial\theta_{k}}:+:1\right]}&{\displaystyle k:=:1}\ {\displaystyle2\sum_{i=1}^{N}\left[,\alpha\left(,i,\right):+:\alpha_{B}:-:\alpha_{m}\left(,i,\right)\right]\frac{\partial\alpha\left(,i,\right)}{\partial\theta_{k}}}&{\displaystyle k:\ne1}\end{array}\right.

{\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}}}={\left[\begin{array}{l l}{\displaystyle2\sum_{i=1}^{N}{\left[{\frac{\partial\alpha\left(i\right)}{\partial\theta_{k}}}+1\right]\left[{\frac{\partial\alpha\left(i\right)}{\partial\theta_{l}}}+1\right]}}&{\displaystyle k=1,l=1}\ {\displaystyle2\sum_{i=1}^{N}{\left[{\frac{\partial\alpha\left(i\right)}{\partial\theta_{k}}}+1\right]\frac{\partial\alpha\left(i\right)}{\partial\theta_{l}}}}&{\displaystyle k=1,l\neq1}\ {\displaystyle2\sum_{i=1}^{N}{\frac{\partial\alpha\left(i\right)}{\partial\theta_{k}}}\left[{\frac{\partial\alpha\left(i\right)}{\partial\theta_{l}}}+1\right]}&{\displaystyle k\neq1,l=1}\ {\displaystyle2\sum_{i=1}^{N}{\frac{\partial\alpha\left(i\right)}{\partial\theta_{k}}},{\frac{\partial\alpha\left(i\right)}{\partial\theta_{l}}}}&{k\neq2,l\neq1}\end{array}\right]}

  

式(10-319)和式（10-320）中的 $\partial\,\alpha/\partial\,\theta_{k}$ 需通过灵敏度方程积分获得。  

6）灵敏度方程组  

状态方程组对待辨识的未知参数求偏导数，得灵敏度方程组  

\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial q}{\partial\theta_{l}},=,\frac{q_{\infty},S l}{I_{y}}\Big[,C_{m\alpha},\frac{\partial,\alpha}{\partial\theta_{l}},+,3,C_{m\alpha}{}^{3},\alpha^{2},\frac{\partial,\alpha}{\partial\theta_{l}},+

5C_{m a}^{;;;}\alpha^{4};\frac{\partial\alpha}{\partial\theta_{l}};+;\left(,\overline{{{C}}}{m q};+;\overline{{{C}}}{m a}^{;;;}\right),\frac{\partial q}{\partial\theta_{l}};\frac{l}{2V}\Biggr]+;U_{1,l}

\frac{\mathrm{d}}{\mathrm{d}t},\frac{\partial\alpha}{\theta_{l}},=,\frac{\partial q}{\partial\theta_{l}}\qquad(l,=,1,{,2},,\cdots,7)

  

式中  

\begin{array}{l l}{{U_{1,1},=,0}}&{{U_{1,2},=,\displaystyle{\frac{q_{\infty},S l}{I_{y}}}}}&{{U_{1,3},=,U_{1,2}\alpha}}\ {{\mathrm{}}}&{{\mathrm{}}}\ {{U_{1,4},=,U_{1,2}\alpha^{3}}}&{{U_{1,5},=,U_{1,2}\alpha^{5}}}&{{U_{1,6},=,U_{1,2}q,\displaystyle{\frac{l}{2,V}}}}\ {{\mathrm{}}}&{{U_{1,7},=,0}}&{{U_{1,8},=,0}}\end{array}

  

灵敏度方程组的积分初值为  

\frac{\partial q\left(0\right)}{\partial\theta_{7}},=,\frac{\partial\alpha\left(0\right)}{\partial\theta_{8}},=,1

  

其余全为零。  

上述辨识算法用于辨识动导数在一个振荡周期内的平均值，给出平均动稳定导数随振幅的变化关系。之后，还需将随振辐变化的平均动稳定导数变换为随攻角变化的动稳定导数，具体变换方法参见参考文献[13］。  

图 10-14 给出了某典型再人飞行器在 Ma = 4 和 Mα = 6下若干次自由振荡试验的平均动导数辨识结果，圆点为辨识结果，实线为拟合曲线。由图可见，辨识获得的平均动稳定导数随振幅的变化具有明显的规律性。当振幅很小时，平均动稳定导数辨识结果跳动较大,这是由于测量误差、测量噪声以及外部扰动等因素的影响所致。将图 10-14所示的随振幅变化的动导数变换为随攻角变  

化的动导数，结果示于图10-15。  

![](images/c26453e0d9a32f74afb4394346e90fd6584b3cb6a3bbd2000c4aae7b22bf42ec.jpg)  
图 10-14某再人飞行器自由振荡试验的平均动导数辨识结果  

![](images/e79b81778d527895f41c7838190a1b79d15b754fe835082c4e837de3289bd7d0.jpg)  
图 10-15某再人飞行器自由振荡试验动导数变换结果  

# 10.8.3大攻角非定常气动力参数辨识  

地面试验研究飞机的大攻角非定常空气动力特性，主要米用大振幅的强迫振荡试验和自由振荡试验。由于强迫振荡试验比较容易实现各种振幅和频率下的运动，进行6分量测量，并且适用于静不稳定飞机的气动特性研究，因而得到最为广泛的应用。2.2节所讨论的非线性非定常气动力数学模型可以利用大振幅强迫振荡风洞试验数据进行参数辨识。这里将给出下述微分方程模型的非定常气动力参数辨识算法(14,15]  

C_{L}\ =\ C_{L s t}\left(,\alpha,\right)\ +\ \left(,C_{L q}^{\ \ \bullet};+;C_{L\dot{\alpha}}^{\ \ \bullet},\right)q;\frac{c_{A}}{2,V},+,C_{L u n s t}

\tau_{1}\ \frac{\mathrm{d}C_{L u n s t}}{\mathrm{d}\tau},+,C_{L u n s t}\ =\ \sum_{i,=,0}^{n},\sum_{j,=,0}^{n,-,i}A_{i j}\alpha^{i}\ \dot{\alpha}^{j,+,1}

  

数学模型（10-323）～式（10-324）的物理意义可参考2.2节。由于静态气动力系数 $C_{L s t}\left(\,\alpha\,\right)$ 和动导数 $\bigl(\,C_{L q}^{\phantom{\dagger}}\cdot\,+\,C_{L\dot{\alpha}}^{\phantom{\dagger}}\cdot\,\bigr)$ 可分别从风洞静态试验和强迫振荡试验获得，上述模型中仅包含未知参数 $\tau_{1}$ 和 $A_{i j}\big(\,i=0,1\,,\cdots,n\,,j=0,1\,,\cdots,n\,-\,i\,\big)$ ，待辨识的未知参数矢量为  

\pmb{\theta};=;(,\tau_{1},;A_{00},,A_{01},,\cdots,,A_{0n},;A_{10},,A_{11},,\cdots,,A_{1,n-1},;\cdots,;A_{n0},)^{\mathrm{,T}}

  

# 1）模型辨识  

对于微分方程模型式（10-323）及式（10-324），需通过模型辨识确定阶次 $\pmb{n}$ ，并筛选候选模型项。  

阶次 $\pmb{n}$ 可根据具体问题给定，例如，对于大振幅谐波振荡运动，可取为试验数据傅里叶分析的阶次；也可以通过模型的 $F$ 统计检验来确定：用式（10-323）计算由非定常效应产生的附加气动力系数 $C_{L u n s t}$ ,并数值微分求其时间导数 ${\mathrm{d}C_{L u n s t}}/{\mathrm{d}t}$ ,这样，式（10-324）就可看做关于参数天量 $\pmb{\theta}$ 的线性回归方程，对不同的阶次 $\pmb{n}$ 构成候选模型集，应用模型 $F$ 统计检验及其相关算法即可确定最优模型,从而确定最佳的阶次 $n_{\circ}$  

阶次 $\pmb{n}$ 确定后，式（10-324）仍可能包含允余项，在参数辨识之前还应进行模型结构辨识。前已述及，式（10-324）可看做关于参数矢量0的线性回归方程，因此，可应用基于 $F$ 统计检验的逐步回归法、主元回归法、主成分分析法、正交分解法等方法进行候选模型项的筛选，确定最优模型结构。  

# 2）频域参数估计算法  

上述模型辨识方法在确定最优模型结构的同时，可求得参数的最小二乘估计。  

对于大振幅谐波振荡风洞试验数据，还可以在频域中用多元  

线性回归法估计未知参数。考虑谐波振荡运动  

\alpha(,\tau,)=\alpha_{0},+,\alpha_{s}\sin k\tau

  

用式(10-323)求出 $C_{L u n s t}$ ,将其傅里叶级数表达式代人式（10- 324),得  

\begin{array}{r c l}{{}}&{{}}&{{\displaystyle\alpha_{0}\big(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},\big),+,\sum_{i,=1}^{n},\bigl{,\big[,\tau_{1},i k b_{i}\big(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},\big),+,a_{i}\big(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},\big),\big]\mathrm{cos},i k\tau,+,}}\ {{}}&{{}}&{{\displaystyle~\big[,-,,\tau_{1},i k a_{i}\big(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},\big),+,b_{i}\big(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},\big),\big]\mathrm{sin},i k\tau,\bigr},=}}\end{array}

a_{0f}!\left(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},,\theta_{1},\right),+,\sum_{i,=,1}^{n},[,a_{i f}!\left(,\alpha_{0},,\alpha_{s},,\boldsymbol{k},,\theta_{1},\right)!\cos i k\tau,+

b_{i f}(,\alpha_{0},,\alpha_{s},,k,,\theta_{1},)\sin i k\tau,]

  

式中 $\alpha_{0\setminus a_{i}\setminus b_{i}}.\longrightarrow C_{L u n s t}(\{\tau\}$ 的傅里叶系数；  

αofαir、bir-—式(10-324)右端项的傅里叶系数;  

\pmb{\theta}{1};=;(,A{00},,A_{01},,\cdots,A_{0n},;A_{10},,A_{11},,\cdots,A_{1,n-1},;\cdots;A_{n0},)^{\mathrm{T}}

  

显然， ${a}_{0f}\!\left(\,{\alpha}_{0}\,,\,{\alpha}_{s}\,,\,{k}\,,\,{\pmb\theta}_{1}\,\right),{a}_{i f}\!\left(\,{\alpha}_{0}\,,\,{\alpha}_{s}\,,\,{k}\,,\,{\pmb\theta}_{1}\,\right)$ 和 $b_{i f}(\,\alpha_{0}\,,\,\alpha_{s}\,,\,k\;,$ $\pmb{\theta}_{1}\,)$ 关于参数矢量 $\pmb{\theta}_{1}$ 是线性的。根据等式两边同阶谐波项的系数相等可得关于参数矢量 $\pmb{\theta}$ 的线性模型，对不同频率、不同攻角均值和不同振幅的试验数据，用多元线性回归法即可求得 $\pmb{\theta}$ 的最小二乘估计值。  

3）时域参数估计算法  

模型辨识方法和上述频域多元线性回归法所得的估计值均为θ的最小二乘估计。由于回归方程的噪声序列是相关的，最小二乘估计是有偏的。为了得到更准确的参数估计值，应采用最大似然法。  

对于风洞试验，攻角和气动力系数有测量值。微分方程模型式（10-323）及式（10-324）的参数估计可看成下述动态系统的参数估计问题：  

状态方程  

\tau_{1}\ \frac{\mathrm{d}C_{L u n s t}}{\mathrm{d}\tau},+,C_{L u n s t}\ =\ \sum_{i,=,0}^{n},\sum_{j,=,0}^{n-i}A_{i j}\alpha^{i},\dot{\alpha^{\ j+1}}

  

# 观测方程  

C_{L m};=;C_{L s t}\left(,\alpha,\right);+;\left(,C_{L q},^{\bullet};+;C_{L\dot{\alpha}},^{\bullet},\right)q;\frac{c_{A}}{2,V};+;C_{L u n s t};+;\varepsilon_{1}

  

下标“ $_m$ ”表示测量值。  

由于只有一个观测量，且不考虑过程噪声，似然准则等价于最小二乘准则  

J(,\pmb\theta);=;\frac{1}{N}\sum_{i,=,1}^{N},[,C_{L}(,t_{i},);-;C_{L m}(,t_{i},),]^{2}

  

未知参数的最大似然估计 $\pmb{\hat{\theta}}$  

\hat{\pmb{\theta}},=,\mathrm{ARG}_{\scriptscriptstyle{\theta\in\vartheta}}J(\pmb{\theta})

  

采用牛顿-拉夫逊算法从 $\pmb{\theta}$ 的某一组初值出发,迭代求解之。在牛顿-拉夫逊算法中，待估计参数的修正公式为  

{\pmb\theta}^{(k+1)};=;{\pmb\theta}^{(k)};-;\left(\frac{\partial^{2}{\cal J}}{\partial{\pmb\theta}^{2}}\right)^{-1}\frac{\partial{\cal J}}{\partial{\pmb\theta}}

\frac{\partial J}{\partial\theta_{l}},=,\frac{2}{N}\sum_{i,=,1}^{N},[,C_{L}(,t_{i},),-,C_{L m}(,t_{i},),],,\frac{\partial C_{L}}{\partial\theta_{l}}

\frac{\partial^{2}J}{\partial\theta_{k}\partial\theta_{l}},=,\frac{2}{N}\sum_{i,=,1}^{N},\frac{\partial C_{L}}{\partial\theta_{k}},\frac{\partial C_{L}}{\partial\theta_{l}}

  

灵敏度方程组为  

\begin{array}{r l}{\displaystyle\frac{\mathrm{d}}{\mathrm{d}\tau},\frac{\partial C_{L u n s t}}{\partial\tau_{1}},=\displaystyle\frac{1}{\tau_{1}}\bigg[-,\frac{\partial C_{L u n s t}}{\partial\tau_{1}},+,C_{L u n s t},\mathrm{-}}&{}\ {\displaystyle\sum_{i=0}^{n},\sum_{j,=,0}^{n-i}A_{i j}\alpha^{j}\dot{\alpha}^{{j}+1},\bigg]}\end{array}

\frac{\mathrm{d}}{\mathrm{d}\tau},\frac{\partial C_{L u n s t}}{\partial A_{i j}},=\frac{1}{\tau_{1}}\bigg[-,\frac{\partial C_{L u n s t}}{\partial A_{i j}},+,\alpha^{i},\dot{\alpha^{'j+1}}\bigg]

(,i,=,0,,1,,\cdots,n,;j,=,0,,1,,\cdots,n,-,i,)

  

积分初值均为零。  

牛顿-拉夫逊算法要求参数的初值在其真值附近。为此,可将模型辨识或频域多元线性回归获得的参数最小二乘估计值作为最大似然辨识算法的参数初值。  

当测量数据始于小攻角或静止状态时,非定常效应很小甚至不存在,式(10-327)的积分初值可取为零;否则,积分初值 $C_{L u n s t}(0)$ 应作为未知参数参加辨识。如果同时处理K次试验数据，则需增加  

![](images/671960c00014724f14ce4c903b2665ede951fd45872dfa496f1e6ab17752bac3.jpg)  
图10-16F-18非定常气动力辨识结果与风洞试验数据的比较  

……静态试验；·动态试验；-辨识结果；…….文献[16]的结果。  

$K$ 个未知参数 $C_{L u n s t}^{(k)}\left(0\right)\left(k=1,2,\cdots,K\right)$ ,，相应地,灵敏度方程组也要增加 $K$ 个方程  

\frac{\mathrm{d}}{\mathrm{d}\tau},\frac{\partial C_{L u n s t}}{\partial C_{L u n s t}^{(k)}(0)},=,\frac{1}{\tau_{1}}\bigg[\frac{\partial C_{L u n s t}}{\partial C_{L u n s t}^{(k)}(0)}\bigg]\quad(,k,=,1,,2,,\cdots,K,)

  

积分初值  

$\left.\frac{\partial C_{L u n s t}}{\partial C_{L u n s t}^{(k)}(0)}\right|_{t=0}=\left\{\begin{array}{l l}{{\bf l}}\\ {{\bf\zeta}}\\ {{\bf\zeta}}\end{array}\right.$ 对于第 $k$ 次试验$(\,k\;=\;1,2,\cdots,K\,)$ 对于其他次试验  

图10-16给出采用上述方法对 ${\bf F}^{-18}$ 大振幅振荡风洞试验数据辨识非定常气动力数学模型与实测数据的比较，图中虚线还给出了文献[16］用阶跃相应函数方法建模的结果，三者的一致性较好。  

# 参考文献  

1蔡金狮.飞行器气动参数辨识进展.力学进展，1987，17（4）：467一478  

2蔡金狮.动力学系统辨识与建模.北京：国防工业出版社，1991  

3蔡金狮等.飞行器系统辨识.北京：宇航出版社，1995  
4  Jategaonkar R V, Thielecke F. Evaluation of Parameter Estimation Methods for Unsta-ble Aircraft. Journal of Aircraft, 1994, 31(3): ${510\!\sim\!519}$   
5  Preissler H, Schaufele H. Equation Decoupling--A New Approach to the AerodynamicIdentification of Unstable Aircraft. Journal of Aircraft, 1991, 28(2): 146 -- 150  
6 Hamel P (Director). Rotorcraft System Identification. AGARD LS-178, 1991  
7  Kaletka J. Identification of Mathematical Derivative Models for the Design of a ModelFollowing Control System. AHS $45^{\mathfrak{t h}}$ Annual Forum Proceedings, 1989, 655 \~ 668  
8  Fu K-H, Kaletka J. Frequency-Domain Identification of BO 105 Derivative Models withRotor Degrees of Freedom. AHS $47^{\mathrm{th}}$ Annual Forum Proceedings, 1991, 3\~ 21  
9蔡金狮，张宏显，安遐令等.无控 $\texttt{K}$ 行器气动参数估值.空气动力学学报创刊号，1980,21 \~ 39  
10蔡金狮.再人体滚转共振与小不对称气动力.空气动力学学报，1985，3（3）： $72\!-\!81$   
11 Chapman G T,etc.根据运动分析确定物体的空气动力特性.蔡金狮译自 AD-713915，高超速气动技术专集，1973，（2）  
12蔡金狮，万宗国.自由飞弹道靶气动参数辨识.第七届跨声速流学术会议论文集，1995,72\~ 77  
13和争春，汪清,蔡金狮.自由振荡风洞试验动导数的应用问题研究.中国 2000 年飞行力学与飞行试验学术年会， $2000\,,\!237\!\sim\!244$   
14汪清，蔡金狮.飞机大攻角非定常气动力建模与辨识.航空学报，1996，17（4）：391～398  
15汪清.飞机大攻角非定常气动力建模及其应用研究［博士学位论文】.西安：西北工业大学，1994  
16 Hu C-C, Lan C E, Brandon J. Unsteady Aerodynamic Modeling for Maneuvering Air-craft. A1AA 93-3626, 1993  

# 第11章 惯性仪表误差系数辩识  

11.1概述  

为保证战略导弹命中预定目标，需要在主动段根据设计弹道对导弹进行制导。制导的基本原理是，制导系统依据从惯性测量装置采集到的有关导弹的飞行参数，由弹载计算机按发射前编排好的制导方程和方法进行导航计算，确定导引控制参数，使实际弹道与标准参考弹道一-致!1\~3],并确定关机时刻。制导过程中方法上的误差和测量装置的测量误差共同构成了弹道导弹的制导误差。  

制导系统的测量元件是惯性仪表，惯性仪表主要有两类，平台式和捷联式。对于平台一计算机式惯性导航系统，平台系统由平台台体、陀螺仪和加速度计构成，陀螺仪和平台为加速度计提供一个惯性测量基准坐标系。对导弹瞬时速度参数的获取由装在平台上的加速度计通过测量导弹三个方向上的视加速度来得到。由于平台系统在制造和安装上的原因，使平台系统在导弹飞行时出现偏移，导致测量基准偏离弹载计算机中的计算参考坐标系。同时，加速度计本身也存在测量误差，这些误差统称为惯性测量误差，又称之为制导工具误差[4.5]  

在所有造成落点偏差的因素中，制导工具误差是最主要的误差源,其造成的偏差占了落点总偏差的 $80\,\%$ 以上[6,7]。因而如何降低制导工具误差成为提高弹道导弹精度的主要课题和手段，减少该项误差可以大大提高导弹的命中精度。降低制导工具误差的手段和途径主要有两种，一是努力提高惯性测量元件的测量精度，即从机械加工和元件组装上降低各项误差因素，使对导弹运动参数测量准确。然而从机械加工上提高惯性器件的精度到一定程度之后,再进一步提高精度就非常困难8,需要花费巨大的人力物力,并且不能保证一定能提高惯性测量装置的测量精度。另一种途径就是对惯性测量器件的测量系统误差进行补偿，通过分析建立准确的误差数学模型，在导弹发射前将误差模型装人弹载计算机中,对测量参数进行修正或在导航计算中加以补偿[9\~12],进而修正制导工具误差，该方法较之第一种途径现实可行，而且有效。目前国内外均采用这种途径来补偿工具误差，经实践证明取得了良好的效果。该方法实施的关键是如何建立起工具误差的较为完备而准确的数学模型，如何对误差模型中的待求参数进行测定，以及如何验证数学模型的正确性。  

随着弹头向高精度方向的发展，制导系统逐渐采用静压液浮式平台系统，它的体积小、质量轻、精度高。该系统在平台台体上配有三个静压液浮单自由度积分陀螺仪，两个静压液浮陀螺加速度表,另外还装有三个石英挠性摆式加速度表l13，其中两个作为调平敏感元件，另一个则用来测量导弹的侧向视加速度。  

制导工具误差的误差源很多，大致可以分为静态误差和动态误差，动态误差与导弹系统的摇摆、角振动、线振动、温度、气压、时滞等众多因素有关，关于这些动态误差，其所涉及的环境函数难以找到，列出具体的误差表达式十分困难，因而通常采用对一些参数严格限制、导弹减振等措施来加以控制，使其产生的误差影响较小。对于先进战略导弹的平台系统，可不予考虑平台的动态误差，而主要针对平台系统的静态误差进行分析和补偿。  

制导工具误差的补偿是导弹精度工程中的重要课题，国外对此作了大量的分析和研究工作，取得了较好的成绩。其关键问题在于建立适当的误差模型，并通过大量的地面实验和飞行试验对误差系数进行分离。美国人针对此问题设计了一些地面实验方法和特殊弹道试验，主要有离心机试验，实验室实验，火箭机试验，普通弹道试验,特殊高弹道试验,低频振动试验[14]等,并且美国人发展了先进的高精度的测量设备，得到的数据质量和数量都很高。美国人对制导工具误差模型的考虑已先后超过84和170项因素[15.,16],在惯性平台系统的设计中采用了严格的控制措施对各种可能的动态误差进行了限制，使动态误差因素的作用小到可忽略不计。  

限于我国的经济条件和技术条件，要进行大量的地面或飞行试验是不现实的，尤其是飞行试验十分的稀少，摆在我国科研工作者面前的艰巨任务就是如何从有限的实验数据中建立起工具误差的模型并对误差系数进行分离。为了弥补原始数据的不足，必须深人开展误差系数分离方法的研究。  

误差模型的建立基于对惯性平台系统构成和物理原理的分析,考虑各种可能的干扰源，形成一定的模型。本章主要针对静压液浮式平台系统，进行误差模型和工具误差系数分离研究。  

# 11.2 制导工具误差一般模型  

制导工具误差由加速度表本身测量误差和测量坐标系偏离基准坐标系引起的误差构成，由于平台系统漂移的存在，基准坐标系实际上是计算机所用的计算系。设导弹飞行的真实视加速度为W,加速度表的测量误差为6W。，并设测量坐标系与惯性基准坐标系之间的欧拉角为（α，αy，α）,于是有平台系统测量的视加速度值  

\dot{\pmb{W}}{c};=;{\cal L}\left(,\alpha{x},,\alpha_{y},,\alpha_{z},\right),\dot{\pmb{W}};+;\delta\dot{\pmb{W}}_{a}

  

式中 L(α，αy，α）——两坐标系之间的转换矩阵，并有  

L\left(,\alpha_{x},,\alpha_{y},,\alpha_{z},\right),=,\left(\begin{array}{c c c}{{\cos\alpha_{y}\mathrm{cos}\alpha_{z}}}&{{,\sin\alpha_{z}\mathrm{cos}\alpha_{x},+,\sin\alpha_{x}\mathrm{sin}\alpha_{y}\mathrm{cos}\alpha_{z}}}&{{}}\ {{-,\cos\alpha_{y}\mathrm{sin}\alpha_{z}}}&{{,\cos\alpha_{z}\mathrm{cos}\alpha_{x},-,\sin\alpha_{x}\mathrm{sin}\alpha_{y}\mathrm{sin}\alpha_{z}}}&{{}}\ {{\mathrm{sin}\alpha_{y}}}&{{-,\cos\alpha_{y}\mathrm{sin}\alpha_{x}}}&{{}}\end{array}\right),+,h.c o s,+,h.c o s,+,h.c o s,-1,=,0.

\begin{array}{r l}&{\sin\alpha_{x}\mathrm{sin}\alpha_{z}\mathrm{-}\sin\alpha_{y}\mathrm{cos}\alpha_{z}\mathrm{cos}\alpha_{x}}\ &{\sin\alpha_{z}\mathrm{sin}\alpha_{y}\mathrm{cos}\alpha_{x}\mathrm{+}\cos\alpha_{y}\mathrm{sin}\alpha_{x}}\ &{~~~~~~~~~~~~~~~~\mathrm{cos}\alpha_{y}\mathrm{cos}\alpha_{x}}\end{array}

  

由于 $\alpha_{x}\,,\alpha_{y}\,,\alpha_{z}$ 均很小,用小角度近似并略去高阶小量,有  

L\left(\alpha_{x},,\alpha_{y},,\alpha_{z}\right)\approx\left(\begin{array}{c c c}{{1}}&{{\alpha_{z}}}&{{-\ \alpha_{y}}}\ {{-\ \alpha_{z}}}&{{1}}&{{\alpha_{x}}}\ {{\alpha_{y}}}&{{-\ \alpha_{x}}}&{{1}}\end{array}\right)

  

于是有  

\Delta\dot{W}{c};=;\left(\frac{}{}\frac{}{}I,-,I\right)\dot{W};+;\delta\dot{W}{a};=;{\bf}A\dot{W};+;\delta\dot{W}_{a}\qquad.

  

式中  

\Delta W_{c}=\pmb{W}_{c}-\pmb{W}

\textbf{\em A}=\left.\begin{array}{c c}{\left(\begin{array}{c c c}{0}&{\alpha_{z}}&{}&{-\alpha_{y}}\ {}&{}&{0}&{}\ {\alpha_{z}}&{0}&{}&{\alpha_{x}}\ {\alpha_{y}}&{-\alpha_{x}}&{}&{0}\end{array}\right)}\end{array}\right.

  

而定义欧拉角 $\boldsymbol{\alpha}=(\,\alpha_{x}\,,\alpha_{y}\,,\alpha_{z}\,)^{\textup T}$ 为基准角偏差,显然  

\pmb{\alpha}=\pmb{\alpha}{g}+\pmb{\alpha}{p}

  

下标“g"和“p”分别表示陀螺和平台偏移引起的偏差角，式（11-4）就是惯性平台系统测量误差的一般算式，换算成视速度差有  

\Delta W_{c}(,t,),=,\int_{0}^{t}A\left(,\tau,\right)\dot{{\pmb W}}(,\tau,)\mathrm{d}\tau,+\int_{0}^{t}\partial\dot{{\pmb W}}_{a}(,\tau,)\mathrm{d}\tau

  

从而测量系统测量误差静态模型取决于式（11-4)中 $\alpha_{g}\,,\,\alpha_{\hat{p}}\,,\,\delta{\dot{W}}_{a}$ 的形成机理和构式。  

# 11.2.1 加速度表误差  

加速度表有两种，一是静压液浮陀螺加速度表，一是石英挠性摆式加速度表。前者用于测量射面内即 x 和y方向的视加速度，后者用于对侧向视加速度的测量。  

静压液浮陀螺加速度表采用二自由度陀螺，其工作原理如图11-1所示,在陀螺输出轴上设置一偏摆质量 m，偏摆至输出轴距离为 $l$ ,则当导弹在输人轴方向以加速度 $\textbf{\em a}$ 作加速运动时,在输出轴上产生一外加力矩 $M_{0}=m l a$ ，由于 $M_{0}$ 的存在，需要通过电动机驱动陀螺外环轴,使之产生一陀螺进动力矩 $T_{0}$ ,使 $T_{0}+M_{0}\,{=}\,0$ ，从而让转子复位。  

![](images/be1f1353d1d250a4d204ba81eb2dcfdf3d05d1cf346061d2fc1cd72e81d69f4e.jpg)  
图 11-1 陀螺加速度计原理图  

设转子的角动量为 $H$ ,进动角速度为 $\pmb{\theta}$ ,有  

T_{0}\ =\ H\dot{\pmb{\theta}}\ =\ m l a

{a\ =\ \frac{H}{m l}{\not!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

  

而 $\theta$ 由测量用于驱动电动机的电压 $V$ 换算得到,令 $\theta=K_{V}V$ ,于是有  

{\boldsymbol{a}}\ ={\frac{H}{m l}}K_{V}{\boldsymbol{V}}

  

上式就是测得的导弹沿陀螺输人轴方向的加速度。  

当沿陀螺输出轴存在其他干扰力矩时，就使陀螺加速度计出现测量误差，设测量值为 $\acute{a}$ ，此时有  

m l a^{\prime}=H K_{V}V=m l a+\Delta M

a^{'},=,a,+,{\frac{1}{m l}}\Delta M

  

$\Delta M$ 中有系统性的干扰力矩以及随机性干扰力矩[6]。系统性干扰  

力矩主要可分为对加速度不敏感的力矩 $\Delta M_{0}$ 以及同导弹运动加速度有关的力矩 $\Delta M(\,a\,)$ 。研究表明[5.6],同加速度有关的力矩可写成加速度 $a$ 的多项式  

\Delta M(,a,),=,k_{1}^{,\prime}a,+,k_{2}^{,\prime}a^{2},+,\cdots

  

式中 $\boldsymbol{k}_{1}^{\prime},\boldsymbol{k}_{2}^{\prime},\cdots$ 为相应的系数,于是  

\Delta a;=;\frac{1}{m l}(,k_{0}^{\prime},+,k_{1}^{\prime}a,+,k_{2}^{\prime}a^{2},+,\cdots);+;\eta

  

写成  

式中 $k_{0}$ —表征与加速度无关的一些系统力矩引起的测量误差；  

n—表示随机干扰力矩引起的加速度测量偏差。  

式(11-15)中 $k_{0}$ 与陀螺系统的弹性力矩、磁性干扰力矩、浮液的涡流力矩、信号传感器偏差等因素有关；而 $k_{1}$ 与陀螺质心偏移引起的不平衡力矩有关； $k_{2}$ 则和陀螺转子轴轴向刚度不均匀引起的弹性变形造成的力矩有关，该项力矩与导弹加速度的二次方成正比。  

用于测量侧向加速度的石英挠性加速度计，其测量的加速度偏差可用下式表述7  

\Delta a_{z};=;k_{0},+,k_{1}a_{z};+;k_{2}a_{;z}^{;2};-;\delta_{!z}a_{x};+;\delta_{!x}a_{y};+;\eta

  

式中 $k_{0}$ 一代表测量加速度计的零偏值,它是机械零位与电气零位变化综合形成的；  

$k_{1}$ 一——考虑了加速度计的标度因素；  
$k_{2}$ 一考虑非线性项的作用；  
n——代表各种随机干扰因素的综合。  

严格地讲,若加速度计之 $\boldsymbol{z}$ 轴与平台 $\mathscr{z}$ 轴不重合，即存在加速度计轴系与平台轴系之间的欧拉角 $\hat{\delta}_{x}\,,\hat{\delta}_{y}$ ，此时，加速度计所敏感的加速度 $a_{z}$ 包含有 $\delta_{y}\,a_{x}$ 和 $\delta_{x}\,a_{y}$ 的分量，即  

a_{z}^{\prime};=;a_{z};-;\delta_{y},a_{x};+;\delta_{x},a_{y}

  

$\hat{\delta}_{x}\,{\setminus}\,\hat{\delta}_{y}$ 是小量,而 $a_{z}$ 本身也是小量， $\alpha_{x}$ 和 $\boldsymbol{a}_{\boldsymbol{y}}$ 较大,在 $\delta_{x}$ 较大时，$a_{z}$ 和 $-\,\delta_{x}\,a_{y}+\delta_{y}\,a_{x}$ 可能具有相同量级,相对而言容易引起较大的误差。综合上式，可写成  

\Delta a_{z};=;k_{0},+,k_{1}a_{z},+,k_{2}a_{,z}^{,2},+,k_{x},a_{x},+,k_{y},a_{y},+,\eta

  

对于 $_y$ 方向和 $\pmb{x}$ 方向加速度的测量，虽有测量轴对不准问题，但对不准引起的加速度附加分量与本轴加速度相比是小量，故可忽略不计。  

# 11.2.2 陀螺漂移误差  

静压液浮平台采用三个单自由度积分陀螺仪，陀螺仪的作用是迫使平台与陀螺转子角动量在空间方向保持一致，当陀螺承受到各种干扰力矩时，将使转子角动量发生进动，形成陀螺的漂移，使平台随之产生角度偏移。  

如图11-2,根据拉格朗日二类方程式  

\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial,T}{\partial,q_{s}}\right)-\frac{\partial,T}{\partial,q_{s}},\approx,Q_{s}

  

式中 4一一—广义坐标;$T$ 一系统总能量；  

![](images/50ab9e780f92072c8a39988781734b1b8b7cffc633c1f8127ac4c1512e1d63bc.jpg)  
图11-2单自由度陀螺仪原理简图  

在单自由度陀螺中,转子只有两个自由度，可用进动角 $\beta$ 和转子转动角 $\gamma$ 作为广义坐标，此时广义力 $Q_{s}$ 为 $M_{O A}$ 及 $M_{S A}$ ，下标OA表示输出轴，SA表示转子轴， $M_{O A}\setminus M_{S A}$ 分别表示沿输出轴和转子轴的干扰力矩。  

设内环相对 $O x y z$ 各轴之转动惯量为 $I_{b x}\,,I_{b y}\,,I_{b z}$ ,此时有内环动能  

T_{b};=;\frac{1}{2}\omega I_{b}\omega;=;\frac{1}{2},I_{b}{\bf\dot{\beta}}^{2}

  

对转子，设 $\boldsymbol{I_{c}}=(\,I_{c x}\,,I_{c y}\,,I_{c z}\,)^{\mathrm{T}}$ ,其角速度 $\pmb{\omega}_{c}$  

{\pmb{\omega}}_{c};=;{\pmb{\dot{\beta}}}i;+;{\pmb{\dot{\gamma}}}{\pmb{k}};=;(,{\pmb{\dot{\beta}}},,0,,{\pmb{\dot{\gamma}}},)^{\intercal}

  

于是有转子动能  

T_{c};=;\frac{1}{2},I_{c}\pmb{\dot{\beta}}^{2},+,\frac{1}{2},I_{c z}\pmb{\dot{\gamma}}^{2}

  

总动能  

T;=;T_{b};+;T_{c};=;\frac{1}{2}(;I_{b x};+;I_{c x},)\dot{\pmb{p}}^{2};+;\frac{1}{2},I_{c z}\dot{\pmb{y}}^{2}

  

代人式（11-19）,有  

\left{\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial,T}{\partial\dot{\pmb{\beta}}}\right)-\frac{\partial,T}{\partial\beta},=,M_{O A}}\ {\left.\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial,T}{\partial\dot{\pmb{\gamma}}}\right)-\frac{\partial,T}{\partial,\gamma},=,M_{S A}}\end{array}\right.

  

整理得  

\left{\left(\frac{\d I_{b x}}{\d I_{c z}}\right.+\left.I_{c x}\right)\ddot{\pmb{\beta}};=;M_{\mathrm{OA}}\right.

  

由上式可知，转子角动量的进动与沿输出轴的作用力矩直接相关。  

$M_{O A}$ 由各种力矩构成，包括阻尼力矩 $\mu\beta$ 、电磁力矩 $M_{\sun}$ 、涡流力矩 M涡、静不平衡力矩、弹性变形力矩等,其中静不平衡力矩可写成  

M_{s};=;k_{S A}\alpha_{S A};+;k_{I A}\alpha_{I A}

  

弹性变形不均匀力矩可写成  

\begin{array}{c}{{M_{e}{}^{-}:k_{S I}a_{S A}a_{I A}+k_{O S}a_{S A}a_{O A}+k_{I O}a_{I A}a_{O A}+}}\ {{{}}}\ {{k_{S A}^{'}a_{S A}^{2}+~k_{I A}^{'}a_{I A}^{2}}}\end{array}

  

另外，如果平台（即陀螺仪之基座）有绕输人轴的转动角速度$\omega_{y}$ 时，会产生陀螺力矩 $\sim H\omega_{y}$ ，把与加速度无关的 $M_{\sun}+M_{\sun}$ 用$\boldsymbol{k}_{0}$ 表示，于是（11-25）第一式变成  

(:I_{b x}:+:I_{c x}:):\dot{\pmb{\beta}}:+:\mu\dot{\pmb{\beta}}:=:H\omega_{y}:+:M_{s}:+:M_{c}:+:k_{0}

  

考虑稳态解， ${\pmb\beta}=0$ ,于是有  

\mu\dot{\boldsymbol{\beta}}:=:H\omega_{y}:+:M_{s}:+:M_{e}:+:k_{0}

  

分析 $H\omega_{y}$ 项，它是基座相对于陀螺输人轴存在转动引起的，显然平台组件由沿陀螺输出轴的加速度导致的静不平衡力矩和弹性变形不均匀力矩会产生转动，即  

\omega_{y},\sim,k_{\mathrm{OA}}\alpha_{\mathrm{OA}},+,k_{\mathrm{OA}}^{,^{\prime}}\alpha_{\mathrm{OA}}^{,2}

  

综合式（11-26）～式（11-30）,为方便计，仍用 $k$ 记各项系数，可把单自由度陀螺的漂移写成  

\beta,=k_{0},+,k_{S A}\alpha_{S A},+,k_{I A}\alpha_{I A},+,k_{O A}a_{O A},+,k_{S A}^{'}a_{S A}^{2},+,k_{I A}^{'}\alpha_{I A}^{2},+

k_{O A}^{\prime}a_{,,O A}^{,\prime}+k_{S I}a_{S A}a_{I A}+k_{S O}a_{S A}a_{O A}+k_{I O}a_{I A}a_{O A}+\eta

  

式中， $k_{\mathrm{()}A}a_{\mathrm{()}A}$ 及 $\dot{k}_{\mathrm{()}A}^{\mathrm{~\prime~}}a_{\mathrm{~\tiny~O/A}}^{2}$ 分别是由于平台在沿陀螺输出轴加速度引起的不平衡力矩和不等弹性力矩作用下，绕输人轴转动引起的陀螺力矩的作用，它们是有其严格的物理意义的，实际上是存在的。  

参考文献[7]认为该两项没有明确的物理含义，只是数学推导的结果，而在实际陀螺仪测试中陷人了矛盾，一方面认为从物理上它们没有意义，另一方面在测试中又发现了 $k_{O A}a_{O A}$ 的贡献18]。通过本文的分析发现，它们的贡献来源于其导致的基座转动，具有明确的物理含义，模型中应当予以保留。  

陀螺漂移还与摩擦力矩、温度漂移、动态漂移有关，在静压液浮平台系统中，摩擦力矩因采用了液浮技术而大大降低，温度漂移则采用恒温系统来加以控制,残余的随机因素用 $\pmb{\eta}$ 表示之。  

# 11.2.3 平台角偏差  

平台是陀螺仪和加速度计的载体，为加速度计提供测量惯性基准，主要的偏差是其初始偏差。  

平台初试角偏差由以下因素构成：平台台体的加工误差，该项误差可导致平台上三轴非严格正交，从而始终至少有一轴不能与惯性基准轴重合；陀螺和加速度表的安装误差，即陀螺和加速度表的三轴与平台三轴之间的角偏差；平台初始瞄准误差，这是在设置平台方位时与弹载计算机方位坐标轴系的差异，可用三个欧拉角描述；平台调平和方位锁定误差也将引起初始偏差。  

陀螺和加速度计各有三个，每个与平台基准坐标系之间因安装引起的角偏差都可能与其他仪表不同，此时的偏差角情况较为复杂,为简单记,把所有初始偏差用三个欧拉角表示，即 $\pmb{\alpha}_{\pmb{\hat{p}}x0}$ $\alpha_{\ensuremath{\,\!\,\!\,p\mathrm{v0}}}\,,\alpha_{\ensuremath{\,\!\,\!p z0}\,\!\circ}$  

除初始偏角外，平台各部分组件的质心偏移，在过载作用下，形成绕各轴的干扰力矩，使平台发生偏移，这些因素与过载是成正比的 $[13\sim16]$ ,同时，各组件的弹性形变不均匀也要产生质心偏移，其影响与过载的二次项成正比。另外，平台的稳定回路失调也会使平台产生偏移，它们与过载变化率和过载平方变化率成正比。  

平台静差最后可写成  

\left{\begin{array}{c}{\displaystyle{\alpha_{p x}=\alpha_{p x0}+k_{p x}^{\prime}\hat{W}{y}+k{p1x}^{\prime}\hat{W}{x}+k{p x}\hat{W}{z}+k{p x}\hat{W}{y}+}}\ {\displaystyle{k{p2x}^{\prime}\hat{W}{y}\hat{W}{z}+k_{p2x}\frac{\mathrm{d}\left(\hat{W}{x}\hat{W}{x}\right)}{\mathrm{d}t}}}\ {\displaystyle{\alpha_{p y}=\alpha_{p0}+k_{p1y}^{\prime}\hat{W}{x}+k{p1y}^{\prime}\hat{W}{z}+k{p x}\hat{W}{x}+k{p x}\hat{W}{x}+k{p x}\hat{W}{x}+}}\ {\displaystyle{k{p2y}^{\prime}\hat{W}{x}\hat{W}{z}+k_{p2y}\frac{\mathrm{d}\left(\hat{W}{x}\hat{W}{z}\right)}{\mathrm{d}t}}}\ {\displaystyle{\alpha_{p z}=\alpha_{p0}+k_{p1z}^{\prime}\hat{W}{x}+k{p1z}^{\prime}\hat{W}{y}+k{p z}\hat{W}{x}+k{p z}\hat{W}{y}+}}\ {\displaystyle{k{p2z}^{\prime}\hat{W}{x}\hat{W}{y}+k_{p2z}\frac{\mathrm{d}\left(\hat{W}{x}\hat{W}{y}\right)}{\mathrm{d}t}}}\end{array}\right.+

  

平台偏差中共有21个系数。  

而陀螺的误差与平台上各陀螺仪相对平台的取向有关，若按照图11-3的取向，陀螺的漂移可写成  

$\begin{array}{r}{\left\{\begin{array}{c}{\dot{\beta}_{g x}\,=\,k_{g0x}\,+\,k_{g11}\,\dot{W}_{z}\,+\,k_{g12}\,\dot{W}_{x}\,+\,k_{g13x}\dot{W}_{y}\,+\,k_{g x x z}\dot{W}_{x}\dot{W}_{z}\,+}\\ {k_{g x y z}\dot{W}_{y}\dot{W}_{z}\,+\,k_{g x x y}\dot{W}_{x}\dot{W}_{y}\,+\,k_{g x x}\dot{W}_{x}^{2}\,+\,k_{g x y}\dot{W}_{y}^{2}\,+\,k_{g x z}\dot{W}_{z}^{2}}\end{array}\right.\,.}\end{array}$ (11 -33)   
$\begin{array}{r}{\dot{\mathsf{\boldmath~\mu~}}_{g y}\;=k_{g0\,y}\,+\;k_{g11\,y}\dot{\mathsf{W}}_{z}\,+\;k_{g12\,y}\dot{\mathsf{W}}_{y}\,+\;k_{g13\,y}\dot{\mathsf{W}}_{x}\,+\,k_{g y x z}\dot{\mathsf{W}}_{x}\dot{\mathsf{W}}_{z}\,+\,}\\ {k_{g y y z}\dot{\mathsf{W}}_{y}\dot{\mathsf{W}}_{z}\,+\,k_{g y x y}\dot{\mathsf{W}}_{x}\dot{\mathsf{W}}_{y}\,+\,k_{g y x}\dot{\mathsf{W}}_{x}^{2}\,+\,k_{g y y}\dot{\mathsf{W}}_{y}^{2}\,+\,k_{g y z}\dot{\mathsf{W}}_{z}^{2}\,}\end{array}$ (11 -34)   
$\begin{array}{r l r}{\dot{\mathsf{\boldmath}}_{g z}\!\!\!}&{=k_{g0z}\,+\,k_{g11z}\dot{\mathsf{W}}_{y}\,+\,k_{g12z}\dot{\mathsf{W}}_{z}\,+\,k_{g13z}\dot{\mathsf{W}}_{x}\,+\,k_{g z x z}\dot{\mathsf{W}}_{x}\dot{\mathsf{W}}_{z}\,+}&\\ &{}&{\qquad\,k_{g z y z}\dot{\mathsf{W}}_{y}\dot{\mathsf{W}}_{z}\,+\,k_{g z x y}\dot{\mathsf{W}}_{x}\dot{\mathsf{W}}_{y}\,+\,k_{g z x}\dot{\mathsf{W}}_{x}^{2}\,+\,k_{g z y}\dot{\mathsf{W}}_{y}^{2}\,+\,k_{g z z}\dot{\mathsf{W}}_{z}^{2}}\end{array}$  

![](images/9fe8d08b748ca1ceb11757cd83e9d4de4795a8885fa86ab4f93496185fee325f.jpg)  
图 11-3静压液浮单自由度陀螺仪与平台安装示意图$O$ -——输出轴， $H$ 一转子轴， $I$ 一—输人轴）  

由此引起的角偏移为  

\alpha_{g i}(,t,);=\int_{0}^{t}!\dot{\pmb{\beta}}_{g i}\mathrm{d},\tau\qquad(,i;=;x,,y,,z,)

  

加速度计的误差模型可写成  

\left{\begin{array}{l l}{\delta\dot{W}{x},=,k{a0x},+,k_{a1x}\dot{W}{x},+,k{a2x}\dot{W}{x}^{2},+,\eta{x a}}\ {\delta\dot{W}{y},=,k{a0y},+,k_{a1y}\dot{W}{y},+,k{a2y}\dot{W}{y}^{2},+,\eta{x a}}\ {\delta\dot{W}{z},=,k{a0z},+,k_{a1z}\dot{W}{z},+,k{a2z}\dot{W}{z}^{2},+,\eta{z a}}\end{array}\right.

  

根据式（11-4）,结合式（11-32）～式（11-37），假设各模型中之系数 $k$ 为常量，误差模型可写成  

\Delta\dot{\pmb{W}}_{c};=;\pmb{S}\pmb{C},+,\pmb{\eta}

  

式中 $\pmb{C}$ —误差系数 $k$ 之集合；  

$\pmb{S}$ --相应的灵敏度函数矩阵；  
n——各项随机误差之和。  

关于 $\pmb{S}$ 和 $\pmb{C}$ 各分量的情况参见附表A1。  

\begin{array}{r l}&{:({\cal k}{a0x},{\cal k}{a0y},{\cal k}{a0z},{\cal k}{a1x},{\cal k}{a1y},{\cal k}{a1z},{\cal k}{a2x},{\cal k}{a2y},{\cal k}{a2z},}\ &{{\cal k}{g0x},{\cal k}{g0y},{\cal k}{g1z},{\cal k}{g11x},{\cal k}{g11y},{\cal k}{g11z},{\cal k}{g12x},{\cal k}{g12y},{\cal k}{g12y},}\ &{{\cal k}{g13x},{\cal k}{g13y},{\cal k}{g13z},{\cal k}{g1x z},{\cal k}{g8x z},{\cal k}{g8x z},{\cal k}{g8x y},{\cal k}{g8y z},{\cal k}{g8y z},}\ &{{\cal k}{g a x y},{\cal k}{g a x y},{\cal k}{g a x y},{\cal k}{g a x y},{\cal k}{g a x},{\cal k}{g a x y},{\cal k}{g a y},{\cal k}{g a y},}\ &{{\cal k}{g a y},{\cal k}{g a x},{\cal k}{g a x},\alpha_{p y0},\alpha_{p0},\alpha_{p0},{\cal k}{p1x},{\cal k}{p1y}^{\prime},{\cal k}{p1z}^{\prime},}\ &{{\cal k}{p1x}^{\prime\prime},{\cal k}{p1y}^{\prime\prime},{\cal k}{p1z}^{\prime\prime},{\cal k}{p2x},{\cal k}{p2x},{\cal k}{p2x y},{\cal k}{p2y},{\cal k}{p2y},}\ &{{\cal k}{p2z}^{\prime\prime},{\cal k}{p2y}^{\prime},{\cal k}{p2z}^{\prime\prime},{\cal k}{p2x},{\cal k}{p2y},{\cal k}_{p2z},1^{\prime\prime}}\end{array}

  

# 11.2.4 误差模型  

模型式（11-38）中，误差项达60项之多，在应用上不但不方便，地面测试中也不可能得到所有各项系数的测量值，必须对模型进行筛选，忽略影响很小的项，保留较为显著的项。对于不同的惯性平台系统，所采用的模型可能不一样，需根据具体情况确定实用的误差模型，使模型项数尽可能少，又能充分表征测量误差的特性。  

实用模型的确定，需根据地面试验中对各误差系数的标定情况或设计指标值，结合飞行试验弹道特性来分析得到。  

一般飞行试验弹道或作战任务飞行时，导弹主要沿射面内飞行，其侧向视加速度和视速度分量 $\dot{W}_{z}\,,W_{z}$ 相对而言很小，第一步可将与之有关的误差项忽略不计，这样，对加速度表可简化成  

\left{\begin{array}{l}{\delta\dot{W}{x},=,k{a0x},+,k_{a1x}\dot{W}{x},+,k{a2x}\dot{W}{x}^{2}}\ {\delta\dot{W}{y},=,k_{a0y},+,k_{a1y}\dot{W}{y},+,k{a2y}\dot{W}{y}^{2}}\ {\delta\dot{W}{z},=,k_{a0z}}\end{array}\right.

  

陀螺仪表的漂移可简化成  

\left{\begin{array}{l}{{\dot{\beta}{g x},=,k{g0x},+,k_{g12}\dot{W}{x},+,k{g13x}\dot{W}{y},+,k{g x x y}\dot{W}{x}\dot{W}{y},+}}\ {{\qquad\quad,k_{g x x}\dot{W}{x}^{2},+,k{g x y}\dot{W}{y}^{2}}}\ {{\dot{\beta}{g y},=,k_{g0y},+,k_{g13y}\dot{W}{x},+,k{g12y}\dot{W}{y},+,k{g x y}\dot{W}{x}\dot{W}{y},+}}\ {{\qquad\quad,k_{g y x}\dot{W}{x}^{2},+,k{g y y}\dot{W}{y}^{2}}}\ {{\dot{\beta}{g z},=,k_{g0z},+,k_{g11z}\dot{W}{y},+,k{g13z}\dot{W}{x},+,k{g z x y}\dot{W}{x}\dot{W}{y},+}}\ {{\qquad\quad,k_{g z x}\dot{W}{x}^{2},+,k{g z y}\dot{W}_{y}^{2}}}\end{array}\right.

  

平台角偏差可初步简化成  

\left{\begin{array}{l}{\alpha_{\beta x},=,\alpha_{\beta x0},+,k_{\beta1x}^{\prime}\dot{W}{y},+,k{\beta x y}\dot{W}{y}}\ {\alpha{\beta y},=,\alpha_{\beta y0},+,k_{\beta1y}^{\prime}\dot{W}{x},+,k{\beta y x}\ddot{W}{x}}\ {\alpha{\beta z},=,\alpha_{\beta z0},+,k_{\beta1z}^{\prime}\dot{W}{x},+,k{\beta1z}^{\prime}\dot{W}{y},+,k{\beta z x}\ddot{W}{x},+,k{\beta z y}\ddot{W}{y},+}\ {\qquad k{\beta2z}^{\prime}\dot{W}{x}\dot{W}{y},+,k_{\beta2z},\frac{\mathrm{d}\bigl(\dot{W}{x}\dot{W}{y}\bigr)}{\mathrm{d}t}}\end{array}\right.

  

模型的进一步简化可利用设计指标，计算各项产生的视速度差大小及对引起落点散布偏差的量级进行分析，保留模型中最主要的项。在进行参数估计之前进行模型简化，大大有利于误差系数的分离，否则要花费大量的时间进行模型辨识，而且模型辨识的结果不一定很好。  

式（11-40）一式(11-42)中相应的 $\pmb{S}$ 和 $\pmb{C}$ 参见附表 $\mathbf{A}2_{\circ}$  

# 11.3 误差系数估计  

惯性平台系统制导工具误差包含有随机误差和系统误差，由于对平台系统的不断改进和完善，使系统误差与随机误差之比越来越大[13,4] ,有的甚至高达 20 倍。这就使工具误差补偿有意义和切实可行。误差补偿的关键是建立足够准确的误差模型，以便通过弹载计算机进行实时的恰当的补偿，从而提高导弹的制导精度。一方面，误差模型以及模型系数需要通过大量的地面试验和理论研究来建立和确定,另一方面必须通过飞行试验来辨识飞行条件下的误差系数,检验地面试验给出的模型,并确定天地关系是否一致。只有二者一致的模型才是正确模型，才能用于精度补偿，而对于天地关系不一致的情形，则必须认真分析不一致的原因，对误差模型进行重构建模，最后达成天地关系一致。  

# 11.3.1 工具误差的试验  

战略导弹在发射前，需在地面测试间对平台制导系统的误差进行测试，分离主要的误差系数，对各项误差系数进行标定，以获得工具误差的地面测试信息，供天地关系分析使用。目前，地面试验方法有离心机试验、重力场静态翻滚试验、火箭机试验、低频振动试验[18]等测试方法,其中最常用的是重力场静态翻滚试验,其他方法需要昂贵的硬件投资。  

对陀螺加速度表的误差  

\Delta\dot{W}{a};=;k{a0},+,k_{a1},\dot{W};+;k_{a2},\dot{W}^{2}

  

目前主要采用正倒置试验法和六位置翻转试验法对零次和-次项系数进行测试[13,4]。测量是在一个“ $g^{\,\ast}$ 的重力场中进行。现有测试方法中，正倒置试验法对 ${\dot{R}}_{a0}\,,{\dot{R}}_{a1}$ 两项系数的测量有效,在生产线上得到了推广和应用。六位置翻转试验法对 $\pmb{k}_{a1}$ 项系数的测量较为有效，对于 $k_{a0}$ ，由于测量中引人了间隙影响，有一定误差。同时，间隙的影响掩盖了二次项的作用，对二次项及以上的非线性项的测量不可靠，数据不能使用。  

对石英挠性加速度表的误差测量，则采用四位置翻滚试验法对其各项系数进行测试和标定。目前的测试仍然集中在对模型中的零次项和一次项系数的标定[15]。  

在国内，关于加速度计的测量误差的地面试验，由于没有高精度的试验设备和方法，对于二次项以上的非线性系数的测量缺乏有效的手段进行测量和标定。因此地面试验数据中一般只包括${k_{a0},k_{a1}}$ 的测量值,而 $k_{a2}$ 只有设计指标值。  

对静压液浮陀螺漂移的测试采用六位置法和 $D$ _最优定位翻滚测试法16]来测试和标定陀螺漂移中的零次项和一次项,关于与过载二次方有关的误差系数的标定技术还有待于研究。虽然 $D$ 最优定位翻滚测试法原则上可以测量二次项,但由于在一个 $"_{g}"$ 的重力场中进行测量，其测量结果不准确，因而通常仅给出设计指标值。  

基于测试手段的原因，对平台角偏差的测试仅限于对调平和方位锁定精度的测试，而对于同过载相关的项一般给出设计指标值。  

由于上述的原因，地面试验数据中主要包括平台系统各个部件的常值偏差和与过载成比例的一次项系数，二次项以上的误差系数的地面测量数据是相当有限的。  

由于地面试验环境同实际飞行中的环境相差较为悬殊，要确切地知道各惯性仪表在飞行环境下的误差系数，还有赖于实际飞行试验条件下的误差系数辨识。因此，必须进行飞行试验。飞行试验有普通弹道试验和有利于误差辨识的各种形式的特殊弹道试验，后者包括早期的用于制导系统鉴定的垂直弹道飞行试验，以及惯性仪表最佳定向飞行试验和特殊高弹道试验。  

# 11.3.2  工具误差的观测方程  

飞行试验中导弹的状态参数由外弹道测量系统测量得到，外测数据中包含有站址测量误差、电波折射误差、时间不同步误差、随机误差及其他误差[1,17]。外测数据要通过一系列处理措施,如电波折射误差修正、站址测量误差修正、数据相容性检验、野值剔除、截断误差修正等，最后得到用于制导工具误差辨识的外测数据。  

导弹在飞行中制导系统的测量值是通过遥测系统测量的，遥测数据包括加速度计输出的视加速度、弹载计算机的导航输出、各分系统的参数等等。加速度计的输出包含了导弹飞行中的真实视加速度、工具误差和遥测系统的测量误差三部分。遥测系统的测量误差包括有起飞零点偏差、遥测取数时间偏差和随机误差。  

对遥测和外测数据进行必要的处理后，把遥测量和外测量换算到同-个参考系，将二者相减，就是惯性仪表的测量误差和遥外测测量噪声，其中的加速度测量数据或位置参数可用做误差辨识的观测值。  

\mathbf{y}=W_{\mathcal{H}\times\overline{{\mathcal{H}}}}-W_{\mathcal{B}\overline{{\mathcal{B}}}}=\Delta W~+\pmb{\eta}=S C+~\xi

  

上式即为工具误差辨识问题的观测方程或称为回归方程。  

# 11.3.3 工具误差辨识难题  

国内外采用的误差模型主要为线性静态模型[2-6],对于系统的动态误差，一方面其机理不够清楚，建立不起适当的表述式，另一方面，即或是能建立一定的表述式，但却给不出测量值来。由于动态因素的复杂性，对于动态误差因素的考虑和分离，需要进行复杂的试验和测量以得到必要的数据。在国内，由于试验条件和试验手段的限制，目前，一般不分离动态误差项，主要通过采取严密的限定措施如液浮、减振和恒温控制等办法来使动态因素的作用最小[ 7,8]  

在上节已推导出辨识问题的一般误差模型如下式  

\Delta\Psi;=;S C;+;\xi

  

式中△W一—惯性平台系统的测量误差矢量,作为观测矢量；  

$\pmb{S}$ 一—一环境函数矩阵；  
$\pmb{C}$ 一一一误差系数矢量；  
$\xi$ 一测量中的随机噪声。  

在飞行试验中，分别通过遥测和外测得到导弹的状态参数，由于外测数据具有较高的精度，对其进行必要的处理后，其与遥测数据的差作为辨识问题的观测数据。  

辩识问题就是从由飞行试验中得到的遥外测试验数据中求得误差系数矢量C的估计值C。如果所用线性模型合适，就是典型的线性模型参数估计问题。将式（11-43)写成更一般的形式  

,\mathbf{y};=;\pmb{X}\pmb{\theta};+;e

  

式中， ${\mathfrak{y}}\in R^{m\times1}$ ： $\pmb{X}\in R^{m^{\times}\,\dot{p}}$ $\pmb\theta\in R^{p\times1}$ $\pmb{e}\in R^{m\times1}$ ，且 $e\sim N$ (0,${\sigma}^{2}{\boldsymbol{B}}\,)\,,{\pmb{B}}$ 正定； ${\mathfrak{y}}\,.{\pmb{\mathfrak{X}}}$ 分别为可观测的矢量和系数矩阵； ${\pmb\theta}$ 为待估计参数矢量。  

按照估计理论有 $\pmb{\theta}$ 的最小二乘估计 $\hat{\pmb{\theta}}_{L S}$  

\hat{\pmb{\theta}}_{L S}:=:(\pmb{X}^{\mathrm{T}}\pmb{B}^{-1}\pmb{X})^{-1}\pmb{X}^{\mathrm{T}}\pmb{B}^{-1},\mathbf{y}

  

众所周知， $\hat{\pmb{\theta}}_{L S}$ 是无偏的,且方差最小。对于一般的估计问题, $\pmb{\hat{\theta}}_{L S}$ 给出令人满意的结果，但对于病态问题， $\hat{\pmb{\theta}}_{L S}$ 结果则相当差。上式进一步可写成  

\hat{\pmb{\theta}}_{L S};=;\pmb{\theta};+;\left(\pmb{X}^{\operatorname{T}}\pmb{B}^{-1}\pmb{X}\right)^{-1}\pmb{X}^{\operatorname{T}}\pmb{B}^{-1}\pmb{e}

  

如果环境函数矩阵 $\pmb{X}$ 存在复共线性，则 $\pmb{X}^{\mathrm{T}}\pmb{B}^{\mathrm{~-~}1}\pmb{X}$ 近似奇异，具有广泛的特征值谱，条件数极大，呈现严重的病态。表11-1给出了一个特征值分布的例子，其最大特征值与最小特征值之间相差12个量级。  

表 11-1 回归矩阵特征值表  


<html><body><table><tr><td>序号</td><td>特征值</td><td>序号</td><td>特征值</td><td>序号</td><td>特征值</td><td>序号</td><td>特征值</td></tr><tr><td>I</td><td>0.6367E + 05</td><td>6</td><td>0.2711E+ 02</td><td>11</td><td>0.9240E -01</td><td>15</td><td>0.1581E - 04</td></tr><tr><td>2</td><td>0.9272E + 04</td><td>7</td><td>0.6314E + 01</td><td>12</td><td>0.5480E -01</td><td>16</td><td>0.8247E - 05</td></tr><tr><td>3</td><td>0.6426E + 03</td><td>8</td><td>0.2423E + 01</td><td>13</td><td>0. 1341E - 01</td><td>17</td><td>0.1154E - 05</td></tr><tr><td>4</td><td>0.1014E + 03</td><td>9</td><td>0.4704E + 00</td><td>14</td><td>0.2189E - 02</td><td>18</td><td>0.3134E - 05</td></tr><tr><td>5</td><td>0.9822E + 02</td><td>10</td><td>0. 1757E + 00</td><td>15</td><td>0.1581E - 04</td><td>19</td><td>0.4576E - 06</td></tr></table></body></html>  

# 由于 $X^{\mathrm{T}}{\pmb{\mathscr{B}}}^{-1}{\pmb{X}}$ 对称,存在正交矩阵 $P$ 使  

$P^{\mathrm{T}}(\,{\bf X}^{\mathrm{T}}{\cal B}^{\,-1}{\cal X})\,P\;=\;{\cal A}\;=\;\mathrm{diag}(\,\lambda_{1}\,,\lambda_{2}\,,\cdots,\lambda_{\rho}\,)$ (11 - 47)其中， $\lambda_{1}\geq\lambda_{2}\geq\cdots\geq\lambda_{p\circ}$ 矩阵条件数定义为  

\operatorname{Cond}(A);=;\lambda_{1}/\lambda_{p}

  

对病态情况，在线性方程求解问题  

{\pmb{\ A}}{\pmb{x}}\ =\ {\pmb{b}}

  

式中，如果右端项b有一微小的误差，将导致解x严重偏离问题真解 $\pmb{x}_{\iota r}^{\{23\}}$ 。在估计问题中，由于随机噪声的存在，必然使 $\pmb{\hat{\theta}}_{L S}$ 远  

442  

离真值 $\pmb{\theta}$ 。考察 $\pmb{\hat{\theta}}_{L S}$ 的欧氏长度  

\begin{array}{r l}{\textbf{\emph{E}}|\hat{\textbf{\em{\theta}}}{L S}}|{\mathrm{2}}=\textbf{\em{E}}|\left(\textbf{\em{\theta}}+(\textbf{\em X}^{\mathrm{T}}\pmb{B}^{\mathrm{-1}}\pmb{X})^{\mathrm{-1}}\pmb{X}^{\mathrm{T}}\pmb{B}^{\mathrm{-1}}e\right)^{\mathrm{T}}\times}&{}\ {\left[\pmb{\theta}\right.+\left.\left(\textbf{\em X}^{\mathrm{T}}\pmb{B}^{\mathrm{-1}}\pmb{X}\right)^{\mathrm{-1}}\pmb{X}^{\mathrm{T}}\pmb{B}^{\mathrm{-1}}e\right]\updownarrow\ =}&{}\end{array}

\parallel\theta\parallel_{2}+\sigma^{2}\sum_{i=1}^{p}{\frac{1}{\lambda_{i}}}

  

因此，当存在某些 $\lambda_{i}{\approx}0$ 时， $\hat{\pmb{\theta}}_{L S}$ 大大偏离 $\pmb{\theta}$  

制导工具误差系数分离，正是这样一种病态问题，传统的最小二乘估计 $\pmb{\hat{\theta}}_{L S}$ 对噪声异常敏感，严重不稳定，远远偏离系统真值。为了获得较好的误差系数分离结果，直观的办法是改进环境函数矩阵的特性，使病态减轻或消除病态，这主要是通过各种特殊弹道飞行试验，来逐步分离出误差系数，美国人采用了这种途径，取得了满意的结果[15]。在我国，由于资金和手段上的原因,无法进行大量的飞行试验，只能靠有限的飞行试验数据分析和处理。因此需要采用有偏估计或子集求取的办法，目前流行的有偏估计方法有超椭球估计、压缩估计、岭估计、主成分估计、特征根估计、贝叶斯估计以及各种带约束的最小二乘估计 $[\,\mathbf{16}\!\sim\!23\,,\,\,\mathbf{44}\!\sim\!50\,]$ 等等。这些方法都试图对最小二乘估计进行改进，其根本的出发点是寻求比最小二乘估计 $\pmb{\partial}_{L S}$ 更接近参数真值 ${\hat{\pmb{\theta}}}_{0}$ 的估计值 $\pmb{\hat{\theta}}$ ，即寻求 $\hat{\pmb\theta}$ ,使  

\mathrm{MSE}(,\hat{\pmb{\theta}},),=,E,,|!|,,\hat{\pmb{\theta}},-,\pmb{\theta},,|!|,^{2}\leqslant\mathrm{MSE}(,\hat{\pmb{\theta}}_{L S},),=

E\parallel\hat{\pmb{\theta}}_{L S}\sim\pmb{\theta}\parallel^{2}

  

对于工具误差辨识，国内认为较好的方法有主成分方法及其改进方法，基于验前信息的贝叶斯估计以及二者的结合方法PB回归法，即主成分贝叶斯估计方法。然而，参考文献[21指出，现有的有偏估计方法，无论从估值或从预测的角度看，不存在一种一致优于另外其余方法的有偏估计或子集选择技术。  

# 11.3.4 仿真应用算例  

利用仿真得到的观测数据和环境函数矩阵，用某发弹工具误差系数的地面测试值进行仿真估计计算。估计方法分别采用正交最小二乘估计（OLSE），主成分估计（PCE)和PB估计方法。  

工具误差模型采用第11.3.2节确定的线性模型的简化模型，因得到的视加速度测量误差包含 $x\setminus y\setminus z$ 三个方向的分量。在估计中将三个方向进行单独处理，这样可以大大减少模型项数。在所采用的20项误差模型中， $x\setminus y$ 方向各含8项， $\mathcal{z}$ 方向含9项。仿真中随机噪声 $e$ 的方差分别取0.01,0.02和0.05。估计结果见表11-2\~表11-5。  

表11-23种方法估计结果比较（无噪声情况）  


<html><body><table><tr><td></td><td>C;</td><td>真值</td><td>范围</td><td>OLSE</td><td>PCE</td><td>PB1</td><td>PB2</td></tr><tr><td>1</td><td>ka0x</td><td>0.87016</td><td>0.74031 ~1.0</td><td>0.87058</td><td>. 45683</td><td>0.87016</td><td>0.94252</td></tr><tr><td>2</td><td>kaoy</td><td>0.88434</td><td>0.76869-- 1.0</td><td>0.88747</td><td>1.7828</td><td>0.8 88434</td><td>0. 96928</td></tr><tr><td>3</td><td>ka0z</td><td>- 0.86085 一</td><td>-1~ -0.72171</td><td>0.86087</td><td>-0.061504 一</td><td>-0.86085</td><td>-0 0.94156</td></tr><tr><td>4</td><td>kalr</td><td>0</td><td>-1~1</td><td></td><td>3.7084</td><td>0.00001</td><td>- 0.07194</td></tr><tr><td>5</td><td>kaly</td><td>0</td><td>-1~1</td><td></td><td>1.4856</td><td>一 -0.00001</td><td>-0 0.11292</td></tr><tr><td>6</td><td>ka2x</td><td>0</td><td>-1-1</td><td></td><td>-1.7743</td><td>0.00000</td><td>-0. .01901</td></tr><tr><td>7</td><td>ka2y</td><td>0</td><td>-1~1</td><td></td><td>1.1118</td><td>1 - 0.00001</td><td>-0 04822</td></tr><tr><td>8</td><td>kg01</td><td>0.84839</td><td>0.69678 - 1</td><td>0.84832</td><td>.0185</td><td>0.84838</td><td>0.8 89764</td></tr><tr><td>9</td><td>kgOy</td><td>- 0.93790</td><td>- 1~ - 0.87580</td><td>0.93798</td><td>-0 0.53540</td><td>一 0.93790</td><td>0300</td></tr><tr><td>10</td><td>20#4</td><td>-0.84902</td><td>- 1 ~- -- 0.69804</td><td>-0.84905</td><td>-1 1.0186</td><td>一 -0.84901</td><td>-0. 89959</td></tr><tr><td>11</td><td>kg121</td><td>0.76161</td><td>0.52322~1</td><td>0.76175</td><td>0.27548</td><td>0.76161</td><td>0.8 80891</td></tr><tr><td>12</td><td>Rx12y</td><td>0.67386</td><td>0.34773- -1</td><td>0.67391</td><td>0.69530</td><td>0 0.67389</td><td>0.8 8 1 1355</td></tr><tr><td>13</td><td>kgllz</td><td>0.95 95851</td><td>0.91702 - 1</td><td>0.95844</td><td>1. 0710</td><td>0.95851</td><td>0548</td></tr><tr><td>14</td><td>kp0r</td><td>0.12112</td><td>- 0.75776 ~-1</td><td>0. 12058</td><td>3. .7590</td><td>0.12106</td><td>-0. 04036</td></tr><tr><td>15</td><td></td><td>0.29239</td><td>-0.41522~1 一</td><td>0.29208</td><td>0 55574 一</td><td>0.29241</td><td>0.38428</td></tr><tr><td>16</td><td>kp)2</td><td>0.40892</td><td>- 0.18215~ 1</td><td>0.40877</td><td>1.1869</td><td>0.40896</td><td>0.36178</td></tr><tr><td>17</td><td>kpix</td><td>0</td><td>[~1</td><td></td><td>- 12.286</td><td>0.00003</td><td>-0 07321</td></tr><tr><td>18</td><td>kp1y</td><td>0</td><td>-1-1</td><td></td><td>- 34.773</td><td>0.00001</td><td>0.01056</td></tr><tr><td>19</td><td></td><td>0</td><td>-1-1</td><td></td><td>2.8100</td><td>0.00001</td><td>-- 0.01060</td></tr><tr><td>20</td><td>k1=</td><td>0</td><td>-1~1</td><td></td><td>-2.5724</td><td>0.00003</td><td>-0.17289</td></tr></table></body></html>  

# 表 11-33种方法估计结果比较(噪声方差0.01)  

<html><body><table><tr><td></td><td>Ci</td><td>真值</td><td>范围</td><td>OLSE</td><td>PCE</td><td>PB1</td><td>PB2</td></tr><tr><td>1</td><td>ka0r</td><td>0.87016</td><td>0.74031~1.0</td><td>0.87326</td><td>0.45694</td><td>0.87022</td><td>0.94258</td></tr><tr><td>2</td><td></td><td>0.88434</td><td>0.76869 ~-1.0</td><td>0.91710</td><td>1.7844</td><td>0.88433</td><td>0.96927</td></tr><tr><td>3</td><td>ka0x</td><td>0.86085</td><td>-- 1 ~ -0.72171</td><td>-0.88822</td><td>- 0.060605</td><td>- 0.86079</td><td>0 0.94150</td></tr><tr><td>4</td><td>kal1</td><td>0</td><td>-1~1</td><td>'.</td><td>3.5150</td><td>0.00057</td><td>- 0.07137</td></tr><tr><td>5</td><td>kaly</td><td>0</td><td>-1~1</td><td></td><td>- 1.4087</td><td>一 - 0.00141</td><td>-0.11432</td></tr><tr><td>6</td><td>ka2r</td><td>0</td><td>-1~1</td><td></td><td>-1.0084</td><td>0.00020</td><td>-0.01881</td></tr><tr><td>7</td><td>ka2y</td><td>0</td><td>-1~1</td><td></td><td>0.91736</td><td>0.00076</td><td>-0.04897</td></tr><tr><td>8</td><td></td><td>0.84839</td><td>0.69678 ~ 1</td><td>0.86593</td><td>0452</td><td>0.84841</td><td>0.89766</td></tr><tr><td>9</td><td>Rgoy</td><td>-0.93790</td><td>- 1~ - 0.87580</td><td>1.0019</td><td>-0.55966</td><td>一 0.93789</td><td>1 0300</td></tr><tr><td>10</td><td>kg0x</td><td>-0.84902</td><td>- 1~ -- 0.69804</td><td>-0.85333</td><td>-1 .0180</td><td>一 -0.84938</td><td>- 0.89996</td></tr><tr><td>11</td><td>kg121</td><td>0.76161</td><td>0.52322~1</td><td>0.79926</td><td>0.25088</td><td>0.76152</td><td>0.80883</td></tr><tr><td>12</td><td>Rg12y</td><td>0.67386</td><td>0.34773- 1</td><td>0.80742</td><td>0.73425</td><td>0.67426</td><td>0.8 1392</td></tr><tr><td>13</td><td>R8llz</td><td>0.95851</td><td>0.91702~1</td><td>0. 96205</td><td>1.0714</td><td>0. 5850</td><td>05 5480</td></tr><tr><td>14</td><td>kp0x</td><td>0.12112</td><td>一 - 0.75776~ 1</td><td></td><td>3.7021</td><td>0. 12176</td><td>一 0 .03966</td></tr><tr><td>15</td><td>cOd4</td><td>-0.29239</td><td>-1~0.41522</td><td>**.</td><td>- 0.54803</td><td>0.2 .29227</td><td>0.38414</td></tr><tr><td>16</td><td>kp0</td><td>0.40892</td><td>- 0.18215~ 1</td><td>0.41071</td><td>1.1840</td><td>0. 40923</td><td>0.36204</td></tr><tr><td>17</td><td>kpix</td><td>0</td><td>-1-1</td><td></td><td>-12.302</td><td>0.00134</td><td>0 07184</td></tr><tr><td>18</td><td>kply</td><td>0</td><td>-1-1</td><td>**</td><td>-- 34.978</td><td>-0.00024</td><td>0.01031</td></tr><tr><td>19</td><td>kp1x</td><td>0</td><td>-1~1</td><td></td><td>2.7586</td><td>0.00039</td><td>→ - 0.01023</td></tr><tr><td>20</td><td>k1x</td><td>0</td><td>-1~1</td><td></td><td>-2.5538</td><td>0.00192</td><td>- 0.17100</td></tr></table></body></html>  

表 11-43种方法估计结果比较(噪声方差0.02)  


<html><body><table><tr><td></td><td></td><td>真值</td><td>范围</td><td>OLSE</td><td>PCE</td><td>PB1</td><td>PB2</td></tr><tr><td>1</td><td>ka0x</td><td>0.87016</td><td>0.74031-1.0</td><td>0.87637</td><td>0.45704</td><td>0.87027</td><td>0.94264</td></tr><tr><td></td><td>RaOy</td><td>0.88434</td><td>0.76869~ 1.0</td><td>0.95020</td><td>1.7861</td><td>0.88432</td><td>0.96926</td></tr><tr><td>3</td><td>ka0z</td><td>0.86085</td><td>-- 1~ -- 0.72171</td><td>-0.86842</td><td>-0.05970</td><td>-0.86074</td><td>-0.94144</td></tr></table></body></html>  

（续）  

<html><body><table><tr><td></td><td>C;</td><td>真值</td><td>范围</td><td>OLSE</td><td>PCE</td><td>PB1</td><td>PB2</td></tr><tr><td>4</td><td>kalr</td><td>0</td><td>-1~1</td><td></td><td>3.3216</td><td>0.0013</td><td>-0.07081</td></tr><tr><td>5</td><td>kaly</td><td>0</td><td>-1~1</td><td></td><td>-- 1.3318</td><td>- 0.00280</td><td>-0.11571</td></tr><tr><td>6</td><td>ka2r</td><td>0</td><td>-1~1</td><td></td><td>- 0.24246</td><td>0.00040</td><td>- 0.01862</td></tr><tr><td>7</td><td>ka2y</td><td>0</td><td>-1-1</td><td></td><td>0.72297</td><td>- 0.00151</td><td>-0.04972</td></tr><tr><td>8</td><td>Rx0r</td><td>0.84839</td><td>0.69678-1</td><td>0.87337</td><td>1. 0719</td><td>0.84843</td><td>0.8 89768</td></tr><tr><td>9</td><td></td><td>- 0.93790 1</td><td>-1~ - 0.87580</td><td>-0.98348</td><td>"0. 58391</td><td>一 - 0.93787</td><td>1.0300</td></tr><tr><td>10</td><td>Rx0x</td><td>- 0.84902</td><td>- 1~ - 0.69804</td><td>-0.85764</td><td>.0173</td><td>一 -0.84975</td><td>-0. 90033</td></tr><tr><td>11</td><td>kx12x</td><td>0.76161</td><td>0.52322-1</td><td>0.76329</td><td>0.22629</td><td>0.76144</td><td>0.8 80875</td></tr><tr><td>12</td><td>kg12y</td><td>0.67386</td><td>0.34773~1</td><td>0.77853</td><td>0.7 7321</td><td>0.67463</td><td>0.8 8 81429</td></tr><tr><td>13</td><td>kg1lz</td><td>0.95851</td><td>0.91702 -1</td><td>0. 96557</td><td>1. 0719</td><td>0.95850</td><td>1.0 05480</td></tr><tr><td>14</td><td>kp01</td><td>0.12112</td><td>- 0.75776 ~ 1</td><td></td><td>3.6451</td><td>12246</td><td>-0 03896</td></tr><tr><td>15</td><td>kp0y</td><td>0.29239</td><td>- 0.41522 ~ 1</td><td></td><td>- 0.54033</td><td>0.29213</td><td>0.38400</td></tr><tr><td>16</td><td>kp0x</td><td>0.40892</td><td>- 0.18215~ 1</td><td>0.41245</td><td>1.1811</td><td>0.40949</td><td>0.36231</td></tr><tr><td>17</td><td>kp1r</td><td>0</td><td>-1~1</td><td></td><td>- 12.317</td><td>0.00272</td><td>-0 .07046</td></tr><tr><td>18</td><td>kp1y</td><td>0</td><td>-1~1</td><td></td><td>- 35.183</td><td>一 0.00049</td><td>0.01006</td></tr><tr><td>19</td><td>k1x</td><td>0</td><td>-1~1</td><td></td><td>2.7071</td><td>0.00076</td><td>- 0.00986</td></tr><tr><td>20</td><td>k1z</td><td>0</td><td>-1~1</td><td></td><td>-2.5352</td><td>0.00381</td><td>- 0.16911</td></tr></table></body></html>  

表11-53种方法估计结果比较（噪声方差0.05)  


<html><body><table><tr><td></td><td>C;</td><td>真值</td><td>范围</td><td>OLSE</td><td>PCE</td><td>PB1</td><td>PB2</td></tr><tr><td></td><td>ka0x</td><td>0.87016</td><td>0. 74031 - 1.0</td><td>0.88569</td><td>0.45736</td><td>0.87045</td><td>0.94281</td></tr><tr><td>2</td><td>kaoy</td><td>0.88434</td><td>0.76869~ 1.0</td><td>1.0495</td><td>1.7911</td><td>0.88429</td><td>0.96923</td></tr><tr><td>3</td><td>20##</td><td>- 0.86085</td><td>- 1~ - 0.72171</td><td>-0.77301</td><td>- 0.05701</td><td>0.86057</td><td>-- 0.94127</td></tr><tr><td>4</td><td>kalr</td><td>0</td><td>-1~1</td><td></td><td>2.7415</td><td>0.00283</td><td>0.06911</td></tr><tr><td>5</td><td>kaly</td><td>0</td><td>-1~1</td><td></td><td>- 1.1010</td><td>- 0.00698</td><td>-0.11989</td></tr><tr><td>6</td><td>ka21</td><td>0</td><td>-1~1</td><td></td><td>2.0552</td><td>0.00099</td><td>0.01802</td></tr></table></body></html>  

（续）  

<html><body><table><tr><td></td><td>C;</td><td>真值</td><td>范围</td><td>OLSE</td><td>PCF</td><td>PB1</td><td>PB2</td></tr><tr><td>7</td><td>ka2y</td><td>0</td><td>-1-1</td><td></td><td>0.13980</td><td>-- 0.00376</td><td>- 0.05197</td></tr><tr><td>8</td><td>kg0x</td><td>0.84839</td><td>0.69678 - 1</td><td>0.91213</td><td>1.1519</td><td>0.84849</td><td>0.89775</td></tr><tr><td>6</td><td>kx0y</td><td>-- 0.93790</td><td>0.87580 1</td><td>0.93128</td><td>- 0.65668</td><td>-0.93784</td><td>-1.0300</td></tr><tr><td>10</td><td>20#4</td><td>- 0.84902</td><td>- 1 ~ - 0.69804</td><td>-0.87057</td><td>1.0153</td><td>0.85086</td><td>-0.90143</td></tr><tr><td>11</td><td>Rg12x</td><td>0.76161</td><td>0.52322- 1</td><td>0.61741</td><td>0.15250</td><td>0.76120</td><td>0.8 80850</td></tr><tr><td>12</td><td>kg12y</td><td>0.67386</td><td>0.34773~ 1</td><td>0.69182</td><td>0.89007</td><td>0.6 67574</td><td>0.8 8 31540</td></tr><tr><td>13</td><td>kg1lz</td><td>0.95851</td><td>0.91702 2-1</td><td>0.97611</td><td>1.0733</td><td>0.9 95848</td><td>1.05480</td></tr><tr><td>14</td><td>kpOx</td><td>0.12112</td><td>- 0.75776 ~ 1</td><td></td><td>3.4743</td><td>0.12457</td><td>一 0 03685</td></tr><tr><td>15</td><td>kp0y</td><td>0.29239</td><td>- 0.41522 ~ 1</td><td>ww</td><td>-- 0.51722</td><td>0.29171</td><td>0.38358</td></tr><tr><td>16</td><td>kp0z</td><td>0.40892</td><td>-0.18215~1</td><td>0.41767</td><td>1.1725</td><td>0.41028</td><td>0.36310</td></tr><tr><td>17</td><td>kpix</td><td>0</td><td>-1~1</td><td></td><td>- 12.365</td><td>0.00684</td><td>- 0.06634</td></tr><tr><td>18</td><td>kp1y</td><td>0</td><td>-1~1</td><td></td><td>-- 35.798</td><td>0.00124 一</td><td>0.00931</td></tr><tr><td>19</td><td>kx</td><td>0</td><td>-1-1</td><td></td><td>2.5528</td><td>0.00188</td><td>一 -0.00874</td></tr><tr><td>20</td><td>k12</td><td>0</td><td>-1~1</td><td></td><td>- 2.4794</td><td>0.00948</td><td>-- 0.16345</td></tr></table></body></html>  

表中第2列是各误差系数的代表符号，第3列是仿真计算中误差系数的真值，第4列数据是各误差系数的验前范围，即 $m_{i}\pm$ $2.\,7\sigma$ ，第5列至第8列数据分别是用正交最小二乘估计、主成分估计、PB估计的估计结果。表中列出了PB1和PB2，其中PB1用验前真值作为验前信息，PB2是在真值的基础上人为地引人误差，以考察PB估计与验前信息的关系（表中数据均作了归一化）。  

OLSE法根据各项贡献的大小进行了模型筛选，表中斜杠表示舍去未估之项。  

从表11-2中数据可以看到，在没有噪声的精确情况下，OLSE估计和PB1估计都得到了较好的结果，估计值与真值之.差在小数点后第3位上才表现出来。而主成分估计则有较大的偏差，估计值落在验前信息范围内的只有第12和15两项,其他估计值都超出了验前的范围。PB2结果中由于在验前均值中人为引人了  

$10\,\%$ 的误差，估计结果与仿真真值存在较大的偏差。  

由表11-3～表11-5数据,当观测量中存在随机白噪声时,正交最小二乘估计对模型中主项系数的估计结果仍然令人满意，除表 11-4中第12项系数估计略大而外,其他估计值与真值之差很小,由于第 14、15两项对模型贡献很小,在观测量中所占的比重小于 $0.1\,\%$ ,在估计过程中被逐一剔除，剩余项估计值可信。可见，OLSE在不同噪声水平下，其估计结果较为稳定，估计结果还表明，该方法对模型的结构确定是合理的。  

从表中结果可以看出，OLSE对模型主项的估计较好，而主成分估计的结果较差，主成分贝叶斯估计在利用准确的验前信息 $\theta_{0}$ 后其估计结果相当好，但当验前信息给定不准时，其结果偏离真值，对观测量 $y$ 之拟合也较差。可见，贝叶斯方法和PB估计对验前信息具有一定的依赖性。  

# 11.4天地关系检验与地面数据纠错  

飞行试验和误差分离的主要目的之一是验证地面试验给定的模型和分离的误差系数是否正确,即检验天地关系是否一致[1,2]由于在地面试验建立的模型中认为惯性平台系统的动态误差项得到了较好的控制，仅考虑线性的静态模型，即忽略动态误差项。这样的考虑是否合适，涉及到模型是否完备的问题，也就是说所用的线性模型是否能较好地表述飞行中系统的性能，关于这一点，目前尚没有有效的办法来验证。  

地面试验中标定的误差系数是否准确，特别是一些重要项的系数是否准确，直接影响到飞行试验结果与地面试验数据的一致性。由于制导工具误差分离问题的严重病态特性，要想纯粹通过参数估计的办法，把模型中各项误差系数估计准确，进而确定不相符的误差项,这是相当困难的，因此必须采用别的办法来对数据进行检验。本节讨论利用估计问题中的组合不变量来对地面试验数据进行检错与纠正的方法。  

# 11.4.1 组合不变量  

对于线性模型参数估计问题  

\left{!!\begin{array}{l}{{{\pmb y},=,{\pmb X}{\pmb\theta},+,e}}\ {{e,\sim,{\pmb N}\left({\bf0},,\sigma^{2},{\pmb I}\right)}}\end{array}\right.

  

式中 $\mathbf{y}\in\mathbb{R}^{m\times1}$  

\begin{array}{l}{\pmb{X}\in\pmb{R}^{m}\times\mathscr{p},;}\ {\pmb{\theta}\in\pmb{R}^{\mathscr{p}\times1}\circ}\end{array}

  

按照正交最小二乘估计方法中的变换，有  

\mathbf{y}~=Q R\pme

  

式中 $\b{Q}\in\b{R}^{m\times\b{n}}$ ,满足 ${\pmb{Q}}^{\mathrm{T}}{\pmb{Q}}=\mathbf{diag}\,;$  

$R\in R^{\phi\times\phi}-$ 上三角阵，且对角元素 $r_{i i}=1\,(\,i=1\,,2\,,\cdots,$  

\phi,)_{\circ}

  

令 ${\pmb W}={\pmb Q}\,,{\pmb g}={\pmb R}{\pmb\theta}$ ,于是式（11-52)化成  

\pmb{{\mathtt y}}=\pmb{{\cal W}}\pmb{{\mathtt g}}+\pmb{\ell}

  

由此可得到 $\pmb{g}$ 之估计值 $\pmb{\hat{g}}$  

\hat{\textbf{g}}=(,W^{\intercal}\pmb{W})^{-1},\pmb{W}^{\intercal}\pmb{y}\ =\ (,W^{\intercal}\pmb{W})^{-1},\pmb{W}^{\intercal}(,\pmb{W}\pmb{g}\ +\ \pmb{e},)\ =

\pmb{g},+,(\pmb{W}^{\intercal}\pmb{W})^{-1},\pmb{W}^{\intercal}\pmb{e}

  

在正交最小二乘估计[3]中,用各项的贡献大小确定主项,因而对于贡献较大的项而言，其估计值 $\hat{g}_{i}\!\sim\!g_{i}$ ，即估计值比较准确，对噪声不敏感，具有良好的估计性能。  

对于病态问题，不同的方法对系统参数 $\pmb\theta$ 的估计具有较大的差异，即不同方法所得到的结果不一致。但是，如果各方法对观测量 $\pmb{y}$ 的估计 $\hat{\mathbf{y}}$ 一致，那么对于正交最小二乘估计中的主项 $\pmb{g_{i}}$ 应为一致，即设有任两个估计 $\hat{\pmb{\theta}}_{1}$ 和 ${\hat{\pmb{\theta}}}_{2}$ ,其对 $\pmb{y}$ 的估计分别为 $\hat{\mathbf{y}}_{1}$ 和 $\hat{\mathbf{y}}_{2}\,\mathrm{o}$ 若  

\hat{\bf y}{1}\approx\hat{\bf y}{2}

  

用 $\hat{\mathbf{y}}_{1}$ 和 $\hat{\mathbf{y}}_{2}$ 代替式（11-54)中的 $\pmb{y}$ ,则对于若干主项 $\pmb{g}$ 有  

\hat{\mathbf{y}}{1},=,\sum{i,=,1}^{r}\hat{g}{1,i}w{i}

\hat{\pmb y}{2}\ =\ \sum{i,=,1}^{r}\hat{g}{2,i}{\pmb w}{i}

  

式中 $\pmb{r}$ 为模型主项数;  

$w_{i}$ —矩阵W的第 $_i$ 行。  

根据上述三式有  

\hat{\pmb{y}}{1}\ =\ \sum{i,=,1}^{r}\hat{g}{1,i}\pmb{w}{i}\approx\hat{\pmb{y}}{1},=\ \sum{i,=,1}^{r}\hat{g}{1,i}\pmb{w}{i}

  

由于 $\pmb{{w}}_{i}$ 是确定量,并满足正交特性，于是有  

\hat{g}{1i}\approx\hat{g}{2i}

  

上式也就是式（11-56）,式（11-60)仅对主项成立，对于次要项,因 $\pmb{\hat{g}}$ 对误差极为敏感，上式不能成立。  

主项中 $\dot{g}_{i}$ 的这种特性称之为估计中的不变量，它与所采用的估计方法关系不大，只要估计对于观测量的拟合良好即可。一旦拟合一致，则这些 $\hat{g}_{i}$ 还与真值 $g_{i}$ 相一致。  

下面举一例子加以说明，仍用11.3节中的仿真算例，分别采用正交最小二乘估计、主成分估计和PB方法进行估计，并将主成分和PB法的估计值 $\pmb{\hat{\theta}}$ 换算成 $\pmb{\hat{g}}$ ,最后的结果列于表11-6～表11-8，从表中数据可以看出这些不变量的一致性。  

表 11-6 $\boldsymbol{x}$ 方向组合量  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>g2</td><td>g3</td><td>g4</td></tr><tr><td colspan="2">真值</td><td></td><td>0.248280E - 2 0.372033E-6</td><td>10.301529E - 6</td><td>0.959860E -- 4</td></tr><tr><td rowspan="2">OLSE</td><td>α =0.01</td><td>0.248315E - 2</td><td>0.366833E-6</td><td>0.302680E - 6</td><td>[0.964053E - 4</td></tr><tr><td>α =0.02</td><td>0.248325E - 2</td><td>0.361435E - 6</td><td>0.303818E-6</td><td>0.968138E - 4</td></tr><tr><td rowspan="2">PCE</td><td>α =0.01</td><td>0.248287E -2</td><td>10.367290E - 6</td><td>0.302894E -- 6</td><td>0.962341E - 4</td></tr><tr><td>α =0.02</td><td>0.248293E-2</td><td>0.361836E -6</td><td>0.304776E - 6</td><td>0.965402E - 4</td></tr><tr><td rowspan="2">PB</td><td>0 =0.01</td><td>0.248292E - 2</td><td>0.372293E -6</td><td>0.301766E - 6</td><td>0.962054E - 4</td></tr><tr><td> =0.02</td><td>0.248279E -2</td><td>0.372332E-6</td><td>0.301995E - 6</td><td>0.964131E - 4</td></tr></table></body></html>  

表11-7 $y$ 方向组合量  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>g2</td><td>g3</td></tr><tr><td colspan="2">真值</td><td>0.197678E - 2</td><td>- 0.254888E - 5</td><td>0.271423E -6</td></tr><tr><td rowspan="2">OLSE</td><td>0 =0.01</td><td>0.201241E - 2</td><td>- 0.248003E - 5</td><td>0.265863E -6</td></tr><tr><td>α =0.02</td><td>0.201382E -2</td><td>- 0.248420E - 5</td><td>0.266943E - 6</td></tr><tr><td rowspan="2">PCE</td><td>0 =0.01</td><td>0.201215E - 2</td><td>- 0.248000E - 5</td><td>0.265649E -6</td></tr><tr><td>0 =0.02</td><td>0.201352E - 2</td><td>0.248416E - 5</td><td>0.266010E - 6</td></tr><tr><td rowspan="2">PB</td><td>o =0.01</td><td>0.201224E -2</td><td>- 0.247865E - 5</td><td>0.264811E - 6</td></tr><tr><td>α =0.02</td><td>0.201382E - 2</td><td>- 0.248135E -- 5</td><td>0.264845E- 6</td></tr></table></body></html>  

表 11-8 $\pmb{z}$ 方向组合量  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>g2</td><td>g3</td></tr><tr><td colspan="2">真值</td><td>- 0.216181E - 1</td><td>0.166248E - 5</td><td>- 0.437728E - 5</td></tr><tr><td rowspan="2">OLSE</td><td>=0.01</td><td>- 0.216156E - 1</td><td>0.167094E - 5</td><td>- 0.438009E - 5</td></tr><tr><td> =0.02</td><td>- 0.216138E- 1</td><td>0.167938E - 5</td><td>0.438305E - 5</td></tr><tr><td rowspan="2">PCE</td><td>0 =0.01</td><td>- 0.216154E - 1</td><td>0.167096E - 5</td><td>- 0.438135E - 5</td></tr><tr><td>α =0.02</td><td>- 0.216139E - 1</td><td>0.167956E - 5</td><td>-0.438475E- 5</td></tr><tr><td rowspan="2">PB</td><td>=0.01</td><td>- 0.216158E - 1</td><td>0.166866E - 5</td><td>- 0.437362E - 5</td></tr><tr><td>α =0.02</td><td>- 0.216143E - 1</td><td>0.167486E - 5</td><td>- 0.437006E - 5</td></tr></table></body></html>  

从表11-6到表11-8的数据发现，在 $\boldsymbol{x}$ 方向真有四个不变量，y和z方向各有三个不变量。这些不变量对应的模型项在观测量中所占的比重列于表11-9,可以看出，它们之和构成了误差的主要部分，超过99.9%。表11-6中，三种方法估值换算的g1同其真值十分一致，其误差不超过 $0.1\,\%\,,\hat{g}_{2}$ 项的误差不超过 $\,3\,\%\,,\,\hat{g}_{3}\,$ 项的误差不超过1%，g4项的误差不超过1%。同样，y方向和z 方向的各g；量也十分接近,相对偏差很小。这是因为三种方法虽然估计的 $\hat{\pmb\theta}$ 相互有差异，但其对观测量的拟合较为一致，从而使表征观测量y的各主要项坐标值也十分一-致。同时，由于他们是模型中的主要项，噪声误差对其影响很小。  

表11-9各组合量对应项在观测量中所占的比重 $(\,\%\,)$   


<html><body><table><tr><td></td><td>g1</td><td>g2</td><td>g3</td><td>g4</td></tr><tr><td>x方向</td><td>97.86</td><td>0.475</td><td>1.105</td><td>0.477</td></tr><tr><td>y方向</td><td>66.81</td><td>32.117</td><td>1.056</td><td></td></tr><tr><td>z方向</td><td>99.677</td><td>0.0456</td><td>0.271</td><td></td></tr></table></body></html>  

由此可以看出，这些不变量不但同所使用的方法关系不大，而且对噪声不敏感。由表可见，不同噪声只影响到第三位有效数字，因而具有良好的估计性能。之所以有它们的存在，是由于它们构成了观测量之主要部分，而观测量的主要部分在给定正交基下的投影不变。  

# 11.4.2 天地关系是否一致的检验  

在对惯性平台测量系统误差进行实时补偿中，希望补偿模型能较好地描述平台系统的实际情况，即具有与飞行试验数据相一致的地面模型。飞行试验及工具误差系数分离的主要任务和目的之就是对天地关系是否一致进行有效的检验，只有相一致的模型才能用于对平台系统测量的实时修正。如果得到的飞行试验结果与地面试验结果不一致，则必须对不一致的原因进行深人的分析，或者对试验数据进行再处理，或者对地面模型进行重建，直到天地关系基本一致。理想的情况是二者十分一致，此时就可利用地面的模型来设计工具误差的补偿方法。然而，由于影响平台系统测量误差的因素十分复杂，地面试验又存在手段的限制，同时测试结果可能出现极性错误，天地关系达到理想的完全一致状态的可能性不大。较多的是出现两种情况，即基本一致和不一致。天地关系不-致大致可分为两种情况，即模型不完备和误差系数的标定不准确，或者两种情况兼而有之。需要有效的方法来对大地关系进行深人分析。  

参考文献[41在考察天地关系是否-致时，根据误差系数的设计指标和测量均值，计算出平台误差引起的视速度差的上下限随时间变化曲线，通过与飞行试验得到的遥、外测视速度差曲线的比较，考察飞行试验结果是否在上下限范围内，随时间变化规律情况，进而对天地关系作出评价。  

对地面试验模型式（11-52），设有关于参数 $\pmb\theta$ 的地面测试值${\pmb\theta}_{\mathfrak{0}}$ ，设计指标方差 $\pmb{\sigma}$ ，在飞行试验得到环境函数 $\pmb{X}$ 后，可求得  

{\bf y_{0}};=;{\bf X}\pmb{\theta_{0}}

\begin{array}{r}{\pmb{y}{\mathrm{sup}};=;\pmb{X}\pmb{\theta}{0},+,2,.,7,\mid,\pmb{X\sigma}\mid}\ {\mathbf{y}{\mathrm{inf}};=;\pmb{X}\pmb{\theta}{0},-,2,.,7,\mid,\pmb{X\sigma}\mid}\end{array}

  

式中，下标“sup”和“inf”分别代表上限和下限。若在整个试验段 内，观测值 ${\bf{y}}$ 满足  

{\mathbf{y}}{\mathrm{inf}}\leqslant{\mathbf{y}}\leqslant{\mathbf{y}}{\mathrm{sup}}

  

且. $\pmb{y}$ 与 ${\mathfrak{y}}_{0}$ 规律基本一致，则认为天地关系一致。  

这样的判断较为直观和简洁，但可能出现复杂的情况，甚至出现误判。下面以某发弹的飞行试验数据为例，加以说明。图11-4和图11-5分别是用两组地面数据 $\pmb{\theta}_{01}$ 和 ${\pmb\theta}_{02}$ 经计算得到的比较曲线图，两组数据中的第一项系数 $k_{a0x}$ 、第二项系数 $k_{a0y}$ 和第十九项系数 $k_{g13x}$ 正好反号，即极性相反。图中FT表示飞行试验测得的数据；GT表示用地面测量的系数换算出的视速度偏差数据。从图中曲线可以看出，两组数据换算的结果均满足式（11-64），且yo1,yo2变化规律与y 的规律均较为一致。按照上面的思想,两组结果都可以认为与飞行试验一致。从 ${\mathfrak{y}}_{01},{\mathfrak{y}}_{02}$ 与 $\b{y}$ 的关系来看，明显 $\pmb{y}_{02}$ 要比 $\pmb{y}_{0\textup{\AA}}$ 更接近 ${\mathfrak{y}}_{\circ}$ 而第一组数据恰恰是实际的地面测试结果。由此不容易判断哪一组数据更接近参数真值。  

可见，用上述的思想来判别天地关系是否一致过于宽松。并且对于较为复杂的线性多项式模型，即使是飞行试验曲线满足式（11-64），仍然不一定存在参数 $\theta\!\in\!\left(\,\theta_{0}-2.7\,\sigma\,,\theta_{0}+2.7\,\sigma\,\right)$ ，使 X0较好地拟合飞行试验的观测数据 ${\mathfrak{y}}_{\circ}$  

有人提出用下述条件作为天地关系基本一致的判别准则：  

![](images/8b44f2ccc7da91471d37a62160709bb956e7503c20519e9ec232ddabc2440dab.jpg)  
图 11-4飞行试验曲线与地面曲线比较(第一组）  

当存在 $\hat{\pmb{\theta}}\in(\,\pmb{\theta}_{0}\,-\,2\,.\,7\,\pmb{\sigma}\,,\pmb{\theta}_{0}\,+\,2\,.\,7\,\pmb{\sigma}\,)$ ,使 $\pmb{X}\hat{\pmb{\theta}}$ 对 $x$ 行试验的观测数据 $\pmb{y}$ 拟合的残差在容许范围内，即  

\parallel\textbf{y}-\textbf{X}\hat{\pmb{\theta}}\parallel_{2}\leqslant C_{1}

  

或者在试验时段范围内满足  

\operatorname*{max}\mid;\mathbf{y};-;\mathbf{X}\hat{\pmb{\theta}};\mid;\leqslant C_{2}

  

时，天地关系基本一致。  

上述条件中， $C_{1}$ 和 $C_{2}$ 为给定的容许值，可根据实际情况确定。利用条件式（11-66)时对野值要慎重，须对各种野值和跳点进行剔除。很显然，天地基本一致时，地面试验信息可信，可以作为实时补偿的依据。  

1）天地关系基本一致时的检验  

454  

![](images/bc802e7d6ebb83519c36cc42025266331f7cb96d9a974a8ab386846bdc6def65.jpg)  
图 11-5 飞行试验曲线与地面曲线比较(第二组）  

按上述判别条件，如果天地关系基本一致，则地面试验的信息较为准确可信，此时可直接用贝叶斯估计方法来进行检验。因为贝叶斯估计的优点是利用地面验前信息（实际上就是地面试验数据）,并能克服估计中的病态特性，因而当天地关系一致时其估计量与验前信息也基本一致。贝叶斯估计的目标函数是  

J;=;\frac{1}{\sigma^{2}};\Vert;{\bf y};-;X\hat{\pmb{\theta}};\Vert_{;2};+;\frac{1}{\sigma^{2}};\Vert;\hat{\pmb{\theta}};-;{\pmb{\theta}}{0};\Vert{;2}

  

考察估计值 $\pmb{\hat{\theta}}$ ，以及 $\hat{\bf y}$ 与观测值 $\pmb{y}$ 的拟合程度,若拟合一致，则表明天地关系基本一致。如果估计值 $\pmb{\hat{\theta}}$ 中存在一些重要参数不在验前范围内，说明天地关系不太一致。  

2）天地关系不一致时的检验  

（1）模型不一致之检验。在3.3节已经知道，正交最小二乘  

估计方法一个重要的特性就是它具有模型结构确定之功能。这一性质可以用来检验地面试验与飞行试验二者模型的不匹配问题。  

飞行试验后误差分离的模型一般采用地面试验模型，若地面模型考虑不完备，则可能导致模型的不相容。  

考察模型是否完备，用下式  

\sum_{i,=,1}^{\beta}\cos(,i,)\geqslant C_{e}

  

$C_{e}$ 一般取99.9,或者根据实际情况给定。若上式成立，则表明所论模型已经完备，无需再考虑其他模型项，即现有模型能足以描述系统之性能。如果式（11-67）在现有模型情况下不成立，则可能是噪声太大或者模型不完备，那么现有模型就不能够充分表述系统的特征，必须对模型进行更加深入的分析，引入其他线性项或者非线性项，对模型进行扩展，直到满足上式，再进行工具误差系数的分离。因此式（11-67)是模型完备性的重要判据。  

（2）误差系数标定不准确。这种误差系数标定不准确也会影响天地关系，在实践中是容易出现的一种情况，其表现形式可能是某些项的标定符号不对，发生极性错误，或者某些重要的误差系数标定不准确，从而导致飞行试验数据与地面试验数据之间的差异。这时尤为关键的是一些重要项的标定出现误差，而那些影响很小的项却并不那么紧要，完全可以忽略。于是，误差分离的目的并不仅局限于得到待估参数的一个估计值，而应该是找出不一致的根源，并尽可能地对地面标定量出现错误的重要项进行纠正。这就是下一节的内容，利用组合不变量进行纠错。  

# 11.4.3 变量重组与地面数据纠错  

正如制导工具误差系数辨识问题一样，存在一类线性多项式模型问题，其自变量具有强烈的复共线性，准确地估计各个参数十分困难，并且其试验输人有限，而又希望尽可能多地辨识出模型参数，以用于其他输人情况。关于未知参数，具有一定的验前信息，日部分信息是可信的，要求辨识出不太可信的参数来。  

由于工具误差的补偿主要还是根据地面测量信息进行，因而如果完全否定宝贵的地面信息十分不可取，必须充分利用它们，同时要求对地面数据中的主要参数中确实存在的极性不正确和标定错误的项加以识别和校正，以利于对工具误差进行有效的补偿，提高导弹的落点精度。这也是平台系统设计部门十分关心的问题。由于正交二乘估计中的不变量特性，可以用不变量来进行地面数据校正。  

注意3.3节中的式（3-27），其中  

g_{\flat}\ =\ \theta_{\flat}

g_{j}=\theta_{j}+\sum_{\scriptscriptstyle{i,=,j+1}}^{!!!\beta}\eta_{j i}\theta_{i}\qquad(j~=p-1,p-~2,\cdots,1)

  

对 $_{j}=1,2,3$ 情形重写上式，有  

\begin{array}{l}{\displaystyle\begin{array}{l l}{\displaystyle\varrho_{1},=,,\theta_{1},+,\sum_{i=2}^{p},\eta_{1},{i}\theta{i}}\ {\displaystyle g_{2},=,,\theta_{2},+,\sum_{i=3}^{p},\eta_{2},{i}\theta{i}}\end{array}}\ {\displaystyle\begin{array}{l l}{\displaystyle g_{3},=,,\theta_{3},+,\sum_{i=4}^{p},\eta_{3},{i}\theta{i}}\end{array}

  

从上述式子可知， $\theta_{1}$ 仅影响 $g_{1},\theta_{2}$ 仅影响 $g_{1}\,,g_{2}$ ，而 $\theta_{3}$ 仅影响g1、g2-g3,换言之,若地面试验给定值0 中仅θ,和 02有问题,则在组合量 ${\pmb g}$ 的表现中， $\pmb{g}_{1}$ 和 $g_{2}$ 会出现偏值。  

组合不变量具有良好的估计性能，因为，如表11-9中数据，它们构成了观测量中的主要部分，其贡献和大约占总的 $99\,\%$ 以上，对噪声不敏感，从而使模型中主项 $\pmb{g}$ 的估计性能得到保证，估计值结果稳定可靠。从表 $11\!-\!6\!\sim$ 表11-8的仿真结果可以看出这些项确实得到了很好的估计，也就是说，对于这些项，在不知道真值的情况下，可以用其估计值 $\pmb{\hat{g}}$ 来代替而不会有较大的误差。  

不失一般性，假设地面试验数据中 $\theta_{1}$ 和 $\theta_{2}$ 给错，而其余 $\theta_{i}$ 值给定较为准确，则用这些数据利用关系式（11-70）～式（11-72）  

得出的地面值 $g_{\mathrm{~t~}}$ 地丶g2地、 $g_{3}$ 地中， $g_{3}$ 地与 $g_{3}$ 值一致,而g1地 $,\,\times\,g_{21}$ 地分别与 $\hat{g}_{1},\hat{g}_{2}$ 出现偏差,可用下述方法求出 $\theta_{2\#\Sigma},\theta_{1\#\Sigma}$ 的值。  

已知 $g_{3\#2}$ 地与 $\hat{g}_{3}$ 一致,则可认为 $\theta_{i\neq\notin}({\it i}>2)$ 正确,于是有  

\begin{array}{l}{{\displaystyle\theta_{2:\not\equiv}=g_{2}-\sum_{i:=:3}^{\beta},\eta_{2:i}\theta_{i:\not\equiv}}}\ {{\displaystyle\theta_{1:\not\equiv}=g_{1}-\sum_{i:=:2}^{\beta},\eta_{1:i}\theta_{i:\not\equiv}}}\end{array}

  

通过上式求出 $\theta_{2}.\mu_{3}.\theta_{1}.\mu_{2}$ 之后，再用它们求出观测值 $Y_{\#\mathbb{B}}$ ，并与飞行试验结果相比较,如果一致,说明 $\theta_{2}\mu_{2}\cdot\theta_{1/2}$ 求取正确。  

实际上，不太可能恰好是 $\theta_{1}$ 和 $\theta_{2}$ 出错，可能是任两个 $\theta_{i}$ 和$\theta_{j}$ ,这时总可以通过变量顺序之重构，把 $\theta_{i}$ 和 $\theta_{j}$ 调整为 $\theta_{1}^{'}$ 和 $\boldsymbol{\theta}_{2}^{\prime}$ ，然后用上述的方法加以分辨纠错。这可通过搜索的办法来完成，对于 $g_{1},g_{2},g_{3}$ ,若出现 $g_{3}{\approx}g_{3{\#}\!\!\!\perp}$ ,而 $\hat{g}_{1},\hat{g}_{2}$ 与 $g_{1\mathrm{tra}},g_{2\mathrm{tra}}$ 不对，则可以认为只有 $\theta_{1},\theta_{2}$ 不对。  

按照表11-6\~表 11-8的仿真数据,在 $_{x}$ 方向有4个 $g_{i}\,,y\,,z$ 方向各有3个 $g_{i}$ ，因此，在该仿真情况，最多可以查出7个错误数据，考虑到3个方向某些变量的重叠，实际上可能达不到7个。  

# 11.4.4 仿真算例  

仍采用前述算例中的观测仿真量和环境函数矩阵，在进行仿真时采用了一套系数 $\pmb\theta$ 的数据，称之为 $\pmb{\theta}_{t r}$ 。而给 $\pmb{\theta}_{t r}$ 某些项人为的偏差成为 $\theta_{\pmb{\mathscr{H}}_{0}\circ}$ 利用观测量 $\pmb{y}$ 和环境函数矩阵，首先能得到不变量 $\pmb{g}$ 的估计值 $\hat{g}$ ，我们把 $\pmb{\hat{g}}$ 视作 $\pmb{g}_{t r}$ ，同时在采用估计时获得了的变换关系  

\begin{array}{l}{{g_{\phi}\ =\ \theta_{\phi}}}\ {{\ }}\ {{g_{i}\ =\ \theta_{i},-,\displaystyle\sum_{i,=,j+1}^{,\phi}\eta_{j i}\theta_{i}}}\end{array}

  

利用 $\theta_{H E}$ 替换上式可得  

g_{i j k!!!/!\frac{1}{2}};=;\theta_{i j k!!!/\frac{1}{2}};-;\sum_{i,=,j+1}^{p}\eta_{j i}\theta_{i}\dag!!!/\frac{1}{2}

  

比较 $\hat{g}_{i}$ 与 $g_{i}\not=\pmb{\mathrm{k}}$ ,若所有 $g_{i}$ 均偏差较大,则交换模型中各项的秩序，重新比较，当满足最后一个不变量基本一致时，用上节所述的方法求出这些有偏差的 $\pmb{\theta}$ 量,并与 $\pmb{\theta}_{t r}$ 进行比较。  

表 11-10和表 11-11是检测过程的结果数据,仿真计算中在 $y$ 方向的第1和第5项系数中引人偏差，初次检测时，这两项并未处于前两位，因而影响了各个不变量，表中各对应的不变量数据均有较大的偏差，此时无法确定是那些项有偏差，需要进一步检测。于是对模型项交换顺序，检测结果为表11-10。从表11-11数据看出, $g_{3}$ 的估计值和地面数据值基本一致，此时认为偏差项包含在前两项之中，利用式（11-72)和式（11-73），可求出该两项的实际值，结果见表11-11后三行的值，纠错的结果与真值十分接近。  

表 11-10 $_y$ 方向检测结果(1)  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>g2</td><td>g3</td></tr><tr><td colspan="2">真值</td><td>- 0.956576E - 7</td><td>- 0.488910E -5</td><td>0.300351E - 3</td></tr><tr><td rowspan="2">OLSE</td><td>估计值</td><td>- 0.956318E - 7</td><td>-0.487826E - 5</td><td>0.293232E -3</td></tr><tr><td>地面计算值</td><td>0.451703E-7</td><td>- 0.312825E - 5</td><td>0.100351E-6</td></tr></table></body></html>  

表 11-11 $y$ 方向检测结果(2)  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>g2</td><td>g3</td></tr><tr><td colspan="2">真值</td><td>0.197678E - 2</td><td>-0.254888E - 5</td><td>0.271423E - 6</td></tr><tr><td rowspan="2">OLSE</td><td>估计值</td><td>0.201241E - 2</td><td>0.248003E - 5</td><td>0.265863E - 6</td></tr><tr><td>地面计算值</td><td>- 0.117102E -- 2</td><td>- 0.476049E - 6</td><td>0.264775E - 6</td></tr><tr><td colspan="2">真 值</td><td>0.62784E - 3</td><td>-0.52259E - 5</td><td>（第1,5项）</td></tr><tr><td colspan="2">错值</td><td>0.42784E - 3</td><td>- 0.32259E - 5</td><td></td></tr><tr><td colspan="2">校正值</td><td>0.62773E - 3</td><td>~0.52299E- 5</td><td></td></tr></table></body></html>  

采用类似的步骤可得到 $_{x}$ 和 $\mathcal{z}$ 方向的检测结果,如表11-12 和表11-13给出的数据。从检测结果推知， $_{\l,\tau}$ 方向是其第1、5、8项系数未给准， $_y$ 方向是1、5项系数不准,而 $\mathcal{Z}$ 方向是第4项未给准。  

表11-12 $_x$ 方向检测结果  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>A g2</td><td>g3</td><td>g4</td></tr><tr><td colspan="2">真值</td><td>0.248280E-2</td><td>0.372033E - 6</td><td>0.301529E -6</td><td>0.959860E -4</td></tr><tr><td rowspan="2">OLSE</td><td>估计值</td><td>0.248315E-2</td><td>0.366833E - 610.302680E - 6↓0.964053E - 4</td><td></td><td></td></tr><tr><td></td><td>地面计算值0.427928E-2</td><td>0.192561E - 5</td><td>0.277529E - 6</td><td>0.968138E - 4</td></tr><tr><td colspan="2">真值</td><td>0.18639E - 2</td><td>- 0.52259E -- 5</td><td>0.24659E - 6</td><td>（第1,5,8项）</td></tr><tr><td colspan="2">错值</td><td></td><td></td><td>0.22259E - 6</td><td></td></tr><tr><td colspan="2">校正值</td><td>0.16639E - 2 0.18642E - 2</td><td>- 0.32259E - 5 -0.52297E-5</td><td>0.24752E - 6</td><td></td></tr></table></body></html>  

表 11-13 $\mathcal{Z}$ 方向检测结果  


<html><body><table><tr><td colspan="2"></td><td>g1</td><td>g2</td><td>g3</td></tr><tr><td colspan="2">真值</td><td>0.216181E - 1</td><td>0.166248E - 5</td><td>0.437728E - 5</td></tr><tr><td rowspan="2">OLSE</td><td>估计值</td><td>-0.216156E - 1</td><td>0.167094E - 5</td><td>0.438009E - 5</td></tr><tr><td>地面计算值</td><td>- 0.164247E - 1</td><td>~0.233752E- 5</td><td>- 0. 437728E - 5</td></tr><tr><td colspan="2">真值</td><td></td><td>0.87163E - 5</td><td>（第4项）</td></tr><tr><td colspan="2">错 值</td><td></td><td>0.47163E - 5</td><td></td></tr><tr><td colspan="2">校正值</td><td></td><td>0.87243E - 5</td><td></td></tr></table></body></html>  

# 11.5 实测数据处理  

本节对某发弹的实测飞行试验数据进行分析处理，对误差系数进行分离。  

# 11.5.1 实测数据  

用于制导工具误差系数辨识的实测数据包括地面试验对各误差系数的测量数据，以及飞行试验时用遥测系统和外测系统测量得到的导弹主动段运动状态参数的观测值，误差系数的地面数据中还包括设计指标值。  

地面试验的测量数据给出了导弹飞行试验前在地面试验测量中测得的模型中的各个零次项和一次项系数的值和标准差，同时给出了各误差系数的设计指标值。从实验数据看，地面测试值同给出的设计指标值具有不同程度的差异，其中加速度表的三个零次项以及第12项系数均超出了给定的设计指标范围,尤其是 $k_{a\mathrm{oy}}$ 的测试值比设计指标值大几倍。设计指标值仅仅是平台系统在设计时对系统制造和安装精度的要求，而实际使用的惯性元件并未达到要求的精度。另外，表中数据为0者，并不一定代表该项误差系数的测试期望值为0，而是因为测量手段的限制，在地面测试中无法测出该项的大小，或者对其测量极不准确。关于它们的值，正有赖于从飞行试验数据中去辨识分离出来。  

飞行试验是一次小射程常规弹道试验，导弹在飞行中的状态参数分别由外弹道测量系统和遥测系统测量得到。  

图 $11{\cdot}6\sim$ 图11-8是经过处理后得到的视速度遥外测差的飞行试验数据曲线，图中同时给出了用地面测试的误差系数和设计指标值换算得到的视速度偏差值及其上下限曲线。其中  

\begin{array}{r}{\Delta W_{\mathrm{sup}},=,S C_{0},+,2.7\mid S\Sigma\mid}\ {\Delta W_{\mathrm{inf}},=,S C_{0},-,2.7\mid S\Sigma\mid}\end{array}

\Delta W_{0};=;{\cal S C}_{0}

  

式中 Co—地面试验测试中各误差系数的均值；  

2-误差系数标准差的设计指标值；  
下标“sup”和“inf”"——分别代表上、下限值。  

从图中数据看到  

\Delta W_{\mathrm{int}}<\Delta W_{\mathrm{0}}<\Delta W_{\mathrm{sup}}

  

即飞行试验得到的数据处于地面数据的上、下限之间。比较地面试验测试给出的△W。曲线和飞行试验曲线，两者之间存在较大的差异。  

飞行试验数据得到的是 $t_{0}\!\sim t_{f}$ 的数据，数据采样频率是每秒20个数据点，从图中数据分析，当 $t<t_{1}$ 时，曲线跳动很大，极不规则，这是因为导弹飞行初始时段系统不稳定和其他误差因素引  

![](images/862e22ee6674b97d63ca373fbe970fdfaad0b6ad3ed1b304c60b6c70bf090d26.jpg)  

图 11-6  实测视速度差比较曲线 $(x)$  

![](images/78502c444a29bfb4bbeeea945b7dc1caf7000ab65609a9d0f3a63caa2cb150d1.jpg)  
图 11-7  实测视速度差比较曲线 $(y)$  

![](images/256696a8a9300883c850bea86d91b4f548ca9158eb14c10abb94bf0f43f26a11.jpg)  
图11-8实测视速度差比较曲线 $(z)$  

起的,此时段外测数据的误差也较大,图 11-9 给出了外测数据的精度曲线,在 $\pmb{t}<\pmb{t_{1}}$ 区段，精度很差，使该段数据不能用于工具误差的辨识。另外,根据参考文献[8］,当导弹距测试地面站斜距超过保精度的极限距离后,外测数据的误差变大。外弹道测量数据在 $t\in(t_{2},t_{3})$ 秒范围内，基本上满足精度  

\sigma_{v_{i}}<0.03\mathrm{m/s}\quad(,i;=;x,,y,,z,)

  

![](images/6937a24e21ad6439596990d659ddafa8905d71ee789d730bbdcaacf1a6f49a06.jpg)  
图 11-9外测数据方差曲线  

因此，从外测数据的精度和质量来分析，最适宜于工具误差辨识的数据应是上述区段内的测量数据。本章利用该段数据进行误差系数的辨识分析和处理。  

# 11.5.2 误差模型的初选  

地面测试所用的误差系数值，考虑的误差项有40项，其中第37项 $\sim\!39$ 项考虑数据中可能存在的系统性测量误差（外测数据）的影响，第40项考虑了遥外测时间零点不对齐效应。根据系统辨识理论，模型项太多不利于参数估计。况且制导工具误差辨识本身就是一个病态问题，过多的项只能加重病态的程度。因此有必要根据地面测试的信息和设计指标的信息对误差模型进行预分析，初步确定误差模型。  

利用飞行试验数据计算的环境函数矩阵，根据各误差系数的地面测试值和标准差，计算出各误差项可能引起的视速度偏差。  

表 $11-14\sim$ 表11-16分别列出了这些误差项引起的 $x\,,y\,,z$ 三个方向的视速度偏差值( $\pmb{t}_{3}$ 时刻值),误差系数分别取 $m_{i},m_{i}+2,7\sigma_{i}$ $m_{i}-2.7\sigma_{i}$ 。同时，考虑到环境函数随时间变化，表 11-17列出各误差系数所能引起的最大视速度偏差值（取绝对值）。从表中数据知道，模型中各项引起的视速度偏差相差较为悬殊，对那些视速度偏差很小的项有必要进行剔除。  

由于测量数据中不可避免地伴有随机噪声，外测数据（经辨识前的各种处理后）的测量精度大致为 $0.03\mathrm{m/s}$ ，因而那些视速度偏差值小于该精度值的误差项，其作用易被噪声所湮没。从估计角度看，其估计精度很差，不但估计不准，而且还会影响其他系数的估计精度。同时，这些项的作用本身较小，造成的落点偏差也很小,因而忽略这些项对模型没有多大影响，相反可以简化辨识模型，有利于工具误差系数的估计。  

由表 11-14\~表 11-17 以及地面测试中各误差系数的测量值和设计指标值，首先可以看到第 6、9、13、14、18、22、23、24、31、32、34、35、36 等 13 项因素引起的视速度偏差很小，小于 $0.03\mathrm{m}/\mathrm{s}_{\mathrm{c}}$ 也就是说这些项的贡献不显著，在模型初选时完全可以消去，即使考虑到地面测试数据的不准确性，假设其实际误差系数值有可能超过其设计指标值几倍（这样的假设是合理的，例如第二项误差系数，地面测试值为0.82，而其设计指标值却是 $0.18\pm0.18)$ 。这些误差项在其系数放大后其作用仍然相当小，因此对它们不予考虑不会造成大的偏差。剩余的其他各误差项，虽然某些项的作用也比较小，但考虑到其实际系数与设计指标之间的实际差异，在模型初选中仍加以保留。在辨识过程中确定其作用的主次。它们是第4、5、7、8、28、29、30、33等项。这样，初步用于工具误差系数辨识的模型共有27项。  

表 11-14 各误差系数引起的 $_{x}$ 方向视速度偏差 $(\mathbf{m}/\mathbf{s})$   


<html><body><table><tr><td>序号</td><td>m</td><td>m + 2.7α</td><td>m - 2.7α</td><td>序号</td><td>m</td><td>m +2.7a</td><td>m -2.7α</td></tr><tr><td>1</td><td>- 1.0835</td><td>- 0.8973</td><td>- 1.2696</td><td>24</td><td>0</td><td>0.0001</td><td>- 0.0001</td></tr><tr><td>4</td><td>0</td><td>0.1473</td><td>-- 0.1473</td><td>26</td><td>0</td><td>0.0002</td><td>- 0.0002</td></tr><tr><td>7</td><td>0</td><td>0.0822</td><td>- 0.0822</td><td>27</td><td>0</td><td>0.3058</td><td>- 0.3058</td></tr><tr><td>11</td><td>0.0009</td><td>0.0019</td><td>0</td><td>29</td><td>0</td><td>0.0001</td><td>- 0.0001</td></tr><tr><td>12</td><td>6.5194</td><td>6.8620</td><td>6.1767</td><td>30</td><td>0</td><td>0.0566</td><td>- 0.0566</td></tr><tr><td>14</td><td>0</td><td>0</td><td>0</td><td>32</td><td>0</td><td>0</td><td>0</td></tr><tr><td>15</td><td>- 8.2831</td><td>- 7.6279</td><td>- 8.9384</td><td>33</td><td>0</td><td>0.1406</td><td>- 0.1406</td></tr><tr><td>17</td><td>0.0039</td><td>0.0057</td><td>0.0021</td><td>35</td><td>0</td><td>0</td><td>0</td></tr><tr><td>18</td><td>0.0013</td><td>0.0022</td><td>0.0003</td><td>36</td><td>0</td><td>0.0053</td><td>- 0.0053</td></tr><tr><td>20</td><td>- 0.0013</td><td>- 0.0007</td><td>- 0.0020</td><td>37</td><td>0</td><td>0.0405</td><td>- 0.0405</td></tr><tr><td>21</td><td>0.5213</td><td>0.8256</td><td>0.2170</td><td>40</td><td>0</td><td>0.1964</td><td>- 0.1964</td></tr><tr><td>23</td><td>0</td><td>0</td><td>0</td><td></td><td></td><td></td><td></td></tr></table></body></html>  

表 11-15各误差系数引起的 $y$ 方向视速度偏差 $(\mathbf{m}/\mathbf{s})$   


<html><body><table><tr><td>序号</td><td>m</td><td>m +2.7o</td><td>m -2.7o</td><td>序号</td><td>m</td><td>m +2.7o</td><td>m -2.70</td></tr><tr><td>2</td><td>0.4235</td><td>0.4694</td><td>0.3763</td><td>24</td><td>0</td><td>0.0004</td><td>- 0.0004</td></tr><tr><td>S</td><td>0</td><td>0.0526</td><td>0.0526 一</td><td>25</td><td>0</td><td>0</td><td>0</td></tr><tr><td>8</td><td>0</td><td>0.0604</td><td>一 0.0604</td><td>27</td><td>0</td><td>- 0.0504</td><td>0.0504</td></tr><tr><td>10</td><td>- 0.0016</td><td>- 0.0018</td><td>-0.0013</td><td>28</td><td>0</td><td>0</td><td>0</td></tr><tr><td>12</td><td>-2.2911</td><td>- 2.4116</td><td>2.1707</td><td>30</td><td>0</td><td>- 0.0119</td><td>0.0119</td></tr><tr><td>13</td><td>0</td><td>0</td><td>0</td><td>31</td><td>0</td><td>0</td><td>0</td></tr><tr><td>15</td><td>2.3245</td><td>2.1406</td><td>2.5084</td><td>33</td><td>0</td><td>-0.0142</td><td>0.0142</td></tr><tr><td>16</td><td>0.0011</td><td>- 0.0013</td><td>- 0.0009</td><td>34</td><td>0</td><td>0.0000</td><td>0</td></tr><tr><td>18</td><td>0</td><td>0</td><td>0</td><td>36</td><td>0</td><td>0.0006</td><td>0.0006</td></tr><tr><td>19</td><td>0.0008</td><td>- 0.0013</td><td>- 0.0003</td><td>38</td><td>0</td><td>0.0101</td><td>- 0.0101</td></tr><tr><td>21</td><td>- 0.2296</td><td>-0.3635</td><td>- 0.0956</td><td>40</td><td>0</td><td>- 0.0065</td><td>0.0065</td></tr><tr><td>22</td><td>0</td><td>0</td><td>0</td><td></td><td></td><td></td><td></td></tr></table></body></html>  

表 11-16各误差系数引起的 $_z$ 方向视速度偏差 $(\mathbf{m}/\mathbf{s})$   


<html><body><table><tr><td>序号</td><td>m</td><td>m + 2.7o</td><td>m - 2.7o</td><td>序号</td><td>m</td><td>m + 2.7o</td><td>m -2.7o</td></tr><tr><td>3</td><td>- 0.3363</td><td>- 0.2781</td><td>-0.3944</td><td>23</td><td>0</td><td>0.0005</td><td>- 0.0005</td></tr><tr><td>6</td><td>0</td><td>- 0.0003</td><td>0.0003</td><td>25</td><td>0</td><td>- 0.0956</td><td>0.0956</td></tr><tr><td>６</td><td>0</td><td>0</td><td>0</td><td>26</td><td>0</td><td>0.1004</td><td>0.1004</td></tr><tr><td>10</td><td>- 1.1523</td><td>- 1.3305</td><td>-- 0.9738</td><td>28</td><td>0</td><td>- 0.0439</td><td>0.0439</td></tr><tr><td>11</td><td>0.2403</td><td>0.4907</td><td>-0.0105</td><td>29</td><td>0</td><td>0.0149</td><td>0.0149</td></tr><tr><td>13</td><td>0.0002</td><td>- 0.0005</td><td>0.0002</td><td>31</td><td>0</td><td>0</td><td>0</td></tr><tr><td>14</td><td>0</td><td>0</td><td>0.0001</td><td>32</td><td>0</td><td>0</td><td>0</td></tr><tr><td>16</td><td>0.6492</td><td>-0.7443</td><td>-0.5541</td><td>34</td><td>0</td><td>0</td><td>0</td></tr><tr><td>17</td><td>0.8270</td><td>1.2102</td><td>0.4439</td><td>35</td><td>0</td><td>0</td><td>0</td></tr><tr><td>19</td><td>0.6115</td><td>0 0.9528 一</td><td>0.2702</td><td>39</td><td>0</td><td>0.0127</td><td>- 0.0127</td></tr><tr><td>20</td><td>0.3398</td><td>-0.1723</td><td>-- 0.5073</td><td>40</td><td>0</td><td>0</td><td>0</td></tr><tr><td>22</td><td>0</td><td>0.0004</td><td>-0.0004</td><td></td><td></td><td></td><td></td></tr></table></body></html>  

表 11-17误差系数地面值引起的最大视速度偏差值 $(\mathbf{m}/\mathbf{s})$   


<html><body><table><tr><td>序号</td><td>△Wx</td><td>Wy</td><td>△Wz</td><td>序号</td><td>△W,</td><td>Wy</td><td>△W.</td></tr><tr><td>1</td><td>0.14558E + 1</td><td></td><td></td><td>21</td><td>0.11605E + 1</td><td>0.49755E + 0</td><td></td></tr><tr><td>2</td><td>1</td><td>0.51592E + 0</td><td></td><td>22</td><td></td><td>0.13790E - 5</td><td>0.80547E-3</td></tr><tr><td>3</td><td></td><td></td><td>0.45259E + 0</td><td>23</td><td>0.90461E - 5</td><td></td><td>0.95756E -- 3</td></tr><tr><td>4</td><td>0.29455E + 0</td><td></td><td></td><td>24</td><td>0.24714E -2</td><td>0.76605E -3</td><td></td></tr><tr><td>5</td><td></td><td>0.10572E + 0</td><td></td><td>25</td><td></td><td>0.35870E - 30.92247E + 0</td><td></td></tr><tr><td>6</td><td></td><td></td><td>0.20554E -3</td><td>26</td><td>0.14348E - 2</td><td></td><td>0.42837E + 0</td></tr><tr><td>7</td><td>0.16437E + 0</td><td></td><td></td><td>27</td><td>0.61498E + 0/0.10709E + 0</td><td></td><td></td></tr><tr><td>8</td><td></td><td>0.12087E + 0</td><td></td><td>28</td><td></td><td>0.84400E - 4</td><td>0.28126E + 0</td></tr><tr><td>9</td><td></td><td></td><td>0.46475E - 5</td><td>29</td><td>0.19879E - 4</td><td></td><td>0.28827E - 1</td></tr><tr><td>10</td><td></td><td>0.20276E -2]0.15373E + 1</td><td></td><td>30</td><td>0.11417E + 00.23904E - 1</td><td></td><td></td></tr><tr><td>11</td><td>0.28371E -2</td><td></td><td>0.54144E +0</td><td>31</td><td></td><td>0.21628E - 5</td><td>0.10536E -3</td></tr><tr><td>12</td><td>0.73386E + 1</td><td>0.25320E + 1</td><td></td><td>32</td><td>0.86513E - 5</td><td></td><td>0.62122E - 4</td></tr><tr><td>13</td><td></td><td>0.16856E - 5</td><td>0.81997E - 3</td><td>33</td><td>0.28126E + 0 0.28543E - 1</td><td></td><td></td></tr><tr><td>14</td><td>0.88412E -5</td><td></td><td>0.22928E -3</td><td>34</td><td></td><td>0.10043E-6</td><td>0.16587E --4</td></tr><tr><td>15</td><td>0.97015E + 1</td><td>0.26923E + 1</td><td></td><td>35</td><td>0.10510E -6</td><td></td><td>0.32306E - 5</td></tr><tr><td>16</td><td></td><td>0.14369E - 2|0.86216E + 0</td><td></td><td>36</td><td>0.12368E - 1</td><td>10.13418E - 1</td><td></td></tr><tr><td>17</td><td>0.74762E -- 2</td><td></td><td>0.15933E + 1</td><td>37</td><td>0.81000E - 1</td><td></td><td></td></tr><tr><td>18</td><td>0.34174E - 2</td><td>0.24036E - 3</td><td></td><td>38</td><td></td><td>0.20250E - 1</td><td></td></tr><tr><td>19</td><td></td><td>0.17040E - 2]0.13086E + 1</td><td></td><td>39</td><td></td><td></td><td>0.25313E - 1</td></tr><tr><td>20</td><td>0.26228E - 2</td><td></td><td>0.67475E +0</td><td>40</td><td></td><td>0.64366E + 0 0.42975E + 0 0.28117E - 2</td><td></td></tr></table></body></html>  

# 11.5.3 工具误差系数估计  

对实测的数据的处理分别采用主成分估计、贝叶斯估计、PP回归法和正交最小二乘估计法来估计制导工具误差系数。  

用OLSE方法进行参数估计时，为了充分利用地面试验的信息，首先将飞行试验数据与地面试验值相减，即  

\delta{\pmb{W}},=,\Delta{\pmb{W}},-,{\pmb{S}}{\pmb{C}}_{0}

  

式中， $\pmb{C_{0}}$ 取各误差系数在地面试验中测得的均值。令  

\pmb{C}^{\prime}:=:\pmb{C}:-:\pmb{C}_{0}

  

估计问题变成从  

\delta W;=;{\cal S C}^{\prime};+;\eta

  

中先估计出各误差系数与地面测试值之间的差值，最后得到各误差系数的估计结果。  

原则上，在用格拉姆-施密特法构造正交基时，对基变量的选择可自由选择，但在线性模型估计中应采用优先原则，即按自变量对观测值的相关程度进行选择，从而将重要项系数估计准确。其选择过程如下：  

为书写方便，仍记式（11-85）为  

{\textbf{y}}=,{\pmb{X}}{\pmb{\theta}},+,{\pmb{\xi}},=,\theta_{1}\pmb{x}{1},+,\theta{2},{\pmb{x}}{2},+,\cdots,+,\theta{p}{\pmb{x}}_{p},+,{\pmb{\xi}}

  

首先，求 $\pmb{x}_{i}$ 与 $\pmb{y}$ 之间的相关系数 $r_{i}$ ，有  

r_{i};=;\frac{\displaystyle\sum_{j,=,1}^{m}\left(,x_{i j},-,\overline{{{x}}}{i},\right)(,y{j},-,\overline{{{y}}},)}{\displaystyle\sqrt{,\sum_{j,=,1}^{m}\left(,x_{i j},-,\overline{{{x}}}{i},\right)^{2}},\sqrt{,\sum{j,=,1}^{m}\left(,y_{j},-,\overline{{{y}}},\right)^{2}}}

  

式中  

\begin{array}{c}{{\overline{{{x}}}{i},=,\displaystyle\frac{1}{m}\sum{j,=,1}^{m}x_{i j}}}\ {{\overline{{{y}}},=,\displaystyle\frac{1}{m}\sum_{j,=,1}^{m}y_{j}}}\end{array}

  

取 $^r$ 最大者对应的变量 $\pmb{x}_{k}$ 作为第一个基矢量  

进一步得到 $\hat{g}_{\textsc{i}}$  

\mathbf{y}^{\prime};=;\mathbf{y},-,\hat{\pmb{g}}{1},\pmb{w}{1}

  

对其余变量 $\pmb{x}_{i}\left(\,i\!\neq\!k\,\right)$ ，作变换使之与 $w_{1}$ 正交得 $\pmb{x}_{i}^{\prime}\left(\,i\neq k\,\right)$ ，并用$y^{\prime}$ 置换 $\pmb{y}$ 。重复上面步骤可求得第二、第三个基变量，直到最后。  

估计中考察各项对观测数据的贡献，当其贡献不足0.1%时，认为其对模型贡献不显著，予以剔除。  

用 OLSE方法和主成分估计、贝叶斯估计、PB 回归法分别对各误差系数进行估计，其估计结果列于表11-18。表中第一列是  

表 11-18 工具误差系数估计结果  


<html><body><table><tr><td>序号</td><td>下限</td><td>上限</td><td>PC</td><td>贝叶斯</td><td>PB</td><td>OLSE</td></tr><tr><td>1</td><td>-- 2.047</td><td>-1.</td><td>-1.732</td><td>- 2.377</td><td>- 2.041</td><td>- 1.524</td></tr><tr><td>2</td><td>0.639</td><td>1.</td><td>- 0.701</td><td>0.913</td><td>-0.346</td><td>0.803</td></tr><tr><td>3.</td><td>-1</td><td>- 0.486</td><td>0.342</td><td>-0. 0.537</td><td>-0.795</td><td>1.363</td></tr><tr><td>4</td><td>- 1.0</td><td>1.0</td><td>-0.189</td><td>0.672</td><td>- 0.183</td><td>0.0</td></tr><tr><td>5</td><td>- 1.0</td><td>1.0</td><td>1.047</td><td>- 0.460</td><td>0.864</td><td>0.0</td></tr><tr><td>7</td><td>-1.0</td><td>1.0</td><td>- 0.144</td><td>1.004</td><td>0.122</td><td>0.0</td></tr><tr><td>8</td><td>-1.0</td><td>1.0</td><td>1.912</td><td>- 0.876</td><td>1.402</td><td>-2.6 678</td></tr><tr><td>10</td><td>1.0</td><td>1.898</td><td>0.383</td><td>-0.135</td><td>0.359</td><td>1.449</td></tr><tr><td>11</td><td>-0.65</td><td>1.0</td><td>0.946</td><td>1. .089</td><td>0.995</td><td>0.901</td></tr><tr><td>12</td><td>1.0</td><td>1.235</td><td>0.115</td><td>1.616</td><td>0.114</td><td>2.612</td></tr><tr><td>15</td><td>-- 1.376</td><td>-1.0</td><td>0.009</td><td>- 1.801</td><td>0.053</td><td>- 2.354</td></tr><tr><td>16</td><td>1</td><td>1.829</td><td>0.835</td><td>1.424</td><td>0.850</td><td>1.414</td></tr><tr><td>17</td><td>0.038</td><td>1.0</td><td>-0.026</td><td>0.6 654</td><td>0.000</td><td>0.519</td></tr><tr><td>19</td><td>-0.055</td><td>1.0</td><td>1.124</td><td>1.2 248</td><td>1.088</td><td>0.473</td></tr><tr><td>20</td><td>-1.0</td><td>- 0.007</td><td>0.498</td><td>-0.716</td><td>0.516</td><td>- .503</td></tr><tr><td>21</td><td>0.078 #</td><td>1.0</td><td>0.985</td><td>2.232</td><td>1.079</td><td>0.461</td></tr><tr><td>25</td><td>-1</td><td>1</td><td>-- 2.397</td><td>-2 868</td><td>- 2.537</td><td>0.0</td></tr><tr><td>26</td><td>-1</td><td>1</td><td>0.494</td><td>0.623</td><td>0.538</td><td>0.0</td></tr><tr><td>27</td><td>-1</td><td>1</td><td>-1.301</td><td>1.629</td><td>-1.534</td><td>0.0</td></tr></table></body></html>  

（续）  

<html><body><table><tr><td>序号</td><td>下限</td><td>上限</td><td>PC</td><td>贝叶斯</td><td>PB</td><td>OLSE</td></tr><tr><td>28</td><td>-1</td><td>1</td><td>- 0.139</td><td>- 0.029</td><td>- 0.146</td><td>- 0.407</td></tr><tr><td>29</td><td>-1</td><td>1</td><td>0.017</td><td>- 0.025</td><td>0.018</td><td>0.0</td></tr><tr><td>30</td><td>-1</td><td>1</td><td>- 0.031</td><td>0.077</td><td>- 0.023</td><td>1.424</td></tr><tr><td>33</td><td>-1</td><td>1</td><td>- 0.128</td><td>0.091</td><td>-0.122</td><td>0.0</td></tr><tr><td>37</td><td>-1</td><td>1</td><td>- 0.296</td><td>0.728</td><td>-0.481</td><td>0.0</td></tr><tr><td>38</td><td>-1</td><td></td><td>0.247</td><td>- 2.358</td><td>0.272</td><td>0.0</td></tr><tr><td>39</td><td>- 1</td><td>1</td><td>1.136</td><td>1.741</td><td>1.185</td><td>0.0</td></tr><tr><td>40</td><td>-1</td><td>1</td><td>- 0.037</td><td>0.111</td><td>0.000</td><td>0.185</td></tr><tr><td colspan="3">在上下限范围以内项</td><td>10</td><td>15</td><td>12</td><td>22</td></tr><tr><td colspan="3">在上下限范围以外项</td><td>17</td><td>12</td><td>15</td><td>5</td></tr></table></body></html>  

各误差系数的序号，第2、3列分别是误差系数地面试验值的下限和上限，后面4列是几种方法的估计值，表中最后两行统计了各方法估计结果落入上下限范围的项数。从表中的数据看出，PC法有10 项系数的估计值落在验前信息范围以内,有 17项系数的估计值不在其验前范围内。贝叶斯方法有15项系数的估计值洛在地面值的范围内,有 12 项在该范围以外。PB 法估计值则相反,有12 项系数的估计值在给定的范围内，15项在范围以外。而OLSE的估计结果有 22项系数估计值在它们各自的上下限范围内,只有5项系数的估计值不在该范围。不仅如此,而且其对飞行试验数据的拟合程度较之其他三种方法要好。图 11-10～图 11-13 给出了它们各自对视速度差的估计曲线图。从拟合的曲线可以看出，OLSE方法对三个方向的视速度差的拟合优度均较好，贝叶斯估计对y方向视速度差拟合较好，其余PB法和PC法对视速度差的拟合则不如OLSE估计的拟合效果好。  

从表中的估计结果可以看出，儿种方法的估计值彼此之间具有一定的差异，但相对于上下限值而言，基本上没有量级上的差别,大多数估计值都在验前范围附近。从几种方法的估计看来，模型中的第29，40均很小,第11项系数的估计值非常接近。  

![](images/12d85344fd7b54ddce7a907b344484af988eab53a6c61d342a809f5d59eea5a3.jpg)  
图 11-10 视速度差辨识曲线（PC）  

![](images/2c843554c463aa7e090007953468b3b3b4d58e6235327363fe5ca2c12d465f38.jpg)  
图 11-11 视速度差辨识曲线（PB）  

![](images/d09954f97704e0517e5c1d0a803f2a9d9227e0437345f04943c127430d80c666.jpg)  
图 11-12视速度差辨识曲线(Bayes)  

![](images/628137f8570cee8e285aefa144a97faf5f2b620e332f42543856ce46f73e1ad4.jpg)  
图 11-13 视速度差辨识曲线（OLSE）  

OLSE估计的结果中，第三项系数 $\hat{k}_{a0z}$ 与其地面测试值反号，大小是其地面值的近2倍， $\mathbf{\Deltay}$ 向加速度计的二次误差系数 $\hat{k}_{a2y}$ 超出了其地面设计指标值1.68倍,同时,系数 $\hat{k}_{g0z}$ 和 $\hat{k}_{g11z}$ 也分别超出了其地面测试值区间，另外，第30项系数平台 $\pmb{z}$ 向的一次项$\hat{k}_{\textsc{p l z}}^{\prime}$ 也落在了其设计指标范围以外。除此而外，其他参数全在其地面测试值范围以内且与地面数据十分吻合。  

按照参考文献[7]对估计方法性能优劣的评价标准，估计结果落人验前信息范围内的越多，估计的拟合优度越高，则估计方法越优良。显然，用OLSE估计方法来处理工具误差问题是有效的。  

# 附录A静态误差模型中的环境函数  

附表 A1静态误差模型式(11-38)中环境函数表  


<html><body><table><tr><td>序号</td><td>C:</td><td>S(t)</td><td>S:(t)</td><td>S:(t)</td></tr><tr><td>1</td><td>ka0x</td><td></td><td></td><td></td></tr><tr><td>2</td><td>Raoy</td><td></td><td>t</td><td></td></tr><tr><td>3</td><td>kaoz</td><td></td><td></td><td></td></tr><tr><td>4</td><td>kalr</td><td>W.</td><td></td><td></td></tr><tr><td>5</td><td>katy</td><td></td><td>W,</td><td></td></tr><tr><td>6</td><td>kalx</td><td></td><td></td><td>W.</td></tr><tr><td>7</td><td>ka2r</td><td>W²(t)dz 30</td><td></td><td></td></tr><tr><td>8</td><td>ka2y</td><td></td><td>[w?(t)dt J0</td><td></td></tr><tr><td>9</td><td>ka2r</td><td></td><td></td><td>W²(t)dr J0</td></tr><tr><td>10</td><td>kg0r</td><td></td><td>rWdt 0</td><td>rW,dt 0</td></tr><tr><td>11</td><td>x04</td><td>rW_dt</td><td></td><td>['cWdt J0</td></tr><tr><td>12</td><td></td><td>f'eW,dt J0</td><td>rW,dt 0</td><td></td></tr><tr><td>13</td><td>kgllr</td><td></td><td>0.5w2</td><td>W:W,dt /0</td></tr><tr><td>14</td><td>kxlly</td><td>0.5w?</td><td></td><td>WWdt</td></tr></table></body></html>  

(续）  

<html><body><table><tr><td></td><td></td><td></td><td></td><td>S(t)</td></tr><tr><td>序号</td><td></td><td>S(t)</td><td>S(t)</td><td></td></tr><tr><td>15</td><td>kgl1z</td><td>0.5 W2</td><td>W,Wdt 0</td><td></td></tr><tr><td>16</td><td>kg121</td><td></td><td>Wwdt J0</td><td>WW,dt 0</td></tr><tr><td>17</td><td>kg12y</td><td>W,Wdt</td><td>WWdt</td><td>w,W&dt</td></tr><tr><td>18</td><td>kg12x</td><td>WW,dr Jo</td><td>Jo W,W-dt</td><td>W,Wydr</td></tr><tr><td>19</td><td>kg13x</td><td>WW.dr</td><td></td><td>0.5w2</td></tr><tr><td>20</td><td>kx13y</td><td></td><td>- 0.5w2</td><td></td></tr><tr><td>21 22</td><td>kx13z</td><td>Jw,w,dt</td><td>Weferdr</td><td>ft Wyferdt</td></tr><tr><td></td><td>Rgrt</td><td>Ct Weferdt</td><td></td><td>J0 {'Wserdt</td></tr><tr><td>23</td><td>RRX</td><td>J0</td><td>Wzferdt</td><td>Jo</td></tr><tr><td>24</td><td></td><td>Wferdt Ja</td><td>{t Wefadt</td><td>Wfndt</td></tr><tr><td>25</td><td>Rxxya</td><td></td><td>Jo</td><td>Wfydt</td></tr><tr><td>26</td><td></td><td>2p"fM, J0</td><td></td><td>0</td></tr><tr><td>27</td><td>Rgzyz</td><td>Wfadt J0</td><td>Wrfadt Wefaydt</td><td>Wfaydt</td></tr><tr><td>28</td><td>Rgrry</td><td></td><td>0</td><td>0 Wzfzydt</td></tr><tr><td>29</td><td>RAyIy</td><td>Jo</td><td></td><td></td></tr><tr><td>30</td><td>Rgzry</td><td>Wfndt J0</td><td>Wefxydt</td><td></td></tr></table></body></html>  

(续）  


<html><body><table><tr><td>序号</td><td>Ci</td><td>S(t)</td><td>S(t)</td><td>S(t)</td></tr><tr><td>31</td><td>RgII</td><td></td><td>Wefrrdt</td><td>Ct Wfxrdt Ja</td></tr><tr><td>32</td><td></td><td>Wefdt V0</td><td></td><td>Wzfcrdt 0</td></tr><tr><td>33</td><td>RgZr</td><td>Wfxxdt Jo</td><td>Wfrrdr</td><td></td></tr><tr><td>34</td><td>Rgry</td><td></td><td>Wfndt</td><td>Wafndt</td></tr><tr><td>35</td><td></td><td>Wefndt Jo</td><td></td><td>Wefydt</td></tr><tr><td>36</td><td>Rgry</td><td>Wsndt 00</td><td>Wfydt</td><td></td></tr><tr><td>37</td><td></td><td></td><td>Wfdt 0</td><td>'Wfadt Jo</td></tr><tr><td>38</td><td></td><td>Wfadt</td><td></td><td>Wsadt √0</td></tr><tr><td>39</td><td></td><td>Wfeadt</td><td>Wefndt</td><td></td></tr><tr><td>40</td><td>α par</td><td></td><td>Wx</td><td>-Wy</td></tr><tr><td>41</td><td>αpoy</td><td>- W.</td><td></td><td>Wx</td></tr><tr><td>42</td><td>α pox</td><td>Wy</td><td>-Wx</td><td></td></tr><tr><td>43</td><td>kp1x</td><td></td><td>['wW,dt J0</td><td>W2dr</td></tr><tr><td>44</td><td>kpty</td><td>WWdt</td><td></td><td>W2dt Jo</td></tr><tr><td>45</td><td>kp1z</td><td>['WW,dt 0</td><td>W2dt 0</td><td></td></tr><tr><td>46</td><td>kp1r</td><td></td><td>'wdt J0</td><td>WW,dt 0</td></tr></table></body></html>  

(续）  

<html><body><table><tr><td>序号</td><td>Ci</td><td>S(t)</td><td>S(t)</td><td>S,(t)</td></tr><tr><td>47</td><td>k1y</td><td>W²dt 0</td><td></td><td>WWdt J0</td></tr><tr><td>48</td><td>klz</td><td>rt Wdt 0</td><td>WW,dt 0</td><td></td></tr><tr><td>49</td><td>kp2x</td><td></td><td>Wd( w,W)</td><td>Wd(w,W)</td></tr><tr><td>50</td><td>kp2y</td><td>Wd(WW)</td><td></td><td>Wd(WW)</td></tr><tr><td>51</td><td>Rp2z</td><td>Wd(WW)</td><td>Wd(WW,)</td><td></td></tr><tr><td>52</td><td>Rprz</td><td></td><td>WWdt Jo</td><td>W,Wdt Jo</td></tr><tr><td>53</td><td>kpyu</td><td>WW -dt</td><td></td><td>['wW-dt J0</td></tr><tr><td>54</td><td>Rpzz</td><td>W,Wdr J0</td><td>W-Wrdt 0</td><td></td></tr><tr><td>55</td><td>kpry</td><td></td><td>WW,dt</td><td>W,W,dt Jo</td></tr><tr><td>56</td><td>kpr</td><td>W,Wdt 0</td><td></td><td>WWedt</td></tr><tr><td>57</td><td>kp2y</td><td>WWydr</td><td>W W,dr</td><td></td></tr><tr><td>58</td><td>k2x</td><td></td><td>WW,Wdt 10</td><td>WW=dt J0</td></tr><tr><td>59</td><td>kp2y</td><td>W2Wdt</td><td></td><td>W2W-dt</td></tr><tr><td>60</td><td>k2x</td><td>WWdt J0</td><td>W2W,dr J0</td><td></td></tr><tr><td colspan="6">注:表中 f = W;W; du (i,j = x,y,z) 0</td></tr></table></body></html>  

附表 A2静态误差模型 $(11\!-\!40)\!\sim\!(11\!-\!42)$ 中环境函数表  


<html><body><table><tr><td>序号</td><td>Ci</td><td>S(t)</td><td>S(t)</td><td>S(t)</td></tr><tr><td></td><td>kaor</td><td></td><td></td><td></td></tr><tr><td>2</td><td>kaoy</td><td></td><td></td><td></td></tr><tr><td>3</td><td>ka0z</td><td></td><td></td><td></td></tr><tr><td>4</td><td>ka1x</td><td>Wr</td><td></td><td></td></tr><tr><td>5</td><td>kaly</td><td></td><td>W,</td><td></td></tr><tr><td>6</td><td>kalx</td><td></td><td></td><td>W.</td></tr><tr><td>7</td><td>ka2x</td><td>W²(t)dt J0</td><td></td><td></td></tr><tr><td>8</td><td>Ra2y</td><td></td><td>'W(t)dt J0</td><td></td></tr><tr><td>6</td><td>ka2z</td><td></td><td></td><td>W²(r)dt</td></tr><tr><td>10</td><td>kg0r</td><td></td><td>['W-dt 0</td><td>tW,dt</td></tr><tr><td>11</td><td>kg0y</td><td>tW,dt Jo</td><td></td><td>'tWdt Jo</td></tr><tr><td>12</td><td>204</td><td>JW,dz √0</td><td>'tWzdr Jo</td><td></td></tr><tr><td>13</td><td>hgll1</td><td></td><td>0.5 W?</td><td>WW,dt</td></tr><tr><td>14</td><td>kgl1y</td><td>0.5w2</td><td></td><td>WW-dt</td></tr><tr><td>15</td><td>Rgll2</td><td>0.5 W2</td><td>W,Wzdt</td><td></td></tr><tr><td>16</td><td>kx12x</td><td></td><td>ft WWzdt J0</td><td>W-W,dt</td></tr><tr><td>17</td><td>kg12y</td><td>W,Wdt</td><td></td><td>W,Wrdt √0</td></tr><tr><td>18</td><td>kg12x</td><td>WW,dt</td><td>W-W-dr 0</td><td></td></tr></table></body></html>  

(续）  

<html><body><table><tr><td>序号</td><td>C;</td><td>S(t)</td><td>S,(t)</td><td>S,(t)</td></tr><tr><td>19</td><td>kx13x</td><td></td><td>W,W-dt 0</td><td>W,W,dt 0</td></tr><tr><td>20</td><td>kg13y</td><td>WWzdt J0</td><td></td><td>0.5 w2</td></tr><tr><td>21</td><td>kx13x</td><td>W,W,dt 0</td><td>-0.5w2</td><td></td></tr><tr><td>22</td><td>Rgrry</td><td></td><td>Wefrydt Jo</td><td>Wfxdt √0</td></tr><tr><td>23</td><td>Rgxry</td><td>Wefzydt</td><td></td><td>Wfrydt Jo</td></tr><tr><td>24</td><td>Rgzry</td><td>Wfrydt Jo</td><td>Wfndt 0</td><td></td></tr><tr><td>25</td><td>Ra</td><td></td><td>Wfxxdr</td><td>Wfrdt 0</td></tr><tr><td>26</td><td></td><td>Wfudt 0</td><td></td><td>Wferdt</td></tr><tr><td>27</td><td>kger</td><td>Wfadt 00</td><td>Wzfxxdt Jo</td><td></td></tr><tr><td>28</td><td>kgry</td><td></td><td>Wfndt</td><td>Wzfydt J0</td></tr><tr><td>29</td><td></td><td>Wfndt</td><td></td><td>Ct Wefndt 0</td></tr><tr><td>30</td><td>K</td><td>Wyndt 0</td><td>Wafndt Jo</td><td></td></tr><tr><td>31</td><td>αpor</td><td></td><td>Wz</td><td>W</td></tr><tr><td>32</td><td>α poy</td><td>- W,</td><td></td><td>Wz.</td></tr><tr><td>33</td><td>α pox.</td><td>W,</td><td>-Wx</td><td></td></tr><tr><td>34</td><td>kpiz</td><td></td><td>fww,dt J0</td><td>W2dt</td></tr></table></body></html>  

(续）  


<html><body><table><tr><td>序号</td><td>C;</td><td>Sx(t)</td><td>S,(t)</td><td>S(t)</td></tr><tr><td>35</td><td>kp1y</td><td>WWdt</td><td></td><td>W2dr 0</td></tr><tr><td>36</td><td>k1x</td><td>WWdt Jo</td><td>W2dt</td><td></td></tr><tr><td>37</td><td>k1y</td><td>ft W2dr 0</td><td></td><td>WWdr Jo</td></tr><tr><td>38</td><td>k1z</td><td>W²dt J0</td><td>WWydt</td><td></td></tr><tr><td>39</td><td>kp2z</td><td>{Wd(WW)</td><td>Wd(wW,)</td><td></td></tr><tr><td>40</td><td>kpyuz</td><td>WWrdt 0</td><td></td><td>WWdt 0</td></tr><tr><td>41</td><td>Rprr</td><td>WWdz 0</td><td>WWdt</td><td></td></tr><tr><td>42</td><td>kpry</td><td></td><td>WWydr 0</td><td>W,Wdt 0</td></tr><tr><td>43</td><td></td><td>W,W=dr</td><td></td><td>WWdt</td></tr><tr><td>44</td><td>kp2y</td><td>WWydt J0</td><td>WW,dt 0</td><td></td></tr><tr><td>45</td><td>kp2x</td><td>[wwdt V0</td><td>W2W,dr</td><td></td></tr></table></body></html>  

# 参考文献  

1 Constant J N. Fundamentals of Strategic Weapons Offence and Defense Systems. Martinus Vigholf Publishers, 1981  

2杨辉耀．弹道导弹精度提高与再人误差分析研究[博士学位论文］．西安：西北工业大学，1995  

3沙钰等编·弹道导弹精度分析概论．长沙：国防科技大学出版社，1995  

4蔡金狮等．飞行器系统辨识．北京：宇航出版社，1995  

5DrukerAN．火箭飞行器制导系统的性能分析．王永平译，1992  
6  Weinman R W , Rutkoskie J V. Development, Performance Assessment, and Verifica-tion of a Calibration and Alignment Technique for a Precision IMU. AIAA 81 - 1745,19857宗绍录等．战略导弹精度分析论文选集．航空航天工业部科技司，1991  
8程光显．误差分离演练报告．航天工业总公司一院一部技术报告，1998  
9陈希孺，王松桂．近代回归分析．合肥：安徽教育出版社，198710张金槐．线性模型参数估计及其改进．长沙：国防科技大学出版社，1992  
11 刘利生，刘德怡．外测系统模型误差的辨识．飞行器测控技术，（2），1987  
12 刘希珠，雷田玉．陀螺力学原理．北京：清华大学出版社，1987  
13张金槐．远程火箭精度分析与评估，长沙：国防科技大学出版社，1995  
14 Huddle J R. Inertial Navigation System Error -- Model Consideration in Kalman Filter-ing Applications. Control and Dynamic Systems, 20  
15  Sun Mei. Use of GPS for Evaluating Inertial Measurement Unit Errors. AD A -3065216, 1996  
16  Bateman V 1. Drift Prediction for a Roll - Stabilized Inertial Measuremcnt System.SAND - 82 - 1877C  
17 Heck M. The Adaptation of a Strap Down Formulation for Processing Inertial PlatformData. AIAA 82 - 1332, 1982  
18 张金槐，利用验前信息的-种序贯检验方法，国防科技大学学报，13，1991  
19  Peterson E. Sled Testing of the Missile X ADP/AIRS System. AD A - 1076162  
20张国瑞．美国洲际弹道导弹制导精度的鉴定．国外导弹技术，9，1982  
21张宗美，惯性仪表误差的分离技术，国外导弹技术，8，1984  

# 第12章分布参数系统辨识  

12.1 概述  

分布参数系统辨识是系统辨识的一个重要分支，在工程热物理、石油地质勘探、航空航天领域有着广阔的应用前景。它是近年来随着计算技术和集中参数系统辨识研究的发展而发展起来的。集中参数系统是指具有有限个自由度的物理系统，而分布参数系统是指具有无限个自由度的物理系统。用数学语言讲，集中参数系统是用常微分方程或代数方程来描述其运动规律的系统，分布参数系统则是用偏微分方程，或偏微分积分方程，或偏微分方程与常微分方程的耦合方程来描述其运动规律的系统。例如，热传导系统、导弹结构弹性振动动力学系统、柔性和刚性机器人系统等都是分布参数系统[1。目前,工程上对集中参数系统辨识的研究比较深人，并在工程实际问题中得到了广泛应用。分布参数系统的辨识研究则是与集中参数系统辨识的研究大致同时进行的，从某种意义上来说，分布参数系统辨识方法是集中参数系统辨识理论和方法的推广。但是，由于分布参数系统所描述物理现象的复杂性，考虑的是无限维系统，它不仅要考虑时间，还要考虑空间，这就决定了分布参数系统辨识有其区别于集中参数系统辨识的固有特点，形成了一些特殊的方法[2!  

集中参数系统辨识在飞行器设计和试验中得到较为广泛的应用，本书前11章主要是针对集中参数系统辨识进行论述，其中一些辨识准则和算法在分布参数辨识系统中仍可应用。本章阐述分布参数系统辨识的一般算法及其在气动热参数辨识和工程湍流模  

# 型辨识中的应用。  

# 12.2 基本辨识算法  

分布参数系统状态方程组的一般形式可写为  

\left{\begin{array}{l l}{E\left(\left.u,,x,,\theta,,\iota\right)=0}&{x\in\Omega\quad\iota\in[0,,T]}\ {B\left(\left.u,,x,,\theta,,\iota\right)=0}&{x\in\partial\Omega\quad t\in[0,,T]}\ {I\left(\left.u,,x,,\theta,,0\right)=0}&{x\in\Omega}\end{array}\right.\right.

  

观测方程为  

\pmb{Z}(,\pmb{x}{m},,t{m},)=\pmb{C}[,\pmb{u},(,\pmb{x}{m},,\pmb{\theta},,t{m},),]+\pmb{\varepsilon}(,t_{m},)

  

式中 ${\pmb u}$ -状态矢量；  

$\pmb{x}$ 位置矢量；$\pmb{\theta}$ —未知参数矢量；$\pmb{\varepsilon}(t)$ ——测量噪声；$\Omega$ -—状态矢量的定义域；$\partial\Omega\!\!\!\!\longrightarrow\!\!\!\!\Omega$ 的边界；${\pmb E}$ ——状态函数；$\pmb{B}$ --边界条件函数；I—初值条件函数；$\pmb{C}$ —观测函数；下标“m”表示测量值。  

所谓分布参数系统辨识，就是由该系统的观测信息来确定系统函数 $\mathbf{\nabla}E\,,B\,,I\,,C$ 中的未知部分。其辨识方法大致可分为两大类：一类是基函数法，又称为直接方法，该方法是将偏微分状态方程投影到有限维空间，从而将分布参数系统辨识向题转化为一集中参数系统辨识问题来处理；另一类是最优化方法，将辨识问题转化为优化问题来求解，也称为间接方法，在这类方法中，根据优化策略选取的不同，又可分为伴随方程法和灵敏度法等。以下各节将分别对这两类辨识方法进行介绍。  

# 12.2.1 基函数方法  

1）基本思想  

基函数方法是用“有限”来逼近“无限”，将状态变量展开为基函数的有限级数或用基函数作插值逼近，从而将分布参数系统的偏微分状态方程化为常微分方程或代数方程，再用集中参数系统和代数系统的辨识方法来辨识系统中的未知参数3。分布参数系统的状态方程可写为  

F(,{\pmb u},,x,,{\pmb\theta},,t,,\partial{\pmb u}/\partial{\pmb x},,\partial{\pmb u}/\partial t,,\partial^{2}{\pmb u}/\partial{\pmb x}^{2},,\cdots)={\bf0}

  

将状态矢量 $\pmb{u}$ 的诸分量 $u_{i}$ 均在各自的基函数系 $\left\{\right.\oint_{i j}\big\}_{j}=1\,,2\,,\cdots,N$ 展开，当基函数只是位置的函数时，有  

\pmb{u}{i}\ =\ \sum{j\mathop{=}1}^{N}a_{i j}\left(\ t\right)\pmb{\phi}{{i j}}(\pmb{x})

  

此时的式（12-3)化为  

G\left(,{a}{i j},,\mathrm{d}{a}{i j}/\mathrm{d}t,,{\pmb x},,{\pmb\theta},,t,,{\pmb\phi}{i j},,\mathrm{d}{\pmb\phi}{i j}/\mathrm{d}{\pmb x},,\cdots\right),=,{\bf0}

  

上式对应的则是-一以常微分方程为状态方程的集中参数系统辨识问题，可以套用集中参数系统的辨识方法来处理。这类方法中比较典型的有伽辽金（Galerkin）方法和有限元法。  

当基函数同时是位置和时间的函数时，则有  

u_{i};=;\sum_{j,=,1}^{N}a_{i j}\psi_{i j}\left(,\pmb{x},,t,\right)

  

从而可将式（12-3）化为  

H(,a_{i j},,\pmb{x},,\pmb{\theta},,t,,\pmb{\phi}{i j},,\partial,\pmb{\phi}{i j}/\partial,\pmb{x},,\partial,\pmb{\phi}_{i j}/\partial,t,,\cdots),=,\pmb{0}

  

此式对应的是一个代数系统的参数辨识问题，易于进行处理。这类方法中比较典型的有切比雪夫（Chebyshev）多项式法和块脉冲算子法。其中，块脉冲算子法是以块脉冲函数系为正交基函数系，而块脉冲函数系与著名的沃尔什（Walsh）函数系类似，是一类取离散值的正交函数系，由它导出的算法一般具有形式简单、计算方便、便于递推处理的优点，特别是其运算中普遍采用了运算矩阵的形式，使它的表达和计算更为简洁。近年来，块脉冲函数系和块脉冲算子已被广泛应用于系统分析、辨识和控制等诸多领域，成为一种很有特色的方法[4]。下面两小节将以块脉冲算子法为例来进一步说明基函数法辨识分布参数系统的方法及其在实际问题中的应用。  

2）块脉冲算子法简介  

块脉冲算子法以块脉冲函数系为正交基函数系。下面给出块脉冲函数系和块脉冲算子的定义。  

定义1在区间 $[0,T]$ 上定义如下函数系：  

\phi_{i}(,t,),=,\left{\sqrt{,m/,T,},,,,,t,\in,[,(,i,-,1),T/,m,,i T/,m,]\right.

  

式中 m——自然数;  

i=1,2,\cdots,m\circ

  

函数系 $\left\{\;\phi_{_i}\;\right\}{_{i}}=1,2,\cdots,m$ 称为 $[0,T]$ 区间上的块脉冲函数系。可以证明， $\left\{\,\oint_{i}\,\right\}_{i}=1\,,2\,,\cdots,m$ 是希尔伯特(Hilbert)空间 $L^{2}[0,T]$ 的一组完全的正交基。其中 $L^{2}$ 上的内积定义为  

\langle f(x),g(x)\rangle_{L^{2}},=\int_{0}^{T}f(x)g(x)\mathrm{d}x

  

定义 2对任意自然数 $^{m}$ 和任一函数 $f(x)\in L^{2}[0,T]$ ，定义一维块脉冲算子 $B_{1}$ 如下：  

B_{1}f(,t,),=,\boldsymbol{F}^{\mathrm{T}},=,(f_{1},f_{2},\cdots,f_{m})

f_{i},=,\left\langle,f(,t,),,\phi_{i}(,t,),\right\rangle,=,\sqrt{,m/,T}\int_{,(,i-1),T/m}^{i T/m}f(,t,),\mathrm{d}t

  

若定义 $f_{m}\left(\,t\,\right)=\ \sum_{i\mathop{=}1}^{m}f_{i}\phi_{_i}\left(\,t\,\right)$ ,则当 $m\rightarrow\infty$ 时， $f_{m}\left(t\right)$ 均方收敛于$f(t)_{0}$  

定义 3  设 $f(\v{e}_{x}\,,\v{y})$ 表示区域 $E_{2}$ （定义为 $\{\,(\,x\,,y\,)\,\}\mid x\in[\,0\,,$ $T_{1}\big]\,,y\in\lbrack0\,,T_{2}\rbrack\,\big\}\,\big.$ 上的平方可积函数,即 $f\!\in\!L^{2}(\,E_{2})\circ\,E_{2}$ 上的二元块脉冲函数系定义为  

\phi_{{i j}}(,x,,y,),=,\left{\sqrt{\frac{m,1,m,2}{T{1},T_{2}}}\quad(,x,,y,),\in,\Delta_{{i j}}\right.

\Delta_{i j};=;\left{,(,x,,y,),\bigg\vert;x,\in,\Big[,\frac{(,i,-,1,),T_{1}}{m,1},,\frac{i T_{1}}{m,1}\Big],;\right.

y\in\left[\frac{\left(j\mathrm{-}1\right)T_{2}}{m2},\frac{j T_{2}}{m2}\right]\bigg}

  

式中 $i=1,2,\cdots,m\,1$  

j=1,,2,,\cdots,m,2,_{\circ}

  

由 $\big\{\,\phi_{_{i j}}\,\big\}$ 张成的线性子空间记为  

N_{m,1,m,2},=,\operatorname{span}{,\phi_{_{i j}},(,i,=,1,,2,,\cdots,m,1,;j,=,1,,2,,\cdots,m,2,),}

  

二元块脉冲函数矢量记为  

\Phi_{2}(,x,,y,);=;(,\pmb{\phi}{11},,\pmb{\phi}{12},,\cdots,,\pmb{\phi}{1m2},,\cdots,,\pmb{\phi}{m1m2},)^{\intercal}

  

则 $f(x\,,y)$ 的二元块脉冲算子定义为  

B_{2}f(\l,x,,y,),=,(,f_{11},,f_{12},,\cdots,,f_{1m2},,\cdots,,f_{m1m2},)

f_{i j}^{\phantom{}}=\sqrt{\frac{m,1,m^{2}}{T_{1},T_{2}}}\underset{^\Delta_{i j}}{\iint}f(,\boldsymbol{x},,\boldsymbol{y}),\mathrm{d}\boldsymbol{x},\mathrm{d}\boldsymbol{y}

  

若用 $f_{m\,1\,m\,2}^{}(\,x\,,y\,)=[\,B_{2}^{}f]\cdot\Phi_{2}^{}$ 表示 $f(\v{e}_{x}\,,\v{y})$ 在 $N_{m\,1\,m\,2}$ 上的投影，则 $m\!\mathrm{~}1\,,m\!\mathrm{~}2\!\!\rightarrow\!\infty$ 时， $f_{m,1m2}(x\,,y)$ 均方收敛于 $f(x\,,y)$ 。  

从上述定义出发，可以推出块脉冲算子的诸多性质与运算规则。其中，关于块脉冲算子积分运算的规则是进行分布参数系统辨识的基础。一维块脉冲算子的积分运算规则由下式给出  

B_{1}\Bigl[\int_{0}^{t}f(,\d x)\mathrm{d}x\Bigr]\simeq[,B_{1}f(,t),]P_{m}

B_{1}\biggl[\int_{t}^{T}!f(x)\mathrm{d}x\biggr]\simeq[,B_{1}f(,t,),]P_{m}^{T}

  

式中 $^{\bullet}\simeq^{\bullet}-$ 渐近相等”,即 $\alpha{\simeq}\beta{\leftrightarrow}\parallel\alpha-\beta\parallel{\rightarrow}0($ 当 $_{m\rightarrow\infty})$ ’$\boldsymbol{P}_{m}$ 运算矩阵：  

P_{m},=,\frac{T}{m}\left[\begin{array}{c c c c}{{1/2}}&{{1}}&{{\cdots}}&{{1}}\ {{0}}&{{1/2}}&{{\cdots}}&{{1}}\ {{\vdots}}&{{\vdots}}&{{\ddots}}&{{\vdots}}\ {{0}}&{{0}}&{{\cdots}}&{{1/2}}\end{array}\right]\quad

  

二维块脉冲算子的积分运算规则由以下诸式给出：  

B_{2}\biggl[\int_{0}^{x}\biggr\lbrack f(x^{'},t^{'})\mathrm{d}x^{'}\mathrm{d}t^{'}\biggr]\simeq\bigl\lbrack B_{2}f(x^{'},t)\bigr\rbrack\bigl\lbrack P_{m1}\otimes P_{m2}\bigr\rbrack

B_{2}{\biggl[}\int_{x}^{T_{1}}!!!\int_{\iota}^{T_{2}}!!!f(x^{\prime},t^{\prime}){\mathrm{d}}x^{\prime}{\mathrm{d}}t^{\prime}{\biggr]}!!\simeq[,B_{2}f(x,,t,),]{,}[,P_{m1}^{T}\otimes P_{m2}^{T},]

B_{2}\biggl[\int_{0}^{x}f({\bf\Phi}x^{'},t)\mathrm{d}x^{'}\biggr]\simeq[,B_{2}f({\bf\Phi}x,t),][,P_{m1}\otimes I_{m2},]

B_{2}\Bigl[\int_{x}^{T_{1}}!!f(,x^{\prime},,t,)\mathrm{d}x^{\prime},\Bigr]!\simeq\left[,B_{2}f(,x,,t,),\right]!\left[,P_{m1}^{T}\otimes I_{m2},\right]

B_{2}\biggl[\int_{0}^{t}f(x^{'},t^{'})\mathrm{d}t^{'}\biggr]\simeq\bigl[,B_{2}f(x^{},t),\bigr]\bigl[,I_{m1}\otimes P_{m2},\bigr]

B_{2}\biggl[\int_{t}^{T_{2}}!!f(,x,,t^{\prime},),\mathrm{d}t^{\prime}\biggr]\simeq[,B_{2}f(,x,,t,),],[,I_{m1}\otimes{\cal P}_{m2}^{T},]

B_{2}[,f(\l_{x}),],=,\big[,B_{1}f(\l_{x}),\big]\otimes e_{2}^{T}\quad B_{2}[,g(\l_{t}),],=,e_{1}^{T}\bigotimes\big[,B_{1}g(\l_{t}),\big]

  

式中 $I_{m i}(\,i=1\,,2\,)$ —单位矩阵；  

Pm:(i=1,2)-—积分运算矩阵,与其一维情况下的表达形式相同；  

$\pmb{e}_{i}^{T}=\sqrt{T_{i}/m_{i}}\left(1,1\,,\cdots,1\right)_{1\times m};$ $^{\bullet}\bigotimes^{\bullet\bullet}$ 一矩阵直积，即设 $\pmb{A}=\left(\mathbf{\,}a_{i j}\right),\pmb{B}=\left(\mathbf{\,}b_{i j}\right)$ 为二矩阵,其直积为  

\mathbf{A}\otimes B,=,{\left[\begin{array}{l l l l l}{a_{11}B}&{a_{12}B}&{\cdots}&{a_{1n}B}\ {}&{}&{}&{}\ {a_{21}B}&{a_{22}B}&{\cdots}&{a_{2n}B}\ {}&{}&{}&{}\ {\cdots}&{\cdots}&{\cdots}&{\cdots}\ {}&{}&{}&{}\ {a_{m1}B}&{a_{m2}B}&{\cdots}&{a_{m n}B}\end{array}\right]}

  

3）块脉冲算子法辨识算例  

考虑如下热传导系统,其主控方程为  

\begin{array}{r l}&{\left|\begin{array}{l l}{\displaystyle\frac{\partial u}{\partial t},=,\alpha,\frac{\partial^{2}u}{\partial x^{2}}}&{x\in,[0,1],;t\in,[0,1]}\ {\displaystyle u\left(x,0\right),=,0}&{x\in,[0,1]}\end{array}\right|}\ &{\left|\begin{array}{l l}{\displaystyle\frac{\partial u}{\partial x}(0,t),=,0}&{t\in,[0,1]}\ {\displaystyle\frac{\partial u}{\partial x}(1,t),=,1}&{t\in,[0,1]}\end{array}\right|}\end{array}

  

观测方程为  

u_{m}\left(,x,,t,\right);=;u\left(,x,,t,\right);+;\epsilon\left(,x,,t,\right)

  

式中 α— 一待辨识参数;  

——观测噪声。  

当用块脉冲算子法来辨识 $\pmb{\alpha}$ 时，先在式（12-6)中第一式的两边分别对空间积分两次，再对时间积分一次，并代人边界条件后，化简得  

\begin{array}{r}{\frac{1}{\alpha}{\displaystyle\int_{0}^{x}}{\displaystyle\int_{0}^{x}u\left(x,,,t\right)}\mathrm{d}x,=!\int_{0}^{t}!\left[,u\left(,x,,t,\right),-,u\left(0,,\t\right),\right]\mathrm{d}t;=;}\ {\displaystyle\int_{0}^{t}u\left(,x,,t\right)\mathrm{d}t;-\int_{0}^{t}u\left(0,,\t\right)\mathrm{d}t;=;}\end{array}

  

对上式两端做二维块脉冲算子 $B_{2}$ 运算后，由式（12-5)知  

左端项 $=\,(1/\alpha\,)[\,B_{2}\,u\,]P_{_x}^{2}$ $\left(\boldsymbol{P}_{x}\right)$ 定义为 $P_{m1}\otimes I_{m2})$ 右端第一项 $\mathbf{\chi}=\{\,B_{2}\,u\,\}\,P_{t}$ $\left(\boldsymbol{P}_{\iota}\right)$ 定义为 $I_{m\,1}\otimes P_{m\,2})$  

右端第二项 $\mathbf{\Psi}=\pmb{e}_{1}^{\mathrm{T}}\bigotimes(\mathbf{\Psi}(C_{1},C_{2},\cdots,C_{m2})$  

其中， $C_{i}(\,i=1,2\,,\cdots,m\,2\,)$ 亦为未知量。将以上诸式代人式(12-8)  

后，得  

(,1/\alpha,)[,B_{2},u,],{\pmb P}{x}^{2},=,[,B{2},u,],{\pmb P}{t},-,e{1}^{,\mathrm{T}}\otimes(,C_{1},C_{2},\cdots,C_{m2},)

  

写为矩阵形式即为  

\begin{array}{c}{{\boldsymbol{[},(,[,B_{2},u,],\pmb{P}{x}^{2})^{\mathrm{T}}(e{1}^{\mathrm{T}}\otimes s_{1})^{\mathrm{T}}\quad\cdots\quad(e_{1}^{\mathrm{T}}\otimes s_{m2})^{\mathrm{T}}}\times}\ {{\quad\quad(1/\alpha,,C_{1}\quad C_{2}\quad\cdots\quad C_{m2})^{\mathrm{T}},=,(,[,B_{2},u,],\pmb{P}_{t},)^{\mathrm{T}}\quad}}\end{array}

  

式中 $\pmb{\mathscr{s}}_{i}\longrightarrow\mathscr{m}2$ 维行矢量，其元素除了第 $\dot{\pmb{\imath}}$ 列为1外,其余均为 ${\boldsymbol{0}}_{\circ}$ 上式可简记为  

\mathbf{A}\theta\ =\ b

  

式中 $\overbrace{\phantom{\left.\sum_{k=1}^{3}\sum_{i=1}^{2}\sum_{p=1}^{P_{k}^{(i)}}\left(\left.m\,2+1\right)\right.}}^{A\,\mathrm{-}}\left(\left.m\,1\!\cdot m\,2\right)\right)\times\left(\left.m\,2+1\right)$ 维矩阵;$\theta\mathrm{-}\mathrm{-}(\,m\,2+1\,)$ 维列矢量；$\scriptstyle b\longrightarrow(\,m\,1\,\cdot\,m\,2\,)$ 维列矢量。  

由此可得出参数的最小二乘估值为  

\pmb\theta\ =\ \big(\pmb A^{\textsf{T}}\pmb A\ \big)^{-1}\pmb A^{\textsf{T}}\pmb b

  

由于当 $\alpha=1$ 时,系统(12-6)有解析解[5]  

u\left(,x,,t,\right),=T_{0}+\left[,t,+\frac{1}{3},-,(1,-,x,),+\frac{1}{2}(1,-,x,)^{2},-,

\frac{2}{\pi^{2}}\sum_{n=1}^{\infty};\frac{1}{n^{2}}\mathrm{exp}(,\overline{{{n,\pi}}}^{2},t,)\mathrm{cos},n,\pi(1,-,x,)\Biggr]

  

因此，下面为了验证算法，用此解析解的采样值作为实测结果来辨识参数 $\pmb{\alpha}_{\circ}$ 先取 $m\,1=\,m\,2=\,10$ ，代人辨识算法后,辨识得 $_{\alpha}=$ 1.020122,与参数真值1.0的相对误差为 $2.01\,\%$ 。当进一步减小时间和空间方向上的采样间隔，取 $m\,1=m\,2=20$ 时，辨识得 $\pmb{\alpha}=$ 1.005318，与参数真值1.0的相对误差减小为 $0.53\,\%$ 。这表明，要减小辨识算法引人的系统误差，提高辨识结果精度，需要在测量时减小时间和空间方向上的采样间隔,增加实测信息量。  

若在系统解析解的基础上选加均值为零、标准差为 $\pmb{\sigma}$ 的白噪声来作为实测结果,代人前述的辨识算法中,在 $m\,1={\mathit{m}}\,2=10$ 与$m1=m2=20$ 情况下的辨识结果如表 12-1 所列。从表中可以看出，虽然随着测量噪声的增加，辨识结果与真值的相对误差增大，但是，从具体数值上来看，由于块脉冲算子法的辨识过程中用到的实测信息量比较大，辨识结果受测量噪声的影响并不大。  

表12-1块脉冲算子辨识结果  


<html><body><table><tr><td rowspan="2">噪卢标准差。</td><td colspan="2">m 1 = m2=10</td><td colspan="2">m 1 = m2 =20</td></tr><tr><td>参数α辨识值</td><td>相对误差/%</td><td>参数α辨识值</td><td>相对误差/%</td></tr><tr><td>0 =0.01</td><td>1.018785</td><td>1.879</td><td>1.004048</td><td>0.405</td></tr><tr><td>0 =0.1</td><td>1.007914</td><td>0.791</td><td>0.994487</td><td>0.551</td></tr><tr><td>0=0.2</td><td>0.998260</td><td>0.174</td><td>0.987484</td><td>1.252</td></tr><tr><td>α=0.5</td><td>0.983971</td><td>1.603</td><td>0.985856</td><td>1.414</td></tr></table></body></html>  

由以上分析可以看出，块脉冲算子法具有推导简便、计算方便、受测量噪声影响小的优点，但是，由于作块脉冲运算的需要，同时也是为了保证辨识结果有较高精度，该算法要求在时间和空间上尽量多布置采样点，这就对实测的信息量提出了相当高的要求。基函数法这-类辨识方法大都存在这一缺陷。此外，基函数法的计算量还会随状态变量个数的增加而成倍增加，不适用于处理状态变量个数较多的情况。  

# 12.2.2 伴随方程法  

# 1）基本思想  

分布参数系统辨识的另一类方法是最优化方法，该方法从分布参数系统的原始方程出发，将辨识问题转化为优化问题来处理[6。以式(12-1)和式(12-2)描述的分布参数系统为例,根据最优化的思想，很容易地就可以用输出误差法将这个参数辨识问题转化为一个优化问题，即求参数矢量0使如下目标函数J达极小  

J\left(,\pmb\theta,\right);=;;\left|;{\cal C}\left[,\pmb u\left(x_{\L_{m}},,\pmb\theta,,t_{\L_{m}},\right),\right],-,{\cal Z}\left(,x_{\L_{m}},,t_{\L_{m}},\right),\right|,^{2}

  

式中的“ $||\cdot||$ ”表示某种范数。  

求解这一优化问题的方法很多，不同的优化策略就对应看不同的参数辨识方法。伴随方程法所采取的优化策略是先将系统的偏微分状态方程看做为对未知参数的约束，利用拉格朗日乘数法将有约束的参数优化问题转化为无约束优化问题；再对目标函数做变分，求出伴随矢量应满足的伴随方程；然后，数值求解状态方程和伴随方程，求出目标函数下降的梯度方向；最后，利用基于梯度的优化算法来优化未知参数。下面将给出这种方法的具体算法和步骤。  

2）伴随方程法的辨识算法与步骤  

对于式（12-1）和式（12-2）描述的分布参数系统，采用拉格朗 日乘数法后，目标函数变换为  

J\left(,\pmb{u},,\theta,\right);=;\left|;\pmb{C}\left[,\pmb{u},(,\pmb{x}{m},,\pmb{\theta},,t{m},),\right],-,\pmb{Z}\left(,\pmb{x}{m},,t{m},\right),\right|^{;2};+

\int_{\Omega}!!\int_{0}^{T}!E\left(,u,,x,,\theta,,t,\right)p\left(,x,,t,\right)\mathrm{d}t,\mathrm{d}x

  

式中,新引人的 $\pmb{p}(\pmb{x}\,,t)$ 称为伴随矢量。对上式作变分，得  

\delta J;=;\frac{\partial J}{\partial,{\pmb u}},(,{\pmb u},,,{\pmb\theta},,,{\pmb p},),\delta{\pmb u},+,\frac{\partial J}{\partial,{\pmb\theta}},(,{\pmb u},,,{\pmb\theta},,,{\pmb p},),\delta{\pmb\theta}

  

其中的aJ/au 和aJ/a0 实际上是-算子,称为 Frecht 导数[7,即$\frac{\partial J}{\partial\pmb{u}}\delta\pmb{u}$ 不是 $\partial J/\partial{\pmb u}$ $\delta\pmb{u}$ 简单相乘，而是前者算子作用于后者; $\delta\pmb{u}\in$ $\delta U$ ，集合 $\delta U$ 元素 $\pmb{v}$ 的定义域为 $\Omega\times[0,T]$ ，值域为实数域 $R$ ，且满足如下的边界与初始条件  

\frac{\partial\boldsymbol{B}}{\partial\boldsymbol{u}}\boldsymbol{v},=,0(\mathrm{\boldmath~\forall~}\boldsymbol{x},\in,\partial\Omega)\ \quad\frac{\partial\boldsymbol{I}}{\partial\boldsymbol{u}}(\boldsymbol{x},,0),\boldsymbol{v}(\boldsymbol{x},,0),=,0(\mathrm{\boldmath~\forall~}\boldsymbol{x},\in,\Omega)

  

因此,如果能选取 p(x，t)使得式(12-10)中的第-项为零,则式（12-10）可化为  

\delta J;=;\partial J/\partial,\pmb\theta,(,\pmb u,,\pmb\theta,,\pmb p,),\delta\pmb\theta

  

由此式出发可以很容易地求出目标函数对参数的梯度  

\partial J/\partial\pmb{\theta};=;\delta J\left(\pmb{u},,\pmb{\theta},,\pmb{p},\right)/\delta\pmb{\theta}

  

由此梯度出发就可以用最速下降法、共轭梯度法等优化算法来对参数做优化[8]。  

现在剩下的关键问题就是如何选取伴随矢量 p(x,t)。显然， $\pmb{p}(\pmb{x}\,,t)$ 应满足  

\partial J/\partial,u\left(,u,,\theta,,p,\right)v;=;0\quad(;\forall;v;\in;\delta U,)

  

由此式出发,并考虑到 $\pmb{v}$ 的任意性，可以导出一组 $\pmb{p}(\pmb{x}\,,t)$ 应满足的偏微分方程，称之为伴随方程（有关伴随方程的具体导出方法将在后面的算例中做详细介绍），求解该伴随方程就可以得出伴随矢量在时间和空间上的分布。  

综上所述，伴随方程法辨识分布参数系统的步骤为：  

（1）首先将辨识问题转化为优化问题，再用拉格朗日乘数法将其转化为无约束极值优化问题，并导出伴随方程；  

（2）给定参数初值；  

（3）数值求解状态方程，得状态矢量 ${\pmb u}(\,{\pmb x}\,,t\,)$  

（4）数值求解伴随方程，得伴随矢量 $p(x\,,t)$  

（5）对各参数作摄动，代人计算目标函数变分 $\delta J$ 的表达式，从而由式（12-11)可求出目标函数对各参数的梯度；  

（6）从梯度出发，用基于梯度的优化算法来优化参数；  

（7）判断目标函数收敛与否，若收敛，则停止计算；否则，将优化出的参数值代人步骤（3)继续计算。  

3）伴随方程法的辨识算例  

本节讨论的算例与12.2节中的算例相同，热传导系统的主控方程仍为式(12-6)，此时的观测点只取在 $x=0$ 处，观测方程为  

u_{\scriptscriptstyle m}\left(0,,t,\right);=;u\left(0,,t,\right);+;\varepsilon\left(,t,\right)

  

取目标函数的范数为2一范数，采用拉格朗日乘数法后，目标函数为  

J\ =\int_{0}^{T},[;u\left(0,,t\right);-;u_{{\L}_{m}}\left(0,,{\t}\right)]^{2}\mathrm{d}t\ +

\int_{0}^{T}!!!\int_{0}^{1}\left(\frac{\partial,u}{\partial{t}},-,\alpha;\frac{\partial^{2},u}{\partial{x}^{2}}\right),!!,\rho\left(,x,,t,\right)\mathrm{d}x\mathrm{d}t

  

对此式做变分后，形式上可写为  

\delta J;=;\frac{\partial J}{\partial u}\delta u;+;\frac{\partial J}{\partial\alpha}\delta\alpha

  

其中，目标函数对参数 $\pmb{\alpha}$ 的Frecht导数易于求出为  

\frac{\partial J}{\partial\alpha}\delta\alpha;=;\int_{0}^{T}!!!\int_{0}^{1};-;\left(\frac{\partial^{2}u}{\partial x^{2}}\right)\phi!\left(,x,,t,\right)\delta\alpha\mathrm{d}x\mathrm{d}t

  

为了求目标函数对状态量 $\pmb{u}$ 的Frecht 导数,对式（12-13)作分部 积分，得  

J,=!\int_{0}^{T}!\left[,u\left(0,,t\right),-,u_{m}\left(0,,t\right)\right]^{2}!\mathrm{d}t,+\int_{0}^{1}!\phi!\left(,x,,T\right)u\left(,x,,T\right)!\mathrm{d}x,-,

\int_{0}^{T}!!!\int_{0}^{1}!\left({\frac{\partial\phi}{\partial t}},+,\alpha,{\frac{\partial^{2}\phi}{\partial x^{2}}}\right)u,(x,,,t,){\mathop{\mathrm{d}x}},{\mathop{\mathrm{d}t}},-,\alpha{\int_{0}^{T}!!!\phi,(1,,,t,)}{\mathop{\mathrm{d}t}},+

\alpha{\int_{0}^{T}}\biggl[;u\left(1,t\right),\frac{\partial\phi}{\partial x}(1,t),-,u\left(0,t\right),\frac{\partial\phi}{\partial x}(0,t)\biggr],\mathrm{d}t

  

则此时目标函数对状态量 $\pmb{u}$ 的 Frecht导数为  

\frac{\partial J}{\partial u}\hat{\partial u};=\int_{0}^{T}\biggl{2\bigl[,u,(0,t),-,u_{m},(0,t),\bigr],-,\alpha,\frac{\partial,\phi}{\partial x}\bigl(0,t\bigr),\biggr},\hat{\partial u},(0,t),\mathrm{d}t,+,\frac{\partial,\phi}{\partial x},\hat{\partial,\phi},

\int_{0}^{1}!!!p(,x,,T),\delta u(,x,,T)\mathrm{d}x,-\int_{0}^{T}!!!\int_{0}^{1}!!\left({\frac{\partial\phi}{\partial t}},+,\alpha,{\frac{\partial^{2}\phi}{\partial x^{2}}}\right)

\delta u\left(x,,t\right)\mathrm{d}x\mathrm{d}t,+,\alpha!\int_{0}^{T}!\bigg[,\delta u\left(1,t\right)\frac{\partial\phi}{\partial x}(1,t),\bigg]\mathrm{d}t

  

伴随变量满足的条件为式（12-12），即对任意 $\delta u\in\delta U$ ，均有上式等于零。因此，根据 $\delta\pmb{\mathscr{u}}$ 的任意性可知，上式等于零的充要条件为上式右端的四项均等于零，由此可以导出伴随变量 $\pmb{\dot{p}}$ 满足的伴随方程为(此算例中 $T\!\approx\!1$  

\left.\begin{array}{l l}{\displaystyle\frac{\partial\phi}{\partial t}+\alpha,\frac{\partial^{2}\phi}{\partial x^{2}}=0}&{x\in[0,1];t\in[0,T]}\ {\displaystyle\partial\phi/\partial x(0,t)=(2/\alpha)\big[,u,(0,t)-u_{m}(0,t)\big]}&{t\in[0,T]}\ {\partial\phi/\partial x(1,t)=0}&{t\in[0,T]}\ {\displaystyle\phi(x,T)=0}&{x\in[0,1]}\end{array}\right}

  

式(12-6)和伴随式(12-15)都是抛物型方程,可以采用有限控制体积法来数值求解。求得状态量 $\pmb{u}$ 和伴随变量 $\pmb{\dot{p}}$ 后，由式（12-14)就可以很容易地推出目标函数对参数 $\pmb{\alpha}$ 的梯度为  

\frac{\partial J}{\partial\alpha},=,\int_{0}^{T}!!!\int_{0}^{1},-,\left(\frac{\partial^{2}u}{\partial{x}^{2}}\right)!p(,x,,t,),\mathrm{d}x,\mathrm{d}t

  

将此梯度代人优化算法中，就可对参数 $\pmb{\alpha}$ 进行优化，以最速下降法为例,其选代式为[8]  

\alpha^{(k+1)};=;\alpha^{(k)},-,\lambda,(\partial J/\partial\alpha)

  

式中的上标 $k$ 和 $k+1$ 分别表示优化前后的值， $\lambda$ 为步长，由一维寻优求得。  

在辨识仿真计算中,类似12.2.1节，仍先以 ${\boldsymbol x}=\mathbf{0}$ 处时间方向10个采样点（采样间隔 $\Delta t=0.\,1\,)$ 上的解析解作为实测值来辨识参数 $\pmb{\alpha}$ ,辨识得 $\alpha=0.\,999746$ ，与参数真值1.0十分接近，相对误差仅为 $0.025\,\%$ 。再在系统解析解的基础上迭加均值为零、标准差为 $\pmb{\sigma}$ 的白噪声来作为实测结果，代人伴随方程法的辨识算法中，辨识结果如表12-2所列。从表中知，伴随方程法的辨识结果受测量噪声的影响较大，随测量噪声的增加，参数辨识结果与真值的相对误差增加。  

表12-2停随方程法辨识结果  


<html><body><table><tr><td>噪声标准差α</td><td>α = 0.001</td><td> =0.01</td><td>o=0.1</td><td>α =0.2</td></tr><tr><td>参数α 辨识值</td><td>1.000682</td><td>1.007267</td><td>1.070430</td><td>1.140757</td></tr><tr><td>相对误差/%</td><td>0.068</td><td>0.727</td><td>7.043</td><td>14.076</td></tr></table></body></html>  

由上述分析及算例可以看出，伴随方程法解决辨识问题的-个最大优点在于：由式（12-11）可以较容易地求出自标函数对各参数的梯度，因此该辨识方法整个辨识过程的计算量受参数个数多少的影响不大，适用于处理待辨识参数较多的情况。但是，这一万法也有以下不足之处：一是伴随方程的推导较为繁琐，且伴随变量的物理意义不明确；二是其优化过程对梯度计算精度的要求较高；三是该方法从目标函数的梯度出发来寻优，当参数个数较多时，选取步长时一维寻优的计算量比较大。目前，伴随方程法辨识分布参数系统在工程上的－个典型应用就是基于欧拉方程和 $N-S$ 方程的翼型与机翼反设计，参考文献【9对此问题作了详细介绍。  

此外，在农业工程研究、地质勘探研究等诸多领域中，用伴随方程法来辨识分布参数系统也有着较为广泛的应用。  

# 12.2.3 灵敏度法  

1）基本思想和辨识算法  

灵敏度法辨识分布参数系统的基本思想与伴随方程法-一样，也是先用输出误差法将辨识问题转化为优化问题，然后用数值方法来计算状态变量，并求取状态变量对参数的导数敏度。有了状态变量和灵敏度矢量的计算结果后，就可以用优化算法来对参数进行优化。其中，牛顿-拉夫逊算法是目前应用得较多，较为有效的一种优化方法，其优化策略如下[10,11]  

目标函数 $J\left(\,\pmb{\theta}\,\right)=\ \left\|\begin{array}{l}{\pmb{C}\left[\,\pmb{u}\left(\,\pmb{x}_{m}\,,\,\pmb{\theta}\,,\,t_{m}\,\right)\,\right]\,-\,\pmb{Z}\left(\,\pmb{x}_{m}\,,\,t_{m}\,\right)\,\right\|^{\,2}}\end{array}$ 达极小的必要条件为 $\partial J(\,\pmb\theta)/\partial\pmb\theta=\mathbf0$ 。当在第 $k$ 迭代层次上 $J(\pmb\theta_{k})$ 不是极小值时,必须调整 $\pmb\theta_{k}$ 使 $J_{k+1}$ 达极小值,则令  

\frac{\partial J^{(k+1)}}{\partial\pmb{\theta}},=,\frac{\partial J(\pmb{\theta}^{(k)},+,\Delta\pmb{\theta})}{\partial\pmb{\theta}},=,\frac{\partial J(\pmb{\theta}^{(k)})}{\partial\pmb{\theta}},+

\frac{\partial^{2}J(\mathbf{\pmb{\theta}}^{(k)})}{\partial\mathbf{\pmb{\theta}}\partial\mathbf{\pmb{\theta}}^{T}}\Delta\pmb{\theta}^{(k)}+O(\mathbf{\epsilon}|\Delta\pmb{\theta}^{(k)}|^{2})\mathbf{\epsilon}=\mathbf{0}

  

略去二阶以上小量后得  

\pmb{\theta}^{(k+1)}\ =\ \pmb{\theta}^{(k)}\ +\ \Delta\pmb{\theta}^{(k)}\quad\Delta\pmb{\theta}^{(k)}\ =-\ \pmb{M}^{-1}\left(\frac{\partial\pmb{J}}{\partial\pmb{\theta}}\right)\quad\pmb{M}\ =\ \frac{\partial^{2}\pmb{J}}{\partial\pmb{\theta}\partial\pmb{\theta}^{T}}

  

# 式中 $\pmb{M}$ ——信息矩阵；  

矢量 $\partial J/\partial\pmb\theta$ 和矩阵 $M$ 中都含有状态变量对参数的导数，该导数称为灵敏度，由式（12-16)构成的算法就称为灵敏度法。  

采用灵敏度法求解分布参数系统解主要问题的具体步骤可概括为：  

（1）化辨识问题为优化问题，选取目标函数 $J$  

（2）给定参数初值。  

（3）数值求解状态方程，得状态变量。  

（4）求取灵敏度。方法有两种：一一种方法是就状态方程对参数求导，得出灵敏度应满足的灵敏度方程，再数值求解灵敏度方程；另一种方法是对参数摄动，用差分代替导数的方法来求取灵敏度。例如,状态矢量 $\pmb{u}$ 对参数 $\theta_{i}$ 在 $\theta_{i}=\theta_{i0}$ 处的灵敏度可用中心差分近似为  

\left.\left(\frac{\partial,{\pmb u}}{\partial,\theta_{i}}\right),\right|{\theta{i}=\theta_{i0}}\approx\frac{{\pmb u}\left(,\theta_{i0},+,\Delta\theta_{i},\right),-,{\pmb u}\left(,\theta_{i0},-,\Delta\theta_{i},\right)}{2\Delta\theta_{i}}

  

(5）由式（12-16)来对参数做优化。  

（6）判断目标函数收敛与否,若收敛,则停止计算；否则,将优化出的参数值代人步骤（3）继续计算。  

# 2）灵敏度法的辨识算例  

本节讨论的算例与 12.2.1 和 12.2.2 节中的算例相同,热传导系统的主控方程仍为式（12-6），观测点仍取在 $x=0$ 处，观测方程为式（12-7)。 此时的目标函数取为  

J,=,\int_{0}^{T}\bigl[,u\left(0,,t,,\alpha,\right),-,u_{\L_{m}}\left(0,,t,\right)\bigr]^{2}\mathrm{d}t

  

则有  

\frac{\partial J}{\partial\alpha};=;\int_{0}^{T}!2\big[;u\left(0,,t,,\alpha\right);-;u_{_m}\left(0,,{t}\right)\big];\frac{\partial u}{\partial\alpha}\mathrm{d}t

  

矩阵 $M$ 也退化为单个元素  

{\bf{\cal M}},=,\int_{0}^{T}!2{\left[{\bf\Psi}{u}\left({\bf0},,t,,\alpha\right),-,u{m}\left({\bf0},,t,\right)\right]};\frac{\partial^{2}u}{\partial\alpha^{2}}\mathrm{d}t,+,\int_{0}^{T}!2,\frac{\partial u}{\partial\alpha};\frac{\partial u}{\partial\alpha}\mathrm{d}t

  

当辨识过程收敛时，上式右端的第一项应趋于零，所以在送代过程中可将上式简化为  

M:=:\int_{0}^{T}2:\frac{\partial,u}{\partial\alpha}:\frac{\partial,u}{\partial\alpha}\mathrm{d}t

  

式(12-17)和式(12-18)中的 $\partial u/\partial\alpha$ 就是灵敏度，在本算例中通过解灵  

敏度方程来获取,灵敏度方程的具体形式为( $U$ 定义为 $\partial u/\partial\alpha)$  

\begin{array}{r l}&{\left{\displaystyle\frac{\partial U}{\partial t},=,\alpha,\frac{\partial^{2}U}{\partial x^{2}}+\frac{\partial^{2}u}{\partial x^{2}}\quad x,\in,[0,1],;t,\in,[0,1]\right.}\ &{\left.!!!U(x,,0),=,0\qquad\qquad\quad x,\in,[0,1]\right.}\ &{\left.!!!\partial U/\partial x(0,t),=,0\qquad\quad t,\in,[0,1]\right.}\ &{\left.!!!\partial U/\partial x(1,t),=,0\qquad\quad t,\in,[0,1]\right.}\end{array}

  

此方程也是一抛物型方程，仍可以较容易地用有限控制体积法来数值求解。  

将以上诸式代人灵敏度法的辨识步骤中，为验证辨识算法，仍先以 $x=0$ 处时间方向10个采样点（采样间隔 $\Delta t=0.1)$ 上的解析解作为实测值来辨识参数 $\pmb{\alpha}$ ，辨识得 $_{\alpha}=1.000223$ ，与参数真值1.0十分接近，相对误差仅为 $0.022\,\%$ 。随后,在系统解析解的基础上叠加均值为零、标准差为 $\pmb{\sigma}$ 的白噪声来作为实测结果，代人灵敏度法的辨识算法中,辨识结果如表12-3所列。从表中知，与伴随方程法类似，灵敏度法的辨识结果受测量噪声的影响也较大，随测量噪声的增加，参数辨识结果与真值的相对误差增加。  

表 12-3灵敏度法辨识结果  


<html><body><table><tr><td>噪声标准差o</td><td>0 =0.001</td><td>α =0.01</td><td>0 =0.1</td><td>α =0.2</td></tr><tr><td>参数α辨识值</td><td>1.000994</td><td>1.007399</td><td>1.071549</td><td>1.142367</td></tr><tr><td>相对误差</td><td>0.099 %</td><td>0.740 %</td><td>7.155 %</td><td>14.237%</td></tr></table></body></html>  

由以上分析可以看出，灵敏度法的辨识精度和伴随方程法相当，但与伴随方程法相比，灵敏度法的推导更为简捷，而且其优化过程是从灵敏度出发来进行优化，具有优化速度快，计算量较小的优点，适合于工程应用。  

# 12.3 再人飞行器气动热参数辨识  

再人飞行器在再人大气层过程中，由于气动加热，会经历十分恶劣的热环境[12,13]。例如,远程导弹以马赫数25 再人时,其头部的最高表面温度可达15000K；美国的阿波罗飞船指令舱和苏联联盟号飞船返回舱再人时的最高表面温度也分别达到2950K和1900K。因此,再人飞行器防热系统的成功设计成为决定再人体成败与否的关键因素。  

在防热系统的设计中，首先考虑的是其可靠性，以免冉人时的高温将飞行器的舱体烧坏。同时，为了提高飞行器的有效载荷，也应该在满足防热要求的前提下尽量减轻防热系统的结构重量。这就需要准确确定飞行器再人时的气动热环境并选用合适的防热方案和防热材料。  

要确定飞行器再人时的气动热环境，可以通过3种手段：理论分析及数值模拟、风洞实验和飞行试验。通常，当飞行器处于平衡流区时，通过数值模拟和风洞实验可以较准确地确定出飞行器表面热流等参数；但是，当飞行器处于非平衡流区时，工程算法表明，冻结流和平衡流的热流率相差好几倍，而壁面催化系数难于准确确定，致使非平衡流区的理论计算误差很大，同时，地面风洞实验模拟也有一定困难。此时，飞行试验成为获取飞行器表面热流等气动热环境参数的主要手段。然而，由于再人时飞行器的表面温度极高，不能在飞行器表面安装温度传感器或热流传感器来直接测量表面温度和表面热流。因此，可以考虑在飞行器的防热层内某些点上安装温度传感器，再通过这些点上的温度测量历程来确定飞行器的表面热流和温度，如图 12-1所示。这是一个与经典热传导问题恰恰相反的问题，称之为热传导逆问题。  

![](images/46858719825f2ddea0186eccec24a7d6454d896b50919d987598c634930fa337.jpg)  
图 12-1 飞行器表面热流辨识示意图  

另一方面，由于飞行器再人时经受的热流量较大，防热层内的温度会较高且变化范围广，因此，防热材料的热物理特性必然会随温度变化[14]。要确定防热材料此时的热物性参数,可以借助于地面高温传热实验,通过测量一定热流条件下材料内部的温度分布来确定。这也与经典热传导问题研究的情况相反，是热传导逆问题的另一类型。  

因此，为了确定再人飞行器的表面热流，首先要在地面试验设备中做试验,测定防热材料的 $\rho\,,c_{p}$ 并辨识出热传导系数 $\pmb{k}$ ；然后再利用地面测定的 $\rho\,,c_{p}\,,k$ 和飞行试验实测的温度历程来辨识飞行器表面热流[15]。本节内容相应地分为防热材料热传导系数辨识和飞行器表面热流辨识两大部分，由于这两个问题对应的主控方程都是偏微分方程，所以这两个问题实际上都属于分布参数系统辨识的研究范畴，统称为气动热参数辨识。下面首先给出防热材料热传导系数的辨识算法，然后再介绍已知材料热传导系数情况下辨识飞行器表面热流的算法。  

# 12.3.1 非线性热传导系数的辨识算法  

# 1）问题描述  

通常,地面实验测定材料热传导系数的示意图如图12-2所示，受测材料试样的左端受常值均匀热流 $\boldsymbol{Q}$ ，其余三面为绝热壁，温度传感器置于右端 $P$ 点处测量该点的温度历程 $T_{m}\left(\,l\,,t\,\right)$ 。则  

![](images/a0b8a894aa4e4aa32c7ef8cc113b2d2c2288a4ee1b1c9f030fe6e7d1dda7771c.jpg)  
图12-2 辨识热传导系数示意图  

这一传热问题可简化为一维热传导方程来描述，即  

主控方程  

\begin{array}{r l}&{\left[\displaystyle\frac{\partial}{\partial x}!\left[k\left(T\right)\displaystyle\frac{\partial T}{\partial x}\right]=,\rho c_{\dot{p}},\frac{\partial T}{\partial t}\quad x\in,\left(0,L\right),t>0\right.}\ &{\left.T(x,0),=,T_{0}\qquad\qquad\qquad\quad x\in,\left[0,L\right]}\ &{\quad-,k\left(T\right)!\frac{\partial T}{\partial x}\bigg|{x=0},=,Q\qquad\quad t>0}\ &{\quad-,k\left(T\right)!\frac{\partial T}{\partial x}\bigg|{x=L},=,0\qquad\quad t>0}\end{array}

  

观测方程  

T_{m}(,L,,t,);=;T(,L,,t,),+,\epsilon,(,t,)

  

式中 $\rho$ —材料密度；$c_{p}$ 一—材料的比定压热容；  

${\pmb k}={\pmb k}\left(\,T\right)$ -—材料的热传导系数，是温度的函数；  

$\varepsilon\left(\t\right)$ ——测量噪声。  

现在的热传导逆问题就是由观测方程式（12-20）来辨识材料的热传导系数 $k\left(T\right)$ 。由材料热物性实验的结果知[15},材料的热传导系数可以假设为温度的二次函数，即  

k,(,T,),=,A,+,B T,+,C T^{2},=,(1,,T,,T^{2}),\pmb\theta

  

其中， $\pmb{\theta}=(\,\theta_{1}\,,\theta_{2}\,,\theta_{3}\,)=(A\,,B\,,C)$ 为未知参数矢量。因此，如果为该矢量赋值后，可由式(12-19)求出P点处温度历程T（L，t，0)。于是，辨识问题转化为在给定约束条件式(12-19)下求9使目标函数 $J\left(\,\pmb\theta\,\right)$ 达极小的非线性优化问题。  

\begin{array}{r l}{J(\pmb\theta)!!!}&{=;|\ T_{m},-,T(L,,t,,\pmb\theta);|^{2},=}\ {\quad}&{}\ {\displaystyle\int_{0}^{t_{\mathrm{max}}}!!\left[,T_{m}(,t,),-,T(L,,t,,\pmb\theta),\right]^{2}!\mathrm{d}t}\end{array}

  

牛顿-拉夫逊算法是解决这类优化问题的有效方法，其选代过程  

为  

\left{\begin{array}{l}{\displaystyle\pmb{\theta}^{(k+1)},=,\pmb{\theta}^{(k)},+,\Delta\theta^{(k)},r_{e x}}\ {\Delta\pmb{\theta}^{(k)},=,-,M^{-1}\bigg(\frac{\partial J}{\partial\theta}\bigg)}\ {\displaystyle M,=,2\bigg[{0}^{\prime{\mathrm{max}}}\frac{\partial T}{\partial\theta},\frac{\partial T}{\partial\theta^{T}}\mathrm{d}t}\ {\displaystyle\frac{\partial J}{\partial\theta},=,2!!\int_{0}^{t_{\mathrm{max}}}!!!\big[,T(L,t,\theta),-,T_{m}(t),\big],\frac{\partial T}{\partial\theta}\mathrm{d}t}\end{array}\right.,

  

式中,参数矢量的下标 $k\,,k+1$ 分别表示迭代前、后的参数值; $r_{e x}$ 是亚松弛因子； $\pmb{M}$ 称为信息矩阵；状态量 $T$ 对参数的导数称为灵敏度向量，可通过求解灵敏度方程来获得，而灵敏度方程则是由式(12-19)对参数 $A\,,B\,,C$ 求导后得到的。其具体形式为  

\left{\begin{array}{l l}{\displaystyle\alpha_{r},\frac{\partial}{\partial t}!\left(\frac{\partial T}{\partial\phi_{i}}\right)!=\frac{\partial}{\partial x}!\left[k(,T,),\frac{\partial}{\partial x}!\left(\frac{\partial T}{\partial\theta_{i}}\right)\right],+\frac{\partial}{\partial x}!\left[,U_{i},\frac{\partial T}{\partial x},\right]}&\ {\displaystyle-,k\left(,T,),\frac{\partial}{\partial x}!\left(\frac{\partial T}{\partial\theta_{i}}\right){x,=,0},=,U{i},\frac{\partial T}{\partial x},\right\vert_{x,=,0}}&\ {,-,k\left(,T,\right),\frac{\partial}{\partial x}!\left(\frac{\partial T}{\partial\theta_{i}}\right){x,=,L},=,0}&\ {\displaystyle\frac{\partial T(,x,,0)}{\partial\theta{i}},=,0}&{(,i,=,1,)}\end{array}\right. $$(\,i\,=\,1\,,2\,,3)

U_{i}=T^{i\,-\,1}+B\left(\partial\,T/\partial\theta_{i}\right)+2C T(\partial\,T/\partial\theta_{i}\,)\,\mathrm{~o~}

因此，整个热传导系数辨识的步骤为：

（1）为参数 \pmb\theta 赋初值；

(2）数值求解式(12-19),得温度 T(L,t,0)和目标函数J的值；

（3）数值求解灵敏度方程式（12-23），得灵敏度天量；

（4）用牛顿-拉夫逊算法对参数值进行优化，得 \Delta\pmb{\theta}

（5）判断收敛与否，若收敛，则停止辨识计算；杏则返回步骤（2）重复迭代。

2）求解一维热传导问题的有限控制体积法

在热传导系数的辨识过程中，需要对式（12-19）和式（12-23）进行求解，这两个方程组都是非线性抛物型方程组，因而只有采用数值方法，如有限差分法、有限体积法、有限元法等方法来求解。其中，有限控制体积法从能量守恒观点出发，将积分形式的基本方程离散到有限小的体积单元里来求解，从而使方程的阶次下降，保证了数值解具有较高的精度[16]。其具体处理方法如下:首先,对计算域进行网格划分（如图 12{\-}3\left(\,a\,\right) 所示），区间 [0,L] 划分为 N 个有限控制体，除第1个和第 N 个控制体的长度为 \Delta x/2 外，其余控制体的长度均为 \Delta x\big(\Delta x=L/(N-1\big)\big) 。因此，对于第 _i 个控制体 (\,i\neq1\,,\,i\neq N\,) ，如图 12^{-3(b)} 所示，式（12-19)的第一个方程离散为

图12-3有限控制体积法示意图

k\,(\,T\,)\frac{\partial T}{\partial x}\,\bigg|_{w}^{\ e}\;=\;\rho c_{\rho}\left(\int_{w}^{m}\,\frac{\partial T}{\partial t}\mathrm{d}x\,+\int_{m}^{e}\,\frac{\partial T}{\partial t}\mathrm{d}x\,\right)

用中心差分来处理 _x 方向上的导数，用隐式格式来处理时间方向上的导数，从而可得

A_{i}T_{\phantom{n-1}i\,-1}^{n+1}\,+\,B_{i}T_{\phantom{n+1}i}^{n+1}\,+\,C_{i}T_{\phantom{n+1}i\,+1}^{n+1}\,=\,F_{i}\quad(\,i\,=\,2,\cdots,N\,-\,1)

式中

\begin{array}{c}{{A_{i}\;=\;s k\left(\,T w_{i}\,\right)\,-\,1/8}}\\ {{{}}}\\ {{B_{i}\;=-\;\,s k\left(\,T e_{i}\,\right)\,-\,s k\left(\,T w_{i}\,\right)\,-\,3/4}}\end{array}

C_{i}~=~s k\left(~T w_{i}\right)~-~1/8

F_{i}\,=\,-\,\left(3\,T_{i}^{n}/4\,+\,T_{i-1}^{n}/8\,+\,T_{i+1}^{n}/8\right)

T w_{i}\ =\ (\ T_{\ i}^{n\,+\,1}\ +\ T_{\ i\,-\,1}^{n\,+\,1})/2

T e_{i}\ =\ (\ T_{\ i}^{n\,+\,1}\ +\ T_{\ i\,+\,1}^{n\,+\,1})/2

s\;=\;\Delta t/(\,\rho c_{p}\Delta x^{\frac{2}{}})

T 的下标对应于空间坐标， T 的上标对应于时间推进的时层; \Delta t
为推进的时间步长。

在左边界处，对第一个控制体（图 12{\cdot}3(\,c\,)\,) ，积分后有

k\,(\,T)\frac{\partial T}{\partial x}\,\bigg|_{\iota}^{\,\epsilon}\,=\,\rho c_{\hat{p}}\!\int_{\iota}^{\,e}\frac{\partial T}{\partial t}\mathrm{d}x

将左边界条件代人上式后可得

B_{1}\,T_{1}^{n\,+\,1}\,+\,C_{1}\,T_{2}^{n\,+\,1}\,=\,F_{1}

式中

\begin{array}{c}{{B_{1}\,=\,-\,s k\,(\,T e_{1})\,-\,3/8}}\\ {{}}\\ {{C_{1}\,=\,s k\,(\,T e_{1})\,-\,1/8}}\\ {{}}\\ {{F_{1}\,=-\,\left(\,Q\Delta t/(\rho_{e}_{p}\Delta x\,)\,+\,3\,T_{1}^{n}/8\,+\,T_{2}^{n}/8\right)}}\end{array}

同样，对右边界处的第 N 个控制体也可导出

A_{N}T_{\;\;N-1}^{n+1}\,+\,B_{N}T_{\;\;N}^{n+1}\,=\,F_{N}

式中

\begin{array}{c}{{A_{N}\,=\,s k\,(\,T w_{N})\,-\,1/8}}\\ {{}}\\ {{B_{N}\,=\,-\,\,s k\,(\,T w_{N})\,-\,3/8}}\\ {{}}\\ {{F_{N}\,=\,-\,\,3\,T_{N}^{n}/8\,-\,\,T_{N-1}^{n}/8}}\end{array}

因此,由式(12-24)式(12-25)和式(12-26)就构成了一个 \eta_{\,i}^{n+1}\left(\,i=\right.

1,2,\cdots,N) 应满足的三对角代数方程组

\pmb{S}\pmb{T}^{n+1}\pmb{\mathrm{~=~}}\pmb{b}

S\;=\;\left[\begin{array}{c c c c c c}{{B_{1}}}&{{C_{1}}}&{{}}&{{}}&{{}}&{{}}\\ {{A_{2}}}&{{B_{2}}}&{{C_{2}}}&{{}}&{{}}&{{}}\\ {{}}&{{\ddots}}&{{\ddots}}&{{\ddots}}&{{}}&{{}}\\ {{}}&{{}}&{{A_{N-1}}}&{{B_{N-1}}}&{{C_{N-1}}}&{{}}\\ {{}}&{{}}&{{}}&{{A_{N}}}&{{B_{N}}}&{{}}\end{array}\right]\;

\begin{array}{r l r}{\pmb{T}^{n+1}\;=\;\left(\begin{array}{c}{T_{1}^{n+1}}\\ {T_{2}^{n+1}}\\ {\vdots}\\ {T_{N-1}^{n+1}}\\ {T_{N}^{n+1}}\end{array}\right)\qquad\pmb{b}\;=\;\left(\begin{array}{c}{F_{1}}\\ {F_{2}}\\ {\vdots}\\ {F_{N-1}}\\ {F_{N}}\end{array}\right)}\end{array}

由于矩阵 \pmb{S} 中的元素是 T^{\frac{\eta}{\lambda}\pm1} 的函数，所以这是一非线性代数方程组，只有采用迭代的方法来求解。并且，在每步迭代过程中都需要求解一个三对角代数方程组，可以用追赶法来快速求解。

以上介绍了用有限控制体积法来求解式（12-19）的具体过程，式（12-23）的处理方法与之类似，没有本质上的区别。

3）非线性热传导系数辨识仿真算例

酚醛材料是工程上常用的一-种防热材料，当温度超过800K时，其热传导系数近似为温度的二次函数

k\;=\;2.08\,-\,0.0025\,T\,+\,1.6\,\times\,10^{-6}\,T^{2}

由此关系式和式（12-19）,就可以用有限控制体积法求出 P 点处的温度历程 T_{c}(L\,,t\,) 。下面首先把 T_{c}\left(\,L\,,t\,\right) 作为 P 点处的温度测量值，用12.3.1节中介绍的灵敏度法来辨识材料的热传导系数。其他条件取为： L=0.\;{\bf1m};\,\rho=1400{\bf k g}/{\bf m}^{3};\,c_{_{P}}=1256{\bf J}/({\bf\ k g}\cdot{\bf\nabla}) K); T_{0}=800\mathrm{K} Q=200\mathrm{kW}/\mathrm{m}^{2} 。辨识结果列于表12-4,从表中可以看出，当测量结果中没有测量噪声时，辨识出的参数值和真值十分接近。但是，在实际情况中，测量结果中不可避免地会含有测量噪声,因此,为模拟实际情况,在 T_{c}(L\,,t) 上叠加均值为0,标准差为 20K 的白噪声，并将叠加后得到的温度历程作为温度实测值来辨识热传导系数。热传导系数中的参数 A\,,B\,,C 的辨识结果列于表12-5，几个温度下热传导系数的辨识结果列于表12-6。从表中可以看出，在考虑了测量噪声的情况下，参数 A\,,B\,,C 的辨识值以及几个典型温度下热传导系数的辨识值与真值都相差不大。图12-4也示出了辨识得热传导系数的函数形式与真值的比较，二者符合得比较好。图12-5示出了用热传导系数的辨识值来计算得到的 \boldsymbol{P} 点处温度历程与仿真的测量结果的比较，从图中可以看到，测量结果均匀地分布在辨识值计算结果曲线的两边，辨识值计算结果较好地拟合出了测量结果的变化趋势。由此可见，辨识方法在考虑测量噪声的情况下仍然是十分有效的。

表 12-4热传导系数辨识结果(无测量噪声)

<html>

参数	A	B	C
真值	2.08	- 0.0025	1.6e - 6
初值	1.5	- 0.0015	1.0e - 6
辨识值	2.080015	- 0. 00250014	1. 600003e - 6
相对误差/%	0.00072	0.0056	0.00019

</html>

表12-5热传导系数中参数辨识结果

<html>

参数	A	B	C
真值	2.08	-0.0025	1.6e - 6
辨识值	2.1472	-0.002482	1.5678e -6
相对误差/%	3.23	0.72	2.01

</html>

表 12-6热传导系数辨识结果

<html>

参数	k( T =800K)	k(T = 1400K)	k(T =2000K)
真值	1.1040	1.7160	3.4800
辨识值	1. 1646	1.7446	3.4534
相对误差/%	5.49	1.67	0.763

</html>

本节给出热传导系数是温度二次多项式函数的具体辨识算式。若热传导系数与加热速率有关，则热传导系数表达式（12-21）应含 T 的项。根据各种不同物理过程，可建立不同的热传导系数表达式，这是个复杂的模型辨识过程，可参照第3章模型辨识的方法进行。模型结构确定后，可用本节所述方法进行气动热参数辨识。

图12-4热传导系数辨识值与真值比较

图 12-5 P 点处温度历程比较

通过对酚醛材料热传导系数辨识算例的分析，可以得出以下结论：灵敏度法是辩识材料热传导系数的有效方法,具有较高的辨识精度，即使在考虑测量噪声的情况下仍能得出较好的辨识结

12.3.2 再入飞行器表面热流辨识

1）问题描述及参数估计法

再人飞行器在再入过程中，飞行器大面积防热区的热流可近似处理为一维热传导问题（见图12-1）。飞行器表面热流辨识就是已知 P_{1} 或 P 点处的温度测量历程 T_{m}\left(\,t\,\right) 和内壁的热边界条件，要求辨识外表面的热流 Q\left(\,t\,\right) 。当内壁为绝热壁时，飞行器表面热流的主控方程仍可用式（12-19）表示，唯-的区别在于此时防热材料的热传导系数 k\left(\,T\right) 为已知，而边界条件中的 Q\left(\,t\,\right) 为未知函数。于是，很自然地就会想到沿用12.3.1节中的辨识算法来辨识表面热流，在这里称之为参数估计法[16]

在参数估计法中，假设热流为时间的二次函数，即

Q(\,t\,)\:=\:a\:+\:b t\:+\:c t^{2}\:=\:\left(1\,,t\,,t^{2}\right)\theta

\pmb{\theta}=(\,\theta_{1}\,,\theta_{2}\,,\theta_{3}\,)^{\textup{T}}\!=(\,\alpha\,,b\,,c\,)^{\textup{T}} 为未知参数。从而将辨识问题也转化成了一个参数优化问题。解决此问题的方法和前述的热传导系数的辨识算法大致相同，区别仅在于灵敏度方程的形式有所改变，此时灵敏度方程的具体形式为

\left\{\begin{array}{l l}{\displaystyle\rho_{\nu}\,\frac{\partial}{\partial t}\!\left(\frac{\partial T}{\partial\theta_{i}}\right)\!=\frac{\partial}{\partial x}\!\left[k(T)\,\frac{\partial}{\partial x}\!\left(\frac{\partial T}{\partial\theta_{i}}\right)\right]\!+\frac{\partial}{\partial x}\!\left[\frac{\mathrm{d}k(T)}{\mathrm{d}T}\,\frac{\partial}{\partial\theta_{i}}\right]\!}&{{}}\\ {\displaystyle-\,k(T)\,\frac{\partial}{\partial x}\!\left(\frac{\partial T}{\partial\theta_{i}}\right)_{x\,=\,0}-\left(\frac{\mathrm{d}k(T)}{\mathrm{d}T}\,\frac{\partial T}{\partial\theta_{i}}\,\frac{\partial T}{\partial x}\right]_{x\,=\,0}\,=\,U_{i}}\\ {\,-\,k(T)\,\frac{\partial}{\partial x}\!\left(\frac{\partial T}{\partial\theta_{i}}\right)_{x\,=\,L}\,-\left(\frac{\mathrm{d}k(T)}{\mathrm{d}T}\,\frac{\partial T}{\partial\theta_{i}}\,\frac{\partial T}{\partial x}\right]_{x\,=\,L}\,=\,0}\\ {\displaystyle\frac{\partial T(x,0)}{\partial\theta_{i}}\,=\,0}&{{}(i\,=\,0)}\end{array}\right.

其中 U_{i}=t^{i^{\mathrm{~-~}1}} 。此方程也可以用有限控制体积法来求解。下面给出一个用参数估计法来辨识表面热流的例子。

某材料的热传导系数为 k=10+0.\,01\,T+0.\,00001\,T^{2}(\mathbf{W}/(\mathbf{m}^{.} K)),受到的表面热流为 Q=200000+500\,t+2\,t\left(\mathbf{W}/\mathbf{m}^{2}\right) ，其余条件为 L=0.1\ \mathrm{m};T_{0}=300\ \mathrm{K};\rho_{c_{\beta}}=10000\ \mathrm{J}/(\mathrm{K}\cdot\mathrm{m}^{3}) 。先用以上参数来计算正问题,得到测点处温度的计算值 T_{c}\left(\tau\right) ,再将此计算值作为测量值来辨识表面热流,参数 \theta_{i} 的辨识结果列于表12-7,参数辨识值与真值的差别很小。当在 T_{c}\left(\,t\,\right) 上叠加标准差为5K的测量白噪声，并将叠加后的值作为测量值来辨识热流参数时，参数 \theta_{i} 的辨识结果与真值有所差别，但是，就热流值而言，各个时刻热流的辨识值与真值的差别并不大，二者的比较列于表12-8和图12-6，从表和图中可以看出，辨识结果是令人满意的。

表 12-7　 热流参数辨识结果

<html>

参数			C
真值	20000	500	2
初值	15000	450	1.5
辨识值	19999.8	500.5	2.00012
相对误差/%	0.001	0.01	0.006

</html>

表 12-8 热流辩识结果

<html>

时间(秒)	t = 0	t = 4	t = 12	t = 20
真值	20000	22032	26288	30800
辨识值	19815.7	22163.1	26311.9	29732.9
相对误差/%	0.922	0.595	0.09	3.465

</html>

2）辨识热流的顺序函数法

从上一节的算例可以看出，参数估计法是辨识热流的一种有效方法。但是，这种方法有一个明显的缺陷，即必须用已知热流的函数形式逼近实际热流量，才能对参数进行有效估计，当热流的函数形式未知时，用参数估计法处理起来困难很大。此外，由热传导问题的物理特性可知，非稳态热传导是扩散型的，一方面具有阻尼性和延迟性，阻尼性表现为边界热流的扰动将对边界附近的温度产生大的影响，而随着离扰动点距离的增加，扰动的影响将减小，延迟性则表现为内部温度对边界热流的反应在时间上具有延迟性；另一方面，输入热流在经过一段时间后将达到热平衡，也就是说温度对相邻两个时刻热流的灵敏度经过一段时间以后将线性相关，从而导致相邻时刻两个同量级的热流输人经过一定的时间以后将不可区分。因此，辨识表面热流最有效的方法是按时间顺序估计而不是在全时间域-次估计。这里的按时间顺序估计是指通过 i_{M}\,,\,t_{M+1}\,,\,\cdots,t_{M+r\,-\,1} 共 r 个未来时刻所测的温度来估计 t_{M} 时刻的热流,亦称为顺序函数法[5]。

图 12-6热流辨识值与真值的比较

当用顺序函数法来辨识未知热流 Q\left(\tau\right) 时，问题可描述为：已知 t_{M} 时刻的前 M-1 个时刻处的热流 \hat{Q}_{1}^{\phantom{\dagger}},\hat{Q}_{2}^{\phantom{\dagger}},\cdots,\hat{Q}_{M-1} 和后 r 个时刻的温度值 T_{M},\,T_{M+1},\cdots,\,T_{M+\,r\,-\,1} ,要求辨识 t_{M} 时刻的热流 Q_{M} 。例如,当 M=1 时，即需已知初始热流 Q_{0} 及后 ^r 个温度测值 T_{1},T_{2},\cdots,T_{m} ,再由 Q_{0},T_{1},T_{2},\cdots,T_{r} 的信息来确定 Q_{1}\circ 由于热传导的延迟性， Q_{M} 决定 t_{M} 时刻之后时间里的温度值，即T_{M+\,r-1} 不仅取决于 Q_{M} ,还取决于 \boldsymbol{Q}_{M+1}\,,\cdots,\boldsymbol{Q}_{M+r-1} ,因此，在辨识 Q_{M} 时,还必须建立 Q_{M+\,i}\,(\,i=1\,,2\,,\cdots,r\,) 与 Q_{M} 的关系。若设 Q_{M} ，至 Q_{M+\,r\,^{\,-}\,1} 是线性变化的,当时间间隔是常数时,则有

{Q}_{M+n}\;=\;{Q}_{M}\,+\,\,n\,(\,{Q}_{M}\,-\,\hat{{Q}}_{M-1}\,)\;\;\;\;\left(\,n\;=\;1,2,\cdots,r\;-\;1\,\right)

因此,辨识 Q_{M} 的状态方程为

\left\{\begin{array}{l l}{\displaystyle\frac{\partial}{\partial x}\bigg[k\left(T\right)\frac{\partial T}{\partial x}\bigg]=\,\rho_{\nu}\,\frac{\partial T}{\partial t}}&{x\in\left(0,L\right),t\in\left[t_{M-1},t_{M+r-1}\right]}\\ {\displaystyle T(x\,,t_{M-1})\,=\,T^{\prime}(x)}&{x\in\left[0,L\right]}\\ {\displaystyle-\,k\left(T\right)\!\frac{\partial T}{\partial x}\bigg\rvert_{x\,=\,0}=\,Q_{M+n}}&{t\in\left[t_{M+n-1},t_{M+n}\right];n\,=\,0,1,\cdots,r-1}\\ {\displaystyle-\,k\left(T\right)\!\frac{\partial T}{\partial x}\bigg\rvert_{x\,=\,L}=\,0}&{t\in\left[t_{M+n-1},t_{M+n}\right];n\,=\,0,1,\cdots,r-1}\end{array}\right.

观测方程为（设采样为等时间间隔）

T_{M+i}\,=\,T(\,L\,,t_{M+i}\,)\,+\,\epsilon(\,i\,)\quad(\,i\,=\,0\,,1\,,\cdots,r\,-\,1\,)

辨识的目标函数取为

J\;=\;\sum_{i\,=\,0}^{r\,-1}\,[\:T_{M+\,i}\;-\;T(\:L\:,t_{M+\,i}\:)\:]^{2}

视 Q_{M} 为参数，采用灵敏度法来辨识，则其迭代形式为

Q_{M}^{(k+1)}\;=\;Q_{M}^{(k)}\;+\;\left\{\sum_{i=0}^{r-1}\left[\;T_{M+i}\;-\;T(\;L\,,t_{M+i}\,)\;\right]\;\frac{\partial\,T(\;L\,,t_{M+i}\,)}{\partial Q_{M}}\right\}\,\left(\;L\,,t_{M+i}\;-\;L\,,t_{M+i}\;\right)\;.

\sum_{i\mathop{=}0}^{r-1}\left[\frac{\partial\,T(\,L\,,t_{M+i}\,)}{\partial\,Q_{M}}\right]^{2}

式申 \boldsymbol{Q} 的上标 k\dots k+1 迭代层次；\partial\,T/\partial\,Q_{M} —灵敏度。

可由灵敏度方程(12-34)求得

\begin{array}{r l}&{\left|\frac{\partial}{\partial x}\left[k^{(T)}\frac{\partial}{\partial x}\left(\overline{{g}}\overline{{t}}_{q}\right)\right]=\rho_{k}\;\frac{\partial}{\partial t}\left[\frac{\partial}{\partial q_{k}}\right]\right.}\\ &{\qquad\qquad\qquad\quad\varepsilon\in\{0,L\},\;t\in\{t_{k+1},t_{k+1},\ldots,t\}}\\ &{\qquad\qquad\quad\left.\frac{\partial}{\partial Q_{k}}\left(x,t_{k+1}\right)=0\qquad\qquad\quad x\in\{0,L\}}\\ &{\qquad\qquad\quad\partial\overline{{t}}_{q}\left(x,t_{k+1}\right)=0\qquad\qquad\quad\left.\right.}\\ &{\qquad\qquad\qquad\quad\left.t\in[t_{k+1},t_{k+1}]:n=0,1,\ldots,r=1}\\ &{\qquad\qquad\quad\left.t\in\{t_{k+1},t_{k+1}\}:n=0,1,\ldots,r=1}\\ &{\qquad\qquad\quad\;\partial\overline{{t}}_{x}\left(\overline{{g}}\overline{{t}}_{q}\right)\right|_{x=L}=0}\\ &{\qquad\qquad\qquad\quad\varepsilon\in\{t_{k+1},t_{k+1}\}:n=0,1,\ldots,r=1}\\ &{\qquad\qquad\quad\left.\qquad\quad(12)}\end{array}

综上所述,用顺序函数法辨识热流时，是在时间方向上按顺序向后辨识。当 M=1 时， Q_{0} 已知，方程式（12-30)中的 T^{\prime}\left(x\right) 即为初始时刻已知的全场温度分布，由初估的 Q_{1} 及式（12-30）可求出后 \pmb{r} 个时刻的温度值 T(L\,,t_{i})(\,i=1\,,2\,,\cdots,r\,) ,再由式(12-34)求出灵敏度

\partial\,T(L\,,t_{i})/\partial Q_{M}

(\,i=1\,,2\,,\cdots,r\,) 后，用式(12-33)来对 Q_{M} 优化，优化得 Q_{M} 的最优估值则取为 Q_{1} 的辨识值。然后，再沿时间方向推进,用 Q_{1} 及T_{2},T_{3},\cdots,T_{r+1} 按照同样的方法来辨识 Q_{2} ,依此类推。

接下来用一算例来对上述算法进行验证。表面热流取为一抛物型热流 Q=20\,t+10\,t^{2}(\,\mathrm{W/m}^{2}) ，其余条件为 L=1\mathrm{~m}\,;\,T_{0}=0\mathrm{~K~} \rho C_{\rho}=1~{\mathrm{J}}/(~{\mathrm{K}}\cdot\mathbf{m}^{3})~;k=1~{\mathrm{W}}/(~\mathbf{m}\cdot\mathbf{K}) ,测量点取在 x=L 处。先用以上参数来计算正问题,得到测点处温度的计算值 T_{c}\left(\it{t}\right) ,再将此计算值作为测量值,用顺序函数法来辨识表面热流,顺序函数法中的 ^r 取为4。表面热流的辨识结果示于图 12-7中,辨识值与真值完全重合。当在 T_{c}\left(t\right) 上叠加标准差 \pmb{\sigma} 为0.01K的测量白噪声，并将叠加后的值作为测量值来辨识表面热流时，顺序函数法中的\pmb{r} 取为8,辨识结果较好地反映出了表面热流的变化趋势，与真值差别不大，二者的比较也示于图 12^{-7}<

图 12-7 顺序函数法辨识算例

3）导弹表面热流辨识仿真算例

导弹在再人大气层过程中，会经历较严重的气动加热。因此，型号设计部门希望通过在导弹的防热层内安装传感器来测定其表面热流。从弹体结构强度来考虑，设计部门希望将传感器安装在弹体内壁，以避免在防热层中钻孔来安装传感器。但是，冉人弹头的飞行时间很短，急剧气动加热的时间仅十几秒，而热传导问题又具有较强的滞后性，防热层内壁的温升通常在设计时被控制在150K以下，这就使得防热层内壁处温度的变化不能“及时”地反映出表面热流当前的变化情况。这表明，简单地将传感器置于防热层内壁来确定表面热流是很困难的。但另一方面，传感器又不能放置得太靠外，以免被烧坏。因此，在飞行试验前有必要分析如何放置传感器，使用何种精度的传感器才能安全而准确地确定出飞

行器再人时的表面热流。

仿真辨识是解决这一问题的有效方法。首先，通过气动热环境工程算法[13}]对弹道的仿真计算可以大致确定出弹体表面的热流分布；再用有限控制体积法可以求解出测点上的温度历程；以此温度历程加上测量噪声作为实测得到的温度历程,用顺序函数法来辨识表面热流；如果该热流的辨识值与仿真计算值符合得比较好，就表明当前传感器的位置是合适的，否则，应将传感器位置前移。下面分两种情况来对导弹弹体上某特征点处的热流进行仿真辨识。该特征点处的防热层由两层材料组成,外层为 L=12\,\mathrm{\mm} 厚的斜缠碳酚醛,物性参数为： \rho=1350~{\mathrm{kg/m}}^{3}\,,\,c_{_{P}}=1260~{\mathrm{J/(\kg\cdot\k^{2}}}\, K) , \pmb{k}=1.1\ \mathbf{W}/(\mathbf{m}\cdot\mathbf{K}) ；内层为 3\,\textrm{m m} 厚的铝,物性参数为： \rho= 2800~{\bf k g/m}^{3}\,,c_{_p}=1000~{\bf J}/({\bf k g}\cdot{\bf K})\,,k=130~{\bf W}/({\bf m}\cdot{\bf K})\,\mathrm{o}

（1）不考虑防热层烧蚀后退的情况。为讨论方便，首先分析不考虑防热层烧蚀后退的理想情况。在这一情况下，弹体表面热流主要由两部分组成，一部分是气动加热热流，正是需要辩识确定的热流（其仿真计算值如图12-8所示）；另一部分是弹体表面向周围环境的辐射热流，由斯蒂芬-玻耳兹曼（Stephen-Boltzmann）定律[17],可表示为

Q_{\mathrm{rad}}\;=\;\epsilon\delta(\mathrm{\nabla}T_{\mathrm{sur}}^{4}\;-\;T_{\mathrm{{env}}}^{4})

图12-8仿真计算的表面热流历程

式中 T_{\mathrm{sur}} 一—弹体表面温度；

Tenv 一—环境温度；\delta 斯蒂芬-玻耳兹曼常数， 5.67\times12^{-8}\;\mathrm{W}/(\mathrm{m}^{2}\!\cdot\!\mathrm{K}^{4}) \boldsymbol{\epsilon} 物体的黑度,亦称为发射系数，这里取为0.8。

在有限控制体积法的计算过程中，辐射热流可以直接加人到式(12-25)的 \boldsymbol{Q} 中，再代人式（12-27）中进行温度的迭代计算（注意 T_{\mathrm{sur}}(\,t_{n+1}\,)\geq T_{1}^{n+1})

当温度传感器置于碳酚醛防热层的内壁（即 x=L )时，用有限控制体积法和仿真计算出的热流可以计算出该处的温度变化历程，,如图12-9所示，以此计算值作为测量结果（采样间隔取为\Delta t=0.4\mathrm{s}) ，用顺序函数法来辨识表面热流， \pmb{r} 取值为 28。 热流辨识结果与仿真计算结果的比较示于图12-10，从图中可看出，在16s以前，热流的辨识值和仿真计算值符合得比较好，但是，由于热传导的滞后性，在16s以后，表面热流传到 x=L 处的温度信息很少，以致于被计算机的截断误差和算法本身的系统误差所湮没，不能反映出16s以后的表面热流变化情况。在实际辨识计算中，x=L 处温度信息的不足就具体表现为16s后减小 r 值会导致计算发散。

图12-9各测点温度仿真计算值

将传感器前移至 x=2L/3 处，该测点处温度仿真计算值也示于图12-9中，以此温度历程作为实测值来辨识表面热流，辨识结果示于图12-11。由图中知,虽然此时的热流辨识结果较传感器置于 x=L 处时的辨识结果有所好转，但仍未能模拟出仿真计算值后段的下降趋势。

图 12-10表面热流辨识结果比较

图 12-11表面热流辨识结果比较

将传感器进一步前移至 x=L/2 处，此时测点处温度仿真计算值也示于图12-9中，以此温度历程作为实测值来辨识表面热流，辨识结果示于图12-12。由图中可以看出，此时的热流辨识结果与仿真计算值符合得很好，辨识结果不仅模拟出了热流仿真计算值先升后降的变化趋势，而且热流峰值处的相对误差仅为4\cdot31\,\% 。但是，在实际的温度测量过程中，不可避免地会引人测量噪声。在此问题中，由图12-9知，测点 x=L/2 处的温度会达到

图 12-12表面热流辨识结果比较

800K以上,则温度传感器的量程至少应为1000K,当传感器的测量精度为 0.5\,\% 时，测量噪声可以用一均值为0,标准差为 \sigma=5\mathrm{K} 的白噪声来模拟。将测点温度仿真计算值叠加该白噪声后作为实测值来辨识表面热流，辨识结果示于图12-13中（用空心圆圈表示）,该辨识结果未能模拟出仿真计算值后段的下降趋势。当传感器的测量精度为 0.25\,\% 时，测量噪声用标准差为 \sigma=2.\,5\mathrm{K} 的白噪声来模拟，将白噪声叠加到测点温度仿真计算值上后作为实测值来辨识表面热流，辨识结果示于图12-13中（用空心三角形表示），该辨识结果比 \sigma=5\mathrm{K} 时的辨识结果更为光滑，但仍未能模拟出仿真计算值后段的下降趋势。进一步提高传感器的测量精度到0.15\,\% 时，同样，测量噪声用标准差为 \sigma=1.5\mathrm{K} 的白噪声来模拟，再将白噪声叠加到测点温度仿真计算值上后作为实测值来辨识表面热流，辨识结果示于图12-13中（用实心三角形表示），此时的热流辨识结果模拟出了热流仿真计算值先升后降的变化趋势，其峰值与仿真计算值的峰值在大小上很接近，但在峰值位置上有一定偏差，辨识值的峰值有所滞后。

通过以上分析可以看出：

\textcircled{1} 通过在防热层内放置温度传感器来辨识表面热流时，传感器不能放置得太靠里，否则测得的温度信息不足以及时反映出表面热流的变化情况。

图12-13 有噪声时热流辨识结果

\circledcirc 传感器的测量精度对辨识结果也有影响，当传感器精度较低时，测得的温度信息不能很准确地反映出表面热流的变化情况。就当前讨论的算例而言，将温度传感器置于 x=L/2 处，传感器精度达到 0.15\,\% 时，即可安全而又较准确地辨识出表面热流。

（2）考虑防热层烧蚀后退的情况。在实际的飞行器再人过程中，防热层在高温作用下通常会产生烧蚀后退。此时的表面热流主要由3部分组成：一是气动加热；二是辐射传热；另一部分是防热材料烧蚀带走热量，可表示为

Q_{a b l}\;=\;m_{a}\left(\frac{}{}c_{p g}T_{\mathrm{sur}}\:-\:c_{p}T_{\mathrm{sur}}\right)

式中CpC—— -分别为防热材料在气态和固态时的比定压热容；

m_{a} —一材料的质量烧蚀率。

在有限控制体积法的计算过程中，烧蚀带走热量也可以直接加人到式（12-25)的 \boldsymbol{Q} 中，再代人式（12-27）中进行温度的送代计算。同时，烧蚀后退可以用近似的方法来处理，即在每一个时间推进区间 \left[\,t\,,t+\Delta t\,\right] 中假设材料的厚度不变，用有限控制体积法解出 t+\Delta t 时的全场温度分布 T_{i}(\,i\,\{\,=\,1\,,2\,,\cdots,N\,\} ，然后将材料的厚度减去烧蚀量 V_{{\mathfrak{a}}}(t)\Delta t(V_{{\mathfrak{a}}} 为材料烧蚀后退率），重新生成计算网格，并将各网格点上的值近似地用 T_{i}\,(\,i=1\,,2\,,\cdots,N\,) 来代替，再进行后续计算，当 \Delta t 较小时，该近似方法具有足够的数值精度。

就前面讨论的某型导弹弹体上的特征点处而言，用工程算法仿真计算出的质量烧蚀率随再人时间的变化如图 12-14所示,仿真计算出的材料烧蚀后退率 V_{a} 随再人时间的变化如图12-15所示。通过烧蚀后退率对时间积分可以得出防热层厚度随再人时间的变化规律,由此可知,再人结束时,此时防热层后退约 4\mathsf{m m} 。地面安装传感器时如果是将传感器置于 P 点（ \chi=L/2) 处，再人结束时传感器距离表面就只有约 2\mathbf{mm} 。由仿真的热流、质量烧蚀率、烧蚀后退率,用有限控制体积法可以计算出再人过程中 P 点的最高温度达到了约2000K,因此,此时传感器有可能被烧坏,其安装位置需适当后移。

图 12-14仿真计算的质量烧蚀率

图 12-15 仿真计算的烧蚀后退率

考虑将传感器移至 Q 点 (x=2L/3) 处，该处的温度仿真计算值如图 12-16 中实线所示,该处最高温度约为 1000K。以此温度历程作为实测值来辨识表面热流，辨识结果如图12-17中虚线所示，与仿真计算值符合得很好，比图12-11中的辨识结果有很大改进，究其原因，这是由于再人过程中的烧蚀引起防热层变薄，测点离表面的距离越来越近，使得表面热流的信息在测点处得到了更多更及时的反映。当考虑测量噪声且温度传感器的测量精度为1%时（传感器量程取为1000K）,在Q点温度仿真计算值上叠加均值为0、标准差为 \sigma=10\mathrm{K} 的白噪声后作为实测值来辨识表面热流，辨识结果如图12-16中空心圆圈所示，该辨识结果在前段与仿真计算值差别较大，在后段也未能有效地模拟出表面热流的下降趋势。因此，将温度传感器的测量精度提高到 0.5\,\% ，在 \boldsymbol{Q} 点温度仿真计算值上叠加均值为0标准差为 \sigma\approx5\mathrm{K} 的白噪声后作为实测值（在图12-16中用实心三角形表示)来辨识表面热流，辨识结果如图12-17中实心三角形示，该辨识结果较好地模拟出了表面热流的变化趋势，但热流峰值的位置有一定滞后。这一结果表明，在当前情况下，传感器的放置位置和测量精度是合乎要求的。

图 12-16考虑烧蚀时测点温度计算值

图 12-17考虑烧蚀时热流辨识结果

通过对本节算例的分析可以看出，用仿真辨识结合气动热环境工程估算的方法可以大致确定出飞行试验中温度传感器的放置位置和测量精度，从而为进一步从实际飞行试验数据中安全而又准确地辨识出飞行器的表面热流奠定了基础。

4）航天飞机表面热流辨识仿真算例

航天飞机在再人大气层过程中，也会经历恶劣的热环境。但与再人弹头相比，航天飞机再入过程中的气动加热热流值不太高，而其再人时间比较长。并且，由热传导问题的延迟性知，航天飞机在着陆以后，尽管其表面已只有辐射放热而无气动加热热流传人，但防热层内仍有早些时刻传人的气动加热热流在传递，对防热层内某些点上的温度还有较大影响。因此，当测温点选择在防热层内壁附近时，尽管测温点上的温升并不大，但已包含了航天飞机冉人过程中气动加热热流变化的足够信息，使得我们能够借助参数辩识的方法由测温点上的温度变化历程来较准确地确定出航大飞机表面的气动加热热流。下面以某模型航大飞机迎风中心线上的某特征点为例，用顺序函数法来对该特征点上的表面热流进行仿真辨识。

某模型航天飞机迎风面的防热系统采用的是高温重复使用表面隔热材料（HRSI）,其具体结构如图12-18所示，黄振中对各层材料的热物性参数值随温度的变化情况曾进行过收集分析，在他发表的内部报告中有详细列表，其大致取值如表12-9所列。基于此防热结构，下面以迎风中心线的中点为研究对象，用顺序函数法来对航天飞机再人过程中该点上的表面热流进行仿真辨识。

<html>

涂层3.81×10^米
瓦(LI-900RSI)7.97X10²米
胶合剂(RTV-560)1.78×10米
应变隔离垫(SIP)4.064×10 3米
胶合剂(RTV-560) 1.78×10 4米 铝结构6.35×103米

</html>

表 12-9各层防热材料热物性参数大致取值情况
图 12-18防热层结构示意图

<html>

材料	p/(kg·m -3)	c/(W·m-'·K-1)	k/(J·kg-'·K-')
涂层	1666	1200	1.2
瓦	144.17	1000	0.06
胶合剂	1409.7	1464.4	0.3115
应变隔离垫	86.5	1100	0.03 *
铝结构	2803.4	006	130

</html>

在航天飞机再人过程中，表面热流主要由两部分组成，一是气动加热热流,正是需要确定的热流;二是航天飞机表面向周围环境的辐射热流，表面涂层的发射系数值为0.85。

参考文献[18]给出了用数值计算方法计算出的迎风中心线中点上的气动加热热流,其时间历程如图12-19所示。利用此热流和有限控制体积法，可以计算出防热层内各点的温度变化历程。这里需要指出的是，由于热传导问题的延迟性，航天飞机在着陆以后，尽管其表面已只有辐射放热而无气动加热热流传人，但防热层内仍有早些时刻传人的气动加热热流在传递，使得防热层内某些点的温度还有一个上升,继而平缓,然后再下降的变化过程。图12-20 给出了表面温度的变化历程，图 12-21 给出了瓦的内壁处，即图12-18中 P 点所示位置的温度变化历程。铝结构内壁处的温度历程同样也可以计算出来,温升大致为 30\mathrm{K}

图 12-19气动加热热流计算值

图12-20.表面温度变化历程

下面以 P 点为测温点，首先以该点温度计算结果作为实测值，用顺序函数法辨识其气动加热热流。 ^r 取为 \pmb{r}=450 （时间采样间隔为 1s）,该热流的辨识结果示于图 12-22。由图中可以看出，该辨识结果很好地反映出了表面气动加热热流数值计算值的变化趋势，在具体数值上也符合得较好。

再在计算结果上叠加标准差为1K的白噪声来作为温度的测量值，同样用顺序函数法辩识其气动加热热流。 \pmb{r} 取为 r=650 ,辨识结果示于图12-23。由图中也可以看出，该辨识结果也与表面气动加热热流数值计算值符合得比较好。图12-24给出了在测温点上用热流辨识结果计算出的温度值与仿真模拟的实测值的比较，二者拟合得相当好。

图12-21 P 点温度变化历程

图12-22表面热流辨识结果比较（无测量噪声）

由以上结果可以看出，由于航天飞机再人时间长，且其早些时刻的气动加热热流在着陆后仍能在防热层中继续向内传递，使得防热层内壁附近测温点上的温度历程包含了航天飞机再人过程中气动加热热流变化的足够信息，从而可以借助参数辨识的方法来较准确地确定出航天飞机表面的气动加热热流。这就为返回式再人飞行器表面热流的确定提供了又一有力手段，为飞行器表面热流的数值计算结果和风洞实验结果的验证提供了依据，在航天研究领域有着良好的实际工程应用前景。

图 12-23表面热流辨识结果比较(考虑测量噪声)

图12-24测点温度值比较

12.4 工程湍流模型辨识

自然界和工程技术所涉及的流动,在绝大多数情况下是湍流状态的。然而，由于人们至今对湍流流动机理的认识尚不完善。因此,关于湍流流动的数值模拟,长期以来都是计算流体力学研究最为活跃,最具有挑战性的领域之一[19,20]

目前，对湍流的数值模拟方法大致可分为3类：直接模拟、大涡模拟和雷诺平均方程法。在直接模拟方法中，认为包括脉动在

内的湍流瞬时运动也服从NS方程，而 NS方程本身是封闭的。因此，可以数值求解完整的三维非定常NS方程，对湍流的瞬时运动进行直接的数值模拟，再对结果作平均计算就可得出感兴趣的各种统计平均量。但是,直接模拟方法一直受着计算机速度与内存容量的限制，其主要困难在于湍流脉动运动中包含着大大小小不同尺度的涡运动，其最大尺度可与流动平均运动尺度相当，而最小尺度则取决于粘性耗散速度，即柯尔莫哥洛夫（Kolmogonov）定义的内尺度 \pmb{\eta}=(\left.v^{3}/\epsilon\,\right)^{0.25}(\,\pmb{v} 为层流粘性系数， \pmb{\epsilon} 为湍能耗散率)。因此，在数值模拟时，一方面要求计算域的尺寸应大到足以包含最大尺度的涡,另一方面又要求计算网格尺度应小到足以分辨最小尺度的涡。同时，计算模拟的时间长度也应大于大涡的时间尺度，而时间步长又应小于小涡的时间尺度。这就要求计算机具有相当大的内存和相当快的计算速度，但就目前计算机水平而言，这些要求还难以达到，使得直接数值模拟的方法目前在工程上还难以实现和应用，已有的研究工作也仅限于雷诺数较低的一些简单几何外形的流动。大涡模拟方法的基本思想则是把包括脉动运动在内的湍流瞬时运动通过某种滤波方法分解成大尺度运动和小尺度运动两部分。大尺度运动通过数值求解NS方程来直接计算出来，小尺度运动对大尺度运动的影响则在运动方程中通过建立模型来模拟。这一方法的计算量仍较大，而且方法本身也有一些缺陷，例如，现有的亚格子应力模型，尤其是近壁区内的模型仍很不完善；怎样才是正确的人流出流边界条件等，都是需要解决的问题。迄今为止，大涡模拟的应用还主要是在大气与环境科学领域，在工程问题中的应用还为数不多119]

雷诺平均方程法是目前工程上解决湍流流动问题的常用方法。在这一方法中，将非定常NS方程对时间作平均，在所得出的关于时均物理量的控制方程中包含了二阶脉动速度关联量的时均值等未知量，于是所得方程个数少于未知量个数，这时，不可能依靠进一步时均处理来使方程组封闭，必须作出假设，建立湍流模型来使控制方程组封闭。以动量方程为例，其时均形式为

524

\frac{\partial(\rho U_{i})}{\partial t}\,+\,\frac{\partial(\rho U_{i}U_{j}\,)}{\partial x_{j}}\,=\,-\,\frac{\partial\,\phi}{\partial x_{i}}\,+\,\frac{\partial}{\partial x_{j}}\Bigg(\mu\,\frac{\partial U_{i}}{\partial x_{j}}\,-\,\rho\,\overline{{u_{i}u_{j}}}\Bigg)

式中 廿 U 时均速度；

\pmb{u} 一脉动速度；u;u; 雷诺应力,时均后新引人的未知量（上划横线表示取时均)。

不同的湍流模型对雷诺应力的模拟方法不同。目前在工程湍流计算中常用的湍流模型总体上可以划分为两大类：一类是基于布辛涅斯克(Boussinesq)假设的涡粘性模型；另一类是基于雷诺应力输运方程的二阶矩封闭模型。前者根据所附加引人的偏微分方程的数目又可细分为零方程模型、一方程模型和两方程模型；后者则可分为代数应力模型和雷诺应力输运方程形式模型。

随着人们对湍流认识的不断深人,湍流模型也在不断得到改进与完善。目前对湍流模型的改进大致可概括为3个方面。第一方面是湍流模型的低雷诺数修正。现今通常所用的两方程模型和二阶矩封闭模型,其基准形式都只适用于充分发展的湍流流动，这类模型一般称为高雷诺数模型。但是,这类模型不能很好地模拟壁面附近粘性次层和过渡层中的流动。因而,为了使同一封闭模型既适用于充分发展的湍流流动，也适用于粘性效应起重要作用的近壁流动，有必要对高雷诺数封闭模型进行修正，修正后的模型就称为低雷诺数封闭模型。1972 年,琼斯（Jones)和伦德尔（Laun-der)提出了低雷诺数 k^{-}\varepsilon 模型，随后，不少学者也提出了自己的低雷诺数修正方法并用之于工程实际[21]。同时,还有一些学者致力于研究低雷诺数的二阶矩模式，也已取得了许多可喜的结果。

对湍流模型改进的第二个方面则是模型的非线性化。就 k\!-\!\varepsilon 两方程模型而言，虽然该模型在工程上得到了广泛应用，但该模型对一些较复杂的流动或者精度下降，或者完全失败。例如，在激波后边界层内、在边界层分离点附近以及有分离区的流动中，流动沿流向有显著变化，正应力的梯度要起重要作用，涡粘性模型不能恰当地描写流动的发展;在非圆截面管流和明渠流中,在横截面内由于湍流应力场的强各向异性引起的二次流是很重要的，而涡粘性模型则完全不能计算出二次流。究其原因，一是由于湍流模型中的许多模化项是建立在各向同性假设之上；二是由于在布辛涅斯克假设中，雷诺应力与平均速度梯度线性关联，从而使得 k^{-}\varepsilon 模型未能反映出上述流动的基本物理特性。因此，近年来，国内外的不少专家学者，如国外的斯伯扎那（SpezialeCG）、勒西兹那（Leschziner M A）、义泽（Yoshizawa A)教授，以及国内的符松、陈义良、窦国仁教授等从物理分析和张量分析的角度人手来对布辛涅斯克假设进行非线性扩充，以此来表征流动的各向异性与非线性特性[22~27]。这些模型统称为非线性 k^{-}\varepsilon 模型（或各向异性 k^{-}\varepsilon 模型），现已在工程上得到了初步应用。

对湍流模型改进的第三方面则是考虑拟序结构影响的湍流模型研究。所谓拟序结构（亦称为相干结构），是指在切变湍流场中不规则地触发的一种序列运动，它的起始时刻和位置是不确定的，但一经触发，它就以某种确定的顺序发展特定的运动状态。切变湍流中拟序结构的发现是湍流研究的一个重大进展，它表明湍流并非完全无规则的运动，而是在表面上看来无规则运动中具有可检测的有序运动。因此，以往经典湍流模型研究中认为湍流是完全随机运动的假设将不再成立，同时也不能再用简单统计平均的方法来处理湍流方程，以免在平均过程中将拟序结构和其他不规则运动一起过滤掉，从而失掉拟序结构至关重要的信息。在这种情况下，只有采用多点统计矩才能对拟序结构的几何外形和方向性进行适当的描述[27]。然而,构造含有多点统计矩信息、考虑拟序结构影响的湍流模型的难度很大，目前研究它的学者虽然很多，采用的方法也各不相同，但至今还未建立起一个公认比较通用的模型[ 28] O

由以上分析可知，就目前的计算机计算能力与湍流理论研究现状来看，在今后相当长的一段时间里，基于雷诺平均方程并引人湍流模型仍将是解决工程湍流实际问题的有力手段，因此，工程端流模型的改进与完善是一项值得深人开展的研究工作。本节介绍的工程湍流模型辨识研究就是借助系统辨识的思想对工程湍流模型改进与完善的一种探索。所谓工程湍流模型辨识,是将湍流流动视为一部分模型结构已知，部分模型结构未知的非线性系统；将含有工程湍流模型的NS方程组视为其数学模型；将多个典型流动情况下的实验结果视为系统在不同输人情况下的输出，从而可以根据数值模拟结果和实验结果的比较，用分布参数系统辨识的方法来确定湍流模型结构中未知的部分，以期达到对湍流模型改进与完善的目的。本节的研究对象选取的是标准 k^{-}\varepsilon 两方程模型，因为这一模型虽已被广泛地应用于工程湍流的数值模拟之中，但是该模型本身仍还有许多比较明显的缺陷，需要做一些工作来对其进行改进与完善。对于其他形式的湍流模型，本节介绍的方法仍然适用。

12.4.1 不可压瑞流流动数值模拟方法

湍流模型的参数辨识从数学上讲是一个逆问题。因此，用灵敏度法进行湍流模型的参数辨识时，必须首先研究其正问题的求解方法。这一节便主要介绍不可压湍流流动 k^{-}\varepsilon 两方程模型的数值模拟方法[29]

1）控制方程

引人 k^{\,-}\varepsilon 两方程湍流模型后，不可压流动的时均定常NS方程的通式为

\begin{array}{r}{\textbf{\small v}\cdot\left(\,U\phi\,\right)\;=\;\textbf{V}\cdot\left(\,{\cal T}_{\phi}\,\textbf{V}\phi\,\right)\,+\,{\cal S}_{\phi}\,}\end{array}

对连续性方程而言

\phi\;=\;1\;\;\;\;\;{\Gamma}_{\phi}\;=\;0\;\;\;\;\;\;\;\;\;{S}_{\phi}\;=\;0

对动量方程

\phi\;=\;U_{i}\;\;\;\;\;F_{\phi}\;=\;v_{\mathrm{{eff}}}\;\;\;\;S_{\phi}\;=\;-\;{\frac{\partial\,\rlap/{\,/}\,_{\mathrm{eff}}}{\partial\,x_{i}}}\,+\,{\frac{\partial\,}{\partial\,x_{j}}}\left(\,v_{\mathrm{{eff}}}\;{\frac{\partial\,U_{j}}{\partial\,x_{i}}}\,\right)-\,{\frac{\partial\,Q_{i j}}{\partial\,x_{j}}}

对湍动能方程

\phi~=~k~~~~{\cal{F}}_{\phi}~=~v~+~v_{t}/\sigma_{k}~~~~S_{\phi}~=~G~-~\varepsilon

对瑞能耗散率方程

\phi\ =\ \ \ F_{\phi}\ =\ v\ +\ v_{t}/\sigma_{\epsilon}\ \ \ S_{\phi}\ =\ \left(\,C_{1}G\ -\ C_{2}\varepsilon\,\right)\varepsilon/k

式中

v_{\mathrm{\scriptsize{eff}}}\;=\;v\;+\;v_{\prime}\;=\;v\;+\;C_{\mu}\dot{k}^{2}/\epsilon

\ensuremath{\phi_{\mathrm{eff}}}\,=\,\ensuremath{\phi}\,+\,2k/3

G\;=\;-\;\overline{{{u_{i}}{u_{j}}}}(\partial\,U_{i}/\partial.x_{j})

\overline{{u_{i}u_{j}}}\;=\;\frac{2}{3}\delta_{i j}k\;-\;v_{t}\left(\partial\,U_{i}/\partial\,x_{j}\:+\:\partial\,U_{j}/\partial\,x_{i}\right)\;+\;Q_{i j}

对标准 k-\varepsilon 两方程模型而言， C_{\mu}=0\,.\,09\,,\,Q_{i j}=0 ,其余参数值通常取为： C_{1}=1\,.44\,,C_{2}=1\,.92\,,\sigma_{k}=1\,.0\,,\sigma_{\varepsilon}=1\,.3\,\mathrm{{o}}

2）数值离散

下面以二维流动为例来说明用有限体积法对以上控制方程组（12-35）进行数值模拟的方法。首先须对流场进行有限体积划分。图12-25中示出了-典型的有限体积单元（有限体积的中心为 P ，其四周相邻体积的中心分别为 E\,,\,W\,,N\,,S ；有限体积的四个边界面分别用 \boldsymbol{e}\mathrm{~,~}\boldsymbol{w}\mathrm{~,~}\boldsymbol{n}\mathrm{~,~}\boldsymbol{s} 表示；四个顶点分别用 n e\,,s e\,,s w\,,n v\omega 表示）。在该有限体积上对方程组（12-35)进行离散。方程组（12-35）包含3部分:对流项、扩散项和源项。根据高斯定理，向量散度的体积分等于该向量的面积分。因此，连续方程离散为

F_{e}-F_{w}+F_{n}-F_{s}=0

式中 F_{e}=U_{e}\cdot{\boldsymbol{n}}_{e}\,,F_{n}=U_{n}\cdot{\boldsymbol{n}}_{n} 一有限体积东、北界面上的质量流量 (\boldsymbol{F}_{w}\,\!,\!\boldsymbol{F}_{s} 的表达式类似）;

图 12-25 有限体积示意图

\pmb{U} 和 \pmb{n} 一有限体积单元界面上的速度矢量和界面的法向矢量。

动量方程则分3部分来离散:对流项的离散、扩散项的离散、源项的离散。

（1）对流项的离散。对流项为 \mathrm{div}(\,U\phi\,) 的形式,由高斯定理，有

I^{C}\,=\,\int_{\delta V}\!\mathrm{div}(\,U\phi\,)\mathrm{d}v\,=\,\oiint_{S}\!U\phi\,\cdot\,\mathrm{d}s\,=

\sum_{b}\,(\,{\cal U}\phi\,\cdot\,\mathrm{d}s\,)_{\,b}\ =\ \sum_{b}\,(\,\phi_{b}F_{b}\,)

式中 ^b 一一有限体积的界面，即 \boldsymbol{b}=\boldsymbol{e}\,,\boldsymbol{w}\,,n\,,s_{\circ}

下面以东边界面 e 为例来说明对流项的求法。

在东边界面上， I_{e}^{C}=\phi_{e}F_{e} ，此处的 \pmb{\phi}_{e} 有多种取法,不同的取法就代表着不同的差分格式。

当采用迎风差分格式(UDS)时

\phi_{e}\,=\,\left\{\begin{array}{l l}{{\phi_{p}}}&{{F_{e}\,>0}}\\ {{\phi_{E}}}&{{F_{e}<0}}\end{array}\right.

当采用中心差分格式（CDS）时

\phi_{_{e}}\,=\,f_{_{e}}\phi_{_{E}}\,+\,(1\,-\,f_{_{e}}\,)\,\phi_{_{P}}

式中 f_{e} -几何插值因子 f_{e}=\{\,e P\,|\,/\,|\,P E\,|\,

当采用中心与迎风差分相结合的混合格式(HUCD)时 (\,r 为权因子）

\phi_{e}\,=\,r\phi_{e}^{\mathrm{CDS}}\,+\,\left(1\,-\,r\,\right)\phi_{\,e}^{\mathrm{UDS}}\,=\,\phi_{\,e}^{\mathrm{UDS}}\,+\,r\,\big(\,\phi_{\,e}^{\mathrm{CDS}}\,-\,\phi_{\,e}^{\mathrm{UDS}}\big)

此时东边界面上的对流通量为

\begin{array}{r l r}{I_{e}^{C}\;=\;I_{e\,\mathrm{UDS}}^{C}\,+\,\Delta I_{e}^{C}}&{{}}&{\Delta I_{e}^{C}\;=\;r\,(\:I_{e\mathrm{CDS}}^{C}\,-\,I_{e\mathrm{UDS}}^{C})}\end{array}

当采用 HLPA（Hybrid Linear/Parabolic Approximation）格式130]时

\pmb{\phi}_{e}\;=\;U_{e}^{+}\pmb{\phi}_{P}\;+\;U_{e}^{-}\pmb{\phi}_{\mathrm{~E~}}+\Delta\pmb{\phi}_{e}

U_{\epsilon}^{+}\,=\,(1\,+\,\mid{\cal F}_{\epsilon}\,\mid/{\cal F}_{\epsilon}\,)/2\qquad U_{\epsilon}^{-}\,=\,1\,-\,U_{\epsilon}^{+}

\Delta\phi_{e}\;=\;U_{e}^{+}\alpha_{e}^{\;+}\left(\frac{\not p_{\mathrm{E}}^{}}{\not p_{\mathrm{E}}^{}}\,-\,\not p_{P}^{}\right)\left(\frac{\not p_{P}^{}\,-\,\not p_{_W}^{}}{\not p_{\mathrm{E}}^{}\,-\,\not p_{_W}^{}}\right)+

U_{e}^{-}\alpha_{e}^{-}\left(\right.\not\Phi_{p}\,-\,\not\Phi_{\mathrm{E}}\right)\left(\frac{\not\Phi_{\mathrm{E}}\,-\,\not\Phi_{\mathrm{EE}}}{\not\Phi_{p}\,-\,\not\Phi_{\mathrm{EE}}}\right)

\boldsymbol{\alpha}_{\epsilon}^{\dagger} 和 \ddot{\alpha_{\textit{e}}} 则取为

\alpha_{\it e}^{-}=\left\{\begin{array}{l l}{1}\\ {1}\\ {0}\end{array}\right. 如果 \mid\pmb{\phi}_{P}-2\pmb{\phi}_{\mathrm{E}}+\pmb{\phi}_{\mathrm{EE}}\mid<\mid\pmb{\phi}_{P}-\pmb{\phi}_{\mathrm{EE}}\mid 当 F_{e}\!<\!0 时，其他

该格式实质上是一种迎风加权格式，虽然形式上较为复杂，但具有二阶精度。

当采用 QUICK(Quadratic Upwind Interpolation of Convective Kinematics)格式[31]时

\begin{array}{r}{\pmb{\phi}_{e}\;=\;U_{e}^{+}\pmb{\phi}_{P}\,+\,U_{e}^{-}\pmb{\phi}_{\scriptscriptstyle\mathrm{E}}\,+\,\Delta\pmb{\phi}_{e}}\end{array}

式中

\Delta\phi_{e}\,=\,\left\{\!\!\begin{array}{l l}{{\displaystyle(-\,\,\phi_{\mathrm{w}}-2\,\phi_{_{P}}+3\,\phi_{_\mathrm{E}})/8}}&{{F_{e}\gg0}}\\ {{\displaystyle(3\,\phi_{_P}-2\,\phi_{_\mathrm{E}}-\,\phi_{_{\mathrm{EE}}})/8}}&{{F_{e}<0}}\end{array}\!\!\right.

{U}_{e}^{+} 和 U_{e}^{-} 的定义同HLPA格式，该格式也具有二阶精度。

由式(12-37)和式(12-38)知,HLPA 和 QUICK 格式都是在-阶迎风格式通量的基础上进行修正而得来的，在这两种格式下，东界面上的通量可写为

\begin{array}{r}{I_{e}^{C}\,=\,I_{e\mathrm{UDS}}^{C}\,+\,\Delta I_{e}^{C}\,;\,\Delta I_{e}^{C}\,=\,F_{e}\Delta\phi_{e}}\end{array}

因此,由式(12-36)和式(12-39)知 ,UDS、CDS、HUCD、HLPA和QUICK等五种格式对动量方程中东界面上对流通量的离散在形式上得到了统一。

在其余三个界面上，对流项的离散类似。

(2）扩散项的离散。式（12-37)中的扩散项移到左边后为

\mathrm{div}(\,-\,P_{\phi}\mathrm{~}\nabla\phi) ，由高斯定理，积分此式后有

I^{D}\,=\,\int_{\delta V}\!\mathrm{div}(\ -\ \Gamma_{\phi}\ \nabla\ \phi\,)\mathrm{d}v\,=\,\int_{S}\,-\,{\cal T}_{\phi}\ \nabla\ \phi\,\cdot\,\mathrm{d}s\,\,=\,\,

-\,\sum_{b}\left(\Gamma_{\phi}\,\,\nabla\phi\,\cdot\,\mathrm{d}s\,\right)_{b}

就东界面而言，将上式中的 \Delta\phi 用中心差分格式进行离散后，上式变为

I_{e}^{D}\;=\;I_{e1}^{D}\;+\;I_{e2}^{D}

式中

I_{e1}^{D}\;=\;D_{e}(\,\pmb\phi_{p}\:-\:\pmb\phi_{E}\,)

D_{e}\,=\,\frac{{\cal{T}}_{e}[\,(\,y_{n e}\,-\,y_{s e})^{2}\,+\,(\,x_{n e}\,-\,x_{s e})^{2}]}{(\,x_{E}\,-\,x_{P})(\,y_{n e}\,-\,y_{s e})\,-\,(\,y_{E}\,-\,y_{P})(\,x_{n e}\,-\,x_{s e})}

\mathsf{\Pi}_{\tau2}^{D}\;=\;\frac{{\cal{T}}_{e}[\,(\,y_{E}\,-\,y_{P})(\,y_{n e}\,-\,y_{s e})\,+\,(\,x_{E}\,-\,x_{P})(\,x_{n e}\,-\,x_{s e})\,]}{(\,x_{E}\,-\,x_{P})(\,y_{n e}\,-\,y_{s e})\,-\,(\,y_{E}\,-\,y_{P})(\,x_{n e}\,-\,x_{s e})}(\,\phi_{n e}\,-\,\phi_{s e})\,

其余三个界面上的离散也类似。

（3）源项的离散。设源项可写为 S_{\phi}=S_{\phi}^{u}\,+\,\phi\cdot S_{\phi}^{P} 的形式，则积分后为

\int_{\delta V}\!S_{\phi}\mathrm{d}\,v\ =\ \big[\,\big(\,S_{\phi}^{P}\,\big)\,_{P}\delta V\,\big]\,\cdot\,\phi_{p}\,+\,\big(\,S_{\phi}^{u}\,\big)\,_{P}\delta V

因此，综上所述，离散后的动量方程为

\begin{array}{c}{{\lbrack\;I_{e\mathrm{UDS}}^{C}+\,\Delta I_{e}^{C}\,+\,I_{e1}^{D}\,+\,I_{e2}^{D}\rbrack\,-\,\bigl[\;I_{w\mathrm{UDS}}^{C}\,+\,\Delta I_{w}^{C}\,+\,I_{w1}^{D}\,+\,I_{w2}^{D}\bigr]\,+}}\\ {{\bigl[\;I_{n\mathrm{UDS}}^{C}+\,\Delta I_{n}^{C}\,+\,I_{n1}^{D}\,+\,I_{n2}^{D}\bigr]\,-\,\bigl[\;I_{s\mathrm{UDS}}^{C}\,+\,\Delta I_{s}^{C}\,+\,I_{s1}^{D}\,+\,I_{s2}^{D}\bigr]\,=\,}}\end{array}

\int_{\delta V}\!S_{\phi}\mathrm{d}\,v\ =\ \big[\,\big(\,S_{\phi}^{P}\,\big)_{P}\delta V\,\big]\,\cdot\,\phi_{p}\,+\,\big(\,S_{\phi}^{u}\,\big)_{P}\delta V

将上式中的 I_{\mathrm{\ast_{UDS}}\,\mathrm{`}\,I_{\mathrm{~\ast~1~}}^{D}\left(\mathrm{~\ast~}=e\,,\,w\,,\,n\,,\,s\,\right)}^{C} 和右端第一项留在方程左端,其中的 \phi 作隐式处理。而其余项则移到方程右端作显式源项处理，从而得

a_{P}\pmb{\phi}_{P}-\ a_{E}\pmb{\phi}_{E}\,-\,a_{W}\pmb{\phi}_{W}\,-\,a_{N}\pmb{\phi}_{N}\,-\,a_{S}\pmb{\phi}_{S}\,=\,S

式中

\begin{array}{r l}&{a_{E}\,=\,\operatorname*{max}\{-\,F_{e}\,,0\}\,+\,D_{e}}\\ &{\,\,\,a_{W}\,=\,\operatorname*{max}\{\,F_{w}\,,0\,\}\,+\,D_{w}}\\ &{\,\,\,a_{N}\,=\,\operatorname*{max}\{-\,F_{n}\,,0\,\}\,+\,D_{n}}\end{array}

a_{S}\,=\,\operatorname*{max}\,\{\,F_{s}\,,0\,\}\,+\,D_{s}

a_{P}\;=\;a_{E}\:+\:a_{\psi}\:+\:a_{N}\:+\:a_{S}\:-\:(\:S_{\phi}^{P}\:)_{P}\delta V

S\,=-\,\Delta I_{e}^{C}\,+\,\Delta I_{w}^{C}\,-\,\Delta I_{n}^{C}\,+\,\Delta I_{s}^{C}\,-\,I_{e2}^{D}\,+\,I_{w2}^{D}\,-\,I_{n2}^{D}\,+\,I_{s2}^{D}\,+\,(\,S_{\phi}^{u}\,)_{P}\Delta V

因此，对流场内的所有有限体积进行离散后，最终得到一个五对角代数方程组,可以用斯通(Stone)提出的强隐算法来求解[32]。对于湍动能方程、湍能耗散率方程，也都能类似地离散为五对角代数方程组的形式。

3）压力修正方法

用以上方法来求解NS方程组时会出现一个问题：压力本身没有控制方程，如何通过其与速度的耦合来求解呢？帕坦卡(Patankar S V)与斯伯丁(Spalding D B)提出的 SIMPLE 方法[33],较好地解决了这一问题。SIMPLE方法的基本思想如下：:对于给定的压力场（它可以是假定的，也可以是上一迭代层的计算结果），按次序求解 U,V 的动量方程。由此所得的速度场未必能满足质量守恒的要求,因此必须对给定的压力场加以校正。为此，把由动量方程离散形式所规定的压力与速度的关系代人连续性方程的离散形式，从而得到压力修正值方程。由压力修正值方程解出压力修正值，进而去改进速度，以得出在这一迭代层能满足连续性方程的解。然后用计算所得的新的速度值去计算湍动能与湍能耗散率，并对动量离散方程中的系数加以改进，以开始下一层次的迭代计算。如此反复，直至获得收敛解。但是，由于SIMPLE算法中采用的是压力-速度分离式求解法，非交错网格的使用会引起非物理性质的压力波动[33]。瑞(Rhie)和周(Chow)[34)最早提出了一种改进的压力-速度耦合方法，有效地克服了这种压力波动，其关键在于对单元体界面上通量的插值方式。瑞和周的方法中，单元体界面上的速度不是通过线性插值得到，而是通过该界面相邻节点所代表的两个控制体积的动量方程插值而获得。同时，界面上压力梯度也是由相邻两中心节点的压力差分而得。这一方法已被成功地应用于许多二维及三维流场计算之中。本文就是采用瑞、周和马加姆达（Majumdar）等提出的动量插值法来进行压力修正。

就 P 点对应有限体积而言， \pmb{x} 方向的动量方程可写为

{\alpha}_{P}^{U}U_{P}\;=\;\sum_{n b}{\alpha}_{n b}^{U}U_{n b}\:+\:C_{x}^{U}(\:{\phi}_{e}\:-\:{\phi}_{w}\:)\:+\:C_{y}^{U}(\:{\phi}_{n}\:-\:{\phi}_{s}\:)\:+\:S_{U}

y 方向的动量方程可写为

a_{P}^{V}V_{P}~=~\sum_{n b}\!a_{n b}^{V}V_{n b}~+~C_{x}^{V}(~\!\rho_{e}~\!-~\!\rho_{w})~+~C_{y}^{V}(~\!\rho_{n}~\!-~\!\rho_{s})~+~S_{v}

设修正速度为 U^{\prime},\,V^{\prime} ，相应的压力修正值为 \pmb{\dot{p}}^{\prime} ，则 \boldsymbol{U}+\boldsymbol{U}^{\prime} V+\,V^{\prime}\,,p+\,\acute{p}^{\prime} 仍满足上两方程，相减后得

\begin{array}{l}{{U_{\,\,P}^{\prime}\,=\,\displaystyle\sum_{n b}\frac{a_{n b}^{\,U}}{a_{P}^{\,U}}U_{\,\,n b}^{\prime}\,+\frac{C_{\,\,x}^{U}}{a_{P}^{\,U}}(\,\displaystyle\beta_{e}^{\prime}\,-\,\displaystyle\beta_{w}^{\prime}\,)\,+\frac{C_{\,\,y}^{U}}{a_{P}^{\,U}}(\,\displaystyle\beta_{n}^{\prime}\,-\,\displaystyle\beta_{s}^{\prime}\,)}}\\ {{V_{\,\,P}^{\prime}\,=\,\displaystyle\sum_{n b}\frac{a_{n b}^{\,V}}{a_{P}^{\,V}}V_{\,\,n b}^{\prime}\,+\frac{C_{\,\,x}^{V}}{a_{P}^{\,V}}(\,\displaystyle\beta_{e}^{\prime}\,-\,\displaystyle\beta_{w}^{\prime}\,)\,+\frac{C_{\,\,y}^{V}}{a_{P}^{\,V}}(\,\displaystyle\beta_{n}^{\prime}\,-\,\displaystyle\beta_{s}^{\prime}\,)}}\end{array}

由SIMPLE算法思想，令 \tilde{\mathcal{X}}_{n;}^{\prime} 和 V_{n b}^{\prime} 为零后，有

\begin{array}{l}{{U_{P}^{\prime}\,=\,{\displaystyle\frac{C_{x}^{U}}{a_{P}^{U}}}\,(\,\hat{p}_{e}^{\prime}\,-\,\hat{p}_{w}^{\prime})\,+\,{\displaystyle\frac{C_{y}^{U}}{a_{P}^{U}}}\,(\,\hat{p}_{n}^{\prime}\,-\,\hat{p}_{s}^{\prime}\,)}}\\ {{\displaystyle V_{P}^{\prime}\,=\,{\displaystyle\frac{C_{x}^{V}}{a_{P}^{V}}}\,(\,\hat{p}_{e}^{\prime}\,-\,\hat{p}_{w}^{\prime}\,)\,+\,{\displaystyle\frac{C_{y}^{V}}{a_{P}^{V}}}\,(\,\hat{p}_{n}^{\prime}\,-\,\hat{p}_{s}^{\prime}\,)}}\end{array}

下面求压力修正值,将式(12-41)在 P 点与 E 点写为

U_{P}\,=\;H_{P}\,+\,{\frac{C_{x}^{U}}{a_{P}^{U}}}(\,\widehat{p}_{e}\,-\,\widehat{p}_{w})\,+\,{\frac{C_{y}^{U}}{a_{P}^{U}}}(\,\widehat{p}_{n}\,-\,\widehat{p}_{s})\,+\,{\frac{S_{U}}{a_{P}^{U}}}

U_{E}\,=\,H_{E}\,+\,\left\{\frac{C_{x}^{U}}{a_{P}^{U}}\right\}_{E}\left(\,\phi_{E e}\,-\,\phi_{E w}\right)\,+\,\left[\frac{C_{y}^{U}}{a_{P}^{U}}\right]_{E}\left(\,\phi_{E n}\,-\,\phi_{E s}\right)\,+\,\left[\frac{S_{U}}{a_{P}^{U}}\right]_{E}

对界面 e 上的 U ，采用动量插值得

U_{e}\;=\;\hat{H}\;+\;\left[\frac{C_{x}^{U}}{a_{P}^{U}}\right]_{e}\left(\;\rho_{E}\;-\;\rho_{P}\right)\;+\;\;\left[\frac{C_{y}^{U}}{a_{P}^{U}}\right]_{e}\left(\;\rho_{n e}\;-\;\rho_{s}\right)\;+\;\;\left[\frac{S_{U}}{a_{P}^{U}}\right]_{e}

式中 \hat{H}{\longrightarrow}H_{P} 与 H_{E} 的线性插值;

(1/a_{P}^{U})_{e}{\longrightarrow}(1/a_{P}^{U})_{P} 与 (\mathfrak{l}/a_{P}^{U})_{E} 的线性插值;

其余 V_{e}\,,\,U_{w}\,,\,V_{w}\,,\,U_{w}\,,\,V_{w}\,,\,U_{n}\,,\,V_{n}\,,\,U_{s}\,,\,V_{s} 等量的处理方法类似。将这些值代人连续方程后，有

F_{e}\,-\,F_{w}\,+\,F_{n}\,-\,F_{s}\,=\,S^{\,*}\,\neq\,0

只有对速度修正后才能使上式为零。设 U_{e}\,,\,\rlap{/}{p} 的修正值为 U_{e}^{\prime} \pmb{\mathscr{p}}^{\prime} ，则有

U_{e}^{\prime}\;=\;\hat{H}^{\prime}\;+\;\left[\frac{C_{x}^{U}}{a_{P}^{U}}\right]_{e}\big(\hbar_{E}^{\prime}\;-\;\hat{p}_{\dot{P}}^{\prime}\big)\;+\;\left[\frac{C_{y}^{U}}{a_{P}^{U}}\right]_{e}\big(\hbar_{n e}^{\prime}\;-\;\hat{p}_{s e}^{\prime}\big)

令 U_{\ n b}^{'} 为零，则 \hat{H}^{\prime}\;\approx\;0 ；且略去交叉方向上的压力修正值 (\:\phi_{n e}^{'}\:-\:p_{s e}^{'}\:) ，则得

U_{e}^{\prime}\;=\;\left(\frac{C_{x}^{U}}{a_{P}^{U}}\right)_{e}(\,\boldsymbol{p}_{E}^{\prime}\,-\,\boldsymbol{p}_{P}^{\prime})

对 V",U"，V”等作类似处理,再将U。+U’等代人连续方程后,得

a_{P}\!p_{P}^{\;^{\prime}}\;=\;a_{E}\!p_{E}^{\;^{\prime}}\;+\;a_{\pi}\!p_{W}^{\;^{\prime}}\;+\;a_{N}\!p_{N}^{\;^{\prime}}\;+\;a_{S}\!p_{S}^{\;^{\prime}}\;-\;S^{\;^{\star}}

式中

{\begin{array}{r l}{a_{E}\,=\,\left({\frac{1}{a_{P}^{U}}}\right)\left(y_{n e}\,-\,y_{e}\right)^{2}\,+\,\left({\frac{1}{a_{P}^{V}}}\right)\left(x_{n e}\,-\,x_{e}\right)^{2}}\\ {a_{W}\,=\,\left({\frac{1}{a_{P}^{U}}}\right)_{w}\left(y_{n e}\,-\,y_{n e}\right)^{2}\,+\,\left({\frac{1}{a_{P}^{V}}}\right)_{w}\,(x_{n e}\,-\,x_{n e})^{2}}\\ {a_{N}\,=\,\left({\frac{1}{a_{P}^{U}}}\right)_{n}\left(x_{n e}\,-\,x_{n e}\right)^{2}\,+\,\left({\frac{1}{a_{P}^{V}}}\right)_{n}\,(y_{n e}\,-\,y_{n e})^{2}}\\ {a_{S}\,=\,\left({\frac{1}{a_{P}^{U}}}\right)_{n}\left(x_{n e}\,-\,x_{n e}\right)^{2}\,+\,\left({\frac{1}{a_{P}^{V}}}\right)_{n}\,(y_{n e}\,-\,y_{n e})^{2}}\end{array}}

a_{P}\;=\;a_{E}\;+\;a_{W}\;+\;a_{N}\;+\;a_{S}

这也是一个五对角代数方程组，可用SIP法求解。在解得 \phi_{l}^{'} 后，则可得 U_{P}^{\prime},V_{P}^{\prime} 来修正速度场和压力场。

因此，综合以上的推导，可得出求解不可压湍流流动的整个步骤如下：

（1）假定速度场、压力场以及 \boldsymbol{v}_{t} 分布；

（2）求解 x\,,y 方向动量方程得 \boldsymbol{U}^{\star}\,,\boldsymbol{V}^{\star}

（3）用SIMPLE方法进行压力修正，求解式（12-43）得 P^{\prime} U^{'},V^{'}

（4）将速度修正为 U^{\,^{\star}}\,+\,U^{\prime}\,,V^{\,^{\star}}\,+\,V^{\prime} 后，代人湍动能方程和湍能耗散率方程，得 k 和 \boldsymbol{\varepsilon} 值；

（5）根据连续性方程判断选代过程收敛与否。若收敛，则停止计算；否则，更新 \boldsymbol{v}_{t} 的分布后返回（2)继续选代求解。

4）壁面边界条件处理的壁面函数法

在不可压流场计算中，常常会遇到固壁边界，这一边界条件处理的好坏对计算结果的影响很大。本节采用壁面函数方法来处理固壁边界条件[3]

由于动量方程中的通量代表着作用在控制体上的速度方向的力。因此，在与壁面相连的控制体上，该控制体与壁面相接的界面上的通量等于该处壁面的剪应力。而壁面剪应力可表示为

\tau_{w}\;=\;\lambda\,\frac{\partial\,U}{\partial\,y}\;\bigg|_{\,{\bf w}}\;=\;\lambda\;\frac{\delta U_{P}}{\delta_{n}}

\lambda\;=\;\left\{\begin{array}{l l}{{\mu}}&{{y_{\mathfrak{p}}^{+}<11.6}}\\ {{(\rho C_{\mu}^{1/4}\cdot X\cdot K_{P}^{1/2}\cdot\delta_{\mathfrak{n}})/\mathrm{ln}(\,E\cdot y_{P}^{+})}}&{{y_{\mathfrak{p}}^{+}\geqslant11.6}}\end{array}\right.

式中 \delta U_{P} ——壁面上节点速度和近壁同处节点 P 的平行于壁

面的速度分量之间的差值；

\delta_{n}{\longrightarrow}\!-\!P 到壁面的距离；
Kp——P点处的湍动能值；

E\,,X\,,C_{\mu} 一常数， E=8.\,143\,,X=0.\,41\,,C_{\mu}=0.\,09\,;

y_{p}^{+} ——节点 P 到壁面的无因次距离， y_{P}^{\,^{+}}=\bigl(\,\rho C_{\mu}^{1/4}\,{\cdot}\,K_{P}^{1/2} \delta_{n}\,\rangle/\mu_{\circ}

此外， P 点处的湍能耗散率值则由下式确定

\varepsilon_{p}\:=\:\frac{C_{\mu}^{3/4}\cdot\:K_{P}^{3/2}}{X\:\cdot\:\delta_{n}}

12.4.2 k-z 两方程模型参数辨识研究

1）湍流模型参数辨识算法

在12.4.1节中介绍了不可压湍流流动 k-\varepsilon 两方程模型的数值模拟方法。于是，当给定湍流模型中的一组经验参数值后，就可由上节方法计算出各状态变量（如 U\,,V\,,p\,,k\,,\varepsilon\,) 及由这些状态变量组成的一些物理量。而实验中观测得到的量，也是这些物理量中的一部分。记这些观测量的实测值为 {\boldsymbol{\phi}}_{m} ，在一组参数 \pmb{\theta} 下的计算值为 \pmb{\phi}_{c}(\pmb{\theta}) 。而湍流模型的参数辨识就是调整湍流模型中的参数，使湍流模型尽可能地反映出湍流流动的本质特征，也就是使观测量的计算结果和实测结果尽可能接近。这实际上是将参数辨识问题转化成一个给定约束条件下的非线性优化问题[2，即选取参数0,使得下列目标函数达极小

J\;=\;\parallel\;\pmb\phi_{{\pmb m}}\;-\;\pmb\phi_{{\pmb c}}\left(\pmb\theta\right)\parallel^{2}

在本节的工作中，通常将 \phi 取为湍流流动在流向儿个站位上的速度型,将向量范数取为2-范数。因此，目标函数 J 可表示为

J\;=\;\sum_{\stackrel{i\,=\,1}{i\,=\,1}}^{N I}w_{i}J_{X i}

J_{X i}\;=\;\int_{Y_{i}}\big[\oint_{c}\big(\,x_{i}\,,y\,,\pmb\theta\,\big)\,-\,\oint_{m}\big(\,x_{i}\,,y\,\big)\,\big]^{2}\mathrm{d}y

式中 N I{\longleftarrow}x 方向测量站位数；

\boldsymbol{\varpi}_{i} 权系数；

Y;——第 i 个站位 y 方向的测量范围。

针对式（12-44）中的目标函数，用灵敏度法来对参数进行辨识，其算法可写为

\left\{\begin{array}{l l}{\pmb{\theta}^{(k+1)}\,=\,\pmb{\theta}^{(k)}\,+\,\Delta\pmb{\theta}^{(k)}\,\cdot\,r_{e x}}\\ {\Delta\pmb{\theta}^{(k)}\,=\,-\,\pmb{M}^{-1}\,\frac{\partial\pmb{J}}{\partial\pmb{\theta}}}\\ {\pmb{M}\,=\,\frac{\partial^{2}\pmb{J}}{\partial\pmb{\theta}\partial\pmb{\theta}^{\top}}}\end{array}\right.

式中参数矢量 \pmb{\theta} 的上标 k 和 k+1 一迭代的层次；

亚松弛因子；

\partial J/\partial\pmb\theta\cdot 梯度矢量，它表示为

\frac{\partial J}{\partial\pmb{\theta}}\;=\;\sum_{i\,=\,1}^{N I}\left\lbrace\vphantom{\frac{1}{\partial}}w_{i}\int\left[\oint_{c}\left(\left.x_{i}\left,\pmb{y}\,,\pmb{\theta}\right)\,-\,\oint_{m}\left(\left.x_{i}\,,\pmb{y}\right)\right.\right]\,\frac{\partial\oint_{c}\left(\left.x_{i}\,,\pmb{y}\,,\pmb{\theta}\right)}{\partial\pmb{\theta}}\mathrm{d}\boldsymbol{y}\right\rbrace

\pmb{M} 一一信息矩阵，其中的元素

M_{s t}\;=\;\sum_{i\;=\;1}^{N I}\left\{w_{i}\int\frac{\partial\phi_{c}^{\;}(\boldsymbol{x}_{i}\,,\boldsymbol{y}\,,\pmb{\theta})}{\partial\theta_{s}}\;\frac{\partial\,\phi_{c}^{\;}(\boldsymbol{x}_{i}\,,\boldsymbol{y}\,,\pmb{\theta})}{\partial\theta_{t}}\mathrm{d}\boldsymbol{y}\right\}

因此，整个湍流模型参数辨识的步骤为：

（1）为参数 \pmb{\theta} 赋初值；

（2）将参数 \pmb{\theta} 代人含湍流模型的NS方程中进行数值求解得\boldsymbol\phi_{c} 后，再参照实验结果 \boldsymbol{\phi}_{m} ，用数值积分的方法求目标函数 J ，并判断 J 收敛与否，若收敛，则停止辨识；否则继续以下步骤；

（3）对参数矢量 \pmb\theta 的各分量 \theta_{i} 进行摄动，并用差分代导法来计算状态变量对各参数的灵敏度（以中心差分为例）：

\frac{\partial\phi_{c}}{\partial\theta_{i}}\,=\,\frac{\phi_{c}(\,\theta_{i}\,+\,\Delta\theta_{i}\,)\,-\,\phi_{c}(\,\theta_{i}\,-\,\Delta\theta_{i}\,)}{2\Delta\theta_{i}}

(4) 将 \boldsymbol{\phi}_{c}\,,\boldsymbol{\phi}_{m} 和灵敏度矢量代人优化算法，即式（12-45），以求得 \Delta\pmb{\theta}^{(k)} 和 {\pmb\theta}^{(k+1)}

(5)令 {\pmb\theta}^{(k)}={\pmb\theta}^{(k+1)} ,并返回步骤(2)继续辨识计算。

下面用该算法来对轴对称管道流动、二维后向台阶分离流动、轴对称突扩管道流动等三种流动情况下标准 k^{-}\varepsilon 两方程模型中的参数进行辨识与研究。

2）轴对称管流 k^{-}\varepsilon 模型参数辨识

为了检验辨识算法，首先对轴对称管道流动情况下标准 k^{-}\varepsilon 两方程模型中的参数进行辨识。该流动的雷诺数为388,000（基于人口处速度 U_{0} 和管道直径 D)^{\{35\}} 。在计算时,取计算域为[0\,,45D]\times[0\,,D/2] ，用 200\times60 的方网格来模拟，网格在固壁附近作适当加密。四个边界的边界条件处理方法各不相同。在入口处采用第一类边界条件，给定人口处的速度 U_{\mathrm{in}}=\left.U_{0}\right. 、湍动能k_{\textrm{i n}}\,{=}\,6\,.\,62\times10^{-\,5}\,U_{0}^{2} 和湍能耗散率 \varepsilon_{\mathrm{in}}=C_{\mu}k_{\mathrm{in}}^{2}/16\,v ;在出口处令诸物理量沿流向( \pmb{x} 向）的导数为0；在对称边界上令诸物理量沿法向( y 向）的导数为0；固壁边界则用12.4.1节中介绍的壁面函数法处理。在给定了网格和边界条件后，整个流场就可以用12.4.1节中的算法来进行数值求解。

参考文献[35]中同时提供了流向四个站位 (\,x/D=1.\,5,4.\,5 ，16.5,40.5)的 _{x} 向无因次平均速度 U/U_{\mathbf{0}} 的实测值，现利用这四组实测数据作为观测量来对 k^{-}\varepsilon 两方程模型中的参数进行辨识。辨识得 $C_{\mu}{\approx}0,.,0878,,C_{1}{\approx}1,.,3907,,C_{2}{\approx}1,.,8251,($ （由于状态量对参数o：和α，的灵敏度较小,故略去不辨识）,与这几个参数的通用值相差很小,其中 C_{\mu} 相差 2.2\,\%\,,C_{1} 相差 3.4\,\%\,,C_{2} 相差 4.9\,\% 。图1-26示出了流向后两个站位上用湍流模型参数通用值、参数辨识值的计算结果和实测值的比较，从图中可看出，用参数辨识值计算的速度型有了较大的改进，与实验结果更为贴近。

通过此辨识算例的结果可以看出：对轴对称管道流动这一简单剪切湍流流动而言， k-E 两方程模型较好地反映出了流动的特征，在此情况下辨识得出的参数值与通用值很接近，这表明，参数辨识方法是确定湍流模型中经验参数值的一种有效方法。

538

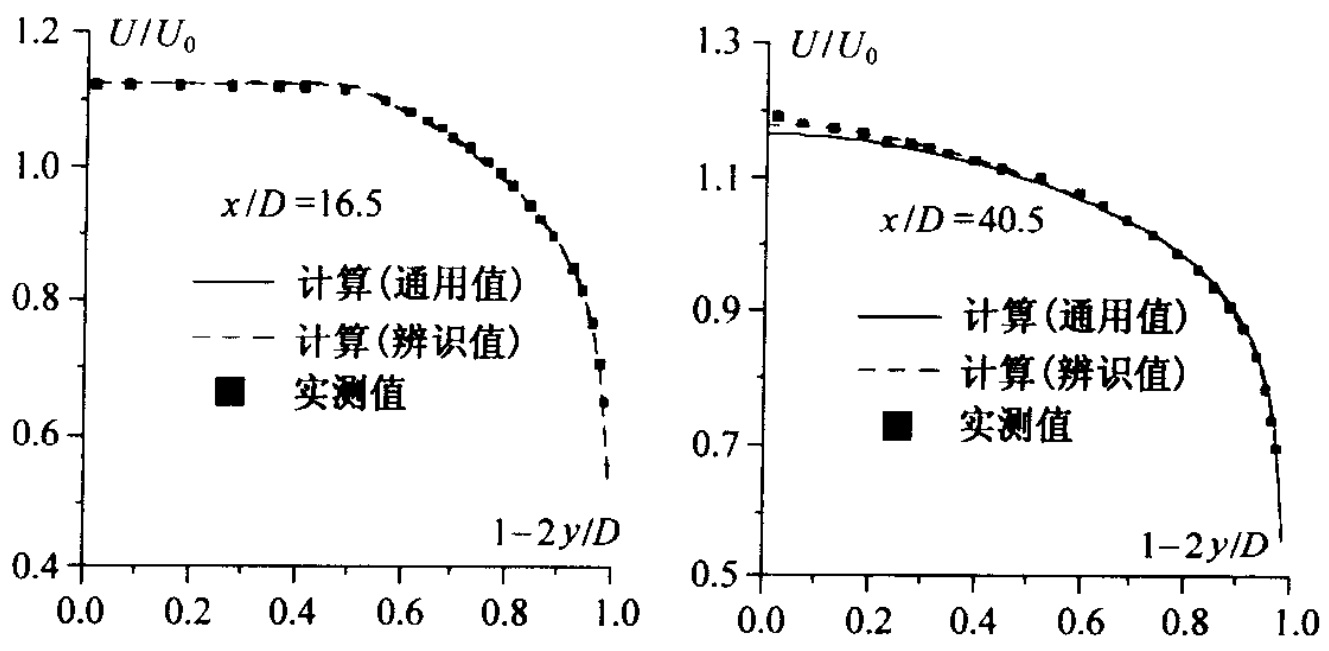
图 12-26 轴对称管流参数通用值、辨识值计算得流向速度型与实测值比较

3）后台阶流动 k^{-}\varepsilon 模型参数辨识

（1）后向台阶流动 k\!-\!\varepsilon 两方程模型参数辨识。二维后向台阶流动是一类典型的分离流动，许多学者都对它进行了实验研究和数值模拟,并常将该流动作为检验湍流模型的标准算例。本节所讨论流动的雷诺数为4400(基于人口平均速度和台阶高 H )，流场扩比(定义为流场扩张后与扩张前的高度比)为 D2:D1=3:2^{{\{3\}}} 在数值模拟时,计算域取为 [\,-4H,18H]\times[0,3H](z) \pmb{x} 轴零点取在流场突扩处， H 为台阶高)。在将台阶视为流场中粘性无穷大的流体后，对全流场用 12\times60 的方网格来模拟，网格在台阶和上下固壁附近作适当加密。人口处的边界条件取为

U_{\mathrm{in}}\,=\,U_{0}\quad k_{\mathrm{in}}\,=\,1.\,5(0.\,04\,U_{0})^{2}\quad\varepsilon_{\mathrm{in}}\,=\,C_{\mu}k_{\mathrm{in}}^{2}/100\,v

出口处仍令各物理量沿流向的导数为零；在上下固壁边界及台阶附近,则用壁面函数法来处理。差分格式采用HUCD格式。

取流向六个站位(x/H=1.33,2.66,5.33,6.22,7.11,8.0)的_{x} 方向无因次速度作为观测量 \phi ,利用参考文献[3]提供的实验结果来辨识湍流模型中的参数。辨识得 C_{\mu}\!\approx\!0.3711,C_{1}\!\approx\!1.4805 C_{2}{\approx}0\,.\,6874(\,\sigma_{k}\,,\sigma_{s} 的灵敏度很小,仍略去不辨识)。此时计算出的回流区长度为6.7H，比用参数通用值计算出的结果（6.02H)有改进，和实测值（约7H)更为接近。图1-27示出了流向两个典型站位上用湍流模型参数通用值、辨识值计算的结果和实测结果的比较。从图中可看出，计算结果有了较大改进，尤其是回流区的后半部分，使得下壁面压力系数分布的计算结果也有一定改进（示于图 12-28) 。

图 12-27后台阶流动流向三个典型站位上流向速度型比较

图12-28后台阶流动下壁面压力系数比较

（2）差分计算格式对参数辨识结果的影响。对后台阶流动而言，不同差分格式下的计算结果有较大差别，用3种不同差分格式，即HUCD格式、HLPA格式和QUICK格式计算出的回流区长度分别为 6.02H、6.27H 和 6.22H。因此，不同差分计算格式下的参数辨识结果也会有差别。表12-10列出了针对1)节中讨论的流动在不同差分计算格式下辨识出的参数值的比较。

表12-10不同差分格式下参数辨识结果比较

<html>

	HUCD格式	HLPA 格式	QUICK格式
参数C，辨识值	0.3711	0.3139	0.2983
参数C，辨识值	1.4805	1.4322	1.4991
参数 C2 辨识值	1.6874	1.6581	1.7367

</html>

（3）参数摄动量对参数辨识结果的影响。由12.4.2.1节中的辨识算法知，状态变量对参数的灵敏度需要用差分代导法来求得。因此，在求灵敏度时用差分来代替导数势必也会给辨识结果带来误差。一种比较保险的处理方法是将参数摄动量的值减小后，再求一次灵敏度，如果灵敏度第二次的计算结果与前一次的计算结果相差不大，则可认为计算得到的灵敏度的值是合理的；如果两次的计算结果相差较大，则需进一步减小摄动量值来求灵敏度，直至两次计算得到的灵敏度的值差别不大为止。在1）节的辨识计算中，参数的摄动量取为

\Delta C_{\mu}/C_{\mu}\;=\;0.\;003\quad\Delta C_{1}/C_{1}\;=\;\Delta C_{2}/C_{2}\;=\;0.\;00125

为验证这一一组摄动量选取得是否合适，将此摄动量的值减半后冉对湍流模型中的参数进行了参数辨识。辨识得 C_{\!_{\mu}}\!\approx\!0.\;3755\,. C,~1. 4813, C_{2}\!\approx\!1.6879. 。两组摄动量下目标函数收敛状况的比较示于图12-29,图中的Case1表示摄动量取式（12-47）时的收敛状况，Case2表示摄动量减半时的收敛状况，坐标横轴为迭代步数。由图可见，两种情况下诸参数与目标函数的收敛状况大致相同，最终收敛结果也十分接近，这说明用式（12-47）给出的摄动量值来进行湍流模型的参数辨识是合理的。

（4）流场扩比对参数辨识结果的影响。为分析流场扩比对辨识结果的影响，下面采用参考文献[37给出的扩比为1.125，雷诺数为36,000 的后台阶流动五个站位 (\,x/H\,{=}\,2\,,4\,,6\,,8\,,12\,) 上 \pmb{x} 方向速度的实测结果作为观测量来辨识湍流模型中的参数，数值计算采用 HLPA 格式。辨识得 C_{\mu}\!\approx\!0 .1020, C_{1}\approx1 .1797, C_{2}\approx 1.5134，此辨识结果与表12-10中扩比为1.5的后台阶流动的参数辨识值有很大差别。究其原因,还是由于湍流模型本身有缺陷，模型参数的通用性不强，从而使得在一种流动情况下辨识优化出的参数值对另一种流动未必适用。图12-30示出了此时用参数通用值、辨识值计算得下壁面上摩阻系数分布的比较。

图 12-29不同参数摄动量下目标函数及参数收敛情况比较

图 12-30下壁面摩阻系数比较

（5）目标函数选取对参数辨识结果的影响。首先分析目标函数式（12-44）中各站位上权系数值的选取对辨识结果的影响，以扩比为1.5的流动为例，在1)节的辨识计算中，各站位上的权系数相等，即 w_{i}=1/6(\,i=1\,,2\,,\cdots,6\,) 。现将后两个站位上的权系数减小为零，位于分离区中的四个站位上的权系数加大为 w_{i}=1/4 (\,i=1\,,2\,,3\,,4\,) ，辨识得 C_{\mu}{\approx}0.3984\,,C_{1}{\approx}1.4587,C_{2}{\approx}1.6526\,, 与1)节的辨识结果有一定差别，此时回流区长度的计算结果为6.77H ，比1)节中辨识值算出的回流区长度有所伸长，但分离区后再发展流动的模拟结果却变差，这也从一个侧面反映出了 k^{-}\varepsilon 两方程模型模拟能力的不足。

不仅流向各站位上权系数值的选取对辨识结果有影响，法向各测量点上权值的选取对辨识结果也有影响。下面讨论一极端情况，以扩比为1.125的流动为例，在4）节的辨识计算中，法向各测量点上的权值相等，现在则只以最靠近下壁面的一层网格点为观测点，以这些点上的摩阻系数为观测量来辨识模型参数。辨识得C_{\mu}{\approx}0.1393\,,C_{1}{\approx}1.4943\,,C_{2}{\approx}1.8238\,, ，此辨识结果与4）节中的辨识值也有很大差别。图12-31中示出了两种自标函数形式下的辨识值计算出下壁面摩阻系数的比较，二者差别很大。

图 12-31 下壁面摩阻系数比较

4）轴对称突扩管流 k^{-}\varepsilon 模型参数辨识

（1）轴对称突扩管流 k-\varepsilon 两方程模型参数辨识。轴对称突扩管道流动亦是一类分离流动。本节讨论流动的雷诺数为110，000（基于人口处最大速度 U_{0} 和扩张前管道直径 D1 ）,管道扩张前后的面积比为 1:4^{[38]} 。取计算域为 [\mathbf{\Gamma}-2.6H,29H]\times[\mathbf{0},2H](x 轴零点取在突扩处， H 为台阶高，等于扩张前管道半径值），用 100\,\times 60网格来模拟。计算格式采用HUCD格式，上边界用对称边界条件，令诸物理量沿法向的导数为0；下固壁边界用壁面函数法处理；出口处的处理方法同前。而在人口处，由于实验时的人口采用的是充分发展管流，因此这时的人口速度型取为 1/7 幂次型，人口的湍流量取为

k_{i n}\;=\;0.0013\,U_{0}^{2}\big[1\,+\,4\big(\,r/R1\big)^{2\cdot5}\big]\,,\epsilon_{i n}\;=\;C_{\mu}^{0.75}k_{i n}^{\,1.5}\big/l_{m}

流动混合长由尼古拉兹（Nikurades）公式计算 \langle R1=D1/2\rangle

l_{m}\,=\,R1[0.14\,-\,0.08(\,r/R1)^{2}\,-\,0.06(\,r/R1)^{4}]

取流向七个站位 \left({{x}/{H}}=1,3,5,7,9,11,15\right) 的 \pmb{x} 方向速度作为观测量 \phi ,利用参考文献[38】提供的实验结果来对湍流模型进行参数辨识。辨识得 C_{\mu}{\approx}0.\,1961\,,C_{1}{\approx}2.\,8329\,,C_{2}{\approx}3.\,4563\,(\,\sigma_{k}\,, \pmb{\sigma}_{s} 仍略去未辨识）。图12-32中示出了在流向两个典型站位上分别利用参数通用值、辨识值计算得速度型和实验结果（图中 R 为扩张后管道半径）的比较。从图中可看出，各站位速度型计算结果有了较大改进。

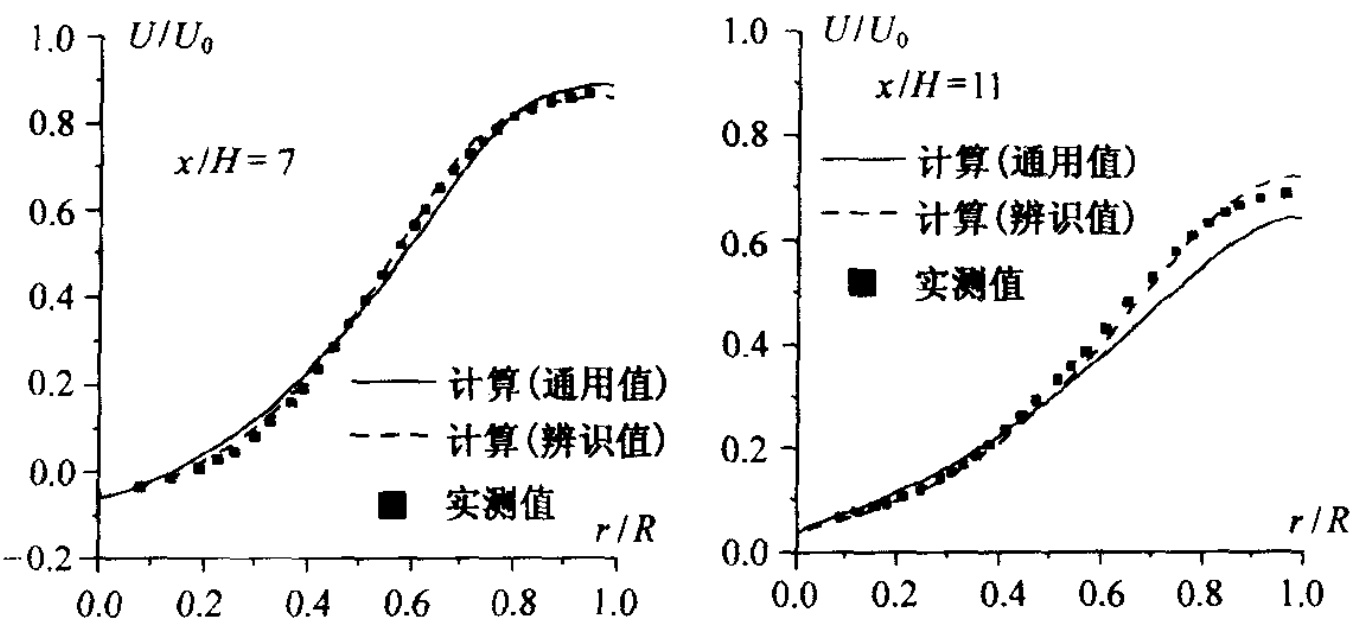
图 12-32轴对称突扩管流参数通用值、辨识值计算得速度型与实测值比较

（2）流场计算人口条件设置对参数辨识结果的影响。就上述流动而言，若将人口处的湍流量用式（12-46）来计算，湍流模型的参数辨识结果为： C_{\mu}{\approx}0.2294\,,C_{1}{\approx}1.6511\,,C_{2}{\approx}1.9698\,, 与1)书中的辨识结果有很大差别。由此可见，由于在流场数值计算中，人口条件的设置对计算结果有比较大的影响，使得湍流模型的参数辨识结果也会受到流场计算人口条件设置的影响。比较合理的处理方法还是尽量用实测值来给定入口条件。

（3）流动雷诺数对参数辨识结果的影响。参考文献[38］中同时还给出了同一突扩管道流动雷诺数为60，000的情况下流向六个站位 (x/D1=1\,,2\,,3\,,4\,,6\,,8\,) 的 \boldsymbol{\mathcal{x}} 方向速度的实验结果。用这些结果作为观测量，采用式(12-48)做人口条件后,辨识得 C_{\mu}\approx 0.1027, C_{1}{\approx}1.5072 C_{2}\!\approx\!1.\,9463 ，与1)节中的辨识结果也有差别。这表明，即使是同一类型，同一扩比下的分离流动，在不同雷诺数下的参数辨识结果都不相同。由此可以想见，就标准 k^{-}\varepsilon 两方程模型而言，要想概括出一组对所有分离流动都适用的参数值是相当困难的。

5）初步结论

本节工作将系统辨识方法用于辨识标准 k\!\cdot\!\varepsilon 工程瑞流模型中的参数，通过对以上几种流动辨识结果的分析，可以总结出以下儿个初步结论：

（1）参数辨识方法是确定湍流模型中经验参数值的一种有效方法。

（2）湍流模型参数辨识的结果受流场计算方面因素的影响很大。差分格式、边界条件处理都会对辨识结果有影响，因此在辨识前应先对流场计算进行较透彻的分析。并尽量选用较高精度的差分格式（如HLPA格式、QUICK格式），人流条件尽量由实验值给出。

（3）由于标准k-e两方程湍流模型本身还有缺陷，对有分离的流动不能很成功地进行模拟，从而使得不同分离流动情况下的湍流模型参数辨识结果差别很大，即使是对于同一类型的流动，辨识结果也会受到目标函数选取形式、流场的几何参数（如扩比）、流动雷诺数等因素影响，因而很难概括出一组对所有分离流动都适用的参数值。

（4）对于有分离的流动，通过参数辨识方法对标准 k^{-}\varepsilon 两方程模型中参数进行适当调整后，可以使流动回流区长度、压力分布、摩阻分布等物理量的模拟精度有所提高。但是，由于模型本身有缺陷，这样的调整不具有通用性，并且对结果改进的幅度也有限。因此，要想进一步提高模型的模拟能力，有必要在湍流模型结构的改进与完善上做工作。

（5）在标准 k^{-}\varepsilon 模型的五个经验参数中， \sigma_{k} 和 {\pmb\sigma}_{\pmb\varepsilon} 对计算结果的影响很小，而其他三个参数，尤其是参数 C_{\mu} ,对计算结果的影响很大。因此,在对标准 k^{-}\varepsilon 模型作改进时，如果能对参数 C_{\mu} 在流场中的分布进行合理处理，则有望使模型的模拟能力有较大提高。

本节采用系统辨识算法，对各种不同的端流流动，辨识出标准k-e工程模型的各个参数,希望能求得适用于各种流动的 k-e 模型。辨识结果表明，不同流动状态下辨识所得参数相差较大，这说明 k^{-}\varepsilon 模型存在固有缺陷，无法求得适用于各种流动的 k^{-}\varepsilon 模型。

12.4.3 对标准 \pmb{k}\!-\!\pmb{\varepsilon} 两方程模型结构改进的探讨

目前，在航空航天、能源交通、桥梁建筑、环境与大气科学等诸多研究领域的工程湍流计算中，标准k-e两方程湍流模型以其结构形式简单，使用方便，且具有一定模拟精度的优点，得到了相当广泛的应用。但是,该模型也存在着一些明显缺陷。一是模型中的许多模化项建立在各向同性假设之上[19,例如,模型中的涡粘系数，是一与方向无关的标量,即是一个各向同性的扩散系数;k 和ε方程中耗散项的模拟也都引人了各向同性假设,这就使得该模型对于各向异性较强的流动,如分离流动,不能成功模拟。二是在ε方程中，湍流扩散项、小涡拉伸引起的产生项和粘性破坏项的模拟还不够完善,没有比较严格的理论与实验基础。三是在布辛涅斯克假设中，雷诺应力与平均速度梯度线性关联，这一线性关系使得标准 k^{-}\varepsilon 模型无法模拟出方截面管流中的二次流动[26]因此,为了克服标准 k^{-}\varepsilon 两方程模型的以上缺陷,再现湍流流动的基本物理特性，近年来，国内外的不少专家学者从物理分析、张量分析、概率统计分析等多个不同角度人手来提出对 k^{-}\varepsilon 两方程模型进行改进与完善的方案。在这些改进方案中，有些是较为成功的，而有些则只适用于某些特殊类型的流动情况，缺乏通用性。本节的工作就是借助模型辨识的思想来对一些典型的改进方案进行探讨。

所谓模型辨识，是系统辨识的一个重要组成部分，其含义是指对于给定的数学模型结构形式（候选模型集合），根据已测得的输人和输出数据，用建模准则确定数学模型的项数、阶数，选出最优的数学模型。模型辨识的关键是建模准则和优选算法，建模准则应该使优选出的数学模型具有以下性质[11]：

（1）模型能很好地拟合现有的实验数据；
（2）模型能预测类似条件下的实测数据；
（3）模型各项有物理意义；
（4）在性能相当条件下是阶次最低的模型。

目前工程上常用的建模准则主要有最大信息量准则、最大可信度准则、 F 统计检验、最小预测误差平方和准则等。其中，最小预测误差平方和准则在工程上有较广泛的应用，其基本思想为：将实验数据分为两部分，一部分数据用于估计候选模型集合中各模型的待定系数；得到待定系数之后，再用之预测第二部分数据的误差平方和,取误差平方和最小者为最优模型[11]

在工程上常见的湍流流动中，后向台阶流动是一类典型的分离流动，流场中包含有逆压梯度、漩涡流动等流动现象，参考文献「36]中介绍的扩比为1.5的后向台阶流动实验和参考文献［37|中介绍的扩比为1.125的后向台阶流动实验是这类流动的代表性实验，其实验结果常常被用于工程湍流模型的验证性计算。但是，仅仅将后向台阶流动的模拟好坏作为检验工程湍流模型的标准是不够的，因为在工程上经常要涉及到的钝体绕流中，还包含有驻点区域流动、曲率流动等更为复杂的流动现象。基于此考虑，本节提出如下的模型优选算法：首先提出候选的湍流模型；分别用每个模型对扩比为1.5的后向台阶流动进行数值模拟和参数辨识；再将模型和辨识值用于预测扩比为1.125的后向台阶流动和典型的钝体绕流流动，如果两种流动情况下的预测结果和实测结果都符合得比较好，则认为该模型是较为成功的，将其选出做进一步的验证与分析，否则，认为该模型是不够成功的，还有待做进一步的完善。

基于上述思想，参考文献[2]对各种 k\!\sim\!\varepsilon 改进模型（包括：金\langle{\bf K}{\bf i m}\ S\ {\bf W}\rangle 和陈(Chen Y S)的 k\!\cdot\!\varepsilon 改进模型[39]、重整化群 k\!-\!\varepsilon 两方程模型[40]、陈义良等提出的非线性 k^{-}\varepsilon 模型、显式代数应力模型(EASM)和一种新提出的 k^{-}\varepsilon 非线性两方程模型等）进行模型辨识。下面给出辨识的初步结果。

1)对 \pmb{\epsilon} 方程改进形式的探讨

本节的概述中已指出， k^{-}\varepsilon 两方程模型中 \pmb{\varepsilon} 方程的推导是最不严格的，函待改进与完善。金 (\operatorname{Kim}\ S\ \mathbb{W}) 和陈(Chen Y S)为了使 \pmb{\epsilon} 对流动的应变更为敏感,在 \varepsilon 方程中加人了-额外源项,提出了一种ε方程的改进方案(下简称为改进 k-ε 模型),其具体形式为[39]

\nabla\,\cdot\,\left(\,U_{\varepsilon}\,\right)\;=\;\nabla\,\cdot\,\left[\,\left(\,v\,+\,\frac{v_{t}}{\sigma_{\varepsilon}}\,\right)\nabla\,\varepsilon\,\right]+

\left(C_{1}G\mathrm{~-~}C_{2}\varepsilon\mathrm{~+~}C_{3}\,\frac{G^{2}}{\varepsilon}\right)\frac{\varepsilon}{k}

模型参数的推荐值为： C_{1}=1.\,15\,,C_{2}=1\,.\,90\,,C_{3}=0.\,25\,,\sigma_{\epsilon}=1.\,15\,\mathrm{{o}}

利用上述模型进行辨识的结果并不理想，其主要原因是，改进k^{-}\varepsilon 模型是通过加大 \pmb{\varepsilon} 方程中的源项，减小流场中计算出的涡粘性，来达到对计算结果改进的目的。但是，该模型中 \boldsymbol\varepsilon 方程的导出缺乏比较严格的理论基础，而且在实际流动的模拟中，尤其是流动中产生项G比较大的情况下，该模型对湍流特征量的计算值与实测值存在着明显的偏差，这表明改进 k^{-}\varepsilon 模型并未能揭示出流动

的本质特征。

因此，由模型优选算法知,式(12-49)对 \pmb{\varepsilon} 方程的改进对于后台阶类型分离流动以及钝体绕流中平均量的模拟是较为有效的，但模型中的湍能产生项 G 与 \pmb\varepsilon 的相互作用机制不尽合理， \pmb\varepsilon 方程的改进形式不具备很强的通用性，还有待于做进一步的深人研究。

2）重整化群 k^{-}\varepsilon 两方程模型

雅克荷（Yakhot V)和俄扎格（Orszag S A）于1986年首次将重整化群理论用于湍流模型研究，其基本思想是将流动对等于高斯平衡态，将大尺度结构对涡的影响用无序力来表示，冉应用统计物理中研究变换的方法来逐次消除湍流的小尺度。例如，消除最小瑞流尺度后可以得到用于大涡模拟的亚格子尺度模式，如再逐次消去较大的湍流尺度，最终可得到雷诺应力模型和 k^{-}\varepsilon 模型。对高雷诺数湍流，用重整化群方法导出的 \pmb{k}-\pmb{\varepsilon} 模型与标准 k^{-}\varepsilon 模型很类似，只在 \boldsymbol{\varepsilon} 方程中多出一附加项，当流动快速畸变时，这一项将显著加大。该模型中ε方程的具体形式为[40]

\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,(\,U\varepsilon\,)\;=\;\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\left[\left(\,\boldsymbol{v}\,+\,\frac{v_{t}}{\sigma_{\epsilon}}\right)\boldsymbol{\nabla}\,\boldsymbol{\epsilon}\,\right]+\,\left(\,C_{1}\,G\,-\,C_{2}\,\varepsilon\,\right)\,\frac{\varepsilon}{k}

(12 - 50)

式中

C_{1}\,=\,1.42\,-\,\frac{\eta(1\,-\,\eta/\,\eta_{0})}{1\,+\,{\beta\eta}^{3}}\;\;\;\;\eta\,=\,\frac{S k}{\varepsilon}\;\;\;\;\;\;\;\;\;\;S\;=\;(2\,S_{i j}S_{i j})^{1/2}

C, = 1. 68\qquad\eta_{0}\,=\,4\,.\,38\qquad\beta\,=\,0\,.\,015\quad\,\sigma_{\epsilon}\,=\,0\,.\,7179 模型中的参数都是通过重整化群方法确定出来的（用重整化群方法确定出模型参数值被认为是重整化群方法研究湍流模型的一大优势），其他模型参数值取为 C_{\mu}=0.\,085\,,\,\sigma_{k}=0.\,7179\,. 。模型中的S_{i j} 定义为

S_{i j}\,=\,(\,U_{i\,,\,j}\,+\,U_{j\,,\,i}\,)/2

式中 U_{i} .i一偏导数的表达形式，即 U_{i\,,\,j}=\partial\pmb{\phi}_{i}/\partial x_{j}\circ 计算结果表明，重整化群 k^{-}\varepsilon 模型的理论基础较为完备，对后台阶流动和翼型绕流都计算出了大体上与实验结果符合得比较好的结果。该模型的不足之处在于对应变较大区域流动的模拟还不够成功。因此,由模型辨识建模准则知,基于重整化群思想对 k^{-}\varepsilon 模型的改进方案是比较成功的，有一定的工程实用价值，可将其优选出来做进一步深人分析与改进。目前，该模型已在工程上得到了实际应用。

3）陈义良、西须磨提出的非线性 k^{-}\varepsilon 模型

在标准 k^{-}\varepsilon 两方程模型中，除了 \boldsymbol{\varepsilon} 方程有明显缺陷外，还有-个较大的缺陷就是模型中的许多项都作了各向同性假设，雷诺应力与流动应变之间线性关联。为了克服此缺陷，可以考虑对雷诺应力表达式进行非线性扩充，以此来更好地描述流动的各向异性与非线性特性。这样得出的新模型可笼统地称之为非线性 k^{-}\varepsilon 模型(或各向异性 k^{-}\varepsilon 模型）。近年来，非线性 k^{-}\varepsilon 模型的研究与应用已成为工程湍流模型研究的热点之一，国内外的不少专家学者，如国外的斯伯扎那、义泽教授，国内的符松、窦国仁、陈义良教授等都分别从物理分析、张量分析和概率统计等角度人手提出了各自的非线性 k^{-}\varepsilon 两方程模型。本节下面将对其中两类典型的非线性模型进行探讨。

在参考文献[27]中，陈义良应用张量不变性理论导出了-类满足不变性原理的非线性 k^{-}\varepsilon 模型。所谓不变性，是指模型公式和坐标系的选择无关，即当坐标系变换时，模型表达式不变。在参考文献[23］中，西须磨和义泽根据概率统计中的 DIA（Direct In-teractionApproximation)理论也提出了一种非线性k-e模型，这两种模型在形式上是一致的，其雷诺应力表达式可写为

\overline{{u_{i}u_{j}}}\,=-\,2\,v_{t}S_{i j}\,+\,\frac{2}{3}\delta_{i j}k\,+\,\frac{k^{3}}{\varepsilon}Q_{i j}

式中

\begin{array}{c}{{Q_{i j}\;=\;A_{1}\displaystyle\left(\left.S^{2}\,-\,\frac{1}{3}\,\right\{S^{2}\}\,\delta_{i j}\right)+\,A_{2}\left(\frac{}{}W^{2}\,-\,\frac{1}{3}\,\O\left\{W^{2}\,\right\}\delta_{i j}\right)+}}\\ {{{}}}\\ {{A_{3}(\,S_{i l}W_{l j}\,-\,W_{i l}S_{l j}\,)}}\end{array}

550

\begin{array}{l l}{{S_{i j}\,=\,(\,U_{i,j}\,+\,U_{j,\,i}^{\,})/2\,}}&{{W_{i j}\,=\,(\,U_{i,\,j}\,-\,U_{j,\,i}^{\,})/2}}\\ {{\,}}&{{\,}}\\ {{S^{2}\,=\,S_{i k}S_{k j}}}&{{}}\end{array}

\{\,\cdot\,\} 表示张量的迹， A_{1},A_{2},A_{3} 是参数。陈义良给出的参数值为：A_{1}=0.\,02\,,A_{2}=0.\,074\,,A_{3}=0.\,054 西须磨和义泽给出的参数值为： A_{1}=0\,.\,055\,,A_{2}=0\,.\,001\,,A_{3}=0\,.\,055\,_{\circ}

辨识结果并不理想。该模型的一个较明显的缺陷在于：雷诺应力三个附加项的系数 A_{i} 和参数 C_{\mu} 被简化取为常数，而由张量不变性理论知，雷诺应力表达式中的二阶独立张量的系数不是简单的常数,而应是张量不变量 \{S^{2}\},\{W^{2}\} 的函数,即系数应与流动的应变、涡量相关。下一节介绍的 GS非线性 k^{-}\varepsilon 模型就是这样的--个模型。

4）格兹克和斯伯扎那提出的非线性 k^{-}\varepsilon 模型

此模型也称为显式代数应力模型（EASM），其思想及二维情况下的开创性工作是由波伯（PopeSB)于20世纪70年代中期提出来的[24],后由格兹克(Gatski T B)和斯伯扎那加以完善并推广到三维情况[25]（以下将此模型简称为 GS非线性 k^{-}\varepsilon 模型),其大致推导过程如下。

对NS方程进行雷诺平均与模化后可以得到封闭的二阶矩湍流模型，其中的雷诺应力表达式为

D(\overline{{u_{i}u_{j}}})/D t\ =-\ \overline{{u_{i}u_{k}}}U_{j\,,k}\ -\ \overline{{u_{j}u_{k}}}U_{i\,,k}\ +\ \Phi_{i j}\ -\ \epsilon_{i j}

引人罗迪（Rodi)假设，即假设雷诺应力 \overline{{{\bf{u}}_{i}{\bf{u}}_{j}}} 与瑞动能 \pmb{k} 成正比，上式可简化为代数应力模型（ASM），其中的雷诺应力满足卜列方程

(\,P\,-\,\varepsilon\,)\ \overline{{u_{i}u_{j}}}/k\ =-\ \overline{{u_{i}u_{k}}}U_{j\,,\,k}\ -

\widehat{u_{j}u_{k}}U_{i\,,\,k}\,+\,\Phi_{i j}\,-\,2\,\epsilon\delta_{i j}/3

上式右端的前两项为端流的生成，第四项为作了各向同性假设后的应力耗散项。而第三项为压力与应变率的相关项,可模化为(41]

\Phi_{i j}\,=-\,\,C_{1}\,\,\frac{\varepsilon}{k}\left(\overline{{u_{i}u_{j}}}\,-\,\frac{2}{3}\,k\delta_{i j}\,\right)-\,C_{2}\left(\,P_{i j}\,-\,\frac{2}{3}\,\delta_{i j}P\,\right)

式中,生成项 P_{i j}=\,-\,(\,\overline{{u_{i}u_{k}}}U_{j\,,k}^{}\,+\,\overline{{u_{j}u_{k}}}U_{i\,,k}^{}\,)\,,P=P_{k k}^{}/2 ,经验参数C_{1},C_{2} 取为1.8和0.6。

因此,若定义： {\theta_{i j}}=\overline{{{u_{i}}{u_{j}}}}/2k-{\delta_{i j}}/3 ,则式(12-53)可化为

\Phi_{i j}\,=-\,2\,C_{1}^{\prime}\varepsilon b_{i j}\,+\,C_{2}^{\prime}k S_{i j}\,+\,C_{3}^{\prime}k\,(\,b_{i k}S_{k j}\,+\,b_{j k}S_{k i}\,-

2\,\delta_{i j}b_{l k}S_{k l}/3\,)\,-\,C_{4}^{\prime}\,k\,(\,b_{i k}W_{k j}\:+\:b_{j k}W_{k i}\,)

式中的参数值分别为： C_{2}^{'}=4\,C_{2}/3\,,C_{3}^{'}=2\,C_{2}\,,C_{4}^{'}=2\,C_{2} 。将上式代人式(12-52),则可得到一关于雷诺应力 \overline{{{\pmb u}_{i}{\pmb u}_{j}}} 的隐式方程。由张量不变性理论125,2],雷诺应力 \widetilde{\mathbf{\omega}_{u_{i}}\pmb{u}_{j}} 可展开为如下形式：

\overline{{{u_{i}u_{j}}}}\,=\,\sum_{\lambda}G^{\lambda}\mathbf{T}^{\lambda}

式中 T^{\lambda} -田 S_{i j} 和 \boldsymbol{W}_{_{i j}} 构成的独立张量;

G^{\lambda} 一—由张量不变量组成的系数。

为了确定 G^{\lambda} 的形式,将式(12-54)代人式（12-52)后，对二维流动情况可以得到[25]

\begin{array}{l}{{\displaystyle\overline{{{u_{i}u_{j}}}}\ =\frac{2}{3}\delta_{i j}k\ -\ 2\,v_{t}\biggl[S_{i j}\,+\,\beta_{2}k\,(\,S_{i k}W_{k j}\,+\,S_{j k}W_{k i}\,)/\varepsilon\ -\ }}\\ {{\displaystyle\beta_{3}k\,\biggl(\,S_{i j}^{2}\,-\,\frac{1}{3}\,\delta_{i j}S_{k k}^{2}\,\biggr)/\varepsilon\ \biggr]\qquad\qquad\qquad(12)}}\end{array}

式中

\begin{array}{r l r l}&{v_{t}=C_{\mu}k^{2}/\epsilon}&&{C_{\mu}=3\beta_{1}/(3-2\,\eta^{2}+6\,\xi^{2})}\\ &{\beta_{1}=(2/3-C_{2}^{\prime}/2)/g}&&{\beta_{2}=(1-C_{4}^{\prime}/2)/g}\\ &{\beta_{3}=(2-C_{3}^{\prime})/g}&&{g=C_{1}+C_{S}-1}\\ &{\eta^{2}=(\beta_{3}S)^{2}/8}&&{\xi^{2}=(\beta_{2}\Omega)^{2}/2}\\ &{S=(k/\epsilon)\sqrt{2S_{k k}^{2}}}&&{\Omega=(k/\epsilon)\sqrt{-2\,W_{k k}^{2}}}\\ &{S_{i j}^{2}=S_{i k}S_{k j}}&&{S_{k k}^{2}=S_{i k}S_{k l}}\end{array}

C_{5} 通常取值为2。从式（12-56）可以看出，对于 \eta\>1 的流动，式中的 C_{\mu} 有可能出现奇性。究其原因，这实际上是由于代数应力模型对于 \eta\!>\!1 的流动已不再适用而造成的。然而,在工程应用

中,常常会遇到一些流动,只在流场中某些局部区域,或者在流场计算的迭代过程中出现 \eta\!>\!1 的情况。为了使上述模型在这些情况下仍能使用，参考文献[25]中作了如下的正则化假设：

1\ensuremath{\mathrm{~\boldmath~\cdot~}}\ensuremath{\eta}^{2}\approx1/(1\ensuremath{\mathrm{~\boldmath~\cdot~}}\ensuremath{\eta}^{2})

从而得到 C_{\mu} 的表达式为

C_{\mu}\;=\;3\beta_{1}(1\;+\;\eta^{2})/[3\;+\;\eta^{2}\;+\;6\xi^{2}(1\;+\;\eta^{2})\;]

由式（12-55)和式（12-57)就构成了GS非线性 k^{-}\varepsilon 两方程模型。 可以看出，式 (12-55) 右端前两项在形式上和布辛涅斯克假设完全 相同，因而式（12-55）可看做是对布辛涅斯克假设的非线性扩充， 即式（12-55）可另写为

\widehat{u_{i}u_{j}}\ =\ \frac{2}{3}\,\hat{\partial}_{i j}k\,-\,2\,v_{i}S_{i j}\,+\,Q_{i j}

式中 Q_{i j} 一一代表非线性扩充项。

用该模型来计算扩比为1.5的后向台阶流动，计算出流动的回流区长度为 6.98H ，与实测值很接近。计算出的速度型、下壁面压力系数分布比上一节所介绍非线性模型计算出的结果有改进，与实测结果更为接近。

模型辨识结果表明，GS非线性 k^{-}\varepsilon 模型的结果比较好，这主要由于GS非线性 k^{-}\varepsilon 模型中的雷诺应力表达式是由代数应力模型导出，具有较严格的理论基础，对后台阶型流动和翼型绕流也计算出了较好的结果。但是，从理论和实践来看，GS非线性 k^{-}\varepsilon 模型对于 \pmb{\eta} 较大的流动区域的模拟还存在着明显不足。因此，可以将其优选出来做进一步深人分析与改进，尤其应重点探讨该模型对 \eta 较大区域流动的处理方法。

5）一种新的非线性 k^{-}\varepsilon 两方程湍流模型

由上节的探讨可知，非线性 k\!-\!\varepsilon 模型，尤其是GS非线性 k\!\cdot\!\epsilon 模型，通过在雷诺应力的表达式中加人非线性项来反映流动的各向异性与非线性特性是对标准 k^{-}\varepsilon 两方程模型的一种比较有效的改进。但是，GS非线性 k^{-}\varepsilon 模型中的雷诺应力表达式是由代数应力模型导出来的，当流动状况不满足罗迪假设时，代数应力模型不再适用,此时的GS非线性 k\!-\!\varepsilon 模型适用与否难以预料；此外，式（12-55）仅仅给出了二维情况下的雷诺应力表达式，三维情况下雷诺应力表达式的推导相当复杂,使用起来很不方便{25]。本节将在理论分析和对标准 k\!-\!\varepsilon 模型、GS非线性 k\!\cdot\!\varepsilon 模型计算结果分析的基础上,在标准 k^{-}\varepsilon 模型的涡粘性系数 {\boldsymbol{\mu}}_{t} 中考虑流动各向异性的影响，将涡粘性系数中的参数 C_{\mu} 取为表征流动各向异性的参数A 的一个线性函数，并保留GS非线性 k^{-}\varepsilon 模型雷诺应力中的高阶非线性项，提出一种新的非线性 k^{-}\varepsilon 两方程湍流模型。

首先，沿用GS非线性 k^{-}\varepsilon 模型的雷诺应力表达式形式，将雷诺应力写为

\begin{array}{l}{{\overline{{{u_{i}u_{j}}}}\ =\displaystyle\frac{2}{3}\,\delta_{i j}k\,-\,2\,v_{t}S_{i j}\,-\,2\,v_{t}\,[\,\beta_{2}k\,(\,S_{i k}W_{k j}\,+\,S_{j k}W_{k i}\,)/\varepsilon\ -\ 4\,\beta_{1}}}\\ {{\beta_{3}k\,\Big(\,S_{i j}^{2}\,-\,\frac{1}{3}\,\delta_{i j}S_{k k}^{2}\,\Big)/\varepsilon}}\end{array}

式中 \beta_{2} 和 \beta_{3} —待定参数。

\boldsymbol{v}_{t} 中参数 C_{\mu} 的形式也待定。

其次,由于 k^{-}\pmb{\varepsilon} 两方程模型中涡粘性系数 \boldsymbol{v}_{t} 的各向同性是 k^{-}\varepsilon 两方程模型的一个明显缺陷，且 k^{-}\varepsilon 模型中涡粘性系数 \pmb{\mathscr{V}}_{t} 中的经验参数 C_{\mu} 的合理取值对计算结果有较大影响。于是，可以考虑将参数 C_{\mu} 取为某一表征流动各向异性的量的函数，以此来反映涡粘性系数和流动的各向异性。

对于-一个流场，若定义一无量纲的雷诺应力各向异性张量：

a_{_{i j}}\;=\;\overline{{{u_{{i}}}{u_{j}}}}/\,k\;-\;2\,\delta_{_{i j}}/3

其二次和三次不变量定义为： A_{2}=a_{i k}a_{k i}\,,A_{3}=a_{i k}a_{k j}a_{j i}\,\circ 可以证明[2],当某一个速度脉动分量的相对值为零 (\stackrel{\scriptscriptstyle-\sim}{u}_{i}^{2}/k=0) 时，无论另两个分量的相应值如何，必有

A_{2}\mathrm{~-~}A_{3}\,=\,8/9

若引人参数 A=1-\left(9/8\right)\left(A_{2}-A_{3}\right) ,则对于各向同性湍流 (A_{2}

A_{3} 均为零）， A=1 ;而对于各向异性较强的流动， A 趋于零。因此，参数 A 实际上表征了流动的各向异性程度[19]。

为了确定参数 C_{\mu} 和 A 之间的函数关系，采用如下方法：对于扩比为1.5的后台阶流动，GS非线性 k\!\cdot\!\varepsilon 模型计算出了比较好的结果,因而可以认为此时计算出的参数 C_{\mu} 在流场中的分布是较为合理的；再来计算此时流场中流动各向异性因子 A 的分布；并分析这两个分布之间的对应关系。图12-33示出了两个流向站位上用GS非线性模型计算得出的参数 C_{\mu} 与 \boldsymbol{A} 的分布。从图中可以看出，参数 C_{\mu} 与 \mathbf{A} 有着大致相同的变化趋势，二者之间存在一近似的线性关系，即近似有

C_{\mu}\ =\ \alpha\ +\ \beta A

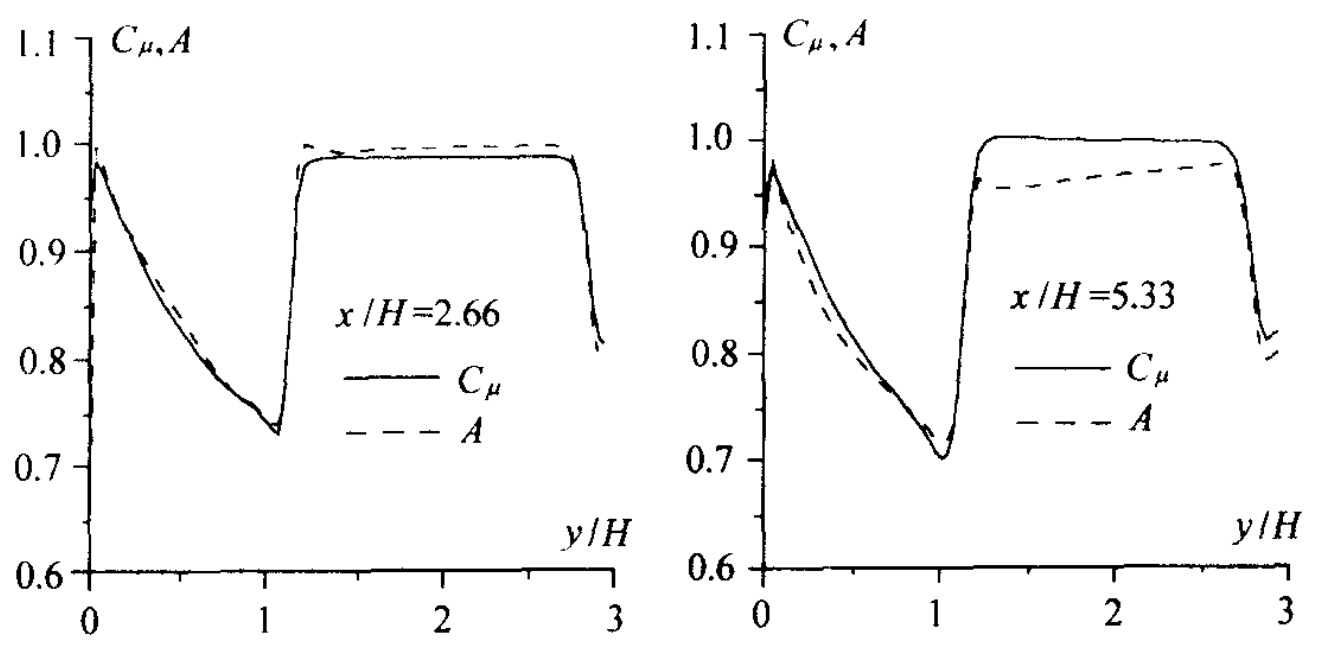
图12-33GS非线性 k^{-}\varepsilon 模型计算得流向站位上 C_{\mu} 与 \pmb{A} 的分布

由于标准 k^{-}\varepsilon 模型对各向同性流动能计算出较好的结果，因而可引人约束条件

\alpha\,+\,\beta\,=\,0.09

将式(12-59)代人式(12-58)中 \pmb{v}_{t} 的表达式里，就可得到一种新的非线性 k\!-\!\varepsilon 模型的雷诺应力表达式。式中共有三个待定系数\alpha\setminus\beta_{2} 和 \beta_{3}

采用两组不同扩比下后台阶流动的实验数据来辨识模型（12-

58）和（12-59）中的待定系数，一组数据是前面章节已多次用到的扩比为1.5的后台阶流动，另一组数据则是参考文献1421给出的扩比为 1.25,雷诺数为 28,000(基于人口处速度 \boldsymbol{v}_{0} 和台阶高 H 一的后台阶流动。

将两组辨识结果的算术平均取为参数辨识的最终结果：

(\,\alpha\,,\beta_{2}\,,\beta_{3}\,)\,=\,(0.0293\,,0.096\,,0.28\,)

将以上参数代人式（12-58）和（12-59)中，就得到了新的非线性 k^{-}\varepsilon 模型中雷诺应力表达式的确定形式。

采用此模型对四种流动进行数值模拟并与标准 k^{-}\varepsilon 模型、实验结果作比较，以验证此模型的正确性。

（1）扩比为 1.5、1.25、1.125的后台阶流动；(2）绕方块的二维分离流动[43]；(3）二维U型管道内的流动[44];(4）接近失速攻角下绕 \mathbf{A} 翼型[45]和GAW-1翼型[46]的低速流动。

验证比较的内容包括速度型 {v}/{v_{\infty}} 、压力系数 C_{p} 、摩阻系数C湍动能 K/²、雷诺应力xy/2等。验证结果表明[2],在k-ε两方程模型的雷诺应力表达式中考虑非线性与各向异性的影响后，在一定程度上反映出了流动的部分本质特征，使得 k^{-}\varepsilon 模型的适用性和数值模拟精度有了较大的提高。而且，该非线性 k^{-}\varepsilon 模型在形式上对标准 k^{-}\varepsilon 两方程模型的改动不大，从而文保留了标准 k\!\sim\!\varepsilon 模型结构简单，使用方便经济，便于推广应用到三维情况的优点。因此,该模型具有较强的工程应用价值。但该模型的不足之处有两方面：一是在有曲率的流动情况下,尤其是沿凹壁的流动情况，该模型不能对流动特性做出准确的模拟；二是该模型对各向异性特别强的流动区域的模拟效果欠佳。这两方面是今后对该非线性模型做进一步改进与完善的主要方向。

在我国，分布参数系统辨识在气动领域中的应用起步于20世纪90年代初，现仍处于探索阶段。本章介绍了辨识的基本算法，并给出在气动热参数辨识和工程湍流模型参数辨识中的应用。文中内容不很成熟，结果也不尽人意，但是给出了初步的研究方法，其辨识结果也给读者一些启示，以免重走已走过的路。

参考文献

1李言俊.系统辨识.西安：西北工业大学出版社，1991
2钱炜祺.分布参数系统辨识及其在航空航天研究领域中的应用[博士学位论文].西安：西北工业大学航天工程学院，1999
3 Banks H T , Ito K. A Unified Framework for Approximation in Inverse Problerns for Dis-tributed Parameter Systems. AFOSR-TR-88-0392 (ADA193780),1987
4王行愚，蒋慰孙.块脉冲算子及其应用.上海：华东化工学院出版社，1989
5 Beck J V, Blackwell B, Clair C R S Jr. Inverse Heat Conduction-Iil-Posed Problems. NewYork: John Wiley & Sons,1985
6 Chavent G. Identification of Distributed Parameter Systems: about the Output LeastSquare Method , Its Implementation , and Identifiability. Proc. of 5^{\tan} IFAC Symp. on Iden-tification and System Parameter Estimation, Darmstadt,FRG, 1979: 85 ~ 97
7 何淑芷等.数学物理方程中的近代分析方法.广州：华南理工大学出版社，1995
8张可村.工程优化的算法与分析.西安：西安交通大学出版社，1988
9 Reuther J ,Jameson A. Aerodynamic Shape Optimization of Wing and Wing-Body Con-figurations Using Control Theory. AIAA-95-0123,1995
10任斌，蔡金狮.用灵敏度法对分布参数系统的参数辨识.空气动力学学报，1994，12(4) : 455~459
11蔡金狮.动力学系统辨识与建模.北京：国防工业出版社，1991
12 黄志澄等.航天空气动力学.北京：宇航出版社，1994王希季等.航天器进人与返回技术（上）.北京：宇航出版社，1991王希季等.航天器进人与返回技术（下）.北京：宇航出版社，1991
15蔡金狮.飞行器系统辨识.北京：宇航出版社，1995

18航天部第十一研究所.V-2 火箭航天飞机概念论证文集(第二分册)一—气动力、气动热.1988

20 Hallback M,ed. Turbulence and Transition Modelling. Netherlands: Kluwer Academic Publishers, 1996
21 Brankovic A,Stowers S T. Review of Low Reynolds Number Turbulence Models for Complex Internal Separated Flows. AIAA 88-3006, 1988
22 Speziale C G. Turbulence Modeling for Time-Dependent RANS and VLES: A Review. AIAA 97-2051,1997
23 Nisizima S, Yoshizawa A. Turbulent Channel and Couette Flows Using an Anisotropic k -ε Model. AIAA Journal, 1987 ,25(3): 414 ~ 420
24 Pope S B. A More General Effective Viscosity Hypothesis. Journal of Fluid Mechanics, 1975,72: 331~340
25 Gatski T B,Speziale C G.On Explicit Algebraic Stress Models for Complex Turbulent Flows. Journal of Fluid Mechanics,1993,254: 59 ~ 78
26符松.非线性湍流模式研究及进展.力学进展,1995,25(3)：318～327
27陈义良.湍流计算模型.合肥：中国科学技术大学出版社,1991
28 Laporta A,Bertoglio J P. A Model for Inhomogeneous Turbulence Based on Two-Point Correlations. In: Benzi R,ed. Advances in Turbulence V- Proc. of 5^{\ast} European Turbulence Conference. Netherlands: Kluwer Academic Publishers, 1995 ,286 ~ 297
29朱国林,M.Kronast.用二维NS方程计算汽车流场的地面效应.空气动力学学报， 1993,11(1): 21~32
30 Zhu J. A Low-Diffusive and Oscillation-Free Convection Scheme. Communications in Applied Numerical Methods, 1991,7: 225 ~ 232
31 OH C S,Choi D H. An Improved Navier-Stokes Procedure for Analysis of Two-Dimensional Aerofoils in Laminar and Turbulent Flows. International Journal for Numerical Method in Fluids. 1997,25(2) : 167 ~ 182
32马铁犹.计算流体动力学.北京：北京航空学院出版社,1986
33陶文铨.数值传热学.西安：西安交通大学出版社,1988
34 Rhie C M, Chow W L. Numerical Study of the Turbulent Flow past an Airfoil with Edge Separation. AIAA Jourmai,1983,21(11): 1525 - 1553
35 Goldsmith M, ed. Comparisons of Turbulent Flow Calculations with Experiments. WAPD-TM-1473,1981
36 Kim J , Kline S J,Johnston J P. Investigation of a Reattaching Turbulence Shear Layer: Flow Over a Backward- Facing Step. Journal of Fluid Engineering, Transactions of ASME. 1980 ,102: 302 ~ 308
37 Driver D M,Seegmiller H L. Features of a Reattaching Turbulent Shear Layer in Divergent Channei Flow. AIAA Journal,1985,23(2) : 163 ~ 171
38 Sultanian B K, etc. Turbulent Flow Prediction in a Sudden Axisymmetric Expansion.

In: Chen C J,ed. Turbulence Measurements and Flow Modelling. New York: Hemi sphere,1985,655 ~664

39 Zuercher J W,Rozon B J. Validation of a Two-Layer Turbulence Model Using Channel , Step and Turnaround Duct Data. AIAA 93-3028,1993
40 Papp J L,Ghia K N.Study of Turbulent Compressible Mixing Layers Using Two-Equation Turbulence Models Including an RNG k-s Model. AIAA 98-0320,1998
41 Gibson M M, Launder B E. Ground Effect on Pressure Fluctuation in the Atmospheric Boundary Layer. 1978,86: 491 - 511
42 Vogel J C, Eaton J K. Combined Heat Transfer and Fluid Dynamics Measurements Downstream of a Backward - Facing Step. Journal of Heat Transfer, Transactions of ASME.1985,107: 922 ~ 929
43 Durst F, Rastogi A K. Theoretical and Experimental Investigation of Turbulent Flows with Separation. In: Durst F,ed. Turbulent Shear Flow I. Berlin: Springer Verlag, 1979,208 ~219
44 Monson D J, etc. Comparison of Experiment with Calculations Using Curvature- Corrected Zero and Two Equation Turbulence Models for a Two-Dimensional U-Duct. AIAA 90-1484,1990
45 Lien F S,Leschziner M A. Modelling 2D Separation from a High Lift Aerofoil with a Nonlinear Eddy- Viscosity Model and Second- Moment Closure. Aeronautical Journal, 1995,99(984) : 125 ~ 144
46 Guilmineau E,Piquet J,Queutey P. Two-Dimensional Turbulent Viscous Flow Simulation past Airfoils at Fixed Incidence. Computers & Fluids,1997,26(2) : 135 ~ 162

Document generated by Anna's Archive around 2023-2024 as part of the DuXiu collection (https://annas-blog.org/duxiu-exclusive.html).

Images have been losslessly embedded. Information about the original file can be found in PDF attachments. Some stats (more in the PDF attachments):

"before_pdg2pic_conversion": {
"filename": "MTE1NzU4MDEuemlw",
"filename_decoded": "11575801.zip",
"filesize": 16109370,
"md5": "71c07c453bcd6f40b9d858027e798073",
"header_md5":"8aa8f3e725cac9750b851bb6a1c82d1c", "sha1":"59796ac2e3cb419af2a76f8dedf20fe815639a71",
"sha256":"a4f88062134919097ffa595ba230378c58403dcacda04b2d737c8d25ff2f7aee",
"crc32":2332852573,
"zip_password": "",
"uncompressed_size": 16783207,
"pdg_dir_name": "",
"pdg_main_pages_found": 558,
"pdg_main_pages_max": 558,
"total_pages": 579,
"total_pixels": 14053376 "after_pdg2pic_conversion": {
"filename":"MTE1NzU4MDEuemlw",
"filename_decoded": "11575801.zip",
"filesize": 28254960,
"md5": "911581c115b085a18c295e30edf7019d",
"header_md5": "711740846532dc86360f8d02b5ac3fd5",
"sha1": "64a14d25dbeb5678a6717fe05e3093501076006e",
"sha256": "936a989a4377f476f2bd1a24c069a676be957db157216fa3d5c6324b7ebc50e4", "crc32": 1660187800,
"zip_password": ",
"uncompressed_size": 29137148,
"pdg_dir_name": "",.
"pdg_main_pages_found": 558,
"pdg_main_pages_max": 558,
"total_pages": 579,
"total_pixels": 2036655616
1,
"pdf_generation_missing_pages": false